Abstract
The instrumental temperature record is of insufficient length to fully express the natural variability of past temperature. High elevation tree-ring widths from Great Basin bristlecone pine (Pinus longaeva) are a particularly useful proxy to infer temperatures prior to the instrumental record in that the tree-rings are annually dated and extend for millennia. From ring-width measurements integrated with past treeline elevation data we infer decadal- to millennial-scale temperature variability over the past 4,500 years for the Great Basin, USA. We find that twentieth century treeline advances are greater than in at least 4,000 years. There is also evidence for substantial volcanic forcing of climate in the preindustrial record and considerable covariation between high elevation tree-ring widths and temperature estimates from an atmosphere–ocean general circulation model over much of the last millennium. A long-term temperature decline of ~−1.1 °C since the mid-Holocene underlies substantial volcanic forcing of climate in the preindustrial record.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Multiple lines of evidence, including comparisons with instrumental climate data over the last century, show that patterns in the ring widths of upper treeline bristlecone pine are strongly influenced by temperature variability, particularly at decadal to centennial scales (LaMarche 1974; Hughes and Funkhouser 2003; Salzer and Kipfmueller 2005; Salzer and Hughes 2007; Salzer et al. 2009; Kipfmueller and Salzer 2010; Towlinski-Ward et al. 2010; Bunn et al. 2011). Some of the most recent bristlecone pine research has focused on the contrasting signals present in the ring widths of trees at the upper treeline (positive growth correlations with temperature) and in trees below upper treeline (negative or no correlation with temperature; e.g. Salzer et al. 2009; Kipfmueller and Salzer 2010; Bunn et al. 2011). These studies suggest that upper treeline ring widths contain an appreciable temperature signal at decadal to multi-centennial timescales, whereas trees below the treeline do not. However, using bristlecone pine ring widths to infer paleotemperature has been complicated by the discovery that trees somewhat below, yet still very near the upper treeline environment, as close as 150 vertical m, do not contain the same temperature signal as trees within ~100 m of treeline. For example, we have shown in the White Mountains of California, that the growth patterns of Pinus longaeva trees growing at treeline are quite different from growth patterns of the same species of tree growing only 150 m below treeline (see Salzer et al. 2009, Fig. 4a). The elevational threshold for bristlecone temperature-sensitivity is unknown and has not been widely studied. Also, it has been argued that microtopographical features such as cold air pooling, for example, could complicate defining temperature-sensitive trees based solely on elevation or distance from treeline (Bunn et al. 2011).
In spite of these challenges, we suggest the most accurate estimates of past temperature will come from ring widths formed in trees within ~100 m of the species upper elevation ecotonal boundary. This elevational sector corresponds to a cold zone where temperatures are most limiting to growth (Fritts 1976) and above which cold temperatures preclude tree establishment entirely. However, these ecotonal boundaries have changed with time as climate has evolved, and quantifying the narrow elevation band occupied by trees with a ring-width temperature signal can be particularly problematic when working with material that predates the age of modern, established treeline. Due to past climatic change and the fluctuation of past treeline elevations, it becomes necessary to first determine the elevation of past treelines, and then, when developing temperature-sensitive ring-width chronologies, it is important to use only those trees that were growing within the cold zone (~100 m of treeline) during their lifetimes. We systematically avoid the use of rings formed in a past warmer era of higher treeline if these rings were sampled from wood at a location much lower than the remnant treeline. For example, old deadwood samples taken near modern upper treeline elevation or just below are avoided, as these rings would have been below the 100 m cold zone during their time of formation, and thus are inappropriate for paleotemperature inference. This line of reasoning is based on the assumption that the same, or a very similar, temperature-growth threshold relationship existed in past eras as exists currently. The existence of temperature-sensitive trees near treeline at the upper-elevational limit of their distribution has been confirmed in our previous work on bristlecone pine (Salzer et al. 2009). In this study, we first derive estimates of past treeline elevations, and then use samples collected within ~100 vertical m of these elevations to create a 4,582-year regional ring-width index chronology (2575 BC-AD 2006), hereafter referred to as GB3rwi. We then estimate millennial-scale temperature variability based on treeline elevational change, and estimate decadal to multicentennial-scale temperature variability using the regional ring-width index chronology scaled to regional temperature output from a climate model millennium run.
2 Materials and methods
2.1 Chronology construction
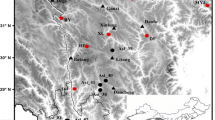
We use samples from bristlecone pine living trees and remnant wood in the upper treeline zone (within 100 m of known treeline or estimated past treeline) in three separate mountain ranges in western North America: (1) Sheep Mountain, White Mountains, CA (SHP, 37.52 N. lat., 118.20 W. long.); (2) Mt. Washington, Snake Range, NV (MWA, 38.91 N. lat., 114.31 W. long.); and (3) Pearl Peak, Ruby Mountains, NV (PRL, 40.23 N. lat., 115.54 W. long.) (Fig. 1). Previous work at these sites has revealed strong correspondence in growth patterns, despite lengthy distances between sites (500 + km) and strong replication for millennia (Fig. 1, S1, S2) (Salzer and Hughes 2007; Salzer et al. 2009). The high correlation between the three chronologies over long intervals is indicative of similar biological responses by the trees to the same factor or factors limiting growth at all three sites.
Mean ring-width index chronologies were developed both for individual sites, and also for the region (GB3rwi) using samples from all three sites: SHP, MWA, and PRL. To gain maximum temporal coverage, we used dendrochronologically-dated materials from both living trees and from relict wood. We standardized each of the individual tree-ring width series to eliminate tree age/size related influences on ring width. Low-frequency variability was retained by limiting the minimum series length allowed to 100 years and standardizing with a negative exponential curve, a trend line with negative slope, or a mean line as determined by standardization option two in the dendrochronological software ARSTANL (Cook 1985; available at http://www.ltrr.arizona.edu/pub/dpl/). This standardization approach is designed to retain decadal to multi-centennial scale variability and to minimize the “segment length curse” (Cook et al. 1995). The individual series lengths were typically between 500 and 800 years from 2000 BC on, suggesting that the chronology should retain variations whose wavelength is a few to several centuries. Samples were dated and measured using established dendrochronological methods (Stokes and Smiley 1968). The GB3rwi chronology was created by using the same dating, measuring, and standardization techniques described above. The GB3rwi chronology differs in that each individual index series after standardization was smoothed with a 20-year cubic smoothing spline to emphasize decadal- to centennial-scale variability prior to averaging the smoothed index series into a chronology of low-frequency variation. This approach allows for the calculation of 95 % confidence intervals for each mean value of the low-frequency chronology (Sheppard 1991). A non-standardized “raw” chronology (GBR3raw) was similarly constructed, but without any standardization procedures—using instead the raw growth measurements. An additional step was taken with GB3raw to eliminate some juvenile growth; each growth curve that resembled a negative exponential as determined by ARSTANL (Cook 1985) was truncated for its first 100 years. However, all analyses in the main paper are based on the standardized version (GB3rwi) to eliminate as much potential bias from non-climatic tree-growth influences as possible. The GB3rwi ring-width chronology is built from series at all three mountain ranges, and extends 4,582 years, from 2575 BC to AD 2006.
2.2 Treeline elevation change
Climatic-treeline elevation is primarily controlled by minimum summer temperature at large spatial scales (Körner and Paulson 2004; Körner 2012). Both SHP and MWA sites contain extensive amounts of deadwood above modern treeline, while PRL contains less due to limited available elevation gain above modern treeline (Figs. S3-S5). Older higher treelines have been documented previously in both the White Mountains of California (LaMarche 1973) and in the Sierra Nevada (Lloyd and Graumlich 1997). We estimated the elevation of past treelines at SHP and MWA based on the elevation of the highest living trees sampled at that point in time (Figs. S3, S4). Past treeline at PRL was estimated based on the data from MWA (Fig. S5). The estimates of past treeline elevations serve a dual purpose. First, they allow for identification of three ~100 m elevational zones (one for each site), which have varied through time, and within which temperature-sensitive trees can be expected to have grown. We use only these trees for our regional ring-width chronology (GB3rwi). Second, independent of the growth records of the rings, the treeline elevation through time is also a record of past environmental change. We use the changing upper treeline at SHP and a local lapse rate to estimate long-term temperature change (see Sect. 3.1).
2.3 Ring-width index and model output
The GCMs used for comparisons to the GB3rwi tree-ring chronology include the Max Planck Institute ECHO-G model (ERIK2, AD 1,000–1,990, single simulation; Legutke and Voss 1999; Stevens et al. 2008), the Max Planck Institute COSMOS system (MPI, AD 800-2005, 5 simulations; Jungclaus et al. 2010), and the National Centers for Atmospheric Research Community Climate Model (CSM, AD 850–1999, single simulation) (Ammann et al. 2007). Two important differences between these simulations are (1) the amplitude of the changes in total solar irradiance (Maunder Minimum to present) used in the ERIK2 and CSM (~4 W m−2) simulations is about 3 times the 1.3 W m−2 that was used in the MPI (COSMOS) simulations, and (2) the ERIK2 and CSM models use prescribed greenhouse gas concentrations while the MPI (COSMOS) model uses a full carbon cycle model. We use area-averaged near-surface temperature from the GCM grid points over the western USA (40°–34°N and from 104° to 124°W) for comparison with the ring-width data.
The scaling of GB3rwi to the GCM output can be formally expressed as follows:
T(t) = f · R(t) + c, where T is the modeled temperature data, R is the ring-width index chronology, f is a variance scaling factor, c is a constant that adjusts the mean, and t is time. The factor f and constant c are derived by: f = S T /S R and c = T (mean) – f · R (mean) where S T and S R are the respective standard deviations of the modeled temperature data and the ring-width index chronology in the AD 1276 to 1990 interval, and T (mean) and R (mean) are the corresponding means. Error bars are the RMSE statistic. Temperature anomalies were originally computed based on the AD 1000–1990 July–September mean of 20.32 °C ‘near surface’ from the ERIK2 model. They were then adjusted for the preindustrial period of 2575 BC to AD 1328 by adding a negative trend of 1.102 °C based on the empirical data from treeline elevation change. There were no adjustments made to the period after AD 1328. The results are a 4,000 + year record of decadal- to millennial-scale variability in past summer temperature. We acknowledge a high level of uncertainty in these past temperature estimates. This is unavoidable, given the multiple sources contributing to the uncertainty: (1) the ring-width chronology itself, (2) the ECHO-g modeling effort (3) the scaling of the tree rings to the modeled data, and (4) the trend adjustment.
3 Results and discussion
3.1 Treeline elevation and temperature inference
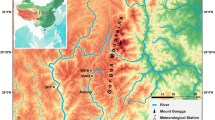
Past treeline estimates from the SHP site extend into the mid-Holocene (Fig. 2a). The SHP estimated treeline is broadly similar to that from MWA, roughly 400 km distant, for their period of overlap (Fig. 2b). Both mountains show substantially higher past treelines, greater than 100 m relative to recent levels, and both decline to modern levels in the fourteenth century AD. At SHP, treeline reaches its maximum elevation approximately 5,000 years ago. Prior to that, estimated treelines range from 45 m above modern level in 4410 BC at the beginning of the record, to 76 m above modern levels in 3755 BC. Treeline reaches its highest point, at 116 m above modern levels, in 2997 BC (Fig. 2a). We are less confident in the completeness of the record prior to 3000 BC and so concentrate our interpretations on the last 5,000 years.
Upper treeline elevation and past estimated treeline elevations. a White Mountains, CA (SHP). Green triangles represent the elevations of clusters of juvenile Pinus longaeva establishing above established modern upper treeline. b Upper treeline elevation and past estimated upper treeline elevations in White Mountains, CA (SHP, red) and Snake Range, NV (MWA, blue)
Estimated past treelines are generally slightly higher at MWA than at SHP. This could result from a variety of reasons. Possibilities include a more complete record or a different lapse rate at MWA. It is worth noting that all the estimates are necessarily the minimum past treeline elevations, as we can never be sure we have found the highest trees that were growing at any particular time. Also, it is difficult to determine the precise timing of climate change by treeline movement for several reasons. Most notably because remnant wood samples often crack and erode over time obliterating many rings. In addition, reproductive lags cause treeline change to unavoidably lag behind climate change. While many different phenomena, such as fragmentation by disturbance, might contribute to local treeline positions, there is abundant evidence on a global scale that climatic treeline positions occur where growing season temperatures are 5–7° C, with a global mean of 6.4 ± 0.7 (Körner 2012). This global correlation between treeline position and temperature demonstrates that temperature is a primary driver of treeline position and challenges the concept that treeline position is a multifaceted phenomenon with complex interactions between multiple environmental drivers (Körner 1998). If the latter were correct, global mountain treeline positions would not correlate with one explicit climatic parameter, which they do (Paulsen et al. 2000).
Two meteorological stations have at times operated at the SHP site simultaneously, but at differing elevations. From these station data we know that the summer surface air temperature gradient at SHP varies at 0.95 °C per 100 m—very near the dry adiabatic lapse rate of 0.98 °C per 100 m (LaMarche 1973). From the 0.95 °C lapse rate and the treeline data we can infer a temperature decline during the growing season (summer) of approximately 1.1 °C from 2209 BC to AD 1328, from the time of the highest treeline elevations to when treeline stabilized and persisted near modern levels until the late twentieth century (Fig. 2a). Modern treeline also stabilized in the early AD 1300 s at MWA (Fig. 2b). Trees were growing at least 25 m above modern treeline in both mountain ranges prior to AD 1300, suggesting warmer temperatures of at least 0.24 °C during this interval before subsequent cooling and treeline decline.
Earlier in the SHP record there is a very sharp treeline decline of about 65 m (0.6 °C) between 2209 and 2139 BC. This decline is not in the MWA treeline record most likely because the MWA summit is only 118 m above modern treeline, whereas the summit at SHP is 295 m above modern treeline. The MWA summit is a very harsh and inhospitable environment that precludes seedling establishment. Without the suitable and available high elevation habitat during the warmest mid-Holocene interval the MWA trees were unable to move up the mountainside. Hence, there is no record of a substantial treeline drop around 2200 BC at MWA. The 2209 BC treeline decline at SHP corresponds temporally to the apparent 4.2–3.9 ka BP abrupt climate change event indicated in many widely distributed proxy records (Zhang and Hebda 2005; Booth et al. 2006; Fischer et al. 2008; Menounos et al. 2008; Baker et al. 2009). This “event” may have been a major contributing factor for massive old-world cultural change (Stanley et al. 2003; An et al. 2005; Staubwasser and Weiss 2006).
At the SHP site at least four clusters of juvenile trees are growing well above modern treeline. The highest of these clusters is 73 m above treeline and contains at least one tree which has reached reproductive maturity. To avoid injury to these young trees they were not cored to determine exact age. However, counting the number of needle whorls suggested an approximate age of 35–50 years in 2012. It is possible that we are witnessing the incipient stages of treeline advance due to modern warming. A 73 m treeline advance is indicative of a modern warming of 0.7 °C, and local PRISM (Daly et al. 2008) modeled summer temperature for this elevation since AD 1895, is consistent with a mid-twentieth century establishment period. There is no evidence that treelines at SHP have established at these altitudes since before the 2200 BC treeline drop. The nature of the treeline-change data precludes us from knowing exactly how long it has been since trees established at this elevation, as it is possible that some smaller remnant material from more recent incipient treeline advances has eroded away or not been found. Yet, it is likely that full-size trees have not grown at this elevation since before 2200 BC and quite possible that high elevation ecosystems are now responding in a manner unprecedented in approximately 4,200 years.
3.2 Ring-width variability and temperature inference
To complement the millennial-scale treeline-change information, we used the GB3rwi ring-width index chronology that spans much of the last five millennia (Fig. 3). We do not interpret GB3rwi from 2140 to 1795 BC due to poor agreement and low sample size during that period (SSS <0.85) (Wigley et al. 1984) (Fig. S2). This “gap” occurs immediately following the 65 m treeline decline at SHP. It coincides with both the 4.2–3.9 ka BP abrupt climate event and with a severely frost-damaged ring that occurs in trees at all three sites in 2036 BC. Cold-damaged high-elevation tree rings (“frost rings”) have been shown to be associated with volcanically-forced short-term cooling events (LaMarche and Hirschboeck 1984; Salzer and Hughes 2007). The event at 2036 BC is the most visually severe in our period of record. The wood has often fractured along the 2036 BC latewood annual boundary and eroded along both sides. This cracking and subsequent erosion has, in many cases, effectively erased the ring-width record for decades to centuries around the 2036 BC ring, which contributes to the “gap” in the record.
Time-series plots of Great Basin 3 (GB3rwi) low-frequency tree-ring chronologies with 95 % confidence intervals (grey dotted lines). Included are a the standardized ring-width index chronology (GB3rwi); b the non-standardized raw ring-width chronology (GB3raw); and c the number of samples used in GB3rwi and the mean length of those segments over the length of the chronology
Past work has demonstrated significant correspondence between ring-widths from trees at these sites and meteorological temperatures over the relatively short period of overlap provided by the instrumental record (Salzer et al. 2009; Bunn et al. 2011). We expanded on this by comparing the GB3rwi chronology to results from forced coupled global climate model (GCM) simulations for the past millennium. These models simulate past changes in climate in response to estimated changes in external forcing such as solar variability, volcanic activity, and greenhouse gas concentrations.
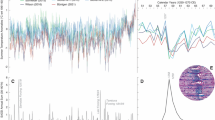
The tree-ring data agree much more closely with the ECHO-G (ERIK2) results than with those from the MPI (COSMOS) model; the CSM results fall somewhere in between (Fig. 4). The correlations over 991 years between non-smoothed monthly-modeled data and non-smoothed ring-width indices are highest using ERIK2 and for the summer months (July–September, r = 0.32, n = 991, Neff = 589, p < 0.001). The correlation increases to 0.64 when the GB3rwi chronology is compared to the July–September ERIK2 data smoothed in a similar manner to GB3rwi over the common interval of the two data sets, AD 1000–1990 (Fig. 4a). For comparison, the AD 1000-1990 correlations using a mean of the five MPI (COSMOS) ensemble members (20-year smooth) is 0.08 (Fig. 4c), while the CSM results give a value of 0.41 (Fig. 4b). The better agreement between the proxy data and the ERIK2 and CSM models is possibly a result of the larger solar variability used in those simulations. [We note that the difference between the ERIK2 and the MPI (COSMOS) temperature records, both for the Great Basin and for the Northern Hemisphere, closely resembles the solar irradiance record (Crowley 2000) used as forcing for the ERIK2 simulation (not shown)]. ERIK2 and GB3rwi, two completely independent records, show some strong similarities, particularly after AD 1275 (r = 0.75, n = 716); in contrast, the first 276 years show no correspondence (AD 1000–1275, r = −0.13). The lack of agreement in the 11th through late-thirteenth centuries may be due to shortcomings in the forcing data used in the models. It is not uncommon for tree-ring temperature proxy records and model results to disagree during the medieval period, particularly with regard to volcanic signals (Mann et al. 2012). To obtain estimates of temperature from the ring-widths, we scaled the GB3rwi chronology to the smoothed July–September ERIK2 temperature data over the 716-year period from AD 1276–1990 where the two data sets show strong agreement (Fig. 5a). If the entire overlap period (AD 1000–1990) were used in the scaling, the temperature scale would be similar to what was found using the more highly correlated AD 1276–1990 scaling interval. The mean difference between estimates when using the two different scaling intervals is only 0.014 °C; the maximum difference, found in years with larger ring-widths and as a result higher estimated temperature, is only 0.040 °C. Scaling allows estimates of decadal to multi centennial variability for past summer temperature in degrees C for years prior to the model (before AD 1000). Hence, we can interpret the paleoclimatic record for much of the second half of the Holocene based on both the GB3rwi tree-ring data and on the treeline elevation change data discussed above.
GB3rwi (blue) and July–September Great Basin temperature from three millennial-run climate models. The tree-ring data agrees most strongly with the ECHO-g model (a red), and less well with the CSM model (b grey) and the MPI model (c black). Modeled temperature anomalies are based on the period AD 1000–1990 with respective mean values in degree celsius of: ECHO-g = 20.32, MPI = 23.33, CSM = 19.03
GB3rwi chronology scaled to ECHO-G climate modeled temperature data (Legutke and Voss1999; Stevens et al. 2008) for period AD 850–2006. Temperature anomalies are based on the AD 1000–1990 July–September mean of 20.32 °C and no trend adjustment is used. a Red is the modeled temperature anomaly data, the solid red line indicates the interval used in the scaling (1276–1990). Blue is the scaled tree-ring data with error bars (±1 RMSE). b GB3rwi inferred temperature anomalies (blue) with no trend adjustment compared to volcanic data (black and grey, Gao et al. 2008; Crowley et al. 2008)
3.3 Inferred paleotemperature record
The negative trend of 1.1 °C, derived from the treeline decline data, equates to a long-term preindustrial Holocene cooling rate of −0.31 °C per 1,000 years over the length of the tree ring record prior to treeline stabilization (2575 BC to AD 1328) (Fig. 6). This is greater than the −0.23 °C per 1,000 years (AD 300–1900) reported for the northern Hemisphere (Mann et al. 2008) and the −.21 °C per 1,000 years (AD 1–1900) reported for the Arctic (Kaufman et al. 2009). The exact same rate of temperature decline, −0.31 °C per 1,000 years, was recently reported over the last ~2,000 years from high latitude Scandinavia on the basis of tree-ring maximum latewood density (MXD) (Esper et al. 2012).
Scaled paleotemperature from Great Basin, USA with a millennial-scale trend adjustment for the period before AD 1328. The negative trend is based on empirical data from treeline elevation change. Blue is inferred past temperature from treeline position (July); black is adjusted temperature anomaly from ring-widths (July–September GB3rwi, see “Materials and methods”); grey is error component from scaling (±1 RMSE); red is ECHO-g ERIK2 climate model (Legutke and Voss1999; Stevens et al. 2008). The black and blue lines are not independent as trend has been added to the portion of the black curve before AD 1328 based on estimated change in temperature from treeline elevation change (blue curve). No trend has been added after AD 1328
The overall range of summer temperature variability over 4,582 years is approximately 3.44 °C, with departures from −1.25 °C to +2.19 °C (Fig. 6). A similar scale of temperature change (~3.1 °C) is produced using PRISM (Daly et al. 2008) modeled instrumental temperature data, unadjusted “raw” ring widths, and regression-based techniques (not shown). The magnitude of temperature anomalies depends on the detail of the scaling of the GB3rwi chronology and partly, prior to AD 1328, on the fact that the chronology has been adjusted using the trend calculated from the tree line changes. The negative trend of 1.1 °C is superimposed upon decadal to century timescale positive departures that exceed +2 °C in the fifth century BC, the warmest period at +2.19 °C, and in the seventeenth century BC at +2.11 °C. There is a strong upward excursion of +1.52 °C in the twentieth century AD. However, the inferred temperature of the modern period was exceeded twice in the Common Era: +1.69 °C in the mid first century AD (centered on AD 33) and +1.58 °C in the mid seventh century (centered on AD 634). The coldest interval is in the mid to late fifteenth century AD (centered on AD 1469) with a temperature departure of −1.25 °C. Consistent with these results and suggesting that some of the departures from mean conditions are at least hemispheric in scale, the MXD estimates of northern Scandinavian summer temperatures indicate nearly identical dates for their warmest and coldest 30-year periods over the last ~2,000 years, at AD 21–50 and AD 1451–1480 respectively (Esper et al. 2012). These similar results are derived from different methods (MXD and ring-width), from different species (Pinus sylvestris and Pinus longaeva) from different ecosystems (lakeshore and alpine/subalpine), and from two distant regions, northern Europe and western North America.
The GB3rwi temperature estimates are likely “missing” some variance in the multi-century part of the variance spectrum because variance at that scale is less evident in the treeline changes and is not as well preserved in the standardized chronology as it is in the “raw” chronology (Fig. 3b). The decadal- to centennial-scale variability in the temperature estimates is likely mainly a result of volcanic and/or solar forcing and of internal climate variability. Direct comparisons between scaled GB3rwi and estimates of volcanic (Crowley et al. 2008; Gao et al. 2008) forcing since AD 850 show an association between volcanic forcing and periods of low temperature (Fig. 5b). It is interesting to note four episodes when volcanic activity is high that correspond with periods of inferred low temperature in the late-thirteenth, mid-fifteenth, late-seventeenth, and early-nineteenth centuries. Moreover, the period with the lowest inferred temperature since AD 850 (mid-fifteenth century; −1.25 °C) is associated with very high volcanic activity. In fact, many of the negative departures in temperature coincide with known periods of climatically effective volcanic eruptions (Salzer and Hughes 2007). This is particularly apparent for the five cool temperature episodes between AD 1280 and 1850 (Fig. 5b). Many of the dips earlier in the record are most likely the result of currently unknown and undated eruptions. It is interesting to note that the large volcanic peak of AD 1258 is not associated with inferred cooling. Warm temperature anomalies of ~ + 0.7 °C are found for several decades in the second half of the tenth and mid eleventh centuries. The Medieval period is a fairly minor warm interval in our record compared to some earlier periods with higher inferred temperatures.
Other paleotemperature proxy records from the Great Basin region often extend farther back into the Holocene than our record, but with less than annual resolution. These proxy archives, such as lacustrine and meadow sediment cores, packrat middens, and glacial moraine dynamics (Thompson et al. 1994; Clark and Gillespie 1997; Smith and Betancourt 2006; Reinemann et al. 2009) are in general agreement with our results, recording higher temperatures during the middle Holocene. Unfortunately, the other proxy archives lack the resolution to be effectively compared to our results in detail. Additionally, the estimates presented here are in agreement with a high-resolution regional-climate model (Diffenbaugh and Sloan 2004). This model uses mid-Holocene orbital forcing and simulates a mid-Holocene summer warming of 1–2.5 °C over most of western USA.
Annually dated multi-millennial length proxy records that contain information about past temperature are extremely rare. We have combined information from two separate aspects of the biological system of long-lived bristlecone pine trees: (1) reproduction and survival at the upper elevational limit of tree distribution resulting in temporal variability in treeline elevation and (2) radial growth measurements of annual rings from trees at their upper elevational limit. This combination allows us to include millennial-scale variability, in addition to decadal to multi-centennial scale, in our estimates of past summer temperatures over several millennia. This is a promising approach for high resolution paleoclimatology that could provide ring-width-based temperature estimates of summer temperature with improved fidelity at millennial timescales. Using this approach we have found: (1) covariation between upper treeline Pinus longaeva ring widths and regional GCM surface temperature data, (2) treeline evidence of a long-term temperature decline of approximately −1.1 °C since the mid-Holocene, (3) abrupt treeline decline (cooling) around 2200 BC coincident with the 4.2 k climate event reported in many proxy data-sets globally, (4) substantial volcanic forcing of climate in the preindustrial record, (5) severe frost damage recorded in the 2036 BC upper treeline rings with few extant treeline samples covering this time, and (6) initial evidence of twentieth century treeline advances greater than in approximately 4,000 years.
References
Ammann CM, Joos F, Schimel D, Otto-Bliesner BL, Tomas R (2007) Solar influence on climate during the Last Millennium. Proc US Natl Acad Sci 104:3713–3715
An CB, Tang L, Barton L, Chen FH (2005) Climate change and cultural response around 4,000 cal year B.P. in the western part of Chinese loess plateau. Quat Res 63:347–352
Baker PA, Fritz SC, Burns SJ, Ekdahl E, Rigsby CA (2009) The Nature and Origin of Decadal to Millennial Scale Climate Variability in the Southern Tropics of South America: The Holocene Record of Lago Umayo, Peru. In: Vimeux F, Sylvestre F, Khodri M (eds) Past climate variability in South America and surrounding regions: from the Last Glacial Maximum to the Holocene, Developments in Paleoenvironmental Research vol 14. Springer, pp 301–322
Booth RK, Jackson ST, Forman SL, Kutzbach JE, Bettis EA III, Kreig J, Wright DK (2006) A severe centennial-scale drought in mid-continental North America 4,200 years ago and apparent global linkages. Holocene 15:321–328
Bunn AG, Hughes MK, Salzer MW (2011) Topographically modified tree-ring chronologies as a potential means to improve paleoclimate inference. Clim Change 105:627–634
Clark DH, Gillespie AR (1997) Timing and significance of late-glacial and Holocene cirque glaciation in the Sierra Nevada. California. Quat Int 38(39):21–38
Cook ER (1985) A time series approach to tree-ring standardization. University of Arizona, Dissertation
Cook ER, Briffa KR, Meko DM, Graybill DA, Funkhouser GS (1995) The ‘segment length curse’ in long tree-ring chronology development for palaeoclimatic studies. Holocene 5:229–237
Crowley TJ (2000) Causes of climate change over the past 1,000 years. Science 289:270–277
Crowley TJ, Zielinski G, Vinther B, Udisti R, Kreutz K, Cole-Dai J, Castellano E (2008) Volcanism and the little ice age. PAGES Newsl 16:22–23
Daly C et al (2008) Physiographically-sensitive mapping of temperature and precipitation across the conterminous United States. Int J Clim 28:2031–2064
Diffenbaugh NS, Sloan LC (2004) Mid-Holocene orbital forcing of regional-scale climate: a case study of western North America using a high-resolution RCM. J Clim 17:2927–2937
Esper J et al (2012) Orbital forcing of tree-ring data. Nat Clim Change. doi:10.1038/nclimate1589
Fischer D et al (2008) The Mt Logan Holocene–late Wisconsinan isotope record: tropical Pacific–Yukon connections. Holocene 18:667–677
Fritts HC (1976) Tree rings and climate. Academic, New York
Gao C, Robock A, Ammann CM (2008) Volcanic forcing of climate over the past 1,500 years: An improved ice core-based index for climate models. J Geophys Res (D23111). doi:10.1029/2008JD010239113
Hughes MK, Funkhouser GS (2003) Frequency-dependent climate signal in upper and lower forest border tree rings in the mountains of the Great Basin. Clim Change 59:233–244
Jungclaus JH et al (2010) Climate and carbon-cycle variability over the last millennium. Clim Past Discuss 6:1009–1044
Kaufman DS et al (2009) Recent warming reverses long-term arctic cooling. Science 325:1236–1239
Kipfmueller KF, Salzer MW (2010) Linear trend and climate response of five-needle pines in the western United States related to treeline proximity. Can J For Res 40:134–142
Körner C (1998) A reassessment of high elevation tree line positions and their explanation. Oecologia 115:445–459
Körner C (2012) Alpine treelines. Springer, Basel
Körner C, Paulsen JA (2004) World-wide study of high altitude treeline temperatures. J Biogeogr 31:713–732
LaMarche VC Jr (1973) Holocene climatic variations inferred from treeline fluctuations in the White Mountains, California. Quat Res 3:632–660
LaMarche VC Jr (1974) Paleoclimatic inferences from long tree-ring records. Science 183:1043–1048
LaMarche VC Jr, Hirschboeck KK (1984) Frost rings in trees as records of major volcanic eruptions. Nature 307:121–126
Legutke S, Voss R (1999) The Hamburg atmosphere-ocean coupled circulation model ECHO-g. Technical Report 18, German Climate Computing Center, Hamburg
Lloyd AH, Graumlich LJ (1997) Holocene dynamics of treeline forests in the Sierra Nevada. Ecol 4:1199–1210
Mann ME et al (2008) Proxy-based reconstructions of hemispheric and global surface temperature variations over the past two millennia. Proc US Natl Acad Sci 105:13252–13257
Mann ME, Fuentes JD, Rutherford S (2012) Underestimation of volcanic cooling in tree-ring-based reconstructions of hemispheric temperatures. Nat Geosci 5:202–205
Menounos B, Clague JJ, Osborn G, Luckman BH, Lakeman TR, Minkus R (2008) Western Canadian glaciers advance in concert with climate change. Geophys Res Lett 35 (L07501). doi:10.1029/2008GL033172
Paulsen JA, Weber UM, Körner C (2000) Tree growth near treeline: abrupt or gradual reduction with altitude? Arc Antarc Alp Res 32:14–20
Reinemann SA, Porinchu DF, Bloom AM, Mark BG, Box JE (2009) A multi-proxy paleolimnological reconstruction of Holocene climate conditions in the Great Basin, United States. Quat Res 72:347–358
Salzer MW, Hughes MK (2007) Bristlecone pine tree rings and volcanic eruptions over the last 5,000 year. Quat Res 67:57–68
Salzer MW, Kipfmueller KF (2005) Reconstructed temperature and precipitation on a millennial timescale from tree-rings in the southern Colorado Plateau. Clim Change 70:465–487
Salzer MW, Hughes MK, Bunn AG, Kipfmueller KF (2009) Recent unprecedented tree-ring growth in bristlecone pine at the highest elevations and possible causes. Proc US Natl Acad Sci 106:20348–20353
Sheppard PR (1991) Identifying low frequency tree-ring variation. Tree-Ring Bull 51:29–38
Smith FA, Betancourt JL (2006) Predicting woodrat (Neotoma) responses to anthropogenic warming from studies of the palaeomidden record. J Biogeogr 33:2061–2076
Stanley JD, Krom MD, Cliff RA, Woodward JC (2003) Nile flow failure at the end of the Old Kingdom, Egypt: strontium isotopic and petrologic evidence. Geoarchaeology 18:395–402
Staubwasser M, Weiss H (2006) Holocene climate and cultural evolution in late prehistoric-early historic West Asia. Quat Res 66:372–387
Stevens MB, González-Rouco JF, Beltrami H (2008) North American climate of the last millennium: underground temperatures and model comparison. J Geophys Res. doi:10.1029/2006JF000705
Stokes M, Smiley T (1968) An Introduction to Tree-Ring Dating. University of Arizona Press, Tucson
Thompson RS, Whitlock C, Bartlein PJ, Harrison SP, Spaulding WG (1994) Climatic changes in the western United States since 18,000 yr B.P. In: Wright HE, Kutzbach T, Webb TI, Ruddiman WF, Street-Perrott FA, Bartlein PJ (eds) Global climates since the Last Glacial Maximum. University of Minnesota Press, Minneapolis, pp 468–513
Tolwinski-Ward SE, Evans MN, Hughes MK, Anchukaitis KJ (2010) An efficient forward model of the climate controls on interannual variation in tree-ring width. Clim Dyn 36:2419–2439
Wigley TML, Briffa KR, Jones PD (1984) On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J Clim Appl Meteorol 23:201–213
Zhang QB, Hebda RJ (2005) Abrupt climate change and variability in the past four millennia of the southern Vancouver Island, Canada. Geophys Res Lett 32 (L16708). doi:10.1029/2005GL022913
Acknowledgments
We gratefully acknowledge support from the National Science Foundation’s Paleo Perspectives on Climate Change (P2C2) Program (Grants ATM-090227 and ATM-1203749). We thank the US Forest Service, the US National Park Service, and the Long Now Foundation for site access, and Kurt Kipfmueller, Evan Larson, and Jim Parks for their assistance.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Salzer, M.W., Bunn, A.G., Graham, N.E. et al. Five millennia of paleotemperature from tree-rings in the Great Basin, USA. Clim Dyn 42, 1517–1526 (2014). https://doi.org/10.1007/s00382-013-1911-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-013-1911-9