Abstract
In this study the added value of a ensemble of convection permitting climate simulations (CPCSs) compared to coarser gridded simulations is investigated. The ensemble consists of three non hydrostatic regional climate models providing five simulations with ~10 and ~3 km (CPCS) horizontal grid spacing each. The simulated temperature, precipitation, relative humidity, and global radiation fields are evaluated within two seasons (JJA 2007 and DJF 2007–2008) in the eastern part of the European Alps. Spatial variability, diurnal cycles, temporal correlations, and distributions with focus on extreme events are analyzed and specific methods (FSS and SAL) are used for in-depth analysis of precipitation fields. The most important added value of CPCSs are found in the diurnal cycle improved timing of summer convective precipitation, the intensity of most extreme precipitation, and the size and shape of precipitation objects. These improvements are not caused by the higher resolved orography but by the explicit treatment of deep convection and the more realistic model dynamics. In contrary improvements in summer temperature fields can be fully attributed to the higher resolved orography. Generally, added value of CPCSs is predominantly found in summer, in complex terrain, on small spatial and temporal scales, and for high precipitation intensities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Regional climate models (RCMs) (Dickenson et al. 1989; Giorgi and Bates 1989) are capable of providing additional regional details beyond the resolution of global climate simulations and re-analysis products. With RCMs only limited areas of the globe are simulated. The required information at the lateral boundaries is usually provided by either global models, reanalyses, or from larger scale regional models. Over the last decade RCMs have proven themselves as important tools in climate sciences (e.g., Wang et al. 2004; Rummukainen 2010) and climate change impact research (e.g., Finger et al. 2012; Heinrich and Gobiet 2011) and considerable efforts were made to further develop and improve RCMs by increasing their complexity and resolution. The horizontal grid spacing of state-of-the-art RCMs typically ranges from 50 to ~25 km [e.g., Christensen and Christensen 2007 (PRUDENCE 50 km); van der Linden and Mitchell 2009 (ENSEMBLES 25 km); Mearns et al. 2009 (NARCCAP 50 km)]. More recently, due to advancements in the field of computer sciences, it is now possible to have higher resolved climate simulations with ~10 km horizontal grid spacing (e.g., Loibl et al. 2011; Gobiet et al. 2012). Nevertheless, even with a mesh size of 10 km there are still numerous processes which cannot be resolved on the model grid and therefore have to be parameterized. These parameterizations are important sources of model errors (Randall et al. 2007) and introduce large uncertainties in the projections of future climate (e.g., Déqué et al. 2007). One challenging task for modelers is the parameterization of deep convection. Although much progress has been made in terms of improvement of old parameterization schemes as well as formulation of new ones, they are still the source of major errors and uncertainties. The most important benefit of convection permitting climate simulations (CPCSs) is that error-prone deep convection parameterization schemes can be omitted as deep convection can be (at least partly) resolved explicitly (Weisman et al. 1997). Furthermore, increasing resolution leads to a more realistic representation of the orography and land surface. However, CPCSs are far from being established because of their immense demand of computational resources and their still widely unknown quality.
In numerical weather prediction (NWP) convection resolving models are already widely used for operational forecasts and research purposes (e.g., Mass et al. 2002; Kain et al. 2006; Schwartz et al. 2009; Gebhardt et al. 2011). According to Weisman et al. (1997) the critical horizontal grid spacing for CPCSs is ~4 km. For grid spacings between 8 and 12 km certain aspects of deep convection are still reasonably represented, but deep convection evolves too slowly and net heat transports, rainfall rates, and net strength of deep convection systems are overestimated. By using the fractions skill score (FSS) Roberts and Lean (2008) showed that convection resolving forecasts are able to produce more realistic precipitation patterns due to a more accurate distribution of the rain and a better prediction of high accumulations. Weusthoff et al. (2010) investigated forecasts from three different NWP models over Switzerland with the FSS and the upscaling method from Zepeda-Arce et al. (2000) and found significantly improvements particularly for convective, more localized precipitation events. Langhans et al. (2012) found that in convection permitting simulations with different horizontal grid spacings (4.4, 2.2, 1.1, and 0.55 km) bulk flow properties, like heating or moisture tendencies (but also precipitation), converge towards the 0.55 km solution. They concluded that convection permitting grid-spacings seem to be sufficient for physical convergence of bulk properties in real case studies.
On longer time scales (14 months) Grell et al. (2000) found similar results and showed that spatial precipitation patterns are changing between CPCSs and coarser resolved simulations with parameterized convection in complex orography. Hohenegger et al. (2008) showed that in their CPCS the precipitation maxima were better localized, a cold bias was reduced, and the timing of the summertime precipitation diurnal cycle was improved compared to a larger scale reference simulation.
This study extends the investigations of previous work by using an ensemble of non-hydrostatic RCMs, which allows more general conclusions than the analysis of single models. Furthermore, we evaluate not only precipitation but also 2 m air temperature, relative humidity, and global radiation, compare the results of a mountainous with a hilly sub-region, and use specific methods for the evaluation of precipitation fields at high temporal and spatial resolution. The major scientific question, which leads us through our study is: which aspects can be consistently improved by CPCSs compared to coarser gridded simulations?
To answer this question, results which are consistent in the majority of the simulations are emphasized. The analyzed ensemble consists of five simulations on a ~10 km horizontal grid and five simulations on a ~3 km grid which are performed with three different RCMs. In the next section we provide basic information about our model ensemble, reference data and methods used to evaluate model results. In the following two sections results are presented and discussed into details. In the last two sections we summarize our results and draw our conclusions.
2 Data and methods
2.1 Experimental setup, data, and models
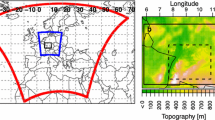
Figure 1 depicts the model and evaluation domains which are used in this study. The domain setup differs between the different simulations, but all 10 km simulations cover at least the European Alpine region and all 3 km simulations cover at least the Eastern Alps (domain D3). The evaluations are focusing on domain D3 and the sub-regions D4a and D4b. The minimum distance between the evaluation domain D3 and the lateral boundaries of the RCMs is eight grid boxes and therefore larger than the relaxation zones. The first sub-region D4a represents a hilly area in the south eastern part of Styria which lies on the foothills of the Alps. The climate of this region is characterized by the predominant influence of Mediterranean cyclones and deep convection especially in summer. From the North and the West, the region is shielded by the Alps. In summer, convective precipitation events on the one hand and partly long lasting dry spells on the other hand characterize this region. The typical weather conditions in winter are dry ones. The second sub-region (D4b) is centered on the highest peaks of the Austrian Alps which are in the Hohe Tauern National Park. The Großglockner, with an elevation of 3,798 m, is the highest summit in this region, and the valleys are roughly on a height of 550 m. Precipitation patterns in this area reveal a great spatial variability from the scale of single slopes upwards. There is a precipitation maximum in summer and a minimum in spring or autumn (Barry 2008). The strong surface height variation and the diversity of weather and climate regimes within a relatively small region are challenging tasks for RCMs.
In order to capture a significant part of the broad range of weather regimes the periods June, July, and August 2007 (JJA) and December 2007, and January and February 2008 (DJF) are chosen for the simulations. Compared to the climatological mean, JJA was warmer than on average and had at the same time an average amount of precipitation. In DJF warm and dry conditions were predominant. The main reason for the selection of these two seasons was the availability of homogeneous, highly resolved lateral boundary conditions (LBCs) and reference data.
Three RCMs have been used for the simulations.
-
The Wegener Center of the University of Graz (WEGC) used the Consortium for Small Scale Modeling (COSMO) Model in Climate Mode (CCLM) in the version 4.0. The CCLM is the climate version of the former “Lokalmodell” of the German weather service with a non hydrostatic core. A detailed description of the COSMO model is given by Steppeler et al. (2003) and Doms and Förstner (2004) and for the CCLM model by Böhm et al. (2006) and Rockel et al. (2008).
-
CCLM was also used by the Brandenburg University of Technology Cottbus (BTU) but in the version 4.8. The major differences to CCLM 4.0 are that, beside corrections and modifications of the source code, a new reference atmosphere (vertical temperature profile) and a subgrid-scale orography scheme were introduced in version 4.8. However, there are also some differences in the model setup (see Table 1). These simulations are described into some details by Georgievski et al. (2011).
Table 1 Listing of all simulations with their acronyms and key settings -
WEGC also applied the Pennsylvania State University (PSU)/National Center for Atmospheric Research (NCAR) Fifth-Generation Mesoscale Model (MM5) version 3.7.4. Details about the model are given in Dudhia (1993).
-
The Weather Research & Forecasting Model (WRF) version 2.2.1 was again used by WEGC. Like the other RCMs it has a non-hydrostatic core and is developed by several research institutes in the USA. A detailed description can be found in Skamarock et al. (2005).
The major difference between the simulations with 10 km horizontal grid spacing and those with 3 km is that the deep convection parameterizations are switched off in the latter. Simulations on the 3 km grid are permitting deep convection and hence they are referred to as CPCSs. The 3 km simulations use the results of the coarser simulations as lateral boundary conditions in two different ways. The first one is called one-way coupling, which means that there is no feedback of information from the 3 km simulation to the 10 km run and information from the 10 to the 3 km simulation is only provided via the lateral boundaries. This approach was used for the CCLM simulations and one pair of MM5 runs (M10_O and M03_O; see Table 1 for acronyms). In CCLM, hourly data from the 10 km simulations were provided as lateral boundaries of the CPCSs, while the CPCS of MM5 was updated every time step of its parent simulation (20 s). The second approach is called two-way coupling, meaning that there is a feedback from the 3 to the 10 km simulation. Thereby, information from the interior of the 3 km domain is fed into the 10 km domain every time step and the 10 km simulation is fed into the 3 km simulation via the lateral boundary conditions, in turn. The feedback from the interior of the 3 km domain is realized by replacing the coarse grid solution with the solution of the coincident points of the fine grid. For numerical stability, the fed back fields are additionally smoothed with a five point 1-2-1 smoother that removes two-grid-length noise, and damps other short wavelengths strongly. The models thereby do not conserve mean values. The advantage of a two-way nesting approach is a better behavior at outflow boundaries of the finer gridded simulation. Similar two-way coupling approaches were used in the WRF simulations and the second pair of MM5 runs (M10_T and M03_T). Detailed information about the model setups, the nesting strategies, and the hereafter used acronyms of the simulations can be found in Table 1.
For the 10 km simulations the LBCs were taken from the integrated forecast system (IFS) of the European Centre for Medium-Range Weather Forecasts (ECMWF). Those data have a T799 L91 resolution (roughly 25 km horizontal grid spacing at mid latitudes, and 91 vertical levels). A temporal resolution of 3 h is achieved by combining IFS analyses (00, 06, 12, and 18 UTC) and short term forecast fields (+3 and +9 h of the 00 and 12 UTC forecasts; see also Suklitsch et al. 2011). It is assumed that these boundary conditions represent the real weather conditions adequately, and hence the RCMs performance can be judged apart from the quality of the LBCs.
The surface boundary conditions (SBCs) were initialized with two different spin-up periods. For the CCLM 4.0 and MM5 simulations a long spin-up period was imitated by initializing the SBCs from simulations which start at the beginning of January 2007. This has the advantage that the soil with its long term memory for initial conditions (Seneviratne et al. 2006) can be assumed to be in a more balanced state at the beginning of the simulations. A shorter spin-up period of 1 month (May for JJA 2007 and November for DJF 2007–2008) was used in the WRF and CCLM 4.8 simulations.
The evaluations in this study are performed with the Integrated Nowcasting through Comprehensive Analysis (INCA) dataset (Haiden et al. 2011), provided by the Austrian Central Institute for Meteorology and Geodynamics (ZAMG). The INCA data set has a 1 km × 1 km resolution on an hourly basis and covers the Austria territory. It is derived through a combination of numerical weather predictions (NWPs) (ALADIN, ECMWF) with current observation data from stations, radars, and satellites, and is further refined with highly resolved orographic information. The station density is especially high in mountainous regions. However, most of the stations are located in the valleys. More technical details about the INCA system and its data processing can be found in Haiden et al. (2010).
The usage of the INCA dataset as reference data has two major advantages. First, its high spatial and temporal resolution and second, it allows for an assessment of the RCMs performance by providing the following four atmospheric parameters: air temperature two meter above surface (T2M), precipitation amount at surface (PR), relative humidity two meters above surface (RH), and global radiation at surface (GL).
However, the advantage of the high spatial and temporal resolution of INCA has also a disadvantage. Even though INCA is constrained by observations, the output contains errors especially in regions with low station density. For temperature, a mean absolute error of 1.0 to 1.5 K in lowland areas and 1.5 to 2.5 K in Alpine valleys is estimated (Haiden et al. 2011). Precipitation mean absolute errors for point values and 15 min time scale can reach up to 50 % in summer and more than 100 % in winter. For larger scales of the order of 100 km² the errors get significantly smaller. Relative humidity was found to be very accurate (5 to 7 %) in a hilly sub-region in southern Styria (Kann et al. 2011). However, no information is available about the accuracy of relative humidity in mountainous areas and global radiation in general.
2.2 Methods
The evaluation process of this study focuses on a broad range of performance metrics to give a holistic view of performance differences, changes in error ranges, and possible benefits of the CPCSs compared to their parent runs.
In the first step of the evaluation process, the characteristics of the seasonally averaged spatial fields are analyzed. Box and whisker plots (e.g., Wilks 2005) help to compare the deviations in the medians, the 25 and 75 % quantiles, and in the tails of the distributions.
In the second step, diurnal cycles of the spatially averaged fields are depicted to analyze the accuracy of sub-daily processes in the simulations. Furthermore, Taylor diagrams (Taylor 2001) are used to evaluate the temporal correlations and standard deviations normalized by the standard deviation of the reference data on a grid point basis.
The third evaluation step focuses on the representation of extremes in the combined temporal and spatial distributions (1 km grid on hourly basis) by comparing differences in the maximum (Q100) and minimum (Q0) values and the 0 to 5 % (Q0–Q5) and 95 to 100 % (Q95–Q100) quantile values.
The fourth evaluation step analyzes high resolution precipitation features on grid-point basis which demands specialized methods, because precipitation is partly non-deterministic and unpredictable at small scales (e.g. Hohenegger et al. 2008). The evaluation of spatial precipitation fields with traditional statistical methods (like correlations and root mean squared errors) often leads to a ‘double penalty’ problem, because modeled and observed precipitation may not match exactly in space and time. For example, if a precipitation object (e.g., a convective cell) is slightly shifted in the simulated precipitation field compared to the observed field, the simulation is penalized twice: first, because it missed the observed precipitation object and second, because it produced precipitation where none was observed. To account for such evaluation problems special methods were developed (particularly by the numerical weather prediction community). A methodological overview is given by Prein and Gobiet (2011).
In this study, two of these methods are applied which evaluate different aspects of the precipitation fields. The corresponding evaluation is performed on D3 only, because the sub-domains D4a and D4b contain too few grid cells to achieve robust results. The first evaluation technique is the FSS developed by Roberts and Lean (2008). It is based on the assumption that a useful simulation has a similar spatial frequency of precipitation events as the observation. A set of precipitation thresholds (q) are used to transfer the original precipitation fields [both simulated (M r ) and observed (O r )] into binary fields I O and I M by setting grid cells with precipitation values larger or equal to a threshold to one and all others to zero (cf. Eq. 1).
In the next step, a simple two dimensional moving average is applied to the binary fields with a squared window of side length n and uniform weights.
O (n)i,j is the field with observed fractions for a squared moving window of length n calculated from the binary field I O and M (n)i,j contains the simulated fractions obtained from the I M binary field. In Eqs. 2 and 3 i goes from 1 to N x , where N x is the number of grid-cells in the longitude direction and j goes from 1 to N y where N y , is the number of grid-cells in the latitude direction. The value of n is denoted as neighborhood size or horizontal scale and varies from n = 1 to n = 2 N−1 where N = max(N x , N y ). If grid points in the moving window lie outside of the domain, their values are considered as zero. After O (n)i,j and M (n)i,j are derived mean squared errors (MSE) are calculated for all n:
From the MSE the FSS can be calculated as follows:
In Eq. 6 MSE (n)ref can be thought of the largest obtainable MSE with the given observed and simulated fractions. The FSS can take values between zero and one, where one means perfect fractional coverage. These steps are done for every hourly field which has either precipitation in the simulation or in the observation. The final FSS is calculated as the seasonal median over all hourly FSSs. By varying the threshold and the size of the window, the FSS allows for intensity- and scale-dependent analysis. A more detailed description of the FSS can be found in Roberts and Lean (2008).
The second applied method to evaluate high resolution precipitation fields is the structure, amplitude, and location (SAL) method (Wernli et al. 2008). As the name indicates, this method analyzes three statistical properties of precipitation fields. The amplitude component (A) consists of the normalized differences of the domain average precipitation values. It can have a maximum/minimum value of ±2 where positive values mean an overestimation and negative values an underestimation of precipitation. A = 0 denotes a perfect agreement of hourly precipitation sums. The location component (L) is derived from two additive terms. The first one accounts for the location of the center of mass of the domain wide precipitation. This component becomes zero if both centers of mass are at the same place and one if the centers are separated by the maximum possible distance within the domain. The second component is necessary, because many different precipitation fields can have the same center of mass. Therefore, the second value accounts for the distance between the center of mass of the total precipitation field and the center of mass of individual precipitation objects. The result is normalized to have values between zero and two, with zero denoting the same average distances of the objects in simulated and observed precipitation. However, L = 0 does not mean a perfect match, because the L value is, for example, insensitive to rotation around the center of mass. The third value in the SAL evaluation is the structure (S) component. It compares the volumes of the precipitation objects and contains information about the mass and the shape of the objects. To avoid double counts of the precipitation bias, which is already accounted for in the A component, the accumulated precipitation in each object is divided by the objects maximum precipitation. S becomes negative if too small or too peaked objects are simulated and positive, if widespread precipitation is modeled but small convective cells are observed. For more details about the SAL evaluation method see Wernli et al. (2008).
Note, before doing any statistics all simulations are resampled to the INCA grid. Thereby, no interpolation and no height correction are applied because in this study added value is defined as comparison of the raw model output to observations. This approach enables to evaluate the simulations with the high spatial details of the INCA dataset and simultaneously conserves the spatial structure (effective resolution) of the individual simulations. A description of the applied resampling technique can be found in Suklitsch et al. (2008). An alternative approach to compare the simulations with each other would be to resample the INCA dataset to the individual model grids. In this case, the spatial resolution of INCA (1 km grid) would be degraded to the resolution of the models. This approach has been followed in parallel in this study (not shown) and leads to similar basic conclusions.
In addition to the RCM simulations also the performance of the IFS data is evaluated to compare the effect of RCM downscaling directly to the original driving data. Therefore, the three hourly IFS data is linearly interpolated to hourly values in advance to be comparable to the temporal resolution of the INCA data and the RCM output. This has to be kept in mind, since it leads to artificially degraded performance of IFS if hourly data are evaluated (like for the FSS and SAL statistic).
3 Results
This chapter is made up of four parts according to the different evaluation aspects of the simulations. In Sect. 3.1 the error ranges of the seasonal mean fields are analyzed. In Sect. 3.2 the representation of sub-daily processes, temporal variability and correlation on grid-point scale is focused. In Sect. 3.3 the representation of extremes in the models are analyzed and in Sect. 3.4 advanced evaluation methods are used to evaluate hourly precipitation fields.
3.1 Spatial error ranges and variability
Figure 2 shows spatial error ranges of the seasonal bias fields. The term “error range” used here denotes the distance between the 25 to the 75 % quantile of the error and is visible as box lengths in Fig. 2.
Spatial box-whisker plots of the seasonal mean bias fields of domain D3 for T2M, PR, RH, and GL (top down). Relative differences are depicted for PR and GL. Left column shows results of JJA and right column those of DJF. The box length denotes the 25 and 75 % quantile of the grid cells in D3, the whiskers have maximal one and a half times the length of the box
In JJA the error ranges of all CPCSs for air temperature two meters above ground (T2M) are smaller than those of the corresponding 10 km simulations and those of IFS (Fig. 2a). The average error range decreases by 0.6 K from 2.4 K in the 10 km simulations to 1.8 K in the CPCSs. This effect is especially strong in the mountainous region D4b and it is smaller in the hilly region D4a (both not shown).
In DJF (Fig. 2b) the average error ranges of the CPCSs and the 10 km simulations are both 1.9 K. Only the C03_4.8 and M03_O simulations are able to reduce the error ranges of their parent simulations. In DJF the CCLM 4.0 simulations have a remarkably strong cold bias of −3 K whereas the median biases of the other simulations are similar to those in JJA.
The JJA relative precipitation amount (PR) and the relative error ranges in both 3 km CCLM simulations are increased compared to the 10 km simulations (Fig. 2c). This is different in the one-way nested MM5 simulations because in M10_O PR is highly overestimated in large areas of D3 which is not the case in the M03_O run leading to decreasing error ranges. In all three one-way coupled simulations, the median JJA precipitation sums are not improved in the CPCS. For the two-way coupled MM5 and WRF simulations the error ranges stay nearly constant, because the 3 km fields are fed back to their driving 10 km parent simulation.
In DJF (Fig. 2d) the relative error ranges of PR are much larger than those in JJA. However, the absolute error ranges (not shown) are smaller because there is generally less PR in winter and DJF 2007–2008 was remarkably dry in many parts of the Eastern Alps. In this season IFS has clearly a smaller error range than all RCM simulations. There is a slight decrease in median PR of the CPCSs which improves the general wet bias of the 10 km simulations (except for M03_O). Like in JJA the error ranges of the two-way coupled 3 and 10 km simulations of MM5 and WRF are very similar but in DJF also those of the one-way coupled simulations do not differ notably.
The median errors of relative humidity (RH) in JJA and DJF are roughly within ±10 %. MM5 and WRF are generally too dry and both versions of CCLM are too wet (Fig. 2e, f). In DJF the error ranges are larger than in JJA, but an improvement of the median biases of the CPCSs can be seen except for M03_O. The error ranges are not reduced in the CPCSs in general.
All CPCSs have higher global radiation (GL) values compared to their parent simulations which is stronger pronounced in JJA (Fig. 2g) but also visible in DJF (except for C03_4.0 and M03_O) (Fig. 2h). Comparing the individual RCMs, the CCLM 4.0 has a strong negative bias in JJA GL which is most probably related to an overestimation of cloud cover in this model. All other relative median RCM biases are within a range of ±20 %. Remarkable is the different behavior of the one-way and two-way nested simulations of MM5. The M03_O and M03_T simulations look very similar but the M10_O has much higher GL values than the M10_T. In DJF (Fig. 2h) the relative error ranges are larger for CCLM and WRF than those in JJA. However, the absolute error ranges are smaller because of the lower GL values in DJF. In general, the CPCSs do not reduce the error ranges.
Summing up, the only systematic added value in terms of seasonal mean spatial patterns of CPCSs is found in summertime temperature. Large differences between the two resolutions have been found in summer precipitation patterns in case of one-way coupling. In addition, summertime global radiation is systematically increased in the high resolution simulations. In winter, the differences between the two resolutions are less systematic and less pronounced.
Concerning the overall performance the CCLM 4.0 simulations show often larger error ranges (e.g., GL in DJF Fig. 2h) or larger differences (e.g., T2M in DJF Fig. 2b or GL in JJA Fig. 2g) than the rest of the simulations. Because of this and because the differences between the C10_4.0 and C03_4.0 simulations are similar to the differences between the C10_4.8 and C03_4.8 runs the results of the CCLM 4.0 simulations are not shown in the evaluation results of the next section. This also reduces the information density in the plots and helps to focus on the essential information.
3.2 Diurnal cycles, temporal correlation, and variability
In this subsection the temporal performance of the RCMs is analyzed. For this purpose, two methods are used: diurnal cycles of the spatially averaged fields and Taylor plots where hourly time series are evaluated on grid point basis.
3.2.1 Diurnal cycles
In Fig. 3 the mean diurnal cycles of the spatially averaged fields are displayed for the Eastern Alps (D3) and the two sub-regions D4a and D4b.
Diurnal cycles of the spatially averaged simulations in domain D3, and in the sub-regions D4a, and D4b (left to right). The upper half of the figure (small letters) show results for JJA and the lower half (capital letters) those for DJF. In each panel the rows display T2M (panel a to c and A to C), PR (panel d to f and D to F), and RH (panel g to i and G to I). The shaded area depicts the 25 and 75 % percentiles of spatially averaged diurnal cycles of the reference data (INCA)
The diurnal cycles of JJA T2M (Fig. 3a, b, c) are scattered around those of INCA within a range of ±2 K. In DJF (Fig. 3A, B, C) the performance of the RCMs is roughly the same. In both seasons, the CPCSs have no deviations from their parent simulations in common.
In JJA PR has a distinct diurnal cycle with a maximum in the afternoon due to convective rainfall in D3 (Fig. 3d) which is most pronounced in the mountainous region (Fig. 3f). In the hilly sub-region D4a (Fig. 3e) no distinct diurnal cycle is visible. All RCMs are able to qualitatively reproduce this diurnal cycle and they are generally improving the timing of the afternoon peak compared to IFS. An added value in the one-way nested CPCSs compared to their parent simulations becomes visible in the better timing of the PR peak later in the afternoon and a more correct onset of PR at noon. While the C03_4.8 simulation deteriorates the amplitude of the diurnal cycle the M03_O simulation improves the amplitude of the afternoon peak compared to M10_O. The two-way coupled 10 and 3 km simulations have nearly identical diurnal cycles.
In DJF (Fig. 3D, E, F) PR shows no clear diurnal cycle. The RCMs perform well in D4a (Fig. 3E) and overestimate PR in D4b (Fig. 3F) which contributes to a general overestimation of PR in D3 (Fig. 3D). There is no systematic difference between the 10 km simulations and the CPCSs in winter.
The diurnal cycle of RH is inversely related to T2M, but reveals some additional information and distinct model deficiencies. The shape is captured reasonably well by all simulations during JJA (Fig. 3g, h, i) but the minima occur too early and partly large offsets to INCA exist in the MM5 and WRF simulations. In DJF (Fig. 3G, H, I) the RCMs have more problems to properly reproduce the diurnal cycle of RH. The performance becomes worse in the mountainous region D4b (Fig. 3I) where the CCLM and the WRF simulations have nearly constant RH values during the entire day and all four MM5 simulations even show an inverse diurnal cycle. In both seasons no common differences between the CPCSs and their parent simulations are visible.
Concerning the diurnal cycle of GL (not shown) the amplitude of the CPCSs is higher than those of the 10 km simulations, especially during summer in the mountains. This is consistent with the results from Sect. 3.1 (Fig. 2).
In summary, the major added value of CPCSs in the diurnal cycle is found in the more correct timing of the afternoon maximum and the noon onset of convective precipitation in summer and especially over mountainous terrain.
3.2.2 Temporal correlation and variability
The ability of the RCMs to reproduce the temporal characteristics (Pearson’s correlation coefficients and standard deviations) of the considered atmospheric parameters on an hourly and grid point basis in D3 is analyzed with the help of Taylor plots (Fig. 4).
Taylor plots of hourly values on grid point basis. Different colors and symbols indicate different simulations. The median statistical values are shown as symbols and the spread of the data points (25 % quantile to 75 % quantile) are shown as vertical and horizontal lines. The upper panels show results for JJA and the lower one those for DJF. Columns correspond to T2M, PR, RH, and GL (from left to right)
In all simulations the temporal correlation of T2M lies between 0.88 to 0.93 in JJA (Fig. 4a) and 0.83 to 0.90 in DJF (Fig. 4b). There are only small differences (below 0.02) in the median correlation coefficients between the CPCSs and their parent simulations. Concerning the median normalized standard deviation in JJA the CPCSs show a small (below 5 %) but consistent increase compared to their parent simulations while in DJF there are positive and negative differences. IFS has the highest correlation coefficients in both seasons. The generally high correlation coefficients are not surprising as the main part of the correlation is caused by the diurnal cycle. Correlation is worse for variables that have no regular diurnal variation. In JJA the temporal standard deviation is well captured in all simulations while in DJF the standard deviations are slightly underestimated. The horizontal and vertical lines, which represent the 25 to 75 % quantile distance of individual grid-pint values are not visible, because those values are clustering very dense around the median correlation coefficients and normalized standard deviations. This means, there is no big difference in temporal correlation coefficients and standard deviations in different areas of D3.
For PR in JJA (Fig. 4c) the correlation coefficients are between 0.12 and 0.25 and the standard deviations are spreading widely, which can be seen from the large vertical 25 to 75 % quantile distance. Common in all CPCSs is their higher temporal variability compared to their parent simulations. The poor performance of highly resolved simulations of PR is a well known issue and is related to the “double penalty problem” which was already discussed in Sect. 2.2. To avoid this problem special methods like the FSS or the structure, amplitude, location (SAL) analysis are applied in Sect. 3.4. In DJF (Fig. 4d) the correlation is generally higher than in JJA because of the predominance of large scale precipitation which is more deterministic than convective precipitation. Data-points of individual grid-cells are spreading widely according to the large 25 to 75 % quantile distances. Compared to their parent simulations all CPCSs show an increase in the median normalized spatial standard deviation which is largest (10 %) in the M03_O simulation. All RCMs have too high standard deviations and the differences in the correlation coefficients between CPCSs and their parent simulations are inconsistent.
For RH in JJA (Fig. 4e) the majority of the simulated correlation coefficients are lower than those of IFS. The CPCSs feature slightly smaller correlation coefficients than their corresponding 10 km runs, except for C03_4.8. In common are increased median normalized standard deviations in the CPCSs (4 to 6 %). The CCLM (MM5) simulations have generally too low (high) temporal variability, while it is well represented in WRF. In DJF (Fig. 4f) the correlation coefficients of the CCLM simulations are lower than in JJA. Also the standard deviations are too low which is in agreement with the nearly constant averaged diurnal cycles shown in Fig. 3I. The differences in the median correlation coefficients are inconsistent however, the median normalized standard deviations are commonly larger in the CPCSs (except for C03_4.8).
The RCMs capture the temporal characteristics of GL with median correlation coefficients between 0.85 and 0.93 in JJA (Fig. 4g). Note, a major part of these high values belong to the diurnal cycle of the sun. A shift towards higher temporal variability is visible in all CPCSs compared to their parent simulations, which is consistent with generally higher GL values of the CPCSs (see e.g., Fig. 2g). Similar results are found in DJF (Fig. 4h), but the correlation coefficients are higher than in JJA with values ranging from 0.93 to 0.95.
In summary, there are no systematic changes in the temporal correlation coefficient or variability between the CPCSs and their parent simulations, except an increase of the variability in summer precipitation and global radiation. High correlation coefficients and accurate variability can be found for all simulated temperature and global radiation fields, while for relative humidity the simulations of MM5 and WRF are outperforming those of CCLM which shows too low temporal variability. Results for precipitation are especially poor in summer, partly due to the double penalty problem (see Sect. 3.4).
3.3 Extremes
In this section we analyze the differences between the distributions of hourly, grid-point values of INCA and the RCM simulations by focusing on the representation of extremes, defined as values below the 5 % and above the 95 % percentile.
For T2 M in JJA (Fig. 5a) and DJF (Fig. 5A) the CPCSs have generally lower minima (Q0) and higher maxima (Q100) than their corresponding 10 km simulations, which results in a more realistic distribution in most cases (compare section 3.1). In JJA (Fig. 5a) the simulations have a larger spread and higher deviations from the reference dataset for minimum compared to the maximum T2M. The 0 to 5 % (Q0–Q5) quantile values are slightly colder in all CPCSs than in their parent simulations whereas the 95 to 100 % (Q95–Q100) quantile values are generally warmer. In DJF (Fig. 5A) there are no such common changes. The RCMs are able to improve the extreme values of IFS in JJA, which has too low Q0–Q5 and too high Q95–Q100 values. In D4a (not shown) all simulations have too low minimum T2M while in D4b (not shown) all simulations have too low maximum temperatures.
Simulated minus observed quantile differences (upper panels) and density distributions of INCA (lower panels) for JJA (left) and DJF (right) for T2M, PR, RH, and GL (rows in top- down sequence) on D3. In the quantile differences plots the parts labeled with Q0 and Q100 show the difference in the minimum (Q0) respectively maximum (Q100) of the hourly grid point values (simulations minus INCA). The box-whisker plots show the differences between the zero to fifth (Q0–Q5) (simulated minus INCA) and the 95th to 100th (Q95–Q100) quantile values. The two vertical gray lines in the density plot depict the 5 and 95 % quantiles and the displayed x-axis range shows maximum and minimum values in INCA
Concerning hourly maximum grid point precipitation, all CPCSs have larger and more realistic Q100 values than their parent simulations (Fig. 5b). An especially large improvement can be seen for the C03_4.8 run which reduces the Q100 difference of its parent simulation from −44 mm h−1 to +9 mm h−1 (Fig. 5b). However, there is no systematic difference between the two resolutions in the Q95–Q100 deviations. The lower quantile differences Q0 and Q0–Q5 are zero because of the many non precipitating hours in the distribution of INCA and the simulations. Compared to IFS the RCMs are able to improve the median Q95–Q100 and Q100 difference. In the sub domains D4a and D4b (not shown) similar results are found.
Similar to JJA there is also more intense PR in DJF (Fig. 5B) in the CPCSs than in their parent simulations which reduces the differences to INCA. Nevertheless, the most extreme precipitation events are still underestimated by the CPCSs in all simulations and all domains.
Concerning RH in JJA (Fig. 5c) there is a consistent decrease in the Q0–Q5 values in all CPCSs compared to their parent runs while there are no common differences in the Q95–Q100 values. The W03 simulation and especially the MM5 runs have unrealistically high maxima which are partly close to 300 %. In DJF (Fig. 5C) the WRF simulations have unphysical minimum values which are below 0 % RH. There are no common changes in the Q0–Q5 and Q95–Q100 values between the CPCSs and the corresponding 10 km simulations. All simulations are overestimating the median of the Q95–Q100 values by ~20 %. As in JJA all MM5 simulations have too high maximum values of RH. In D4a (not shown) extremes are better represented than in D3, while in D4b (not shown) the deviations from INCA distribution are especially large.
For GL (Fig. 5d, D), only the upper tail of the frequency distribution is of relevance in this study: the Q0 and Q0–Q5 values refer to nighttime conditions and hence deviations from INCA become vanishingly small. In JJA (Fig. 5d) the Q95–Q100 values of the CPCSs are higher than in their parent simulations, which is not the case for the Q100 values. In DJF (Fig. 5D), no common changes between the CPCSs and their parent runs are visible. The large negative deviations in the Q100 values can be attributed to erroneous maximum values in the INCA dataset
Summing up, there is a consistent improvement in the representation of the most extreme hourly precipitation values in CPCSs. In the case of T2M the CPCSs have lower minimum values and higher maximum values than their parent simulations, which lead to more realistic cold temperature extremes in most cases.
3.4 Evaluation of PR at high temporal and spatial resolution
The evaluation of simulated PR at high spatial and/or temporal resolution is difficult, because at small scales hourly PR partially gets unpredictable and double penalty problems can occur (see e.g., Fig. 4c, d).
In this section two methods are applied, which are able to avoid the double penalty problem and to evaluate the spatial properties of high resolution precipitation fields more appropriate than most traditional statistical methods, like correlations coefficients or mean square errors.
3.4.1 Fractions skill score (FSS)
Figure 6 depicts the average FSSs of all records with precipitation in JJA depending on the selected threshold values and horizontal extension of the moving window (horizontal scale). Compared to IFS the FSSs are widely improved by the simulations especially for threshold above 1 mm h−1 (Fig. 6c). However, this improvement is partly caused by the three hourly resolution of IFS. The CPCSs have higher FSS than their corresponding 10 km simulations (except the M03_T and W03 simulations below 1 mm h−1 threshold and the M03_O at all thresholds). Differences between the two resolutions are larger at higher precipitation thresholds (e.g., 2 mm h−1 in Fig. 6d). The scales on which the simulations have more than random skill are the same in both, the CPCSs and their parent simulations in the two-way coupled simulations. C03_4.8 improves the scales at which C10_4.8 has more than random skill by a factor of 2 (for 0.5 mm h−1) and a factor of 5 (for 2 mm h−1). In the case of the one-way coupled MM5 simulations it is the other way around and the M03_O deteriorates the scale above random skill of the M10_O simulation. The main reason for this might be the general underestimation of PR in the M03_O simulation (cf. Fig. 2). Above 5 mm h−1 threshold (Fig. 6e) only the CPCSs and the M10_O simulation have FSSs greater than zero. The good performance of the M10_O simulation compared to the M03_O run is partly related to the underestimation of precipitation in the latter which is very similar to the M03_T simulation.
In DJF (Fig. 7) the differences between the FSSs of the CPCSs and their corresponding 10 km simulations are smaller than in JJA because winter precipitation is generally more dominated by large-scale and non-convective processes (e.g., frontal precipitation). However, except for the WRF and the one-way nested MM5 simulations, the CPCSs have higher FSSs and a better representation of small scales than their 10 km parent simulations. IFS has large FSSs at 0.1 mm h−1 threshold and outperforms all RCMs except WRF. For higher thresholds most simulations exceed the FSSs of IFS. Only the C03_4.8 run is able to improve the scales on which the simulations have more than random skill compared to its parent simulation (cf. Fig. 7b). For the other simulations there is no difference in this value except for the W03 run which deteriorates the performance of the W10 simulation.
Same as in Fig. 6 but for DJF
Comparing the FSSs of JJA with those of DJF it becomes visible that at small threshold values (e.g., 0.1 mm h−1) the FSSs are generally larger in DJF compared to JJA. This is because DJF precipitation is dominated by large scale processes which are better represented in RCMs than convective precipitation occurring frequently in JJA. For higher thresholds (e.g., 0.5 or 1 mm h−1) the FSS in JJA are larger than those in DJF because precipitation above e.g., 1 mm h−1 occurs more often in JJA than in DJF (Fig. 5b, B), and the probability that it is observed and simulated at the same time is therefore much higher in JJA.
3.4.2 Structure, amplitude, and location (SAL) evaluation
The structure, amplitude, and location (SAL) evaluation is an object based method which evaluates precipitation fields concerning the three characteristics after which it is named. Since we found that there are no large changes in the location (L) component between different simulations, the focus here lies on changes in the structure (S) and amplitude (A) component. It should be noted that the A component is different from the PR bias; because in the SAL evaluation only records with precipitation in the INCA dataset are considered.
In Fig. 8 the two dimensional distribution of the S and A components are shown for JJA. On average the CPCSs have a median shift of −0.72 in the S component which means there are smaller and/or more peaked precipitation objects in the CPCSs than in their parent simulations. For all models but MM5, this also means an improvement of the structure of precipitation objects in the CPCSs because the S components are more centered on zero. Furthermore, the median A components of the CPCSs are 0.15 higher than those of the 10 km simulations which leads to an average overestimation of precipitation in all CPCSs, because the A components of the 10 km simulations (except those of M10_O) are close to zero. The combination of smaller S values and larger A values in the CPCS means that there is more intense rainfall from smaller and/or more peaked precipitation objects. Compared to IFS (Fig. 8i) the RCMs are able to improve the S and A component of precipitation objects to a large extent. The contingency tables in the lower right corner of each panel reveals insights into the representation of correctly simulated precipitation (OJ/MJ), non-precipitation records (ON/MN), the amount of missed events (OJ/MN), and the amount of false alarms (ON/MJ) of each simulation. All CPCS (except MM5) show on average 23 % less missed events than their corresponding 10 km simulations. However, only the C03_4.8 simulation is also able to decrease the amounts of false alarms.
Structure, amplitude, and location (SAL) evaluation diagrams for JJA in domain D3. The left column shows the results for the 10 km simulations (except panel i which depicts IFS) and the right column those of the CPCSs. In rows there are CCLM 4.8, MM5OW, MM5TW, WRF, and IFS in top down order. Each circle in the plot corresponds to one precipitation event. The colors of the circles depict the L-components. The median values of SAL are written above each panel and the box inside the plots shows the 25 to 75 % quantile of the S and A components. In the lower right corner of the panels contingency tables are depicted. Therein OY denotes hours with PR in INCA, ON records without PR in INCA, MY records with PR, and MN records without PR in the simulations. The numbers in the table show the records where PR was simulated and observed (OY/MY), no PR was simulated and observed (ON/MN), PR was observed but not simulated (OY/MN), and no PR was observed but simulated (ON/MY)
In DJF (Fig. 9) the median S components of the CPCSs are decreasing by −0.48 which leads to an improved structure of PR objects in all CPCSs (except for W03). The median A components slightly increase in the CPCSs on average by 0.1. The RCMs are able to improve the S and A component of IFS (Fig. 9i) even though IFS performs better than in JJA. The contingency tables show that the missed events in the CPCSs of MM5 and WRF are reduced by 13.6 % on average while they stay constant for CCLM 4.8. However, at the same time also the false alarms increase by 18 % in M03_T, and 67 % in W03. In case of M03_O they stay relatively constant and only the C03_4.8 simulation can reduce the false alarms by 25 %.
Same as in Fig. 8 but for DJF
4 Discussions
In this chapter the results presented in Sect. 3 are discussed and interpreted. The main focus lies on the explanation and interpretation of consistent (common, model independent) differences between the CPCSs and their parent simulations.
In order to investigate the effects of a higher resolved model orography more properly, a new MM5 simulation is introduced (M03_S). This simulation uses a smoothed 10 km orography while the rest of the model setup is the same as in the M03_O simulation (see Table 1). The smoothing of the 10 km orography with a 1–2–1 smoother is necessary to eliminate features of two-grid interval wavelengths. Even though the orography of the M03_S and M10_O simulation are not identical, the slope angles, the mountain heights, and the elevation of the valleys are similar. The slope angles and vertical difference between valleys and peaks are important because steeper slopes and higher differences can initialize stronger vertical wind speeds and lift air more easily to the level of condensation and free convection. Therefore, comparing results from the M03_S with the M03_O simulation helps to separate the effect of better resolved orography from the effect of better resolved dynamics and deep convection in the CPCSs.
4.1 Improved representation of T2M
In Fig. 2 we showed that spatial differences in the seasonal averaged T2M fields in JJA are commonly decreasing in all CPCSs compared to their parent simulations. In DJF however, only the C03_4.8 and M03_O simulations show such an improvement. The main reason for this can be found in the improved representation of orography in the CPCSs as shown in Fig. 10.
In Fig. 10a the same data is shown as in Fig. 2a for M10_O, M03_O, and additionally for M03_S however, here a height correction of 6.5 K km−1 is applied to account for the height differences between model and the INCA orography. This height correction leads to a similar error range in all three simulations regardless of their grid spacings and the underling orography. Similar results can also be found for the other simulations (not shown).
In DJF (Fig. 10b), contrary to JJA, the application of a height correction does not remove but only decreases the error range differences. This is because the error ranges in the CPCSs are increased. Especially positive differences are getting larger (e.g., the 75 % quantile) because there is already an overestimation of T2M in the valleys in the CPCSs (not shown) which gets even amplified by the height correction (the valleys in INCA are deeper than in the models which leads to a increase of T2M due to the height correction). The reason for the persistent differences compared to JJA might be related to the more stable stratification of the atmosphere (smaller temperature gradients) in DJF. This means height differences do not have such a strong influence as in JJA. Furthermore, inversions which are hard to simulate even with a 3 km grid spacing model occur frequently during DJF. A worse simulation of inversions in the RCMs can lead to an overestimation of T2M in the valleys (in INCA the T2M in the valleys are well captured because of a high station density).
4.2 Improved diurnal cycle of PR in JJA
An improved onset of rising PR at noon and a better timing of the PR peak in the afternoon is shown for average JJA PR in the CPCSs in Fig. 3d, f. The reason for these improvements is the explicit treatment of convective PR and not the better resolved orography, as shown in Fig. 11. By comparing the diurnal cycles of M10_O (solid blue line) with those of M03_O (dashed blue line) and M03_S (dotted blue line) the described improvements becomes visible. The convective (parameterized) part of PR in M10_O (red solid line) contributes more than 50 % to the total PR (blue solid line) and shows a too early onset of increasing pr in the morning and a too early and peaked maximum in the afternoon. However, the resolved part of PR (orange solid line) has the correct onset and a later but rather weak peak in the afternoon. This is continued when the resolution is increased (M03_O and M03_S). Comparing the results of M03_O with M03_S, the resolution of the model orography has no effect on the improved timing of the diurnal cycle of convective precipitation. This indicates that the improvements in capturing the timing of convective PR is driven by the higher resolved atmospheric dynamics rather than the higher resolved orography.
4.3 Improvements of extreme PR
In Fig. 5 an improvement of the most extreme precipitation rates in DJF (Fig. 5B) and especially JJA (Fig. 5b) in the CPCSs is shown. Figure 12 depicts this improvement exemplarily for M03_O and M03_S and their parent simulation M10_O. In JJA (Fig. 12a), the maxima PR (Q100) is underestimated by −60 mm h−1 in M10_O but only by −33 mm h−1 in M03_O (the maximum in INCA is 85 mm h−1). However, only a small part of this improvement can be attributed to the steeper orography in M03_O, because the M03_S simulation has a similar bias of −36 mm h−1 as the M03_O. Fig. 12b shows the same data as Fig. 12a, but here all fields are spatially averaged to the 10 km grid of M10_O. On this scale there is only a small difference in the Q100 PR between the CPCSs and their parent simulation and also the differences to the maximum PR in INCA are much smaller. In addition, the Q95–Q100 differences show only minor changes. The reason for the improved extreme precipitation rates in Fig. 5b therefore relies on the fine spatial structures of such events, which are more properly captured by the model when the dynamic of the atmosphere is higher resolved.
Simulated minus observed quantile deviations (upper panels) for PR in JJA (left panels a and b) and DJF (right panels A and B) on D3. The upper panels (a and A) show results on the original grid spacing while the lower panels (b and B) display the results averaged to the 10 km M10_O grid. The right quantile differences plot (labeled with Q100) shows the difference in the maximum of the hourly grid point values (simulations minus INCA). The box-whisker plots show the differences between the 95th to 100th (Q95–Q100) quantile ranges
In DJF (Fig. 12A), the differences between the M03_O/M03_S and the M10_O simulation are not as large as in JJA. Still there is an improvement in the Q100 difference in the CPCSs visible. Similar to JJA, also in DJF the evaluation on the 10 km grid (Fig. 12B) reveals that the underestimation of the maximum PR relies on the grid spacing of the simulations and that it is nearly vanishing within an evaluation on a 10 km scale.
4.4 Improved spatial properties of PR
The more accurate spatial distribution of hourly rainfall in CPCSs, which is shown in the FSS evaluations in Sect. 3.4.1, is likely attributed to improvements in the deep convective dynamics during JJA and a more accurate representation of predictable local effects (e.g., orographic uplift). The results agree well with findings of Roberts and Lean (2008) and Weusthoff et al. (2010) even though some differences exist. Weusthoff et al. (2010) found highest improvements in the FSS of convection permitting simulations for lower precipitation threshold whereas Roberts and Lean (2008) found them for higher thresholds similar to those in this study. Furthermore, improvements of scales on which simulations have more than random skill found by Roberts and Lean (2008) can only be seen in the C03_4.8 simulation.
The general more realistic structure of precipitation object (smaller and/or more peaked) which was shown in the SAL evaluations in Sect. 3.4.2 is in good agreement with findings by Wernli et al. (2008) who compared high resolution precipitation forecasts with coarser scale global model forecasts.
4.5 Increase of GL
In Fig. 2g, h a consistent increase of GL in most CPCSs is depicted. This increase can be up to 20 % in JJA, is especially large in the two-way coupled simulations, and leads to changes in the surface energy budged (not shown). For instance, the additional energy increases the latent heat flux in W03 and M03_T simulation, while in the M03_O run the sensible heat is increased. In C03_4.8 both reactions occur, depending on the region. In this subsection atmospheric fields which are important for GL are investigated in JJA between 06:00 am and 06:00 pm.
To understand the reason for the increase in GL it is important to understand how the shortwave radiation is interacting with the atmosphere in the models. In the MM5 and WRF simulations the Dudhia short wave radiation scheme (Dudhia 1989) referred to as D89, is used. Within this scheme a simple downward integration of solar flux is applied which knows three interaction mechanisms: (1) cloud albedo and absorption parameterized with the cloud liquid water (CLW) (2) water vapor absorption (Lacis and Hansen 1974), and (3) clear air scattering. In Fig. 13a the parameterized transmission coefficient of shortwave radiation and its dependency on CLW, as it is parameterized in the D89 scheme, is depicted. At CLW values below 10 g m−2 more than 90 % of the shortwave radiation can transmit while above 1,000 g m−2 the transmission part is only 10 %. In the CCLM simulations the Ritter and Geleyn (1992) radiative transfer scheme, referred to as RG92, is used which is more complex than the D89 scheme. Solar radiation in the RG92 scheme interacts with cloud water droplets, cloud ice crystals, water vapor, ozone, and takes into account effects of Rayleigh scattering. In the RG92 scheme also partial cloudiness is treated by attributing two sets of optical properties and fluxes to each layer, one for the cloudy and one for the cloud free part (Geleyn and Hollingsworth 1979). Thereby, clouds in adjacent model layers have maximum overlap while clouds which are separated by cloud free layers are independent from each other (random overlap assumption).
Panel a shows a quantile–quantile plot of cloud liquid water (CLW) from the 10 km (x-axis) and 3 km simulations (left y-axis) on D3 for hourly grid point values between 06:00 am and 06:00 pm in JJA. The secondary y-axis gives the shortwave transmission coefficient depending on CLW as it is parameterized in the MM5 and WRF simulations for a solar zenith angle of 37° and zero surface albedo (Stephens 1978). The box-whisker plots below (panels b to e) show hourly grid point values for global radiation (GL, panel b), integrated cloud liquid water (CLW, panel c), atmospheric water vapor (AWV, panel d), and cloud area fraction (CAF, panel e) between 06:00 a.m. and 06:00 p.m. The dots show the arithmetic mean values of the distributions. Note, not all parameters are available for every simulation
A general feature in all CPCSs are the higher values of CLW above ~500 g m−2 compared to their parent simulations (all lines are above the diagonal in Fig. 13a). This means that already dense clouds become even denser in the CPCSs. This should not have a very strong effect on the GL values in the CPCSs because the transmission coefficients do not change a lot at these high values and the total amount of values higher than ~500 g m−2 in the entire distribution is marginal (cf. Fig. 13c).
In case of the M03_T simulation, the number of low CLW values (smaller ~300 g m−2) is higher than in the M10_T run (the violet line is below the diagonal for small CLW values in Fig. 13a). Also the GL is increased (Fig. 13b) while the mean CLW stays constant (~38 g m−² Fig. 13c). However the 75 % quantile (upper box) of CLW is clearly decreased (from 34 to 2 g m−2). This shifts the transmission coefficients towards higher values and supports the increase of GL. If one-way coupling is applied less CLW values below ~300 g m−2 occur in the M03_O simulation compared to the M10_O run (blue line is above the diagonal below ~300 g m−2) and GL values are only slightly increasing (Fig. 13b). The boxes and whiskers of CLW are quiet similar even though M03_O has a slightly higher mean and upper whisker value (Fig. 13c). The water vapor absorption is a function of the atmospheric water vapor (AWV) which stays the same in both, the CPCSs and their parent simulations in MM5 (Fig. 13d). In the D89 scheme the clear air scattering is proportional to the atmosphere’s mass path length and can therefore only be responsible for small changes in GL.
Considering those results the primary effect which causes changes of GL between the CPCSs and the 10 km simulations of MM5 are changes in the low values (lower than ~200 g m−2) of the CLW distribution because the gradient of the transmission curve is much larger and the large majority of CLW values are smaller than ~200 g m−2 (see Fig. 13c). This means that in M03_T there are larger fractions with “cloud free areas” compared to M10_T which directly leads to an increase of GL. Since the W03 and W10 are also two-way coupled and the D89 scheme was used in WRF as well, the reason for the increasing GL values might be similar. In M03_O an increase of the “cloud free areas” fraction is not visible compared to M10_O (because M10_O already has low CLW values) and therefore GL changes are small.
To investigate the reasons of the GL increases in CCLM the simulations of both version (4.8 and 4.0) are considered because in the CCLM 4.8 runs no AWV and CAF fields have been stored. The low CLW values (below ~500 g m−2) are very similar in the C03_4.8 and C10_4.8 runs whereas C03_4.0 has clearly lower values than C10_4.0 (Fig. 13a). However, both show a similar median increase in GL (24 W m−2 in C03_4.0 and 28 W m−2 in C03_4.8) (Fig. 13b). In C03_4.0 the mean and the 75 % quantile (upper box limit) of the CLW is decreasing compared to C10_4.0 (Fig. 13c) while the mean is slightly increasing and the 75 % quantile is constant in the C03_4.8 run (compared to C10_4.8). There is more AWV in the C03_4.0 simulation than in the C10_4.0 run (Fig. 13d) and the median CAF decreases by 14 % (Fig. 13e).
Summing up, for C03_4.0 the increase of GL compared to C10_4.0 can be related to a higher “cloud free area” fraction indicated by increased low CLW values and decreased CAF (similar as in MM5). Changes in the cloud ice content can not be investigated because cloud ice was not stored. The reason for the GL increase in C03_4.8 can not be fully analyzed because of missing data.
4.6 Two-way versus one-way coupling
If two-way coupling is applied the atmospheric fields in the 10 km simulation are overwritten by the values of the CPCS within the area of the 3 km nest. This means that the 3 km run is compared to a coarser (smoothed) version of itself. On the other hand, also one-way coupled CPCSs are often more similar to their corresponding 10 km simulations than to the observations (except for precipitation) or to CPCS of other RCMs. This indicates that a large part of the errors in CPCSs comes from the RCM formulation, the RCM setup, or from the lateral boundary conditions of the CPCSs. The small domains in the CPCSs are contributing to this behavior (see Sect. 4.9). Comparing the one-way coupled M03_O simulations with the two-way coupled M03_T run shows that in this study the benefit of two-way coupling is rather small because the results of both simulations are very similar.
4.7 Added value in the sub-regions and seasons
Detecting added value is generally easier in the mountainous region D4b than in the hilly area of D4a because of the high impact of better resolved orography in complex terrain. For instance, this can be seen in the improvements of the JJA precipitation diurnal cycle where no diurnal cycle is visible in D4a (Fig. 3e) whereas a strongly amplified cycle is visible in D4b (Fig. 3f). Furthermore, improvements in the seasonal mean T2M fields are much stronger in D4b than in D4a because of the large improvements of the complex orography in D4b.
Added value is additionally easier to find in JJA than in DJF mainly because of the more accurate representation of convective processes during the hot season and the well mixed conditions in the troposphere. Furthermore, in DJF the large scale flow is more dominant than in JJA which reduces the influence of small scale processes.
4.8 Domain size
A notable limitation of this study are the relatively small sizes of the 3 km simulation domains (see Fig. 1) which have an East–West/North–South extension between ~580 km/~510 km (in C03_4.0) and ~ 440 km/~370 km (in M03_O, M03_T, and W03). This implicates that the boundary conditions from the 10 km simulations have a strong influence on the CPCSs, especially in situations with strong synoptic scale weather patterns (e.g., passages of cold fronts) which occur more frequently in DJF. In such situations the CPCSs have only a limited degree of freedom and are strongly determined by the solution of their parent simulations. In larger domains the differences between the CPCSs and their parent simulations might be more amplified.
5 Summary
This study focuses on added value of CPCSs compared to coarser gridded simulations. Therefore, an ensemble of three regional climate models (RCMs) is used to perform ten simulations of two seasons (JJA 2007 and DJF 2007–2008). Five simulations are conducted with a horizontal resolution of ~10 km and five with ~3 km (CPCSs without deep convection parameterization) over the Eastern Alpine region. Four atmospheric parameters [air temperature 2 m above ground (T2M), precipitation amount (PR), relative humidity (RH), and global radiation (GL)] are evaluated which enables a holistic view on the RCM performance.
Clear evidence is given that CPCSs can add value to coarser gridded simulations. The most consistent improvement is found in precipitation. Resolving deep convection is essential for the correct development of convective precipitation, which is shown by the improved timing of the diurnal cycle of summer precipitation. A similar result for one particular model (CCLM) was also found by Hohenegger et al. (2008). In addition to those temporal aspects the intensity of the most intense precipitation extreme events is improved. The FSS analysis shows that added value is more apparent at medium to higher, than in low intensities and SAL evaluations reveals that most CPCSs more realistically representation spatial patterns of precipitation objects (smaller and more peaked). It could be demonstrated that the improvements are caused by explicit resolved deep convection and the better represented atmospheric dynamics, rather than by the higher resolved orography.
Improvements are also found in seasonally averaged T2M fields in JJA. However, this is mainly related to the higher resolved orography and can also be achieved with a simple height correction.
Most of the above described improvements can be only found on small spatial and/or temporal scales and become undetectable by averaging. One example is the improved in the most extreme precipitation values (see Fig. 12) which is only visible in hourly- grid point values. Another example is the improvement of the timing of JJA precipitation (see Figs. 3d, f, 11), which is detectable only in sub-daily values. In contrast, monthly or spatial averages are generally not improved or even deteriorated, as can be seen in the median precipitation amounts in JJA (Fig. 2c). On exception for this are the error ranges of T2M which are strongly related to the improved orography (Fig. 2a).
Larger differences, which are not necessarily improvements, of the CPCSs compared with their forcing simulations, are found in the surface energy balance. This is caused by a general increase of GL in all CPCSs (on average 11.5 % in JJA and 3.5 % in DJF) which can be mainly attributed to an increase of areas with low integrated cloud liquid water content and/or a decrease of the cloud area fractions (in the case of CCLM). The RCMs react very differently on this additional energy input and partly large changes in the sensible or latent heat flux occur.
6 Conclusions
We found three types of added value in the 3 km grid spacing CPCSs, compared to their 10 km parent simulations: (1) improved summertime precipitation diurnal cycles; (2), better extreme precipitation intensities; and (3), a more accurate distribution of rain and improved (smaller and more peaked) precipitation objects. A fourth improvement, namely smaller biases in seasonally averaged two meter air temperature fields in summer, can hardly be attributed to the CPCSs, since it is also achievable by very simple altitude correction and without any high resolution dynamical simulation.
The improved fine scale structure of precipitation can have significant benefits for climate change impact studies which focus, for example, on mesoscale river catchments or flash flood prediction because the correct representation of the spatial extend, location and intensity of severe precipitation events is crucial for such applications.
Beside those improvements an increase of global radiation at the surface, which is likely caused by an increase of cloud free areas in the CPCSs, leads to partly large changes in the surface energy budged especially in June, July, and August.
There are two major limitations in this study. First, the small domain sizes in the 3 km simulations are likely to be responsible for the partly small differences between the CPCSs and their parent simulations and CPCSs on larger domains could reveal additional added value. Secondly, the rather short simulation periods of only 3 month do not allow drawing conclusions about improvements on longer time scales, which might be caused by better resolved land–atmosphere interaction processes.
Typically, differences between the CPCSs and their parent simulations are largest on small spatial and temporal scales and do often cancel out by averaging. Differences are typically larger in summer than in winter and in mountainous than in flat regions, because of the stronger dominance of small scale processes like deep convection.
Further current investigations analyze the validity of the results presented here for other regions and longer periods. Thereby, the more detailed investigation of atmospheric processes and surface energy budget of CPCSs will become more important to better understand error-sources and added value and to better support the improvement of convection permitting climate models. A more detailed analysis of scale-induced changes in global radiation is also a promising issue for further investigation. However, also due to the lack of comprehensive reference data with resolutions appropriate for the evaluation of CPCSs, the detection of errors and the further development of CPCSs will remain challenging.
References
Barry RG (2008) Mountain weather and climate, Third Edition. Cambridge University Press, Cambridge
Böhm U, Kücken M, Ahrens W, Block A, Hauffe D, Keuler K, Rockel B, Will A (2006) CLM—the climate version of LM: brief description and long-term applications. COSMO Newsl 6:225–235
Christensen JH, Christensen OB (2007) A summary of the PRUDENCE model projections of changes in European climate by the end of this century. Clim Change 81:7–30. doi:10.1007/s10584-006-9210-7
Déqué M, Rowell MP, Lüthi D, Giorgi F, Christensen JH, Rockel B, Jacob D, Kjellström E, de Castro M, van den Hurk B (2007) An intercomparison of regional climate simulations for Europe: assessing uncertainties in model projections. Clim Change 81:53–70
Dickenson RE, Errico RM, Giorgi F, Bates GT (1989) A regional climate model for western United States. Clim Change 15:383–422
Doms G, Förstner J (2004) Development of a kilometer-scale NWP-system: LMK. COSMO Newsl 4:159–167
Dudhia J (1989) Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J Atmos Sci 46:3077–3107
Dudhia J (1993) A nonhydrostatic version of the Penn state/NCAR mesoscale model: validation tests and simulation of an Atlantic cyclone and cold front. Mon Weather Rev 121:1493–1513
Finger D, Heinrich G, Gobiet A, Bauder A (2012) Projections of future water resources and their uncertainty in a glaciarized catchment in the Swiss Alps and the subsequent effects on hydropower production during the 21st century. Water Resour Res. doi:10.1029/2011WR010733
Gebhardt C, Theisa SE, Paulata M, Ben Bouallèguea Z (2011) Uncertainties in COSMO-DE precipitation forecasts introduced by model perturbations and variation of lateral boundaries. Atmos Res 100(2–3):168–177
Geleyn JF, Hollingsworth A (1979) An economical analytic method for the computing of the interaction between scattering and line absorption of radiation. Beitr Phys Arm 52:1–16
Georgievski G, Keuler K, Will A, Radtke K (2011) Evaluation of Central European and Eastern Alpine seasonal climate simulated with CCLM: double nesting vs. direct forcing techniques. COSMO Newsl 11:133–143
Giorgi F, Bates GT (1989) The climatological skill of a regional model over complex terrain. Mon Weather Rev 117:2325–2347
Gobiet A, Jacob D, EURO-CORDEX Community (2012) A new generation of regional climate simulations for Europe: the EURO-CORDEX initiative, Geophys Res, Abstracts Vol. 14, EGU2012-8211, 2012, EGU General Assembly 2012
Grell GA, Dudhia J, Stauffer DR (1995) A description of the fifth-generation Penn state/NCAR mesoscale model (MM5). NCAR/TN-398 + STR. Tech Rep http://www.mmm.ucar.edu/mm5/mm5-home.html
Grell GA, Schade L, Knoche R, Pfeiffer A, Egger J (2000) Nonhydrostatic climate simulations of precipitation over complex terrain. J Geophys Res 105(24):595–608
Haiden T, Kann A, Pistotnik G, Stadlbacher K, Wittmann C (2010) Integrated nowcasting through comprehensive analysis (INCA) system description. Central Institute for Meteorology and Geodynamics: Vienna, Austria, http://www.zamg.ac.at/fix/INCA_system.doc
Haiden T, Kann A, Wittmann C, Pistotnik G, Bica B, Gruber C (2011) The integrated nowcasting through comprehensive analysis (INCA) system and its validation over the Eastern Alpine region. Weather Forecast 26:166–183
Heinrich G, Gobiet A (2011) The future of dry and wet spells in Europe: A comprehensive study based on the ENSEMBLES regional climate models. Int J Climatol 32(13). doi:10.1002/joc.2421
Hohenegger C, Brockhaus P, Schär C (2008) Towards climate simulations at cloud-resolving scales. Meteorol Z 17(4):383–394
Kain JS (2003) The Kain-Fritsch convection parameterization: an update. J Appl Meteor 43:170–181
Kain JS, Fritsch JM (1993) Convective parameterization for mesoscale models: the Kain-Fritsch scheme. Meteorol Monogr 24:165–170
Kain JS, Weiss SJ, Levit JJ, Baldwin ME, Bright DR (2006) Examination of convection-allowing configurations of the WRF Model for the prediction of severe convective weather: the SPC/NSSL spring program. Weather Forecast 21(2):167–181
Kann A, Haiden T, von der Emde K, Gruber C, Kabas T, Leuprecht A, Kirchengast G (2011) Verification of operational analyses using an extremely high-density surface station network. Weather Forecast 26(4):572–578. doi:10.1175/WAF-D-11-00031.1
Klemp JB, Wilhelmson RB (1978) Simulations of three-dimensional convective storm dynamics. J Atmos Sci 35:1070–1096
Lacis AA, Hansen JE (1974) A parameterization for the absorption of solar radiation in the earth’s atmosphere. J Atmos Sci 31:118–133
Langhans W, Schmidli J, Schär C (2012) Bulk convergence of cloud-resolving simulations of moist convection over complex terrain. J Atmos Sci 69:2207–2228
Loibl W, Formayer H, Schöner W, Truhetz H, Anders I, Gobiet A, Heinrich G, Köstl M, Nadeem I, Peters-Anders J, Schicker I, Suklitsch M, Züger H (2011) Reclip: century 1 Research for climate protection: century climate simulations: models, data and ghg-scenarios, simulations, ACRP final report reclip: century part A, Vienna, 22 pp
Mass CF, Ovens D, Westrick K, Colle BA (2002) Does increasing horizontal resolution produce more skillful forecasts? Bull Amer Meteor Soc 83:407–430
Mearns LO, Gutowski WJ, Jones R, Leung L-Y, McGinnis S, Nunes AMB, Qian Y (2009) A regional climate change assessment program for North America. EOS 90(36):311–312
Prein AF, Gobiet A (2011) Defining and detecting added value in cloud resolving climate simulations. Wegener center report, 39, Wegener center verlag: Graz, Austria. ISBN:978-3-9502940-6-4
Randall DA, Wood RA, Bony S, Colman R, Fichefet T, Fyfe J, Kattsov J, Pitman A, Shukla J, Srinivasan J, Stouffer RJ, Sumi A, Taylor KE (2007) Cilmate models and their evaluation. In: Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Miller HL (eds) Climate change 2007: the physical science basis Contribution of working group I to the fourth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Ritter B, Geleyn JF (1992) A comprehensive radiation scheme for numerical weather prediction models with potential applications in climate simulations. Mon Weather Rev 120:303–325
Roberts NM, Lean HL (2008) Scale-selective verification of rainfall accumulations from high-resolution forecasts of convective events. Mon Weather Rev 136:78–97
Rockel B, Will A, Hense A (2008) Special issue on regional climate modelling with COSMO-CLM (CCLM). Meteorol Z 17(4):477–485
Rogers E, Black T, Ferrier B, Lin Y, Parrish D, Mego GD (2001) Changes to NCEP meso ETA analysis and forecast system: increase in resolution, new cloud microphysics, modified precipitation assimilation, modified 3DVAR analysis. NOAA, NWS technical procedures bulletin
Rummukainen M (2010) State-of-the-art with regional climate models. Wiley Interdiscip Rev Clim Change 1(1):82–96
Schwartz CS, Kain JS, Weiss JS, Xue M, Bright DR, Kong F, Thomas KW, Levit JJ, Coniglio MC (2009) Next-day convection-allowing WRF model guidance: a second look at 2-km versus 4-km grid spacing. Mon Weather Rev 137:3351–3372
Seneviratne SI, Lüthi D, Litschi M, Schär C (2006) Land-atmosphere coupling and climate change in Europe. Nature 443:205–209
Skamarock WC, Klemp JB, Dudhia J, Gill DO, Barker DM, Wang W, Powers JG (2005) A description of the advanced research WRF version 2. NCAR technical note 468, Mesoscale and Microscale Meteorology Division at NCAR, Boulder
Stephens GL (1978) Radiation profiles in extended water clouds part II: parameterization schemes. J Atmos Sci 35:2123–2131
Steppeler J, Doms G, Schättler U, Bitzer HW, Gassmann A, Damrath U, Gregoric G (2003) Meso-gamma scale forecasts using the nonhydrostatic model LM. Meteor Atmos Phys 82:75–96
Suklitsch M, Gobiet A, Leuprecht A, Frei C (2008) High resolution sensitivity studies with the regional climate model CCLM in the Alpine Region. Meteorol Z 17(4):467–476
Suklitsch M, Truhetz H, Prein AF, Gobiet A (2011) NHCM-1: Non-hydrostatic climate modelling. Part II: current state of selected cloud-resolving regional climate models and their error characteristics. Wegener Center Report, 40, Wegener Center Verlag: Graz, Austria. ISBN:978-3-9502940-7-1
Taylor KE (2001) Summarizing multiple aspects of model performance in a single diagram. J Geophys Res 106(D7):7183–7192
Tiedtke M (1989) A comprehensive mass flux scheme for cumulus parameterization in large scale models. Mon Weather Rev 117:1779–1800
van der Linden P, Mitchell JFB (2009) ENSEMBLES: climate change and its impacts: summary of research and results from the ENSEMBLES project. Met Office Hadley Centre, Exeter, 160 pp
Wang YQ, Leung LR, McGregor JL, Lee DK, Wang WC, Ding YH, Kimura F (2004) Regional climate modeling: progress, challenges, and prospects. J Meteor Soc Jpn 82(6):1599–1628
Weisman ML, Skamarock WC, Klemp JB (1997) The resolution dependence of explicitly modeled convective systems. Mon Weather Rev 125(4):527–548
Wernli H, Paulat M, Hagen M, Frei C (2008) SAL-A novel quality measure for the verification of quantitative precipitation forecasts. Mon Weather Rev 136(11):4470–4487
Weusthoff T, Ament F, Arpagaus M, Rotach MW (2010) Assessing the benefits of convection-permitting models by neighborhood verification: examples from MAP D-PHASE. Mon Weather Rev 138:3418–3433
Wiker LJ, Skamarock WC (2002) Time-splitting methods for elastic models using forward time schemes. Mon Weather Rev 130:2088–2097
Wilks DS (2005) Statistical methods in the atmospheric sciences, vol 91, 2nd edn. Academic, New YorK. ISBN 0127519661
Zepeda-Arce J, Foufoula-Georgiou E, Droegemeier KK (2000) Spacetime rainfall organization and its role in validating quantitative precipitation forecasts. J Geophys Res 105(D8):129–146
Acknowledgments
This work was funded by the Austrian Science Fund (FWF) under projects: Nonhydrostatic climate modeling (NHCM-1: ID P 19619-N10; NHCM-2: ID P24758-N29). The authors acknowledge the data providers at Central Institute for Meteorology and Geodynamics (ZAMG) for the Integrated Nowcasting through Comprehensive Analysis (INCA) dataset. This study heavily relied on computing resources. The authors are therefore grateful to the Jülich Supercomputing Centre (JSC), the German Climate Computing Center (DKRZ) in Hamburg, and the European Centre for Medium-Range Weather Forecasts (ECMWF) for providing these resources. ECMWF receives further thanks for providing operational Integrated Forecast System (IFS) analysis and short term forecasts which served as lateral boundary conditions (LBCs) for the simulations. CCLM simulations are funded by German Federal Ministry of Education and Research (BMBF). Additionally, the authors wish to acknowledge two anonymous reviewers for their detailed and helpful comments to the manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Prein, A.F., Gobiet, A., Suklitsch, M. et al. Added value of convection permitting seasonal simulations. Clim Dyn 41, 2655–2677 (2013). https://doi.org/10.1007/s00382-013-1744-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-013-1744-6