Abstract
Ensemble simulations with a coupled ocean-troposphere-stratosphere model for the pre-industrial era (1860 AD), late twentieth century (1990 AD) greenhouse gas (GHG) concentrations, the SRES scenarios B1, A1B, A2, as well as stabilization experiments up to the Twenty-third century with B1 and A1B scenario GHG concentrations at their values at 2100, have been analyzed with regard to the occurrence of major sudden stratospheric warmings (SSWs). An automated algorithm using 60°N and 10 hPa zonal wind and the temperature gradient between 60°N and the North Pole is used to identify this phenomenon in the large data set. With 1990 CO2 concentrations (352 ppmv), the frequency of simulated SSWs in February and March is comparable to observation, but they are underestimated during November to January. All simulations show an increase in the number of SSWs from the pre-industrial period to the end of the twenty-first century, indicating that the increase of GHG is also reflected in the number of sudden warmings. However, a high variability partially masks the underlying trend. Multi-century averages during the stabilization periods indicate that the increase of SSWs is linear to the applied radiative forcing. A doubling of SSWs occurs when the GHG concentration reaches the level of the A2 scenario at the end of the twenty-first century (836 ppmv). The increase in SSWs in the projections is caused by a combination of increased wave flux from the troposphere and weaker middle atmospheric zonal winds.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since the discovery of the first major sudden stratospheric warming (hereafter referred to as SSW) in 1952 (Scherhag 1952) the understanding of stratospheric dynamics and the coupling to tropospheric processes has continuously been improved. It is well established that the coupling of the stratosphere and troposphere is most intense during SSWs (e.g. Charlton and Polvani 2007). SSWs were shown to have large effects on the near surface weather and climate (Baldwin and Dunkerton 2001). However, it is not yet adequately explained to what extent SSWs are influenced by the increase of greenhouse gas concentrations (GHG). Model studies addressing this question show diverging results (e.g. SPARC CCMVal 2010). While one study shows a strong decrease of the number of SSWs under doubled CO2 concentration (Rind et al. 1998), some others show an increase in the occurrence frequency (e.g. Huebener et al. 2007; Charlton-Perez et al. 2008; McLandress and Shepherd 2009a; Bell et al. 2009). Further studies show no significant trend at all (e.g. Butchart et al. 2000; SPARC CCMVal 2010).
The increase in GHG concentrations and the associated changes in the vertically and latitudinally dependent temperature structure leads to a stronger wave forcing from the troposphere into the stratosphere (e.g. Butchart and Scaife 2001; Kodera et al. 2008; Bell et al. 2009). A possible explanation for the different results in the number of SSWs as a consequence of increasing GHG concentrations is the dependence of wave propagation and breaking on the background conditions in the upper troposphere and the stratosphere (Kodera et al. 2008; Sigmond and Scinocca 2010).
In addition, Schimanke et al. (2011) present an analysis of a long control simulation under pre-industrial conditions and emphasize that the number of SSWs in 30 year periods can vary between 1 and 14 SSWs when driving their model with a constant external forcing. Such internal variability has the capability to disguise or generate spurious trends when the analysis is restricted to a few decades. Observations reveal likewise variability with a dramatic reduction at the end of the last century (Gillett et al. 2002), and a reversal of the trend during the last decade (Cohen et al. 2009). Furthermore, a number of parameters deduced for the polar stratosphere reveal similar fluctuations. The trend of the lower stratospheric North Pole temperature depends on the month and period under consideration. Observations show that at 30 hPa a negative trend in December between 1957 and 1979 (−1.6 K/decade) is replaced by a positive trend of +2 K/decade for 1979–2001, resulting in a weak negative trend over the entire 1957–2001 period (Labitzke and Kunze 2005). Variations in the persistence of the Arctic polar vortex are identified by Langematz and Kunze (2006). Therefore, high variability is the main problem for deducing robust trends from observations (Labitzke and Kunze 2005) and model studies (Butchart et al. 2000; Charlton-Perez et al. 2008; Schimanke et al. 2011). In consequence of this variability large data sets need to be considered when analyzing long-term changes in the number of SSWs.
Two methods have been developed to detect SSWs by automated algorithms in recent years (Limpasuvan et al. 2004; Charlton and Polvani 2007). Whereas Limpasuvan et al. (2004) identify SSWs using time series of the leading principal component of the Northern Hemisphere daily zonal-mean zonal wind anomalies at 50 hPa, Charlton and Polvani (2007) use the zonal mean zonal wind at 10 hPa. The method by Charlton and Polvani (2007) is close to the WMO standard which defines SSWs by a reversal of the zonal mean of zonal wind at 60°N and the temperature gradient between 60°N and the North Pole at 10 hPa. For this reason, we use a slightly modified version of Charlton and Polvani (2007) for our analysis (hereafter referred to as new algorithm).
Our study aims at the analysis of future SSW trends under consideration of internal variability. Therefore, we analyze an ensemble of multi-century simulations performed with a coupled Atmosphere-Ocean-GCM (AO-GCM), including a detailed representation of the middle atmosphere. Compared to earlier modeling studies (Huebener et al. 2007) a large data set (more than 1,200 and 2,300 years for past and future conditions, respectively) is used comprising several scenario experiments and idealized simulations. The large data set enables us to get statistically robust results, overcoming uncertainty from internal variability, which may have hampered previous studies and contributed to the spread of the simulated trends that have been published.
In Sect. 2 the model and the experimental setup is described, followed by the introduction of the algorithm employed to identify SSWs. Section 3 presents SSW characteristics for two control climate simulations (pre-industrial and present day) and an ensemble of transient historical simulations. In Sect. 4 the response to GHG concentrations in different ensemble mode scenario experiments and idealized CO2-increase simulations with stabilization of concentrations thereafter is studied. In Sect. 5 the simulated changes relevant for the occurrence of SSWs are quantified on the basis of a proposed mechanisms. The results are summarized and discussed in Sect. 6.
2 Model, experiments and methods
2.1 The model
EGMAM (ECHO-G with Middle Atmosphere Model, Huebener et al. 2007) is a fully coupled AO-GCM. It is based on the AO-GCM ECHO-G (ECHAM4+HOPE-G, Legutke and Voss 1999). The atmospheric component is ECHAM4 with extension for the middle atmosphere (MA-ECHAM4). Here, the vertical domain is extended from 10 (∼30 km) to 0.01 hPa (∼80 km), now including the complete stratosphere and the lower part of the mesosphere (Manzini and McFarlane 1998). The number of levels is increased from 19 to 39 layers. A gravity wave parametrization and changes in the radiation code and horizontal diffusion following Manzini and McFarlane (1998) are implemented. The orographic gravity wave parametrization is based on the formulation of McFarlane (1987). Non orographic gravity waves are represented by parametrization of momentum flux deposition from a continuous spectrum of non stationary waves following Hines (1997a, b). Further details on implementation into MA-ECHAM4 can be found in Manzini et al (1997) and Manzini and McFarlane (1998).
The horizontal resolution of the atmospheric part (ECHAM4) is T30. The coupled ocean model (HOPE-G, Wolff et al. 1997) has a horizontal resolution of 2.8° with equator refinement and 21 vertical levels. A flux correction is used for heat and freshwater. The model includes a dynamic and thermodynamic sea-ice model (cf. Legutke and Voss 1999). A brief description of the model climatology can be found below. However, for more information on the model and its performance the reader is referred to Huebener et al. (2007); Körper et al. (2009); Spangehl et al. (2010).
The long-term mean zonal mean zonal wind structure in EGMAM is very close to ERA40 reanalysis for Northern Hemisphere winter season (Fig. 1). The stratospheric polar night jet is slightly too strong in EGMAM and a bit shifted poleward compared to ERA40. The stratospheric winter-to-winter variability of the northern stratospheric polar vortex is captured quite well by the EGMAM model and only somewhat overestimated at the stratopause level. It should be noted, that the improved vertical resolution of the EGMAM model is not sufficient to produce a quasi-biannual oscillation (QBO) (Giorgetta et al. 2006). The model wind in the tropical lower stratosphere is a permanent weak easterly corresponding to a continuous QBO easterly phase, resulting in the absence of stronger variability in the tropical stratosphere (Fig. 1). The tropospheric westerly winds north of 60°N are too weak by about 2 m/s in EGMAM whereas the subtropical jet is slightly overestimated.
Long term DJF winter mean (colours) and winter-to-winter standard deviation (contours) of zonal mean zonal wind (m/s) for (left) EGMAM present-day control simulation (300 model years) and (right) ERA40 data (time period 1979–2000). Contour interval for SD is 1 m/s for first interval and 2 m/s for other intervals
EGMAM simulates the observed temperature patterns in the middle atmosphere, e.g. the warm stratopause, realistically. However, there is a cold bias of approximately 6 K in the Arctic polar lower stratosphere (Huebener et al. 2007). Such cold bias is relatively large but not an outlier in the range of state-of-the-art models used for instance in the CCMVal2 ensemble (Butchart et al. 2011). Note that EGMAM shows a reasonable relationship between the meridional heat flux at the tropopause level (50 hPa) and the temperature of the stratospheric polar winter vortex (Huebener et al. 2007). Moreover, the model simulates the downward propagation of stratospheric vortex anomalies down to the troposphere similar to observations (not shown). As outlined by Huebener et al. (2007) EGMAM is very close to the tropospheric version of the model (ECHO-G) w.r.t. the simulation of the climate of the lower troposphere, but clearly outperforms the tropospheric model in the simulation of the climate of the upper troposphere and lower stratosphere (e.g. zonal mean zonal wind and temperature structure). Additionally, Spangehl et al. (2010) show that EGMAM is close to a completely different model in the simulation of the northern hemisphere near surface winter climate indicating that EGMAM is in the range of other models.
2.2 Experiments
Two control simulations are investigated for the comparison with the transient experiments: the first represents conditions which occured at the end of the twentieth century (hereafter referred to as 20C); the second, pre-industrial (PI) conditions (Table 1). The impact of GHG concentrations on the frequencies of SSWs is investigated with simulations forced by historical GHG concentrations for 1860–2000 (Huebener et al. 2007) and thereafter concentrations according to the special report on emissions scenarios (SRES) B1, A1B and A2 (Nakicenovic 2000). For each scenario as well as the historical period a 3-member initial conditions ensemble exists. Some experiments are continued with fixed GHG concentrations after 2100 (Table 1).
Furthermore, two additional simulations following the Coupled Model Intercomparison Project, Phase II protocol (Covey et al. 2003) with a 1 % per year increase of CO2 concentrations are taken into account: one simulation reaches a doubling of CO2 concentrations and the other reaches a quadrupling. Thereafter, both simulations are stabilized under constant CO2 concentrations for 300 years each (Table 1).
Information about observed SSW frequencies are derived from the 1958–2001 ECMWF reanalysis (hereafter referred to as ERA40, Uppala et al. 2005) and the Freie Universität Berlin stratospheric analysis (hereafter referred to as FUB-analysis, Table 2). A detailed verification of ERA40 and NCEP-NCAR reanalysis data for representing SSWs can be found in Charlton and Polvani (2007). They conclude that both data sets are very similar and useful for the identification of SSWs.
2.3 Identification of sudden stratospheric warmings
Owing to the quantity of data it is necessary to identify SSWs with an automated scheme. In recent years, two main approaches have been applied to identify SSWs with automated algorithms, one by Charlton and Polvani (2007) and the second by Limpasuvan et al. (2004). The present study uses a new algorithm on the basis of Charlton and Polvani (2007) which takes the reversal of the mean zonal wind at 60°N at 10 hPa as the main criterion. The main difference between the algorithm used here and the one proposed by Charlton and Polvani (2007) is the distinction between SSWs and final warmings. We use the modeled climatology of the daily annual cycle of the zonal wind to distinguish SSWs from final warmings. The circulation has to be restored to the climatology before the climatological zonal mean zonal wind becomes weaker than 5 m/s to distinguish the event from a final warming. In ERA40 the winter circulation is getting weaker than 5 m/s on 4 April and in PI on 14 April (Fig. 2a). The additional criterion improves the distinction of final warmings and prevents an overestimation of late SSWs (e.g. winter 1983/1984, see Table 2). The daily climatology of PI is used as the climatological threshold for all simulations. So, misinterpretations due to changes in the mean climate can be avoided and the number of SSWs remains comparable.
According to the WMO’s SSW-definition (cf. Labitzke and Naujokat 2000) we include also the reversal of the temperature gradient between 60°N and the North Pole at 10 hPa as a criterion. Note that the temperature gradient criterion is fulfilled even if the reversal of the gradient takes places up to three days in advance of the reversal of the mean zonal wind which supports the realistic identification of SSWs (Labitzke 1977; Krüger et al. 2005). The number of classified SSWs decreases slightly when the temperature gradient criterion is added as also noted by Charlton and Polvani (2007).
Once all criteria (easterly wind, temperature gradient, and not a final warming) are satisfied, the starting date of the SSW is set. For each SSW the duration is identified as the time between the starting date and the beginning of a 10-day phase with westerlies.
The influence of the additional criteria [(i) the restoration of zonal wind to the climatological threshold and (ii) the temperature gradient] on the number of classified SSWs is presented for PI. The algorithm including both criteria counts 113 SSWs. Ignoring the climatological threshold leads to a classification of 73 additional SSWs. Omitting the temperature gradient criterion leads to an increase of 2 SSWs. Without both criteria, the total number of SSWs is 188, with the biggest increase in February and March and no change in November and December (not shown). For ERA40 (1958–2001) the new objective method identifies 23 SSWs compared to 26 SSWs with the algorithm of Charlton and Polvani (2007). Five cases identified by Charlton and Polvani are treated as final warmings in our method because the climatological zonal wind is not re-established until 4 April (e.g. winter 1983/1984). On the other hand, there are two cases where the new algorithm counts two separate events which Charlton and Polvani (2007) count as one event, leading to the total difference of 3 SSWs. Note that a larger discrepancy is found in the analysis of model simulations if the algorithm of Charlton and Polvani (2007) and our new algorithm are compared. This can be attributed to an underestimation of SSWs during early and mid-winter and a realistic representation of SSWs during the late winter in the model used compared to ERA40 (cf. Sect. 3.1).
In general, the comparison of ERA40 data with FUB-analysis shows good agreement in the occurrences of SSWs with a small overestimation of SSWs at the beginning of ERA40 when the algorithm is applied (Table 2). Therefore, our comparison with the FUB-analysis confirms that ERA40 is useful for the identification of SSWs as reported by Charlton and Polvani (2007).
3 Control simulations, transient historical simulations and comparison with reanalysis data
3.1 Model climatology
3.1.1 Present day climate
The simulated mean annual cycle of parameters used to determine SSWs (Fig. 2) reveals the characteristic negative temperature gradient in winter and a reversed gradient in summer, corresponding to strong westerly winds in winter and easterly winds in summer. In April the winter circulation breaks down and the summer circulation is established. The simulated temperature gradient between the polar region and 60°N is stronger from the beginning of November until the end of the winter when compared to ERA40. This overestimation is related to the cold bias in the polar lower stratosphere (Huebener et al. 2007). Consequently, the wind speed at 60°N and 10 hPa is overestimated from November until the end of April. During northern winter the westerlies at 60°N at 10 hPa have a long term mean maximum of more than 44.8 m/s compared to 37.5 m/s in ERA40. This implies a stronger, less perturbed polar vortex with fewer warmings than observed. The relatively smooth annual cycle of the zonal mean zonal wind in the simulation is mainly due to the large sample size and only partly to a less perturbed polar vortex (cf. Fig. 2).
Our SSW detection algorithm counts 23 SSWs in 43 analyzed ERA40 winters (1958–2001, cf. Sect. 2.3), accordingly 5.3 SSWs per decade, compared to only half the number of SSWs in the present day control simulation of EGMAM (76 SSWs in 299 winters, 2.5 SSWs per decade, Table 3). However, to compare the performence of the model used with state-of-the-art models we applied the original algorithm of Charlton and Polvani (2007) which is commonly used. Using their algorithm gives a mean number of 3.6 SSWs/dec for 20C which is in the range of state-of-the-art models used for instance in the last CCMVal report (SPARC CCMVal 2010; Butchart et al. 2011).
The monthly distribution of SSWs from November through March is shown for EGMAM in Fig. 3. The mean number of SSWs peaks in ERA40 in January whereas the maximum number in the model is found for February. For February and March the model produces about the same number of SSWs as in ERA40 whereas a clear underestimation is found in December and January. Here, the model simulates 0.2 (0.5) SSWs/decade in 20C in December (January) compared to 0.9 (2.3) SSWs/decade in ERA40. In November only a single event is identified for ERA40 on 28 November 1968, while no November-SSW occurs in 20C.
The meridional heat flux at 100 hPa is commonly used as a proxy for the tropospheric wave flux entering the stratosphere (e.g. Bell et al. 2009). Figure 4 illustrates the climatological 100 hPa eddy heat flux of ERA40 and PI as zonal mean. Apart from an underestimation of the heat flux in the model, the latitudinal distribution and seasonal evolution is overall in agreement with ERA40. The area-averaged (40–80°N) difference for PI and ERA40 reveals the greatest discrepancy in November (−2.7 K m/s), falling to only −1.1 K m/s in March (Table 4). This underestimation of meridional eddy heat flux especially during early winter is related to the underestimation of SSWs in the model in November through January. Nevertheless, the heat flux-temperature relationship (Newman et al. 2001) of the model is in good agreement with observations (Huebener et al. 2007).
Typical features of SSWs are similar in ERA40 and the model, e.g. the spatial characteristics of SSWs (Langematz et al. to be submitted). Good agreement is also found in terms of the duration and the strength of SSWs (Table 5). The application of the new algorithm results in a mean duration of an SSW in ERA40 of 7.6 days, compared to 8.8 days in PI. As a measure of strength, the polar cap temperature deviation from the climatological temperature ±5 days around the starting date is used (Charlton and Polvani 2007; McLandress and Shepherd 2009a). The mean strength of an SSW is 11.8 K in ERA40 and 12.4 K in 20C (Table 5).
3.1.2 Pre-industrial climate
The PI long term mean number of SSWs (2.1 SSWs/dec or 113 SSWs in 548 winters) is somewhat lower than in 20C. Though the difference is not significant according to the Wilcoxon rank sum test (Table 3, Wilks 2006). It is associated with a somewhat stronger stratopause jet in PI. The shape of the monthly SSW distributions does not show significant differences between PI and 20C (Fig. 3). Small differences in the number of SSWs between PI and 20C occur in December, January and February, whereas the mean frequency is the same in March. In November a single event occurs in PI.
3.2 Variability of SSWs
Figure 5 shows the occurrence of SSWs in both control simulations. Despite the lower frequency, the model reveals some winters without and with SSWs, which is similar to the ERA40 and the FUB-analysis (Table 2). Longer periods without any classified SSWs are spread over PI and 20C. This is similar to ERA40 where in ten consecutive winters in the 1990’s no SSW is classified, and which has formerly been linked to increasing GHG concentrations (Gillett et al. 2002). On the other hand longer periods with an increased number of SSWs may be found in both simulations. In ERA40, in the 1960’s and 1970’s up to 9 SSWs/decade are found, and between 1998/1999 and 2008/2009 11 SSWs are recorded in the FUB-analysis (Table 2). In PI a maximum of 9 SSWs/dec is reached only once. On average the number of SSWs during decades with multiple SSWs is 6–7 in PI and 20C.
Besides periods with less SSWs, Fig. 5 indicates also that there are longer periods (spanning number of decades) with an accumulation of SSWs, e.g. close to model year 60 in PI or model year 150 and 250 in 20C. The longest period without any classified SSW lasts for 25 winters under PI- and 19 winters under 20C conditions. The variability in ERA40 and the results of 20C permit the assumption that periods longer than 10 years without any SSW could also occur in the real climate under current GHG concentrations.
In a different study we demonstrate that the number of SSWs fluctuate with a period of 52 years in PI (Schimanke et al. 2011). Furthermore, it is shown that this fluctuation is strongly correlated with ocean-atmosphere heat-fluxes in the North Atlantic during autumn and early winter. Statistical analysis shows evidence that a systematic clustering of SSWs occurs also in PI which differs from a distribution of independent random samples (not shown). But for a detailed analysis of low frequencies as done for PI (cf. Schimanke et al. 2011) the 20C time series is too short.
For the comparison of mean occurrence rates of SSWs we recommend comparing periods of at least 100 years or to use ensemble techniques. This is the case for both model validation and the identification of trends in transient simulations as it will avoid misinterpretation of results due to high internal variability.
3.3 Historical period
The number of SSWs in the historical period (1860–2000) is illustrated for all realizations as 20-year mean values (Fig. 6a, values are also shown in Fig. 6b, c). The period is dominated by high decadal to multi-decadal variability with 20-year mean values ranging from 0 to 4.5 SSWs/dec. Additionally, the 50-year running ensemble mean is shown in Fig. 6d) with the x-axis values assigned to the last year of the 50-year period averaged. Even this 50-year ensemble mean shows high variability. Still, its confidence interval always includes the mean value of PI (black dashed line).
Number of SSWs in transient simulations from the pre-industrial period until the end of the stabilization period for a B1, b A1B, and c A2. 20-year mean values for all members of all scenarios are shown as dots. Values of the same members are connected by dotted, dashed, and solid lines, respectively. Linear trends are indicated by dash-dotted lines for the period 1860–2100 and the stabilization phase. d Ensemble means of 50-year running means (SSWs/dec). Each mean value includes the 50 years prior to the respective calendar year, e.g. the value gathered from the figure for the year 2000 (∼1.3 SSWs/dec) reflects the mean between 1951 and 2000. The shaded area represents the 95 % confidence interval defined as ensemble mean \(\pm2\sigma/\sqrt{ensemble\ size}\). Discontinuity is owing to different numbers (displayed at the bottom) of realizations for different periods. The dashed black line displays the PI-mean (2.1 SSWs/dec) whereas colored lines show the scenario means over certain centuries
Over the whole historical period 1.6 SSWs/dec occur in the ensemble mean. This is less than in PI but the difference is not statistically significant (cf. Table 3). The values for the single members are 1.4, 1.5 and 2.0 SSWs/decade. This indicates once more the high variability for long periods. In comparison to 20C, which uses GHG concentrations similar to the values during the historical period, the number of SSWs is 40 % less (Table 3).
Finally, the time series of SSWs in the ensemble mean and all individual realizations do not reveal a significant trend in the twentieth century (Fig. 6a, dashed line). The ensemble mean and the single members are rather at a minimum stage of internal variability in the second half of the twentieth century. The ensemble mean from 1950 to 1999 is 1.4 SSWs/decade, with the mean values of the individual ensemble members being 1.0, 1.4 and 1.8.
4 Future climate
4.1 Scenario simulations
The model simulates global-mean near surface temperature changes from the end of the twentieth century to the end of the twenty-first century of 3.2, 2.1 and 1.5 K for the scenario simulations A2, A1B and B1, respectively (Huebener et al. 2007, their Fig. 1). The largest GHG induced near surface warming appears in high northern latitudes and is more pronounced over continental areas than over ocean areas which is in line with the results of the IPCC report (IPCC 2007). As a consequence of sea-ice feedbacks the strongest surface warming occurs in the Arctic. In terms of zonal mean temperature change, the largest tropospheric warming occurs in the tropics near the tropopause level and in the Arctic near surface (cf. Sect. 5). While the troposphere generally warms, most parts of the stratosphere cool significantly owing to enhanced radiative long-wave emission by increased GHG concentrations. With respect to the difference of the stabilization period of A1B and PI the maximum cooling amounts to more than 16 K in the mesosphere at 0.3 hPa. A detailed discussion of how these changes influence the frequency of SSWs follows in Sect. 5.
4.1.1 The transient phase
SSW-frequencies from 1860 to 2300 for all scenarios are shown in Fig. 6. The number of SSWs rises in all scenarios until 2100. While it is demanding to see it in the 20-year means due to the high variability it is clearly indicated by the linear trends (dashed lines, Fig. 6a–c). The 50-year running means depict these trends as well for the twenty-first century (Fig. 6d). During the second half of the twenty-first century the confidence intervals rises above the PI mean (black dashed horizontal line in Fig. 6d) for the three scenario experiments. This indicates that changes up to the end of the twenty-first century are statistically significant at the 95 %-significance level at least for the B1 and A2 simulation. The trends are superimposed by internal variability in all scenarios. For instance, the rise in the A1B scenario is strongest in the middle of the twenty-first century with a subsequent decrease in the number of SSWs. For this reason the difference with PI is not significant at the end of the twenty-first century. On the other hand, the increase of SSWs in the A2 scenario is suppressed in the first half of the twenty-first century followed by a strong increase afterwards. However, this does not describe the behavior of all single members (Fig. 6a–c). In A2 only one member has a deep minimum between 2,040 and 2,060 affecting the ensemble mean. In A1B two members have medium values while the third member clearly reduces the ensemble mean value at the end of the twenty-first century. In general, the variability of the 20-year means is very large and emphasizes the need of long term means.
The long term mean frequencies for the twenty-first century are given in Table 3. The centennial mean values are significantly higher than the PI-mean for A1B and A2 according to the Wilcoxon rank sum test. Huebener et al. (2007) analyzed a doubling of SSWs occurrences (detected with a subjective method) when comparing the 1961–2000 and 2061–2100 means for A2. This seems to overestimate the response of the model to GHG forcing as the comparable low SSW numbers at the end of the twenty-first century might partly occur by chance in the ensemble runs. However, in general our results confirm the increase in the number of SSWs due to higher GHG concentrations.
4.1.2 The stabilization period
There is no further increase of the SSW occurrence rates within the stabilization period (2100–2300) in general. Only small trends are found for B1 and A1B which are of opposite sign (Fig. 6a, b). The 50-year running means fluctuate around higher mean values compared to PI (Fig. 6d). The ensemble mean of B1 ends at the end of twenty-second century on a lower level compared to the end of the twenty-first century. However, the change within B1 is not significant. On the other hand, the number of SSWs in the A1B scenario rises throughout the twenty-second century to a maximum of 4.8 SSWs/dec in the ensemble mean. This value is far from what is achieved in the single PI run over 550 years over a 50 year period where the maximum is 3.6 SSWs/dec. The maximum is outnumbered by single members of all scenarios. This is a further indication for a GHG induced shift towards an increase of SSWs.
In the twenty-third century the single A1B realization continues to develop SSWs with a high frequency (in the mean 3.6 SSWs/dec). The drop at the end of the twenty-third century as well as the descent in B1 during the twenty-second century may be attributed to the high internal variability. It is even more obvious in Fig. 6a–c) where the 20-year mean values depict the variability much clearer.
In Sect. 5 a working mechanism is presented to explain the mean increase of the SSW occurrence rates under increasing GHG concentrations using the stabilization period of all A1B members (altogether 400 years) as a reliable data basis.
4.2 Idealized experiments
The analysis of the idealized experiments reveal an increase in the number of SSWs and support the results based on the scenario simulations (Fig. 7). The mean number of SSWs is 2.6 SSWs/dec after the doubling of CO2 concentrations (Table 1). This is similar to the B1 runs in which the radiative forcing is comparable as well. However, the higher mean numbers of SSWs are not significantly different from the PI run. Moreover, values higher than in PI or 20C are reached only towards the end of the stabilization period (Fig. 7). On the other hand, SSWs occur with a significantly higher frequency (3.6 SSWs/dec) under quadrupled CO2 contents. Besides, the variability depicted by the 20-year means is very high. In some 20 year periods occur only 2–4 SSWs whereas other periods are marked with up to 12 SSWs.
Number of SSWs/dec for the idealized experiments 2XCO2 (blue) and 4XCO2 (red) as 20 year means. Results are illustrated for the CO2 increase period (70 years) followed by the stabilization phase (300 years). Starting point for 2XCO2 is year 157 of PI. 4XCO2 simulation starts from 2XCO2 after doubling of CO2 concentrations (model year 227). Dashed lines represent mean values of the corresponding simulation. The shaded area represents the uncertainty in the mean of the 20 year PI values
4.3 Future SSW characteristics
The increase in the number of SSWs takes place in all months with the largest change in absolute values in January (not shown). Changes in percentage distributions over winter months are illustrated in Fig. 8 indicating a shift towards more SSWs during early winter. Changes from January to March are in the range of the PI confidence intervals whereas the increase in November for A1B and December (both A1B and 4XCO2) lies outside the confidence interval indicating significant changes for these months. The stronger increase of early SSWs is reflected by larger changes of the meridional heat flux in early winter. While the heat flux strengthens by 23 % in November and December it increases by only 8 % (10 %) in February (March). Nevertheless, the mean frequencies in November and December are still below the ERA40 mean. The increase in the number of SSWs is accompanied by a slight decrease in the polar cap temperature anomaly (Table 5). On the other hand, there seems to be only little influence on the mean duration of SSWs. If any change takes place it is a slight increase in the duration of SSWs (Table 5). That is the case for the scenario and idealized simulations.
4.4 Multi-century mean values
The number of SSWs in relation to the radiative forcing is illustrated in Fig. 9. Here, only the long term mean values over the stabilization periods are considered (Table 3). All values reflect means over at least 300 years with the exception of B1 (200 years) and A2 (63 years). Therefore, the values can be regarded as very robust.
Besides the already discussed variability for decadal mean values the simulations reveal a clear linear relationship between the number of SSWs and the radiative forcing for the multi-century means. A mean number of 2 SSWs/dec can be expected for GHG concentrations as during the pre-industrial period. A doubling (4 SSWs/dec) is reached when the radiative forcing is 8 W/m2 higher than in PI. This is in the range of the radiative forcing in A2 and 4XCO2. Therefore, the slope of the regression reflects one additional SSW/dec for every 4 W/m2 increase of radiative forcing in the model.
5 Mechanism for increase of SSWs due to increasing GHG
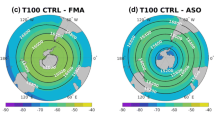
Many studies have recently investigated how the northern polar stratosphere is affected by increasing GHG concentrations during winter (e.g. Langematz and Kunze 2006; Butchart et al. 2006; Kodera et al. 2008; McLandress and Shepherd 2009b). Here, we will develop a possible mechanism for the increase of SSWs utilizing the long ensemble simulations. We use the stabilization periods of A1B (400 years in total) and PI (550 years) to highlight the impact of increasing GHG concentrations. Differences during winter months (DJF) of the scenario and the control simulation are shown in Fig. 10 and are schematically displayed in Fig. 11.
Differences of the stabilization period of A1B (400 years) and the PI control simulation (550 years) for DJF representing the zonal means of a temperature (K), b zonal wind (m/s), and c EP-flux divergence (m/s/day) (shaded) and EP-flux (arrows). For temperature and wind anomalies colored areas indicate that the differences are significant at the 95 %-significance level using a Student’s t test
Schematic mechanism showing how the number of SSWs increase due to increasing GHG concentrations (see Sect. 5 for more details). The schema illustrates the situation during Northern winter and is based on the differences between the A1B-stabilization period (400 years) and PI (550 years) shown in Fig. 10. The numbers reflect differences of the same simulations and are given for: BDC (res. stream function) 40°S–50°N at 1 hPa (kg/s), EP-flux divergence 45°N-75°N and 1–0.1 hPa (m/s/day), eddy heat flux 40°N–80°N at 100 hPa (K m/s), and temperature 30°S–30°N, 250–100 hPa and 80°N–90°N, 100–30 hPa (K)
In our simulations, upper tropical tropospheric temperatures rise by more than 5 K, whereas temperatures in the mid-latitudes stay nearly unchanged at the same altitude (Fig. 10a). According to the thermal wind relation the increase in the meridional temperature gradient is related to a strengthening of the zonal mean zonal wind by more than 6 m/s at 30°N and 100 hPa (Figs. 10b, 11). These changes are within the range of other model studies. Sigmond et al. (2004) get a strengthening of the meridional temperature gradient by 8 K and stronger westerlies of 9 m/s under doubled CO2 concentrations whereas Bell et al. (2009) find only an increase of 2.5 m/s. The altered winds modify the conditions for the propagation of atmospheric Rossby waves from the troposphere into the stratosphere. This results in an increase of upward directed EP-flux in the mid-latitudes above the tropopause (Fig. 10c). In terms of the linear proportional meridional heat-flux the increase between 40–80°N at 100 hPa amounts to approximately 1.8 K m/s or 16 % (Fig. 11). Whereas some studies agree that the vertical component of the EP-flux entering the stratosphere enhances under increasing GHG concentrations (Bell et al. 2009) others do not find a significant trend (SPARC CCMVal 2010).
In the stratopause region the planetary waves are refracted poleward owing to changed conditions for wave propagation (Figs. 10, 11). The increase of the EP-flux convergence (∼14 %, Fig. 11) weakens the westerlies in the middle atmosphere (Fig. 10b) and drives the increase of the residual stream function (∼5 % at 1 hPa, Fig. 11). Hence, the consensus—at least for model simulations—that the residual stream function (also known as Brewer-Dobson circulation, BDC) accelerates with increasing GHG concentrations (e.g. Rind et al. 1998; Butchart et al. 2006; Baldwin et al. 2007; SPARC CCMVal 2010) is confirmed in this study. Moreover, as postulated by Butchart and Scaife (2001) and Butchart et al. (2006), the increase in resolved waves is the primary source for the strengthening of the BDC in a changing climate.
As a consequence of a stronger BDC the lower Arctic stratosphere is warming due to adiabatic heating. The difference of A1B and PI reveals that the dynamical effects counteract the radiative cooling in the polar lower stratosphere and turn it into a net warming of 1 K (Fig. 10a). SPARC CCMVal (2010) does not show temperature trends whereas other studies based on individual models show a slight warming (Sigmond et al. 2004), or even a strong warming up to +7.5 K (Bell et al. 2009, January difference under quadrupled CO2 concentrations). The zonal mean zonal wind at 10 hPa and 60°N is reduced by 5 m/s (Fig. 10b). An even stronger signal is found in the stratopause region with a reduction by more than 12 m/s which is in agreement with the positive EP-flux convergence (Figs. 10b, c, 11). Together with the strengthening of westerlies at 30°N throughout the stratosphere, the signal corresponds to a southward shift of the polar night jet, which is in line with multi-model results reported by Scaife et al. (2012). The decrease at 60°N and 10 hPa is consistent with other studies as for example McLandress and Shepherd (2009a) (−8 m/s) or Bell et al. (2009) (−5 m/s when CO2 concentrations are doubled and −20 m/s after quadrupling) whereas Charlton-Perez et al. (2008) find only a small reduction.
It should be noted that the obtained differences shown in Fig. 10 are not a consequence of the increase in SSWs. In contrast, the pattern is fairly preserved when the analysis is restricted to years without SSWs (not shown).
Finally, the increase in the number of SSWs is caused by two factors as discussed also by McLandress and Shepherd (2009a): First, the increased planetary wave activity emanating from the troposphere (+16 %). Here, the stronger increase in early winter may be responsible for the shift in the seasonal distribution of SSWs (cf. Charlton-Perez et al. 2008). Second, the reduced zonal mean zonal wind at 60°N and 10 hPa. This makes it easier for tropospheric disturbances to turn the wind to easterlies. Altogether, a combination of increased wave activity and reduced climatological zonal wind causes the increase of SSW frequency in our model.
6 Conclusions and discussion
An objective method for identifying SSWs is developed on the basis of the algorithm by Charlton and Polvani (2007). The new algorithm shows improved results due to the inclusion of the temperature gradient and the climatological threshold criterion. Specifically, the latter helps to distinguish SSWs from final warmings. The new algorithm is used to analyze a set of experiments run with a coupled ocean-troposphere-stratosphere GCM, including control simulations and transient simulations with a prescribed increase in GHG concentrations and a stabilization thereafter. The large data set used in this study provides statistically robust results.
The mean number of SSWs in the control simulations is approximately half of the observed value. However, when using the original algorithm of Charlton and Polvani (2007) the modeled SSW frequency is in the range of state-of-the-art models (SPARC CCMVal 2010; Butchart et al. 2011). Moreover, we show for both control simulations a considerable multi-decadal variability and the number of SSWs is close to the observed mean during periods with an anomalously high number of SSWs (cf. Schimanke et al. 2011). In general, SSWs are mainly lacking in early winter whereas the number of SSWs in February and March is similar to ERA40.
The increase of GHG concentrations leads to a significant increase in the number of SSWs for all SRES emissions scenarios and idealized experiments. This result has a high confidence level owing to the use of the large data set based on ensemble simulations and the inclusion of the stabilization periods. The multi century means indicate that a linear relationship exists between the radiative forcing and the number of SSWs. Here, the number of SSWs per decade increases by one for a radiative forcing of 4W/m2. Consequently, the number of SSWs double for the A2 scenario and under quadrupled CO2 concentrations. In contrast, Bell et al. (2009) conclude from their idealized experiments that the response in the number is highly non-linear. However, their results are based on rather short 30-year long experiments which can be highly influenced by multi-decadal variability (Schimanke et al. 2011). Moreover, different results can be achieved by methods that do not apply fixed thresholds such as indices based on the Northern Annular Mode (NAM) (McLandress and Shepherd 2009a). They do not indicate a trend at all. However, we retain the absolute SSW criterion as the appropriate parameter to assess future SSW frequency modulation as it is the absolute zonal wind speed which determines the propagation of tropospheric planetary waves into the stratosphere (Bell et al. 2009). Finally, it is hard to project when the increase might be noticed in the real world owing to the high variability.
The rise in the number of SSWs occurs mainly in the period of increasing GHG concentrations for both the scenario and idealized experiments. Subsequently, no further increase is identified during the stabilization period. However, the long term variability is clearly existing for instance in the A1B scenario which is stabilized until 2300 (see solid line in Fig. 6b). High and low values alternate more or less regularly between the single 20-year averaging periods over the entire stabilization period. A similar feature can be seen for 4XCO2. Even though a frequency analysis is not considered for the rather short stabilization periods these results agree with earlier studies where a multi-decadal variability of 52 years is identified (Schimanke et al. 2011).
The strength of SSWs is moderately reduced with increasing GHG concentrations in comparison with PI throughout the scenarios and the idealized experiments. The weakening varies between 2 % for B1 and 18 % for 4XCO2. This confirms the trend given by McLandress and Shepherd (2009a) but underestimates the reduction of 25 % they estimate for the 2050–2099 period. In addition, the monthly distribution is slightly shifted to more early SSWs in the model whereas other studies even show a more pronounced increase in February and March (Charlton-Perez et al. 2008).
The increased number of SSWs is caused by a combination of simulated climatological changes namely the enhanced wave forcing from the troposphere and the lowered zonal wind speed in the stratosphere where the SSWs are defined (Fig. 11). This pattern is quite consistent over several model studies (e.g. Bell et al. 2009; McLandress and Shepherd 2009a). Moreover, similar effects as pointed out in the schematic figure (Fig. 11) can be found in observations due to increasing GHG concentrations for years of low solar activity (Kodera et al. 2008). Here, Kodera et al. (2008) find a weaker stratopause jet which is sensitive to increased wave activity resulting in a stronger BDC and more adiabatic warming in polar regions. However, in contrast to most model studies observations do not show an overall strengthening of the BDC. Engel et al. (2009) find no increase in the age of air above 24 km.
Finally, some remaining uncertainties and open questions should be addressed for future work. Changes in the stratospheric ozone layer are not included in the simulations. Thus some uncertainty with respect to ozone chemistry feedbacks on the number of SSWs remains. Moreover, in our experiments no QBO is generated and easterly winds prevail in the lower tropical stratosphere. Solar variability is not considered as well though Kodera et al. (2008) reveal evidence that it may modulate the stratospheric response to increasing GHG concentrations. Nevertheless, in this study, the potential role of changes in GHG concentrations is clearly demonstrated independently of other forcings.
References
Baldwin MP, Dunkerton TJ (2001) Stratospheric harbingers of anomalous weather regimes. Science 294:581–584
Baldwin MP, Dameris M, Shepherd TG (2007) How will the stratphere affect climate change. Science 316:1576–1577
Bell CJ, Gray LJ, Kettleborough J (2009) Changes in northern hemisphere stratospheric variability under increased co2 concentrations. Q J R Meteorol Soc 00:1–12 doi:10.1002/qj
Butchart N, Scaife AA (2001) Removal of chlorofluorocarbons by increases mass exchange between the stratosphere and troposphere in a changing climate. Nature 410:799–802
Butchart N, Austin J, Knight JR, Scaife AA, Gallani ML (2000) The response of the stratospheric climate to projected changes in the concentrations of well-mixed greenhouse gases from 1992 to 2051. Journal of Climate 13:2142–2159
Butchart N, Scaife AA, Bourqui M, de Grandpre J, Hare SHE, Kettleborough J, Langematz U, Manzini E, Sassi F, Shibata K, Shindell D, Sigmond M (2006) Simulations of anthropogenic change in the strength of the brewer dobson circulation. Clim Dyn 27:727–741
Butchart N, Charlton-Perez AJ, Cionni I, Hardiman SC, Haynes PH, Krüger K, Kushner PJ, Newman PA, Osprey SM, Perlwitz J, Sigmond M, Wang L, Akiyoshi H, Austin J, Bekki S, Baumgaertner A, Braesicke P, Brühl C, Chipperfield M, Dameris M, Dhomse S, Eyring V, Garcia R, Garny H, Jöckel P, Lamarque JF, Marchand M, Michou M, Morgenstern O, Nakamura T, Pawson S, Plummer D, Pyle J, Rozanov E, Scinocca J, Shepherd TG, Shibata K, Smale D, Teyssèdre H, Tian W, Waugh D, Yamashita Y (2011) Multimodel climate and variability of the stratosphere. J Geophys Res 116(D5):D05,102. doi:10.1029/2010JD014995
Charlton AJ, Polvani LM (2007) A new look at stratosphric sudden warmings. Part I: climatology and modeling benchmarks. J Clim 20:449–469
Charlton-Perez AJ, Polvani L, Austin J, Li F (2008) The frequency and dynamics of stratospheric sudden warmings in the 21st century. J Geophys Res 113:D16,116
Cohen J, Barlow M, Saito K (2009) Decadal fluctuations in planetary wave forcing modulate global waming in late bareal winter. J Clim 22:4418–4426. doi:10.1175/2009JCLI2931.1
Covey C, AchutaRao KM, Cubasch U, Jones P, Lambert SJ, Mann ME, Phillips TJ, Taylor KE (2003) An overview of results from the coupled model intercomparison project. Global Planet Change 37:103–133
Engel A, Möbius T, Bönisch H, Schmidt U, Heinz R, Lewin I, Atlas E, Aoki S, Nakazawa T, Sugawara S, Moore F, Hurst D, Elkins J, Schauffler S, Andrews A, Boering K (2009) Age of stratospheric air unchaged within uncertainties over the past 30 years. Nat Geosci 2:28–31. doi:10.1038/NGEO388
Gillett NP, Allen MR, McDonald RE, Senior CA, Shindell DT, Schmidt GA (2002) How linear is the arctic oscillation response to greenhouse gases? J Geophys Res 107:D3
Giorgetta M, Manzini E, Roeckner E, Esch M, Bengtsson L (2006) Climatology and forcing of the quasi-biennial oscillation in the maecham5 model. J Clim 19:3882–3901. doi:10.1175/JCLI3830.1
Hines CO (1997a) Doppler spread parameterization of gravity wave momentum deposition in the middle atmosphere, 1, basic formulation. J Atmos Solar Terr Phys 59:371–386
Hines CO (1997b) Doppler spread parameterization of gravity wave momentum deposition in the middle atmosphere, 2, broad and quasi monochromatic spectra and implementation. J Atmos Solar Terr Phys 59:387–400
Huebener H, Cubasch U, Langematz U, Spangehl T, Niehörster F, Fast I, Kunze M (2007) Ensemble climate simulations using a fully coupled ocean-troposphere-stratosphere general circulattion model. Philos Trans R Soc A 365:2089–2101
IPCC (2007) Climate change. In: Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Miller HL (eds) The physical science basis. Contribution of working group I to the fourth assessment report of the intergovernmental panel on climate change
Kodera K, Hori ME, Yukimoto S, Sigmond M (2008) Solar modulation of the northern hemisphere winter trends and its implications with increasing co2. GRL 35:L03,704
Körper J, Spangehl T, Cubasch U, Huebener H (2009) Decomposition of projected regional sea level rise in the North Atlantic and its relation to the amoc. Geophys Res Lett 36:L19,714. doi:10.1029/2009GL039757
Krüger K, Naujokat B, Labitzke K (2005) The unusual midwinter warming in the southern hemisphere stratosphere 2002: a comparison to northern hemisphere phenomena. J Atmos Sci 62(3):603–613. doi:10.1175/JAS-3316.1
Labitzke K (1977) Interannual variability of the winter stratosphere in the northern hemisphere. Mon Weather Rev Geophys 105:762–770
Labitzke K, Kunze M (2005) Stratospheric temperatures over the Arctic: comparison of three data sets. Meteorol Z 14(1):65–74
Labitzke K, Naujokat B (2000) The lower arctic stratosphere in winter since 1952. SPARC Newsletter 15:11–14
Langematz U, Kunze M (2006) An update on dynamical changes in the arctic and antarctic stratosphere polar vortices. Clim Dyn 27:647–660
Legutke S, Voss R (1999) The Hamburg atmosphere-ocean coupled circulation model echo-g. DKRZ-Report (18)
Limpasuvan V, Thompson DWJ, Hartmann DL (2004) The life cycle of the northern hemisphere sudden stratospheric warmings. J Clim 17:2584–2596
Manzini E, McFarlane N (1998) The effect of varying the source spectrum of a gravity wave parameterization in a middle atmosphere general circulation model. J Geophys Res 103:31523–31539
Manzini E, McFarlane NA, McLandress C (1997) Impact of the doppler spread parameterization on the simulation of the middle atmosphere circulation using the ma echam4 general circulation model. J Geophys Res 102:25751–25762
McFarlane NA (1987) The effect of orographically exited gravity wave drag on the general circulation of the lower stratosphere and troposphere. J Atmos Sci 44:1775–1800
McLandress C, Shepherd T (2009a) Impact of climate change on stratospheric sudden warmings as simulated by the Canadian middle atmosphere model. J Clim 22:5449–5463. doi:10.1175/2009JCLI3069.1
McLandress C, Shepherd TG (2009b) Simulated anthropogenic changes in the brewer-dobson circulation, including its extension to high latitudes. J Clim 22:1516–1540
Nakicenovic N (2000) Special report on emissions scenarios. Cambridge University Press, Cambridge
Newman PA, Nash ER, Rosenfield JE (2001) What controls temperature of the Arctic stratosphere during spring? J Geophys Res 106:19999–20010
Rind D, Shindell D, Lonergan P, Balachandran NK (1998) Climate change and the middle atmosphere. Part III: the doubled CO2 climate revisited. J Clim 11:876–894
Scaife A, Spangehl T, Fereday D, Cubasch U, Langematz U, Akiyoshi H, Bekki S, Braesicke P, Butchart N, Chipperfield M, Gettelman A, Hardiman S, Michou M, Rozanov E, Shepherd T (2012) Climate change projections and stratosphere-troposphere interaction. Clim Dyn 38:2089–2097. doi:10.1007/s00382-011-1080-7
Scherhag R (1952) Die explosionsartige Stratosphärenerwärmung des Spätwinters 1951/1952. Deutscher Wetterdienst (US Zone) 6:51–63
Schimanke S, Körper J, Spangehl T, Cubasch U (2011) Multi-decadal variability of sudden stratospheric warmings in an aogcm. Geophys Res Lett 38:L01,801. doi:10.1029/2010GL045756
Sigmond M, Scinocca JF (2010) The influence of basic state on the northern hemisphere circulation response to climate change. J Clim 23(6):1434–1446. doi:10.1175/2009JCLI3167.1
Sigmond M, Siegmund P, Manzini E, Kelder H (2004) A simulation of the separate climate effects of middle-atmospheric and tropospheric co2 doubling. J Clim 17:2352–2367
Spangehl T, Cubasch U, Raible CC, Schimanke S, Körper J, Hofer D (2010) Transient climate simulations from the Maunder Minimum to present day: Role of the stratosphere. JGR 115(D00I10):1–18. doi:10.1029/2009JD012358
SPARC CCMVal (2010) SPARC report on the evaluation of chemistry-climate models. SPARC report no. 5, WCRP-132, WMO/TD-No. 1526. URL: http://www.atmosp.physics.utoronto.ca/SPARC
Uppala SM, Kallberg PW, Simmons AJ, Andrae U, Bechtold VDC, Fiorino M, Gibson JK, Haseler J, Kelly AHGA, Li X, Onogi K, Saarinen S, Sokka N, Allan RP, Andersson E, Arpe K, Balmaseda MA, Beljaars ACM, Berg LVD, Bidlot J, Bormann N, Caires S, Chevallier F, Dethof A, Dragosavac M, Fisher M, Fuentes M, Hagemann S, Holm E, Hoskins BJ, Isaksen L, Janssen PAEM, Jenne R, Mcnally AP, Mahfouf JF, Morcrette JJ, Rayner NA, Saunders RW, Simon P, Sterl A, Trenberth KE, Untch A, Vasiljevic D, Viterbo P, Woollen J (2005) The ERA-40 re-analysis. Q J R Meteorol Soc 131:2961–3012. doi:10.1256/qj.04.176
Wilks DS (2006) Statistical methods in the atmospheric sciences. Academic Press, New York
Wolff J, Maier-Reimer E, Legutke S (1997) The hamburg ocean primitive equation model. DKRZ-Report Nr. 13:110
Acknowledgments
Parts of this work were funded by the EU project ENSEMBLES (contract no GOCE-CT-2003-505539) and by the DFG project ProSECCO/CAWSES (contract no LA 1025/5-1). The authors thank the Deutsches Klimarechenzentrum (DKRZ) for providing computing time and Irina Fast and Falk Niehörster for running the experiments.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Schimanke, S., Spangehl, T., Huebener, H. et al. Variability and trends of major stratospheric warmings in simulations under constant and increasing GHG concentrations. Clim Dyn 40, 1733–1747 (2013). https://doi.org/10.1007/s00382-012-1530-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-012-1530-x