Abstract
The West African monsoon has over the years proven difficult to represent in global coupled models. The current operational seasonal forecasting system of the UK Met Office (GloSea4) has a good representation of monsoon rainfall over West Africa. It reproduces the various stages of the monsoon: a coastal phase in May and June, followed by onset of the Sahelian phase in July when rainfall maxima shift northward of 10N until September; and a secondary coastal rainfall maximum in October. We explore the dynamics of monsoon onset in GloSea4 and compare it to reanalyses. An important difference is the change in the Saharan heat low around the time of Sahelian onset. In Glosea4 the deepening heat low introduces moisture convergence across an east-west Sahelian band, whereas in the reanalyses such an east-west organisation of moisture does not occur and moisture is transported northwards to the Sahara. Lack of observations in the southern Sahara makes it difficult to verify this process in GloSea4 and also suggests that reanalyses may not be strongly constrained by station observations in an area key to Sahelian onset. Timing of monsoon onset has socio-economic importance for many countries in West Africa and we explore onset predictability in GloSea4. We use tercile categories to calculate probabilities for onset occurring before, near and after average in four different onset indicators. Glosea4 has modest skill at 2–3 months’ lead time, with ROC scores of 0.6–0.8. Similar skill is seen in hindcasts with models from the ENSEMBLES project, even in models with large rainfall biases over the Sahel. Forecast skill derives from tropical SST in June and many models capture at least the influence of the tropical Atlantic. This suggests that long-range skill for onset could be present in other seasonal forecasting systems in spite of mean rainfall biases.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For the largely rain fed agriculture of West Africa long-range forecasts of season-total rainfall are potentially useful, e.g. to decide on the type of crops to plant. Sivakumar and Hansen (2007) give examples of applications of long-range forecasts in agriculture and also describe practical problems with this. Apart from season-total rainfall the temporal distribution of rain throughout the rainy season is also very important. For example, the start of the rainy season is important for determining the optimal planting time, by assuring continuous water availability at the stage of germination or early growth (Sultan et al. 2005; Marteau et al. 2011). WMO Global Producing Centres for Long Range Forecasts routinely issue operational long-range forecasts for rainy-season totals (Graham et al. 2011). However, long-range forecasts for timing of the onset are not currently produced despite a clear demand for this information in many parts of Africa (Ingram et al. 2002; Graham 2011). Here we will investigate whether the current generation of dynamical seasonal forecast models can provide skilful forecasts for timing of the monsoon onset over West Africa. Such long-range information, together with short range forecasts, should assist agricultural planning and decision-making across a range of time windows.
Monsoon onset in the Sahel region of West Africa is characterised by an apparent rapid northward shift in rainfall maxima in early July from the Gulf of Guinea coast to the Sahel/Sudan (see Fig. 1). This is accompanied by changes in the African Easterly Jet (AEJ) and the tropical-equatorial jet (TEJ) (e.g. Sultan and Janicot 2003). The average date for the onset, as derived from GPCP rainfall estimates between 1979 and 2009 (Xie et al. 2003) is 29 June, with a standard deviation of 8 days (see Sect. 3.1). Various studies have examined the processes controlling monsoon onset. From these studies there is a consensus that the seasonal northward migration of the monsoon is strongly linked to the pressure difference between the Sahara and Gulf of Guinea which builds up from April onward. Different explanations have been given for the suddenness of the onset. Ramel et al. (2006) attribute it to a sudden shift in position of Saharan heat low resulting from the difference in surface albedo of the Sahara and the Sahel. Sultan and Janicot (2003) argue that the interaction between monsoon flow and topography is important for the northward shift of the rain, by providing a means to release the convective energy that is trapped in the lower troposphere on the poleward side of the monsoon front because of dry subsidence. Cook and Vizy (2006), instead, suggest that inertial instability acts to advance the moisture convergence northward, away from the coast. Gu and Adler (2004) see the rainfall in the coastal and Sahelian zones as largely independent, with the former controlled by tropical sea surface temperature (‘SST’) and the latter controlled by changes in large-scale flow (AEJ and TEJ) and African easterly waves. Thorncroft et al. (2011) interpret the apparent jump as a temporary reduction in rainfall, super-imposed on an otherwise smooth seasonal northward migration of the latitude of maximum moisture convergence. They attribute the reduction in rainfall to the combined effect of cooling sea surface temperature (‘SST’) in the Gulf of Guinea and the arrival of dry southerly flow aloft as part of the monsoon circulation. Sijikumar et al. (2006) argue that the Gulf of Guinea may not be the only source of moisture supply associated with onset on the Sahel. They find that increased westerly flow from the eastern Atlantic into the continent at the time of onset is an important source of moisture
Much of the understanding that has been gained from those and other studies comes from model simulations and re-analyses. The conclusions about what controls monsoon onset are therefore inevitably affected by the different representations of physical processes in the models and reanalyses that are used. Global coupled GCMs generally have a poor reputation for their simulation of the West African monsoon (‘WAM’) and its variability (e.g. Cook and Vizy 2006; Joly and Voldoire 2010), and a dry bias over the Sahel during July–September is a common error. Biases in SST in coupled models are an important source of error for the monsoon because of the strong impact on the boundary layer moisture fluxes and diabatic heating (Levine and Turner 2012). Re-analyses rely heavily on the underlying model in parts of West Africa where data coverage is low (section 3.1 of this paper) and, like coupled models, have difficulty reproducing the observed northward migration of rainfall from the coast to the Sahel between July–September (Thorncroft et al. 2011).
Coupled models used in seasonal forecasts are initialised in each forecast. SST drift and their impact on the WAM are therefore restricted to the length of each forecast (typically 6–7 months) but can still be substantial. Other biases in seasonal forecast models are structural and shared with uninitialised models, e.g. insensitivity of Sahelian rainfall to SST anomalies in the south tropical Atlantic (Philippon et al. 2010). However, we will show in this paper that the current UK Met Office operational seasonal forecasting system GloSea4 (‘G4’, Arribas et al. 2011) has a much improved representation of the mean monsoon onset compared to some previous generation seasonal forecasting models.
The purpose of this paper is twofold: (1) to show how dynamical seasonal forecast models can be used to formulate a forecast for onset of the WAM; (2) to explore the sources of forecast skill for onset of the WAM. In Sect. 2 we introduce the models and observational data that are used in this study, and define four different monsoon onset indicators. In Sect. 3 we evaluate these indicators in observations, reanalyses and GloSea4 to determine forecast skill. In Sect. 4 we will explore the reasons for the realistic mean onset in retrospective forecasts (‘hindcasts’) with GloSea4 and compare it to onset in two reanalyses. We also investigate the source of forecast skill for the main onset indicator and the physical mechanisms for late onset in GloSea4 and in reanalyses. Conclusions follow in Sect. 5.
2 Data and methods
2.1 Dynamical seasonal forecasting systems
The main seasonal forecasting system that we use in this study is GloSea4 (‘G4’). It is an ensemble prediction system that uses the HadGEM3 coupled GCM to model interactions across all physical components of the climate system: ocean, atmosphere, land surface and sea ice. Arribas et al. (2011) describe G4 and its performance in detail. In this paper we use the version that became operational in November 2010. Compared to Arribas et al. (2011) this version has increased vertical resolution in the ocean (20 layers in the top 60 m), and increased vertical resolution in the atmosphere, with 21 additional levels in the troposphere and an extended lid to resolve the stratosphere; 3-hourly ocean-atmosphere coupling instead of daily coupling. Separate analyses for ocean, atmosphere, land surface and sea ice are used to initialise the model.
The inherent uncertainty of forecasting climate anomalies at seasonal timescales motivates the use of ensemble techniques in G4. Our seasonal forecasts provide probabilities for a range of outcomes, rather than a single deterministic forecast. To evaluate model skill and for bias correction hindcasts with G4 are available for the period 1996–2009. Hindcasts are initialised 8 days apart with three ensemble members per hindcast start date. To increase ensemble size we pool three adjacent start dates (say 25 April, 1 May, 9 May) giving a total of 3 × 3 = 9 members. The 9-member ensemble thus aggregated is assigned, nominally, the start date of the middle set (1 May in this example). For further details about G4 the reader is referred to Arribas et al. (2011).
We have also used hindcasts from the ENSEMBLES project. These are 9-member hindcasts with six different coupled seasonal forecasting systems, described by Weisheimer et al. (2009). We used ENSEMBLES 1 May hindcasts for the years 1979–2005. Although this is a different hindcast period than G4, the ENSEMBLES models offer a good way to quantify model skill in structurally different seasonal forecasting systems and thus assess the robustness of the G4 results.
2.2 Observations and reanalyses
To evaluate model skill in seasonal forecasts we need to determine onset dates from observations. For this we require datasets with spatially complete coverage and a temporal resolution of 5–10 days. For rainfall we use satellite-based estimates. We use pentadal GPCP data (Xie et al. 2003) for years 1979–2010 (vn 1.0, using real time ‘rt’ data for 2008–2010). We also used TRMM (1998–2010), daily accumulations of 3-hourly rainfall rates 3B42 vn6 (Simpson et al. 1988) which we averaged into 5-day means. TRMM uses precipitation radar measurements which are not used in GPCP making it a valuable additional rainfall estimate data set, even if its record is short. In addition to these rainfall estimates we will also use NOAA OLR observations from 1975 to 2010 (Liebmann and Smith 1996).
Throughout this study we will use two recent, state-of-the-art reanalysis products: MERRA (Rienecker et al. 2011) and ERA-interim (‘ERAI’, Dee et al. 2011) for a number of variables. We use reanalysis data from the period 1979–2010.
2.3 Onset definitions
We need to specify a definition for monsoon onset that can be evaluated in dynamical seasonal forecast models, global reanalyses and gridded observations. With this definition we can then formulate a forecast for timing of the onset and evaluate forecast skill. Definitions of onset of WAM fall into two categories: onset is either defined (1) in terms of local rainfall occurrences and constraints on wet/dry periods or (2) in terms of large-scale changes to the monsoon system, not limited to rainfall (e.g. changes in longwave radiative flux or circulation). Local onset indicators are usually defined with agricultural applications in mind, e.g. Ati et al. (2002), Sivakumar (1988). They are often formulated for a particular region. Marteau et al. (2009) show that local onset dates that are defined in this way tend to be characterised by weak spatial coherence of interannual variability across stations reporting rainfall. If at the individual station level small-scale processes are important in controlling local onset then that may turn out to be difficult to predict at seasonal timescales. Local onset defined at the station level can also be difficult to evaluate in global models, requiring downscaling or calibration steps to account for model biases and limitations in resolution. Large-scale onset indicators have been used extensively in scientific studies of the West African monsoon and are meant to capture large-scale changes that occur in the monsoon system around the time of onset.
A single definition is unlikely to fully cover all aspects of monsoon onset which occurs through various stages (Fontaine et al. 2008; Gazeaux et al. 2011). Basing a forecast on a single indicator could therefore result in an over-confident forecast. Nor is a single indicator likely to be very useful to a wide user community of the forecast. For example, large-scale indicators may be preferable to organisations with broad regional interest e.g. aid agencies, while National Meteorological Services and similar users will prefer more localised information. Therefore we use several onset indicators and forecast skill is evaluated in each indicator separately. We use three large-scale onset indicators (1–3) and one local onset indicator (4) that is relatively insensitive to model bias:
-
1.
Rainfall indicator: determines the time when the rainfall maxima shift from the Gulf of Guinea (‘GoG’) coast to north of 10N
-
2.
Outgoing longwave radiation (‘OLR’) indicator: determines the time when the OLR minima (indicative of the areas of most active atmospheric convection) shift north of 10N.
-
3.
Dynamical indicator: determines the time when, jointly, (1) the monsoon circulation over W Africa (5–15N) has become sufficiently established and (2) the difference in boundary layer moist-static energy over the Sahel minus that over the GoG coast has become positive (i.e. increased warming and moistening over the Sahel).
-
4.
Local onset indicator: for each location we calculate the calendar day when a specified fraction of the average rainy-season total rainfall amount has fallen. Onset can then be defined locally as the arrival of (for example) the 20 % of average season total rainfall. This threshold value can be chosen so as to give a similar onset date to more traditional local onset definitions.
Indicators 1–3 capture important large-scale meteorological changes of the WAM around onset. Indicator 4 has potentially more value for user applications because it contains spatial information, even if it is not identical to standard local onset definitions. More details of these indicators are given in Appendix 1.
3 Results
3.1 Onset in observations and reanalyses
We calculated onset dates using onset definition (1) in the GPCP and TRMM rainfall estimates and reanalyses. Time series of onset dates shown in Fig. 2. The means are very similar. We calculated correlations between the GPCP onset time series and the other data for overlapping years and this is shown in brackets in Fig. 2. There is good correlation between TRMM and GPCP onset (0.83), although they overlap for only 13 years. Correlation between onset dates in GPCP and MERRA is also strong (0.71), with ERAI it is smaller (0.58) but significant at the 5 % level of a 2-tailed T test. The reason for these different correlations in the reanalyses is further explored in Sect. 4.2.
The onset time series for definition (2) from the NOAA OLR data is also shown in Fig. 2. Overall it tracks the GPCP series well. It has larger year-to-year standard deviation than GPCP, as already pointed out by Fontaine et al. (2008): 14 days for NOAA-OLR compared to 8 days for GPCP for the years considered here. Fontaine et al. (2008) argue that this larger variability is a more realistic indication of the true year-to-year fluctuations in monsoon onset than the rainfall-based onset variability. For the dynamical onset indicator (3) we use the required fields (see Appendix 1) from MERRA (3-hourly) and ERAI (6-hourly) data, averaged into daily means. The mean dynamical onset date (day 173) and its standard deviation (8 days) are similar in both datasets. The two dynamical onset series are weakly correlated with GPCP-based onset dates (correlation ≈ 0.3) but reasonably well with each other (correlation 0.5). The local onset indicator (4) is evaluated in GPCP and the climatology for 1996–2009 is shown in the top panel of Fig. 4.
3.2 Onset in GloSea4 and ENSEMBLES models
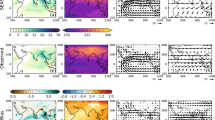
The rainfall climatology over W Africa for the 1 May G4 hindcasts is shown in Fig. 1. The model has maximum rainfall near the Gulf of Guinea from May to July. At the beginning of July the rainfall maxima shift north of 10N, similar to the observations. Rainfall in the Sahel is too strong in the model during July compared to observations. In TRMM Sahelian rainfall reaches a maximum in the second half of August, which is reproduced by G4. In summary, key features of the monsoon rainfall evolution over West Africa are well reproduced by G4. This is an important improvement over some other seasonal forecast models (cf. Fig. 17 in the Appendix 3) or CMIP3 coupled models (Cook and Vizy 2006).
Time (horizontal) versus latitude (vertical) diagrams of time-average pentadal rainfall (mm/day), zonally averaged between 10°E–10°W, for TRMM satellite-based observations, MERRA and ERAI reanalyses and GloSea4 (indicated at top of each panel). The onset date in each of these time-mean datasets is stated in the subpanels and indicated by a vertical line
Time series of onset dates inferred from GPCP rainfall (red), TRMM rainfall (dark blue), NOAA OLR (black), dynamical onset from MERRA and ERAI reanalyses (light blue and green). Linear correlation between GPCP onset dates and the other onset dates (in overlapping years) is shown in brackets in the legend. Day 150 is 30 May, day 210 is 29 July
We now calculate onset dates for all four indicators in G4 hindcasts with a nominal start date of 1 May. Distributions of onset dates are shown in black in Fig. 3, the corresponding observed equivalents (Sect. 3.1) are shown in blue. It is encouraging to see that without any bias correction the mean and standard deviation of model onset dates for all three definitions of onset is very similar to the observed date. This suggests the possibility that, on average, the model is able to capture the right processes that determine the onset and its variability. We will explore these processes more in Sects. 4.1 (for mean) and 4.2 (for variability).
Histograms and fitted normal distributions of observed (blue) and GloSea4 (black) onset dates for the hindcast period 1996–2009. Onset dates from GloSea4 are for 1 May model start dates, observations are described in text. Distributions are shown for each of the three large-scale onset indicators (stated above each panel). Mean and standard deviation are shown in the top left of each panel
For local onset indicator (4) we show the G4 climatology in the lower panel of Fig. 4. Model onset timings are broadly similar to GPCP except over the central Sahel (10W–10E, 15–20N), where onset in the model is around 20 days too early. This is consistent with the wet bias early in the season noticed before (Fig. 1). Because there is proportionally too much rain in the early season in the model, it reaches 20 % level earlier than the observations. The area north of 20°N should be ignored because it receives very little rain and onset is not meaningful here.
3.3 Forecast skill for onset
We have calculated two different kinds of skill score for onset in G4 hindcasts initialised from late March till late May: anomaly correlations and ROC scores. In the left column of Fig. 5 we show anomaly correlations between the observation and the ensemble mean hindcast for each year. It is calculated as the correlation between anomalies in the observed timeseries and the ensemble-mean model hindcast. This is a deterministic way of quantifying model skill and does not convey any information about spread in the hindcasts. Leave-one-out correlations have a median that corresponds closely to the correlations of the full timeseries (dash-dotted lines in left column of Fig. 5). The correlations are good estimates of the true model correlation.
GloSea4 skill scores for onset forecasts over the hindcast period 1996–2009. Anomaly correlation (left column, solid black lines) and ROC areas for tercile categories (‘early’, ‘normal’ and ‘late’ onset, right column) are shown as a function of model start date for the large-scale onset indicators: precipitation (top, verified against GPCP), OLR (centre, verified against NOAA OLR) and dynamical (bottom, verified against ERAI). Start dates on the horizontal axis are shown as ‘month date’, e.g. ‘0325’ is 25 March. Skill scores from 1 May ENSEMBLES hindcasts (1979–2005) are included for precipitation and OLR based onset: anomaly correlation is shown by coloured squares for individual ENSEMBLES models; for ROC areas we show the ENSEMBLES range (minimum, maximum and ensemble-mean) for the three tercile onset categories. The dashed curve on the right in the anomaly correlation plots shows the estimated PDF of anomaly correlation for a random forecast, with some upper percentiles of this PDF indicated by dotted straight lines (see text for details). The dash-dotted curves in the anomaly correlation plots show the median values of leave-one-out correlations
Random forecasts provide a useful benchmark for the G4 anomaly correlations: we define a random forecast as a random sequence of the observed onset dates over the 14 years spanning the G4 hindcast period. We then estimated the distribution of anomaly correlations for a random forecast from 10,000 such random forecasts. The empirical PDFs of these random anomaly correlations are shown at the right-hand side of the panels in Fig. 5, for each of the three indicators. Also shown are percentiles (50th, 75th, 90th, 95th and 99th) of the cumulative PDF of random anomaly correlations (dotted lines). From these one can see what the probability is that a random forecast would outperform a G4 forecast for a given start date. For example, there is a less than 5 % chance that a random forecast would outperform a G4 forecast issued in mid/late April for OLR-based onset. Forecasts initialised from early April onward have anomaly correlations that vary between 0.15 and 0.4 for precipitation and OLR onset, weaker correlations are seen for the dynamical indicator from mid April. The positive correlations indicate that the ensemble mean of G4 has some weak skill in predicting anomalies in timing of the onset 2–3 months ahead. Skill does not increase monotonically for smaller lead time, the reasons for this can be complex. For example we have found that model bias varies with start date which can affect the model’s dynamical behaviour and forecast skill. We have not explored this point further. Overall, it is clear that the ensemble mean of G4 only captures a small fraction of the year-to-year fluctuations in the observed onset dates. The usefulness of longrange deterministic onset forecasts based on the ensemble mean will be limited.
We have also calculated ROC areas (see for example, Kharin and Zwiers 2003) to quantify probabilistic skill for tercile categories of timing of the onset. These ROC areas are shown in the right column of Fig. 5. In the current context tercile categories correspond to whether in a given year onset occurs before average (lower tercile, i.e. lower third of the onset dates over the full hindcast period), near-average (middle tercile, or central third of the onset dates) or later than average (upper tercile, or top third of the onset dates). To evaluate tercile boundaries for both model and observed climatologies we fit a normal distribution to the onset dates, and define the boundaries of the 33rd and 66th percentiles of the fitted normal distribution as lower and upper tercile boundaries. We found that fitting a distribution gives a more robust estimate of the tercile boundaries than calculating these directly from the raw onset dates: the discrete nature of onset dates at pentadal resolution means that population samples can occur in clusters, from which tercile boundaries can not be determined very accurately. We carried out the Lilliefors version of the K–S test (Wilks 2011) which indicated that the sample data are consistent with normal distributions at the 20 % level (not shown). ROC scores > 0.5 indicate when the ensemble can, with more skill than climatology, distinguish whether onset is likely to be late, early or average (climatological probabilities for these categories are by definition 33 %). The ‘dynamical indicator’ 3) is again the least skilful of the three indicators considered here.
It is useful to compare the information conveyed by the various skill measures. We will do this here for 1 May forecasts with the precipitation-based indicator (top row Fig. 5). For this start date the G4 ensemble mean forecast for the onset date has only a correlation of 0.2 with the observed onset dates, so it only captures around 4 % of the observed variance. A random forecast has a probability of nearly 25 % of having a larger correlation with the observations than a 1 May G4 forecast. Next we consider 1 May probabilistic forecasts for three onset categories: early, normal or late. 1 May G4 forecasts have ROC scores > 0.5 for all onset categories: 0.55 for early, 0.7 for late, 0.75 for normal. Following Mason and Graham (2002) we interpret these values as the probabilities that G4 will distinguish an event from a non-event, i.e. 55 % for early, 70 % for late and 75 % for normal onset. This example shows that the G4 probabilistic onset forecasts have skill even if the deterministic (i.e. ensemble-mean) forecasts explain relatively little of the observed variance. This applies to most startdates in Fig. 5. It suggests that is generally better to consider probabilistic than deterministic longrange onset forecasts with G4.
We also calculated onset dates for large-scale indicators (1) and (2) in the ENSEMBLES hindcasts (there are insufficient data available to evaluate indicator 3, OLR data were only useable for 4 models). Mean rainfall over the region in each of the models is shown in the Appendix 3, Fig. 17. Anomaly correlation and ROC area for the ENSEMBLES models are by the whiskers in Fig. 5. We used the same verification datasets as for G4 but for years 1979–2005. This hindcast period is different from that of G4 which could affect the values of the skill scores. However, Fig. 5 indicates that skill in G4 is largely similar to those of the ENSEMBLES models, in spite of the different hindcast periods.
For the local onset indicator (4) we show in Fig. 6 maps of ROC area. It shows that in the western Sahel and in the east (southern Sudan/Ethiopia) the forecasts have skill compared to climatological forecasts, with ROC scores of 0.5–0.8 or above. There are large areas in the central Sahel where the 1 May hindcasts have no skill for local onset indicator (ROC area < 0.5).
Statistical forecasts for onset have been described in the literature, e.g. using boundary layer humidity (Omotosho et al. 2000), rainfall and winds between mid May and mid June (Fontaine and Louvet 2006) and OLR and MSE in May (Fontaine et al. 2008). Anomaly correlations range between 0.4 and 0.8 in a range of verification periods. Comparing this to Fig. 5 indicates that the statistical prediction schemes are as good as or better than the ensemble mean of dynamical seasonal forecasting systems like G4. The advantage of the seasonal forecasting systems is that they have useful skill at longer lead times than the statistical schemes. Furthermore, model spread in the dynamical forecasts provides an estimate of the uncertainty in the forecast, which is not normally available from statistical forecasts. As noted, probabilistic longrange forecasts for onset have better skill than deterministic ones.
4 Mechanisms of onset in GloSea4 and reanalyses
Having shown that, on average G4, has a good simulation of the northward progression of the rains throughout the monsoon season (Fig. 1), and that there is some predictability of interannual variations in onset timing, we now explore the mechanisms that control onset. The mean properties of WAM onset in G4 and reanalyses are explored in Sect. 4.1. Onset variability and the source of forecast skill, as found in the previous section, are investigated in Sect. 4.2. Throughout this section we will use the rainfall-based onset indicator (1) (Sect. 2.3) to quantify onset.
4.1 Mean onset
We have seen in Sect. 3.2 (Fig. 1) that WAM onset simulated by G4 compares favourably to observations: the rainfall maxima move north from the Gulf of Guinea coast to the Sahel in early July, similar as the observations although G4 is wetter over the Sahel in July than the observations. As noted before, in the ERAI and MERRA reanalyses the rainfall maxima do not penetrate far enough north into the Sahel, i.e. north of 10N (Fig. 1), or do so later than observed. The aim is to understand what causes the mean evolution of G4 and reanalyses rainfall to be different at the time of onset in early July, as evident from Fig. 1.
For G4 we use 1 May hindcasts for years 1992–2005 which have additional diagnostic output. For ERAI and MERRA we use the full range of available years (1979–2010) to obtain the best possible estimate of the atmosphere’s mean state. For the period 1992–2005 average onset dates are very similar in all datasets: 2 July (G4), 29 June (MERRA), 3 July (ERAI), 28 June (GPCP) and we will analyse differences averaged between 15–29 June and 30 June–14 July, i.e. the 15 days before and after the nominal mean onset date.
Average MSLP, rainfall and horizontal moisture transport at 925 hPa from G4 in the second half of June are shown in the top panel of Fig. 7 (mean fields for ERAI and MERRA are qualitatively similar and not shown here). The Saharan heat low is well established with cyclonic low-level winds advecting maritime air into the western and central Sahel. Flow from the Gulf of Guinea towards the Sudan region appears to be driven by the pressure difference between the tropical Atlantic and the Red Sea. To determine the changes that occur in these variables around the mean onset date we calculate the composite difference of the average over 30 June–15 July minus the average over 15–29 June. In G4 (middle panel of Fig. 7) the Saharan heat low deepens by 2 hPa in early July on the Atlantic side of its centre. The high pressure over the Gulf of Guinea increases by 1 hPa, following the seasonal cooling of local SST at this time (see also Thorncroft et al. 2011). These anomalous pressure gradients induce increased moist flow into the continent near the Gulf of Guinea coast and Senegal/Mauretania with moisture convergence (shown by the white ‘+’ signs) in the central Sahel (between 10E–10W and 10–15N). This eastward flow establishing around the onset is reminiscent of the regional model study by Sijikumar et al. (2006). This region also has increased ascent (indicated by ‘o’) and increased rainfall. This is associated with increased low level convergence from the west and south which provides a source of latent heating in this region (not shown here, but its zonal mean may be seen in Fig. 9). A noticeable feature of the MSLP anomalies in G4 in early July is their largely zonal orientation between 15–20N.
Top panel MSLP (contours), rainfall (shading, mm/day) and moisture transport at 925 hPa (arrows) from Glosea4 averaged between 15–29 June, i.e. the 15 days before the mean onset date. Middle panel (for GloSea4) and lower panel (for ERAI) show the difference of the average from 30 June to 15 July minus the average from 15 to 29 June (i.e. the 15 days after the mean onset minus 15 days before the onset) for MSLP (white contours, interval 0.5 hPa, negative values dashed), precipitation (colours, mm/day), horizontal moisture transport at 925 hPa (arrows). Gridpoints where moisture convergence changes by more than +(−) 2 · 10−8 s−1 are shown by white plus and minus signs, respectively. Changes in ascent at 700 hPa in excess of −0.02 Pa/s are shown by ‘o’ , changes in descent larger than 0.02 Pa/s shown by ‘v’. For clarity arrows are only shown at every other grid point
In ERAI (Fig. 7 lower panel) the Saharan heat low also deepens by 2 hPa but pressure changes in the Sahel and central Sahara are weaker than in G4. As a result the pressure anomaly in ERAI in early July is less zonal and dominated by the cyclonic feature in the western Sahara. Pressure increase over the Gulf of Guinea is smaller than in G4, about 0.5 hPa. As a result of these different pressure changes moisture transport anomalies at 925 hPa do not penetrate into the central Sahel but instead are diverted northward to the western Sahara. Near the Gulf of Guinea coast the change in moisture transport is orientated more zonally than in G4 and mostly non-divergent. There is no extra ascent between 10E–10W and 10–15N as in G4 and more extensive descent of dry air from aloft over Mali and Mauretania. Rainfall changes in ERAI in early July are limited to the ocean and the eastern Sahel with a gap over the central Sahel. We note that G4 and ERAI are in broad agreement about changes over the eastern Sahel/central Sudan.
Verification of these changes in G4 requires observations made for long enough and with sufficient temporal resolution to reliably estimate 15-day changes. We use HadISD, a dataset of quality-controlled sub-daily WMO station reports (Dunn et al. 2012). Note that many of these data will have been assimilated in ERAI and this should be kept in mind when comparing ERAI and HadISD. We use HadISD to estimate average MSLP changes between early July and late June 1979–2010, Fig. 8 (see Appendix 2 for details of the calculation). Local minima of negative pressure change are seen over Morocco and Egypt, positive pressure change is seen south of the Sahara with perhaps a local maximum around 12N. The available observations show that model and ERAI reanalyses get the large scale pattern right: positive in the south, negative in the northwest (compare Figs. 7 and 8). The changes in the Sahel in ERAI are perhaps somewhat weaker than in the station data; those in GloSea4 in the northern Sahara (Algeria and Libya) are too strongly negative. Unfortunately there is little data coverage in HadISD between 15 and 25N, i.e. in the northern Sahel and southern Sahara. This means that we cannot determine if the pressure pattern of G4 or ERAI in this region is more realistic. If this gap in coverage of station data in HadISD is representative of the station data assimilated in ERAI then it suggests that, on average, over the course of the reanalysis period ERAI is perhaps not strongly constrained by station observations in the region between 15 and 25N.
Locations of WMO observing stations with sufficient data coverage (see text for details) to calculate average MSLP change between 30 June and 15 July minus 15–29 June for the years 1979–2010. Pressure change in hPa is indicated by the colour. Values significantly different from zero (at the 90 % level) are shown by filled symbols, non-significant values by open symbols. Pressure changes greater than 0.5 hPa or −1 hPa are shown by squares, smaller changes by circles
We extend this analysis of the near-surface changes to that of changes aloft, in a meridional/vertical plane. We do this for specific humidity, zonal, meridional and vertical pressure velocity at pressure levels between 1,000 and 400 hPa, and supplement this with precipitation, MSLP, surface skin temperature, sensible heat (‘SH’) and latent heat (‘LH’) flux and total cloud cover changes. We calculate zonal means between 10E and 10W and calculate composite differences in these variables before and after onset. (Figs. 9, 10, see captions for legend).
Mean differences associated with monsoon onset in GloSsea4. Difference fields are calculated as the average over 30 June–14 July minus average over 15–29 June for the years 1992–2005. All fields are zonally averaged between 10°E–10°W. Colours: specific humidity (units kg kg−1, see colour bar), arrows: meridional velocity and vertical pressure velocity, contours: zonal velocity (m s−1, negative dashed). Surface fields are shown by curves centred around the red zero line in the lower panel, with scale for each variable shown in lower right: precipitation (heavy solid line); skin temperature (heavy dotted line); MSLP (purple dash-dotted); surface latent heat flux (thin solid, upward positive); surface sensible heat flux (thin dotted, upward positive), total cloud cover (dashed). GPCP rainfall difference is shown by the thin green line at the same scale as GloSea4. The approximate position of the coast line is shown by the black bar at 6.25°N
In G4 the northward shift in rainfall is clearly visible, centered around 10N. This shift is accompanied by a drying south of 10N (5N at higher levels) and a moistening north of 10N across most of the troposphere. There is also an increase in cloud cover north of 10N. We see an increase in low-level northward flow between 5 and 25N. Cooler SSTs mean there is reduced latent heat (‘LH’) flux and anomalous descent over the ocean, which is consistent with the drying of the atmosphere south of 5N. Over land we see an increase in surface LH flux around 15N that is collocated with anomalous rising across most of the troposphere (cf. ‘o’ in Fig. 7). At the latitudes where LH flux increases (12–18N) sensible heat (‘SH’) flux is reduced. To the north we see an increase in SH flux. Hagos and Zhang (2010) calculated the divergent circulation response of the WAM to SH and LH fluxes, with the circulation driven by SH flux instrumental in advancing the monsoon circulation inland. It is beyond the scope of this paper to repeat their analysis for G4. However, we note a similar colocation as Hagos and Zhang (2010) of LH changes and deep overturning changes (increase around 15N, decrease south of 10N) and, to a lesser extent, of SH increase and shallow overturning (north of 20N). We note that the African Easterly Jet weakens near 10N, as observed by Sultan and Janicot (2003) in the NCEP reanalyses. For most variables we lack the independent observations to verify these changes in G4, except for precipitation. Comparing zonal mean precipitation in G4 and GPCP (green line in bottom panel of Fig. 9) suggests that G4 gets the right pattern of rainfall change but overestimates its amplitude. A possible interpretation is that in G4 the processes controlling onset are working in the right way but are overly active.
The ERAI (Fig. 10) and MERRA (Fig. 19, Appendix 4) reanalyses show essentially the same response as G4 south of 5N (i.e. over the ocean and the coast), but differ substantially from G4 over land. Moistening of the troposphere over land is weaker and does not extend much above 800 hPa. Instead we see drying between 500 and 700 hPa and increased southward flow of dry air from the Sahara (stronger and reaching further south than in G4). Between 10 and 15N there is downward flow of dry air in the reanalyses (see also ‘V’ in Fig. 7), whereas G4 has upward motion here. Changes in the boundary layer (e.g. MSLP and latent heat flux) and the enhanced monsoon inflow at 925 hPa are smaller than in G4. Like G4, the reanalyses overestimate rainfall changes over the ocean and just north from the coast (0–10N) compared to GPCP.
Summarising, the key difference between G4 and the reanalyses is the presence of dry air over the Sahel across most of the middle and lower troposphere. The reanalyses have weaker low-level inflow of moist air from the ocean than G4 and a stronger flow aloft of dry air from the Sahara. This implies that the reanalyses have a smaller increase in moisture supply to the lower and middle troposphere and less increased upward motion or convection over the Sahel, consistent with the dry rainfall bias in the Sahel north of 10N. G4 and reanalyses do generate a reduction in rainfall over the coastal region, as seen in GPCP, and this is one of the two components of onset indicator (1). It explains why onset dates from the reanalyses have some correlation with GPCP-based onset in spite of their shortcomings in reproducing rainfall changes over the Sahel.
4.2 Onset variability
Seasonal forecast skill in the atmosphere arises from the interaction between the atmosphere and more slowly evolving (i.e. more predictable) components of the climate system, e.g. sea surface temperature (SST). In this section we will therefore investigate the relation between SST and the rainfall-based onset indicator (1) (Sect. 2.3)
4.2.1 Teleconnection with SST
To see how June SST anomalies affect timing of the onset we calculate a regression between these variables (units °C/day). We do this for observations (HadISST SST (Rayner et al. 2003) and GPCP-derived onset dates); G4 hindcasts (initialised on 1 May) and ERAI and MERRA reanalyses, Fig. 11. Positive teleconnections show where warm SST delays the onset and cold SST hastens onset (opposite for areas of negative teleconnections). The observed teleconnection pattern (top left panel) shows that warm SSTs in the Gulf of Guinea (‘GoG’) and S tropical Atlantic delay onset. There is a significant signal in the Pacific (mainly in W Pacific and off equator, i.e. outside the Niño 3 and 4 regions). G4 captures the pattern in the S Atlantic but it is too weak, i.e. effect of warm SST anomalies in delaying the onset is too small compared to observations. The model does not capture the contribution from SST outside the equatorial Atlantic. The reanalyses have teleconnections similar to the observed in the equatorial Atlantic, but over the Pacific both differ substantially from the observed pattern. Teleconnections in the six ENSEMBLES hindcasts are shown in the Appendix 3, Fig. 18. Most ENSEMBLES models capture the teleconnection in the Atlantic but differ in the simulated strength. Like the reanalyses, none of these models accurately reproduce the observed pattern over both the Pacific and Indian Ocean.
Teleconnection patterns between June SST and monsoon onset, expressed as a regression: days of delay in onset per K. GPCP-onset and HadISST (top left, 1979–2010), GloSea4 (1 May startdates in extended hindcast, 1989–2009), ERAI and MERRA reanalyses (1979–2010). Areas of significant regressions (at the 95 % level) are enclosed by contours
To confirm the robustness of the observed teleconnection pattern of Fig. 11 we also calculated it using different observational SST datasets: Reynolds OIv2 (Reynolds et al. 2002) and HadSST3 (Kennedy et al. 2011). June SST teleconnections using these SST observations are very similar to that for HadISST (not shown). Pattern correlation with the HadISST-derived pattern is strong: 0.82 for Reynolds and 0.70 for HadSST3. None of the teleconnection patterns change much if they are calculated over the G4 extended hindcast period 1989–2009 (not shown). Therefore we believe that the observed teleconnection pattern in Fig. 11 is a robust feature. On its own, however, a statistical relation between SST and monsoon onset date does not necessarily mean that SST affects the timing of the onset directly. For example both could be driven by some other process, or the statistical relation could just be picking up random fluctuations in the climate system that happen to co-incide but have no physical connection. However, we found additional support for a direct physical link in two ways.
Firstly, we found that the more accurately a model reproduces the observed teleconnection pattern, the better its hindcast skill is of monsoon onset: Fig. 12 shows the anomaly correlation of onset in hindcasts and observed onset (vertical axis) against pattern correlation between simulated and observed teleconnection (horizontal axis) for models and reanalyses. Better hindcast skill is found in models with better pattern correlation. This suggests that the observed teleconnection pattern is not merely noise but indicates a pathway for SST to affect timing of the monsoon onset. This forcing pathway forms a source of potential skill in models, provided they can reproduce this teleconnection. The Meteo France and CMCC-INGV are best at capturing this teleconnection pattern and have the best anomaly correlation with observed onset. This is perhaps surprising, given that these models have the largest mean biases in Sahelian rainfall of the ensemble (Fig. 17). It suggests that processes controlling the mean rainfall amount over the Sahel and those that control variability of timing of onset are not the same.
Projection of simulated teleconnection on observed teleconnection pattern (horizontal) versus anomaly correlation between simulated and observed onset (vertical). Shown are results for GloSea4, the ENSEMBLES models developed by IFM-GEOMAR (IFMGM), ECMWF, UK Metoffice HadGEM (HDGEM) and DePreSys (DPSYS), CMCC-INGV (CMCCB) and Meteo France (METOF). Triangles indicate the values for ERAI and MERRA reanalyses. ‘S3’ and ‘R’ denote projections of teleconnections using HadSST3 and Reynold SST data onto the HadISST1 derived pattern
Establishing how Atlantic SST anomalies can affect onset date provides a second argument for the importance of the teleconnection of Fig. 11. We will investigate this in the following section. Previous studies have highlighted the possibility of remote influences on the African monsoon at intra-seasonal timescales: model experiments by Lavender and Matthews (2009) have suggested that SSTs in the Pacific warm pool can affect convection in West Africa through the MJO. Flaounas et al. (2011) describe how westward propagating Rossby waves, triggered by onset of the Indian monsoon, can inhibit convection over West Africa. We will focus on the role of Atlantic SST, the nearest ocean basin. All models and reanalyses capture its teleconnection to some extent, whereas many struggle to reproduce the observed SST teleconnection over the combined other basins (i.e. the tropical Pacific as well as Indian oceans).
4.2.2 Monsoon response to Atlantic SST
In this section we investigate what processes give rise to a late monsoon onset and how they are linked to SST. Footnote 1 We compare processes in G4 and in MERRA and ERAI re-analyses. As seen in the previous section, G4 has problems with onset being too unresponsive to Atlantic SST. Reanalyses also have problems with monsoon onset, e.g. their failure to reproduce the observed shift of the rainfall maximum to north of 10N during JAS (Fig. 1). Neither G4 nor reanalyses should therefore be thought of as completely representative of the real atmosphere and their comparison should be viewed as a sensitivity study of the processes that can cause late onset.
For G4 we use the same hindcast (1992–2005) as in Sect. 3.2. For the reanalyses we use the maximum range of available years (1979–2010) to obtain the best possible estimate of the processes. Building on our analysis of the mean onset (Sect. 3.2, Fig. 7) we start by looking at low-level changes first and subsequently analyze the latitude-height cross sections. In Fig. 13 we show regressions of all variables onto onset date, in order to quantify how they change when onset is late.
Regression of Glosea4 (top) and ERAI (bottom) fields onto onset date: colours are for rainfall (units mm/day/day, only shown where significant at the 90 % level), black contours are for MSLP (10−2 hPa/day) purple contours for skin temperature (10−2 K/day). Negative values are dashed, significant values are shown by thick contours. Arrows are for horizontal moisture transport at 925 hPa (significant regression shown by thick arrows). Left column is for fields time averaged between 15 and 29 June, right column is for fields time averaged between 30 June and 14 July
In G4 (Fig. 13 top row) warm SST in late June in the Gulf of Guinea (‘GoG’) causes a local reduction of MSLP and consequently a reduction in the north-south pressure gradient between the ocean and the land (see the mean state in Fig. 7, top panel). Furthermore, there is a shift in the center of the Saharan heat low to the north-east (cf. Fig. 7 top panel). Over the GoG the pressure change drives anomalous low-level moisture transport towards the coast (strongest from the ocean side) which sees an increase in rainfall. The changes in the Saharan heat low cause a weakening of the westerly moisture transport between 10 and 20N from the Atlantic and cause a reduction of rainfall over the Sahel. In the first half of July the pressure anomaly over the GoG has largely subsided (although, interestingly, the warm SST anomaly is still present there). In the Sahel the warm surface air temperature anomaly has increased and there is a large negative pressure anomaly here. The now increased pressure difference between the GoG and the Sahel reinstates the northward moisture transport to the Sahel from the GoG. Westerly moisture transport from the Atlantic between 10 and 15N is still weakened. The rainfall anomalies in early July reflect this, with reduced deficit in the east but sustained deficit in the west. In the second half of July (not shown) most anomalies over land have disappeared.
In ERAI (Fig. 13 bottom row) in late June there is a warm SST anomaly in the GoG associated with a late onset, but no sign of related MSLP change here. Instead, we note a large positive pressure anomaly over the central and eastern Sahara (Algeria, Libya and Egypt), with signs of a cold anomaly at the surface. This reduces the north-south pressure difference between the land and the ocean, reducing the low-level moisture transport from the GoG into the central Sahel. The increased low-level moisture convergence near the GoG causes increased rainfall there. In the Sahel there is little change in rainfall, apart from a region over Niger. In early July the pressure anomaly over the Sahara has disappeared. There are still rainfall anomalies over the coast and eastern Sahel/Sudan region but the regression of onset date onto SST shows a weakened signal over the GoG.
To verify these relations in observations we again use the HadISD station data and the GPCP-derived onset date. Regressions from the station data onto the onset date are shown in Fig. 14 (details in Appendix 2). It confirms the presence of negative MSLP and warm air temperature anomalies in the Sahel and near the GoG coast in both periods, similar to G4 but with a smaller amplitude. As before, there are insufficient observations in the southern Sahara (15–25N). In the northern Sahara the observations in late June show no significant MSLP signal like ERAI does. The observations do show a positive MSLP anomaly north of 30N in early July by which time the MSLP anomaly has disappeared in the ERAI reanalyses.
Regression of observed MSLP (top row, in 10−2 hPa/day) and 1.5 m temperature (bottom row in 10−2 °C/day) HadISD station data onto GPCP-derived onset date for the periods 15–29 June (left column) and 30 June–14 July (right column) during the years 1979–2009. Values significantly different from zero (at the 90 % level) are shown by filled symbols, non-significant values by open symbols
We use the same variables as for the mean onset in Sect. 3.2 and calculate zonal means of these fields between 10E and 10W for latitudes 10S–30N. The zonal mean fields were then time-averaged over two 15-day periods before and after average GPCP monsoon onset: 15 June–29 June and 30 June–14 July. Finally, we regressed the zonally and temporally averaged fields against the respective model/reanalysis monsoon onset dates, to determine the linear change ‘per day of late onset’ for each data set (Fig. 15).
Regression of GloSea4 (top) and ERAI (bottom) fields on onset dates. Format is the same as in Fig. 9. Units are now change in variable per day of delayed onset, e.g. for precipitation: mm/day/day
In G4, warm SST in the second half of June causes a strong upward LH flux or evaporation over the ocean, and deep upward motion, with low-level meridional convergence: northward flow south of 5N, southward flow between 5 and 10N where it opposes ‘normal’ monsoon inflow. There is an increase in precipitation around the Gulf of Guinea (‘GoG’) coast (5N) and a reduction in the Sahel (north of 10N). The low-level flow is consistent with anomalous gradients in MSLP (purple line). Over the land area north of 10N there is anomalous poleward flow above 700 hPa and a strengthening of the AEJ. In the area of anomalous ascent over the ocean specific humidity increases, whereas over land around 15N there is drying, strongest between 925 and 800 hPa. Consistent with the drier air, rainfall and total cloud cover are reduced around 15N. A warm skin temperature anomaly appears at 15N, accompanied by increased surface SH flux and decreased LH flux. In the first half of July the warm anomaly over land near 15N amplifies, as do the SH and LH flux changes. MSLP over land deepens further, with a local minimum near 15N. At this latitude increased ascent develops with increased northward and eastward low-level flow towards 15N. The anomalous circulation is again reminiscent of that described by Hagos and Zhang (2010): near LH flux anomalies there is deep ascent and low-level convergence that acts to delay northward progression of the monsoon; near SH maxima there is shallow ascent (up to about 700 hPa) whose low-level convergence promotes the inland penetration of the monsoon flow.
In the ERAI reanalyses we see in the second half of June a similar behaviour as G4: a warm SST, with anomalous ascent/moistening and increase in precipitation near the GoG coast, and a southward low-level flow between 5 and 20N. Differences are the amount of moistening over the ocean, which is smaller than G4 and the drying over land, which is stronger than G4. Also, the anomalous flow over the Sahel above 700 hPa is southward, bringing dry air from the Sahara, whereas it is northward in G4, i.e. coming from the ocean. During the first half of July ERAI also has an amplification of the warming at 15N, SH flux and low pressure anomaly at 15N, but not as strong as G4. The main differences with G4 in this period is that ERAI does not bring in more humid air around 10N in the lower troposphere and that the southward flow anomaly between 5–10N and 1,000–850 hPa persists to the first half of July. It is not until the second half of July that a small increase is seen in the low-level northward flow near 15N (not shown).
In MERRA the changes over the ocean in the second half of June are similar to G4 and ERAI (Fig. 20). Over land the flow aloft is southward (like in ERAI), but the drying over land is not as large as ERAI and more like G4. In the first half of July anomalous northward flow develops around 10N (between 925–850 hPa), like in G4.
In summary: Reanalyses and G4 all show that warm SSTs in the equatorial Atlantic in late June cause anomalous evaporation, and anomalous ascent near the GoG coast. The ascent is fed by low-level southward flow between 5 and 10N that opposes the monsoon inflow. This causes a drying of the lower troposphere and reduction of rainfall over the Sahel. There is less consensus about what happens next, in the first half of July. All models show a warming of the land in the Sahel. In G4 this causes a strong increase of SH flux and a local drop in MSLP near 15N that acts to accelerate the monsoon inflow. This is followed by the arrival of more humid air over the Sahel in late July. In ERAI and MERRA the response of the land surface is smaller than G4. A small increase of the monsoon inflow into the Sahel is seen in MERRA (early July) and ERAI (late July), but otherwise there is little sign of any anomalies in the reanalyses from mid-July onwards.
The scarcity of model-independent observations in this region over long enough periods makes it difficult to assess how realistic model and reanalyses are in simulating processes associated with variability of onset. However, we can compare the simulated changes in precipitation with those in GPCP observations (green lines in Fig. 15). The good agreement between observations and models (as well as between G4/reanalyses) near the coast in the second half of June suggests that we can have confidence in this part of the response to warm SST. Over land the surface response is quantitatively different in model/reanalyses, and we are therefore less confident about this part of the response associated with late onset. One interpretation of these results is that over land G4 is too active, whereas the reanalyses are too inactive.
5 Discussion and conclusions
Providers of climate and weather information are increasingly asked to supply user-specific forecasts. This may involve forecast information that is very different from what is produced at present. For the largely rain fed agriculture in Africa long-range forecast information of seasonal rainfall is obviously very important. Forecasts with dynamical seasonal forecast models for total rainfall have been produced for many years now and form an important input to WMO’s Regional Climate Outlook Forums. Footnote 2 Temporal distribution of rainfall throughout the rainy season is also important for many user applications in Africa (Graham 2011). However, longrange forecasts for this are not usually produced at present by forecast models. In this study we have investigated if current dynamical seasonal forecast models can be used to provide long-range forecasts for timing of onset of the West African monsoon.
We formulated four definitions for monsoon onset that capture different aspects of the onset process. The definitions we chose do not rely on absolute rainfall amounts because most models have rainfall biases. We evaluated these definitions in the UK Met Office seasonal forecasting system GloSea4 and in six forecasting systems from the ENSEMBLES project, where possible.
We found that models generally have modest probabilistic skill in forecasting timing of the start of the Sahelian rainfall season at 2–3 months lead time (ROC scores 0.6–0.8). This is perhaps surprising because (1) reproducing the observed mean rainfall amounts in the Sahel remains a challenge for most models; (2) rainfall in the Sahel is influenced by various intraseasonal phenomena that are generally assumed to have little or no longrange predictability, but can influence the temporal evolution of the rainy season (and hence timing of the onset): MJO (Pohl et al. 2009; Lavender and Matthews 2009), African easterly waves (Gu and Adler 2004; Mekonnen et al. 2006), midlatitude intrusions (Vizy and Cook 2009) to name a few. We find that longrange forecast skill for onset derives largely from the atmosphere response to SST in the tropical oceans, reproducing a teleconnection that we also see in observations of rainfall and SST. An important aspect of this response is the delay that warm SST in the tropical Atlantic can cause on the northward migration of the ITCZ. Most models reproduce this basic response.
GloSea4 is one the models that has a comparatively good simulation of the average spatial and temporal evolution of rainfall over West Africa. Over and near the Gulf of Guinea coast the atmosphere of GloSea4 behaves in a similar way as the ERAI and MERRA reanalyses, in terms of the mean onset as well as onset variability. This qualitative agreement between model and reanalyses over the ocean and coastal area means that we are relatively confident that model skill for onset is because GloSea4 captures some of the key physical processes in this region. In contrast, over the continent (the Sahel and Sahara) processes controlling timing of onset are quantitatively very different in model and reanalyses. There are not enough station observations to verify GloSea4 or the reanalyses in the Sahara, but data in the Sahel suggests that the GloSea4 atmosphere is perhaps over-simulating some of the processes here. The lack of data over the Sahara suggests that the reanalyses may not be strongly constrained by station observations in an area that we found to be key for monsoon onset. Sustained observations in this region would be clearly beneficial to better understand the processes controlling monsoon variability. Targeted field campaigns like AMMA (Redelsperger et al. 2006) may offer the best opportunity to acquire observations in this region and thereby contribute to improving models on the short (NWP) range, potentially improving longrange forecasts (Senior et al. 2010).
We have found modest longrange forecast skill for onset in various seasonal forecasting systems that are typical of current operational systems. We think that there is some scope for the levels of forecast skill to increase in the future. Firstly, model improvements should enable models to capture the observed influence of SST from the tropical Pacific and Indian Oceans. This is something that many models studied here fail to do and therefore is an unexploited source of longrange skill. Secondly, if the coupling between land surface and atmosphere is modelled well (Seneviratne et al. 2006), local soil moisture may provide another source of longrange forecast skill. Soil moisture has been shown to have the potential to influence interseasonal (Fontaine et al. 2007) and intraseasonal (Moufouma-Okia and Rowell 2009) rainfall variability over West Africa. The relative importance of soil moisture on monsoon onset compared to that of SST has not been studied systematically, though, and some of the models used in our study (including Glosea4) already use some form of soil moisture initialisation.
Our results suggests that it is worthwhile to investigate probabilistic forecast skill for monsoon onset in other operational seasonal forecasting systems, even if mean biases in rainfall are present. Based on this study we expect that a multi-variate approach (i.e. use of multiple onset indicators) in a multi-model context could yield skilful longrange information for monsoon onset in West Africa. This would address a clear user need.
Notes
The remainder of this section is formulated in terms of late onset. Early onset is assumed to be caused by processes of opposite sign. We have not investigated non-linearity in the response.
References
Arribas A, Glover M, Maidens A, Peterson K, Gordon M, MacLachlan C, Graham R, Fereday D, Camp J, Scaife AA, Xavier P, McLean P, Colman A, Cusack S (2011) The GloSea4 ensemble prediction system for seasonal forecasting. Mon Weather Rev 139:1891–1910. doi:10.1175/2010MWR3615.1
Ati OF, Stigter CJ, Oladipo EO (2002) A comparison of methods to determine the onset of the growing season in northern Nigeria. Int J Climatol 22(6):731–742. doi:10.1002/joc.712
Cook KH, Vizy EK (2006) Coupled model simulations of the West African monsoon system: twentieth- and twenty-first-century simulations. J Clim 19(15):3681–3703. doi:10.1175/JCLI3814.1
Dee DP, Uppala SM, Simmons AJ et al (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteorol Soc 137(656):553–597. doi:10.1002/qj.828
Dunn RJH, Willett KM, Thorne PW, Woolley EV, Durre I, Dai A, Parker DE, Vose RS (2012) HadISD: a Quality Controlled global synoptic report database for selected variables at long-term stations from 1973–2010. Clim Past Discuss 8:1763–1833. doi:10.5194/cpd-8-1763-2012
Flaounas E, Janicot S, Bastin S, Roca R, Mohino E (2011) The role of the Indian monsoon onset in the West African monsoon onset: observations and AGCM nudged simulations. Clim Dyn. doi:10.1007/s00382-011-1045-x
Fontaine B, Janicot S (1992) Wind field coherence and its variations over West Africa. J Clim 5:512–524. doi:10.1175/1520-0442(1992)005<0512:WFCAIV>2.0.CO;2
Fontaine B, Louvet S (2006) Sudan-Sahel rainfall onset: Definition of an objective index, types of years, and experimental hindcasts. J Geophys Res 111(D20103). doi:10.1029/2005JD007019
Fontaine B, Philippon N (2000) Seasonal evolution of boundary layer heat content in the West African monsoon from the NCEP/NCAR reanalysis (1968–1998). Int J Climatol 20:1777–1790. doi:10.1002/1097-0088(20001130)20:14<1777::AID-JOC568>3.0.CO;2-S
Fontaine B, Louvet S, Roucou P (2007) Fluctuations in annual cycles and inter-seasonal memory in West Africa: rainfall, soil moisture and heat fluxes. Theor Appl Climatol 88:57–70. doi:10.1007/s00704-006-0246-4
Fontaine B, Louvet S, Roucou P (2008) Definition and predictability of an OLR-based West African monsoon onset. Int J Climatol 28:1787–1798. doi:10.1002/joc.1674
Gazeaux J, Flaounas E, Naveau P, Hannart A (2011) Inferring change points and nonlinear trends in multivariate time series: application to West African monsoon onset timings estimation. J Geophys Res 116(D05101). doi:10.1029/2010JD014723
Graham R (2011) CSRP stakeholder consultation for long-range forecast requirements in Africa, internal report
Graham RJ, Yun WT, Kumar A, Jones D, Bettio L, Gagnon N, Kolli RK, Smith D (2011) Long-range forecasting and the Global Framework for Climate Services. Clim Res 47:47–55. doi:10.3354/cr00963
Gu G, Adler RF (2004) Seasonal evolution and variability associated with the West African monsoon system. J Clim 17:3364–3377. doi:10.1175/1520-0442(2004)017<3364:SEAVAW>2.0.CO;2
Hagos S, Zhang C (2010) Diabatic heating, divergent circulation and moisture transport in the African monsoon system. Q J R Meteorol Soc 136(S1):411–425. doi:10.1002/qj.538
Ingram KT, Roncoli MC, Kirshen PH (2002) Opportunities and constraints for farmers of west Africa to use seasonal precipitation forecasts with Burkina Faso as a case study. Agric Syst 74:331–349. doi:10.1016/S0308-521X(02)00044-6
Joly M, Voldoire A (2010) Role of the Gulf of Guinea in the inter-annual variability of the West African monsoon: what do we learn from CMIP3 coupled simulations. Int J Climatol 30(12):1843–1856. doi:10.1002/joc.2026
Kennedy JJ, Rayner NA, Smith RO, Parker DE, Saunby M (2011) Reassessing biases and other uncertainties in sea surface temperature observations measured in situ since 1850: 1. Measurement and sampling uncertainties. J Geophys Res 116(D14103). doi:10.1029/2010JD015218
Kharin VV, Zwiers FW (2003) On the ROC score of probability forecasts. J Clim 16:4145–4150
Lavender SL, Matthews AJ (2009) Response of the West African monsoon to the Madden–Julian oscillation. J Clim 22:4097–4116. doi:10.1175/2009JCLI2773.1
Levine RC, Turner AG (2012) Dependence of Indian monsoon rainfall on moisture fluxes across the Arabian Sea and the impact of coupled model sea surface temperature biases. Clim Dyn 38(11–12):2167–2190. doi:10.1007/s00382-011-1096-z
Liebmann B, Smith CA (1996) Description of a complete (interpolated) outgoing longwave radiation dataset. Bull Am Meteorol Soc 77:1275–1277
Marteau R, Moron V, Philippon N (2009) Spatial coherence of monsoon onset over western and central Sahel (1950–2000). J Clim 22(5):1313–1324. doi:10.1175/2008JCLI2383.1
Marteau R, Sultan B, Moron V, Alhassane A, Baron C, Traore SB (2011) The onset of the rainy season and farmers’ sowing strategy for pearl millet cultivation in Southwest Niger. Agric For Meteorol 151(10):1356–1369. doi:10.1016/j.agrformet.2011.05.018
Mason SJ, Graham NE (2002) Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: statistical significance and interpretation. Q J R Meteorol Soc 128:2145–2166. doi:10.1256/003590002320603584
Mekonnen A, Thorncroft CD, Aiyyer AR (2006) Analysis of convection and its association with African Easterly Waves. J Clim 19:5405–5421. doi:10.1175/JCLI3920.1
Moufouma-Okia W, Rowell DP (2009) Impact of soil moisture initialisation and lateral boundary conditions on regional climate model simulations of the West African Monsoon. Clim Dyn 35(1):213–229. doi:10.1007/s00382-009-0638-0
Omotosho JB, Balogun AA, Ogunjobi K (2000) Predicting monthly and seasonal rainfall, onset and cessation of the rainy season in West Africa using only surface data. Int J Climatol 20:865–880. doi:10.1002/1097-0088(20000630)20:8<865::AID-JOC505>3.0.CO;2-R
Philippon N, Doblas-Reyes FJ, Ruti PM (2010) Skill, reproducibility and potential predictability of the West African monsoon in coupled GCMs. Clim Dyn 35(1):53–74. doi:10.1007/s00382-010-0856-5
Pohl B, Janicot S, Fontaine B, Marteau R (2009) Implication of the Madden–Julian Oscillation in the 40-day variability of the West African monsoon. J Clim 22:3769–3785. doi:10.1175/2009JCLI2805.1
Ramel R, Gallee H, Messager C (2006) On the northward shift of the West African monsoon. Clim Dyn 26(4):429–440. doi:10.1007/s00382-005-0093-5
Rayner NA, Parker DE, Horton EB, Folland CK, Alexander LV, Rowell DP, Kent EC, Kaplan A (2003) Global analyses of SST, sea ice and night marine air temperature since the late nineteenth century. J Geophys Res 108(D14). doi:10.1029/2002JD002670
Redelsperger JL, Thorncroft CD, Diedhiou A, Lebe T, Parker DJ, Polcher J (2006) African monsoon multidisciplinary analysis: an international research project and field campaign. Bull Am Meteorol Soc 87:1739–1746. doi:10.1175/BAMS-87-12-1739
Reynolds RW, Rayner NA, Smith TM, Stokes DC, Wang WQ (2002) An improved in situ and satellite SST analysis for climate. J Clim 15(13):1609–1625
Rienecker MM, Suarez MJ, Gelaro R et al (2011) MERRA—NASA’s modern-era retrospective analysis for research and applications. J Clim 24:3624–3648. doi:10.1175/JCLI-D-11-00015.1
Seneviratne S, Koster RD, Guo Z, authors C (2006) Soil moisture memory in AGCM simulations: analysis of global land-atmosphere coupling experiment (GLACE) data. J Hydrometeorol 7:1090–1112. doi:10.1175/JHM533.1
Senior CA, Arribas A, Brown AR, Cullen MJP, Johns TC, Martin GM, Milton SF, Webster S, Williams KD (2010) Synergies between numerical weather prediction and general circulation climate models. In: Donner L, Somerville R, Schubert W (eds) The development of atmospheric general circulation models: complexity, synthesis, and computation. Cambridge University Press, Cambridge
Sijikumar S, Roucou P, Fontaine B (2006) Monsoon onset over Sudan-Sahel: Simulation by the regional scale model MM5. Geophys Res Lett 33(L03814). doi:10.1029/2005GL024819
Simpson J, Adler R, North G (1988) A proposed tropical rainfall measuring mission (TRMM) satellite. Bull Am Meteorol Soc 69(3):278–295
Sivakumar MVK (1988) Predicting rainy season potential from the onset of rains in Southern Sahelian and Sudanian climatic zones of West Africa. Agric For Meteorol 42(4):295–305. doi:10.1016/0168-1923(88)90039-1
Sivakumar MVK, Hansen J (eds) (2007) Climate prediction and agriculture: advances and challenges. Springer, Berlin
Sultan B, Janicot S (2003) The West African monsoon dynamics. Part II: the preonset and onset of the summer monsoon. J Clim 16:3407–3427
Sultan B, Baron C, Dingkuhn M, Sarr B, Janicot S (2005) Agricultural impacts of large-scale variability of the West African monsoon. Agric For Meteorol 128:93–110. doi:10.1016/j.agrformet.2004.08.005
Thorncroft CD, Nguyen H, Zhang C, Peyrillé P (2011) Annual cycle of the West African monsoon: regional circulations and associated water vapour transport. Q J R Meteorol Soc 137:129–147. doi:10.1002/qj.728
Vizy EK, Cook KH (2009) A mechanism for African monsoon breaks: Mediterranean cold air surges. J Geophys Res 114(D01104). doi:10.1029/2008JD010654
Weisheimer A, Doblas-Reyes FJ, Palmer TN, Alessandri A, Arribas A, Deque M, Keenlyside N, MacVean M, Navarra A, Rogel P (2009) ENSEMBLES: a new multi-model ensemble for seasonal-to-annual predictions—skill and progress beyond DEMETER in forecasting tropical Pacific SSTs. Geophys Res Lett 36(L21711). doi:10.1029/2009GL040896
Wilks DS (2011) Statistical methods in the atmospheric sciences, International geophysics series, vol 100, 3rd edn. Academic Press, New York
Xie PP, Janowiak JE, Arkin PA et al (2003) GPCP pentad precipitation analyses: an experimental dataset based on gauge observations and satellite estimates. J Clim 16(13):2197–2214
Acknowledgments
This work was carried out under the joint UK DFID/ Met Office Hadley Centre Climate Science Research Partnership (CSRP), which is funded by the UK Department for International Development (DFID) for the benefit of developing countries. The views expressed are not necessarily those of DFID. Pentadal GPCP data were provided by NOAA NCDC from their web site at http://lwf.ncdc.noaa.gov/oa/wmo/wdcamet-ncdc.html Interpolated OLR and NOAA_OI_SST_V2 data were provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, from their web site at http://www.esrl.noaa.gov/psd Daily TRMM 3B42_vn6 rainfall estimates were provided by NASA Goddard Space Flight Center and made available at http://mirador.gsfc.nasa.gov The HadISST and HadSST3 data were made available by the Met Office Hadley Centre and obtained from http://www.metoffice.gov.uk/hadobs MERRA reanalysis data were provided by Global Modeling and Assimilation Office (GMAO) and the GES and available from http://disc.sci.gsfc.nasa.gov/daac-bin/FTPSubset.pl ECMWF ERA-Interim data used in this study have been obtained from the ECMWF data server. The ENSEMBLES data used in this work were produced by the EU FP6 Integrated Project ENSEMBLES (Contract number 505539). The provision of data by all these centres is gratefully acknowledged and has been instrumental to the research described in this paper. Comments by three reviewers have helped to improve the manuscript and are very much appreciated.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Onset definitions
1.1 Precipitation-based onset indicator
This indicator identifies the time of the northward shift in rainfall maxima from the Gulf of Guinea coast to the Sahel. We follow the method by Fontaine and Louvet (2006). They calculate the difference between the area-averaged, standardised rainfall amounts in a southern box (0–10N) and a northern box (10–20N), both averaged zonally between 10W and 10E. Data are smoothed by a ten-day running mean. The timing of the zero-crossing of the difference time series is taken as the onset date in this method, provided the difference remains positive for at least 15 days to reject false onsets. Because this method uses standardised differences it is relatively insensitive to biases in absolute rainfall amounts, a common problem in GCMs.
1.2 OLR-based onset indicator
This indicator uses the timing of the northward shift of the main convective regions to define monsoon onset. As a proxy for convective activity we use outgoing longwave radiation (‘OLR’) at the top of the atmosphere, following the method described by Fontaine et al. (2008). The idea behind their method is that high convective cloud corresponds to low OLR values. Because medium-level cloud and land and sea surface can confuse the signal Fontaine et al. (2008) do not simply calculate area-average values of OLR. They determine gridpoints for which OLR is below a pre-specified threshold value of 180 W m−2. For each latitude between 0 and 20N all gridpoints between 10W and 10E with OLR < 180 W m−2 are flagged. The number of occurrences is then zonally summed, totalled over 5-day periods and scaled by the maximum possible number of gridpoints in that latitude range and pentad (see Fig. 4 of Fontaine et al. 2008 for an example). We then define onset as the pentad when the latitude of maximum occurrence (‘Cmax’ in the terminology of Fontaine et al. 2008) shifts north of 10N, remains north of that latitude for at least 3 out of the 4 following pentads, and the fraction of points satisfying the threshold criterion does not exceed 30 %. When applying this method in models we found it necessary to alter the OLR threshold, as model and observed OLR values are not identical. We modified the threshold value used for models so that the fraction of points at the latitude of maximum occurrence is on average 20 %. For G4 this meant changing the threshold to 170 W m−2.
1.3 Dynamical onset indicator
This indicator is based on the timing of changes in the energy content of the boundary layer and in the large-scale monsoon circulation. For the energy content we calculate moist static energy (‘MSE’), which is defined as : MSE = g*z + L*q + Cp*T, with g the acceleration from gravity, z geopotential height, L latent heat of evaporation, q specific humidity, Cp heat capacity at constant pressure and T absolute temperature. Fontaine and Philippon (2000) analysed seasonal evolution of MSE in the boundary layer and found it is linked to the seasonal evolution of precipitation in the monsoon region, as well as interannual rainfall variability. These authors showed that MSE is largest over the ocean and Gulf of Guinea coast in early spring (March–April), but that the maximum moves north as a result from the increasing surface warming and moistening inland. It becomes largest over the Sahel during the rainy season (July–September). We evaluate MSE at 925 hPa, typically the lowest standard pressure level that is defined over a large part of the region. We follow Fontaine et al. (2008) and define the day when MSE over the Sahel (10–15N) becomes larger than over the Gulf of Guinea coast (5–10N) for a period of at least 20 days as date of the dynamical onset (using 5-day averages). This onset date is then modified by the condition that the large-scale monsoon circulation also needs to be ‘sufficiently’ strong. Circulation is measured by the West African monsoon indicator (‘WAMI’, Fontaine and Janicot 1992). WAMI is defined as the standardised value of the wind speed at 925 hPa (in the monsoon inflow layer) minus the standardised value of the zonal wind at 200 hPa (in the TEJ). A more established monsoon circulation yields a larger WAMI than a weak monsoon circulation early in the season. We apply this to seasonal forecasts which are initialised between March and May and use the period May-July to calculate the standardised values of the winds. This captures pre-onset, onset and post-onset stages. A WAMI index of >0.5 is used as a second constraint on the dynamical onset date, which typically adds several days to the onset-date based on the MSE-gradient being directed northward.
1.4 Local onset indicator
First we define the start and end (in pentads) of the average rainy season, with a buffer of several weeks before the start to allow for a possible early onset. For the Sahel we have used periods that span May–October, with the exact date dependent on the actual start dates of the model hindcasts (in our example of Fig. 4 we use 11 May–27 October). In each grid point the rainfall climatology is accumulated over that period, and scaled by the total amount at the end (i.e. 27 October), i.e. it runs from 0 to 1 (black curve Fig. 16). The same is then done for an individual year in the observations or model, which is scaled by the same climatological accumulation on 27 October (red curve Fig. 16). Onset is defined as the time when the curve passes the 20 % threshold of the climatological mean (dashed black line). In this example onset occurs around 14 June for the climatology (vertical black line) and around 10 days later for the individual year (vertical red line). Note that in this example onset is ‘late’ but the season as a whole is wetter than climatology. When applied to all locations in the region we can draw lines of equal arrival time, or isochrones, Fig. 4 The threshold value is a free parameter. We have chosen 20 % because that gives on average a local onset in the central Sahel at the beginning of July (for GPCP), similar to precipitation-based indicator (1).
The isochrone method is applied identically to rainfall from the model and observations. Because accumulations are all scaled with the average season-total rainfall this method allows a comparison between model and observed isochrones, in spite of model biases in absolute rainfall amounts. In that respect the isochrone method is better suited for use in forecast models than agronomical onset definitions that use absolute rainfall amounts, e.g. Ati et al. (2002), Sivakumar (1988). The isochrone method clearly needs the model to generate a realistic distribution of rainfall throughout the season in order to yield a realistic onset time.
It is important to re-iterate that the isochrone method that we use for local onset is not identical to agronomical local onset definitions. Marteau et al. (2009) showed that the potential for longrange predictability of agronomical onset appears to be low. The isochrone method described here aims to provide longrange information with a spatial structure for use in global seasonal forecast models.
Appendix 2: Station data
The MSLP observations used in this study are taken from HadISD (Dunn et al. submitted) a quality-controlled Integrated Station Data set. HadISD uses as its input sub-daily reports from WMO reporting stations between 1973 and 2010. We used HadISD MSLP data from stations in western Africa. For the months of June and July in the period 1979–2010 we calculated a daily mean for each station if at least six observations were reported that day. From these daily means we calculated two 15-day means: one for 15–29 June and one for 30 June–14 July if at least 10 daily means exist for each station for each 15-day period. The average pressure change of Fig. 8 is then calculated for each station as the difference between the average over all early July values (provided there are at least 15 years’ worth of 15-day means) minus the average over all late June averages (again requiring a minimum of 15 15-day means). If there are fewer than 15 years’ worth of either 15-day period (late June and early July) then that station is disregarded. Similarly, a regression of MSLP or surface temperature onto onset date (Fig. 14) is only calculated if there are at least 15 years’ worth of 15-day averages.
Appendix 3: Results from ENSEMBLES hindcasts
Rainfall climatologies of the six ENSEMBLES models for the West African monsoon are shown in Fig. 17, together with the onset date determined with precipitation-based onset indicator (1). The teleconnection between June SST and onset date in these hindcasts are shown in Fig. 18.
Time (horizontal) versus latitude (vertical) diagrams of time-average pentadal rainfall (mm/day), zonally averaged between 10°E and 10°W for 1 May hindcasts between 1979 and 2005 with ENSEMBLES models (names at top of each panel): ECMWF, Meteo France (METOF), CMCC-INGV (CMCCB) IFM-GEOMAR (IFMGM), UK Metoffice HadGEM (HDGEM) and DePreSys (DPSYS). The onset date in each of these time-mean datasets is stated in the subpanels and indicated by a vertical line
Teleconnection patterns between June SST and monsoon onset date in hindcasts with the ENSEMBLES models (1 May startdates for 1979–2005), units days/K. Significant regressions (at the 95 % level) are enclosed by contours. Model names are abbreviated as in Fig. 17
Appendix 4: Onset in MERRA reanalyses
The mean changes in MERRA reanalyses at the time of onset are shown in Fig. 19. The changes accompanying a late onset in MERRA are shown in Fig. 20.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Vellinga, M., Arribas, A. & Graham, R. Seasonal forecasts for regional onset of the West African monsoon. Clim Dyn 40, 3047–3070 (2013). https://doi.org/10.1007/s00382-012-1520-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-012-1520-z