Abstract
Based on a decade of research on cloud processes, a new version of the LMDZ atmospheric general circulation model has been developed that corresponds to a complete recasting of the parameterization of turbulence, convection and clouds. This LMDZ5B version includes a mass-flux representation of the thermal plumes or rolls of the convective boundary layer, coupled to a bi-Gaussian statistical cloud scheme, as well as a parameterization of the cold pools generated below cumulonimbus by re-evaporation of convective precipitation. The triggering and closure of deep convection are now controlled by lifting processes in the sub-cloud layer. An available lifting energy and lifting power are provided both by the thermal plumes and by the spread of cold pools. The individual parameterizations were carefully validated against the results of explicit high resolution simulations. Here we present the work done to go from those new concepts and developments to a full 3D atmospheric model, used in particular for climate change projections with the IPSL-CM5B coupled model. Based on a series of sensitivity experiments, we document the differences with the previous LMDZ5A version distinguishing the role of parameterization changes from that of model tuning. Improvements found previously in single-column simulations of case studies are confirmed in the 3D model: (1) the convective boundary layer and cumulus clouds are better represented and (2) the diurnal cycle of convective rainfall over continents is delayed by several hours, solving a longstanding problem in climate modeling. The variability of tropical rainfall is also larger in LMDZ5B at intraseasonal time-scales. Significant biases of the LMDZ5A model however remain, or are even sometimes amplified. The paper emphasizes the importance of parameterization improvements and model tuning in the frame of climate change studies as well as the new paradigm that represents the improvement of 3D climate models under the control of single-column case studies simulations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The representation of turbulent, convective and cloud processes is critical for climate modeling for a series of reasons. Clouds affect the latitudinal gradients of diabatic heating in the atmosphere, thereby forcing the general circulation. Their representation is key for the simulation of prominent climate features such as the Inter Tropical Convergence Zone (ITCZ) organization (Lindzen and Hou 1988; Hou and Lindzen 1992) or Madden-Julian Oscillation (Zhang 2005). Cloud feedbacks also constitute a major source of dispersion in global warming projections (Bony and Dufresne 2005; Webb et al. 2006). A good representation of boundary layer and convective processes is also a key issue for the coupling with the other components of the climate system: surface energy fluxes (which depend on turbulence and clouds) and rainfall for coupling with the ocean and continental surfaces, vertical transport of gaseous molecules or lifting and scavenging of aerosols. It is also essential for so-called impact studies which generally rely on statistics on the near surface meteorological variables and fluxes which determine the climates in the geographers’ sense.
In the last two decades, significant progress was made in the understanding of cloud and convective processes and paths towards new parameterizations were proposed. These works were coordinated at an international level in the framework of the GCSS Footnote 1 or Eurocs Footnote 2 projects. They benefited from the progress in observations—both satellite and in-situ on the occasions of coordinated field campaign experiments—and from the development of limited area non-hydrostatic models. Explicit simulations, with so-called cloud resolving models (CRM, with horizontal resolution of 1–2 km) are indeed able to represent reasonably well some important aspects of deep convection (Guichard et al. 2004; Redelsperger et al. 2000). Large Eddy simulations (LES), with a resolution of 20–100 m, are able to accurately simulate boundary layer dynamics (Moeng and Wyngaard 1988; Couvreux et al. 2005), cumulus clouds (Siebert and Frank 2003; Brown et al. 2002) or the transition from shallow to deep convection (Petch et al. 2002). A series of such explicit simulations, concerning various types of clouds or meteorological situations, were made available to the community. Evaluation against those reference simulations has become a central tool for the development of new parameterizations (see e.g. Lenderink et al. 2004; Guichard et al. 2004).
In the team of Laboratoire de Météorologie Dynamique (LMD) in charge of the development of the atmospheric general circulation model LMDZ (Z standing for the model zoom capacity), we have tried to pursue a double objective. In parallel with the development of the IPSL Footnote 3 climate system model, which required robust rather than sophisticated versions of the atmospheric code, work was done on the parameterization of boundary layer turbulence, dry and deep moist convection and clouds. These efforts have been capitalized recently in a brand new version of the physical package. The previous version LMDZ5A, based on “Standard Physics” (SP), was used in IPSL-CM5A to explore a large sample of the climate change simulations defined by the CMIP5 project. The “New Physics” (NP) package, that defines the LMDZ5B version of the atmospheric model, was used to produce a subset of CMIP5 simulations with IPSL-CM5B.
The boundary layer parameterization now relies on the combination of a classical eddy diffusion (Yamada 1983) with a mass-flux representation of the organized thermal structures of the convective boundary layer, the so-called “thermal plume model” (Hourdin et al. 2002; Rio and Hourdin 2008). The idea of combining a diffusive scheme with a mass flux scheme was first proposed by Chatfield and Brost (1987). It enables one to represent the upward convective transport in the mixed layer although this layer is generally marginally stable (Hourdin et al. 2002), solving a long recognized limitation of eddy diffusion (Deardorff 1966). This approach was developed independently by two teams and since adopted in several groups (Soares et al. 2004; Siebesma et al. 2007; Pergaud et al. 2009; Angevine et al. 2010; Neggers et al. 2009; Neggers 2009). Mass-flux schemes account reasonably well for the organized structures (thermal plumes, or rolls) of the convective boundary layer. Their properties are used in the new model version for coupling with deep convection and also to better parameterize the boundary layer clouds (Rio and Hourdin 2008; Jam et al. 2011).
With respect to deep convection, the developments were motivated in particular by what was long considered as a deadlock: parameterized deep convection tends to peak at noon, in phase with insolation, while the observed convection is usually maximum between mid afternoon and midnight. The SP and NP versions of LMDZ5 share the same Emanuel (1991) scheme but the convective closure (that determines the convective mass flux at cloud base) and triggering which were relying in the SP version on the large scale vertical profiles of temperature and humidity (through notions like Convective Available Potential Energy or CAPE) are now based on the sub-cloud processes. The coupling of the convective parameterization with those of sub-cloud processes is done through the notions of Available Lifting Energy (ALE, which must overcome the convective inhibition, or CIN, for triggering) and Available Lifting Power (ALP) that controls the convective closure. Both quantities are computed from internal variables of the “thermal plume model” and of a new parameterization of the cold pools created by re-evaporation of convective rainfall in the sub-cloud layer (Grandpeix and Lafore 2010; Grandpeix et al. 2010). The potential role of cold pools in controlling the life cycle of continental convection has been recognized for a while (Zipser 1969; Houze 1977; Lima and Wilson 2008) but no parameterization has been available as yet.
The developments of the new parameterizations were essentially conducted and evaluated in single-column versions of the LMDZ model by comparison with explicit CRM or LES simulations on a series of case studies. Several important improvements of the new parameterizations were demonstrated in that framework: (1) accounting for the organized structures of the convective boundary layer through the thermal plume model allows the boundary layer thermodynamical and wind profiles to be well represented both in terms of quasi-stationary state over the ocean and of diurnal cycle over the continents (Rio and Hourdin 2008); (2) coupling with a bi-Gaussian statistical cloud scheme leads to a good representation of the associated cumulus clouds (Jam et al. 2011); (3) coupling of the convective mass-flux scheme with the thermal plume model and cold pools results in a shift of several hours of the diurnal cycle of convective rainfall over continents, which is in much better agreement with observations and CRM results (Rio et al. 2009).
The aim of the present paper is twofold. It describes the development of the new LMDZ5B 3D model. It also documents and analyses the effect of its new parameterizations on its climatology, its variability and its sensitivity to greenhouse gases as represented in the IPSL-CM5 coupled atmosphere-ocean simulations. We insist on the importance of free model parameters tuning, an often hidden but fundamental aspect of climate modeling. Tuning is needed because the models, and in particular the parameterizations of physical processes, are only approximate representation of reality. The picture of a mean plume representing the organized structures of the boundary layer allows to derive a set of mathematical equations at the basis of the parameterization. But, in fine, the parameters of the models must be tuned so that the mean plume accounts as closely as possible for the behavior of an ensemble of clouds. In this particular case, the tuning can be done in a large part on simulations of case studies validated by comparison with observations or explicit high resolution simulations. However, even after the tuning of individual parameterizations, when possible, the 3D model still requires a final tuning of free parameters, in order to insure in particular that radiative fluxes balance globally at atmospheric top for present-day condition.
Here, we present (Sect. 2) the rationale that drove the development of the NP version. We show illustrations from the single-column simulations that underline the main improvements and describe the work which had to be done to pass from parameterization new concepts and developments to 3D climate modeling. Section 3 addresses the issue of free parameters tuning for the 3D atmospheric model, and to the compromises done to guarantee some important constraints for the coupled IPSL model. In Sect. 4, we illustrate how the changes in physics did modify some important aspects of the model mean climatology and variability, as well as its sensitivity to greenhouse gases. Climate sensitivity results are based on climate change simulations which will be available on the CMIP database. The conclusions (Sect. 5) underline the robust improvements that come from the change in physical parameterizations, the importance of the tuning phase as well as the change of paradigm that constitutes the fact that the new parameterizations were evaluated in details in single-column mode on selected case studies.
2 The LMDZ5 “New Physics”
2.1 LMDZ5 and IPSL-CM5
LMDZ5 is the current version of the LMDZ atmospheric general circulation model (Hourdin et al. 2006) which is used for climate studies, climate change projections and environmental studies. LMDZ5 is the atmospheric component of the IPSL Coupled Model (IPSL-CM5) used in particular for climate change projections in the frame of CMIP5. In IPSL-CM5, LMDZ5 is coupled to Orchidee over continental surfaces (Krinner et al. 2005) and Nemo3.2 over the oceans, which uses the Orca2 grid, Lim2 for sea-ice and Pisces for biochemistry (see Dufresne et al., submitted).
The LMDZ dynamical core is based on a mixed finite difference/finite volume discretization of the primitive equations of meteorology and transport equations. It is coupled to a set of physical parameterizations. The Morcrette (1991) code is used for radiative transfer. Effects of subgrid-scale orography are accounted for both through drag and lifting effects on the obstacles and through generation and propagation in the atmosphere of gravity waves (Lott and Miller 1997). The LMDZ5A and LMDZ5B configurations of LMDZ5 differ by the activation of a different set of parameterizations for turbulence, convection and clouds.
The parameterizations of the SP version LMDZ5A are close to that of the previous LMDZ4 version (Hourdin et al. 2006). The boundary layer turbulence is parameterized as a diffusion with an eddy diffusivity which depends on the local Richardson number. A counter-gradient term on potential temperature (Deardorff 1972) as well as a dry convective adjustment are added to handle dry convection cases which often prevail in the boundary layer. The standard version also includes the Emanuel (1993) scheme for deep convection and the Bony and Emanuel (2001) statistical cloud scheme. This version is described further by Hourdin et al. (submitted).
2.2 The NP version LMDZ5B
The development of the new set of physical parameterizations that defines the LMDZ5B version was motivated by the importance of clouds for climate and climate sensitivity (Bony et al. 2006), and by known weaknesses of current climate model parameterizations such as the under-estimation of shallow cumulus clouds (Zhang et al. 2005) or the unrealistic phasing of the diurnal cycle of parameterized convection over continents (Guichard et al. 2004).
The new set of parameterizations relies on the separation of three distinct scales for the turbulent and convective subgrid-scale vertical motions:
-
1.
The small scale (10–100 m), associated with random turbulence, dominant in particular in the surface layer.
-
2.
The boundary layer height (500 m-3 km) that corresponds to the vertical scale of organized structures of the convective boundary layer.
-
3.
The deep convection depth (10–20 km) of cumulonimbus, meso-scale convective systems or squall lines.
The way parameterizations separate the various components of the convective/turbulent motions is debated in the community. Some authors favor for instance the idea of unified convection schemes (Kuang and Bretherton 2006; Hohenegger and Bretherton 2011). Here, the treatment of dry and cloudy shallow convection is unified while there is a separate treatment for deep convection. This separate treatment is motivated by the differences in dominant processes and spatial organization. While shallow convection can be seen as an organization mode of the convective boundary layer turbulence, rainfall plays a crucial role in deep convection, both locally in the convective column, and through the cold pools created below cumulonimbus by rainfall re-evaporation.
2.2.1 Boundary layer
The first two scales dominate the vertical subgrid-scale transport in the boundary layer. In the “new physics”, the parameterization of this vertical transport relies on the combination of a diffusion scheme for small scale turbulence and a mass-flux model of the organized structures of the convective boundary layer, the so-called “thermal plume model” (Hourdin et al. 2002; Rio and Hourdin 2008).
The computation of the eddy diffusivity K z is based on a prognostic equation for the turbulent kinetic energy, according to Yamada (1983). It is mainly active in practice in the surface boundary layer, typically in the first few hundred meters above surface.
The mass flux scheme represents an ensemble of coherent ascending thermal plumes in the grid cell as a mean plume. A model column is separated in two parts: the thermal plume and its environment. The vertical mass flux in the plume f th = ρ α th w th —where ρ is the air density, w th the vertical velocity in the plume and α th its fractional coverage—varies vertically as a function of lateral entrainment e th (from environment to the plume) and detrainment d th (from the plume to the environment):
For a scalar quantity q (total water, potential temperature, chemical species, aerosols), the vertical transport by the thermal plume (assuming stationarity) reads
q th being the concentration of q inside the plume (air is assumed to enter the plume with the concentration of the large scale, which is equivalent to neglect the plume fraction α th in this part of the computation). The time evolution of q finally reads
with
The vertical velocity w th in the plume is driven by the plume buoyancy g (θ th − θ)/θ. The thermal plume fraction is also an internal variable of the model. The computation of w th , α th , e th and d th is a critical part of the code. We test here two different versions of the e th and d th computation presented in details by Rio and Hourdin (2008) and Rio et al. (2010) respectively.
2.2.2 Cold pools
The wake model is fully described in Grandpeix and Lafore (2010) and Grandpeix et al. (2010). Only a sketch of the scheme is presented here.
The model represents a population of identical circular cold pools (the wakes) with vertical frontiers over an infinite plane containing the grid cell. The wakes are cooled by the convective precipitating downdrafts, while the air outside the wakes feeds the convective saturated drafts.
The wake centers are assumed statistically distributed with a uniform spatial density D wk. The wake state variables are their fractional coverage \(\sigma_w$ ($\sigma_w = D_{\rm wk} \pi r^2\) where r is the wake radius), the potential temperature difference δθ(p) and the specific humidity difference δq v (p) between the wake region (w) and the off-wake region (x). δθ(p) and δq v (p) are non zero up to the homogeneity level p h = 0.6p s (where p s is the surface pressure). Above p h the sole difference between (w) and (x) regions lies in the convective drafts (saturated drafts in (x) and unsaturated ones in (w)).
Wake air being denser than off-wake air, wakes spread as density currents, inducing a vertical velocity difference δω(p) between regions (w) and (x) (δω(p) > 0). The vertical profile δω(p) is imposed piecewise linear. Especially, between surface and wake top (the altitude h w where δθ crosses zero) the slope corresponds to wake spreading without lateral entrainment nor detrainment.
The wake geometrical changes with time are due to the spread, split, decay and coalescence of the wakes. Split, decay and coalescence are merely represented by imposing a constant density D wk and by assuming that when σ w reaches a maximum allowed value (=0.5) some wakes vanish (i.e. mix with the environment) while others split so that the fractional cover σ w stays constant. The spreading rate of the wake fractional area σ w reads:
where C *, the mean spread speed of the wake leading edges, is proportional to the square root of the WAke Potential Energy WAPE: \(C_{\ast} = k_{\ast} \sqrt{2 {\rm WAPE}}\) and \({\rm WAPE} = -g \int_0^{h_{w}} {\frac{\delta \theta_v}{\overline{\theta_v}}}dz\) where, k *, the spread efficiency, is a tunable parameter in the range 1/3–2/3 and θ v is the virtual potential temperature.
The energy and water vapor equations are expressed at each level yielding prognostic equations for δθ(p) and δq v (p) as well as contributions to the average temperature \(\overline{\theta}\) and average humidity \(\overline{q_v}\) equations.
The convective scheme is supposed to provide separately the apparent heat sources due to saturated drafts and to unsaturated drafts, which makes it possible to compute the differential heating and moistening feeding the wakes.
2.2.3 Deep convection
As in the standard LMDZ5 version, the LMDZ5B version uses the buoyancy sorting mass-flux scheme of Emanuel (1993), with modified mixing (Grandpeix et al. 2004) and splitting of the tendencies due to saturated and unsaturated drafts. The precipitation efficiency is computed as a function of the in-cloud condensed water and temperature following Emanuel and Zivkovic-Rothman (1999). It is bounded by a maximum value ep max which is slightly less than unity to allow some cloud water to remain in suspension in the atmosphere instead of being entirely rained out (Bony and Emanuel 2001).
The parameterizations of triggering and closure have been deeply modified in the NP version as explained in the introduction, using the Available Lifting Energy (ALE) and Available Lifting Power (ALP) provided by sub-cloud lifting processes. The ALE allows to overcome the Convective INhibition (CIN) so that convection is triggered when ALE > |CIN|. The closure consists in prescribing the mass flux M at the top of the inhibition zone as:
where w B is the updraft speed at the level of free convection. The original constant value w B = 1 m/s was replaced by a function of the level of free convection as explained below.
In the NP version of LMDZ, two processes are taken into account for both ALE and ALP: (1) the ascending motions of the convective boundary layer, as predicted by the thermal plume model and (2) the air lifted downstream of gust fronts. ALE is the largest of the lifting energies provided by the two processes: ALE = max(ALE th , ALE wk) where ALE th scales with w 2 th and ALE wk = WAPE. ALP is the sum of the lifting powers provided by the two processes: ALP = ALP th + ALP wk where ALP th scales with w 3 th and ALP wk scales with C 3* .
This coupling between cold pools (generated by convection) and convection (triggered in turn and fed by cold pools) allows for the first time to get an autonomous life cycle of convection, not directly driven by the large scale conditions.
2.2.4 Clouds
The fractional cloudiness α c and condensed water q c are predicted by introducing a subrid-scale distribution P(q) of total water q so that:
where q sat (T) is the grid averaged saturation specific humidity in the mesh.
For deep convection, we assume that the subgrid-scale condensation and rainfall can be handled by the Emanuel scheme, so that this statistical cloud scheme is used only to predict the fractional cloudiness for the radiative transfer. Following Bony and Emanuel (2001), the in-cloud water (q inc = q c /α c ) predicted by the convective scheme is used, through an inverse procedure, to determine the variance σ of a generalized log-normal function bounded at 0. With this particular function, the skewness of P(q) increases with increasing values of the unique width parameter ξ = σ/ q.
For other types of clouds, the statistical cloud scheme is used to compute not only the cloud properties for radiation but also “large scale” condensation.
If the thermal plume is not active in the grid box (in practice if f th = 0), the width parameter ξ of the generalized log-normal function is specified as a function of pressure: ξ(p) increases linearly from 0 at surface to ξ600 = 0.002 at 600 hPa, then to ξ300 = 0.25 at 300 Pa. It is kept constant above.
When f th > 0 in the grid box, two options are available. Either we use the Bony and Emanuel (2001) procedure to invert the width parameter ξ from the knowledge of the condensed water computed in the thermal plumes (like what is done for deep convection) or we use a new statistical cloud scheme proposed by Jam et al. (2011) in which the sub-grid scale distribution of the water saturation deficit (rather than total water) is parameterized as the sum of two Gaussian functions, representing the variability within and outside the thermal plume respectively. The width of each Gaussian varies as a function of the thermal plume fractional cover α th and of the contrast in saturation deficit between the plume and its environment.
A fraction f iw of the condensed water q c is assumed to be frozen. This fraction varies as a function of temperature from f iw = 0 at 273.15 K to f iw = 1 at 258.15 K.
The condensed water is partially precipitated. Derived from Zender and Kiehl (1997) formula for an anvil model, the associated sink is
where w iw = γ iw × w 0, w 0 = 3.29(ρq iw )0.16 being a characteristic free fall velocity (in m/s) of ice crystals given by Heymsfield and Donner (1990) and γ iw a parameter introduced for the purposes of model tuning (ρ in kg/m3).
For liquid water, following Sundqvist (1978), rainfall starts to precipitate above a critical value clw (0.6 g/kg in the reference version) for condensed water, with a time constant for auto-conversion τ convers (=1,800 s) so that
A fraction of the precipitation is re-evaporated in the layer below and added to the total water of this layer before the statistical cloud scheme is applied. For ice particles, we assume that all the precipitation re-evaporates. For liquid water, following Sundqvist (1988), we assume that
where P is the precipitation flux, and β a tunable parameter.
The effective radius of cloud droplets depends on the aerosol concentration which is specified as a function of space and season as explained by Dufresne et al., this issue. The effective radius of ice crystals varies linearly as a function of temperature between er iw,max at 0 °C and er iw,min at −84.1 °C.
2.3 1D evaluation
2.3.1 The single-column framework
In the last decades, single-column models have become a central tool for the development and evaluation of physical parameterizations. In this approach, the coupling between the local atmospheric column and large scale dynamics is replaced by an imposed forcing: surface fluxes or temperature, large-scale advection of heat and moisture plus radiative heating if not computed interactively. A number of case studies have been developed addressing in particular convection and clouds. The case studies are often derived from field campaign experiments for which a lot of in-situ or remote sensing observations are available.
If enough observations are available to prescribe properly the large-scale forcing and adequately sample the relevant variables, one can evaluate single-column simulations against real observations. However, they are more often compared with the results of full 3D non-hydrostatic high-resolution simulations. This approach presents several advantages: (1) the same forcing can be applied to the 3D explicit simulation and to the single-column model, (2) the explicit simulation gives access to any variable at any time and location in the domain and (3) the forcing parameters can be arbitrarily varied to test the response of the physical parameterizations in the single-column model. The counterpart is that the explicit simulations can depart from observation.
Most developments and improvements of the LMDZ new physical parameterizations were undergone in this single-column framework. We show below results of single-column simulations that illustrate the improvements of the new parameterizations with respect to the previous SP version. Those tests are performed with the NPv3 version of the NP parameterizations, which is used in the 3D simulations as explained later on.
2.3.2 Boundary layer clouds
Figures 1 and 2 illustrate two cases of convective boundary layer with shallow cumulus. The first one is the Eurocs fair-weather cumulus case, built from observations of the ARM site in Oklahoma (Brown et al. 2002; Lenderink et al. 2004). This case has been used systematically during the development of the thermal plume model (Rio and Hourdin 2008; Couvreux et al. 2010; Rio et al. 2010). The difference with previously published results is that the single-column simulations shown here are performed with exactly the same version of the model as in the full climate model, with the same tuning of free parameters (see next section). In particular, the deep convection parameterization is uninhibited here, whereas it was intentionally switched off in the publications mentioned above. The second one is a case of marine drizzling cumulus based on the Rico campaign (Rauber et al. 2007; VanZanten et al. 2011). This case was not used during the model development and so offers an independent evaluation of the new scheme.
Time evolution of the vertical profile of cloud fraction (in %, colors) for two test cases of shallow cumulus: the Eurocs cumulus continental case (left) and the Rico oceanic case (right). Results of the SP (lower panels) and NP (middle) versions of LMDZ5 ran in single-column mode are compared with LES results (upper panels). The contours show the specific humidity (in g/kg) for the Eurocs case and the difference of the specific humidity with its initial value for Rico
Vertical profile of liquid potential temperature θ l (K), specific humidity r t (g/kg), zonal and meridional wind (m/s) for the 8th hour of the Eurocs cumulus simulation (13:30 local time). We show the results of the MesoNH LES (gray) and SP and NP single-column simulations with LMDZ5. The last two panels show the thermal plume vertical velocity (m/s) and fractional cover in the NP simulation and diagnosed through the tracer-based sampling of thermal plumes in LES (Couvreux et al. 2010)
The LMDZ single-column results are compared with those of 3D Large Eddy Simulation (LES) performed with the MesoNH model with meshes of the order of 50 m (see Couvreux et al. 2010, for more details). The Eurocs single-column simulation is performed with 40 levels on the vertical between the surface and 4 km and the Rico simulation with 80 layers covering the whole troposphere.
We first show in Fig. 1 the time evolution of the cloudiness vertical profile. The improvement from the SP to NP version is clear on those graphs, with much deeper clouds, even if the vertical extent remains a bit underestimated. The comparison of vertical profiles of liquid potential temperature and specific humidity (first two panels in Fig. 2) shows that the boundary layer is also better represented in the NP version with a well-mixed layer below 1 km and a cloud layer between 1 and 2 km. Note also the better representation of the horizontal wind which is well mixed between the top of the surface layer (at 200 m) and the cloud base (1 km) and gradually reaches the imposed geostrophic wind (U, V) = (10, 0) m/s in the free troposphere. In the SP version, the boundary layer is confined to the first kilometer or so, and almost no cloud layer develops above.
In addition, the thermal plume model provides a characterization of the organized structures of the convective boundary layer. As an illustration, we show for the same hour of the Eurocs case, the plume vertical velocity and fractional cover obtained in the NP simulation (last two panels in Fig. 2). It is compared with values obtained thanks to a tracer-based sampling of the thermal plumes of the LES (Couvreux et al. 2010). The adequate representation of these internal variables is crucial for the simulation of the vertical transport of trace species. These variables also enter in the definition of the ALE and ALP used for triggering and closure of the deep convection parameterization.
2.3.3 Diurnal cycle of convection
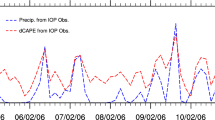
The second improvement, concerning the representation of the diurnal cycle of deep convection over continents (Rio et al. 2009), is illustrated in Fig. 3 for the ARM case of Guichard et al. (2004). The SP version tends to predict a rainfall in phase with insolation, as most convective parameterizations do. The convection maximum is delayed by about four hours with the NP version, in much better agreement with CRM results. The thermal plume model plays a key role in preconditioning the boundary layer in the morning and controlling the early phase of deep convection while the addition of the cold pool parameterization allows an amplification and self-maintenance of convection in late afternoon, with a slightly underestimated intensity when compared with CRMs.
Diurnal cycle of rainfall for the Eurocs ARM continental case of deep convection. The dots correspond to four of the results of CRM simulations presented in Guichard et al. (2004)
2.4 Switching to new parameterizations in the 3D model
2.4.1 From case studies to global climate
To be qualified for 3D climate modeling, a parameterization must be valid both over ocean and continents, from the poles to the equator, on deserts or wet lands. Two important points had to be addressed in that respect when finalizing the LMDZ5B version.
The first issue concerns the convective closure: the set of free parameters which was retained by Rio et al. (2009) for the ALP convective closure, based on the 1D ARM case, was not satisfactory for oceanic cases. Introducing a height dependency in the vertical velocity at cloud base (w B ) used in the ALP-closure (Eq. 6) allowed to reconcile the case of continental convection with oceanic cases. This modified ALP closure is discussed in details by Rio et al. (submitted).
The second point concerns the treatment of strato-cumulus. Although some encouraging work is done currently on the thermal plume model in that direction, the current version does not represent properly strato-cumulus clouds. Strato-cumulus are known to be especially prominent at the eastern side of tropical oceans. On the other hand, the Yamada (1983) scheme alone performs quite well for those particular conditions. A kludge is thus introduced in the model, which consists in identifying the atmospheric columns with a sharp temperature inversion at the boundary layer top, and turning off the thermal plume model in those particular cases. In practice, if
then the thermal plume parametrization is arbitrarily switched off. This test is in fact inherited from the standard LMDZ5 model where it was used to switch between two different computations of the K z coefficient with the same goal of contrasting the regions of strato-cumulus and trade-wind cumulus on tropical oceans. We show in Fig. 4 the regions selected by this criteria on a typical simulation done with LMDZ5B (the NPv3 simulation which is analyzed later on).
2.4.2 Vertical resolution
A major difference between 1D and 3D is the issue of numerical cost. This puts some constraints on the complexity of the parameterizations but also on the resolution at which those parameterizations are used.
The vertical and horizontal discretization are often a compromise between the expected improvement coming from an increased resolution, and numerical cost. The question of horizontal resolution is discussed by Hourdin et al. (submitted). For grid mesh coarser than a few tens of km, the horizontal resolution is not an issue for the parameterizations, except for the organization of deep convection which covers a very large range of scales.
The question of vertical discretization is more crucial for boundary layer and cloud parameterizations. The parameterizations of the convective boundary layer presented above require an explicit representation of the decrease of potential temperature with height in the first few hundreds meters above surface. The parameterization of lateral entrainment and detrainment (Rio et al. 2010) also shows very sharp variations at the inversion level, where water vapor can vary by an order of magnitude and the temperature by several degrees over only a few tens of meters.
In the current version, we retained the same L39 discretization as in the LMDZ5A configuration. It was found to be fine enough to capture most of the boundary layer structures.
We illustrate in Fig. 5 for the Rico case of precipitating shallow cumulus how the cloudiness and specific humidity degrade when using the L39 vertical grid of the 3D model (red curve) rather than the L80 grid used for single-column simulations (black curve). The use of a coarser grid and time step clearly impacts the cloud cover but less than the change of parameterization. However, an increase of vertical resolution, or alternatively a modification of the parameterization which would allow to account for subgrid scale transitions on the vertical (in particular at cloud bottom and cloud top) would be better.
Effect on the LMDZ5B single-column simulations of the Rico case of changing the vertical grid or time step. We show the mean cloudiness (left) and specific humidity (g/kg, right) profiles averaged between hour 6 and 12 of the simulation. The single-column integration shown in Figs. 1 and 8 are run with the L80 vertical grid and a time step of 60 s. They correspond to the black curve here. The L39 grid is that of the 3D model. The green curve corresponds to the L39 vertical discretization and 450 s time step of the 3D climate simulations
2.4.3 Numerical stability
The parameterizations presented above, although being a crude representation of the full meteorology, are already quite sophisticated. The number of equations and internal variables of those parameterizations grows, with often poor control on the behavior of the mathematical equations and appropriate numerical methods to handle them in a climate model. In particular, the parameterizations of boundary layer presented above tend to show important numerical oscillations when long time steps are used.
In the current version of the LMDZ model, the primitive equations are integrated with a 3 min time step (there is no filtering of gravity waves). In the standard version LMDZ5A, the physical parameterizations are coupled to primitive equations every 30 min. This is not a fine enough time step for the NP parameterizations. The single-column simulations of case studies are typically performed with a 1 or 2 min time step. For the 3D simulation, a 7.5 min time step is used, which does not inhibit all numerical oscillations.
We show in Fig. 5 results obtained for the Rico case using the L39 vertical grid with either a 60 s time step (red) or the 450 s time step of the 3D model (green). Once again, the impact of using a larger time step is significant, but weaker than the impact of changing parameterization.
2.4.4 Tuning of free parameters
The last but essential step in the finalization of a model version to be used in climate change projections is the tuning of free parameters.
In forced simulations, the imposed distribution of Sea Surface Temperatures (SSTs) puts a strong constraint on the atmospheric general circulation. Even in this case, significant biases can be obtained in the mid-troposphere or over continents if, for instance, cloud parameters have not been tuned. The issue is even more crucial when coupling the atmosphere to an ocean model. In the range of uncertainty of the model free parameters, the radiative impact of clouds can vary by several tens of W/m2. Systematic biases in surface fluxes will produce significant biases in SSTs which, in turn, will strongly affect the climate over continents.
When tuning the model, choices and compromises must be made, which may depend on the scientific question addressed and will remain, at the end, arbitrary. The strategy followed for the LMDZ5B tuning and the sensitivity of the model results to parameterization changes and tuning is discussed in the next section.
3 Improvements and tuning
3.1 Tuning strategy
3.1.1 Key targets for tuning
When tuning the LMDZ5B free parameters, the first priority was given to the global radiative balance.
The tuning of the net top-of-the-atmosphere (TOA) radiative balance determines the global energy budget of the climate system. With a perfect model, it is expected that an exact balance in simulations forced by present day observed SSTs should guarantee a stable climate in the coupled atmosphere-ocean simulations, i.e. with no drift in the SSTs. In fact, since we are in a warming transient phase due to greenhouse gases increase, the present-day balance is probably closer to 0.5–1 W/m2 which corresponds to heat storage in the ocean.Footnote 4 In practice for LMDZ5B, an unbalance of −2.5 W/m2 is needed in the forced-by-SSTs simulation in order to obtain, in the coupled model, a stable climate with a mean surface temperature close to present day observations.
The final tuning of the net balance is a key issue. Changing this tuning by 1 W/m2 will typically shift the mean surface temperature by 1 K. Because of the robust spatial patterns of the SST biases in global climate models, this gives a certain degree of freedom. One can favor having the best global SSTs, or best average surface temperature over continents, or best mean temperature in a particular region of the globe.
Regarding radiative fluxes, we also consider the following targets for tuning:
-
1.
the latitudinal variations which drive the atmospheric general circulation;
-
2.
the absolute global values of the absorbed solar radiation and outgoing long-wave radiation at TOA (the difference of which gives the net balance);
-
3.
the decomposition between clear sky fluxes and cloud radiative forcing (CRF);
-
4.
the dependency of the radiative flux on the large scale dynamics, using the ω500 regime sorting of Bony et al. (1997);
-
5.
ocean/continent contrasts, in the tropics, which is key for monsoon circulation.
Regarding meteorological variables, reducing as far as possible the biases in the mean meridional structure of the zonal wind, temperature and humidity was the main target.
3.2 A set of sensitivity experiments
The model depends on probably more than one hundred parameters. Some of them have a well-known value such as the gravity or the solar constants. About 15 of them, mostly related to clouds and convection, were actually used for the tuning of the LMDZ5B model. Those parameters were chosen somewhat arbitrarily, both because they are quite uncertain and for their significant impact on the radiative fluxes.
During the development and tuning of the NP version of LMDZ5, many simulations were performed with the same set of values of the tunable parameters for both the 1D test cases and 3D forced-by-SSTs simulations. In the 3D simulations, the mean seasonal cycle of the AMIP SSTs (Hurrell et al. 2008) for the period 1970–2000 was used as boundary condition. The grid used for the 3D simulations is the low resolution grid retained at IPSL for the CMIP5 experiments. It is based on 96 longitudes (3.75° resolution) and 95 latitudes (1.9°) on the horizontal. The standard L39 vertical grid of LMDZ5 is also used in these simulations. See Hourdin et al. (submitted) for a discussion on the choice of this particular grid.
To demonstrate the added value of the new parameterizations and underline the importance of parameter tuning, we defined a posteriori a set of nine sensitivity experiments, in which we start from the final tuning of the model. This final tuning defines the NPv3 version used for CMIP5 simulations.
The list of the sensitivity experiments is given in Table 1 together with the value of the modified parameter. The first four simulations (TH08, TH10, CLDTAU and CLDLC) are expected to modify mainly the low and mid-level clouds. The following four (EPMAX, FALLICE, RQD and ICEER) are expected to modify humidity, temperature and cloudiness in the mid and upper troposphere. The last one (DRAGOCE) concerns surface drag on the oceans. Because of the low reliability of the surface drag computation in the LMDZ5 SP and NP versions, a factor is applied to the surface exchange coefficient for water and temperature, and used as a tunable parameter. This parameter is set to 0.8 in the SP and DRAGOCE experiments and to 0.7 in the NPv3 simulation.
3.3 Clouds
The tuning of the 3D model was done mainly on parameters that control radiative fluxes through clouds and atmospheric humidity.
A consistent comparison between model clouds and space observations is made possible by the use of so-called observations simulators (Yu et al. 1996), which diagnose from model outputs what different satellites would observe from space if they were flying in orbit around the model’s atmosphere.
Figure 6 shows the zonal and annual mean of the cloud fraction as simulated with the NPv3 version of the model and as observed by the Caliop Lidar onboard the Calipso satellite (Winker et al. 2007). The Calipso-GOCCP (Chepfer et al. 2010) data set is used here as it has been developed to be consistent with the Calipso-COSP simulator outputs (Chepfer et al. 2008; Bodas-Salcedo et al. 2011). We separate the low (surface to 680 hPa), mid (680–440 hPa) and high (above 440 hPa) level clouds. We compare with observations both the model cloud cover and that derived from the Calipso-COSP simulator.
The use of the simulator is particularly important in the case of low or mid-clouds overlapped by upper-levels clouds. A difference between model (viewed through the simulator) and observed low clouds can be due to a difference in the masking effect of higher clouds.
3.3.1 Low- and mid-level clouds
We illustrate in Fig. 7 how the changes in boundary layer parameterizations improved the representation of the low and mid-level cloud coverage with respect to the SP version. The SP version strongly underestimates the low and mid-level clouds, a common feature in climate models (Zhang et al. 2005). The increase in low level clouds in the NP version is consistent with the single-column results (Fig. 1). Significant changes, although not systematic, are also visible when comparing NPv3 with TH08 and TH10. TH08 and TH10, which differ from each other by the specification of lateral entrainment/detrainment of the thermal plume, are close to each other.
Mid and low level cloud fraction (%) obtained with the SP and NPv3 versions of LMDZ, and in the TH08 and TH10 simulations. The gray dots correspond to GOCCP observations. The black curve and gray dots are the same as in Fig. 6
On the other hand, introducing the bi-Gaussian cloud scheme (Jam et al. 2011) induces a stronger effect (comparing TH10 and NPv3).
The NPv3 version also systematically simulates more mid-level clouds than SP and a little bit more than TH08 and TH10. The changes here may not be due only to the change in the boundary layer parameterizations but also to the modification of the convective closure.
These changes are highlighted by the 1D simulations shown in Fig. 8. For the Eurocs cumulus case, the improved parameterization of the thermal plume lateral entrainment and detrainment (from TH08 to TH10) produces a better representation of the deepening of the boundary layer in the afternoon. However, both simulations produce vertical profiles of the cloud fraction that do not peak at cloud base, as it does in the LES (Fig. 1). Using the bi-Gaussian scheme coupled to the thermal plumes (NPv3 simulation in Fig. 1) produces much more realistic vertical profiles. The impact is even stronger in the Rico case as illustrated in the right panels of Fig. 8. During the first hours of the Rico simulation, as for Eurocs, the cloud cover shows a marked and unrealistic maximum in the upper part of the cloud in TH08 and TH10. In-cloud condensation produces rainfall that re-evaporates in the sub-cloud layer which rapidly moistens, explaining the later apparition of clouds close to the surface. Note that this behavior was not visible in the case of non precipitating marine cumulus used for the development of the thermal plume model (see e.g. Rio et al. 2010).
Time evolution of the vertical profile of cloud fraction (in %, colors) for the Eurocs cumulus continental case (left) and the Rico oceanic case (right). Results are shown for the TH08, TH10, CLCTAU and CLDLC simulations. The contours show the specific humidity (in g/kg) for the Eurocs case and the difference of the specific humidity with its initial value for Rico
Increasing from 30 min to 2 h the time constant of the cloud autoconversion rate τ convers (CLDTAU) or reducing from 0.6 to 0.1 g/kg the critical value for the in-cloud condensed water clw (CLDLC) has a much weaker effect than the changes of parameterizations, as seen both for the 3D model (by comparing Figs. 7 with 9) and in the single-column simulations (Figs. 8, 1). The mid-level clouds are also weakly affected in the tuning experiments.
3.3.2 High-level clouds
For high clouds, changes in parameterizations and tuning of free parameters have a comparable impact (see Fig. 10). High clouds significantly depend on the fall velocity of ice crystals (FALLICE) and on the maximum precipitation efficiency (EPMAX) of the convective scheme. The difference between the SP and NPv3 simulations actually comes for a large part from the use of a larger value of ep max and a smaller value of γ iw . Increasing ep max (i.e. reducing the condensed water detrained by the convection in the upper troposphere) slightly reduces the high cloud fraction close to the convective regions, while reducing γ iw has an effect along the trajectory of air parcels at all latitudes. This explains the over estimation of high cloud cover in the SP and FALLICE simulations with respect to NPv3, particularly strong in mid to high latitudes. A decrease of the parameter ξ300, which controls the width of the sub-grid scale total water distribution for large-scale clouds in the upper troposphere (RQH), has a similar impact.
3.4 Radiative fluxes
The effect of changes in parameterizations (left column) and free parameters tuning (right column) on the TOA radiative fluxes is shown in Fig. 11 for the latitudinal variations and Fig. 12 for tropical dynamical regimes, the corresponding global mean values being given in Table 2.
Zonal mean of the 10-year average of the TOA total (LW+SW) net radiation (upper row), total CRF (second row), SW CRF (third row) and LW CRF (fourth row) in W/m2. The left column shows the sensitivity to parameterization changes and the right one the free parameter sensitivity experiments. For the right column, the sensitivity experiments that affect more the low clouds are shown in red (CLDLC, CLDTAU, DRAGOCE) and those that affect more the high clouds in green (EPMAX, FALLICE, ICEER, RQH). For each panel, a thick line is used (red or green) to highlight one particular sensitivity experiment. Observations (gray dots) correspond to the The CERES Energy Balanced and Filled (EBAF) dataset, developed to remove the inconsistency between average global net TOA flux and heat storage in the Earth-atmosphere system Loeb et al. (2009)
Regime sorting (as a function of the vertical velocity ω500 at 500 hPa) of the TOA total (LW+SW) net radiation (upper row), total CRF (second row), SW CRF (third row) and LW CRF (fourth row) in W/m2. Same conventions and remarks as for Fig. 11
The latitudinal variations of the TOA total radiation (upper panels in Fig. 11), which in part reflect the latitudinal variations of insolation, are captured rather well. All simulations except CLDLC (highlighted as a thick red curve) tend however to underestimate the net radiation in the southern mid-latitudes. The regime dependence of this TOA total radiation (upper panels in Fig. 12) is rather well simulated for the various sensitivity experiments.
Among the various tunings of the NP version, differences in net radiation are dominated by the changes in cloud radiative forcing, the clear-sky radiation (not shown) being less affected.
The impact of the switch from SP to NP is particularly strong in the tropics. The SW CRF in the tropics was strongly underestimated in the SP version, and in particular in convective regimes (large negative values of ω500 in Fig. 12). The TH10 and NPv3 versions are closer to observations, both in terms of latitudinal variations and regime sorting. Tuning experiments do not really affect the shape of the SW CRF in the tropics but can change the mean value by several W/m2. The improvement of tropical SW CRF is thus a robust feature of the new parameterizations. In the mid-latitudes, the SW CRF is more sensitive to parameter tuning. The tuning retained for NPv3 is significantly too negative in the southern mid-latitudes, which explains the bias already mentioned for the total net radiation.
Changes in LW CRF are closely related to the changes in high-level clouds discussed above. Decreasing ep max, γ iw or ξ300 increases the high-levels cloud cover and in turn the LW CRF. As already discussed, the effect of ep max is particularly strong in regions of deep convection. This is clearly illustrated in the regime sorted graph. Both the SW CRF and LW CRF are in fact intensified in the convetive regimes (large negative values of ω500) in EPMAX (thick green versus black curves in the two lower panels in the right column of Fig. 12). The SW and LW effects compensate in the total CRF. Also γ iw has a particularly strong effect in mid-latitudes (thick green versus black curves in the lower right panel of Fig. 11), as already discussed for the high clouds.
Altogether, the NPv3 version constitutes a satisfactory tuning of radiative fluxes. A lower value of clw may be seen as preferable in view of the zonal averages (second column of Fig. 11). However, reducing clw has a strong effect on the global energy balance. The difference in the global balance between NPv3 and CLDLC is around 7 W/m2 (Table 2).
As mentioned earlier, it turns out that the tuning of the TOA global net flux in the forced-by-SSTs model must be of about −2.5 W/m2 in order to obtain a realistic simulation of the global surface temperature in the coupled model. Thus the combination of values retained for the tunable parameters must ensure, in the end, a balance of −2 to −3 W/m2. In addition to this global constraint, we retained a tuning with a good simulation of separate SW and LW fluxes. The global mean clear-sky OLR being too weak by about 2 W/m2 (it was not the case for the SP version), the final tuning corresponds to an underestimation of the LW CRF by 2.6 W/m2 so that the total-sky OLR is close to observation. The clear-sky absorbed solar radiation is close to observation (about 287 W/m2 as can be checked by adding the ASR and SW CRF in Table 2) and does not depend much on the parameterizations nor on the parameter tuning. In the final NPv3 tuning, the global balance of −2.3 W/m2 was obtained with an overestimated SW CRF by about −3 W/m2.
This final tuning is the result of a 2-year-long iterative process, during which series of tuning simulations were redone regularly, in particular after each significant change in the parameterizations. It is possible that a better set of tuning values could be reached. Attempts to automatize the tuning procedure were made several times: once a series of sensitivity experiments is available, one could try to build sensitivity functions on which optimization procedures could be applied. But the compromise that is done at the end is difficult to translate into objective functions so far. Also, some systematic biases seem to be intrinsically linked to the particular model or model version, and one may not want to correct too far this model signature by a tuning which would be too negative for other aspects. So, up to now, this tuning phase remains somewhat manual and the results sometimes disappointing.
3.5 Tropospheric biases
The NPv3 simulation shows a strong bias in the mean zonal wind (Fig. 13), positive on the equatorial flank of the mid-latitude jets and negative at higher latitudes. This bias is a robust signature of the LMDZ model and corresponds to a shift of the mid-latitude jets toward equator. It has been analyzed by Hourdin et al. (submitted). This bias is significantly reduced when refining the horizontal grid (see also Guemas and Codron 2011). More surprisingly, this bias appears to be sensitive to the tuning of the cloud parameters. The NPv3 version is worse than the SP version in that respect.
Zonal averages of the 10-year mean zonal wind (U, m/s), temperature (T, K) and relative humidity (RH, %) in the SP, NPv3 and FALLICE simulations. Contours correspond to the simulated values and colors to the difference with the ERA-Interim (Dee et al. 2011) re-analysis
Improvement in the representation of the boundary layer thermodynamics visible in the 1D simulations is responsible for the reduction of a robust dry bias of the SP version at boundary layer top (around 900 hPa) in the tropics. The moister top boundary layer in the NP version directly comes from the vertical transport of humidity by thermal plumes which extends all through the depth of the boundary layer. The moist bias of the mid latitudes is however reinforced in the NP version compared to SP.
Regarding temperature, both SP and NP show a cold bias in mid-latitudes. This bias is largely due to the over-estimation of the cooling-to-space associated with the overestimated humidity there.
The lower panels of Fig. 13 illustrate how tuning may affect these biases. The FALLICE simulation interestingly produces biases in the temperature field which are closer to the SP version. The effect on the zonal wind biases goes in the direction of a reduction, but is not enough to reconcile the results with the SP version. Note however that an even smaller value of γ iw = 0.25 was used in the SP version.
Whether the mid-latitude biases in zonal wind, temperature and humidity could be reduced in the NP version by refining the horizontal grid or by a different tuning has to be investigated further.
3.6 Rainfall
The zonally and annually averaged rainfall is shown in Fig. 14 for the various model versions. Even with the change from SP to NP, the changes are weak. The impact of parameter tuning is even smaller (not shown). The global mean rainfall is a little bit stronger in the NP version than in SP, and too strong when compared to GPCPFootnote 5 observations (see Table. 2). This is the reason why the value of the surface drag tuning parameter was reduced in NPv3 with respect to SP. The DRAGOCE simulation documents the effect of this parameter. Changing this scaling factor from 0.8 (the value of the SP version and of the DRAGOCE sensitivity experiment) to 0.7 (retained for NPv3) decreases a little bit the global precipitation, from 2.95 to 2.85 mm/day, while GPCP suggests a still smaller value of 2.61 (Table 2). The factor was not reduced further because the impact on the radiative balance (+1.4 W/m2 when passing from DRAGOCE to NPv3) is not negligeable and would have been to be compensated, for instance by a worse tuning of clouds. No significant change was noticed in this sensitivity experiment, except the change in global parameters.
4 Climate of the NPv3 model
In the present section, important aspects of the mean climate and its variability, as simulated by the NP version of the forced-by-SSTs and coupled ocean-atmosphere models, are documented and compared to the previous SP version.
4.1 Mean climate of the atmospheric LMDZ5B simulations
The impact of the new parameterizations and free parameters tuning on the zonally averaged cloudiness was already discussed. The improvement in the seasonal and geographical distribution of clouds is illustrated further for northern summer in Fig. 15.
High (upper panels), mid (middle) and low (lower panels) clouds coverage (%) averaged for the months of June–July–August–September for the NPv3 and SP simulations with the LMDZ5 model and for the Calipso/GOCCP climatology. The Calipso/Cosp simulator is applied on-line on the model thermodynamical variables for the comparison
Concerning high clouds, the contrast between the cloudy and clear regions is stronger in the NP version and the patterns over South Asia, the warm pool and West Pacific are better represented. However, as discussed above, the differences may come in part from the use of a smaller fall velocity for ice crystal in the SP version, which makes it possible for cirrus clouds to be advected farther away from convective regions. A major deficiency of the NP version is the underestimation of high clouds coverage over West and Equatorial Africa.
There is a clear improvement in the representation of mid-level clouds even if they are still underestimated.
Trade-wind cumulus, on the western side of the tropical ocean basins are still underestimated in LMDZ5B while strato-cumulus, on the eastern side, are well captured. The contrasts between continents and oceans are also simulated well in the NP version.
Figure 16 presents the 10-year annual mean of rainfall for the LMDZ5A and B versions together with GPCP observations. Differences in the precipitation field are not as strong as for clouds. Rainfall over Amazonia and central Africa is weaker in the NP version, in better agreement with observation. On the contrary, rain is too strong (and stronger than in the SP simulation) over the “Maritime continent” and extends too much westward over the Indian ocean. Rainfall in the monsoon regions, over South Asia and over Africa, north of the Guinean coast, are simulated rather well in the two versions. Over Africa, the three maximum over Guinea, Cameroon and Sudan are well represented in the NP version. The overestimation in the SP version of the (very weak) rainfall on the eastern side of tropical oceans (a classical bias of climate models) is slightly amplified in the NP version. Finally the South Pacific Convergence Zone (SPCZ) as well as the SACZ over Atlantic are better captured in the NP version.
Shifting the continental convection from noon to late afternoon was one of the major achievements of the development of the new parameterizations. The single-column results of Rio et al. (2009) are confirmed in 3D as illustrated in Fig. 17. The shift in time of the rainfall maximum is quite systematic over continents. Here also, the results are not affected by the tuning of clouds parameters (not shown), and are directly related to changes of physical parameterizations, as discussed in details by Rio et al. (submitted).
Local hour of the maximum rainfall in the SP (upper) and NPv3 (lower) simulations. The maximum is computed on the first harmonic of the diurnal cycle. Results are displayed only if the peak-to-peak amplitude of this first harmonic is larger than 15 % of the maximum rainfall. The NP version shows results closer on continents to that obtained from observations by Yang and Slingo (2001)
4.2 Biases in IPSL-CM5B
We document here the mean biases obtained in the IPSL-CM5B-LR version of the IPSL coupled model, which uses LMDZ5B as atmospheric component. The results are compared with the IPSL-CM5A-LR version, based on LMDZ5A. All the simulations presented in this paper are performed with the Low Resolution (LR) horizontal grid based on 96 by 95 points regularly spread in longitude and latitude and we will omit the -LR suffix in the name.
Figure 18 compares the structure of the SSTs biases. Because the historical simulations were not available for IPSL-CM5B at the time of paper submission, pre-industrial simulations are considered here. The mean SST value from the models and observations is subtracted before bias computation so that only the structure of the bias is seen.
Biases in the mean SSTs in a pre-industrial control IPSL-CM5A (upper panel) and IPSL-CM5B (lower panel) simulations. The mean difference with the observed averaged SST in the 60S-60N domain is subtracted in order to focus on the bias structure. This averaged difference is of −1.8 K for IPSL-CM5A and −0.5 K for IPSL-CM5B
IPSL-CM5A shows warm biases in the tropics and cold biases in the high-latitudes, essentially symmetrical with respect to the equator. The model also tends to show stronger positive biases on the eastern side of tropical oceanic basins.
In IPSL-CM5B, biases show an hemispheric asymmetry with a warm bias in the southern high latitudes and a cold bias in the north. This asymmetry is probably associated with another strong deficiency of the IPSL-CM5B coupled model which drastically underestimates the intensity of the Atlantic thermohaline circulation. It is typically of the order of 3–4 Sverdrup against 16–18 in the observation and 10–12 in the IPSL-CM5A version. This underestimation of the thermohaline circulation is probably itself related to the strong biases in the mid-latitudes jet.
The biases are significantly reduced in the tropical Pacific as well as in the South Atlantic. However, the contrast between the warm bias in the region of upwelling, on the west coast of Africa, south of the equator, and the cold bias in the north Atlantic is, at least, as strong as in IPSL-CM5A. The cold bias in the West Pacific is also much more pronounced in IPSL-CM5B than in IPSL-CM5A.
Regarding the mean rainfall (Fig. 19), the IPSL-CM5A model shows a so-called double ITCZ structure over the Pacific ocean, with a secondary convergence zone around 5S. This deficiency is still present but significantly reduced in the NP version IPSL-CM5B. A similar improvement is noticeable over the Atlantic Ocean. Interestingly, the tendency of LMDZ5B to simulate a too strong rainfall over the maritime continent in Southeast Asia is less marked in the coupled than in the forced-by-SSTs simulations which may be related to the simulation of colder SSTs than observed in this region. The monsoon rainfall over the Indian sub-continent and over West Africa does not extend far enough north in the two versions of the IPSL-CM5 model if compared with GPCP observations and with the forced-by-SSTs simulations. For West Africa at least, this deficiency can be attributed to the bias in the inter-hemispheric contrast over the Atlantic Ocean, the presence of a warm (resp cold) bias south (resp north) of the equator counteracting the northward migration of the rainfall band during summer. However, monsoon rainfall are reasonably well represented here, if compared for instance to the previous IPSL-CM4 version (see Hourdin et al., submitted)
4.3 Atmospheric variability in the IPSL-CM5B model
Although the mean rainfall turns out to be fairly similar in the SP and NP simulations, we note a huge impact on the rainfall variability, as illustrated by comparing the standard deviation of daily rainfall anomalies for the winter season (November to April, Fig. 20).
Standard deviation of daily rainfall anomalies (mm/day) of the a GPCP dataset (1996–2009), b IPSL-CM5A and c IPSL-CM5B preindustrial simulations, for the winter season (November to April—NDJFMA). 30 years of simulations were used for the two IPSL-CM5 versions. Daily rainfall anomalies were computed against their mean seasonal cycle
Precipitation intraseasonal variability was much too weak in the SP version (Fig. 20b), while it is too strong in the new version (Fig. 20c). This new behavior of precipitation is also present in the forced version of LMDZ5B. These results do not depend much on the tuning parameters of LMDZ5 (not shown), indicating that they originate mainly from the change in parameterizations.
A space-time analysis of tropical rainfall anomalies, similar to that of Wheeler and Kiladis (1999) was then performed (Fig. 21), in order to assess how rainfall variability projects onto major Convectively-Coupled Equatorial Waves (CCEWs, e.g., Kiladis et al. 2009) or how it relates to the Madden-Julian Oscillation (MJO, Zhang 2005; Waliser et al. 2009). The raw spectrum of rainfall anomalies (Fig. 21a–c) was computed for each latitude between 15S and 15N, for successive overlapping segments of data (256-day long, with 206 days of overlap), and then averaged. As demonstrated in Wheeler and Kiladis (1999), the structure of CCEWs is either symmetric or antisymmetric about the equator, consistently with the shallow water theory. Therefore, precipitation anomalies were further decomposed into their symmetric and antisymmetric parts. The space-time spectra were computed for each of these two components, and background spectra were estimated through successive passes of a 1-2-1 filter in frequency and wavenumber. The ratio between the raw spectra and this background spectra (Fig. 21d–f for the symmetric component) should emphasize significant peaks of variance in the space-time domain (see the discussion in Wheeler and Kiladis 1999).
Raw space-time spectrum of rainfall anomalies for the a GPCP dataset (1996–2009), b IPSL-CM5A and c IPSL-CM5B preindustrial simulations. The power has been summed over latitudes between 15S and 15N, and its base-10 logarithm is taken for plotting. The ratio between the raw spectrum and a background spectrum of the symmetric component of rainfall anomalies is also shown for the d GPCP dataset, e IPSL-CM5A and f IPSL-CM5B. Shading begins at a value of 1.1 for which the spectral signatures are statistically significant above the background at the 95 % level (see Wheeler and Kiladis 1999). Superimposed are the dispersion curves of the odd meridional mode-numbered equatorial waves for five equivalents depths of h = 8, 12, 25, 50 and 90 m
In accordance with Figs. 20, 21b–c show an increase of rainfall variance at all frequencies and wavenumbers, from IPSL-CM5A to IPSL-CM5B. Precipitation variability in the NP version is now overestimated at low frequencies/high wavenumbers, while it still remains underestimated in the right upper part of the diagram (periods shorter than 7 days and eastward wavenumbers). This last deficiency is symptomatic of the lack of Kelvin waves in both the SP and NP version (Fig. 21e, f).
A new peak in the spectrum now stands out for wavenumber 1–4 and periods between 30 and 80 days (Fig. 21c), consistent with the GPCP dataset (Fig. 21a), and should indicate that the IPSL-CM5B is able to produce a MJO-like signal. Even though this signal is still weak compared to that of the GPCP dataset, it is highly significant for the symmetric component of rainfall anomalies (Fig. 21f), as well as for their antisymmetric component (not shown). In IPSL-CM5A, a significant peak can also be highlighted near 80 days (Fig. 21e), but the period is too long to be attributed to MJO-like variability.
4.4 Sensitivity to greenhouse gases
Finally, we present here how the switch from the SP to NP physical package modifies the climate sensitivity. For that purpose we perform simulations where the CO2 concentration is instantaneously quadrupled and then held constant (the so-called abrupt 4CO2 experiment in the CMIP5 design). For such experiments, Gregory et al. (2004) suggest to use a regression of the perturbation of the net flux at TOA (N) as a function of the perturbation \(\Updelta T\) of the global mean surface temperature in order to estimate the radiative forcing, the total climate feedback and the temperature change at equilibrium. The radiative forcing is obtained by the intersection of the regression line and the Y axis (for \(\Updelta T=0\), i.e. at the beginning of the simulation) whereas the temperature change at equilibrium is obtained by the intersection of the regression line and the X axis (N = 0). The variations of N and \(\Updelta T\) for the SP and NP 4CO2 experiments are reported in Fig. 22. In contrast with IPSL-CM5A, IPSL-CM5B shows a change of slope after 5–8 years. A time dependence of the climate feedbacks was in fact pointed out in other models as well (Senior and Mitchell 2000; Winton et al. 2010). It makes the radiative forcing estimate more difficult. For the estimate of the temperature change at equilibrium, we use a linear regression on years 10–160. This temperature change is of about 8 K for IPSL-CM5A and 5.4 for IPSL-CM5B (Fig. 22). The climate sensitivity of the new IPSL-CM5B model is thus much smaller than that of the previous IPSL-CM5A model. For a doubling of CO2, the temperature increase is approximately half of that for a quadrupling of CO2, i.e. around 2.7 K for IPSL-CM5B and 4 for IPSL-CM5A. The first one is in the lower part of the CMIP3 models sensitivities and the second one in the upper part (Meehl et al. 2007).
Scatter plot of the net flux change (N in W/m2) at TOA as a function of the global mean surface temperature increase (\(\Updelta T\) in K) simulated by the two versions of the model in response to an abrupt quadrupling of the CO2 concentration. A 3-year running mean is applied to the 160 years of the simulations. One value is displayed for each year, in red for IPSL-CM5A and in black for IPSL-CM5B. The straight lines corresponds to linear regressions of the data, for years 10–160. Intersection with the horizontal axis gives the expected temperature change at equilibrium (N = 0 W/m2). The flux and temperature changes are computed relative to the values of the control experiment where the CO2 concentration is held fixed
We show in Fig. 23 the structure of the global warming in the two model versions as well as the impact on rainfall. Because the asymptotic state of the 4CO2 simulations was not reached, and in order to focus on patterns, we show differences normalized by the change in the global mean temperature. For illustration, we assume a global warming of 3 K which is the approximate averaged value of the CMIP3 models for a CO2 doubling.
Temperature change (T2m, K, left) and precipitation relative change (%, right) in Abrupt 4CO2 experiments. The computation is done on the difference between the 4CO2 and corresponding control experiment. The difference is divided by the change in global mean temperature, and then multiplied by 3 to illustrate the changes that would be associated with a change of 3 K in the global mean temperature. The average is computed on the years 100–160 of the 4CO2 simulations
Classical features of the climate change simulations are recognized: a stronger warming over continents (where evaporation is limited by the water availability) than over oceans, a stronger warming at the (more continental) northern hemisphere than in the south, and in high than in low latitudes in the northern hemisphere due to both local albedo feedbacks and dynamical reasons (Alexeev et al. 2005). The simulations show also, in a rather consistent way, a weak warming in the southern mid-latitudes. The signature of the two simulations is quite different in other regions, for instance in the North Atlantic, where the difference could come from the quite different thermohaline circulation in the two models.
Regarding rainfall, some aspects appear to be robust as well, such as the global increase of rainfall in the ITCZ/SPCZ region, and a relative drying at around 30–40 degrees latitude in both hemispheres, also a rather robust feature of CMIP3 projections (Held and Soden 2006). However, the structure in the ITCZ region is very different in the two models. The IPSL-CM5B version tends to predict a larger increase in rainfall (or less drying) over semi-arid regions like South Europa, West Africa, India or in the southern part of the USA. Patterns over tropical forest (Amazonia, Central Africa, Indonesia) are also strongly modified from one model to the other.
5 Conclusions
The present paper is an outcome of 15 years of research on clouds and convection parameterization in the community in general, and in the team that develops the LMDZ model in particular. A version of the model, LMDZ5B, with new parameterizations has been developed, which is used for CMIP5. Important improvements in the climate simulations arise from the improvement of the physical parameterizations.
-
1.
The low-levels cloud coverage is better represented in the new version as well as the thermodynamic and diurnal cycle of the boundary layer. Additional evaluation by comparison with continuous in-situ observations in the Paris area is presented by Cheruy et al. (submitted).
-
2.
The improvement of the boundary layer parameterization results in a better representation of the SW CRF in the tropics, both in terms of spatial distribution and dependency on large scale dynamical regimes.
-
3.
The mid-level cloud coverage is also simulated better with the NP version, although the coverage is still underestimated when compared with the Calipso-GOCCP dataset.
-
4.
The maximum of the diurnal cycle of convective rainfall over continents is shifted by several hours.
-
5.
Tropical rainfall variability is much larger in the NP version, in better agreement with observations, in particular in the location, and spectral range associated with the Madden Julian Oscillation.
The improvements described above are robust in the sense that the conclusions are not modified by tuning the free parameters in the range of acceptable values. Also, for points 1 and 4, the confidence comes for a large part from the fact that the same improvements are observed in single-column simulations of test cases as in the 3D forced or coupled model.
The NP version, as any climate model, is however subject to significant biases, and some of those biases are even stronger in the NP than in the SP version. Some of them are also significantly affected by the tuning of free parameters needed to minimize biases and drifts in the coupled ocean-atmosphere simulations. Note that this tuning is crucial as well for forced-by-SST global and regional climate simulations, a point which is too often neglected and could explain strong biases observed in some regional climate studies (Oettli et al. 2011).
When tuning the model, particular care was given to the latitudinal variations of the TOA radiative flux, to the dependency to dynamical regimes in the tropics and to the decomposition between SW and LW or clear sky and CRF. As discussed above, a significant improvement of the SW CRF representation in the tropics comes directly from the better simulation of boundary layer clouds. As for mid-latitude balance and LW CRF, it is much more dependent on the values chosen for the tunable parameters, and in particular to the three parameters that control the non convective upper levels clouds (ep max, γ iw and ξ300).
Except for the moistening of the top of the tropical boundary layer, the NP version shows generally stronger biases than the SP version with regards to the representation of mean meteorological variables in the troposphere. In particular, the jets are located even closer to the equator than in the SP version, for which this was already a problem. Also the cold and moist biases of the mid-latitudes troposphere are amplified. The bias in the zonal wind might be responsible for a major deficiency of the IPSL-CM5B model: a quasi collapse of the North Atlantic deep water formation and, probably linked to it, a strong hemispheric asymmetry in the SSTs biases, with too warm SSTs around Antarctica and too cold SSTs in the north.
A number of shortcomings or features should be improved in future model versions. For instance, the reasonable representation of strato-cumulus relies in the current NP version on an arbitrary bypass of the thermal plume model when a strong inversion is present in the temperature profile. The turbulence in stable conditions and the representation of surface drags have not been looked at with enough attention so far. Also the 2-layer model for surface hydrology is responsible for significant biases over continents as illustrated by Cheruy et al. (submitted).
The switch from the SP to NP version of LMDZ5 constitutes (at least for us) a change in the paradigm of climate modeling. Most of the pieces of the new parameterizations were developed and tested in a single-column framework and compared with detailed 3D LES or CRM simulations of the parameterized processes. Note that it was already partly the case before for convective clouds (Bony and Emanuel 2001), which parameterization was evaluated in single-column simulations of the Toga-Coare experiment, and for the effect of sub-grid scale orography (Lott and Miller 1997; Lott 1999). With the development of the NP version, the iterative work between single-column simulations on test cases and 3D evaluation and tuning has become a corner stone of the model development. In practice, the sensitivity experiments were run systematically in 3D simulations and on a series of test cases of shallow cumulus or deep convection on both continents and ocean. Single-column simulations of test cases serve as a guide for model improvement and help in understanding some biases of the 3D model. It also put strong additional constraints on the model. If this strategy is not always sufficient to solve the problems identified in the 3D model, it prevents improving the 3D results with changes in parameterizations or tuning that would degrade the representation of cloud processes.
Finally, our results confirm that the representation of clouds and convection has a strong impact on the simulation of climate changes, in terms of both global warming and regional climate change. Progress in physical parameterizations of boundary layer, clouds or soil processes may be a crucial issue for improving our assessment of regional climate change, as important as progress in down-scaling techniques.
The model new version can be seen less pessimistic with both a weaker global warming and a tendency to simulate a more rainy future climate in semi-arid regions. Improvements of the representation of some fundamental processes could lead to give more credit to the NP projections. It must be kept in mind, however, that the new processes have been evaluated in terms of the representation of current climate but not in terms of climate sensitivity. An important issue for the confidence building will be to understand why the sensitivity of the SP and NP versions are so different. This will require deep analysis of the model results and simulations in a range of configurations including, for instance, aqua-planets. The evaluation of the sensitivity and mechanisms involved through detection/attribution studies on the observations of the past decades will also be essential.
The work on parameterizations is often difficult to promote in research programs or scientific institutions. It is sometimes considered as an old-fashioned question. A more serious argument comes from the difficulty of the subject itself. In view of the slow progress in that field, authors even suggested that we were facing a deadlock (Randall et al. 2003). Because centenal climate simulations with global explicit CRM or LES will not be possible for a while, intermediate strategies were explored with so-called super-parameterizations, in which a local 2D or 3D CRM model is nested in each column of the climate model (Randall et al. 2003; Khairoutdinov et al. 2005; Zhu et al. 2009). If this approach is worth exploring and has already shown promising results concerning, in particular, tropical variability, we argue here that significant progress in parameterizations are indeed possible.
Parameterizations are only an approximation of the real system, or of the explicit simulations used here as a reference. Models with parameterized physics are also more complex since new equations are introduced in addition to the fundamental equations of fluid mechanics. This additional complexity is however payed-off by a gain in numerical cost when compared with explicit simulations. Parameterizations are also conceptual models that summarize the effect of subgrid-scale processes and their coupling with the large scale dynamics. As such, the improvement of a model with parameterized convection represents a step forward in our understanding of the role of clouds in the climate system.
References
Alexeev VA, Langen PL, Bates JR (2005) Polar amplification of surface warming on an aquaplanet in “ghost forcing” experiments without sea ice feedbacks. Clim Dyn 24:655–666. doi:10.1007/s00382-005-0018-3
Angevine WM, Jiang H, Mauritsen T (2010) Performance of an eddy diffusivity-mass flux scheme for shallow cumulus boundary layers. Mon Weather Rev 138:2895–2912
Bodas-Salcedo A, Webb MJ, Bony S, Chepfer H, Dufresne JL, Klein SA, Zhang Y, Marchand R, Haynes JM, Pincus R, John VO (2011) COSP: satellite simulation software for model assessment. Bull Am Meteorol Soc 92(8):1023–1043. doi:10.1175/2011BAMS2856.1
Bony S, Dufresne JL (2005) Marine boundary layer clouds at the heart of tropical cloud feedback uncertainties in climate models. Geophys Res Lett 32:20,806
Bony S, Emanuel KA (2001) A parameterization of the cloudiness associated with cumulus convection; evaluation using TOGA COARE data. J Atmos Sci 58:3158–3183
Bony S, Lau KM, Sud YC (1997) Sea surface temperature and large-scale circulation influences on tropical greenhouse effect and cloud radiative forcing. J Clim 10:2055–2077. doi:10.1175/1520-0442(1997)010<2055:SSTALS>2.0.CO;2
Bony S, Colman R, Kattsov VM, Allan RP, Bretherton CS, Dufresne JL, Hall A, Hallegatte S, Holland MM, Ingram W, Randall DA, Soden BJ, Tselioudis G, Webb MJ (2006) How well do we understand and evaluate climate change feedback processes? J Clim 19:3445. doi:10.1175/JCLI3819.1
Brown AR, Cederwall RT, Chlond A, Duynkerke PG, Golaz JC, Khairoutdinov M, Lewellen DC, Lock AP, MacVean MK, Moeng CH, Neggers RAJ, Siebesma AP, Stevens B (2002) Large-eddy simulation of the diurnal cycle of shallow cumulus convection over land. Q J R Meteorol Soc 128:1075–1093. doi:10.1256/003590002320373210
Chatfield RB, Brost RA (1987) A two-stream model of the vertical transport of trace species in the convective boundary layer. J Geophys Res 92:13,263–13,276
Chepfer H, Bony S, Winker D, Chiriaco M, Dufresne JL, Sèze G (2008) Use of CALIPSO lidar observations to evaluate the cloudiness simulated by a climate model. Geophys Res Lett 351:L15,704. doi:10.1029/2008GL034207
Chepfer H, Bony S, Winker D, Cesana G, Dufresne JL, Minnis P, Stubenrauch CJ, Zeng S (2010) The GCM oriented calipso cloud product (CALIPSO-GOCCP). J Geophys Res 115:D00H16. doi:10.1029/2009JD012251
Couvreux F, Guichard F, Redelsperger JL, Kiemle C, Masson V, Lafore JP, Flamant C (2005) Water-vapour variability within a convective boundary-layer assessed by large-eddy simulations and IHOP_2002 observations. Q J R Meteorol Soc 131:2665–2693
Couvreux F, Hourdin F, Rio C (2010) Resolved versus parametrized boundary-layer plumes. Part I: a parametrization-oriented conditional sampling in large-Eddy simulations. Boundary-layer Meteorol 134:441–458. doi:10.1007/s10546-009-9456-5
Deardorff JW (1966) The counter-gradient heat-flux in the lower atmosphere and in the laboratory. J Atmos Sci 23:503–506
Deardorff JW (1972) Theoretical expression for the countergradient vertical heat flux. J Geophys Res 77:5900–5904
Dee DP, Uppala SM, Simmons AJ, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda MA, Balsamo G, Bauer P, Bechtold P, Beljaars ACM, van de Berg L, Bidlot J, Bormann N, Delsol C, Dragani R, Fuentes M, Geer AJ, Haimberger L, Healy SB, Hersbach H, Hólm EV, Isaksen L, Kållberg P, Köhler M, Matricardi M, McNally AP, Monge-Sanz BM, Morcrette JJ, Park BK, Peubey C, de Rosnay P, Tavolato C, Thépaut JN, Vitart F (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. doi:10.1002/qj.828
Emanuel KA (1991) A scheme for representing cumulus convection in large-scale models. J Atmos Sci 48:2313–2335
Emanuel KA (1993) A cumulus representation based on the episodic mixing model: the importance of mixing and microphysics in predicting humidity. AMS Meteorol Monogr 24(46):185–192
Emanuel KA, Zivkovic-Rothman M (1999) Development and evaluation of a convection scheme for use in climate models. J Atmos Sci 56:1766–1782. doi:10.1175/1520-0469(1999)056<1766:DAEOAC>2.0.CO;2
Grandpeix J, Lafore J (2010) A density current parameterization coupled with Emanuel’s convection scheme. Part I: the models. J Atmos Sci 67:881–897. doi:10.1175/2009JAS3044.1
Grandpeix J, Lafore J, Cheruy F (2010) A density current parameterization coupled with Emanuel’s convection scheme. Part II: 1D simulations. J Atmos Sci 67:898–922. doi:10.1175/2009JAS3045.1
Grandpeix JY, Phillips V, Tailleux R (2004) Improved mixing representation in Emanuel’s convection scheme. Q J R Meteorol Soc 130:3207–3222
Gregory JM, Ingram WJ, Palmer MA, Jones GS, Stott PA, Thorpe RB, Lowe JA, Johns TC, Williams KD (2004) A new method for diagnosing radiative forcing and climate sensitivity. Geophys Res Lett 31(3):L03205. doi:10.1029/2003GL018747
Guemas V, Codron F (2011) Differing impacts of resolution changes in latitude and longitude on the mid-latitudes in the lmdz gcm. J Clim. doi:10.1175/2011JCLI4093.1
Guichard F, Petch JC, Redelsperger JL, Bechtold P, Chaboureau JP, Cheinet S, Grabowski W, Grenier H, Jones CG, Köhler M, Piriou JM, Tailleux R, Tomasini M (2004) Modelling the diurnal cycle of deep precipitating convection over land with cloud-resolving models and single-column models. Q J R Meteorol Soc 130:3139–3172
Held IM, Soden BJ (2006) Robust responses of the hydrological cycle to global warming. J Clim 19:5686. doi:10.1175/JCLI3990.1
Heymsfield AJ, Donner LJ (1990) A scheme for parameterizing ice-cloud water content in general circulation models. J Atmos Sci 47:1865–1877. doi:10.1175/1520-0469(1990)047<1865:ASFPIC>2.0.CO;2
Hohenegger C, Bretherton CS (2011) Simulating deep convection with a shallow convection scheme. Atmos Chem Phys Discuss 11(3):8385–8430
Hou AY, Lindzen RS (1992) The influence of concentrated heating on the Hadley circulation. J Atmos Sci 49:1233–1241
Hourdin F, Couvreux F, Menut L (2002) Parameterisation of the dry convective boundary layer based on a mass flux representation of thermals. J Atmos Sci 59:1105–1123
Hourdin F, Musat I, Bony S, Braconnot P, Codron F, Dufresne JL, Fairhead L, Filiberti MA, Friedlingstein P, Grandpeix JY, Krinner G, Levan P, Li ZX, Lott F (2006) The LMDZ4 general circulation model: climate performance and sensitivity to parametrized physics with emphasis on tropical convection. Clim Dyn 27:787–813. doi:10.1007/s00382-006-0158-0
Houze RA (1977) Structure and dynamics of a tropical squall-line system. Mon Weather Rev 105:1540–1567
Huffman GJ, Adler RF, Morrissey MM, Bolvin DT, Curtis S, Joyce R, McGavock B, Susskind J (2001) Global precipitation at one-degree daily resolution from multisatellite observations. J Hydrometeorol 2:36. doi:10.1175/1525-7541(2001)002<0036:GPAODD>2.0.CO;2
Hurrell JW, Hack JJ, Shea D, Caron JM, Rosinski J (2008) A new sea surface temperature and sea ice boundary dataset for the community atmosphere model. J Clim 21:5145. doi:10.1175/2008JCLI2292.1
Jam A, Hourdin F, Rio C, Couvreux F (2011) Resolved versus parametrized boundary-layer plumes. Part iii: a diagnostic boundary-layer cloud parameterization derived from large eddy simulations. submitted to BLM
Khairoutdinov M, Randall D, Demott C (2005) Simulations of the atmospheric general circulation using a cloud-resolving model as a superparameterization of physical processes. J Atmos Sci 62:2136–2154. doi:10.1175/JAS3453.1
Kiladis GN, Wheeler MC, Haertel PT, Straub KH, Roundy PE (2009) Convectively coupled equatorial waves. Rev Geophys 47:RG2003. doi:10.1029/2008RG000266
Krinner G, Viovy N, de Noblet-Ducoudré N, Ogée J, Polcher J, Friedlingstein P, Ciais P, Sitch S, Prentice IC (2005) A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system. Glob Biogeochem Cycles 19:B1015
Kuang Z, Bretherton CS (2006) A mass-flux scheme view of a high-resolution simulation of a transition from shallow to deep convection. J Atmos Sci 63:1895–1909
Lenderink G, Siebesma PA, Cheinet S, Irons S, Jones GC, Marquet P, Müller F, Olmeda D, Calvo J, Sánchez E, Soares MMP (2004) The diurnal cycle of shallow cumulus clouds over land: a single-column model intercomparison study. Q J R Meteorol Soc 130:3339–3364. doi:10.1256/qj.03.122
Lima MA, Wilson JW (2008) Convective storm initiation in a moist tropical environment. Mon Weather Rev 136:1847. doi:10.1175/2007MWR2279.1
Lindzen RS, Hou A (1988) Hadley circulation for zonally averaged heating centered off the equator. J Atmos Sci 45:2416–2427
Loeb NG, Wielicki BA, Doelling DR, Smith GL, Keyes DF, Kato S, Manalo-Smith N, Wong T (2009) Toward optimal closure of the earth’s top-of-atmosphere radiation budget. J Clim 22(3):748–766. doi:10.1175/2008JCLI2637.1
Lott F (1999) Alleviation of stationary biases in a GCM through a mountain drag parameterization scheme and a simple representation of mountain lift forces. Mon Weather Rev 127:788. doi:10.1175/1520-0493(1999)127<0788:AOSBIA>2.0.CO;2
Lott F, Miller M (1997) A new sub-grid scale orographic drag parametrization: its formulation and testing. Q J R Meteorol Soc 123:101–128
Meehl GA, Stocker TF, Collins WD, Friedlingstein P, Gaye AT, Gregory JM, Kitoh A, Knutti R, Murphy JM, Noda A, Raper SCB, Watterson IG, Weaver AJ, Zhao ZC (2007) Global climate projections. In: Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Miller HL (eds) Climate change 2007: the scientific basis. Contribution of working group I to the fourth assessment report of the intergovernmental panel on climate change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, Chap 10, pp 747–846
Moeng C, Wyngaard JC (1988) Spectral analysis of large-eddy simulations of the convective boundary layer. J Atmos Sci 45(23):3573–3587
Morcrette J (1991) Radiation and cloud radiative properties in the European Centre for Medium Range Weather Forecasts forecasting system. J Geophys Res 96:9121–9132
Neggers RAJ (2009) A dual mass flux framework for boundary layer convection. Part II: clouds. J Atmos Sci 66:1489–1506
Neggers RAJ, Köhler M, Beljaars ACM (2009) A dual mass flux framework for boundary layer convection. Part I: transport. J Atmos Sci 66:1465
Oettli P, Sultan B, Baron C, Vrac M (2011) Are regional climate models relevant for crop yield prediction in West Africa? Environ Res Lett 6(1):014,008. doi:10.1088/1748-9326/6/1/014008
Pergaud J, Masson V, Malardel S, Couvreux F (2009) A parameterization of dry thermals and shallow cumuli for mesoscale numerical weather prediction. Boundary-layer Meteorol 132:83–106
Petch JC, Brown AR, Gray MEB (2002) The impact of horizontal resolution on the simulations of convective development over land. Q J R Meteorol Soc 128:2031–2044
Randall D, Khairoutdinov M, Arakawa A, Grabowski W (2003) Breaking the cloud parameterization deadlock. Bull Am Meteorol Soc 84:1547–1564. doi:10.1175/BAMS-84-11-1547
Rauber RM, Ochs HT III, di Girolamo L, Göke S, Snodgrass E, Stevens B, Knight C, Jensen JB, Lenschow DH, Rilling RA, Rogers DC, Stith JL, Albrecht BA, Zuidema P, Blyth AM, Fairall CW, Brewer WA, Tucker S, Lasher-Trapp SG, Mayol-Bracero OL, Vali G, Geerts B, Anderson JR, Baker BA, Lawson RP, Bandy AR, Thornton DC, Burnet E, Brenguier JL, Gomes L, Brown PRA, Chuang P, Cotton WR, Gerber H, Heikes BG, Hudson JG, Kollias P, Krueger SK, Nuijens L, O’Sullivan DW, Siebesma AP, Twohy CH (2007) A supplement to rain in shallow cumulus over the ocean: the RICO campaign. Bull Am Meteorol Soc 88:12. doi:10.1175/BAMS-88-12-Rauber
Redelsperger JL, Brown PRA, Guichard F, Hoff C, Kawasima M, Lang S, Montmerle T, Nakamura K, Saito K, Seman C, Tao WK, Donner LJ (2000) A GCSS model intercomparison for a tropical squall line observed during TOGA-COARE. I: cloud-resolving models. Q J R Meteorol Soc 126:823–863. doi:10.1002/qj.49712656404
Rio C, Hourdin F (2008) A thermal plume model for the convective boundary layer: representation of cumulus clouds. J Atmos Sci 65:407–425
Rio C, Hourdin F, Grandpeix J, Lafore J (2009) Shifting the diurnal cycle of parameterized deep convection over land. Geophys Res Lett 36:7809. doi:10.1029/2008GL036779
Rio C, Hourdin F, Couvreux F, Jam A (2010) Resolved versus parametrized boundary-layer plumes. Part II: continuous formulations of mixing rates for mass-flux schemes. Boundary-layer Meteorol 135:469–483. doi:10.1007/s10546-010-9478-z
Senior CA, Mitchell JFB (2000) The time-dependence of climate sensitivity. Geophys Res Lett 27(17):2685–2688. doi:10.1029/2000GL011373
Siebert P, Frank A (2003) Source-receptor matrix calculation with a lagrangian particle disperion model in backward mode. Atmos Chem Phys Discuss 3:4515–4548
Siebesma AP, Soares PMM, Teixeira J (2007) A combined eddy-diffusivity mass-flux approach for the convective boundary layer. J Atmos Sci 64:1230. doi:10.1175/JAS3888.1
Soares PMM, Miranda PMA, Siebesma AP, Teixeira J (2004) An eddy-diffusivity/mass-flux parametrization for dry and shallow cumulus convection. Q J R Meteorol Soc 130:3365–3383
Sundqvist H (1978) A parameterization scheme for non-convective condensation including prediction of cloud water content. Q J R Meteorol Soc 104:677–690. doi:10.1002/qj.49710444110
Sundqvist H (1988) Parameterization of condensation and associated clouds in models for weather prediction and general circulation simulation. physically-based modelling and simulation of climate and climatic change
VanZanten MC, Stevens BB, Nuijens L, Siebesma AP, Ackerman A, Burnet F, Cheng A, Couvreux F, Jiang H, Khairouidinov M, Kogan Y, Lewellen DC, Mechem D, Nakamura K, Noda A, Shipway BJ, Slawinska J, Wang S, Wyszogrodzki A (2011) Controls on precipitation and cloudiness in simulations of trade-wind cumulus as observed during RICO. J Adv Model Earth Syst 3:6001, M06001
Waliser D, Sperber K, Hendon H, Kim D, Maloney E, Wheeler M, Weickmann K, Zhang C, Donner L, Gottschalck J, Higgins W, Kang IS, Legler D, Moncrieff M, Schubert S, Stern W, Vitart F, Wang B, Wang W, Woolnough S (2009) Mjo simulation diagnostics. J Clim 22:3006–3030
Webb MJ, Senior CA, Sexton DMH, Ingram WJ, Williams KD, Ringer MA, McAvaney BJ, Colman R, Soden BJ, Gudgel R, Knutson T, Emori S, Ogura T, Tsushima Y, Andronova N, Li B, Musat I, Bony S, Taylor KE (2006) On the contribution of local feedback mechanisms to the range of climate sensitivity in two GCM ensembles. Clim Dyn 27(1):17–38. doi:101007s00,38200601112
Wheeler M, Kiladis GN (1999) Convectively coupled equatorial waves: analysis of clouds and temperature in the wavenumber-frequency domain. J Atmos Sci 56:374–399. doi:10.1175/1520-0469(1999)056<0374:CCEWAO>2.0.CO;2
Winker DM, Hunt WH, McGill MJ (2007) Initial performance assessment of caliop. Geophys Res Lett 34(19):L19803. doi:10.1029/2007GL030135
Winton M, Takahashi K, Held IM (2010) Importance of ocean heat uptake efficacy to transient climate change. J Clim 23(9):2333–2344. doi:10.1175/2009JCLI3139.1
Yamada T (1983) Simulations of nocturnal drainage flows by a q 2 l turbulence closure model. J Atmos Sci 40:91–106
Yang GY, Slingo J (2001) The diurnal cycle in the tropics. Mon Weather Rev 129:784. doi:10.1175/1520-0493(2001)129<0784:TDCITT>2.0.CO;2
Yu W, Doutriaux M, Seze G, Le Treut H, Desbois M (1996) A methodology study of the validation of clouds in GCMs using ISCCP satellite observations. Clim Dyn 12(6):389–401. doi:10.1007/BF00211685
Zender CS, Kiehl JT (1997) Sensitivity of climate simulations to radiative effects of tropical anvil structure. J Geophys Res 1022:23,793–23,804. doi:10.1029/97JD02009
Zhang C (2005) Madden-Julian oscillation. Rev Geophys 43:RG2003. doi:10.1029/2004RG000158
Zhang M, Lin W, Klein S, Bacmeister J, Bony S, Cederwall A, Del Genio A, Hack J, Loeb N, Lohmann U, Minnis P, Musat I, Pincus R, Stier P, Suarez M, Webb M, Wu J, Xie S, Yao MS, Zhang J (2005) Comparing clouds and their seasonal variations in 10 atmospheric general circulation models with satellite measurements. J Geophys Res 110:D15
Zhu H, Hendon H, Jakob C (2009) Convection in a parameterized and superparameterized model and Its role in the representation of the MJO. J Atmos Sci 66:2796. doi:10.1175/2009JAS3097.1
Zipser EJ (1969) The role of organized unsaturated convective downdrafts in the structure and rapid decay of an equatorial disturbance. J Appl Meteorol 8:799–814
Acknowledgments
The work presented in this paper has largely benefited from the work of our colleagues of the IPSL Climate Modelling Centre. The development of the new parameterizations which are at the basis of the NP version of LMDZ would not have been possible without the long term and fruitful collaboration of Fleur Couvreux, Francoise Guichard and Jean-Philippe Lafore from the Moana/CNRM team, who develop and use the MesoNH non hydroststic model for process studies. The research leading to these results was supported by CNRS, the INSU-LEFE French Program under the projects Dephy and MissTerre. This work also benefited of the HPC resources of CCRT and IDRIS made available by GENCI (Grand Equipement National de Calcul Intensif).
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper is a contribution to the special issue on the IPSL and CNRM global climate and Earth System Models, both developed in France and contributing to the 5th coupled model intercomparison project.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hourdin, F., Grandpeix, JY., Rio, C. et al. LMDZ5B: the atmospheric component of the IPSL climate model with revisited parameterizations for clouds and convection. Clim Dyn 40, 2193–2222 (2013). https://doi.org/10.1007/s00382-012-1343-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-012-1343-y