Abstract
A principal component decomposition of monthly sea surface temperature (SST) variability in the tropical Pacific Ocean demonstrates that nearly all of the linear trends during 1950–2010 are found in two leading patterns. The first SST pattern is strongly related to the canonical El Niño-Southern Oscillation (ENSO) pattern. The second pattern shares characteristics with the first pattern and its existence solely depends on the presence of linear trends across the tropical Pacific Ocean. The decomposition also uncovers a third pattern, often referred to as ENSO Modoki, but the linear trend is small and dataset dependent over the full 61-year record and is insignificant within each season. ENSO Modoki is also reflected in the equatorial zonal SST gradient between the Niño-4 region, located in the west-central Pacific, and the Niño-3 region in the eastern Pacific. It is only in this zonal SST gradient that a marginally significant trend arises early in the Northern Hemisphere spring (March–May) during El Niño and La Niña and also in the late summer (July–September) during El Niño. Yet these SST trends in the zonal gradient do not unequivocally represent an ENSO Modoki-like dipole because they are exclusively associated with significant positive SST trends in either the eastern or western Pacific, with no corresponding significant negative trends. Insignificant trends in the zonal SST gradient are evident during the boreal wintertime months when ENSO events typically mature. Given the presence of positive SST trends across much of the equatorial Pacific Ocean, using fixed SST anomaly thresholds to define ENSO events likely needs to be reconsidered.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Over the last century, sea surface temperature (SST) trends are generally positive across the global ocean, with the exception of negative trends in the far northern Atlantic Ocean (Deser et al. 2010a). SST trends in the equatorial Pacific Ocean are especially controversial due to the discrepancy in the sign of the trend in the central and eastern Pacific among various SST datasets (Vecchi et al. 2008; Karnauskas et al. 2009; Deser et al. 2010a). However, the disparity in trend largely arises from the coverage and quality of in situ observations in the centennial record, particularly during the early decades of the twentieth century (Deser et al. 2010a; Giese et al. 2010). Identifying and understanding the strength and pattern of trends in SSTs is especially critical if the trends induce, or reflect, changes in the atmospheric circulation and convection. The interplay between the ocean and the atmosphere is most pronounced in the global tropics due to the first order approximation between warm SSTs and the enhancement of deep convection (Back and Bretherton 2009; Johnson and Xie 2010).
Recently, several studies have identified a potential SST trend during El Niño-Southern Oscillation (ENSO) events, which is the leading coupled ocean–atmosphere mode of the tropical Pacific with significant global impacts (Ropelewski and Halpert 1987, 1989; Halpert and Ropelewski 1992). In particular, Yeh et al. (2009), Ashok and Yamagata (2009), Lee and McPhaden (2010), and McPhaden et al. (2011) indicated that there is evidence for the increasing occurrence and intensity of “El Niño Modoki,” which is potentially, but not conclusively, attributable to global warming. Canonical El Niño events are distinguished by above-average equatorial SSTs across the central and eastern Pacific Ocean, often with greatest amplitude in the eastern Pacific (Rasmusson and Carpenter 1982; Deser and Wallace 1990). In contrast, El Niño Modoki is the term first adopted by Ashok et al. (2007) to characterize a secondary pattern of tropical Pacific SST variability, which is described by a zonal SST anomaly dipole across the equatorial Pacific Ocean. While the increasing trend has been associated with only El Niño events (i.e., above-average SSTs in the central Pacific and below-average SSTs in the eastern Pacific), there is also evidence for a La Niña Modoki pattern (Ashok et al. 2007; Yu and Kim 2011), although there is some dispute over whether La Niña Modoki events are truly spatially distinct from other La Niña events (Kug et al. 2009). Even though SST observations imply El Niño Modoki events are increasing in the recent record, 1000 year integrations of a statistical-based Linear Inverse Model (Newman et al. 2011) and a fully coupled general circulation model (Yeh et al. 2011) indicate that the recent increased occurrence of El Niño Modoki events may not be distinct from natural, low-frequency variability.
Irrespective of the potential SST trends, there remains considerable debate over whether ENSO Modoki represents a unique climate mode that is separate from the ENSO phenomenon. Ashok et al. (2007), Kao and Yu (2009), and Kug et al. (2009) document distinctive characteristics associated with Modoki, or central Pacific warm events that are not replicated during more canonical, eastern Pacific ENSO events. Hu et al. (2012) proposed the location and strength of antecedent tropical wind anomalies influences air-sea interaction over the cold tongue and the oceanic thermocline, favoring the development of either a central Pacific or eastern Pacific El Niño. Conversely, others hypothesize that ENSO Modoki is a statistical artifact that arises as a leading mode due to the nonlinearity between El Niño and La Niña (e.g., Monahan and Dai 2004). This notion is supported by the Modoki-like pattern that arises from the summation of El Niño and La Niña SST composites, which is due to larger eastern Pacific SST anomalies during El Niño relative to La Niña (Hoerling et al. 1997). Recently, Takahashi et al. (2011) argued that ENSO events can be described by the superposition of two independent indices representing central and eastern Pacific ENSO variability.
Regardless of whether ENSO Modoki is physically distinct from canonical ENSO events, warming occasionally is mostly restricted to the central Pacific during wintertime El Niño events and this can have implications for expected extratropical impacts. These different “flavors” of ENSO (Trenberth and Stepaniak 2001) and their corresponding forcing onto the tropical atmosphere is related to the longitudinal extent of warm SSTs in the equatorial Pacific. Hoerling and Kumar (2002) showed that weaker, central Pacific El Niño events are linked to a westward shift of the anomalous trough-ridge axis located in the Gulf of Alaska. While the sample size limits significance, it appears that the shift in circulation modifies the downstream impacts of temperature and precipitation anomalies over the United States (Larkin and Harrison 2005a, b; Hu et al. 2012). The notion that the strength and spatial structure of the SST anomalies modify tropical-extratropical impacts motivates a greater understanding of trends in SSTs related to ENSO (e.g., Kumar et al. 2010).
The purpose of this paper is to understand the linear trends in association with the leading patterns of tropical Pacific SST variability and in key SST regions of the tropical Pacific during 1950–2010. Because of prior work indicating a positive trend in the El Niño Modoki, the significance of this pattern and the zonal gradient of equatorial Pacific SSTs is closely examined. Because of limited data coverage prior to the Second World War, we elected to not use the full SST datasets that begin in the nineteenth century. While centennial trends are not assessed here, we note that using a reduced period results in more consistent linear trends in SSTs over the 61-year record (Fig. 1), which are significantly positive throughout the tropical Pacific Ocean. Other papers (e.g., Falvey and Garreaud 2009) have used an even shorter record (1979–2006) with different trends, but we would like to minimize the potential influence of decadal variability on the secular trend. Section 2 documents the datasets and methods used in this study. Section 3.1 describes the four leading patterns of interannual, tropical SST variability and their time series. Section 3.2 examines the linear trends in the time series of the leading tropical patterns and also in the Niño SST regions of the equatorial Pacific Ocean. Section 3.3 assesses the co-variability and linear trends in the zonal gradient of equatorial Pacific SSTs (between Niño-4 and Niño-3) and the corresponding tropical Pacific SST trend pattern during significant seasons. Finally Sect. 4 summarizes the results and discusses future avenues to investigate.
Linear trends of sea surface temperature (in °C over all months, 1950–2010) using (top panel) ERSST.v3b and (bottom panel) HadISST1 data. The red box in the top panel shows the location of the Niño-3 region in the eastern Pacific (5°S–5°N, 150°W–90°W), the blue box indicates the Niño-4 region in the west-central Pacific (5°S to 5°N, 150°W to 160°E), and the black box shows the Niño-3.4 region, which overlaps both Niño-3 and Niño-4 (5°S–5°N, 170°W–120°W). Color shading denotes SST anomalies that are 95 % significant based on a two tailed Student’s t test. The thick black contour interval is 0°C, while remaining intervals are drawn every 0.25°C for above-average SSTs (solid contour) and below-average SSTs (dash-dot contour)
2 Data and methods
Three monthly averaged sea surface temperature (SST) datasets with coverage in the tropical Pacific Ocean are analyzed in this study. The gridded 2° × 2° NOAA Extended Reconstructed SST dataset (ERSST.v3b; Smith et al. 2008) includes in situ data (ships and buoys), but does not include satellite data. The gridded 1° × 1° Met Office Hadley Sea Ice and SST dataset (HadISST1; Rayner et al. 2003) includes both in situ and available satellite data. The gridded 1° × 1° NOAA Optimal Interpolation SST (OISST.v2; Reynolds et al. 2002) incorporates in situ and satellite data, but unlike the other two SST datasets, it is only available in the recent period from November 1981 to the present. Both HadISST1 and ERSST.v3b are available from the mid-to-late 1800s, but only monthly data from 1950 to 2010 was considered in this study. Prior to the satellite era, SST datasets rely heavily on the International Comprehensive Ocean–Atmosphere Data Set (ICOADS), whose coverage of in situ observations begins to sharply increase around 1950, after the Second World War, but remains relatively data sparse in the tropical Pacific Ocean (see Figure 3 from Deser et al. 2010b). Therefore, the SST datasets employ a range of statistical procedures in order to fill gaps in the observing record and to resolve various inhomogeneities. In the recent decades, the coverage of tropical Pacific SSTs observations has improved due to the inclusion of satellite data since the early 1980s and the installation of the Tropical Atmosphere Ocean (TAO) moorings by the mid 1990s. From these SST datasets, the time series of three established SST regions are calculated, which are commonly used to monitor and predict ENSO. The domains of these SST regions are averaged to form the Niño indices and are shown in Fig. 1. Monthly means from 1981 to 2010 are subtracted from the raw SST data to form departures from average.
As an initial step, a Principal Component Analysis (PCA) was used to examine the leading patterns and temporal variations of tropical Pacific SST variability. PCA has the advantage of isolating independent, co-varying patterns across a large spatial domain, whereas a single boxed region cannot distinguish between multiple large-scale patterns of variability. Prior to the eigenanalysis of the covariance matrix, the SST anomalies were area-weighted by the square root of the cosine of latitude. The covariance matrix was selected to diagnose the primary patterns of co-variability in the basin-wide SSTs, rather than the patterns of normalized covariance (or correlation matrix), which is useful for prediction tools, such as CCA (Barnston and Ropelewski 1992). The principal component (PC) time series are displayed in degrees Celsius per standard deviation of the PC and were reconstructed by regressing the monthly averaged SST anomalies onto the eigenvectors or Empirical Orthogonal Functions (EOFs). The SST anomaly patterns are also displayed in degrees Celsius and were calculated by regressing the SST anomalies onto the standardized PC time series. The PCA was performed on all three SST datasets, and even though the SST regression maps are only displayed for HadISST1 (Fig. 2), the SST patterns remain qualitatively similar in ERSST.v3b and OISST.v2. The corresponding PC time series are displayed for all three SST datasets in Fig. 3.
Tropical Pacific sea surface temperature anomalies (°C) regressed onto (top left panel) Principal Component (PC)-1, (top right panel) PC-2, (bottom left panel) PC-3, and (bottom right panel) PC-4. Results are based HadISST1 data from 1950 to 2010 with a 1981–2010 base period. Color shading denotes SST anomalies that are 95 % significant based on a two tailed Student’s t test. Contour intervals are drawn every 0.25°C for above-average SSTs (solid contour) and below-average SSTs (dotted contour)
Monthly mean values of the four leading Principal Components (in °C) associated with Fig. 2. The green line represents ERSST.v3b data from 1950 to 2010. The blue line indicates HadISST1 data from 1950 to 2010, and the red line denotes OISST.v2 data from 1982 to 2010
Significance of the PCs was evaluated using the North et al. (1982) criterion for identifying well-separated climate patterns. However, the ordering of the PCs, by variance explained, is sensitive to the selected monthly mean climatology or “base period.” Using the full base period (1950–2010) results in PC-2 and PC-3 swapping positions, but each time series retains roughly the same trend. Ultimately the 1981–2010 base period was selected and used to form anomalies for three reasons: (1) due to higher quality observations in the post-satellite era and TAO moorings, (2) for consistency in the anomaly calculation among all the SST datasets (OISST.v2 data begins in 1982), and (3) the World Meteorological Organization (WMO) recommendation for 30-year base periods to be updated every 10 years. The ordering of the PCA is also slightly sensitive to the spatial domain considered (herein, the domain from 30°S to 30°N, 130°E–70°W is used), though we note that all four leading tropical Pacific SST patterns identified in this study also appear in a PCA of global SST anomalies.
The linear trends were tested against the null hypothesis of zero linear trend using a Monte Carlo procedure where samples of the same length were drawn randomly with replacement from the full 61-year record (bootstrapping). The significance of the linear trend maps were evaluated using a two-tailed Student’s t test.
3 Results
3.1 Leading tropical Pacific SST patterns
Figure 2 shows the four leading tropical Pacific SST regression maps (in °C per one standard deviation of the PC time series) based on the HadISST1 dataset during 1950–2010. The corresponding un-standardized PC time series (°C) are shown in Fig. 3 along with the time series from the ERSST.v3b and OISST.v2 datasets, whose SST patterns are not shown here but are qualitatively similar. The percent of the monthly variance explained by each pattern is indicated in Fig. 2 and is also plotted in Fig. 4 (top panel), which uses the North et al. (1982) criterion for assessing significance. While the PCs are described below, it is important to recognize that all of the tropical Pacific PCs presented herein do not necessarily reflect true physical modes of the climate system. For this reason, the SST regression maps are referred to as “patterns” in this study, and their interpretation and legitimacy as separate physical climate modes is not ensured unless corroborated by other variables and methods of analysis.
Top panel percent variance explained for the leading ten Principal Components of tropical Pacific sea surface temperature from 1950 to 2010. The error bars are based on the North et al. (1982) significance test. Bottom panel percent of the total linear trend explained by successively removing prior Principal Components. The blue line indicates HadISST1 data, while the red line shows ERSST.v3b data
The first leading pattern, which explains 43 % of SST variability, clearly depicts the canonical ENSO pattern (e.g., Rasmusson and Carpenter 1982), with a broad region of same-sign SST anomalies extending off the coast of South America and then tapering off just west of the International Date Line. The PC-1 time series has a positive linear trend and is well correlated (r = 0.94) with the Niño-3.4 SST index.
A second leading SST pattern (12 % of variance explained) also shares features reminiscent of the first pattern, but same-sign SSTs are more restricted to the equator (5°N–5°S), with a more expansive region of opposite-sign SSTs in the surrounding tropical and subtropical oceans. A smoother version of this pattern is also apparent in ERSST.v3b (also ~12 % of variance explained) and was featured recently in Zhang et al. (2010) who examined a longer time series from 1870-2006 and identified it as a “cooling mode,” acknowledging the pronounced negative trend in the second PC (Fig. 3). However, by either halving the period of record in the datasets or by examining the shorter-record OISST.v2 data (1982–2010), this “cooling mode” disappears and the subsequent leading patterns are promoted (PC-3 becomes PC-2 and so on). Additionally, by removing linear SST trends in the 61-year datasets prior to the PCA, the second leading pattern vanishes, which indicates that its existence is solely dependent on long-term linear trends in the equatorial Pacific. In contrast, the other patterns shown in Fig. 2 remain robust even with the prior removal of linear SST trends. In the concluding section of this paper (Sect. 4), it is further discussed that the lack of stability in PC-2 in combination with other confounding qualities of the PCA seriously cast doubt on the legitimacy of PC-2 as a true mode of SST variability.
Ashok et al. (2007) referred to the third leading SST pattern in Fig. 2 (8 % of variance explained) as El Niño or La Niña “Modoki,” who uncovered it as the second EOF using HadISST from 1979 to 2004. Recall that by using a shorter record or by de-trending the dataset, this third leading pattern is elevated to the second leading pattern. ENSO Modoki is characterized by an east–west dipole encompassing the equatorial Pacific. The westernmost central Pacific SST anomaly broadly extends northeastwards into the Northern Hemisphere subtropics (to ~30°N). This third SST pattern is also reminiscent of the so-called Pacific Meridional Mode, which may precede ENSO events (Vimont et al. 2003; Chang et al. 2007; Zhang et al. 2009). The PC-3 monthly time series reveals no discernible linear trend in contrast to PC-1 and PC-2 (Fig. 3).
The fourth leading SST pattern only describes 4–5 % of the variability, but it is shown here because of the consistency in the spatial pattern among several datasets, and also because of the intriguing decadal variation that is evident in its associated PC (Fig. 3). Like ENSO Modoki, this fourth pattern is also associated with SST anomalies in the central Pacific (Fig. 2). An opposite signed SST anomaly is evident in the far eastern Pacific, but it is located off the equator in the Southern Hemisphere subtropics. While this fourth pattern does not describe a significant percentage of month-to-month variability, it may describe a significant portion of decadal ENSO fluctuations, though this is not analyzed. There are two transitions in the time series: (1) from a more positive state to a negative state occurs in the late 1970s, and (2) from a predominantly negative state to a positive state in the late 1990s. These transitions appear to coincide with inflection points in the Pacific Decadal Oscillation index, the leading SST pattern in the North Pacific (e.g., Alexander 2010).
The overlap of the error bars in Fig. 4 (top panel) indicates the PC-2 (“cooling mode”) is not well separated from PC-3 (“Modoki”) and PC-4 (“decadal”). However, because detrending the SST dataset prior to PCA results in the disappearance of PC-2, the result of using the detrended SST dataset is three leading patterns that are indistinguishable from Fig. 2 (canonical, Modoki, and decadal) and are significantly distinct from each other (i.e., error bars in Fig. 4-top do not overlap).
3.2 Linear trends in the tropical Pacific SST indices
The linear trends in the leading four PCs are indicated by the middle hash mark of the boxes in the left panel of Fig. 5 (°C over 1950–2010). Thin boxes are based on ERSST.v3b and thick boxes are based on HadISST1. The OISST.v2 data is not represented here because of the shorter record length, but during the overlapping period, the leading PCs in OISST.v2 are all highly correlated (in excess of r = 0.85) with their counterparts in HadISST and ERSST.v3b. The bottom and top edges of the box represent the 95 % level of significance based on the likely range of observed trends as indicated by randomizing all months in the observed index. As is evident in Fig. 3, PC-1, or the canonical ENSO time series, has a positive trend that ranges from ~0.2°C to 0.5°C over the 61-year period. In contrast, PC-2 (“cooling mode”) has a negative trend that ranges from ~0.4°C to 0.5°C. Notably PC-3, or ENSO Modoki, has small (0.1°C to near 0°C) and opposite signed trends depending on the dataset examined. Finally, PC-4, which includes significant decadal variation, is nearly indistinguishable from zero. Figure 4 (bottom panel) is constructed as the ratio of the linear trend of the summed PCs with the previous PCs removed and the “total trend” (the linear trend based on the sum of all possible PCs). So, after PC-1 and PC-2 are removed, the percent of the total trend explained is near zero (Fig. 4, bottom panel). Hence, the linear trends are almost entirely confined to the two leading patterns of tropical Pacific SST variability.
While the focus so far has been on the leading SST patterns of variability, the right panel of Fig. 5 also examines the linear trends in three of the Niño indices (SST regions in Fig. 1). Also shown is the zonal SST gradient, or the difference between Niño-4 and Niño-3, which includes two indices that are often invoked in studies involving Central Pacific or Modoki events (Yeh et al. 2009; Kim et al. 2009; Lee and McPhaden 2010) and is an alternative index for an east–west SST dipole pattern. The monthly Niño-4 minus Niño-3 time series is correlated to the monthly PC-3 at r = 0.6 (HadISST1) to 0.7 (ERSST.v3b and OISST.v2) implying this difference significantly captures temporal variations associated with the third leading SST pattern. Both the Niño-3 and Niño-4 indices have significant, positive trends, which range from ~0.1°C to 0.8°C in Niño-3 and ~0.3°C to 0.7°C in Niño-4. However, the index of the difference in Niño-4 and Niño-3 indicates trend in the zonal gradient is not statistically significant from zero. Finally, it appears that Niño-3.4 has a significant positive trend, but the 95 % confidence range is between near zero to ~0.7°C.
3.3 Linear trends in the zonal SST gradient
So far, it is evident that ENSO Modoki, as represented by PC-3 or the Niño-4 minus Niño-3 index, does not have a consistent, significant linear trend during all months from 1950 to 2010. However, is it possible that there is a trend in the covariability between Niño-4 and Niño-3? Figure 6 shows an 11-year sliding window of correlation (left panel) and least squares regression between Niño-4 and Niño-3 (right panel) for HadISST1 (thick lines) and ERSST.v3b (thin lines). While the correlation and regression indicate decadal shifts in the strength of the relationship between Niño-3 and Niño-4 (i.e., negative trends indicate periods of decreasing covariability between Nino-3 and Nino-4), there is no clear long-term trend in the relationship between the two Niño regions.
Left panel the correlation between the monthly values of the Niño-3 and Niño-4 indices, and right panel the regression of Niño-4 onto Niño-3 (dashed) and regression of Niño-3 onto Niño-4 (solid) for HadISST1 (thick line) and ERSST.v3b (thin line). Plotted points represent the center of the period and represent the month number since January 1960 (calculations are on an 11-year sliding window from 1950 to 2010)
Because many of the previous studies focus on linear trends in ENSO Modoki during certain seasons, the Niño-4 and Niño-3 difference index is examined for trends as a function of three-month overlapping seasons, which is displayed in Fig. 7 (black shading shows ERRST.v3b and un-shaded shows HadISST1). Bars in excess of the lower (upper) most whisker are greater than 90 % (95 %) significant based on 10,000 randomized samples with the same degrees of freedom as the observed sample. Based on this approach, there are no significant trends in the zonal gradient (Niño-4 minus Niño-3) as a function of season in either dataset (Fig. 7).
Linear trends (°C over all months, 1950–2010) in seasonally averaged values of the Niño-4 minus Niño-3 region for HadISST.v1 (white bars) and ERSST.v3b (black bars). Bars that exceed the lower whisker are greater than 90 % significant, and bars that exceed the top whisker are greater than 95 % significant using a Monte Carlo test. The ordinate shows twelve overlapping 3-month seasons
However, some interesting features are found in Fig. 8 using a similar approach, which isolates El Niño (red shading; seasonal Niño-3.4 index value equal to or greater than 0.5°C) and La Niña (blue shading; seasonal Niño-3.4 index value equal to or less than −0.5°C). Each sample contains anywhere between 9-20 El Niño or La Niña events depending on the season. Un-shaded bars represent the remaining seasons, or ENSO-neutral events. Linear trends are calculated using just the sample, so contain no temporal information that indicates changes to the frequency of occurrence. The slope is multiplied by the number of events within the 61-year record, so the resulting units are in °C and can be interpreted as the change in the strength of ENSO or ENSO-neutral events over the 1950–2010 period. Positive values indicate that the SST trend is more positive in the westernmost Niño-4 region than in the eastern Niño-3 region. Negative values signify a more positive trend in Niño-3 relative to Niño-4. Over both datasets, during March–May (MAM), there appears to be negative trend in the zonal gradient during El Niño and La Niña near the 90 % level of significance. During ENSO-neutral events this trend is not significant and is of the opposite sign. During July–September (JAS), there is a positive trend in the zonal gradient during El Niño just shy of the 95 % level of significance. The trends during La Niña and ENSO-neutral events are insignificant and near zero. While not significance tested here, trends in both SST datasets exhibit a wave-one appearance about the x-axis (Fig. 8) that implies a distinct seasonality in the temporal evolution of the zonal gradient for El Niño and La Niña, although many individual seasons are insignificant in isolation.
Top panel using ERSST.v3b monthly data, the linear trends in seasonally averaged values of the Niño-4 minus Niño-3 SST index during El Niño (red), La Niña (blue), and ENSO-neutral events (white). Bottom panel same as top panel except for HadISST1 monthly data. The trends are calculated based on all available ENSO events in the 1950–2010 record with no gaps for intervening years. Bars that exceed the lower whisker are greater than 90 % significant, and bars that exceed the top whisker are greater than 95 % significant using a Monte Carlo test
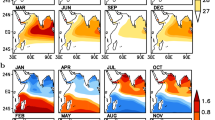
Using the significant zonal gradients in Fig. 8 as a guide for isolating seasons, Fig. 9 shows the linear SST trends across the tropical Pacific for the MAM season (left panels) and the JAS season (right panels). The top row shows the trends based on all 61-year years, the second row shows trends based on just ENSO-neutral events, and the third and bottom rows show the trends for La Niña and El Niño, respectively. Shading denotes SSTs with linear trends larger than ±0.25C and are 95 % significant via a two-tailed Student’s t test. While not shown here, smoother patterns of the same trends were also reproduced in ERSST.v3b. Across both seasons, nearly all of the significant trends in the tropical Pacific Ocean are positive. During MAM, for both El Niño and La Niña, positive SST trends are greatest in the eastern Pacific Ocean, particularly in the region immediately south of the equator (Fig. 9, left panels). However, these eastern Pacific SST trends are only significant during La Niña, so despite that the zonal SST gradient (Niño-4 minus Niño-3) is marginally significant for El Niño (Fig. 8), the positive trend in the eastern Pacific does not reach the 95 % threshold (achieves significance at p < 0.20).
Left panels linear trends in March–May averaged sea surface temperatures for (top row) ENSO-neutral events, (middle row) La Niña events, and (bottom row) El Niño events. Right panels same as in the left panel but for July–September averages. Trends shown for HadISST1. Color shading denotes SST anomalies that are 95 % significant based on a two tailed Student’s t test. The thick black contour interval is 0°C, while remaining intervals are drawn every 0.25°C for above-average SSTs (solid contour) and below-average SSTs (dash-dot contour)
During JAS El Niño events, a significant zonal SST gradient is linked to positive SST trends in the western equatorial Pacific (Fig. 9, right panels). Interestingly, a large region of negative SST trends is apparent in the equatorial eastern Pacific, but it does not reach the 95 % level of significance due to high SST variability in the region over the small number of El Niño events. In contrast, during JAS La Niña events, positive SST trends are strongest in the eastern tropical Pacific, south of the equator, and are accompanied by weaker positive trends that stretch across nearly all longitudes from ~5°S to 15°S. This is consistent with the finding that the zonal SST gradient on the equator is near zero during JAS La Niña events (Fig. 8).
Figure 10 shows the same trends, but for the Northern Hemisphere winter (November-February), which does not have a significant zonal SST gradient in Fig. 8. However, it is shown here because the peak ENSO amplitude occurs during these months and because previous literature has suggested a potential change in the ENSO Modoki trend. Interestingly, positive SST trends are strongest during La Niña events, but only in a zonally elongated region south of the equator (~5°S to 15°S). On the equator, SST trends are weakly negative but insignificant. During El Niño, positive SST trends are relatively small where they are significant.
As in Fig. 9, but based on linear trends in November–February averaged sea surface temperatures
4 Summary and future work
In contrast to previous studies, multiple SST datasets over a long record indicate that ENSO Modoki has an insignificant trend across all months and seasons, while the two leading patterns of Pacific SST variability contain nearly all linear trends. However, when ENSO events are isolated, marginally significant trends are evident in the zonal gradient of SSTs (Niño-4 minus Niño-3) across the tropical Pacific during the Northern Hemisphere spring and late summer/early fall. The significant linear trends in the zonal SST gradient do not correspond well with the ENSO Modoki dipole pattern, but largely arise from significant (p < 0.05) positive trends partially projecting onto either the eastern Pacific anomalies (during MAM La Niña events) or the western Pacific anomalies (during JAS El Niño events). The wintertime (November–February) season is not associated with significant trends in the zonal SST gradient.
While ENSO represents a coupled mode of atmosphere–ocean variability, it is reasonable to presume that significant positive SST trends across much of the equatorial Pacific will impact ENSO categorizations based on SSTs, even if it isn’t clear how the aggregate characteristics of the ENSO phenomenon will be affected by these trends (DiNezio et al. 2009; Collins et al. 2010; Stevenson et al. 2011). The NOAA Climate Prediction Center (CPC) primarily uses ERSST.v3b values of the Niño-3.4 index to categorize El Niño and La Niña events. The Niño-3.4 index seems to have weaker positive trend (0.2°C–0.7°C) over the 61-year record relative to Niño-3 and Niño-4, but this positive trend still needs to be considered given that ENSO events are defined categorically based on the departure from normal (±0.5°C). A non-stationary time series means a shift in the climatological base period (e.g., 30-year WMO climate normal) will likely influence the historical categorization of ENSO events. Other strategies will likely need to be employed in monitoring ENSO variability, such as removing the SST trend or using indices based on other ENSO-related variables with insignificant trends.
It is also clear that the Principal Component Analysis (PCA) is sensitive to the presence and amplitude of linear trends. In addition to the fact that the PC-2 “cooling mode” does not exist without observed linear trends, it is possible that the split into opposite signed trends (Figs. 4-bottom, 5), for the leading two patterns (PC-1 and PC-2), is a mathematical artifact of how PCA decomposes observed linear trends across the Pacific basin into orthogonal components. As a test, a single synthetic de-trended time series was summed to time series of observed basin linear trends and then eigen analysis was performed. The result is two PCs that collectively explain 100 % of the variance and have opposite signed linear trends (not shown). While these PCs are orthogonal (their inner product is zero), when de-trended the PCs become perfectly correlated. Therefore, it is possible that the observed linear trends cause the PCA to decompose Pacific SSTs into two separate, opposite signed PCs that largely reflect the same canonical ENSO variability. This notion is supported by the striking similarity (r = 0.7) between the first and second SST regression patterns for the domain shown Fig. 2. Also, the observed correlation between PC-1 and PC-2 is 0.4 (HadISST1) and 0.5 (ERSST.v3b) after the PC time series are both detrended suggesting their variability is intertwined. Whether there is evidence to support that PC-2 could be an independent physical mode or is merely the result of the orthogonality of PCs is worthy of further investigation.
Lingering questions also remain regarding the third pattern, ENSO Modoki, and whether it is a distinct physical mode separate from canonical ENSO variability or whether it represents non-linear aspects of ENSO. The analyses presented so far do not resolve this debate and, in fact, cast doubt on the usefulness of PCA to provide a physical description of the observed SST trends. Figure 11 shows the count of seasons when zonal SST gradient (Niño-4 minus Niño-3) exceeds one standard deviation (calculated for each season), and it is clear that the dipole is most common during the Northern Hemisphere spring and summer, in contrast to the frequency of the canonical ENSO pattern (Niño-3.4), which peaks during the Northern Hemisphere winter. Although not shown here, PC-3 also appears to peak during the spring and summer. Therefore, the linear trends in ENSO Modoki are most significant in seasons when the ENSO Modoki pattern is most frequent, which also coincides with the time of year when ENSO is often in a state of transition (developing or decaying). So, it may also be worth further investigating whether ENSO Modoki reflects not only asymmetries in the spatial distribution of SSTs (e.g., Hoerling et al. 1997), but that the dipole also reflects the natural phase progression of ENSO through the seasonal cycle. It has also been noted that PC-3 appears to be in spatial quadrature with PC-1 and therefore a Complex EOF analysis is needed to elucidate whether the PC-3/Modoki pattern may simply reflect the evolving ENSO pattern (personal communication, David Enfield).
Regardless, even if not directly linked with variations in Modoki, the documented SST trends in the western or eastern Pacific imply that the progression of El Niño and La Niña events may be altered. For example, trends toward more positive SSTs in the eastern Pacific during springtime La Niña events (Figs. 8, 9) could portend a faster decay in the eastern Pacific relative to the central Pacific. Other variables (convection, zonal winds, ocean heat fluxes, etc.) should be examined to see if the entire coupled system is undergoing a structural adjustment during these transition seasons.
Finally, it may be worth investigating the robustness and potential origin of these equatorial Pacific SST trends by assessing their reproducibility in coupled model simulations. Is the spatial pattern of the positive SST trends apparent in the latest CMIP runs, and, if so, can their relationship to natural and anthropogenic forcings be diagnosed? Also, do these models reproduce the observed SST trends associated with the leading patterns of tropical Pacific SSTs? Casting doubt on the utility of this investigation, Shin and Sardeshmukh (2011) have shown that coupled model simulations inadequately capture the pattern of linear trends over the tropical Pacific basin. Previous work on related questions has also been limited given that many studies indicate coupled models have errors in resolving the structure, amplitude (e.g., Yu and Kim 2010; Collins et al. 2010), and frequency (e.g., Newman et al. 2009; Guilyardi et al. 2009) of ENSO.
References
Alexander MA (2010) Extratropical air–sea interaction, SST variability and the Pacific decadal oscillation (PDO). In: Sun D, Bryan F (eds) Climate dynamics: why does climate vary. AGU Monograph #189, Washington D. C., pp 123–148
Ashok K, Yamagata T (2009) Climate change: the El Niño with a difference. Nature 461:481–484. doi:10.1038/461481a
Ashok K, Behera SK, Rao SA, Weng H, Yamagata T (2007) El Niño Modoki and its possible teleconnection. J Geophys Res 112:C11007. doi:10.1029/2006JC003798
Back LE, Bretherton CS (2009) On the relationship between SST gradients, boundary layer winds, and convergence over the tropical oceans. J Clim 22:4182–4196
Barnston AG, Ropelewski CF (1992) Prediction of ENSO episodes using canonical correlation analysis. J Clim 5:1316–1345
Chang P, Zhang L, Saravanan R, Vimont DJ, Chiang JCH, Ji L, Seidel H, Tippett MK (2007) Pacific meridional mode and El Niño-Southern Oscillation. Geophys Res Lett 34:L16608. doi:10.1029/2007GL030302
Collins M, An SI, Cai W, Ganachaud A, Guilyardi E, Jin FF, Jochum M, Lengaigne M, Power S, Timmermann A, Vecchi G, Wittenberg A (2010) The impact of global warming on the tropical Pacific Ocean and El Niño. Nat Geosci 3:391–397
Deser C, Wallace JM (1990) Large-scale atmospheric circulation features of warm and cold episodes in the tropical Pacific. J Clim 3:1254–1281
Deser C, Phillips AS, Alexander MA (2010a) Twentieth century tropical sea surface temperature trends revisited. Geophys Res Lett 37:L10701. doi:10.1029/2010GL043321
Deser C, Alexander MA, Xie SP, Phillips AS (2010b) Sea surface temperature variability: patterns and mechanisms. Ann Rev Mar Sci 2:115–143. doi:10.1146/annurev-marine-120408-151453
DiNezio PN, Clement AC, Vecchi GA, Soden BJ, Kirtman BP, Lee SK (2009) Climate response of the equatorial pacific to global warming. J Clim 22:4873–4892
Falvey M, Garreaud RD (2009) Regional cooling in a warming world: recent temperature trends in the southeast Pacific and along the west coast of subtropical South America (1979–2006). J Geophys Res 114:D04102. doi:10.1029/2008JD010519
Giese BS, Compo GP, Slowey NC, Sardeshmukh PD, Carton JA, Ray S, Whittaker JS (2010) The 1918/19 El Niño. Bull Am Meteorol Soc 91:177–183. doi:10.1175/2009BAMS2903.1
Guilyardi E et al (2009) Understanding El Niño in ocean–atmosphere general circulation models: progress and challenges. Bull Am Meteorol Soc 90:325–340
Halpert MS, Ropelewski CF (1992) Surface temperature patterns associated with the southern oscillation. J Clim 5:577–593. doi:10.1175/1520-442(1992)005<0577:STPAWT>2.0.CO;2
Hoerling MP, Kumar A (2002) Atmospheric response patterns associated with tropical forcing. J Clim 15:2184–2203
Hoerling MP, Kumar A, Zhong M (1997) El Niño, La Niña, and the nonlinearity of their teleconnections. J Clim 10:1769–1786
Hu ZZ, Kumar A, Jha B, Wang W, Huang B, Huang B (2012) An analysis of warm pool and cold tongue El Niños: air–sea coupling processes, global influences, and recent trends. Clim Dyn. doi:10.1007/s00382-011-1224-9
Johnson NC, Xie SP (2010) Changes in the sea surface temperature threshold for tropical convection. Nat Geosci 3:842–845
Kao HY, Yu JY (2009) Contrasting eastern Pacific and central Pacific types of ENSO. J Clim 22:615–632
Karnauskas KB, Seager R, Kaplan A, Kushnir Y, Cane MA (2009) Observed strengthening of the zonal sea surface temperature gradient across the Equatorial Pacific Ocean. J Clim 22(16):4316–4321
Kim HM, Webster PJ, Curry JA (2009) Impact of shifting patterns of Pacific Ocean warming on North Atlantic tropical cyclones. Science 325:77–80
Kug JS, Jin FF, An SI (2009) Two types of El Niño events: cold tongue El Niño and warm pool El Niño. J Clim 22:1499–1515
Kumar A, Jha B, L’Heureux M (2010) Are tropical SST trends changing the global teleconnection during La Niña? Geophys Res Lett 37:L12702. doi:10.1029/2010GL043394
Larkin NK, Harrison DE (2005a) On the definition of El Niño and associated seasonal average U.S. weather anomalies. Geophys Res Lett 32:L13705. doi:10.1029/2005GL022738
Larkin NK, Harrison DE (2005b) Global seasonal temperature and precipitation anomalies during El Niño autumn and winter. Geophys Res Lett 32:L16705. doi:10.1029/2005GL022860
Lee T, McPhaden MJ (2010) Increasing intensity of El Niño in the central-equatorial Pacific. Geophys Res Lett 37:L14603. doi:10.1029/2010GL044007
McPhaden MJ, Lee T, McClurg D (2011) El Niño and its relationship to changing background conditions in the Tropical Pacific Ocean. Geophys Res Lett 38:L15709. doi:10.1029/2011GL048275
Monahan AH, Dai A (2004) The spatial and temporal structure of ENSO nonlinearity. J Clim 17:3026–3036
Newman M, Sardeshmukh PD, Penland C (2009) How important is air–sea coupling in ENSO and MJO evolution? J Clim 22:2958–2977. doi:10.1175/2008JCLI2659.1
Newman M, Shin SI, Alexander MA (2011) Natural variation in ENSO flavors. Geophys Res Lett 38:L14705. doi:10.1029/2011GL047658
North GR, Bell TL, Cahalan RF, Moeng FJ (1982) Sampling errors in the estimation of empirical orthogonal functions. Mon Weather Rev 110:699–706
Rasmusson EM, Carpenter TH (1982) Variations in tropical sea surface temperature and surface wind fields associated with the Southern Oscillation/El Niño. Mon Weather Rev 110:354–384
Rayner NA, Parker DE, Horton EB, Folland CK, Alexander LV, Rowell DP, Kent EC, Kaplan A (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res 108(D14):4407. doi:10.1029/2002JD002670
Reynolds RW, Rayner NA, Smith TM, Stokes DC, Wang W (2002) An improved in situ and satellite SST analysis for climate. J Clim 15:1609–1625
Ropelewski CF, Halpert MS (1987) Global and regional scale precipitation patterns associated with the El Niño/Southern Oscillation. Mon Weather Rev 115:1606–1626
Ropelewski CF, Halpert MS (1989) Precipitation patterns associated with the high index phase of the Southern Oscillation. J Clim 2:268–284
Shin SI, Sardeshmukh P (2011) Critical influence of the pattern of tropical warming on remote climate trends. Clim Dyn 36:1577–1591. doi:10.1007/s00382-009-0732-3
Smith TM, Reynolds RW, Peterson TC, Lawrimore J (2008) Improvements to NOAA’s historical merged land–ocean surface temperature analysis (1880–2006). J Clim 21:2283–2296
Stevenson S, Fox-Kemper B, Jochum M, Neale R, Deser C, Meehl G (2011) Will there be a significant change to El Niño in the 21st century? J Clim (in press as part of the CCSM4 Special Issue)
Takahashi K, Montecinos A, Goubanova K, Dewitte B (2011) ENSO regimes: reinterpreting the canonical and Modoki El Niño. Geophys Res Lett 38:L10704. doi:10.1029/2011GL047364
Trenberth KE, Stepaniak DP (2001) Indices of El Niño evolution. J Clim 14:1697–1701
Vecchi GA, Clement A, Soden BJ (2008) Examining the tropical Pacific’s response to global warming. EOS 89(9):81–83
Vimont DJ, Wallace JM, Battisti DS (2003) The seasonal footprinting mechanism in the Pacific: implications for ENSO. J Clim 16(16):2668–2675
Yeh SW, Kug JS, Dewitte B, Kwon MH, Kirtman BP, Jin FF (2009) El Niño in a changing climate. Nature 461:511–514. doi:10.1038/nature08316
Yeh SW, Kirtman BP, Kug JS, Park W, Latif M (2011) Natural variability of the central Pacific El Niño event on multi-centennial timescales. Geophys Res Lett 38:L02704. doi:10.1029/2010GL045886
Yu JY, Kim ST (2010) Identification of Central-Pacific and Eastern-Pacific types of ENSO in CMIP3 models. Geophys Res Lett 37:L15705. doi:10.1029/2010GL044082
Yu JY, Kim ST (2011) Reversed spatial asymmetries between El Niño and La Niña and their linkage to decadal ENSO modulation in CMIP3 models. J Clim 24:5423–5434. doi:10.1175/JCLI-D-11-00024.1
Zhang L, Chang P, Ji L (2009) Linking the Pacific meridional mode to ENSO: coupled model analysis. J Clim 22:3488–3505. doi:10.1175/2008JCLI2473.1
Zhang W, Li J, Zhao X (2010) Sea surface temperature cooling mode in the Pacific cold tongue. J Geophys Res 115:C12042. doi:10.1029/2010JC006501
Acknowledgments
The authors appreciate manuscript reviews by Tony Barnston, Arun Kumar, Dave Unger, Caihong Wen, David Enfield, and Michael Alexander, and also discussions with Kathy Pegion and Phil Pegion prior to the preparation of this manuscript.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
L’Heureux, M.L., Collins, D.C. & Hu, ZZ. Linear trends in sea surface temperature of the tropical Pacific Ocean and implications for the El Niño-Southern Oscillation. Clim Dyn 40, 1223–1236 (2013). https://doi.org/10.1007/s00382-012-1331-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-012-1331-2