Abstract
The Intra-Americas Sea (IAS) low-level jet has been studied mainly for the summer and winter seasons. In contrast, spring conditions have been studied less. Here we analyze the boreal spring variability of the IAS low-level jet (IA-LLJ) and its relation with precipitation and tornadic activity in the region of the lower Mississippi, Tennessee and Ohio River basins (MORB). The main mode of variability of the spring IA-LLJ is obtained from a combined principal component analysis of zonal and meridional winds at 925-hPa. The first empirical orthogonal function of the IA-LLJ is a strengthening of the climatological flow with stronger easterlies in the Caribbean and stronger southeasterlies in the Gulf of Mexico. This first mode of variability of the IA-LLJ is related mainly to the Pacific North American (PNA) teleconnection pattern as the PNA modulates the pressure in the southeast region of the U.S. Consequently, there is an increase in precipitation over the MORB region as the moisture fluxes associated with the IA-LLJ increase. Tornadic activity in nine states spanning the MORB region is also significantly related to the IA-LLJ and the PNA index for March, in addition to the Pacific decadal oscillation (PDO) and the Niño indexes. Among the environmental factors that influence tornadic activity are southwesterly wind shear, dry transients at the mid-troposphere, moist transients at low levels, and an increase in convective available potential energy (CAPE). The decadal shifts in MORB precipitation and tornado activity appear to be related to the decadal shift of the IA-LLJ.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Intra-Americas Sea (IAS; Gulf of Mexico and Caribbean Sea) is a source of moisture for the eastern region of the United States of America (US). Previous studies by Rasmusson (1967), Bosilovich and Schubert (2002), Mestas-Nuñez et al. (2007) and Ruiz-Barradas and Nigam (2005) highlight the importance of the influence of IAS atmospheric moisture on the moisture budget of the continental US. The bulk of the moisture transport from the IAS is at the lower-levels below 700 hPa (Helfand and Schubert 1995). It travels through a low-level corridor comprised of the Caribbean easterlies and the Gulf of Mexico southeasterlies. In fact, it is the easterly Caribbean low-level jet (Muñoz et al. 2008) and the Gulf of Mexico southeasterlies (Mestas-Nuñez et al. 2007) that are the main wind components of the IAS moisture corridor.
The focus of the studies mentioned in the previous paragraph has been on the summer and winter seasons, whereas the spring season has received comparatively less attention. For example, Bosilovich and Schubert (2002) performed integrations from June through August. Additionally, Rasmusson (1967) and Mestas-Nuñez et al. (2007) analyzed and contrasted the winter and summer seasons. However, analyzing the spring season is important for several reasons: (1) it is a season typified by frequent Midwest flood events; (2) it is the primary season for tornadoes in the southern US affected by the availability of low-level moisture from the Gulf of Mexico; (3) rainfall anomalies in the spring create soil moisture conditions that can carry over to summer and either exacerbate or ameliorate the tendency for summer floods or drought conditions; and (4) it is observed that over the Mississippi River basin the moisture flux convergence is largest during spring and is associated with the northward flux from the Gulf of Mexico (Berbery and Rasmusson 1999).
The influence of the El Niño-southern oscillation (ENSO) phenomenon on the tropical North Atlantic has been well-documented. However, other teleconnections that are active during winter and spring months also play a role in the IAS. For example, one of the characteristics of the Pacific North American (PNA) oscillation is its anomaly center of sea level pressure straddling the southeastern part of the US (Feldstein 2002; Barnston and Livezey 1987; Wallace and Gutzler 1981). The PNA has also been documented to have a major influence in the region of the Ohio River Valley (Coleman and Rogers 2003) and the Mississippi River region (Roger and Coleman 2003). Also, the Pacific decadal oscillation (PDO) influences the precipitation variability in North America (McCabe et al. 2004; Mantua and Hare 2002). Nevertheless, the PNA and the PDO have been discussed less with respect to their impacts and relation to IAS climate variability.
Tornadic activity is also influenced by moisture fluxes from the Gulf of Mexico. A well-known region of tornadic activity is the “Tornado Alley”, comprised mainly of the states of Texas, Oklahoma, Kansas, Nebraska, eastern Colorado, and South Dakota with most of the activity occurring during May and June. However, other regions of the US are also prone to tornadic activity throughout the year (Brooks et al. 2003a), sometimes more prominent in late winter and early spring and with a different seasonal behavior when compared with Tornado Alley. For example, one of the major tornado outbreaks in the US occurred on April 3–4, 1974 in the region of the Mississippi and Ohio River basins outside of Tornado Alley (Verbout et al. 2006). Additionally, Trapp et al. (2005) found that tornado activity was strongly associated with squall lines and bow echoes (as opposed to cells) for the US states situated along a curved axis from Louisiana to Pennsylvania and that activity was higher in the first few months of the year (i.e., from January to April). Tornadic activity in a similar region was found by Cook and Schaefer (2008) to be susceptible to the influence of ENSO conditions in boreal winter.
The objective of the present study is to analyze the climate factors associated with the principal mode of interannual variability for the Intra-Americas low-level jet (IA-LLJ) in boreal spring and its relation to the precipitation and tornadoes of the Mississippi and Ohio River basins. We analyze the relation of the IA-LLJ variability with Pacific and Atlantic teleconnections with the goal of identifying the dominant regional mechanisms likely forced from outside the IAS.
2 The data and the approach
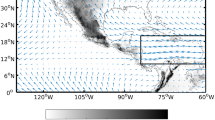
Data were obtained from the ECMWF 40-year reanalysis (ERA-40; Uppala et al. 2005) and the North American Regional Reanalysis (NARR; Mesinger et al. 2006) for 1958–2001 (ERA-40) and 1979–2001 (NARR). To study the boreal spring IA-LLJ, the 925-hPa zonal and meridional monthly winds were analyzed. Previous studies have documented the 925-hPa level to be near the level of strongest winds in the Caribbean region (Muñoz et al. 2008; Amador 2008) and in the southern region of the US (Ting and Wang 2006; Weaver and Nigam 2008). Figure 1 shows the annual mean of the 925-hPa winds and their magnitude from NARR and ERA-40 data. In the annual mean, the Caribbean easterlies and the Gulf of Mexico southeasterlies connect to form the IA-LLJ.
The standard deviation of each component of the wind calculated from the monthly vector winds is shown in Fig. 2. The zonal wind has a greater standard deviation in the Caribbean Sea, the region of the North Atlantic subtropical high, and the region of the Papagayo Jet (over the northeastern tropical Pacific). The meridional wind has a greater standard deviation over the southern states of the US between 88 and 98°W, in the Gulf of Mexico, the Tehuatenpec Jet, the Yucatan Channel, and the North Atlantic region north of 25°N.
Annual mean standard deviation (m/s) of the 925-hPa zonal (top) and meridional (bottom) wind components from NARR (shades) and ERA-40 (contours) data. The anomalies were calculated based on the 1979–2001 climatology. The contour interval for (a) is 0.4 starting at 1.2 m/s and for (b) it is 0.25 starting at 1.0 m/s
To quantify the relation between the interannual variabilities of the Caribbean and Gulf of Mexico winds, an approximation can be achieved by correlating the 925-hPa zonal wind anomalies in the Caribbean region (70–80°W, 12–16°N) with the 925-hPa meridional wind anomalies in the Gulf of Mexico region (87–98°W, 22–30°N) based on the areas of higher standard deviation (Fig. 2) for each wind component. First, the wind anomalies were calculated as the monthly departures from the monthly 1979–2001 climatology and then area-averaged over the indicated domains. The respective zonal and meridional indexes of the monthly anomalies in these regions were correlated separately for each calendar month as shown in Fig. 3. The common data period of the correlation was 1979–2001, and the 97.5% level of significance was a correlation coefficient of ±0.48.
Monthly correlation between Gulf of Mexico 925-hPa meridional wind anomalies and 925-hPa Caribbean zonal wind anomalies for 1979-2001 from ERA-40 and NARR data. The Gulf of Mexico index is the 925-hPa meridional wind anomalies averaged over 87–98°W and 22–30°N. The Caribbean Sea index is the 925-hPa zonal wind anomalies averaged over 70–80°W and 12–16°N
The 925-hPa Caribbean zonal wind and the Gulf of Mexico meridional wind are most highly and significantly anti-correlated in late winter and early spring (February, March, and April) and in September in both the ERA-40 and NARR data sets. This indicates that when the anomalous winds in the Gulf of Mexico are southerly, the anomalous winds in the Caribbean are most likely easterly. It is in these months that the moisture fluxes of the Caribbean would combine with the moisture fluxes of the Gulf of Mexico with greater impact on the US continent. This implies a greater moisturization of the low-level air mass due to the longer fetch over warm waters. The months with the lowest correlation in the NARR data set were July and August, although the ERA-40 data set showed a modest correlation for these summer months.
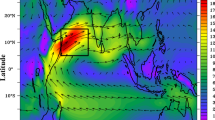
The high correlation between the Gulf of Mexico meridional wind and the Caribbean zonal wind for the months of March and April lends itself to be analyzed with other statistical techniques. To obtain the main mode of variability for the IA-LLJ, a principal component analysis (PCA) was performed by combining both wind components into a single decomposition. The PCA technique separates the variability of the time series of a given field into independent modes, providing a pattern (the eigenvector, also referred to as the empirical orthogonal function, EOF) and a respective time series (the principal component, PC) for each mode. The combined PCA calculation was based on the correlation matrix, thereby maximizing the joint variance of the zonal and meridional winds from the correlation between and among the wind components (Wilks 2006). The PCA was calculated for the March and April monthly anomalies of the 925-hPa zonal and meridional winds for 1958–2001 from the ERA-40 data set in the domain specified by Fig. 4a, the Intra-Americas Sea. That is to say, subsequent individual March and April monthly values were used (not two-month averages). Most of the land areas were masked, with the exception of the Yucatan Peninsula and western Cuba, which are low terrains and over which the Caribbean low-level flow connects with the Gulf of Mexico.
To analyze the main mode of variability of the IA-LLJ the corresponding time series (or PC1) was regressed on other atmospheric and oceanic fields and correlated with the teleconnection indexes. The ERA-40 data set was used for the following atmospheric parameters: sea level pressure (SLP), vertical velocity, geopotential height, divergence, air-sea fluxes, moisture fluxes, specific humidity and winds. For precipitation, the University of Delaware’s 0.5 × 0.5 degree data set was used (Willmott and Matsuura 2007); for sea surface temperature (SST), NOAA’s Extended Reconstructed SST data set (ERSST.v3) was used (Smith et al. 2008).
To analyze the relationship between the IA-LLJ and US precipitation and tornadoes we calculated two additional indexes. One index was for the area-average precipitation anomalies over the region of the lower Mississippi, Tennessee, and Ohio River basins. We refer to this index as the MORB precipitation index. The University of Delaware (Willmott and Matsuura 2007) precipitation data set was used to calculate the MORB precipitation index. The other index was for the monthly average of tornado counts for the region encompassing the MORB precipitation index. The data set used to calculate the tornado activity index was the Storm Prediction Center Tornado Database (McCarthy 2003; Schaefer and Edwards 1999). As Doswell et al. (2009) indicate, analyzing tornado data can be challenging due to issues associated with the temporal inconsistency of the tornado intensity Fujita scale (F-scale). For example, it is likely that pre-1975 tornadoes were rated higher (Verbout et al. 2006). Therefore, we proceeded with caution in creating the tornado activity index and accounted only for those tornadoes of significant strength.
To analyze the environmental conditions related to the tornado activity index, we used the covariance of wind and specific humidity data from the NCEP/NCAR Reanalysis (Kalnay et al. 1996). Mestas-Nuñez et al. (2005) showed the usefulness of the NCEP/NCAR Reanalysis moisture fluxes for the water budget analysis of the IAS. We also used wind shear and convective available potential energy (CAPE) data from NARR (Mesinger et al. 2006). CAPE is a measure of the amount of energy available for convection, and Brooks et al. (2003b) identified the CAPE and the wind shear as quantitative measures that serve to characterize environments conducive to severe storms.
The following teleconnection indexes were also used: the PNA index and the north Atlantic oscillation (NAO) index from NOAA’s Climate Prediction Center calculated according to the methodology of Barnston and Livezey (1987); the PDO index from Miller et al. 1994; and the tropical Pacific SST anomaly Niño indexes.
3 Principal mode of variability of IAS low-level winds
3.1 The atmospheric circulation variability
The main mode of variability for the March–April 925-hPa winds of the Intra-Americas region has a spatial pattern (EOF1) in which the Caribbean easterlies and the Gulf of Mexico southeasterlies change along the axis of their climatological flow (Fig. 4b). This first mode has more than 70% of the explained variance, and out of the first several loading vectors (EOFs) is the only one with a coherent intensification (or weakening) of the climatological flow (the IA-LLJ). The atmospheric flow from the Caribbean into the Gulf of Mexico through the Yucatan Channel weakened, for example, during the years of 1969, 1987, and 1993, while it strengthened for the years from 1973 through 1977 (Fig. 4b, c). In fact, a decadal shift in the late 1970s can be identified as the direction of the IA-LLJ PC1 anomalies is mostly positive before the early 1980s and mostly negative after the late 1970s.
The regression of PC1 for the period 1958–2001 onto the upper-level, mid-level and low-level circulation (Fig. 5) shows significant changes not only in the IAS but also throughout the western North Atlantic, North American continent and northeastern Pacific. Strong positive anomalies of the 200-hPa height are centered over the mid-latitude northeastern Pacific (45°N, 155°W) and straddle the southeastern US, separated by negative anomalies over Canada (Fig. 5a). The large-scale pattern of the 925-hPa wind (Fig. 5c) is comprised of a large anticyclonic circulation centered over the east coast of the US and involves a strengthening of the northeast trades over the tropical North Atlantic extending into the Caribbean. The strengthening of the southerly flow extends from the Gulf of Mexico to the Great Lakes region between the east coast of the US and the Rocky Mountains and the Mexican Sierra Madre Oriental. The low-level strengthening is also accompanied by positive anomalies of specific humidity, indicating a strengthening of the low-level moisture fluxes from the Gulf of Mexico. When considering the difference between the low-level (925-hPa) and mid-level winds (500-hPa), the winds are veering with height, indicating a southwesterly wind shear.
Regression onto the IA-LLJ PC1 of (a) 200-hPa geopotential height (m), (b) 500-hPa wind (m/s, vector) and specific humidity (shades), and (c) 925-hPa wind and specific humidity from ERA-40 data. The 200-hPa geopotential contour interval is 10 m starting at ±10 m. Dashed contours correspond to negative values and solid contours correspond to positive values. Color shaded regions are significant at the 95% level. The gray shaded regions in the bottom panel indicates high land areas
The changes in the large-scale wind pattern lie on the periphery of a pattern of positive SLP anomalies centered over the western mid-latitude North Atlantic (Fig. 6a). Concurrent with a strengthening of the IA-LLJ there is a strengthening of SLP to the east of the US with its core centered at 75°W, 35°N over the ocean. The pattern represents a northward and westward displacement of the climatological core of the north Atlantic subtropical high (NASH). A strong SLP anomaly zonal gradient forms over North America with negative SLP anomalies over northern North America and positive SLP anomalies over the Atlantic (also evident in the 925-hPa wind anomalies) corresponding to a strengthening of the Great Plains LLJ.
Regression onto the IA-LLJ PC1 of (a) mean sea level pressure (MSLP) and (b) sea surface temperature (SST) anomalies. The MSLP contour interval is 10 Pa starting at ±10 Pa. The SSTA contour interval is 0.015°C starting at ±0.015°C. Dashed contours indicate negative values and solid contours indicate positive values. Color-shaded regions are significant at the 95% level. MSLP data are from the ERA-40 data set and SST data are from ERSST.v3 data set
In the Pacific, significant SLP anomalies are observed to the west of the US centered at 45°N, 150°W (Fig. 6a). A similar pattern of anomalies has been associated with the negative phase of the PNA oscillation in the winter season (Barnston and Livezey 1987; Wallace and Gutzler 1981). The 200-hPa height anomalies corroborate the PNA relationship (Fig. 5a). The 200-hPa level is appropriate to distinguish teleconnection patterns since this level exhibits both divergent circulation in the tropics and non-divergent circulation in the mid-latitudes (Nigam 2003). In fact, out of several northern hemisphere teleconnection indexes (Table 1), the correlation of the PNA index with PC1 is the most highly (anti-) correlated, having a correlation coefficient of −0.61. This indicates that when the PNA is in its negative phase, the IA-LLJ most likely intensifies. The NAO index, on the other hand, is not significantly correlated with PC1. The Pacific climatic indexes (PNA, PDO, and the Niño indexes), however, are significantly correlated with the IA-LLJ PC1.
3.2 Sea surface temperature
In the region of the IAS, there is a cooling of the Caribbean Sea and a warming of the Gulf of Mexico associated with a strengthening of the IA-LLJ (Fig. 6b). The warming in the Gulf of Mexico and along the east coast of the US is associated with a decrease in heat loss from the ocean by turbulent and radiative heat fluxes (not presented), of which the latent heat flux is dominant followed by the sensible heat flux. This relation with latent and sensible heat fluxes is consistent with changes in the intensity of frontal passages associated with the anomalous pressure trough over the eastern seaboard (Eichler and Higgins 2006). The oceanic region off the southeastern US also shows positive SST anomalies as a result of the negative windstress curl anomalies. However, the cooling in the Caribbean Sea is associated predominantly with an increase in evaporation (negative latent heat flux anomalies) due to the strengthened northeast trades (Fig. 5c). Muñoz et al. (2009) have done an in-depth analyses of the IAS SST dipole during springtime.
A strengthening of the IA-LLJ is associated with a cooling of the tropical Pacific SST anomalies that serve as background for the influence of the PNA. The negative phase of the PNA is associated with cooling along the west coast of North America and warming farther west as observed in Fig. 6b. The cooling of the tropical Pacific is marginally significant, with a correlation between the Niño3 index and the IA-LLJ PC1 of 0.38. Similarly, the negative (cool) phase of the PDO is associated with a strengthening of the IA-LLJ (Table 1). This tropical Pacific cooling acts as a modulator by strengthening the tropical North Atlantic (TNA) trade winds, inducing latent heat flux anomalies that cool the TNA surface waters. Enfield and Mayer (1997) presented evidence of a lagged and positive correlation between the tropical Pacific conditions in winter and the tropical North Atlantic conditions a few months after in boreal spring. In this case, stronger easterlies induced an increase in evaporative heat loss and consequent cooling of the Caribbean SSTs.
3.3 Precipitation
The regions of increased precipitation over North America are also regions of upper-level divergence and an increase in upward motion (Fig. 7), coinciding with a strengthened IA-LLJ and moisture transport from the IAS. Conversely, those regions of less precipitation over the Atlantic and the IAS (Fig. 7c) are collocated with regions of upper-level convergence (Fig. 7a) and decreased upward motion (Fig. 7b). For example, the precipitation over the Florida peninsula, Bahamas, and Greater Antilles is reduced for those years with a strengthening of the IA-LLJ.
Regression onto IA-LLJ PC1 for 1958–2001 of (a) 200-hPa wind divergence, (b) vertical pressure velocity, and (c) land precipitation. Dashed (solid) contours indicate values less (greater) than zero. Gray shaded areas are significant at the 95% level. The contour interval for divergence is 5.0 × 10−8 s−1 starting at ±5.0 × 10−8 s−1. For vertical pressure velocity, the contour interval is 5 × 10−4 Pa/s starting at ±5 × 10−4 Pa/s, and for precipitation it is 1 mm/month starting at ±1 mm/month. Wind divergence and vertical velocity data are from the ERA-40 data set, and precipitation data are from Willmott and Matsuura (2007)
Precipitation is enhanced in the region of the central Mississippi and Ohio River basins as the IA-LLJ intensifies (Fig. 7c). In fact, the moisture flux towards North America along 30°N has strengthened and more moisture reaches the regions north of the Gulf of Mexico (Fig. 8). This is consistent with the winter and summer relationship as observed by Mestas-Nuñez et al. (2007) and Ruiz-Barradas and Nigam (2005), respectively. In this case, as observed in Fig. 8, the strengthening of the moisture flux is concentrated at the lower levels with the strongest anomalies near 925 hPa. Considering the moisture flux components separately (Fig. 8), it is observed that the specific humidity positive anomalies are stronger as the height decreases (as the pressure level increases), and the southerly wind anomalies are stronger between 90 and 97°W from 850 hPa and higher.
Vertical cross-section along 30°N of regression of the meridional moisture flux (shades), meridional wind (black contours), and specific humidity (red contours) onto the IA-LLJ PC1. The units of moisture flux are g/kg m/s. The contour interval for wind is 0.2 m/s and for specific humidity it is 0.1 g/kg
4 Precipitation variability in the Mississippi and Ohio River basins
As we have shown, the region of greater precipitation anomalies associated with changes in the springtime IA-LLJ is the region of the Mississippi and Ohio River basins (MORB). We corroborate the relation from the standpoint of the precipitation anomalies. To do this, we created an index of March–April MORB precipitation based on the colored area shown in Fig. 9a. That is to say, we averaged the precipitation anomalies over the Mississippi, Tennessee and Ohio River basins. Using the 0.5 × 0.5 degree precipitation data set, the river basins were approximated based on the map of US climate divisions. The MORB precipitation index (Fig. 9b) shows a decrease in precipitation in recent decades most likely associated with the weakening of the IA-LLJ after the early 1980s (Fig. 4).
MORB precipitation index. a Shows the regions of the two precipitation indexes: (1) the Mississippi-Ohio River basins (MORB) area is shaded and (2) the Great Plains area is the purple square. The MORB index is the area-average over the following river basins: (i) Lower Mississippi (green), (ii) Tennessee (orange), and (iii) Ohio (blue). b The March–April time series of the MORB precipitation index is in mm/month
As observed in Fig. 10, the regression of the MORB precipitation index highlights the region between the Appalachian Mountains to the east, the Great Lakes to the north, the Gulf of Mexico to the south, and the states of Texas, Oklahoma, Kansas, and Nebraska to the west. The areas to the west and the area of the coastal southeast US (including the Florida peninsula) do not have a statistically significant relationship with the MORB precipitation index. The region of increased moisture flux convergence is collocated with the region of increased precipitation. The moisture fluxes associated with positive MORB precipitation anomalies corroborate the IA-LLJ regressions with an anticyclonic gyre centered over the northeast of the IAS. That is to say, with an increase in precipitation during March–April in the MORB region there is also a strengthening of the moisture fluxes from the IAS, including a strengthening of the moisture fluxes associated with the Caribbean LLJ.
(a) Shows the regression of precipitation onto the MORB precipitation index. (b) Shows the regression of moisture flux (vectors) and moisture flux divergence (color shades) onto the MORB precipitation index. The reference arrow is 30 kg m−1 s−1. The moisture flux divergence is in units of kg m−2 s−1. The period of the regressions is for 1958–2001. Only the statistically-significant regressions of the moisture flux divergence are color shaded. Arrows for which the magnitude of the correlation vector is greater than (less than) 0.29 are in black (gray). (c) and (d) Correspond to panels (a) and (b) but for the Great Plains index
We compared the IAS moisture flux anomalies related to the MORB precipitation index with those related to the precipitation anomalies of the Great Plains during March–April. To create the Great Plains index of March–April precipitation anomalies, we used the area delimited by Ruiz-Barradas and Nigam (2005) as the area of the Great Plains (i.e., 35–45°N, 90–100°W) (purple square in Fig. 9a). In contrast with the MORB index, the Great Plains precipitation index for March–April shows precipitation anomalies centered over 93°W and 38°N that are weaker than those of the MORB index. The variability of the Great Plains index in March–April is centered in the southeast quadrant of the Great Plains index area. Positive Great Plains precipitation anomalies in March–April are related to stronger moisture fluxes from the Gulf of Mexico but not (statistically significant) from the Caribbean Sea. The moisture flux anomalies extend from the northern area of the central US southward towards Mexico. The anticyclonic circulation centered over the southeastern US is less evident, while a stronger cyclonic flow centered over the states of California and Arizona emerges. The zones of moisture flux convergence are also different, as the stronger Great Plains index is associated with moisture flux convergence over the north-central US and moisture flux divergence to the west of California and the Baja California peninsula. For both precipitation indexes, the moisture fluxes from the Gulf of Mexico are important. However, the associated circulation anomalies are distinct for each case. The Caribbean moisture fluxes are less related to the circulation anomalies that affect the Great Plains region (used for the index) in boreal spring.
The SLP and SST anomalies associated with the MORB precipitation index are highly similar to those related to the IA-LLJ variability (Fig. 6). The SLP and SST patterns (not presented) highlight significant anomalies in the midlatitudes of the North Pacific. A strong positive zonal gradient of SLP from the region of Texas to the east of the US is an indication of the strengthening of the meridional component of the wind at the lower levels. The region of the Gulf of Mexico and to the east of the US also shows warm anomalies associated with an increase in precipitation in the MORB region. These warm anomalies are expected as the precipitation bands associated with storm tracks move north during negative PNA and La Niña events; this results in decreased cloudiness over the Gulf region and decreased heat loss from turbulent fluxes. In fact, the teleconnection index most highly (anti-) correlated with the MORB index in March is the PNA (−0.43). The PNA, however, is not significantly correlated with the MORB index in April. The Niño3.4 index is the teleconnection index most highly correlated with the MORB index in April. A correlation of 0.40 between the February Niño3.4 and April MORB indexes is perhaps an indication of the superposition of the lead influence of the ENSO and the concurrent influence of the PNA.
5 Tornado index
We further explored the relation between the IA-LLJ and extreme events in the region encompassing part of the lower Mississippi, Tennessee, and Ohio River basins in March–April by analyzing the interannual variability of tornadic activity. Tornado data from the Storm Prediction Center (McCarthy 2003; Schaefer and Edwards 1999) were used to create a monthly index of tornado counts for 1950–2006 for the following nine states: Alabama, Arkansas, Illinois, Indiana, Kentucky, Louisiana, Mississippi, Missouri and Tennessee. The tornadoes counted were category F2 and stronger (i.e., significant tornadoes) on the F-scale for tornado intensity. The tornadoes were grouped into a regional monthly tornado count index (TCI) for the nine states. As our interest was for how climate variability relates to tornadic activity, we smoothed the monthly time series with a 1-2-1-month running mean and rounded the values to the nearest integer. For example, the TCI value of March 1973 is substituted by [TCI(February 1973) + 2*TCI(March 1973) + TCI(April 1973)]/4. From the smoothed time series, the tornado count for April 1974 was the largest. The monthly median (1951–2006) for the smoothed time series was rounded to the nearest integer and removed from each respective month. The median was chosen as the measure of central tendency since the tornado index appears to have a skewed distribution. Nevertheless, the values for the year 1974 were not accounted for in the calculation of the median. They were excluded from the time series because 1974 was the most extreme year and would have affected the statistics.
The smoothed March–April tornado time series with the median removed is shown in Fig. 11. From the time series, one can identify tornado outbreaks in March 1961, March–April 1963, April 1973, March 1976, April 1982, March 1997, and March–April 2006. A few of these months have been identified by Verbout et al. (2006) within the group of the top 25 tornado outbreaks between 1954 and 2003. The index also shows low-activity periods for 1987–1994 and 2000–2005 (except perhaps April 2003), high-activity periods in the 1960s and the mid-1970s, and normal-to-high activity for 1996–1998.
6 Climatic conditions related to the tornado index
We regressed the tornado index to the low-level (925-hPa) and mid-level (500-hPa) winds and specific humidity. The regression coefficients (not presented) make evident that the pattern of low-level winds associated with tornadic storms is very similar to the pattern associated with the main mode of variability for the IA-LLJ (Fig. 5). An intensification of the Gulf of Mexico southerly winds and the Caribbean easterly winds occurred and, in the North Pacific, there were significant anomalies in the midlatitudes. It is also evident that the low-level moisture flux from the Gulf of Mexico is important in providing the moisture relevant to the development of tornadic storms in the region of study. At the mid-levels (e.g., 500-hPa), the pattern of the winds was one with strong anomalies coming from the southwest over the Rocky Mountains. Although there are positive anomalies of specific humidity associated with these winds, they are of very low strength.
In fact, as seen in Fig. 12, the transients of the zonal moisture flux show negative anomalies at the mid-levels, whereas at the low levels the transients of both the zonal and meridional components are positive. Therefore, although the steady anomalies of specific humidity do not show dryness in the mid-troposphere, the covariance of the anomalies for zonal wind and specific humidity showed drying (negative anomalies) of the levels between 700 and 600 hPa. The dry transients from the west at the mid-levels and the moist transients from the Gulf of Mexico at the low-levels were found to be main ingredients of tornadic activity.
Zonal average from 100 to 85°W for the regression of the March–April covariance of (a) meridional wind and specific humidity and (b) zonal wind and specific humidity onto the March–April tornado index (1950–2006). The contour interval of the meridional component is 2 × 10−4 m/s kg/kg starting at ±1 × 10−4. The contour interval for the zonal component is 1 × 10−4 starting at ±0.5 × 10−4 m/s kg/kg. Moisture transient data are from NCEP/NCAR Reanalysis data set
Higher tornadic activity is also associated with southwesterly wind shear between the mid-troposphere (i.e., the 500-hPa level) and the low levels (i.e., 10 m from the surface) as observed in Fig. 13a. The contributing wind shear anomalies cover the region from the eastern US coast to the west with greater anomalies centered at the junction of the Mississippi and Ohio Rivers. Additionally, the CAPE showed positive anomalies from the Gulf of Mexico to the north covering the states of Louisiana, Mississippi, Alabama, Tennessee and Georgia. However, positive CAPE anomalies do not cover all the states represented in the tornado index. In fact, the TCI has a higher correlation with precipitation than with CAPE. As the TCI increases, the precipitation anomalies increase in the region encompassed by the TCI. Taking into account the findings of Shepherd et al. (2009) for the state of Georgia, we quantified the relation of the MORB TCI with preceding precipitation. The preceding precipitation anomalies are significant in the northern area of the region (Illinois, Indiana, Ohio and Michigan) but are not significant over the southern states of the regional index.
(a) Wind shear (m/s) and (b) CAPE (J/kg) anomalies regressed onto the tornado index for 1979–2006. The wind shear is calculated as the vector difference between the 500-hPa and 10-m winds. The wind shear contour interval is 0.3 m/s starting at ±0.3 m/s. The CAPE contour interval is 10 J/kg starting at ±10 J/kg. Yellow shaded areas indicate positive values, and blue shaded areas indicate negative values
To identify the teleconnections mainly related to the tornado index, we calculated rank (Spearman) correlations between the tornado index and the following teleconnection indexes: NAO, PNA, PDO, and Niño3.4. Rank correlation was used as a non-parametric measure of correlation which does not assume a specific frequency distribution of the variables. Table 2 shows the dominant correlation with the teleconnection indexes and the dominant correlation with the Niño3.4 index for the period 1950–2007. The teleconnection having the highest correlation with the tornado index is the March PNA. The correlation between the March PNA and the March (April) tornado index is −0.46 (−0.33). The March correlation drops to about −0.37 when a partial correlation is performed controlling for the PDO and the Niño3.4 indexes. Therefore, part of the correlation with the PNA is due to the relation between the PNA and the PDO (and Niño3.4). Similarly, the April tornado index has a higher correlation with the March PNA (−0.33) and a significant correlation with the April NAO (−0.29).
The SLP and SST anomalies associated with the tornado index (Fig. 14) confirm the relation between the tornado index and the teleconnection indexes. The midlatitude North Pacific shows a weakening of the Aleutian low, corresponding to a negative PNA as was also observed with the incidence of excess MORB precipitation and southerly (easterly) wind anomalies over the Gulf of Mexico (Caribbean) (Fig. 5). The equatorial Pacific shows cool SST anomalies, and the midlatitude Pacific shows a SST anomaly pattern akin to the PDO. In the Gulf of Mexico and along the west coast of the US, the SLP anomalies have a positive zonal gradient and warm SST anomalies. In the Caribbean Sea and most of the North Atlantic, the SST anomalies are cool.
Correlation of the tornado index with (a) mean sea level pressure (MSLP) and (b) sea surface temperature (SST) anomalies for 1950–2006. The dashed contours indicate the −0.2 correlation, and the solid contours indicate the 0.2 correlation. MSLP data are from the NCEP/NCAR Reanalysis data set and SST data are from ERSST.v3 data set
7 Summary and conclusions
The IA-LLJ forms a corridor that transports moisture into North America from the Gulf of Mexico and the Caribbean Sea. However, the focus of previous studies has been limited to understanding the winter and summer IAS moisture transport. The objectives of this study were to diagnose the dynamics of the IA-LLJ in boreal spring, its remote forcings, and its impacts.
We found that in recent decades (1980s to mid-2000s) the Caribbean and Gulf of Mexico low-level winds have been highly correlated during March–April. The variability of the IAS 925-hPa wind anomalies in March and April was analyzed here by principal component analysis (PCA) using data for 1958–2001. The PCA reveals a main mode of variability in which the climatological 925-hPa wind weakens or intensifies in unison, indicating a fluctuation of the IA-LLJ and its moisture transport into the US east of the Rocky Mountains. The main teleconnection associated with the IA-LLJ variability is the PNA. Prediction of the IA-LLJ variability may, therefore, be promising given that Hamill et al. (2006) found the PNA to be one of the three most predictable patterns with a 10-day lead.
The strengthening of the IA-LLJ increases the source of moisture from the IAS, having a positive impact on the precipitation in the Mississippi, Tennessee, and Ohio Rivers basins. This moisture influx at low levels not only impacts the precipitation but also the tornadic activity in the region centered at the junction of the Ohio and Mississippi rivers. A regional index of tornado count (TCI) variability was constructed and found to have similar influences as those factors affecting the IA-LLJ variability. Other associated factors that influenced the TCI variability were: (1) wet transients of zonal and meridional moisture fluxes at the low levels; (2) dry transients of zonal moisture fluxes at the levels between 600 and 700 hPa; (3) southwesterly wind shear between the 500-hPa winds and 10-m winds; (4) positive CAPE anomalies over the southeastern gulf states; and (5) positive precipitation anomalies. Yet, the relation of tornadic activity in this region with preceding precipitation is unclear; although Shepherd et al. (2009) found that springtime tornadic activity for the state of Georgia had a tendency to be lower when drought conditions persisted in the preceding fall and winter.
The variability of the three indexes developed for this study (i.e., IA-LLJ index, precipitation index, and tornado index) has a strong relationship with the variability of the PNA and the PDO. Based on our analyses, we conclude that the negative phase of the PNA during boreal spring is related to an intensification of the IA-LLJ, which provides greater moisture to the region of the Mississippi and Ohio River basins, leading to increased precipitation and greater tornadic activity. The significant relation with the PDO is also evident in the decadal shift of the three indexes in the late 1970s, consistent with the behavior observed herein. That is to say, the weakening of the springtime IA-LLJ during the 1980s and 1990s led to weaker moisture influx from the IAS, thereby manifesting as a decadal shift (a decrease) in precipitation and tornadic activity in the region of the Mississippi and Ohio River basins for the same period.
In this study, we have presented evidence that the IA-LLJ (and its associated moisture fluxes) is one dynamic feature by which the PNA, the PDO, and ENSO influence precipitation and tornado variability in the region of the lower Mississippi, Tennessee, and Ohio River basins. This dynamic feature is important with respect to seasonal hydrological and tornadic activity forecasts.
References
Amador JA (2008) The Intra-Americas Sea low-level jet: overview and future research: In: Trends and directions in climate research. Ann NY Acad Sci 1146:153–188
Barnston AG, Livezey RE (1987) Classification, seasonality and persistence of low-frequency atmospheric circulation patterns. Mon Weather Rev 115:1083–1126
Berbery EH, Rasmusson EM (1999) Mississippi moisture budgets on regional scales. Mon Weather Rev 127:2654–2673
Bosilovich MG, Schubert SD (2002) Water vapor tracers as diagnostics of the regional hydrological cycle. J Hydrometeor 3:149–165
Brooks HE, Doswell CA III, Kay MP (2003a) Climatological estimates of local daily tornado probability for the United States. Weather Forecast 18:626–640
Brooks HE, Lee JW, Craven JP (2003b) The spatial distribution of severe thunderstorm and tornado environments from global reanalysis data. Atmos Res 67/68:73–94
Coleman JSM, Rogers JC (2003) Ohio River Valley winter moisture conditions associated with the Pacific-North American teleconnection pattern. J Clim 16:969–981
Cook AR, Schaefer JT (2008) The relation of El Niño-Southern Oscillation (ENSO) to winter tornado outbreaks. Mon Weather Rev 136:3121–3137
Doswell CA III, Brooks HE, Dotzek N (2009) On the implementation of the enhanced Fujita scale in the USA. Atmos Res 93:554–563
Eichler T, Higgins W (2006) Climatology and ENSO-related variability of North American extratropical cyclone activity. J Clim 19:2076–2093
Enfield DB, Mayer DA (1997) Tropical Atlantic Sea surface temperature variability and its relation to El Niño-Southern Oscillation. J Geophys Res 102:929–945
Feldstein SB (2002) Fundamental mechanisms of the growth and decay of the PNA teleconnection pattern. QJR Meteorol Soc 128:775–796
Hamill TM, Whitaker JS, Mullen SL (2006) Reforecasts: an important dataset for improving weather predictions. Bull Am Meteorol Soc 87:33–46
Helfand HM, Schubert SD (1995) Climatology of the simulated Great-Plains low-level jet and its contribution to the continental moisture budget of the United-States. J Clim 8:784–806
Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, Iredell M, Saha S, White G, Woollen J, Zhu Y, Leetmaa A, Reynolds R, Chelliah M, Ebisuzaki W, Higgins W, Janowiak J, Mo K, Ropelewski C, Wang J, Jenne R, Joseph D (1996) The NCEP/NCAR 40-year reanalysis project. Bull Am Meteorol Soc 77:437–471
Mantua NJ, Hare SR (2002) The Pacific decadal oscillation. J Oceanogr 58:35–44
McCabe G, Palecki MA, Betancourt JL (2004) Pacific and Atlantic Ocean influences on multidecadal drought frequency in the United States. Proc Natl Acad Sci 101:4136–4141
McCarthy DW (2003) NWS tornado surveys and the impact on the national tornado database. Preprints, First Symposium on F-scale and Severe Weather Damage Assessment, Long Beach, CA. Am Meteorol Soc., CD-ROM, 3.2
Mesinger F et al (2006) North American regional reanalysis. Bull Amer Meteorol Soc 87:343–360
Mestas-Nuñez AM, Zhang C, Enfield DB (2005) Uncertainties in estimating moisture fluxes over the Intra-Americas Sea. J Hydrometeorol 6:696–709
Mestas-Nuñez AM, Enfield DB, Zhang C (2007) Water vapor fluxes over the Intra-Americas Sea: seasonal and interannual variability and associations with rainfall. J Clim 20:1910–1922
Miller AJ, Cayan DR, Barnett TP, Graham NE, Oberhuber JM (1994) The 1976–1977 climate shift of the Pacific Ocean. Oceanogr 7:21–26
Muñoz E, Busalacchi AJ, Nigam S, Ruiz-Baradas A (2008) Winter and summer structure of the Caribbean low-level jet. J Clim 21:1260–1276
Muñoz E, Wang C, Enfield D (2009) The Intra-Americas Sea springtime surface temperature anomaly dipole as fingerprint of remote influences. J Clim (in press)
Nigam S (2003) Teleconnections. In: Holton JR, Pyle JA, Curry JA (eds) Encyclopedia of atmospheric sciences. Elsevier, London, pp 2243–2269
Rasmusson EM (1967) Atmospheric water vapor transport and the water balance of North America: part I. Characteristics of the water vapor flux field. Mon Weather Rev 95:403–426
Roger JC, Coleman JSM (2003) Interactions between the Atlantic multidecadal oscillation, El Niño/La Niña, and the PNA in winter Mississippi Valley stream flow. Geophys Res Lett. doi:10.1029/2003GL017216
Ruiz-Barradas A, Nigam S (2005) Warm-season rainfall variability over the US Great Plains in observations, NCEP and ERA-40 reanalyses, and NCAR and NASA atmospheric model simulations. J Clim 18:1808–1829
Schaefer JT, Edwards R (1999) The SPC Tornado/Severe Thunderstorm Database. Preprints, 11th conference applied climatology, Dallas
Shepherd M, Niyogi D, Mote TL (2009) A seasonal-scale climatological analysis correlating spring tornadic activity with antecedent fall-winter drought in the southeastern United States. Environ Res Lett 4:024012. doi:10.1088/1748-9326/4/2/024012
Smith TM, Reynolds RW, Peterson TC, Lawrimore J (2008) Improvements to NOAA’s historical merged land-ocean surface temperature analysis (1880–2006). J Clim 21:2283–2296
Ting MF, Wang HL (2006) The role of the North American topography on the maintenance of the Great Plains summer low-level jet. J Atmos Sci 63:1056–1068
Trapp RJ, Tessendorf SA, Godfrey ES, Brooks HE (2005) Tornadoes from squall lines and bow echoes: part I. Climatological distribution. Weather Forecast 20:23–34
Uppala SM et al (2005) The ERA-40 re-analysis. QJR Meteorol Soc 131:2961–3012
Verbout SM, Brooks HE, Leslie LM, Schultz DM (2006) Evolution of the US tornado database: 1954–2003. Weather Forecast 21:86–93
Wallace JM, Gutzler DS (1981) Teleconnections in the geopotential height field during the Northern Hemisphere winter. Mon Weather Rev 109:784–812
Weaver S, Nigam S (2008) Variability of the Great Plains low-level jet: large-scale circulation context and hydroclimate impacts. J Clim 20:1532–1551
Wilks DS (2006) Principal component (EOF) analysis. In: Statistical methods in the atmospheric sciences, 2nd edn. Elsevier, London, pp 463–508
Willmott CJ, Matsuura K (2007) Terrestrial precipitation: 1900–2006 Gridded Monthly Time Series, http://climate.geog.udel.edu/~climate/html_pages/Global_ts_2007/README.global.p_ts_2007.html. Accessed 2008
Acknowledgments
This research was carried out in part under the auspices of the Cooperative Institute for Marine and Atmospheric Studies (CIMAS), a cooperative institute of the University of Miami and the National Oceanic and Atmospheric Administration, cooperative agreement #NA17RJ1226. This work was also supported by base funding of NOAA’s Atlantic Oceanographic and Meteorological Laboratory (AOML). The findings and conclusions in this report are those of the author(s) and do not necessarily represent the views of the funding agency. We thank the reviewers’ comments and suggestions. Gail Derr gave some editorial comments. The ERA-40 data used in this study were provided by ECMWF and NCAR.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Muñoz, E., Enfield, D. The boreal spring variability of the Intra-Americas low-level jet and its relation with precipitation and tornadoes in the eastern United States. Clim Dyn 36, 247–259 (2011). https://doi.org/10.1007/s00382-009-0688-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-009-0688-3