Northern hemisphere storm tracks during the last glacial maximum in the PMIP2 ocean-atmosphere coupled models: energetic study, seasonal cycle, precipitation

Abstract

Mid-latitude eddies are an important component of the climatic system due to their role in transporting heat, moisture and momentum from the tropics to the poles, and also for the precipitation associated with their fronts, especially in winter. We study northern hemisphere storm-tracks at the Last Glacial Maximum (LGM) and their influence on precipitation using ocean-atmosphere general circulation model (OAGCM) simulations from the second phase of the Paleoclimate Modelling Intercomparison Project (PMIP2). The difference with PMIP1 results in terms of sea-surface temperature forcing, fundamental for storm-track dynamics, is large, especially in the eastern North Atlantic where sea-ice extends less to the south in OAGCMs compared to atmospheric-only GCMs. Our analyses of the physics of the eddies are based on the equations of eddy energetics. All models simulate a consistent southeastward shift of the North Pacific storm-track in winter, related to a similar displacement of the jet stream, partly forced by the eddies themselves. Precipitation anomalies are consistent with storm-track changes, with a southeastward displacement of the North Pacific precipitation pattern. The common features of North Atlantic changes in the LGM simulations consist of a thinning of the storm-track in its western part and an amplification of synoptic activity to the southeast, in the region between the Azores Islands and the Iberian Peninsula, which reflects on precipitation. This southeastward extension is related to a similar displacement of the jet, partly forced by the eddies. In the western North Atlantic, the synoptic activity anomalies are at first order related to baroclinic generation term anomalies, but the mean-flow baroclinicity increase due to the presence of the Laurentide ice-sheet is partly balanced by a loss of eddy efficiency to convert energy from the mean flow. Moisture availability in this region is greatly reduced due to more advection of dry polar air by stationary waves, leading to less synoptic-scale latent heat release and hence less precipitation also. In terms of seasonality, the stormy season is shifted later in the year by a few days to a month depending on the season and the model considered. This shift does not directly reflect on the first-order seasonal cycle of precipitation, which also depends on other mechanisms, especially in summer.

1 Introduction

1.1 Context and aims

The climate of the mid-latitudes in winter is mostly determined by synoptic-scale variability, through the occurrence or not of perturbations. The fronts associated with these mid-latitude storms are responsible for most of the precipitation at this time of the year, which is determinant for the availability of water for the whole year by feeding the groundwater reservoir and eventually for heat and drought waves of the next summer like in Europe, which nowadays partly depends on winter soil moisture anomalies around the Mediterranean region (Vautard et al. 2007). It can also play an important role in supplying snow to the continental ice-sheets and therefore contributing to their maintenance, growth or decay (Hall et al. 1996).

In the context of climate change and its modelling, it is important to evaluate whether climate models are able to simulate climates different from the modern one. Indeed, climate models have to rely on parameterizations of small-scale phenomena which are adjusted so that the model correctly reproduce present-day observations. One way to evaluate this ability is through the simulation of paleoclimates, for which independent validation exists from the reconstruction of climatic variables from different proxies. In this context, the Last Glacial Maximum (LGM) is particularly interesting since it concerns a significantly different climate compared to present and since great efforts have been put and are still on the way concerning reconstructions of oceanic conditions (CLIMAP 1981; Mix et al. 2001; Kucera et al. 2005) and of continental climate (e.g. Wu et al. 2007). The comparison between the different models is also very instructive and helps evaluate the consistency of model results. It is therefore important to set common boundary conditions to run the models so that the differences in model results are not due to differences in these ones.

In this context, the Paleoclimate Modelling Intercomparison Project (PMIP1) was launched in the 1990s to run models under the same set of boundary conditions for the LGM (21 ky BP) and the mid-Holocene (6 ky BP) (Joussaume and Taylor 1995). The models consisted of atmospheric-only general circulation models (AGCMs) run using either fixed sea surface temperatures (SSTs) and sea-ice extent from CLIMAP (1981) or using a slab ocean model, for which surface heat fluxes between the ocean and the atmosphere are considered but not the dynamics of the ocean, except for a parameterization of the horizontal heat transport based on a simulation of the modern climate giving the best match to reanalyses. This latter parameterization implies that the same heat is transported by the oceans today and at the LGM, which was probably not the case (Lynch-Stieglitz et al. 2007; Weber et al. 2007). Also, this parameterization is different for each model, leading to a source of external dispersion between the models. In terms of northern hemisphere storm-tracks, the general response of the PMIP1 models consisted of an eastward shift of the storm-tracks, more pronounced for the North Atlantic, the magnitude of the shift and the intensity of the storm-tracks being quite model-dependent (Kageyama et al. 1999). For the prescribed SST models, results were also very tied to the sea-ice reconstruction by CLIMAP, which was extending far South in the North Atlantic in winter, implying a strong temperature gradient constraining the jet and the storm-track. New reconstructions and ocean-atmosphere coupled models suggest that this sea-ice extent was overestimated (Pflaumann et al. 2003; Kageyama et al. 2006).

The second phase of PMIP (PMIP2, Braconnot et al. 2007) continues the first one by running simulations of the LGM climate under similar boundary conditions. The greatest difference compared to PMIP1 simulations concerns the models used, which are fully ocean-atmosphere coupled in PMIP2. Therefore, sea-ice concentrations and SSTs, which have a major impact on storm-tracks, are not imposed anymore but derived by the models. This is a major improvement for considering storm-tracks at LGM, but we might expect a higher dispersion of the simulated storm-tracks due to the higher degree of freedom compared to results by Kageyama et al. (1999). Compared to PMIP1 also, boundary conditions have been modified, only slightly in terms of greenhouse gas (GHG) concentrations (185 ppm for the CO₂ instead of 200 ppm), but more importantly in terms of ice-sheets, with Peltier (2004) ICE-5G being used instead of Peltier (1994) ICE-4G. The major differences concern the Laurentide ice-sheet, much higher in PMIP2 simulations (maximum altitude around 4,000 m instead of around 2,500 m for PMIP1), the Greenland ice-sheet, lower for PMIP2 by a few hundreds of metres and the eastern part of the Fennoscandian ice-sheet (less extensive in ICE-5G). These differences may lead to differences in stationary waves and in storm-tracks. Also, the resolution of the models has increased between the two phases of PMIP, which has been shown to have determinant effects on the magnitude of the storm-tracks (Boville 1991; Kageyama et al. 1999). Finally, the full coupling between the ocean (including sea-ice) and the atmosphere in the PMIP2 models implies major changes in surface temperature over the oceanic regions compared to PMIP1 results (Braconnot et al. 2007; Kageyama et al. 2006).

It is therefore interesting to consider the updated results from PMIP2 in terms of storm-tracks at the LGM. It is the focus of the first part of the paper (Sect. 2.1), for which December–January–February means (DJF) of the standard deviation of the synoptic variability of the total eddy energetics at 500 hPa are shown. Simple considerations on the mean-flow baroclinicity are considered in order to understand the observed changes in synoptic variability (Sect. 2.2). These mean-flow baroclinicity changes explain the behaviour of the eddies in most places of the northern hemisphere but not all. The relationship does not hold for the western North Atlantic, as was already noticed in the conclusion of Kageyama et al. (1999). In fact, the different structure of the mean-flow at LGM compared to today and the difference in moisture content of the air due to colder temperature (cf. the Clausius–Clapeyron expression for the saturation vapour pressure) can imply behaviours not as simple as the linear response of the storm-tracks to the mean baroclinicity as in the Eady model (Eady 1949). Especially, Kageyama et al. (1999) suggested an explanation for the LGM North Atlantic storm-track behaviour similar to the midwinter suppression observed by Nakamura (1992) in the North Pacific. Synoptic activity in the North Pacific was reduced during the mid-winter months of the early 1980s compared to the late automn and early spring months whereas mean-flow baroclinicity was at its strongest at this time of the year. Since then, Chang (2001) and Nakamura et al. (2002) have further studied the mechanisms involved in the North Pacific midwinter suppression of the early 1980s, highlighting the role of diabatic heating and of the efficiency of eddies to convert energy from the mean-flow. Section 2.3 gives an explanation for the complex behaviour of the LGM North Atlantic storm-tracks based on eddy energy generation terms, including latent heating. Finally the interaction between the mean-flow and the eddies is completed with consideration on the forcing of the mean-flow by transient eddies according to the type of wave breaking (Sect. 2.4), following Orlanski (2003) and Rivière and Orlanski (2007).

We also consider the seasonal cycle of the synoptic variability (Sect. 2.5). Intraseasonally, the LGM climate may imply phenomena similar to the mid-winter suppression of the early 1980s with the strength of the synoptic activity not directly related to the strength of the mean-flow baroclinicity. Shifts in the stormy season might also occur. Since precipitation partly depends on storms, but also on the water vapour content of the air, which depends on the season considered, changes in the transient eddy seasonality could also imply important changes in the seasonal cycle of precipitation. Section 3.1 first considers the DJF anomalies of precipitation and its link to storm-tracks and stationary wave anomalies. The seasonal cycle of northern hemisphere precipitation is then studied in Sect. 3.2.

1.2 Models and simulation runs

PMIP2 models are state of the art AOGCMs, equivalent to those run in the IPCC-Ar4 exercise. Atmosphere, ocean and sea-ice are coupled and evolve consistently. The same boundary conditions have been used to run the different models participating to PMIP2 (Braconnot et al. 2007, http://pmip2.lsce.ipsl.fr/pmip2/). For its second phase and for the LGM, they consist of GHG concentrations equal to 185 ppm for the CO₂ (Monnin et al. 2001), 350 ppb for CH₄ (Dallenbach et al. 2000) and 200 ppb for N₂O (Flückiger et al. 1999). The ice-sheets are imposed and based on the reconstruction from Peltier (2004) ICE-5G. They are fixed as boundary conditions but snow on top of them is computed by the atmospheric models. In the LGM runs, excess snow The sea-level decrease by 120 m and coastlines are modified according to the reconstructed ice-sheet ICE-5G. The orbital parameters are set to LGM values, although the insolation is in fact not much different from today’s. Vegetation and river pathways are set to modern conditions.

The control simulations (CTRs) correspond to preindustrial runs with GHG concentrations equal to 280 ppm for the CO₂, 760 ppb for CH₄ and 270 ppb for N₂O. Ice-sheets, coastlines, topography, vegetation, orbital parameters are set to modern conditions.

The daily data, needed for our study of the storm tracks, were available for four of the seven models taking part to the PMIP2 LGM exercise. These models are HadCM3M2, IPSL-CM4-V1-MR, MIROC3.2 and CNRM-CM3. Twenty years of simulations have been used to compute the different means presented in this paper, for the CTR simulations as well as for the LGM. Table 1 summarizes the years taken for each model as well as the resolution of the atmospheric grids. Note that the years do not necessarily correspond to the time of integration of the models but to the years defining the files in the PMIP2 database. The data comes from the database version of PMIP2 of September 2007, except for CNRM-CM3 data, not included at this date.

Table 1 Characteristics of the models and data used in this study

2 Synoptic activity changes at LGM

2.1 DJF total eddy energy changes

We define the storm-tracks using an eulerian representation. The variations of climatic parameters are time-filtered in order to isolate their sub-weekly variations, which are related to the mid-latitude perturbations. The filter used is the simple Lorenz’s “poor man” commonly used in storm-track studies (e.g. Kageyama et al. 1999). Different meteorological fields can be used to characterize the storm-tracks (Hoskins and Hodges 2002). In this study, we use the total eddy energy, a practical measure for which equations can be derived, isolating and defining generation and dissipation terms. The definition of the total eddy energy and the equations governing its evolution in a quasigeostrophic framework are presented in Sect. 2.3, and used as a basis for our understanding of the physics involved. Since daily variables were not available for all vertical levels, we do not consider vertical averages or different levels but only the 500 hPa pressure level. This intermediate level is appropriate to capture the mixed behaviour of both the lower and the upper troposphere and gives a convenient representation of the mean behaviour of the whole troposphere. This idea was tested on two of the models for which we had more data (namely CNRM-CM3 and IPSL-CM4-V1-MR) and gave satisfactory results (not shown). In this section, we consider the winter season (December, January, February; hereafter “DJF”), for which synoptic activity in the mid-latitudes is maximum. Section 2.5 will consider the seasonal cycle of the northern hemisphere storm-tracks.

Figure 1 shows the total eddy energy at 500 hPa calculated from the daily NCEP reanalyses for years 1980–1999. Figure 2 also represents this field, for the CTR simulations as isolines, for HadCM3M2, IPSL-CM4-V1-MR, MIROC3.2, CNRM-CM3 from top to bottom. The representation of the position of the storm-tracks in the CTR simulations is very realistic when compared to reanalyses, with a maximum off Newfoundland for the North Atlantic storm track and one around the dateline around 40°N for the North Pacific using this diagnostic. The dispersion is greater concerning the intensities of the synoptic activity between the different models and compared to reanalyses. NCEP indicates a North Atlantic maximum of around 95 J/kg, value that is underestimated by all models (maximum around 75 J/kg) except for HadCM3M2, which simulates an appropriate value. The NCEP maximum for the North Pacific peaks at 75 J/kg, value that is overestimated in HadCM3M2 and MIROC3.2 (peaks around 100 J/kg), also slightly by CNRM-CM3 model (above 80 J/kg), and slightly underestimated by the IPSL model (around 65 J/kg). We should not expect a very precise equality between the simulated storm-tracks and the reanalyses, especially since the CTR simulations represent preindustrial climates whereas the climate of the period 1980–1999 has already experienced a significant increase in the GHG concentrations compared to the preindustrial levels. Note also that 1980–1999 is a period when the North Atlantic oscillation (NAO) was predominantly in its positive mode, corresponding to a strong North Atlantic storm-track, which can explain its underestimation by the models. The general conclusion is that the representation of the storm-tracks by the models is satisfactory, especially in terms of localization.

Fig. 1

DJF NCEP total eddy energy at 500 hPa for year 1980–1999. Units in J/kg

Fig. 2

DJF total eddy energy at 500 hPa for HadCM3M2, IPSL-CM4-V1-MR, MIROC3.2 and CNRM-CM3 (from top to bottom). CTR values as isolines every 15 J/kg. Anomalies (LGM-CTR) as colours. Units in J/kg

The LGM-CTR anomalies are shown in colour in Fig. 2 for each model. The general behaviour of the models consist of a southward shift of the northern hemisphere synoptic activity. Negative anomalies are usually found North of 40–45°N, where modern storm-tracks stand, and positive ones southward. This is a broad picture of the changes in the northern hemisphere zonally averaged synoptic activity. On a more local scale, many differences are found, especially in the North Atlantic.

The North Pacific storm-track anomalies are robust for all models, corresponding to a southward shift of the storm-track and an eastward extension. Negative anomalies are found North of the CTR storm-track in all models, with the strongest negative anomalies located North of the CTR storm-track maximum, and ranging from −15 to −45 J/kg depending on the models. Positive anomalies are found South of the CTR storm track also in all models, with relatively strong anomalies at the storm-track end and over the western coast of the United States (ranging from 10 to 35 J/kg depending on the models), corresponding to an eastward spreading of the North Pacific storm-track.

In the North Atlantic sector, the models are less consistent, although they all tend to simulate a thinner storm-track (in latitude) on its western part and an eastward extension. Southward shifts are only simulated by HadCM3M2 and IPSL-CM4-V1-MR. Anomalies are negative North of the CTR storm-track maximum at around 45°N, with the greatest values (−10 to −35 J/kg) usually found off the Labrador Sea mouth. Negative anomalies are also found southwestward of the CTR maximum, insignificant for HadCM3M2 and IPSL-CM4-V1-MR models, strong in MIROC3.2 and CNRM-CM3 models (−25 and around −40 J/kg respectively). Anomalies are positive southeastward of the CTR storm-track maximum, weak for the two latter models, strong for the two former, for which anomalies reach 35 J/kg over the Azores Islands for HadCM3M2, further eastward and spreading over Europe in the IPSL model.

2.2 DJF mean-flow baroclinic changes

Storms form baroclinically, in an environment with a strong vertical wind shear. A basic diagnostic for storm-track dynamics is the jet intensity or the horizontal gradient of potential temperature that directly relates to it in the geostrophic framework, following the thermal wind equation (expressed in pressure coordinates):

$$\frac{\partial {{\mathbf{v}}}_{g}}{\partial p}=-\frac{1} {f\rho\theta} {{\mathbf{k}}} \times {{\mathbf{grad}}}_{H} \theta $$

(1)

where v _g represent the geostrophic wind, ρ the density, θ the potential temperature, grad _H the horizontal gradient operator. Jet considerations are useful both in the zones of storm formations but also farther downstream, perturbations staying within the jet region to some extent.

Figure 3 shows the horizontal temperature gradient at 500 hPa, in terms of anomalies (LGM-CTR) in colour, and as black isolines for CTR values. We plot the horizontal temperature gradient rather than the jet intensity because this term enters the baroclinic generation term studied in Sect. 2.3 and leads to the exact same conclusions. The direction of the temperature gradient anomalies is dominated by its meridional component, which implies that the anomalies plotted in Fig. 3 mostly correspond to westerly jet anomalies. The maximum sea-ice extent is also indicated by red lines for CTR and by green lines for the LGM simulations, which indicates that mid-latitude temperature gradient changes are not related to sea-ice extension. Most of the synoptic anomalies shown in Fig. 2 can be understood in terms of jet stream changes. In the North Pacific sector, the jet is intensified and displaced to the South, as indicated by positive and negative anomalies South and North of the latitudinal CTR horizontal temperature maximum respectively. The eastward extension is also apparent, with the greatest anomalies found downstream of the CTR maximum for all models except MIROC3.2 (but for which eastward storm-track extension is weak). The link between synoptic and mean-flow baroclinic anomalies is also quite relevant over the Asian continent. Concerning the North Atlantic sector, the relationship is much weaker or non-existing. The difference in meridional temperature gradient is particularly strong on the southern edge of the Laurentide ice-sheet (around 45°N on the North American continent) and on the western part of the North Atlantic basin where storm forms. As expected from the presence of the ice-sheet, the horizontal temperature gradient is much stronger at the LGM than at present, nevertheless, the synoptic anomalies are not particularly stronger in this sector. Obviously, the simple mean-flow baroclinic argument does not apply in this area. Humidity changes associated with the much weaker temperatures found around the ice-sheet may explain this fact, but might not stand for the strong negative anomalies found in MIROC3.2 and CNRM-CM3 to the South where major temperature changes are not expected. The following section addresses this question.

Fig. 3

Modulus of the DJF horizontal temperature gradient at 500 hPa. CTR values as isolines (every 0.5°C/100 km), (LGM-CTR) anomalies as colour in °C/100 km. Red and green lines delimitate zones with sea-ice concentration greater than 75% for CTR and LGM runs respectively

2.3 DJF eddy energy generation terms analysis

2.3.1 Equations

The total eddy energy E ^′ _T is defined as the sum of the eddy kinetic and eddy potential energy, noted K′ and P′ respectively, with

$$K^{\prime}=1/2(u^{\prime 2}+v^{\prime 2}); P^{\prime}=1/2S\left(\frac{\partial\phi^{\prime}}{\partial p}\right)^{2}={{\mathcal{R}}}^{2}/2S \theta^{\prime 2} $$

(2)

where the static stability S is defined as $S=-1/\rho_{0}\frac{\partial}{\partial p} ln\Theta_{0}=-{{\mathcal{R}}}\frac{\partial}{\partial p}\Theta_{0}$ following notations from Cai and Mak (1990), with Θ₀ the potential temperature average, depending only on pressure, ${\mathcal{R}}=\frac{R}{p_{00}}(\frac{p_{00}}{p})^{c_{v}/c_{p}}$ (p ₀₀ is a reference pressure, 1,000 hPa in this study, c _v and c _p the atmospheric specific heat at constant volume and pressure respectively). Note that our derivation of the vertical derivative is only based on the levels available in the database, i.e. 850, 500 and 200 hPa and is quite a rough estimate of the actual one.

In the quasi-geostrophic framework and decomposing the variables into a high-frequency part (sub-weekly variations in our analysis) representing transient eddy quantities (denoted by primes), and a low-frequency part (monthly means in our analysis) representing mean-flow conditions (denoted by bars), the equation governing the total eddy potential energy in a quasigeostrophic framework (details about the derivation can be found in Cai and Mak (1990) or Orlanski and Katzfey (1991)) is

$$\frac{\partial}{\partial t} E_{T}^{\prime}= -{\bar{{\mathbf{V}}}}\cdot\nabla E_{T}^{\prime}+ {{\mathbf{F}}}^{\prime}\cdot {\bar{\mathbf{T}}}+\frac{{{\mathcal{R}}}^{2}} {S\Pi}\theta^{\prime}Q^{\prime}+{{\mathbf{E}}}^{\prime}\cdot {\bar{\mathbf{D}}}- {{\mathbf{v}}}^{\prime}\cdot\nabla \phi^{\prime}+{\mathbf{R}}^{\prime}$$

(3)

The first term of the right hand side corresponds to the advection of the eddy energy by the mean flow. The second and third ones correspond to the creation of eddy potential energy, by baroclinic conversion and by diabatic heating respectively. The fourth term represents barotropic conversion, the fifth ageostrophic geopotential fluxes, the last one a residual term including dissipation, forcing, and non-linear eddy terms (detailed in Orlanski and Katzfey 1991).

The baroclinic conversion components are defined as

$${{\mathbf{F}}}^{\prime}={{\mathcal{R}}}[u^{\prime} \theta^{\prime},v^{\prime}\theta^{\prime}]; {\bar{{\mathbf{T}}}}=\left(\frac{\partial}{\partial p} \Theta_{0}\right)^{-1}\left[\frac{\partial}{\partial x} \bar{\theta},\frac{\partial}{\partial y} \bar{\theta}\right] $$

(4)

and indicate the role of the eddy heat fluxes to convert energy from the mean flow through their component parallel to the low-frequency temperature gradient. The parameters influencing the strength of baroclinic generation are the strength of the eddy heat flux itself, the strength of the mean horizontal temperature gradient and the angle between the two vectors.

Concerning the diabatic heating term, $\Pi(p)=c_{p}\frac{T}{\theta}$ and Q can be decomposed in

$$Q=-\frac{1}{\rho} (\hbox{div}{{\mathbf{F}}}_{\rm rad}+\hbox{div} {{\mathbf{J}}}_{H}^{\mathbf{D}}+L \hbox{div}{{\mathbf{J}}}_{q}^{D})-L(e-c)+Q_{f} $$

(5)

with F _rad the radiative flux, J ^D _H and J ^D _q the heat and water vapour flux due to conduction, e and c the rates of evaporation and condensation, Q _f the frictional component.

In this study, we only consider the eddy energy generation terms through baroclinic conversion and through the diabatic effect of condensation vs. evaporation (fourth term of the right-hand side of Eq. 5). Their anomalies alone explain most of the total eddy energy anomalies presented in the previous section and are considered as the dominant terms. The other terms are not developped, and were found to be of minor interest in the case of our analyses (studied but not shown on two of the models, namely IPSL-CM4-V1-MR and CNRM-CM3) but readers interested in their expression can refer to Cai and Mak (1990) or Rivière et al. (2004). The quasi-geostrophic framework is used for simplifying the equation of the total eddy energetics, nevertheless it does not change the expression of the two terms studied in this work.

Note that we did not have access to daily values of precipitation and evaporation, therefore, we reconstructed the (e−c) variations from daily means of specific humidity q and wind v at 850 hPa following Eq. 12.6 of Peixoto and Oort (1992)

$$\frac{\partial q}{\partial t} +\hbox{div}(q {{\mathbf{v}}})+\frac{\partial q\omega}{\partial p}=(e-c) $$

(6)

The vertical velocity ω was not available at 850 hPa either, so that we have only considered the horizontal flux divergence, which dominates the signal although the vertical divergence can reach the order of one tenth of the total divergence (tested on CNRM-CM3 for which we had access to more daily variables). Despite this approximation, we are confident that we obtain a relevant idea of what is happening in terms of synoptic diabatic heating.

2.3.2 Results

The left column of Fig. 4 shows the DJF baroclinic generation term at 500 hPa in terms of CTR field (isolines) and LGM-CTR anomalies in colour for each model. In terms of anomalies, the patterns of total eddy energy and baroclinic conversion correspond very well and the former can be explained almost entirely by anomalies of this generation term. The decomposition of this baroclinic term (Eq. 4) indicates that part of the changes can be attributed to mean temperature gradient changes ${\bar{\bf T}}$ and the rest to eddy property changes. In Sect. 2.1, we have discussed changes in the mean horizontal temperature gradient and showed that they explain most of the synoptic changes except for the North Atlantic storm-track. Therefore, in the North Atlantic sector, the main reason for the simulated storm-track changes is related to changes in the eddy-related part of the conversion from mean potential energy into eddy energy. This eddy-related part can be decomposed into the magnitude of the eddy heat flux itself, i.e. the modulus of F′ (Eq. 4), and the angle made by this eddy flux with the mean temperature gradient. The former is related to the eddy activity, and its changes correlate directly to those of the eddy energy (not shown). It can therefore be seen as an amplification factor of the eddy dynamics: more eddy activity favours more conversion of mean flow energy into eddy energy. The latter, the angle made between the eddy heat flux and the mean temperature gradient, is a term related to the eddy efficiency to convert energy from the mean flow (Rivière and Joly 2006). The right column of Fig. 4 shows the anomalies of ${\bf F}^{\prime}\cdot {\bar{T}}/E_{T}^{\prime},$ which give the effective baroclinic conversion rate, which correspond to the rate of conversion of eddy energy if the latter takes an exponential form (cf. Eq. 3). When compared to Fig. 3, it indicates that on the southeastern flank of the Laurentide ice-sheet, the eddies are less efficient to convert the mean-flow energy into eddy energy since the effective conversion rate anomalies are much weaker than the increase in mean-flow energy. The loss of efficiency of the eddies counterbalance the increased mean-flow baroclinicity in this region.

Fig. 4

DJF baroclinic generation term at 500 hPa, noted ${\bf F}^{\prime}\cdot {\bar{T}}$ in text (left column) and DJF exponential baroclinic generation rate at 500 hPa (rigth column), ${\bf F}^{\prime} \cdot {\bar{T}}/E_{T}^{\prime}$ with text notations. CTR values as isolines (every 0.25 mW/kg for the baroclinic generation term, every 0.5 10⁻⁵ s ⁻¹ for the exponential rate), (LGM-CTR) anomalies as colour

DJF Latent heating anomalies (Fig. 5) generally correlate well with eddy energy or baroclinic anomalies. It is not too much of a surprise since we can expect more and/or stronger storms (corresponding to positive eddy energy anomalies) to be related to greater amount of water vapour to be condensated during the storm life cycles, hence releasing more latent energy (the contrary being true for negative anomalies). Exceptions to this relationship are observed in the models in the western part of the north Atlantic sector. Explanation for this fact will be developed in Sect. 3, dealing with precipitation. In conclusion, synoptic latent heating anomalies usually correlate to storm-tracks anomalies, themselves similar at first order to baroclinic anomalies, and therefore amplify the latter. In the western North Atlantic, diabatic anomalies are usually negative, all the more if we normalize it by the total eddy energy (not shown) to infer latent changes not related to the synoptic activity itself. The exception concerning HadCM3M2 south of 40°N will be shown to be an artefact of neglecting vertical advection of specific humidity in Eq. 6 (Sect. 3.1). These negative diabatic anomalies (Fig. 5) counterbalance the positive baroclinic anomalies in IPSL-CM4-V1-MR and MIROC3.2 (Fig. 4) towards moderately positive storm-track anomalies (Fig. 2).

Fig. 5

Approximated DJF synoptic latent heat release at 850 hPa, with text’s notations: $\frac{{{\mathcal{R}}}^{2}}{S\Pi} \theta^{\prime} div(q^{\prime} {\bf v}^{\prime}),$ with v′ the eddy horizontal wind components. CTR values as isolines (every 0.25 mW/kg), (LGM-CTR) anomalies as colour in mW/kg

Although the primary cause for synoptic activity changes seem to be more related to baroclinic conversion changes in terms of direct energetic estimates, humidity changes, and especially the drier conditions over Eastern North America and the Western North Atlantic (cf. also Sect. 3) could explain the loss of efficiency of the eddies in this region. Especially, it could influence the static stability, which is indeed increased in these regions in the simulations at LGM (not shown), and should result in a weaker sensitivity of the synoptic activity to the increased mean-flow baroclinicity (e.g. Chang and Zurita-Gotor 2007).

2.4 Mean-flow forcing by transient eddies

To complete our understanding of the eddy/mean-flow interaction, we consider the forcing of the mean-flow by transient eddies following Hoskins et al. (1983) and Trenberth (1986). Decomposing the zonal wind into an eddy (denoted by primes) and mean flow (denoted by bars) components as in the previous section, and the subscript a referring to ageostrophic wind, the zonal momentum equation for non-divergent flow, neglecting friction and vertical advection gives:

$$\frac{\partial}{\partial t} \bar{U}+\bar{U}\frac{\partial} {\partial x} \bar{U}+\bar{V} \frac{\partial}{\partial y} \bar{U}=f {{\bar{v}}_{a}^{*}}+\hbox{div}({\bar{\bf E}}^{\prime}) $$

(7)

where ${\bf E}^{\prime}=[v^{\prime 2}-u^{\prime 2},-u^{\prime}v^{\prime}]$ and $v_{a}^{*}=v_{a}-f^{-1}\frac{\partial} {\partial x} v^{\prime 2}.$

Several studies have highlighted the role of the meridional derivative of the second component of the E-vector in the displacement of the jet, i.e. the role of the eddy momentum fluxes (cf. Rivière and Orlanski 2007). In fact, u′v′ physically relates to the type of elongation of the eddies, positive values corresponding to a southwest-northeast tilt of the eddies, negative values to a northwest-southeast elongation. These two types of eddy elongation can be related to anticyclonic wave breaking (AWB) and cyclonic wave breaking (CWB) respectively. When AWB occurs, momentum fluxes u′v′ are predominantly positive, which makes the meridional derivative of the second component of the E-vector positive to the north and negative to the south, implying a poleward displacement of the jet. The reverse happens for CWB with an eddy feedback pushing the jet equatorward. Teleconnections such as the North Atlantic Oscillation (NAO), characterized by a meridional displacement of the upper-tropospheric Atlantic jet are now directly understood through this notion of wave breaking (e.g. Benedict et al. 2004; Rivière and Orlanski 2007). The positive (negative) phase of the NAO occurs when AWB (CWB) is predominant over CWB (AWB). It is thus particularly interesting to study the type of wave breaking in order to interpret the jet location at LGM, in particular in the eastern part of the oceans where the eddy feedback is known to be the strongest. Figure 6 shows eddy momentum fluxes at 200 hPa (colours), which are used as a proxy for diagnosing wave breaking, along with the jet intensity and location as isolines for the CTR (left column) and the LGM simulations (right column).

Fig. 6

DJF wind strength as isolines every 10 m/s and DJF eddy momentum flux as colours in m²s⁻² at 200 hPa. CTR simulation left column, LGM right column

In all panels, eddy momentum fluxes are negative on the north side of the jet and positive on the south side. According to Eq. 7, the jet is forced by the eddies to accelerate where the meridional derivative of the fluxes is minimum and negative (i.e. where the meridional derivative of the second component of the E-vector is maximum and positive). This minimum is reached farther southward in LGM plots compared to CTR ones in the eastern part of the storm-tracks as well as the position of the jet. One can think that it just reveals a positive eddy feedback onto the jet. Indeed, the jet will stretch eddies along the SW-NE and NW-SE direction on its south and north sides respectively and the eddy feedback is such that it will accelerate the jet at the same place as it is already. However, the different panels of Fig. 6 provide an additional information concerning the eddy feedback, especially in terms of the asymetry between AWB and CWB, that suggest their implication in the southward jet displacement at LGM. Note first that for a given longitude positive momentum fluxes are much weaker in LGM panels than in CTR ones. It is clearly visible in all models in the Pacific and Atlantic storm-tracks regions. It is only in very specific regions that we do not see such a difference in positive momentum fluxes for example in HadCM3M2 around longitude 100°W or in IPSL-CM4-V1-MR between 20°E and 60°E, but these regions do not correspond to storm-tracks regions. Concerning negative momentum fluxes, a difference also exists even though it is less visible; negative minima reach generally stronger amplitudes at LGM than at CTR apart maybe in MIROC3.2 where they are almost of the same amplitude in both runs of the model. To conclude, the values reached by the positive and negative momentum fluxes strongly suggest a dominance of AWB in preindustrial runs compared to LGM and the reverse for CWB. The fact that there is less AWB and more CWB at LGM offers an explanation for the equatorward shift of the jets in the eastern part of the Pacific and Atlantic storm-tracks. The stronger baroclinicity at LGM acts to favour cyclones over anticyclones and CWB over AWB following the arguments of Orlanski (2003) but less precipitation will have the reverse impact. It is thus not clear why less AWB and more CWB is present at LGM. More work should be done in future studies to investigate in detail wave breaking processes at LGM. Figure 6 can therefore be viewed as a starting point for further studies. As the sign of the momentum fluxes is just a proxy to estimate the type of wave breaking, more work should be done to establish more clearly the occurrence of the different types of wave breaking at LGM and to understand the difference with CTR simulations.

2.5 Seasonality changes

We now consider the seasonality changes at the LGM. Some of the questions we are willing to answer are: Do we expect changes in the amplitude or shifts in the seasonal cycle of northern hemisphere storm-tracks at LGM compared to CTR? Do we get similar behaviours as the midwinter suppression of the North Pacific in the early 1980s first analysed by Nakamura (1992) for the LGM, with weaker synoptic activity during the months of strongest mean-flow baroclinicity? In order to address these questions, we have computed the mean seasonal cycle, i.e. the monthly averages, then extracted the main variability of this cycle by computing the first principal component over the North Hemisphere (North of 25°N). Results are not very different when considering the first principal component on the two storm-tracks regions separately. The results are presented as follow:

• The annual mean value is plotted in colours for CTR and LGM for each model as in Fig. 7. Comparing the CTR and LGM maps indicate general changes between the two climates but no specific seasonal changes;

• The amplitude and the spatial pattern of the first principal component, hereafter called the first EOF, is plotted on the same figures as isolines. It indicates the location of the regions of strong seasonal variability and the amplitude directly reflects the mean amplitude of the cycle since the first principal component time-series (hereafter the first PC) has been normalized. The variance explained by the first EOF is indicated above the maps;

• The information presented in the graphs of the first PC refers to changes in the temporal variation of the seasonal cycle, i.e. shifts or relative changes in the seasonality of specific seasons or months compared to others.

Figure 7 shows the results for the total eddy energy at 500 hPa for the CTR and LGM simulations of each model. From the annual mean value of this field (colour plots), the same general conclusion as for the DJF analysis can be drawn, with a southward displacement and eastward extension of the North Pacific storm-track and a latitudinal thinning (in the western part) and a southeastward extension of the North Atlantic storm-track. The changes in the synoptic activity and their associated reasons detailed in the previous sections are not specific to the winter season but general to the LGM vs. CTR climates.

Fig. 7

Seasonal cycle of total eddy energy at 500 hPa. Left column: standardized first PC of the seasonal cycle (CTR as dashed lines, LGM as solid lines). Central and right columns correspond to CTR and LGM simulations respectively, annual values in colour (J/kg), first EOF as isolines (every 5 J/kg). The variance explained by the first EOF is indicated on top of the plots. Note that when masked values appear for model variables not extrapolated at pressure levels below the surface (IPSL-CM4-V1-MR and MIROC3.2), the same mask has been used in CTR for consistency

Concerning the amplitude of the seasonal cycle (black isolines), no strong consistency is found between the models. The amplitude of the seasonality of the North Atlantic storm-track is increased in HadCM3M2 by around 20%, reduced in IPSL-CM4-V1-MR and CNRM-CM3 (by around 30% and up to 50% respectively), unchanged in MIROC3.2. In the North Pacific, the amplitude of the seasonality is unchanged in HadCM3M2, slightly increased in the IPSL model, and slightly reduced in MIROC3.2 and CNRM-CM3 (more pronounced for the latter). Concerning the spatial localization of the seasonal variability, there is a tendency towards an eastward displacement of the seasonal cycle w.r.t. the annual mean pattern. In the CTR simulation, the seasonal pattern is usually located South of the annual mean pattern, indicating a simple southward and intensification of the storm-tracks during the winter season. In the LGM simulations, the seasonal pattern is also usually displaced to the east w.r.t. the annual mean pattern, indicating a southward and eastward amplification of the synoptic variability during the cold season.

Concerning the seasonal cycle, the models suggest a slight intensification of the synoptic activity in the late winter season (February–March–April) and a slight decrease in the early winter season (October–November). Note that this behaviour is robust between the different models. This shift of the stormy season later in the year is of the order of a few days to a month depending on the month and models (consider on PC graphs of Fig. 7 the temporal translation of the stormy season). In order to understand this shift in the seasonal cycle of the synoptic activity, we consider the mean seasonal cycle of the mean temperature gradient at 500 hPa (Fig. 8, left column), indicating the direct influence of the mean flow baroclinicity on the baroclinic generation term, the exponential baroclinic generation rate $({\bf F}^{\prime} \cdot {\bar{T}}/E_{T}^{\prime}),$ which add the effect of the changes in eddy efficiency (Fig. 8, central column), and of the approximated synoptic latent heating, normalized by the total eddy energy (named “latent heat source” in Fig. 8, right column). The mean-flow baroclinicity is slightly shifted later in the year, except for HadCM3M2, but the order of magnitude of the shift is usually weaker than for the eddy energy (except for CNRM-CM3). The changes of the seasonal cycle when considering also the effect of the changes in the mean seasonal cycle of the eddy efficiency (central column) and the effect of the latent heat source (right column) do not directly relate neither to the shifts in the mean seasonal cycle of the storm-track activity.

Fig. 8

Standardized first PC of the seasonal cycle (CTR as dashed lines, LGM as solid lines) for the horizontal temperature gradient at 500 hPa (left column), for the eddy efficiency (central column, ${\bf F}^{\prime} \cdot\bar{T} /E_{T}^{\prime}$ with text notations), and for latent heat source (right column, $\frac{{{\mathcal{R}}}^{2}} {S\Pi} \theta^{\prime}Q^{\prime}/E_{T}^{\prime})$

During the stormy season, changes are found in the month of maximum synoptic activity. In the CTR simulations, this month is January for all models. Looking at the first PC of temperature gradient at 500 hPa, computed over the same domain, indicates that the CTR seasonal cycle of northern hemisphere storm-tracks corresponds to the one of the mean-flow baroclinicity (dashed lines in Fig. 8, left column). The only model that diverges from this rule is IPSL-CM4-V1-MR, for which the March synoptic activity is found equivalent to the January one, but with a weaker mean-flow baroclinicity. We therefore find something similar to the Pacific midwinter suppression in this model for the CTR climate, although the first PC considered here includes both northern hemisphere storm tracks. For the LGM, the changes in the month of maximum synoptic activity are not associated with a similar shift in the mean-flow baroclinicity, whose maximum strength still occurs in January (Fig. 8, left column). Some of these changes seem at least in part related to changes in the efficiency of the eddies (Fig. 8, central column). Although the shapes of the seasonal cycles do not match directly, the peak in synoptic activity in the HadCM3M2 model in March at LGM is suggested by a local enhancement in the eddy efficiency term, the LGM maxima in February in IPSL-CM4-V1-MR and CNRM-CM3 are also present in the seasonal cycle of the eddy efficiency. The changes in the seasonal variations of the latent heat source (Fig. 8, right panel) could also explain the seasonal variation in synoptic activity as it is partly the case for the North Pacific storm-track nowadays (Chang 2001; Chang and Song 2006), nevertheless they do not correlate directly to the ones of the synoptic activity. The seasonal cycle of the inverse of the static stability at 500 hPa, over the whole domain and over the oceanic surfaces of the domain only, in order to isolate changes influencing the storm-tracks (not shown), do not relate neither to the one of the synoptic activity nor to the one of the eddy efficiency, to which it could also be linked (e.g. Chang and Zurita-Gotor 2007).

Since the baroclinic generation term $({\bf F}^{\prime}\cdot\bar{T})$ exhibits a seasonal cycle very similar to the synoptic activity for all models (not shown), but that neither the mean temperature gradient nor the eddy efficiency part of this term do so (Fig. 8, left and central panels), it suggests that the amplification role played by the synoptic activity itself on the generation of eddy energy is crutial for determining its seasonality. The seasonal shift of the synoptic activity could be primarily due to the shift in the mean-flow baroclinicity, further amplified by the non-linearity of the system, whereas the changes in the seasonal extrema of the synoptic activity could be at least in part related to seasonal changes of the efficiency of the eddies, also enhanced by the eddy activity itself. Further work should be performed in order to better understand the changes in the seasonality of the northern hemisphere storm-tracks between preindustrial and LGM climates.

3 Precipitation changes at LGM

3.1 DJF precipitation changes

First, we consider precipitation anomalies for DJF (Fig. 9), season during which we expect northern hemisphere precipitation to be mostly influenced by storms. Indeed, precipitation anomaly patterns correspond very well to synoptic activity anomalies, with the exception of the North Atlantic region (Fig. 2).

Fig. 9

DJF precipitation. CTR values as isolines (every 2 mm/day), (LGM-CTR) anomalies as colour in mm/day

In the North Pacific, the storm activity reduction on the northern edge of the CTR storm-track is associated with a significant reduction in precipitation ranging from a maximum reduction of 2 mm/day in the IPSL model up to 3.5 mm/day in HadCM3M2 and MIROC3.2, and even 4 mm/day in CNRM-CM3. It corresponds roughly to a 40% reduction of the precipitation on the northern edge of the CTR North Pacific storm-track in each model, of the same order as the synoptic activity loss. The Southeastward extension of the North Pacific storm-track at LGM is also associated with increased precipitation, with a maximum anomaly simulated on the North American coast around 38°N for all models, with values ranging from 2.5 to 4 mm/day. The enhanced precipitation on the southeastern edge of the CTR North pacific storm-strack is about 50–100% greater than the CTR values. This is greater than the synoptic activity anomalies, pointing out the non-linear effect of the displacement of the storm-track over moister areas to the south.

Over the continents, precipitation anomalies also usually correlate well with synoptic activity changes, especially over North America with enhanced precipitation south of the ice-sheet and reduced precipitation over the ice-sheet itself. The cold and dry air imposed by the presence of ice-sheets also acts to reduce the precipitation over the Fennoscandian ice-sheet, i.e. over Northern Europe and the present-day Barents Sea. Furthermore, precipitation is reduced over most of Asia in all models, especially north of 40°N, despite some slight enhanced synoptic activity at 500 hPa in some places in HadCM3M2 and IPSL-CM4-V1-MR. The influence of colder temperatures therefore appears to dominate over synoptic anomalies over this area.

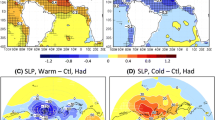
Concerning the North Atlantic region, the relationship between precipitation and storm-track anomalies is not direct, especially on the western part of the basin. A significant reduction in maximum precipitation is observed in all models, with anomalies found at the location of the CTR precipitation maximum, i.e. around 60°W, 37.5°N. This reduction is about 25–30% of the CTR value. This precipitation anomaly can be attributed to storm-track activity reduction in MIROC3.2 and CNRM-CM3, but not in HadCM3M2 nor in IPSL-CM4-V1-MR. Figure 10 shows sea-level pressure LGM-CTR anomalies in colour, along with the CTR values as isolines, the zonal means being removed. This shows the stationary waves which are important in the DJF North Hemisphere circulation: Aleutian and Islandic Lows alterning with American and Asian Highs. The high pressure systems developing over the continents in winter are much stronger at LGM due to even colder temperature compared to oceans, especially due to the presence of the ice-sheets. The strengthening of the American High related to the Laurentide ice-sheet is very strong in IPSL-CM4-V1-MR, but is also present in the other model results. It implies more cold and dry polar air being advected in the zone of storm formation, in the area off Newfoundland. It can explain the strong precipitation loss in this area despite small positive anomalies in storm activity in HadCM3M2 and IPSL-CM4-V1-MR. Note also the low pressure anomalies over the eastern North Atlantic usually centred at around 20°W, 55°N, that correspond to a southward displacement of the winds with westward wind anomalies to the North and eastward anomalies to the south. This is coherent with the eddy forcing of the winds described in Sect. 2.4.

Fig. 10

DJF sea level pressure, zonal mean removed. CTR values as isolines (every 5 hPa), (LGM-CTR) anomalies as colour in hPa

The fact that DJF precipitation anomalies do not correspond to DJF storm-tracks anomalies in the western North Atlantic does not mean that they are not related. In fact, the pattern of synoptic latent heating anomalies shown in Fig. 5 looks similar to the precipitation anomaly pattern shown in Fig. 9. The anomalies of precipitation minus evaporation occurring at the synoptic time-scale therefore seem to determine most of the total precipitation anomalies. One exception is the HadCM3M2 model, in which strong latent heat release is found south of 40°N in the whole western North Atlantic whereas precipitation anomalies are dominantly negative in this region. This is an artefact. In fact, the difference comes from a discrepancy of our approximation consisting in calculating only the horizontal divergence of eddy humidity flux in Fig. 5. Splitting DJF precipitation anomalies between large-scale (resulting from horizontal divergence of humidity fluxes) and convective precipitation (resulting from vertical instability) in the models (Fig. 11) indicates that in the HadCM3M2 model, the convective precipitation anomalies are very important in this region and counterbalance large-scale precipitation anomalies. The DJF latent heating approximated in Fig. 5 in fact correlates very closely to large-scale DJF precipitation anomalies (Fig. 11 left column), but the complete synoptic latent heating anomalies calculated using also the vertical divergence of eddy humidity fluxes would probably look even closer to total precipitation anomalies (Fig. 9). The synoptic activity anomalies determine the precipitation anomalies also in the western North Atlantic but in an overall much drier environment at LGM resulting from more polar air advection by stationary waves in this area.

Fig. 11

DJF Large-scale (left column) and convective (rigth column) precipitation. CTR values as isolines (every 2 mm/day), (LGM-CTR) anomalies as colour in mm/day

3.2 Seasonality changes

We use the same method as the one described in Sect. 2.5 to study the seasonal cycle of precipitation in the CTR and in the LGM simulations (Fig. 12). Concerning the seasonal cycle (left panels), the normalized first principal components indicate only very weak changes between the CTR and LGM climates in the models. Contrary to the synoptic activity variations which capture only one physical process maximum in winter and minimum in summer, the first EOF of the precipitation seasonal cycle captures different physical phenomena occurring dominantly in winter for storm-related precipitation and in summer for local convection or monsoonal precipitation. The first EOF captures both behaviours in one component, not allowing a high degree of freedom for seasonal shifts for each process involved. The higher degree of complexity in the seasonal cycle of precipitation compared to synoptic activity can also be seen from the lower variance explained by the first PC (around 70% for precipitation compared to around 80% for synoptic activity).

Fig. 12

Seasonal cycle of precipitation. Left column: standardized first PC of the seasonal cycle (CTR as dashed lines, LGM as solid lines). Central and right columns correspond to CTR and LGM simulations respectively, annual values in colour (mm/day), first EOF as isolines (every 1 mm/day). The variance explained by the first EOF is indicated on top of the plots

The pattern of the first EOF of the synoptic activity (Fig. 7) is positive everywhere indicating a simple seasonal variation with more synoptic activity in winter, less in summer. The patterns of the first EOF of precipitation (isolines in Fig. 12) are more complex. There are regions with positive values (generally over the oceans and the western ends of continents) and regions with negative values (generally over inner and eastern ends of continents), indicating in the first case more precipitation in winter and in the latter more precipitation in summer. This is consistent with the fact that precipitation can result from different physical systems including frontal structures of midlatitude storms (following synoptic activity, dominant in winter months), local vertical instabilities resulting in the formation of local cumulonimbus (dominant in summer) or monsoonal systems (also dominant in summer months).

First we consider the patterns of positive values of the first EOF, i.e. dominated by winter precipitation. It mostly concerns the oceanic basins and especially their central to eastern parts, and the western part of the continents. In the central to eastern North Pacific, we find a southeastward displacement of the precipitation pattern consistent with conclusion from the DJF analysis of the previous section. The position of the precipitation patterns to the south-east compared to the synoptic activity patterns (Fig. 7) corresponds to the fact that precipitation results from frontal structures developing at the border of the warm and moist air mass advected from the south in front of the storms. In the North Atlantic, the pattern of strong seasonal variability is usually displaced to the east (HadCM3M2, IPSL-CM4-V1-MR, and CNRM-CM3 to a lesser extent) or simply increased over the South eastern Atlantic (MIROC3.2), consistent with the conclusions from the DJF analysis.

In the western part of the oceanic basins (between 140 and 180°E for the Pacific and 80 and 40°W in the Atlantic), we usually have less seasonal variability at the LGM than for the CTR simulations, although they are still regions of strong precipitation. In the CTR runs, precipitations in these regions are dominated by winter precipitations associated with storms. In the LGM runs, precipitations tend to be more year-round phenomena, which can be due to a decrease in storm activity in this region (MIROC3.2, CNRM-CM3 models), but also to weaker availability of moisture in this region due to stationary wave effects (Fig. 10).

Over inner and eastern continents and the far western North Pacific, precipitation are not dominated by any seasons in particular (zero values of the first EOF pattern) or by summer months (negative values). Over North America, south of the ice-sheet, precipitation increases at LGM compared to CTR, partly in winter due to synoptic activity changes (1), but mostly in summer (cf. negative patterns of the first EOF in Fig. 12). Over Asia, the annual mean precipitation is weaker in relationship with a colder climate but the seasonal variations are similar at LGM and for CTR simulations in the models. In western Asia and Europe (west of 70°E), patterns are similar at LGM and at CTR for each model with usually slightly positive EOF values corresponding to predominantly winter precipitation. Between 70°E and 140°E, patterns are similar at LGM and at CTR with usually negative, especially to the South, corresponding to the Asian monsoon.

4 Conclusions

We have studied the synoptic variability during the Last Glacial Maximum from simulations using the same PMIP2 experimental design. We have centred our study on DJF months for which synoptic activity is the greatest, trying to understand the physical mechanisms explaining the differences with respect to preindustrial climate (CTR) simulations based on the generation terms of eddy energetics. We then considered the seasonal variations of storm-tracks. Given the influence of perturbations on precipitation, especially in winter, we have considered precipitation changes first during DJF months, then for the overall seasonal cycle.

Concerning the North Pacific region, all models simulate a consistent southeastward shift of the storm-track in winter (Fig. 2), mostly related to baroclinic effects and a similar displacement of the jet (Figs. 3, 4), partly forced by the eddies themselves (Fig. 6). Latent heat release (Fig. 5) further amplifies the baroclinic anomalies, more and/or stronger storms implying more condensation during the life cycle of the storms. Weaker availability of moisture due to colder air temperature does not change the physics of the perturbations in this region. In terms of winter precipitation (Fig. 9), anomalies relate very well to storm-track changes, with a southeastward displacement of the North Pacific precipitation pattern. A large decrease of precipitation in the western part of the North Pacific is also related to stronger continental high pressure systems in winter bringing more dry polar air in this region (Fig. 10).

Over the North Atlantic, there is a greater dispersion of the models and a greater complexity in the physics involved. The common feature consists of a thinning of the storm-track in its western part and an amplification of synoptic activity to the southeast, around the region between the Azores Islands and the Iberian Peninsula (Fig. 2). The southeastward displacement of the storm-track is related to a similar displacement of the jet (Fig. 3), also forced by eddies (Fig. 6), as for the eastern north Pacific. Concerning the behaviour in the western North Atlantic, the synoptic activity anomalies are at first order related to baroclinic generation term anomalies (Fig. 4), but a loss in the eddy efficiency to convert energy from the mean flow balances a clear increase in the mean-flow baroclinicity due to the presence of the ice-sheet (Fig. 3). Latent heat release anomalies (Fig. 5) in this region does not directly follow neither synoptic nor baroclinic anomalies due to a change in the moisture availability in the region due to the advection of more dry polar due to stationary wave enhancement (Fig. 10). The loss of efficiency of the eddies to convert energy from the mean flow should be further studied. The drier conditions in the Western North Atlantic could contribute to change the eddy properties, as well as the orography imposed by the Laurentide ice-sheet. Also, the presence of this ice-sheet should greatly modify the upstream seeding of the North Atlantic storm-track. Winter precipitation anomalies are related to storm-activity anomalies, but the effect of dry polar air advection has to be taken into account. The latter effect implies less precipitation on the western part of the basin, and the former a southeastward displacement of precipitation at the end of the storm-track (Fig. 9), with more precipitation over the Iberian Peninsula, less over northern Europe.

Compared to the results from the PMIP1 prescribed SST simulations, the LGM synoptic activity is found to be less dependant on the sea-ice edge in the North Atlantic ocean. The sea-ice limit extends farther North in the PMIP2 coupled simulations compared to the CLIMAP reconstruction, which prevents it to force the localization of the North-Atlantic storm-track along its edge. Despite the higher degrees of freedom in PMIP2 models due to the full coupling between the atmosphere and the ocean, the dispersion of the model responses in terms of storm-tracks does not seem greater than for PMIP1 models (cf. Kageyama et al. 1999), which could be due to less differences in the models resolutions, which was a major factor of model result dispersion for the PMIP1 models. The SST differences between PMIP1 and PMIP2 simulations, and especially the sea-ice extent differences, imply major differences in the humidity content of the air and hence in the precipitation patterns, as highlighted in Braconnot et al. (2007).

The seasonal cycle of the synoptic activity follows the overall conclusions of the winter months in terms of patterns and intensities. In terms of seasonal timing, the stormy season is displaced later in the year by a few days to a month depending on the season and the model considered (Fig. 7). This shift, as well as a change in the month of maximum synoptic activity in the LGM runs, seem partly related to changes in mean-flow baroclinicity and eddy efficiency changes (Fig. 8), amplified by the positive feedback of the synoptic activity on the generation of eddy energy. However, further work would be needed in order to clearly understand the seasonality changes of the synoptic activity. In terms of impacts, the seaonality change does not directly reflect on the seasonal cycle of the precipitation studied from its first EOF, probably since the first EOF of precipitation is sensitive to different mechanisms and does not specifically capture the response to storm-related precipitation only. Precipitation over the oceanic basins is maximum in winter and dominantly follows storm-track variations. However, more intense polar air advection on the western part of the oceanic domains also contributes to reduced precipitation in these regions. Over North America, south of the ice-sheet, annual precipitation is increased in all simulations, associated to more synoptic activity in winter, but also due to more summer precipitation at the LGM. Over Eurasia, the overall climate is drier, the precipitation pattern and seasonality do not seem to change much at LGM compared to CTR (Fig. 12).

The different models react in similar manners on many aspects of the storm-tracks. In order to consider if it indeed corresponds to realistic behaviour at LGM, it is important to compare to reconstructions based on proxy data. Concerning storm-tracks directly, the meridional sea-surface temperature gradients can be good indicators of the mean-flow baroclinicity and of storm-track localization over the oceanic basins. Kageyama et al. (2006) compared the different PMIP models to different proxy sea-surface temperature reconstructions over the North Atlantic and noticed a southward shift and stronger gradient of meridional SST in the eastern North Atlantic consistent in both models and reconstructions, suggesting that the southeastward extension of the North Atlantic storm-track is a robust feature. Concerning precipitation changes at LGM, first note that our general conclusions concerning the four models presented here are also found for all PMIP2 model-mean precipitation pattern as shown in Braconnot et al. (2007). Concerning precipitation reconstructions over the continents, recent results using inverse vegetation modelling over Eurasia (Wu et al. 2007) are consistent with the model simulations presented here, at least in its general conclusion of drier conditions. Concerning North America, the drier conditions inferred from reconstructions south of the ice-sheet (Bromwich et al. 2005) is not necessarily in contradiction with PMIP2 model results, since the increased precipitation occurs farther south, South of 40°N in winter (Fig. 9). This increased precipitation over southern North America is suggested by pollen-based reconstructions (Jackson et al. 2000) and from consideration on lake shorelines (Menking et al. 2004). A more detailed and quantitative analysis of model/data comparison would be of interest, especially using new pollen-based reconstructions taking the CO₂ effect into account (Wu et al. 2007).

Despite the higher degree of freedom of PMIP2 models compared to PMIP1 models due to a full coupling between the ocean and the atmosphere, fundamental for storm-track dynamics, the response of the models to LGM conditions is quite robust. Models and data are also consistent, at least at first order, concerning northern hemisphere synoptic activity and precipitation patterns at the Last Glacial Maximum. It is encouraging concerning simulations of future climates under increased CO₂ concentrations, although cold and warm climates might not be completely symmetrical since for instance, the Clausius–Clapeyron equation for saturation vapour pressure is not, potentially leading to different influences of changes in water vapour in the atmosphere. The great ice-sheets also imply a strong constraint on storm-tracks that do not exist for increased-GHG concentration simulations, but consistent results were also found in the North Pacific at LGM, not directly influenced by ice-sheets. Concerning the physics of the storm-tracks, paleoclimate simulations can provide interesting situations, the LGM for instance providing a useful ground for studying strong mean-flow baroclinicity in the North Atlantic. Concerning the understanding of paleo and future climates, it is fundamental to consider the complex behaviour of the storm-tracks, especially when the hydrological cycle of the mid-latitudes is at steak. Changes in the climatological mean of the synoptic activity should also be extended to its interannual variability in order to consider oscillations similar to the modern Arctic Oscillation under different global climatic conditions.