Quantifying changes and their uncertainties in probability distribution of climate variables using robust statistics

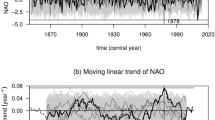
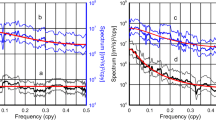
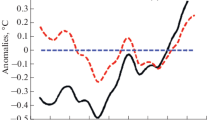
Abstract

Robust tools are presented in this manuscript to assess changes in probability density function (pdf) of climate variables. The approach is based on order statistics and aims at computing, along with their standard errors, changes in various quantiles and related statistics. The technique, which is nonparametric and simple to compute, is developed for both independent and dependent data. For autocorrelated data, serial correlation is addressed via Monte Carlo simulations using various autoregressive models. The ratio between the average standard errors, over several quantiles, of quantile estimates for correlated and independent data, is then computed. A simple scaling-law type relationship is found to hold between this ratio and the lag-1 autocorrelation. The approach has been applied to winter monthly Central England Temperature (CET) and North Atlantic Oscillation (NAO) time series from 1659 to 1999 to assess/quantify changes in various parameters of their pdf. For the CET, significant changes in median (or scale) and also in low and high quantiles are observed between various time slices, in particular between the pre- and post-industrial revolution. Observed changes in spread and also quartile skewness of the pdf, however, are not statistically significant (at 95% confidence level). For the NAO index we find mainly large significant changes in variance (or scale), yielding significant changes in low/high quantiles. Finally, the performance of the method compared to few conventional approaches is discussed.

Appendix

1.1 On quantile estimates and their standard errors

This appendix provides a simple guideline to compute quantiles and few other robust, and resistant measures of scale and shape of pdfs along with their standard errors in independent and dependent data.

1.1.1 Independent data

We consider a time series x _t , t=1,..., n, assumed to be a a realisation of a sequence X ₁,X ₂,...,X _n of independent and identically distributed (iid) random variables having the same continuous distribution as some random variable X whose cdf and its corresponding pdf are respectively F( ) and f( ). The cdf F( ) is monotonically increasing and can be inverted. The number ξ _p =F ⁻¹ (p), for any 0<p<1, is the pth quantile of X. For a given x let $I_{k} (x) = 1_{X_{k} \le x}$ be the indicator of {X _k ≤ x }, i.e. I _k (x) is one only if X _k ≤ x, and zero otherwise. Then I _k (x), k=1, ..., n, are also iid as I(x)=1_{X ≤ x}. The edf of the sample is given by:

$$F_n (x) = \frac{1}{n} \sum\limits_{k=1}^{n} I_k(x). $$

(32)

The use of the edf to express the sample quantile has been initiated first by Bahadur (1966) using the following asymptotic representation:

$$X_{(p)} = \xi_{p} + \frac{p - F_{n} (\xi_{p})}{f (\xi_{p})} + \mathcal{R}_{n} $$

(33)

where $\mathcal{R}_{n}$ is a remainder that goes to zero as n increases. Note that for any 1 ≤ k ≤ n, I _k (ξ _p ) is a binary random variable taking values 0 and 1 with respective probabilities 1−p and p. Now, for large n, X _(p)− ξ _p is approximately normally distributed with zero mean and variance (see also Kendall and Stuart 1977; Wilcox 1997):

$$\sigma_{p}^{2} = \frac{p(1-p)}{n f^{2} (\xi_{p})}. $$

(34)

Both the estimators (Eqs. 33 and 34) are parametric, and they will be used later for dependent data. Here we are interested in non-parametric and resistant estimators for the quantiles and their standard errors. Let x _1:n ≤ x _2:n ... ≤ x _n:n be the sorted sample of the time series. Similarly, let X _1:n ≤ X _2:n ... ≤ X _n:n be the order statistics of the sequence X ₁,X ₂,...,X _n . These order statistics can be used to construct a resistant, robust, and non-parametric estimator X _(p) for the pth quantile, namely:

$$X_{(p)} = X_{p_{0}:n} $$

(35)

where p ₀=[np+0.5], i.e. the integer part of np+0.5 (Kendall and Stuart 1973; David 1981.) Now at a given significance level α, the probability that X _r:n ≤ X _(p) ≤ X _s:n, can be computed, and is given by (see e.g. Kendall and Stuart 1973):

$$1 - \alpha = J_{p} (r, n-r+1) - J_{p} (s, n-s+1), $$

(36)

where $J_p (a,b) = \frac{1}{B(a,b)} \int_{0}^{p} t^{a} (1 - t)^{b-1} {\rm d}t$ is the cdf of the beta distribution with parameters a and b.

For a given n, α, and 0<p<1, Eq. 36 is solved by choosing the interval [r, s] to be centered at the rank p ₀ corresponding to $X_{(p)} = X_{p_{0}:n}.$ Hence, taking p ₀=[np+0.5], we then choose s=2p ₀ − r. The parameter r is then obtained by solving the nonlinear equation:

$$N(x) = J_{p} (x, n-x+1) - J_{p} (2p_{0} - x, n-2p_{0} + x + 1) -1 + \alpha = 0 $$

(37)

Note that in Eq. 37 the arguments n−x+1, 2p ₀ − x, and n−2p ₀+x +1 should all be non-negative and that 1≤ x ≤ n. This readily yields:

$$\max \left(1,2p_{0}-n \right) \le x \le \min \left(n,2p_{0} -1 \right). $$

(38)

Equation 37 is solved using the root finder fzero in MATLAB within the interval provided by Eq. 38.

An approximation of the standard error σ _p of the estimator X _(p) of ξ _p is obtained using:

$$2 \sigma_{p} \Phi^{-1} \left(1 - \frac{\alpha}{2} \right) = E \left( X_{s:n} - X_{r:n} \right), $$

(39)

where Φ is the cdf of the standard normal distribution, and E( ) stands for the expectation operator. The estimate of the standard error from the observed sample is obtained from Eq. 39 by substituting X _s:n and X _r:n for x _s:n and x _r:n respectively. In Table 1 we show values of r for α=5%, sample sizes ranging from 100 to 2,000, and various values of probability p.

In a similar manner it is possible to compute the standard errors of other quantities such as the quantile difference D _p,q (see Eq. 19.) In this case, it can be seen from Eq. 33 that $f(\xi_{p}) f(\xi_{q}) {\rm cov} \left( X_{(p)}, X_{(q)} \right) = \frac{1}{n^{2}} \sum_{k,l} {\rm cov} \left(I_{k} (\xi_{p}), I_{l} (\xi_{q}) \right),$ and since cov (I _k (ξ _p ), I _l (ξ _q ) )=p(1−q) δ _kl , where δ _kl is the Kronecker delta, one gets:

$${\rm cov} \left(X_{(p)}, X_{(q)} \right) = \frac{p(1-q)}{nf(\xi_{p}) f(\xi_{q})}, $$

(40)

which reproduces (Eq. 34) when p=q. The nonparametric expression of σ ²_p,q =E(D _p,q)² (see Eq. 20) is then obtained from σ ² _p , σ ² _q , and Eq. 40 after eliminating f(ξ _p ) and f(ξ _q ) using Eq. 34.

1.1.2 Dependent data

Interest in computing quantiles from data has, since the work of Bahadur (1966), attracted many researchers. Extensions of Eq. 33 to sequences of random variables (or stochastic processes) with dependency structures have been performed to include a broad class of linear processes

$$X_{t} = \sum\limits_{k=1}^{\infty} a_{k} \varepsilon_{t - k}. $$

(41)

with iid ɛ _k satisfying certain regularity properties. Sen (1968, 1972) extended Bahadur’s result to m-dependent and strongly mixing processes. Hesse (1990) extended the result to a broad class of linear short range dependence processes, whereas Ho and Hsing (1996) extended it to include long-range dependence. Wu (2005) generalised and refined those results for linear and some nonlinear processes.

In summary, Eq. 33 is found to apply to a large class of linear and nonlinear time series including short- and long-range dependence. Note that for the latter case a correction term

$$-\frac{1}{2} \overline{X_{n}}^{2} \frac{{\rm d}Log f}{{\rm d}x} (\xi_{p})$$

is included in Eq. 33 (Wu 2005).

From Eq. 33 the variance σ ² _p of X _(p) now involves ${\rm var} \left[\frac{1}{n} \sum_{k=1}^{n} I_{k} (\xi_{p}) \right],$ precisely:

$$n \sigma_{p}^{2} f^{2}(\xi_{p})= \frac{1}{n} {\rm var} \left[ \sum_{k=1}^{n} I_{k} (\xi_{p}) \right]. $$

(42)

Later we give the expression of σ ² _p when the process is Gaussian. Using the stationarity of the sequence I _k (x), k=1,2,..., n, yields, for large n, the approximation:

$$n \sigma_{p}^{2} f^{2} (\xi_{p}) \approx \sum\limits_{k=-(n-1)}^{n-1} {\rm cov} \left[I_{n} (\xi_{p}), I_{n+k} (\xi_{p}) \right]. $$

(43)

Heidelberg and Lewis (1984) interpret the right hand side of Eq. 43 as the value at zero frequency of the spectrum:

$$h(\omega, x) = \sum\limits_{k= -\infty}^{\infty} {\rm cos} (2 \pi \omega k) {\rm cov} \left[I_{n} (x), I_{n+k}(x) \right], $$

(44)

of the binary process I _k (x), k=1,2, ..., for − (1/2) ≤ ω ≤ (1/2). The variance σ ² _p is then given by:

$$\sigma_{p}^{2} = \frac{h(0, \xi_{p})}{n f^{2} (\xi_{p})}. $$

(45)

The ratio R ² _p between variances of quantile estimates is then obtained as the ratio between Eqs. 45 and 34. Here, as in Heidelberg and Lewis (1984), the log-periodogram:

$$L(k, p) = \hbox{Log}\,\left[ \frac{1}{n} \left| \sum\limits_{j=1}^{n} I_{j} (\xi_{p}) {\rm e}^{-2{\rm i}(j-1)k/n}\right|^{2} \right], $$

(46)

estimated from the binary sequence, is used to compute h(0, ξ _p ) using the intercept of a least square regression of the log-periodogram (Eq. 46). Note that the log-periodogram provides an estimator of the logarithm of the spectrum.

Now suppose that the sample is drawn from a zero-mean Gaussian process with covariance and correlation functions γ _k and ρ _k , k=0,1,...,n−1. In this case the joint distribution of any subset (X ₁, ..., X _p ) is completely specified by the covariance matrix $\mbox{\boldmath$\Sigma$}_{p} = \left(\gamma_{i-j} \right)$ of the random vector X=(X ₁, ..., X _p )^T. It can be verified that:

$${\rm cov} \left[I_{k} (\xi_{p}), I_{l} (\xi_{p}) \right] = {\rm Pr} \left(X_{k} \le \xi_{p}, X_{l} \le \xi_{p} \right) - p^{2} = \int\limits_{-\infty}^{\xi_{p}} \int\limits_{-\infty}^{\xi_{p}} g_{k,l} (x,y) {\rm d}x\,{\rm d}y - p^{2}, $$

(47)

which involves the joint pdf

$$g_{k,l}(x,y) = \frac{1}{2\pi\left|\mbox{\boldmath$\Sigma$} \right|^{1/2}} \hbox{exp}\,\left[-\frac{\gamma_{0}}{2\left|\mbox{\boldmath$\Sigma$}\right|} \left(x^{2} - 2 \rho_{k-l} xy + y^{2} \right) \right] $$

(48)

of X _k and X _l , when k ≠ l, which is a bivariate normal with zero mean and covariance matrix

$$ \mbox{\boldmath$\Sigma$} = \left(\begin{array}{*{20}c} \gamma_{0} & \gamma_{k-l} \\ \gamma_{k-l} & \gamma_{0} \\ \end{array}\right). $$

Note that for k=l one gets var(I _k (ξ _p ))=p − p ². Now using Eqs. 42 and 47, and letting

$$\Psi(k) = \frac{1}{2 \pi \sqrt{1 - \rho_{k}^{2}}} \int\limits_{-\infty}^{\xi_{p}/\sqrt{\gamma_{0}}} \int\limits_{-\infty}^{\xi_{p}/\sqrt{\gamma_{0}}} \hbox{exp}\,\left[ -\frac{1}{2(1 - \rho_{k}^{2})} \left(x^{2} - 2 \rho_{k} xy + y^{2}\right)\right] {\rm d}x\,{\rm d}y,$$

(49)

the variance of the pth quantile estimates becomes:

$$\sigma_{p}^{2}=\frac{1}{n f^{2} (\xi_{p})} \left[2 \sum\limits_{k=1}^{n-1} \left(1 - \frac{k}{n}\right) \Psi (k) + p - n p^{2}\right].$$

(50)