Minimal Obstructions for Polarity, Monopolarity, Unipolarity and (s, 1)-Polarity in Generalizations of Cographs

Abstract

It is known that every hereditary property can be characterized by finitely many minimal obstructions when restricted to either the class of cographs or the class of $P_4$-reducible graphs. In this work, we prove that the same is true when restricted to some other superclasses of cographs, including $P_4$-sparse and $P_4$-extendible graphs (both of which extend $P_4$-reducible graphs). We also present complete lists of $P_4$-sparse and $P_4$-extendible minimal obstructions for polarity, monopolarity, unipolarity, and (s, 1)-polarity, where s is a positive integer. In parallel to the case of $P_4$-reducible graphs, all the $P_4$-sparse minimal obstructions for these hereditary properties are cographs.

1 Introduction

All graphs in this paper are simple and finite; we refer the reader to [1] for basic terminology and notation not explicitly defined. For a graph G, we denote its vertex set by $V_G$, and its complement by ${\overline{G}}$. For graphs G and H, we denote by $G + H$ the disjoint union of G and H, and by $G \oplus H$ the join of G and H, i.e., the graph $\overline{{\overline{G}} + {\overline{H}}}$. Naturally, the disjoint union of n copies of a graph G is denoted by nG. Two subsets $V_1$ and $V_2$ of $V_G$ are said to be completely adjacent if every vertex v of $V_1$ is adjacent to any vertex of $V_2 \setminus \{v\}$. Analogously, $V_1$ is completely nonadjacent to $V_2$ if no vertex v in $V_1$ is adjacent to a vertex in $V_2$.

If G and H are graphs, we write $H \le G$ to denote that H is an induced subgraph of G. We say that G is an H-free graph if G does not have induced subgraphs isomorphic to H. Given a family of graphs ${\mathcal {H}}$, we say that G is ${\mathcal {H}}$-free if it is H-free for every $H \in {\mathcal {H}}$. A k-cluster is the complement of a complete k-partite graph, and a cluster is a k-cluster for some integer k. Clusters are characterized as $P_3$-free graphs, while k-clusters are precisely the $\{P_3, (k+1)K_1\}$-free graphs. Complementarily, complete multipartite graphs coincide with the $\overline{P_3}$-free graphs, and complete s-partite graphs are precisely the $\{\overline{P_3}, K_{s+1}\}$-free graphs.

A property ${\mathcal {P}}$ of graphs is said to be hereditary if it is closed under taking induced subgraphs. Given a hereditary property of graphs ${\mathcal {P}}$, a ${\mathcal {P}}$-obstruction is a graph G that does not have the property ${\mathcal {P}}$; if in addition G is such that any proper induced subgraph of G has the property ${\mathcal {P}}$, then G is said to be a minimal ${\mathcal {P}}$-obstruction.

For nonnegative integers s and k, an (s, k)-polar partition of a graph G is a partition (A, B) of V such that G[A] is a complete multipartite graph with at most s parts and G[B] is a k-cluster. A graph G is said to be (s, k)-polar if V admits an (s, k)-polar partition. When we replace s or k with $\infty$, it means that the number of parts of G[A] or G[B], respectively, is unbounded. A graph is said to be monopolar or polar if it is a $(1, \infty )$- or an $(\infty , \infty )$-polar graph, respectively. A unipolar partition of a graph G is a polar partition (A, B) of G such that A is a clique. Naturally, a graph is said to be unipolar if it admits a unipolar partition. Unipolar and monopolar graphs are particularly interesting because many recognition algorithms for polar graphs on specific graph classes first check whether the input graph is either unipolar or monopolar. A (1, 1)-polar partition of a graph G is commonly called a split partition of G. The graphs admitting a split partition are the split graphs and they are characterized as the $\{2K_2, C_4, C_5\}$-free graphs [26].

In the broader context of matrix partitions, it was shown that for any pair of fixed nonnegative integers, s and k, there are only finitely many minimal (s, k)-polar obstructions [25], and therefore the class of (s, k)-polar graphs can be recognized by a brute force algorithm in polynomial time. Also, unipolar graphs have been shown to be efficiently recognizable [9, 22]. In contrast, the problems of deciding whether a graph is polar and deciding whether a graph is monopolar have been shown to be NP-complete [5, 23] even when restricted to triangle-free planar graphs [34]. Such results encouraged the study of polarity and monopolarity in many graph classes as cographs [21], chordal graphs [19, 35], permutation graphs [17, 18], trivially perfect graphs [36], line graphs [6, 20], triangle-free and claw-free graphs [7, 8], comparability graphs [9], and planar graphs [33, 34], just to mention some of the most outstanding classes.

Cographs were introduced in [14], where it was proved that such graphs are precisely the $P_4$-free graphs, and also the graphs that can be obtained from trivial graphs by disjoint union and join operations. Thus, for any nontrivial cograph G, either G or ${{\overline{G}}}$ is disconnected. The first $O(|V |+|E |)$-time algorithm to determine whether a graph G is a cograph, and to construct a rooted labeled tree uniquely representing G (the cotree of G) was introduced in [15]. Other algorithms with the same running time, and building on top of similar ideas, were presented in later years, culminating with an algorithm based on LexBFS which also provides an induced $P_4$ as a no-certificate when G is not a cograph [4]. It follows from the uniqueness of the cotree representation of a cograph that many algorithmic problems which are difficult for general graphs can be efficiently solved on cographs by using its cotree [14]. Additionally, cographs inherit efficient algorithms from some of the superclasses they belong to, such as distance hereditary, permutation, and comparability graphs.

Cographs possess many desirable structural properties and are particularly interesting because real-life applications often involve graph models where paths of length four are unlikely to appear [15]. For the above reasons, the study of cographs was naturally followed by the introduction of a wide variety of cograph superclasses having both few induced $P_4$’s and a unique tree representation. For instance, a graph is said to be a $P_4$-sparse graph if any set of five vertices induces at most one $P_4$, and a $P_4$-extendible graph is a graph such that, for any vertex subset W inducing a $P_4$, there exists at most one vertex $v \notin W$ which belongs to a $P_4$ sharing vertices with W.

Ekim, Mahadev and de Werra found the complete list of cograph minimal polar obstructions as well as the exact list of cograph minimal (s, k)-polar obstructions when $\min \{s,k\} = 1$ [21]. In the past few years, the study of (s, k)-polarity in cographs has continued with the following main results. In [28], Hell, Hernández-Cruz and Linhares-Sales provided a full characterization of cograph minimal (2, 2)-polar obstructions. Bravo, Nogueira, Protti and Vianna exhibited the exhaustive list of cograph minimal (2, 1)-polar obstructions [3], and Contreras-Mendoza and Hernández-Cruz proved a simple recursive characterization for all the cograph minimal (s, 1)-polar obstructions for any arbitrary integer s, as well as the complete list of cograph minimal monopolar obstructions [10]. The authors of the present work provided in [11] complete lists of cograph minimal $(\infty , k)$-polar obstructions for $k = 2$ and $k = 3$, as well as a partial recursive characterization for arbitrary values of k.

In this paper we study (s, k)-polarity on two cograph superclasses, namely $P_4$-sparse and $P_4$-extendible graphs. Additionally, we prove that any hereditary property has only finitely many minimal obstructions when restricted to some cograph superclases, including the aforementioned families. The rest of the paper is organized as follows. In Sect. 2 we introduce some families generalizing cographs. Section 3 is devoted to prove that any hereditary property has finitely many minimal obstructions when restricted to some particular cograph superclasses. In Sects. 4 and 5 we provide complete lists of disconnected minimal (s, 1)- and $(\infty , 1)$-polar obstructions for general graphs, as well as technical results we need to characterize connected $P_4$-sparse and $P_4$-extendible minimal (s, 1)- and $(\infty , 1)$-polar obstructions. Finally, in Sect. 6 we prove our main results about polarity on cograph generalizations: we give complete characterizations for $P_4$-sparse and $P_4$-extendible minimal (s, 1)-, $(\infty ,1)$-, and $(\infty , \infty )$-polar obstructions, as well as complete sets of minimal obstructions for unipolarity for both families. Conclusions, work in progress, as well as some open problems and conjectures, are presented in Sect. 7.

A complementary version of this work can be found in arXiv [13]. In particular, some results which are stated here without proofs have complete proofs there.

2 Cograph Generalizations

In a series of papers, Jamison and Olariu introduced several classes of uniquely tree-representable graphs that, in different senses, have few induced paths of order four. For instance, a graph was called $P_4$-reducible if any vertex belongs to at most one induced $P_4$ [29], $P_4$-sparse if any vertex subset of five vertices induces at most one $P_4$ [31], and $P_4$-extendible if for any vertex subset W inducing a $P_4$, there exists at most one vertex $v \notin W$ which belongs to a $P_4$ sharing vertices with W [30].

Moreover, by generalizing the work done in the graph classes previously introduced, Jamison and Olariu obtained a structural theorem for arbitrary graphs that provides a decomposition scheme similar to the well known modular decomposition. Below, we introduce the basic concepts needed to state the mentioned theorem.

A graph G is said to be p-connected if, for any partition (X, Y) of $V_G$ into two nonempty sets, G contains an induced $P_4$ with vertices from both X and Y. The maximal p-connected induced subgraphs of G are called the p-components of G. A p-component H of G is separable if $V_H$ admits a separable partition, that is, a partition $(H_1, H_2)$ in such a way that every $P_4$ with vertices from both $H_1$ and $H_2$ has its midpoints in $H_1$ and its endpoints in $H_2$.

Theorem 1

([32]) For an arbitrary graph G, precisely one of the following conditions is satisfied.

• 1. G is disconnected.

• 2. ${\overline{G}}$ is disconnected.

• 3. G is p-connected.

• 4. There is a unique proper separable p-component H of G with a separable partition $(H_1, H_2)$ such that $V_G \setminus V_H$ is completely adjacent to $H_1$ and completely nonadjacent to $H_2$.

Notice that cographs and $P_4$-reducible graphs can be thought as special cases of the structure decomposition given by Theorem 1. Cographs clearly are the class of graphs whose p-components are trivial graphs [14], and a graph is $P_4$-reducible if and only if each of its p-components has order at most 4 [29]. As we observe below in Theorems 2 and 3, $P_4$-extendible and $P_4$-sparse graphs also can be seen as restricted cases of Theorem 1.

A graph G of order at least four is said to be a headless spider if there exists a split partition (S, K) of V and a bijection $f :S \rightarrow K$ such that either $N(s) = \{f(s)\}$ for any $s \in S$, or $N(s) = K {\setminus } \{f(s)\}$ for every $s \in S$. A spider is a graph G whose vertex set can be partitioned into into S, K and R in such a way that $G[S \cup K]$ is a headless spider with partition (S, K), R is completely adjacent to K and completely nonadjacent to S. For a spider $G = (S, K, R)$ we say that S is its legs set, K is its body, and R is its head. A spider is called thin (respectively thick) if $d(s) = 1$ (respectively $d(s) = |K |-1$) for any $s \in S$. Notice that the complement of a thin spider is a thick spider, and vice versa, and that a headless spider is precisely a spider with an empty head. The next proposition, which should be compared with Theorem 1, states that a graph is $P_4$-sparse if and only if its p-components are either trivial graphs or headless spiders.

Theorem 2

([31]) If G is a graph, then G is a $P_4$-sparse graph if and only if for every nontrivial induced subgraph H of G, exactly one of the following statements is satisfied

• 1. H is disconnected.

• 2. ${\overline{H}}$ is disconnected.

• 3. H is a (possibly headless) spider.

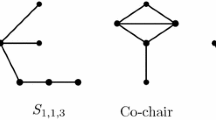
Jamison and Olariu [30] noticed that a graph is $P_4$-extendible if and only if every p-component has at most 5 vertices, that is to say, if and only if each of its non trivial p-components is one of $P_4, C_5, P_5, P, F$ or their complements (see Fig. 1), which they called extension graphs. Observe that every extension graph is trivially a $P_4$-extendible graph but the headless spiders on six vertices are examples of minimal $P_4$-extendible obstructions. Thus, since any headless spider is a $P_4$-sparse graph and all the forbidden $P_4$-sparse graphs are $P_4$-extendible, the classes of $P_4$-sparse graphs and $P_4$-extendible graphs are incomparable.

Fig. 1

The eight extension graphs. Black vertices are the midpoints of separable extension graphs

By mimicking the concept of spiders introduced before in order to characterize the structure of $P_4$-sparse graphs, we define a G-spider as follows. Given a separable extension graph G, a G-spider is an (induced) supergraph H of G such that $V_H - V_G$ (denoted R) is completely adjacent to the midpoints set of G (denoted K), and completely nonadjacent to the endpoints set of G (denoted S). If H is a G-spider, we say that (S, K, R) is a G-spider partition of H, and we refer to K, S and R as the body, the legs set, and the head of H, respectively.

The following structural characterization for the class of $P_4$-extendible graphs was given in [30]; we paraphrase it in terms of G-spiders. Notice that, as it is the case of Theorem 2, Theorem 3 is a restricted version of Theorem 1.

Theorem 3

([30]) If G is a graph, then G is a $P_4$-extendible graph if and only if, for every nontrivial induced subgraph H of G, precisely one of the following conditions is satisfied:

• 1. H is disconnected.

• 2. ${\overline{H}}$ is disconnected.

• 3. H is an extension graph.

• 4. There is a unique separable extension graph S such that H is an S-spider with nonempty head.

In view of Theorems 2 and 3, we can generalize the cograph superclasses introduced before by restricting the family of p-components that a class of graphs can have as follows. Given a family ${\mathcal {E}}$ of p-connected graphs, let ${\mathcal {F}}_{\mathcal {E}}$ be the class of graphs G such that, for any induced subgraph F of G, exactly one of the following conditions is satisfied:

• 1. F is disconnected.

• 2. ${\overline{F}}$ is disconnected.

• 3. $F \in {\mathcal {E}}$.

• 4. There is a unique proper separable p-component $H \in {\mathcal {E}}$ of F with a separable partition $(H_1, H_2)$ such that $V_F \setminus V_H$ is completely adjacent to $H_1$ and completely nonadjacent to $H_2$.

Thus, for instance, $P_4$-reducible, $P_4$-sparse, and $P_4$-extendible graphs are equivalent to ${\mathcal {F}}_{{\mathcal {E}}_1}$, ${\mathcal {F}}_{{\mathcal {E}}_2}$, and ${\mathcal {F}}_{{\mathcal {E}}_3}$, respectively, where ${\mathcal {E}}_1 = \{K_1, P_4\}$, ${\mathcal {E}}_2$ is the infinite set consisting of $K_1$ and all headless spiders, and ${\mathcal {E}}_3 = \{K_1, P_4, C_5, P_5, \overline{P_5}, P, {\overline{P}}, F, {\overline{F}} \}$.

3 Well-Quasi-Orderings

Throughout this section, we show that any hereditary property has a finite number of minimal obstructions when restricted to some cograph superclasses, including $P_4$-sparse and $P_4$-extendible graphs. We will often use the following observation in the rest of the text without mentioning it explicitly.

Remark 4

Let ${\mathcal {P}}$ be a hereditary property of graphs, and let H be a ${\mathcal {P}}$-obstruction. If G is a minimal ${\mathcal {P}}$-obstruction such that $H \le G$, then $G \cong H$.

A poset $(M, \le )$ is called a well-quasi-ordering (WQO) if any infinite sequence of elements $\{ a_i \}_{i \in {\mathbb {N}}}$ from M contains an increasing pair, that is to say, a pair $a_i\le a_j$ such that $i<j$. Equivalently, $(M, \le )$ is a WQO if and only if M contains neither an infinite decreasing chain nor an infinite antichain.

Let ${\mathcal {G}}$ be a graph class ordered by the induced subgraph relation, and let ${\mathcal {P}}$ be a hereditary property on ${\mathcal {G}}$. By Remark 4, the family of minimal ${\mathcal {P}}$-obstructions is an antichain. Moreover, any antichain in $({\mathcal {G}}, \le )$ is the family of minimal $\mathcal Q$-obstructions for a hereditary property ${\mathcal {Q}}$. Then, since graphs ordered by the induced subgraph relation do not have infinite decreasing chains, ${\mathcal {G}}$ is WQO by the induced subgraph relation if and only if it contains no infinite antichain, or equivalently, if every hereditary property on ${\mathcal {G}}$ has only finitely many minimal obstructions. Peter Damaschke [16] used the following theorem to prove that cographs and $P_4$-reducible graphs are WQO under the induced subgraph relation.

Theorem 5

([16]) Let ${\mathcal {G}}$ be a family of graphs, and let $\Sigma$ and $\Pi$ be sets of unary and binary graph operations, respectively. Define partial orderings on $\Sigma$ and $\Pi$ as follows:

$$\begin{aligned} \sigma \preceq \sigma ' \text { if and only if } \sigma (G) \le \sigma '(G) \text { for all graphs } G. \\ \pi \preceq \pi ' \text { if and only if } \pi (G,H) \le \pi ' (G,H) \text { for all graphs } G,H. \end{aligned}$$

Suppose that the following assertions are satisfied:

• 1. ${\mathcal {G}}$ is WQO by the induced subgraph relation.

• 2. Any $\sigma \in \Sigma$ is monotonous (that is, $H \le G$ implies $\sigma (H) \le \sigma (G)$), and extensive (that is, for any graph G, $G \le \sigma (G)$).

• 3. Any $\pi \in \Pi$ is commutative, associative, and satisfies:

  • (a) if $G \le G'$ and $H \le H'$, then $\pi (G,H) \le \pi (G',H')$, and

  • (b) $G,H \le \pi (G,H)$.

• 4. $(\Sigma , \preceq )$ and $(\Pi , \preceq )$ are WQO.

Then, the class $\Gamma ({\mathcal {G}}, \Sigma , \Pi )$ of all graphs obtained by start graphs from ${\mathcal {G}}$ using operations from $\Sigma$ and $\Pi$, is WQO under the induced subgraph relation.

Next, we prove that for any self-complementary family ${\mathcal {E}}$ of p-connected graphs such that $({\mathcal {E}}, \le )$ is WQO, the class ${\mathcal {F}}_{\mathcal {E}}$ is well-quasi-ordered by the induced subgraph relation. Particularly, this implies that for any hereditary property of graphs there is only a finite number of minimal obstructions when restricted to some of $P_4$-sparse or $P_4$-extendible graphs, both of them $P_4$-reducible superclasses.

Let $\Pi ^*$ be the set of binary operations on the class of all graphs whose only elements are the disjoint union and join operations. Observe that any $\pi \in \Pi ^*$ satisfies all the requirements listed in item 3 of Theorem 5.

Given a separable p-connected graph S with separable partition $(S_1, S_2)$, we define $\sigma _S$ as the unary operation such that, for any graph G, $\sigma _S(G)$ is the graph with vertex set $V_S \cup V_G$ and edge set $E_S \cup E_G \cup \{ xy \mid x \in V_G, y \in S_1 \}$. Given a set ${\mathcal {E}}$ of p-connected graphs, we use $\Sigma _{\mathcal {E}}$ to denote the set of all operations $\sigma _S$ associated to separable graphs $S \in {\mathcal {E}}$. Notice that, for any separable p-connected graph S, the operation $\sigma _S$ trivially is both, monotonous and extensive, so $\Sigma _{\mathcal {E}}$ satisfies item 2 of Theorem 5.

Theorem 6

Let ${\mathcal {E}}$ be a family of p-connected graphs. If $({\mathcal {E}}, \le )$ is WQO, then $\Gamma ({\mathcal {E}}, \Sigma _{\mathcal {E}}, \Pi ^*)$ is WQO too. Particularly, $\Gamma ({\mathcal {E}}, \Sigma _{\mathcal {E}}, \Pi ^*)$ is WQO whenever ${\mathcal {E}}$ is finite.

Proof

It is enough to prove that ${\mathcal {E}}$, $\Sigma _{\mathcal {E}}$, and $\Pi ^*$ satisfy the conditions listed in Theorem 5. By hypothesis, ${\mathcal {E}}$ is WQO under the induced subgraph relation, and we previously observed that $\Sigma _{\mathcal {E}}$ and $\Pi ^*$ satisfy items 2 and 3 of Theorem 5. Thus, it only remains to prove that both, $(\Sigma _{\mathcal {E}}, \preceq )$ and $(\Pi ^*, \preceq )$, are WQO. Since $\Pi ^*$ is finite, we have that $\Pi ^*$ is WQO under the relation $\preceq$.

To verify that $(\Sigma _{\mathcal {E}}, \preceq )$ is WQO, let us start noticing that, for any separable graphs S and $S'$, if $S \le S'$, then $\sigma _S(G) \le \sigma _{S'}(G)$ for every graph G, so we have that $\sigma _S \preceq \sigma _{S'}$ whenever $S \le S'$. Now, let $\sigma = \{\sigma _{S_i}\}_{i\in {\mathbb {N}}}$ be an infinite sequence of elements in $\Sigma _{\mathcal {E}}$, and let s be the sequence $\{S_i\}_{i \in {\mathbb {N}}}$. Notice that, from the initial observation of this paragraph, if s has an increasing pair $S_i \le S_j$, then $\sigma$ has $\sigma _{S_i} \preceq \sigma _{S_j}$ as an increasing pair. Now, aiming for a contradiction, assume that $\sigma$ does not have any increasing pair. Thus, s neither has any increasing pair, so for any natural numbers i and j with $i < j$, we have that either $S_j < S_i$ or $S_i$ and $S_j$ are incomparable under the induced subgraph relation. Hence, from the infinite Ramsey’s theorem, there is an infinite subsequence of s that is either an infinite antichain or an infinite decreasing chain, but this is impossible since $({\mathcal {E}}, \le )$ is WQO. The contradiction arose from supposing the existence of an infinite sequence in $\Sigma _{\mathcal {E}}$ without an increasing pair, so it follows that $(\Sigma _{\mathcal {E}}, \preceq )$ is WQO.

Therefore, we have that, for any two separable graphs S and $S'$ in ${\mathcal {E}}$, $S \le S'$ if and only if $\sigma _{S} \preceq \sigma _{S'}$. Hence, since $({\mathcal {E}}, \le )$ is WQO, it follows that $(\Sigma _{\mathcal {E}}, \preceq )$ is WQO too. Since all the conditions of Theorem 5 hold, it follows that the class of graphs $\Gamma ({\mathcal {E}}, \Sigma _{\mathcal {E}}, \Pi ^*)$ is WQO under the induced subgraph relation. $\square$

Remark 7

If ${\mathcal {E}}$ is a self-complementary set of p-connected graphs having the trivial graph, then ${\mathcal {F}}_{\mathcal {E}}$ is self-complementary too.

Lemma 8

Let ${\mathcal {E}}$ be a self-complementary family of p-connected graphs including the trivial graph. Then, $\Gamma ({\mathcal {E}}, \Sigma _{\mathcal {E}}, \Pi ^*) = {\mathcal {F}}_{\mathcal {E}}$.

Proof

Notice that both sets are closures of ${\mathcal {E}}$ under equivalent operations. $\square$

Theorem 9

For every self-complementary family ${\mathcal {E}}$ of p-connected graphs including the trivial graph, if $({\mathcal {E}}, \le )$ is WQO, then ${\mathcal {F}}_{\mathcal {E}}$ is WQO under the induced subgraph relation. Particularly, any hereditary property on either $P_4$-sparse or $P_4$-extendible graphs admits a finite forbidden subgraph characterization.

Proof

The first part of the statement follows directly from Theorem 6 and Lemma 8. The second part is because, as we noticed at the end of Sect. 2, ${\mathcal {F}}_{{\mathcal {E}}_2}$ and ${\mathcal {F}}_{{\mathcal {E}}_3}$ are precisely the classes of $P_4$-sparse and $P_4$-extendible graphs, so both classes are WQO under the induced subgraph relation. $\square$

The rest of the paper is devoted to the characterizations by forbidden induced subgraphs of properties associated with polarity in $P_4$-sparse and $P_4$-extendible graphs.

4 Disconnected Minimal (s, 1)-Polar Obstructions

By means of generalizing Lemmas 2–5 from [10], it is possible to obtain a complete characterization of disconnected minimal (s, 1)-polar obstructions for general graphs. For the sake of brevity, instead of stating the generalization of each of the aforementioned lemmas, we will jump directly to the complete characterization, and we will omit its proof. Statements of all the lemmas together with their proofs can be found in the arXiv version of this work [13].

Theorem 10

Let s be an integer, $s\ge 2$, and let G be a disconnected minimal (s, 1)-polar obstruction. Then G satisfies one of the following assertions:

• 1. G is isomorphic to one of the graphs depicted in Fig. 2.

• 2. $G \cong 2K_{s+1}$.

• 3. $G \cong K_2 + (2K_1\oplus K_s)$.

• 4. $G \cong K_1 + (C_4\oplus K_{s-1})$.

Fig. 2

Some minimal $(\infty ,1)$-polar obstructions

For any nontrivial cograph G, either G or its complement is disconnected [14], so the complement of any nontrivial connected cograph is disconnected. This fact was used in [10] to give a recursive characterization of all cograph minimal (s, 1)-polar obstructions. After giving a complete characterization of the disconnected cograph minimal (s, 1)-polar obstructions, the authors provided a recursive construction for the disconnected cograph minimal (1, s)-polar obstructions (which are precisely the complements of connected cograph minimal (s, 1)-polar obstructions).

In the following section we will present very similar results for $P_4$-sparse graphs and $P_4$-extendible graphs. In particular we will prove that all $P_4$-sparse minimal (s, 1)-polar obstructions are cographs, which turns out to be similar in flavor to a result obtained in [27], stating that all $P_4$-sparse minimal obstructions for $(k,\ell )$-coloring are cographs.

5 Connected Minimal (s,1)-Polar Obstructions

Theorem 10 characterizes disconnected minimal (s, 1)-polar obstructions for general graphs. Thus, to completely characterize minimal (s, 1)-polar obstructions for a given class of graphs it suffices to characterize connected minimal (s, 1)-polar obstructions. To this end, in order to follow the strategy described in the final paragraphs of the previous section for $P_4$-sparse and $P_4$-extendible graphs, we notice that the following lemma, which was stated and proved in [10] for the special case of cographs, is also valid for general graphs.

Lemma 11

Let t be an integer, $t \ge 2$, and for each $i\in \{1, \dots , t\}$, let $G_i$ be a minimal $(1, k_i)$-polar obstruction that is a $(1, k_i+1)$-polar graph. Then, for $k = t-1 + \sum _{i=1}^t k_i$, the graph $G = G_1 + \dots + G_t$ is a minimal (1, k)-polar obstruction that is a $(1, k+1)$-polar graph.

In the following two propositions we show that the converse of Lemma 11 holds for some graph classes with particular properties. That is to say, we prove that any disconnected minimal (1, k)-polar obstruction on such classes is the disjoint union of minimal $(1,k_i)$-polar obstructions for some integers $k_i < k$.

Let ${\mathcal {G}}$ be any hereditary class of graphs such that, for each nonnegative integer k and each connected minimal (1, k)-polar obstruction $G \in {\mathcal {G}}$, if ${\overline{G}}$ is connected, then (i) ${\overline{G}}$ is a $(k+1,1)$-polar graph and, (ii) for any nonnegative integer $\kappa < k$, ${\overline{G}}$ contains a proper induced subgraph that is both, a minimal $(\kappa , 1)$-polar obstruction and a $(\kappa +1, 1)$-polar graph. Since the complement of any nontrivial connected cograph is disconnected, it follows that the class of cographs satisfies the previous contitions. Later, we will prove that both, $P_4$-sparse and $P_4$-extendible graphs, also have these properties.

Lemma 12

Let ${\mathcal {G}}$ be a hereditary class having the properties described in the previous paragraph, let t be an integer, $t \ge 2$, and for each $i \in \{1, \dots , t\}$, let $G_i$ be a connected minimal $(1, k_i)$-polar obstruction in ${\mathcal {G}}$ which is a $(1, k_i+1)$-polar graph. If $G = G_1 + \dots + G_t$, then G is a minimal (1, k)-polar obstruction if and only if $k = t - 1 + \sum _{i=1}^t k_i$.

Proof

Let $k = t-1+\sum _{i=1}^t k_i$. We have from Lemma 11 that G is a minimal (1, k)-polar obstruction which is $(1,k+1)$-polar, so we just need to show that G is not a minimal $(1,\kappa )$-polar obstruction for any $\kappa <k$.

Let $G_i$ be a connected minimal $(1, k_i)$-polar obstruction in ${\mathcal {G}}$ which is $(1, k_i+1)$-polar. Thus, it follows from the choice of ${\mathcal {G}}$ and Theorem 10 that, for any nonnegative integer $\kappa _i$ such that $\kappa _i < k_i$, $G_i$ contains a proper induced subgraph $H_i$ that is both, a minimal $(1, \kappa _i)$-polar obstruction and a $(1, \kappa _i+1)$-polar graph.

Let $\kappa$ be a positive integer such that $\kappa < k$, and let $s_1, \dots , s_t$ be integers such that, for $i \in \{1, \dots , t\}$, $0 \le s_i \le k_i$ and $\kappa = t -1 +\sum _{i=1}^t s_i$. For each $i \in \{1, \dots , t\}$, if $s_i < k_i$, let $H_i$ be a proper induced subgraph of $G_i$ that is both a minimal $(1, s_i)$-polar obstruction and a $(1, s_i+1)$-polar graph, otherwise let $H_i = G_i$. Then, by Lemma 11, $H = H_1 + \dots + H_t$ is a minimal $(1, \kappa )$-polar obstruction that is a proper induced subgraph of G, and therefore G is not a minimal $(1, \kappa )$-polar obstruction. $\square$

The following lemma is a generalization of Lemma 9 in [10], which states the same result for cographs.

Lemma 13

Let ${\mathcal {G}}$ be a hereditary class having the properties described in the paragraph before Lemma 12 and let k be a nonnegative integer. If G is a disconnected minimal (1, k)-polar obstruction in ${\mathcal {G}}$ with components $G_1, \dots , G_t$, then there exist nonnegative integers $k_1, \dots , k_t$ such that, for each $i \in \{1, \dots , t\}$, $G_i$ is a connected minimal $(1, k_i)$-polar obstruction that is a $(1, k_i+1)$-polar graph, and $\sum _{i=1}^t k_i = k -t +1$. (Notice that $k_i < k$ for any $i \in \{1, \dots , t\}$, and G is a $(1, k+1)$-polar graph.)

Proof

It is not hard to argue that each component $G_i$ is a minimal $(1,k_i)$-polar obstruction that is (1, k)-polar, where $k_i$ is the minimum integer such that any proper induced subgraph of $G_i$ is $(1,k_i)$-polar. Thus, we have from Theorem 10 and the choice of ${\mathcal {G}}$ that $\overline{G_i}$ is a $(k_i+1,1)$-polar graph, so $G_i$ is $(1,k_i+1)$-polar. Finally, the result follows from Lemma 12. $\square$

Next, we prove that the classes of $P_4$-sparse and $P_4$-extendible graphs satisfy the properties required for the graph classes ${\mathcal {G}}$ used in Lemmas 12 and 13. We start proving it for $P_4$-sparse graphs.

The following observation is a consequence from the well known fact that $P_3$ is a minimal (0, k)-polar obstruction for any integer $k \ge 2$.

Remark 14

If G is a headless spider or a spider whose head induces a split graph, then G is a split graph that has both, $P_3$ and $\overline{P_3}$, as proper induced subgraphs. Hence, G is not a minimal (s, k)-polar obstruction for any choice of s and k.

Our next proposition provides the basis for showing that any connected $P_4$-sparse minimal (k, 1)-polar obstruction has a disconnected complement.

Proposition 15

Let k be a positive integer, and let $G = (S, K, R)$ be a spider with possibly empty head. Then, G is not a minimal (1, k)-polar obstruction.

Proof

Suppose for a contradiction that G is a minimal (1, k)-polar obstruction, and let $\sigma \in S$ be a leg of G. Let (A, B) be a (1, k)-polar partition of $G-\sigma$. Notice that $|K \cap A |\le 1$ because K is a clique and A is an independent set. Therefore, since K has at least two vertices, $K \cap B \ne \varnothing$. Moreover, since B induces a cluster, R is completely adjacent to K, and $K \cap B \ne \varnothing$, $R \cap B$ is a clique. Also notice that either $K \cap A = \varnothing$ or $R \cap A = \varnothing$.

Now, if $K \cap A \ne \varnothing$, then R is a clique, G is a split graph, and therefore G is a (1, k)-polar graph, which is impossible. Otherwise, if $K \subseteq B$, then $(A \cup \{\sigma \}, B)$ is a (1, k)-polar partition of G, a contradiction. $\square$

Since the complement of a spider is also a spider, and any minimal $(\infty ,1)$-polar obstruction is a minimal (k, 1)-polar obstruction for some positive integer k, we have the following simple consequences of the previous proposition and Theorem 2.

Corollary 16

Let k be a positive integer. If G is a spider, then G is neither a minimal (k, 1)-polar obstruction nor a minimal $(\infty ,1)$-polar obstruction. Therefore, if G is a $P_4$-sparse minimal (k, 1)-polar obstruction, then G or its complement is disconnected.

From Corollary 16, it is clear that Lemmas 12 and 13 can be applied in the class of $P_4$-sparse graphs. Next, we prove an analogous result to Corollary 16 for $P_4$-extendible graphs. For the sake of brevity, since the techniques used to obtain the results for both classes is the same and the only differences come from the connectedness characterizations for said families, we omit the proofs of the following propositions. We begin with some easily verifiable facts.

Remark 17

Let s, k be either in ${\mathbb {N}}$ or equal to $\infty$.

• 1. $P_4$ and F are split graphs but they are neither $(0,\infty )$- nor $(\infty , 0)$-polar graphs.

• 2. $C_5, P_5$, and P are (1, 2)- and (2, 1)-polar, but they are neither (1, 1)-, $(\infty ,0)$- nor $(0,\infty )$-polar graphs.

• 3. An extension graph G is a minimal (s, k)-polar obstruction if and only if $G \cong C_5$ and $s = k = 1$.

The following proposition allows us to show that any connected $P_4$-extendible minimal (1, k)-polar obstruction, other than $C_5$, has a disconnected complement.

Lemma 18

Let k be a nonnegative integer, and let G be a separable extension graph. If $H = (S, K, R)$ is a G-spider with nonempty head, then H is not a minimal (1, k)-polar obstruction.

We have the following consequence of Theorem 3, Remark 17, and Lemma 18. Notice that it follows from Corollary 19 that Lemmas 12 and 13 can be applied also in the class of $P_4$-extendible graphs.

Corollary 19

Let k be a nonnegative integer, and let H be a $P_4$-extendible minimal (1, k)-polar obstruction. If $H\not \cong C_5$, then H or its complement is disconnected.

6 Main Results

In order to analyze the minimal obstructions for polarity in the classes of $P_4$-sparse and $P_4$-extendible graphs we need a final lemma. Notice that it holds for general graphs.

Lemma 20

If G is a graph, then G is a disconnected minimal polar obstruction if and only if $G \cong P_3 + H$ where H is a minimal monopolar obstruction which is not a minimal polar obstruction.

Proof

First, assume that H is a minimal $(1,\infty )$-polar obstruction which is not a minimal polar obstruction, and let $G = P_3 + H$. Assume for a contradiction that G has a polar partition (A, B). Notice that G[A] is not an empty graph because H is not a $(1,\infty )$-polar graph. Then G[A] is completely contained in a component of G. Moreover, since any component of G is either $P_3$ or a component of H, and G[B] is a $P_3$-free graph, we have that $A\cap V_H = \varnothing$ so H is a cluster, a contradiction. Hence, G is not a polar graph.

Let $v \in V_G$. If $v\in V_H$, let (A, B) be a $(1, \infty )$-polar partition of $H-v$, and let $w\in V_G - V_H$ be a vertex of degree 1. Then $(A', V_G - (A'\cup \{v\}))$, where $A' = A\cup \{w\}$, is a $(1,\infty )$-polar partition of $G-v$. Now, let $v \in V_G - V_H$. Then, since H is a polar graph and $P_3-v$ is a cluster, $G-v$ is a polar graph. Therefore G is a disconnected minimal polar obstruction.

For the converse, assume that G is a disconnected minimal polar obstruction. Notice that, if all the components of G are $(1,\infty )$-polar graphs, then G is also a $(1,\infty )$-polar graph, so G has a component $H'$ that contains a minimal $(1,\infty )$-polar obstruction H as an induced subgraph. Notice that by the minimality of G, H is a polar graph. In addition, G has no complete components, so any component of G contains an induced $P_3$, and therefore G contains the disjoint union of $P_3$ with a minimal $(1,\infty )$-obstruction that is a polar graph (H). Together with the minimality of G, this implies that $G \cong P_3 + H$. $\square$

The following result provides complete recursive constructions of $P_4$-sparse and $P_4$-extendible minimal (s, 1)-polar obstructions. Notice that, since $C_5$ is a $P_4$-extendible minimal (1, 1)-polar obstruction, there are $P_4$-extendible minimal (s, 1)-polar obstructions which are not cographs for each positive integer s.

Theorem 21

Let s be an integer, $s \ge 2$. If G is a $P_4$-sparse graph (respectively a $P_4$-extendible graph), then G is a minimal (s, 1)-polar obstruction if and only if G satisfies exactly one of the following assertions:

• 1. G is isomorphic to one of the $P_4$-sparse graphs (resp. $P_4$-extendible graphs) depicted in Fig. 2.

• 2. G is isomorphic to some of $2K_{s+1}, K_2 + (K_s\oplus 2K_1)$ or $K_1 + (K_{s-1}\oplus C_4)$.

• 3. The complement of G is disconnected with components $G_1, \dots , G_t$, each $G_i$ is a minimal $(1, s_i)$-polar obstruction whose complement is different from the graphs in Fig. 2, and $s = t-1+ \sum _{i=1}^t s_i$.

Proof

We prove the proposition for $P_4$-sparse graphs, the proof for $P_4$-extendible graphs is analogous but using Corollary 19 and Item 3 of Remark 17 instead of Corollary 16.

If G is disconnected, it follows from Theorem 10 that G is a minimal (s, 1)-polar obstruction if and only if G is either a $P_4$-sparse graph depicted in Fig. 2 (which can easily be checked to be a cograph), or it is isomorphic to some of $2K_{s+1}, K_2 + (K_s\oplus 2K_1)$ or $K_1 + (K_{s-1}\oplus C_4)$. Otherwise, if G is connected, Corollary 16 implies that ${\overline{G}}$ is a disconnected $P_4$-sparse minimal (1, s)-polar obstruction, and the result follows from Lemma 13. $\square$

For any hereditary property ${\mathcal {P}}$ and any graph classes ${\mathcal {G}}$ and ${\mathcal {H}}$ such that ${\mathcal {G}} \subseteq {\mathcal {H}}$, the set of minimal ${\mathcal {P}}$-obstructions in ${\mathcal {G}}$ clearly is a (possibly proper) subset of the set of minimal ${\mathcal {P}}$-obstructions in ${\mathcal {H}}$. The class of $P_4$-sparse graphs has been observed to have a behavior which is very similar to cographs when computing their minimal obstructions with respect to some hereditary properties. For example, Hannebauer [27] proved that every $P_4$-sparse minimal obstruction for $(k,\ell )$-coloring is a cograph. The following propositions demonstrate that a similar phenomenon arises when considering (s, 1)-, $(\infty , 1)$-, and $(\infty , \infty )$-polarity.

Theorem 22

Let s be a nonnegative integer. Any $P_4$-sparse minimal (s, 1)-polar obstruction is a cograph.

Proof

Let G be a $P_4$-sparse minimal (s, 1)-polar obstruction. We proceed by induction on s. The statement is clearly true for $s \le 1$. Let $s \ge 2$. It follows from Corollary 16 that G is not a spider, hence G or its complement is disconnected.

If G is disconnected, it follows from Theorem 10 that G is a cograph. Otherwise, by Corollary 16, ${{\overline{G}}}$ is disconnected, and Lemma 13 implies that any component H of ${{\overline{G}}}$ is a $P_4$-sparse minimal $(1,k_i)$-polar obstruction for a nonnegative integer $k_i$ with $k_i < k$. Thus, ${{\overline{H}}}$ is a $P_4$-sparse minimal $(k_i,1)$-polar obstruction, and by induction hypothesis ${{\overline{H}}}$ (hence H) is a cograph. Since the disjoint union of cographs is also a cograph, ${{\overline{G}}}$ (hence G) is a cograph. $\square$

Corollary 23

If G is a $P_4$-sparse graph, then G is a minimal $(\infty ,1)$-polar obstruction if and only if G is one of the four cographs depicted in Fig. 2.

Proof

Let G be $P_4$-sparse minimal $(\infty ,1)$-polar obstruction. Then G is a minimal (s, 1)-polar obstruction for some nonnegative integer s. Moreover, by Theorem 22 we have that G is a cograph minimal $(\infty ,1)$-polar obstruction. Then, from Theorem 12 in [10] we have that G is isomorphic to one of the cographs depicted in Fig. 2. The converse follows easily from Theorem 10. $\square$

Theorem 24

If G is a $P_4$-sparse minimal polar obstruction, then G is a cograph.

Proof

First, assume for a contradiction that G is a spider, say $G = (S, K, R)$. Since headless spiders are split graphs, and thus polar graphs, R is not an empty set. Moreover, by the minimality of G, G[R] admits a polar partition (A, B), and then $(A \cup K, B\cup S)$ would be a polar partition of G, contradicting the choice of G. Therefore G is not a spider. Thus, by Theorem 2, G or its complement is disconnected. However, in both cases Lemma 20 and Corollary 23 imply that G is a cograph. $\square$

Unlike $P_4$-sparse graphs, there are $P_4$-extendible minimal monopolar and polar obstructions which are not cographs. We give complete lists of such minimal obstructions in the next results.

Corollary 25

If G is a $P_4$-extendible graph, then G is a minimal $(\infty ,1)$-polar obstruction if and only if G is one of the graphs depicted in Fig. 2.

Proof

Let G be a $P_4$-extendible minimal $(\infty ,1)$-polar obstruction. Then G is a minimal (s, 1)-polar obstruction for some integer s, $s \ge 2$. By Lemma 13 and Theorem21 we conclude that G is isomorphic to one of the seven graphs depicted in Fig. 2. The converse follows easily from Theorem10. $\square$

Theorem 26

If H is a $P_4$-extendible minimal polar obstruction, then H or its complement is the disjoint union of $P_3$ with the complement of one of the graphs depicted in Fig. 2.

Proof

First, let assume for obtaining a contradiction that H is a G-spider for some separable extension G, say $H = (S, K, R)$. By Item 1 and 2 of Remark 17, we have that $R \ne \varnothing$, and by the minimality of H, H[R] admits a polar partition (A, B). But, no matter what separable extension G is, its midpoints induce a complete multipartite graph while its endpoints induce a cluster, so $(A\cup K, B\cup S)$ is a polar partition of H, contradicting the assumption that H was a G-spider. Thus, by Theorem 3, either H or its complement is disconnected, and the result follows from Lemma 20 and Corollary 25. $\square$

Although it is a simple observation, for sake of completeness we close this section with characterizations of unipolar $P_4$-sparse and unipolar $P_4$-extendible graphs in terms of minimal obstructions. Notice that this result implies that any $P_4$-sparse minimal unipolar obstruction is a cograph. For brevity, we omit the proof, which can be consulted in the arXiv version of this work [13].

Theorem 27

Let G be a $P_4$-sparse graph (respectively, a $P_4$-extendible graph). Then, G is a minimal unipolar obstruction if and only if G is a $P_4$-sparse graph (resp., a $P_4$-extendible graph) in the set $\{ 2P_3, K_{2,3}, C_5\}$.

7 Conclusions

In the present work we generalize some results related to hereditary properties in cographs and $P_4$-reducible graphs, providing similar results for some of their superclasses defined in terms of p-connectedess, including $P_4$-sparse and $P_4$-extendible graphs. Notice that the main results of this work, might be stated for any subclass ${\mathcal {G}}$ of either $P_4$-extendible or $P_4$-sparse graphs which is closed under both graph complements and induced subgraphs. In particular, this slight generalization is true for Theorems 21,23 and 27 and Corollaries 25 and 9. Additionally, we state a characterization for polar obstructions synthetizing (and somewhat generalizing) the results of Theorems 24 and 26 and [21].

Theorem 28

Let G be a graph in the class ${\mathcal {G}}$. Then, G is a minimal polar obstruction if and only if either G or its complement is the join of $\overline{P_3}$ with one of the graphs depicted in Fig. 2.

Throughout this work we showed that any $P_4$-sparse minimal obstruction for unipolarity, monopolarity, polarity, and (s, 1)-polarity is a cograph. In addition, Hannebauer [27] showed the following interesting result that generalize its analogue for cographs, which was previously proved in [24].

Theorem 29

([27]) If H is a $P_4$-sparse minimal (s, k)-polar obstruction, then H has at most $(s+1)(k+1)$ vertices.

In view of the observations above we propose the following questions.

Problem 30

For any positive integers s and k, is every $P_4$-sparse minimal (s, k)-polar obstruction a cograph?

Problem 31

Can we establish an O(sk) upper bound for the order of the $P_4$-extendible minimal (s, k)-polar obstructions?

It was independently shown in [2] and [27] that any $P_4$-sparse minimal obstruction for $(k,\ell )$-coloring is a cograph too, so we propose the following problem generalizing Problem 30.

Problem 32

Which hereditary properties ${\mathcal {P}}$ satisfy that every $P_4$-sparse minimal ${\mathcal {P}}$-obstruction is a cograph?

With the help of an interesting graph operation called partial complementation, Hell, Hernández-Cruz and Linhares-Sales [28] gave the complete list of cograph minimal (2, 2)-polar obstructions. In [12], we provide analogous results for $P_4$-sparse and $P_4$-extendible graphs, as well as efficient algorithms for finding maximal unipolar, monopolar, and polar subgraphs on these families. Such algorithms are based on the unique tree representations for the mentioned classes and they generalize those given in [21] for cographs.

As a future line of work, we propose to extend the results in this paper to more general graph classes having few induced $P_4$’s. Another line of work is to characterize some other hereditary properties on cograph superclasses by their sets of minimal obstructions. For example, it remains unknown whether the $P_4$-extendible minimal $(k,\ell )$-obstructions admit a simple structural characterization as their analogous in cographs and $P_4$-sparse graphs.