Coloring Graphs in Oriented Coloring of Cubic Graphs

Abstract

Oriented coloring of an oriented graph G is an arc-preserving homomorphism from G into a tournament H. We say that the graph H is universal for a family of oriented graphs $\mathcal {C}$ if for every $G\in \mathcal {C}$ there exists a homomorphism from G into H. We are interested in finding a universal graph for the family of orientations of cubic graphs. In this paper we present constructive proof that: if there exists a universal graph H on 7 vertices for every orientation of cubic graphs, then minimum out-degree and minimum in-degree of H are equal to 2. That gives a negative answer to the question presented in Pinlou’s PHD thesis.

1 Introduction

In this paper we will use standard graph theory notations. An directed graph G is a pair (V(G), A(G)) where V(G) is a vertex set and $A(G)\subseteq V(G) \times V(G)$ is a set of arcs. An oriented graphs are directed graphs with neither loops nor opposite arcs. For shortness, if an arc is going from u to v, instead of (u, v) we simply write uv. For a vertex $v \in V(G)$, we denote by $N_{out}^G(v)$ the set of out-neighbors of v, by $N_{in}^G(v)$ the set of in-neighbors of v and by $N^G(v) = N_{in}^G(v) \cup N_{out}^G(v)$ the set of neighbors of v. The degree of a vertex v (resp. in-degree, out-degree), denoted by $\deg ^G(v)$ (resp. $\deg _{in}^G(v)$, $\deg _{out}^G(v)$), is the number of its neighbors (resp. in-neighbors, out-neighbors). The minimum in-degree (resp. out-degree) of a graph, denoted by $\delta _{in}^G$ (resp. $\delta _{out}^G$), is the minimum of its vertices’ in-degrees (resp. out-degrees).

Let ${{\,\mathrm{rev}\,}}(G)$ be the graph obtained from G by reversing all arcs. The induced subgraph G[S] is the graph whose vertex set is S and the arc set contains all of the arcs in A(G) that have both endpoints in S. Directed path $P_n$ (resp. cycle $C_n$) is a path (resp. cycle) with n vertices and all arcs going in the same direction.

An oriented k-coloring $\phi$ is an arc-preserving homomorphism from an oriented graph G into an oriented graph H on k vertices. We say that graph G is colored by H and that graph H is a coloring graph. It is easy to see that we can only consider tournaments as coloring graphs. For two oriented graphs G and H if there exists a homomorphism from G into H, we will simply write $G \rightarrow H$, and $G \nrightarrow H$ otherwise.

The oriented chromatic number $\chi _o(G)$ of an oriented graph G is the smallest number k such that there exists a homomorphism from G into a coloring graph H on k vertices. An oriented clique is an oriented graph G such that $|V(G)|=\chi _o(G)$. We say that a coloring graph H is universal for a family of oriented graphs $\mathcal {C}$ if every member of that family can be colored by H. The oriented chromatic number $\chi _o(\mathcal {C})$ of the family $\mathcal {C}$ is the maximum of oriented chromatic number of any member of $\mathcal {C}$.

Over the years many authors determine the bounds or exact values of oriented chromatic number for many families of graphs. We refer to [6] for a short survey of the main results. In 1997 Kostochka et al. [4] considered orientations of graphs with maximum degree $\Delta$ and proved that every such graphs have the oriented chromatic number at most $2\Delta ^22^\Delta$. The version of the problem in which $\Delta =3$ is of particular interest.

Let $\mathcal {G}$ be the family of orientations of graphs with maximum degree 3 and let $\mathcal {G}^c \subset \mathcal {G}$ be the family of orientations of connected graphs with maximum degree 3. It is quite easy to see that there exists a graph $G\in \mathcal {G}^c$ which requires 7 colors for any oriented coloring (for example see Fig. 1). In 1997 Sopena [7] showed $\chi _o(\mathcal {G}) \le 16$ and conjectured that:

Conjecture 1

(Sopena [7]) $\chi _o(\mathcal {G}^c) = 7.$

In order to prove the above conjecture we can consider the disconnected version, i.e. is $\chi _o(\mathcal {G}) = 7$? That question is equivalent to the question if there exists a universal graph for $\mathcal {G}^c$. Indeed, if H is universal for $\mathcal {G}^c$ then it can be used to color every connected component of a graph $G\in \mathcal {G}$. For implication in opposite direction, if for every coloring graph H there exists a graph $G_H$ such that $G_H\nrightarrow H$ then $\bigcup \nolimits _{H} G_H$ is a graph which cannot be colored by 7 colors.

The above-mentioned upper bound $\chi _o(\mathcal {G}) \le 16$ was later improved by Sopena and Vignal [8] to 11. In recent years Duffy et al. [2] proved that 9 colors are enough for members of the family $\mathcal {G}^c$, the same bound for $\mathcal {G}$ was proved by Dybizbański, Ochem et al. [3]. Finally, Duffy [1] proves that $\chi _o(\mathcal {G}^c) \le 8$.

In summary, the difference between known upper bound and lower bound of $\chi _o(\mathcal {G}^c)$ equals 1. This motivated us to examine possible coloring graphs on 7 vertices which can color all orientations of graphs with maximum degree 3. In this article we show that if the coloring graph H is universal for $\mathcal {G}^c$ then $\delta _{out}^H=2$ and $\delta _{in}^H=2$. We can use the following proposition and consider only graphs with $\delta _{out}^G \le \delta _{in}^G$.

Proposition 1

Let H be a coloring graph (tournament) and G be an oriented graph, then $G \rightarrow H \iff {{\,\mathrm{rev}\,}}(G) \rightarrow {{\,\mathrm{rev}\,}}(H)$.

2 Coloring of cubic graphs

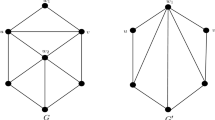
For completeness we start with the following known simple fact. Consider the graph $G_0$ presented in Fig. 1.

Proposition 2

There is no tournament T on 7 vertices such that $\delta _{out}^T = 0$ and there exists a homomorphism from $G_0$ into T.

Fig. 1

Graph $G_0$

Proof

Since every pair of vertices of $G_0$ are neighbors or connected by a directed path $P_3$, the graph $G_0$ is an oriented clique. The graph $G_0$ has 7 vertices and each of them has at least one out-neighbor, so we cannot use color c such that $\deg _{out}^T(c)=0$. $\square$

Consider the graph $G_1$ presented in Fig. 2.

Theorem 1

There are 11 tournaments T on 7 vertices such that: $\delta _{out}^T = 1$ and there exists a homomorphism $\phi : G_1 \rightarrow T$.

Proof

Let $V(T)=\{0,1,2,3,4,5,6\}$ be colors, assume that $\deg _{out}^T(0)=1$ and $N_{out}^T(0)=\{1\}$. It is easy to see that $G_1$ requires 7 colors for any oriented coloring. $\square$

Fig. 2

Graph $G_1$

Vertices in the interior cycle ($v_5, \ldots , v_9$) have two out-neighbors which are connected by directed path $P_3$. Thus, none of the vertices on the interior cycle can be colored with color 0. Without loss of generality assume that $\phi (v_0)=0$ and $\phi (v_1)=1$.

To color the interior directed cycle $C_5$ we have to use 5 colors. Assume first that we do not use color 1, thus we can assume that $\phi (v_i)=i-3$ for $i=5,\ldots ,9$. Consider color $\phi (v_3)$. We can only use colors 2 or 3 to color that vertex. If $\phi (v_3)=2$ (resp. $\phi (v_3)=3$), then we cannot color $v_2$ (resp. $v_4$), a contradiction. Thus we know that color 1 is used in the interior cycle $C_5$. Consider two cases depending on where color 1 is used.

Case 1. $\phi (v_9)=1$. For the other vertices in the interior cycle $C_5$ we use new colors: $\phi (v_5)=2$, $\phi (v_6)=3$, $\phi (v_7)=4$ and $\phi (v_8)=5$. Now, the last three vertices in the exterior cycle can be colored in exactly one way:

• Type 1 $\phi (v_2)=6$, $\phi (v_3)=2$ and $\phi (v_4)=4$. In the coloring $\phi$ we do not use connections between colors: 3 and 5, 3 and 6, 5 and 6. In the adjacency matrix of the coloring graph all other positions are filled. Let a, b and c be the values which represent three unused arcs.

  Depending on values of a, b and c we received 8 tournaments denoted by $T_1^{abc}$. The matrices are presented in Fig. 3a.

Case 2. $\phi (v_8)=1$. For the other vertices in the interior cycle $C_5$ we use new colors: $\phi (v_5)=3$, $\phi (v_6)=4$, $\phi (v_7)=5$ and $\phi (v_9)=2$. Now, the last three vertices in the exterior cycle can be color in exactly three ways:

• Type 2 $\phi (v_2)=3$, $\phi (v_3)=6$ and $\phi (v_4)=4$. Like in Type 1, we have 3 unused connections denoted a, b and c. Compatible tournaments are denoted by $T_2^{abc}$. The matrices are presented in Fig. 3b.

• Type 3 $\phi (v_2)=3$, $\phi (v_3)=6$ and $\phi (v_4)=5$. Compatible tournaments are denoted by $T_3^{abc}$. The matrices are presented in Fig. 3c.

• Type 4 $\phi (v_2)=6$, $\phi (v_3)=3$ and $\phi (v_4)=5$. Compatible tournaments are denoted by $T_4^{abc}$. The matrices are presented in Fig. 3d.

Fig. 3

Matrices of 32 coloring graphs for $a,b,c \in \{0,1\}$. For $0\le i,j\le 6$, $M_{ij}=1$ iff there is an arc ij. Values below diagonal $M_{ij} = 1-M_{ji}$

Summarizing, we have 32 tournaments which, up to the isomorphism, belong to 11 equivalence classes:

• 1. $T_1^{001} \cong T_2^{001}$,

• 2. $T_1^{011} \cong T_2^{011}$,

• 3. $T_1^{110} \cong T_2^{110} \cong T_3^{001} \cong T_3^{110} \cong T_4^{001} \cong T_4^{110}$,

• 4. $T_3^{011} \cong T_4^{111}$,

• 5. $T_1^{111} \cong T_2^{111}$,

• 6. $T_3^{111} \cong T_4^{011}$,

• 7. $T_1^{000} \cong T_2^{000}$,

• 8. $T_1^{010} \cong T_2^{010} \cong T_3^{000} \cong T_4^{100}$,

• 9. $T_1^{101} \cong T_2^{101}$,

• 10. $T_1^{100} \cong T_2^{100} \cong T_3^{100} \cong T_4^{000}$,

• 11. $T_3^{010} \cong T_3^{101} \cong T_4^{010} \cong T_4^{101}$.

$\square$

These eleven equivalent classes presented in the proof of Theorem 1 will be used later in the paper. We will refer to the leftmost tournament of each list.

An oriented graph is called a gadget if it contains one vertex of degree 1 and all others of degree 3. Let G be a gadget with vertex $v_0$ of degree one, H be the coloring graph and $S\subseteq V(H)$ be a set of colors. If for every $c\in S$ there is no homomorphism $\phi : G \rightarrow H$ such that $\phi (v_0)=c$ then the gadget G is called a S -gadget for H or |S|-colors gadget for H.

Lemma 1

Let H be a coloring graph on 7 vertices. If there exists a 3-colors gadget for H then there exists $G\in \mathcal {G}^c$ such that $G \nrightarrow H$.

Proof

Let $G'$ be a 3-colors gadget for H. Let G be a graph that contains five copies of the gadget $G'$ with vertices of degree 1: $v^1$, $v^2$, $v^3$, $v^4$, $v^5$. Additionally, these vertices induce a directed cycle $C_5$. The graph G is clearly an orientation of connected cubic graph.

Since $G'$ is a 3-colors gadget for H, in every homomorphism $\phi : G\rightarrow H$ vertices $v^1$, $v^2$, $v^3$, $v^4$, $v^5$ can be colored using four different colors. On the other hand, the directed cycle $C_5$ requires 5 colors for an oriented coloring, a contradiction. $\square$

Let $S_1=\{ T_1^{001}, T_1^{110}, T_1^{000}, T_1^{010}, T_1^{101}, T_1^{100}, T_3^{010} \}$. Consider gadget $G_2$ presented in Fig. 4.

Lemma 2

For every $T\in S_1$, gadget $G_2$ is a 3-colors gadget for T.

Proof

It is easy to check that every coloring graph $T\in S_1$ has the following properties:

• the only out-neighbor of 0 is the vertex 1,

• for every color $c \in V(T)\setminus \{0\}$, we have $\deg _{in}^T(c)<4$,

• $\deg _{out}^T(1) = 3$.

Consider the graph $G' = G_2 \setminus \{v_0\}$. This graph has 7 vertices and requires at least 6 colors for any oriented coloring—only $v_2$ and $v_3$ can have the same color.

Fig. 4

Gadget $G_2$

First, assume that we use 6 colors in oriented coloring $\phi : G' \rightarrow T$. The vertices $v_4$, $v_5$, $v_6$, $v_7$ induce a directed $C_4$ (requires 4 colors for any oriented coloring) and 0 is the only color with in-degree greater than or equal to 4. From this we conclude that $\phi (v_2)=\phi (v_3)=0$. Hence, $\phi (v_1)=1$ and $v_0$ must have color from $N_{out}^T(1)$.

Next, if we use 7 colors in oriented coloring $\phi : G' \rightarrow T$, then we have to use color 0 on one of the vertices. We can use it for $v_1$, $v_2$ or $v_3$ (others vertices have two out-neighbors). If $\phi (v_2)=0$ or $\phi (v_3)=0$, then $\phi (v_1)=1$ and $v_0$ must have color from $N_{out}^T(1)$. If $\phi (v_1)=0$, then $\phi (v_0)=1$.

Summarizing, to color $v_0$ we can use at most four colors from $N_{out}^T(1) \cup \{1\}$. In other words, $G_2$ is a S-gadget for T, where $S=V(T)\setminus N_{out}^T(1) \setminus \{1\}$ $\square$

Let $S_2=\{ T_3^{011}, T_1^{111} \}$.

Lemma 3

For every $T\in S_2$ there exists a 3-colors gadget G for T.

Proof

For $T=T_3^{011}$, let $G=G_2$ presented in Fig. 4. The proof is very similar to the proof of Lemma 2. The only difference is that we have $\deg _{in}^T(6)=4$. Even so, we cannot use this color at the same time in vertices $v_2$ and $v_3$ because $T[N_{in}^T(6)]$ does not contain a directed cycle $C_4$, but vertices $v_4$, $v_5$, $v_6$, $v_7$ create such a cycle.

$T_1^{111}$ is isomorphic to ${{\,\mathrm{rev}\,}}(T_3^{011})$, we take $G={{\,\mathrm{rev}\,}}(G_2)$ and, by Proposition 1, rest of the proof is the same as for $T_3^{011}$. $\square$

Corollary 1

For every coloring graph $T \in S_1 \cup S_2$ there exists $G\in \mathcal {G}^c$ such that $G \nrightarrow T$. 

Proof

Follows from Lemmas 1, 2 and  3. $\square$

Let $G_3$ be the graph presented in Fig. 5.

Lemma 4

$G_3 \nrightarrow T_1^{011}$.

Proof

Assume that there exists a homomorphism $\phi : G_3 \rightarrow T_1^{011}$. $\square$

Fig. 5

Graph $G_3$

First observe that only one pair of vertices: $v_0$ and $v_5$ is neither neighbors nor connected by a directed path $P_3$. Thus, in every coloring $\phi (v_0)=\phi (v_5)$ and all other vertices have different colors.

Let $X=\phi (v_0)=\phi (v_5)$. Consider three cases depending on X.

Case 1. $X\in \{0,5\}$. Vertex $v_0$ has two in-neighbors: $v_4$ and $v_7$ such that $\phi (v_4)\ne \phi (v_7)$. Similarly, $v_5$ has two out-neighbors: $v_1$ and $v_6$ such that $\phi (v_1)\ne \phi (v_6)$. A contradiction since $\deg _{out}^{T_1^{011}}(0)=1$ and $\deg _{in}^{T_1^{011}}(5)=1$.

Case 2. $X\in \{2,3,4,6\}$. Since $N_{out}^{T_1^{011}}(0)=\{1\}$ and $N_{in}^{T_1^{011}}(5)=\{1\}$, three consecutive vertices on directed cycle ($v_0, \ldots , v_7$) have colors 0, 1 and 5. We have two similar cases: $\phi (v_1)=0$, $\phi (v_2)=1$ and $\phi (v_3)=5$ (resp. $\phi (v_2)=0$, $\phi (v_3)=1$ and $\phi (v_4)=5$). Thus $\phi (v_7)=1$ (resp. $\phi (v_6)=1$). In both cases we have a contradiction since color 1 appears twice in the coloring.

Case 3. $X=1$. First observe that $\phi (v_6)\ne 5$—otherwise $\phi (v_2)=1$. Thus $\phi (v_1)=5$. By a similar argument $\phi (v_4)=0$. Colors 0 and 5 do not appear on other vertices so we have two cases depending on the colors of $v_6$ and $v_7$.

• $\phi (v_6)=4$ and $\phi (v_7)=3$. We can color $v_2$ in only one way ($\phi (v_2)=2$), and we cannot extend that coloring to $v_3$.

• $\phi (v_6)=6$ and $\phi (v_7)=2$. There is one way to color $\phi (v_3)=4$ and we cannot extend that coloring to $v_2$.

$\square$

3 Tournament $T_3^{111}$

Lemma 5

$T_3^{111}$ is self-converse.

Proof

Permutation (02)(13)(46)(5) transforms $T_3^{111}$ into ${{\,\mathrm{rev}\,}}(T_3^{111})$. $\square$

Consider gadgets $G_4$ and $G_5$ presented in Fig. 6.

Lemma 6

Let $\phi : G_4[v_2,\ldots ,v_7] \rightarrow T_3^{111}$ be a homomorphism. If $\phi (v_2)=1$, then $\phi (v_7)=2$.

Proof

If $\phi (v_2)=1$ then to color $v_3$ and $v_4$ we use two different colors from $N_{out}^{T_3^{111}}(1) = \{3,5,6\}$. By symmetry of $G_4[v_2,\ldots ,v_7]$ we can assume that $\phi (v_3)<\phi (v_4)$. We have three cases:

• $\phi (v_3)=3$ and $\phi (v_4)=6$. Therefore $\phi (v_5)=5$, $\phi (v_6)=2$ and we cannot color vertex $v_7$.

• $\phi (v_3)=5$ and $\phi (v_4)=6$. Since $N_{in}^{T_3^{111}}(5) \cap N_{out}^{T_3^{111}}(6) = \emptyset$ we cannot color vertex $v_5$.

• $\phi (v_3)=3$ and $\phi (v_4)=5$. Therefore $\phi (v_5)=4$ and $\phi (v_6)=\{2,6\}$, so vertex $v_7$ can be colored only by color 2.

$\square$

Since $G_4[v_2,\ldots ,v_7]$ is isomorphic to ${{\,\mathrm{rev}\,}}(G_4[v_8,\ldots ,v_{13}])$, then using Lemma 5 and Lemma 6 we know that for every coloring $\phi : G_4[v_8,\ldots ,v_{13}] \rightarrow T_3^{111}$, if $\phi (v_{13})=3$, then $\phi (v_8)=0$

Lemma 7

Let $\phi : G_4[v_2,\ldots ,v_7] \rightarrow T_3^{111}$ be a homomorphism. If $\phi (v_2)=5$, then $\phi (v_7)\in \{2,4\}$.

Proof

If $\phi (v_2)=5$ then to color $v_3$ and $v_4$ we use two different colors from $N_{out}^{T_3^{111}}(5) = \{0,3,4\}$. By symmetry of $G_4[v_2,\ldots ,v_7]$ we can assume that $\phi (v_3)<\phi (v_4)$. We have three cases:

• $\phi (v_3)=3$ and $\phi (v_4)=4$. Therefore $\phi (v_5)=1$, $\phi (v_6)=2$ and we cannot color vertex $v_7$.

• $\phi (v_3)=0$ and $\phi (v_4)=4$. Since $N_{in}^{T_3^{111}}(4) \cap N_{out}^{T_3^{111}}(0) = \emptyset$ we cannot color vertex $v_5$.

• $\phi (v_3)=0$ and $\phi (v_4)=3$. Therefore $\phi (v_6)=1$ and $\phi (v_5)=\{2,6\}$, so vertex $v_7$ can be colored with colors 2 or 4.

$\square$

Fig. 6

Gadgets for $T_3^{111}$

Lemma 8

$G_4$ is $\{3\}$-gadget for $T_3^{111}$.

Proof

We will show that there is no homomorphism $\phi$ from gadget $G_4$ (see Fig. 6a) into $T_3^{111}$ such that $\phi (v_0)=3$. Assume the opposite. Since $\phi (v_1) \in N_{out}^{T_3^{111}}(3)=\{0,2,6\}$ we have three cases:

Case 1. $\phi (v_1)=0$. In this case $\phi (v_2)=1$ and by Lemma 6, $\phi (v_7)=2$. Color 2 has only one in-neighbor in $T_3^{111}$, so $\phi (v_{13})=3$ and again, by Lemma 6$\phi (v_8)=0$, a contradiction since $v_8$ and $v_1$ are neighbors.

Case 2. $\phi (v_1)=2$. It is easy to check that the graph $G' = G_4[v_1,\ldots ,v_{13}]$ is self-converse ($G' \cong {{\,\mathrm{rev}\,}}(G')$). Since Lemma 5 and Proposition 1 the case is the same as Case 1.

Case 3. $\phi (v_1)=6$. We have $N_{out}^{T_3^{111}}(6)=\{0,5\}$. Since $v_3$ and $v_4$ have different colors (they are connected by directed path $P_3$) we cannot use color 0 in $v_2$. Thus $\phi (v_2)=5$ and by Lemma 7, $\phi (v_{7})\in \{2,4\}$ and in consequence $\phi (v_{13})\in \{2,3,5\}$.

• $\phi (v_{13}) = 2$. Since $v_{11}$ and $v_{12}$ have different colors (they are connected by directed path $P_3$) we cannot use color 2 in $v_{13}$, a contradiction.

• $\phi (v_{13}) = 3$. Colors $\phi (v_{11})$ and $\phi (v_{12})$ must both be in $N_{in}^{T_3^{111}}(3)=\{1,4,5\}$ and not be equal. If $\phi (v_{11})=4$ and $\phi (v_{12})=5$ then we cannot color $v_{10}$ ($N_{out}^{T_3^{111}}(5)\cap N_{in}^{T_3^{111}}(4) = \emptyset$). If $\phi (v_{11})=5$ and $\phi (v_{12})=1$ then we cannot color $v_{9}$ because $N_{out}^{T_3^{111}}(1)\cap N_{in}^{T_3^{111}}(5) = \{6\}$ and there is a directed path $P_3$ from $v_9$ to $v_1$. In the last subcase, $\phi (v_{11})=1$ and $\phi (v_{12})=4$, then $\phi (v_{9})=5$ and $\phi (v_{10})=0$ and we cannot color vertex $v_8$, a contradiction.

• $\phi (v_{13}) = 5$. By Lemma 7, $\phi (v_{8}) \in \{0,6\}$, a contradiction since $\phi (v_1)=6$.

$\square$

Lemma 9

$G_5$ is $\{3,4\}$-gadget for $T_3^{111}$.

Proof

Let $G_4^1$ and $G_4^2$ are two copies of $G_4$ and let $v_0^1$ and $v_0^2$ are two vertices of degree 1. Let $G_5$ be the graph obtained from $G_4^1$, $G_4^2$, four new vertices: $v_0, v_1, v_2, v_3$ and 7 new arcs (see Fig. 6b).

By Lemma 8, in every homomorphism $\phi : G_5 \rightarrow T_3^{111}$, $\phi (v_0^1)\ne 3$ and $\phi (v_0^2)\ne 3$. Vertices $v_3$, $v_2$, $v_0^1$ and $v_0^2$ form a directed $C_4$ so they have different colors, and since $N_{in}^{T_3^{111}}(2)=\{3\}$ vertices $v_3$ and $v_2$ do not have color 2.

To prove thesis we will show that there is no homomorphism $\phi : G_5 \rightarrow T_3^{111}$ such that $\phi (v_0)\in \{3,4\}$. In opposite, if $\phi (v_0)\in \{3,4\}$, then $\phi (v_1)\in N_{in}^{T_3^{111}}(v_0) = \{1,2,4,5\}$. Consider 4 cases.

• $\phi (v_1) = 1$. To color vertices $v_2$ and $v_3$ we use colors 0 and 4. Since $N_{out}^{T_3^{111}}(0) \cap N_{in}^{T_3^{111}}(4) = \emptyset$ then the coloring cannot be extended to vertices $v_0^1$ and $v_0^2$.

• $\phi (v_1) = 2$. $N_{in}^{T_3^{111}}(2)=\{3\}$ thus the coloring cannot be extended to vertices $v_2$ and $v_3$.

• $\phi (v_1) = 4$. $N_{in}^{T_3^{111}}(4)=\{2,5\}$ thus the coloring cannot be extended to vertices $v_2$ and $v_3$.

• $\phi (v_1) = 5$. To color vertices $v_2$ and $v_3$ we use colors 1 and 6. Since $N_{out}^{T_3^{111}}(1) \cap N_{in}^{T_3^{111}}(6) = \{3\}$ then the coloring cannot be extended to vertices $v_0^1$ and $v_0^2$.

$\square$

Lemma 10

There exists $G \in \mathcal {G}^c$ such that $G \nrightarrow T_3^{111}$.

Proof

Let $G_5^1$, $G_5^2$, $G_5^3$, $G_5^4$ are 4 disjoint copies of gadget $G_5$ with vertices of degree one: $v_0^1$, $v_0^2$, $v_0^3$, $v_0^4$. Consider gadget $G'$ construct from $G_5^1$, $G_5^2$, $G_5^3$, $G_5^4$ by adding vertex $v_0$ and v, arc $vv_0$ and directed cycle $C_5 = (v_0^1, v_0^2, v_0^3, v_0^4, v_0)$.

Now consider homomorphism $G' \rightarrow T_3^{111}$. We claim that vertex $v_0$ can be colored only by color 3 or 4. If we assume opposite and use Lemma 9, then in any vertex of directed cycle $C_5$ we cannot use color 3 nor 4, so we have to use all colors from $\{0,1,2,5,6\}$. This is impossible since $\{0,1,5,6\} \subset N_{out}^{T_3^{111}}(2)$.

Thus, vertex v can be colored with any color from $N_{in}^{T_3^{111}}(3) \cup N_{in}^{T_3^{111}}(4)$, so $G'$ is a 3-colors gadget for $T_3^{111}$. Using gadget $G'$, the thesis follows from Lemma 1. $\square$

4 Summary

Proposition 3

Let H be tournament on 7 vertices in which every vertex has out-degree equal to 3. There exists graph $G \in \mathcal {G}^c$ such that $\phi : G \nrightarrow H$.

Proof

Consider the graph $G_6$ presented in Fig. 7. We will show that in every oriented 7-coloring of $G_6$, one of the colors has out-degree at least 4. It is clear that $G_6$ is an oriented clique. Assume that $\phi (v_i)=i$ and for every arc $v_iv_j \in A(G_6)$ there exists an arc $ij\in A(H)$. $\square$

Fig. 7

Graph $G_6$

Assume for contradiction that every color in V(H) has out-degree equal to 3. Since there are arcs from 1 to 0, 3 and 4, three other arcs incident with 1 are going in the opposite direction (from 2, 5, and 6 to 1). Now colors 2 and 5 have already three out-neighbors. Those colors are adjacent in H, so one of them have $\deg _{out}^H\ge 4$, a contradiction. $\square$

Theorem 2

If tournament H on 7 vertices is universal graph for class of oriented cubic graphs then $\delta _{in}^H = 2$ and $\delta _{out}^H = 2$.

Proof

This follows from Theorem 1, Lemmas 4, 10, Corollary 1 and Propositions 1, 2, 3. Note that all used graphs are orientations of cubic graphs and their disjoint sum is the graph which cannot be colored by homomorphism into coloring graph H with $\delta _{in}^H \ne 2$ or $\delta _{out}^H \ne 2$. $\square$

5 Discussion and future work

In his PhD thesis, Alexandre Pinlou [5] presented the coloring graph $T_7$ (Figure 2.33). Moreover, together with Édita Máčajová (Comenius University in Bratislava) they worked on the problem of universal graph for family of oriented cubic graphs. Using a computer they have checked that every oriented cubic graph on at most 18 vertices can be colored by $T_7$. Additionally, Pinlou asked question (2.57) whether graph $T_7$ is universal for every orientation of cubic graphs. $T_7 \cong {{\,\mathrm{rev}\,}}(T_3^{010})$, so Proposition 1 and Corollary 1 gives the negative answer to this question.

In this article, for a given coloring graph H on 7 vertices we present orientation of cubic graph G such that $G \nrightarrow H$. More precisely, we consider all tournaments with $\delta _{in}^H \ne 2$ or $\delta _{out}^H \ne 2$. No attempt has been made here to achieve minimal graphs. It is natural to ask what is the minimal size of such graphs.

In our opinion, more interesting is to find oriented cubic graphs for coloring graphs on 7 vertices, which are not considered in this paper. Using popular computer tools, it is easy to check that there are 84 tournaments H such that $\delta _{in}^H=2$ and $\delta _{out}^H=2$. We believe that part of such tournaments do not color some oriented cubic graphs presented in this article. If for every coloring graph H exists an oriented cubic graph which cannot be colored by H, then the disconnected version of Sopena conjecture is false. Equivalently we would know that there is no universal graph on 7 vertices for all members of $\mathcal {G}^c$.

As we mentioned in the introduction, if Sopena conjecture for $\mathcal {G}$ is true then there is an universal graph on 7 vertices for $\mathcal {G}$ (so Sopena conjecture for $\mathcal {G}^c$ is also true). It is very often that for given families of graphs, the authors use one target graph (for example Paley tournament) and show that there is a homomorphism into that tournament. We believe that this method can be used to prove Sopena conjecture and the result of this paper allows us to focus on graphs with minimal out-degree and in-degree equal 2. For example, a very promising tournament is the $QR_7$ (Paley tournament on 7 vertices) with one arc reversed.

On the other hand, if we want to show that Sopena conjecture is false then the result of this paper does not bring us any closer to the solution. Even if for every coloring graph on 7 vertices H exists graph $G\in \mathcal {G}^c$ such that $G \nrightarrow H$, Sopena conjecture still could be true.