Peg Solitaire on Cartesian Products of Graphs

Abstract

In 2011, Beeler and Hoilman generalized the game of peg solitaire to arbitrary connected graphs. In the same article, the authors proved some results on the solvability of Cartesian products, given solvable or distance 2-solvable graphs. We extend these results to Cartesian products of certain unsolvable graphs. In particular, we prove that ladders and grid graphs are solvable and, further, even the Cartesian product of two stars, which in a sense are the “most” unsolvable graphs.

1 Introduction

In [3], Beeler and Hoilman introduced the game of peg solitaire on graphs as a generalization of the classical peg solitaire game:

For a connected, undirected graph $G=(V,E)$, we put pegs in some of the vertices of G. Given three vertices u, v, w with pegs in u and v and a hole in w such that $uv, vw \in E$, we can jump with the peg from u over v into w, removing the peg in v (see Fig. 1). This jump will be denoted as $u \cdot \mathbf{v } \cdot w$.

Fig. 1

A jump in peg solitaire

In general, we begin with a starting state $S \subset V$ of vertices that are empty (i.e., without pegs). A terminal state $T \subset V$ is a set of vertices that have pegs at the end of the game such that no more jumps are possible. A terminal state T is associated to a starting state S if T can be obtained from S by a series of jumps. We will always assume that the starting state S consists of a single vertex.

The goal of the original game is to remove all pegs but one. This is not possible for every graph. Therefore, we use the following notation. A graph $G=(V,E)$ is called

• solvable, if there is some $v \in V$ such that the starting state $S = \lbrace v \rbrace$ has an associated terminal state consisting of a single vertex.

• freely solvable, if for all $v \in V$ the starting state $S = \lbrace v \rbrace$ has an associated terminal state consisting of a single vertex.

• k-solvable, if there is some $v \in V$ such that the starting state $S = \lbrace v \rbrace$ has an associated terminal state consisting of k vertices.

• strictly k-solvable, if G is k-solvable but not l-solvable for any $l<k$. In that case G has solitaire number $\mathrm {Ps}(G)=k$.

Peg solitaire has been considered for quite a few classes of graphs, including paths, complete graphs, stars, double stars and caterpillars (for more results and variants see [1,2,3,4,5,6,7,8,9]).

In this article we will consider the Cartesian product of two graphs. For graphs G and H, we denote the Cartesian product of G and H by $G\,\square\, H$ and use the (common) notation $(g,h)\in V(G\,\square\, H)$ for the vertex induced by $g\in V(G)$ and $h\in V(H)$.

In [3], Beeler and Hoilman gave some results about Cartesian products of graphs, that are either solvable or distance 2-solvable (meaning that they are strictly 2-solvable such that the pegs in the terminal state have distance 2). We will extend these results to Cartesian products of an arbitrary graph and a solvable graph (with an extra condition). We also consider Cartesian products of stars (i.e., graphs that are furthest away from being solvable) and show that these Cartesian products are solvable, too. This gives rise to the conjecture, that all (non trivial) connected Cartesian products are solvable.

2 Ladders and Grids

In this section we will derive some general results. Our main result is the solvability of the Cartesian product of an even Hamiltonian graph and an arbitrary graph.

To deal with Cartesian products, we need the following new concept. A graph G is called super freely solvable if, for any (not necessarily distinct) $v,w \in V$, terminal state $\lbrace w \rbrace$ is reachable from starting state $\lbrace v \rbrace$.

The following (well known) lemma is easy to prove.

Lemma 1

The cycle $C_4$ is freely solvable. Moreover, for any distinct vertices v, w, we can end with a peg in w when starting with a hole in v. On the other hand, $C_4$ is not super freely solvable.

For $m,n \ge 2$, we call $P_n \,\square\, P_2$ a ladder and $P_m \,\square\, P_n$ a grid. In particular, $C_4$ is both, a ladder and a grid. We will show that, apart from $C_4$, all ladders and grids are super freely solvable.

Theorem 1

If $n \ge 3$, the ladder $P_n \,\square\, P_2$ is super freely solvable. Moreover, for each $i \in \lbrace 2,\ldots ,n-1 \rbrace$, at some point in the solving process the subgraph $\lbrace v_i \rbrace \,\square\, P_2$ contains exactly one peg and one hole.

Proof

We divide the proof into several cases, depending on the location of the starting hole and the terminal vertex. In each case it will be clear from the jumps that the second statement in the theorem is fulfilled.

• 1. Suppose that $s = (1,1)$ and $t = (n,i)$. We start with the following jumps:

  $$\begin{aligned} (2,2) \cdot (\overrightarrow{2,1}) \cdot (1,1), (1,1) \cdot (\overrightarrow{1,2}) \cdot (2,2). \end{aligned}$$

  (1)

  This produces a ladder with holes in (1, 1), (1, 2) and (2, 1) and pegs everywhere else. Now we can jump up the ladder in the same fashion until we are left with a ladder with pegs only in $(n-1,2),(n,1)$ and (n, 2). Executing the jumps $(n,2) \cdot (\overrightarrow{n,1}) \cdot (n-1,1)$ and $(n-1,1) \cdot (\overrightarrow{n-1,2}) \cdot (n,2)$ or $(n-1,2) \cdot (\overrightarrow{n-1,1}) \cdot (n,1)$ solves the graph with the desired terminal state.

• 2. Suppose that $s = (1,1)$ and $t = (1,i)$. We start with the jump $(2,2) \cdot (\overrightarrow{2,1}) \cdot (1,1)$. If $t = (1,1)$, we execute the jumps

  $$\begin{aligned} (2j+1,2) \cdot (\overrightarrow{2j+1,1}) \cdot (2j,1), (2j+2,1) \cdot (\overrightarrow{2j+2,2}) \cdot (2j+1,2) \end{aligned}$$

  (2)

  for $1 \le j \le \lfloor \frac{n}{2}\rfloor -1$. If n is odd, we further jump $(n,2) \cdot (\overrightarrow{n,1}) \cdot (n-1,1)$. This sequence of jumps will result in a state where we have pegs in (1, 1), (1, 2), (2j, 1) and $(2j+1,2)$ for $1 \le j \le \lfloor \frac{n}{2}\rfloor -1$ and, if n is odd, also in $(n-1,1)$. Every other vertex is empty. Starting with the jump $(1,1) \cdot (\overrightarrow{1,2}) \cdot (2,2)$, we go up on the second component of the ladder and go down on the other side. This will end with a peg in (1, 1). If $t=(1,2)$, we interchange every second component in the jumps above after the first jump.

• 3. Suppose $s = (1,1)$ and $t = (k,i)$ with $1< k < n$. Consider the ladder up to height k. We solve this using Case 1 with a peg in (k, i) (this is also possible if this ladder is a $C_4$). Now we are left with a ladder of height $n-k+1$ where $t = (1,i)$. If this is the $C_4$, we can solve it since we have a peg in (k, i). If the remaining ladder is not the $C_4$, solve it using Case 2.

• 4. Suppose that $s = (k,1)$ where $1< k < n$ and let $t = (j,i)$. W.l.o.g. assume $j \le k$. Divide the ladder in $L_1$ and $L_2$ where $L_1$ contains the vertices (l, r) with $l \ge k$ and let $L_2$ be the ladder containing the vertices (l, r) with $l \le k$. Solve ladder $L_1$, ending in $(k,i')$ where $i' \ne i$. This is possible if $L_1 \ne C_4$. Now solve $L_2$ ending in t. This is also possible if $L_2 \ne C_4$. The only cases left to consider are the cases $L = P_3 \,\square\, P_2$ and $s=(2,1)$ and $t=(2,i)$. It is easy to check that these are solvable. $\square$

Theorem 2

If $n \ge 3$ or $m \ge 3$, the grid $P_m \,\square\, P_n$ is super freely solvable.

Proof

We prove the theorem by induction. If $m=2$ or $n=2$, the statement follows from Theorem 1. Hence, suppose that both m and n are at least 3. If $G = P_3 \,\square\, P_3$, we find a ladder $P_2 \,\square\, P_3$ in G containing a hole. Since this ladder is super freely solvable, it is easy to see that we can solve it and get a terminal peg (of the ladder) in a vertex such that we can solve the remaining grid with a peg in an arbitrary vertex t.

Now, let $m,n \ge 3$ be arbitrary with $\max \lbrace m,n \rbrace \ge 4$ and let $s=(j,k)$ be the starting hole.

• 1. If $s=(1,1)$, let w.l.o.g. $m \ge 4$ and divide the grid into the two graphs $G_1 \cong P_2 \,\square\, P_n$ and $G_2 \cong P_{m-2} \,\square\, P_n$. If $t \in G_2$, solve the ladder $G_1$ with terminal peg next to $G_2$. After two more jumps, we are left with the graph $G_2$ with exactly one hole. By induction hypothesis this is solvable with peg in t. If $t \in G_1$, start with the jump $(3,1) \cdot (\overrightarrow{2,1}) \cdot (1,1)$. Then, by induction hypothesis, we can solve $G_2$, which is solvable with terminal peg in t.

• 2. If $s=(1,k)$ with $k \ne 1$, we can proceed the same way, provided that $m \ge 4$. If $m=3$, consider the two graphs $G_1$ and $G_2$, where $G_1$ contains all vertices (r, s) such that $s \le k$ and $G_2$ contains all vertices (r, s) with $s \ge k$. Let w.l.o.g. $t \in G_1$. If $G_1$ is a ladder, we can proceed analogously to the case when $G= P_3 \,\square\, P_3$, solving $G_2$ first and dealing with the remaining 4 pegs later. If $G_1$ is not a ladder, solve $G_2$ with terminal peg in $(1,k+1)$. Next do the jumps $(1,k-2) \cdot (\overrightarrow{1,k-1}) \cdot (1,k)$ and $(1,k+1) \cdot (\overrightarrow{1,k}) \cdot (1,k-1)$. We are left with the grid $G_1$ which is freely solvable by induction hypothesis.

• 3. If $s = (j,k)$ with $1< j < m$ and $1< k < n$, divide the grid into two grids $G_1$ and $G_2$ that form a partition of G. Let w.l.o.g. $s \in G_1$. This can always be done in a way such that $G_1$ and $G_2$ are grids, neither of them is the grid $C_4$, and s has distance 1 from its nearest vertex in $G_2$. If $t \in G_2$ we can proceed analogously to case 1. If $t \in G_1$, there exist $v \in G_1, w \in G_2$ such that the jump $w \cdot \overrightarrow{v} \cdot s$ is possible. After this jump, we solve $G_2$ with terminal peg in the unique vertex $u \in G_2$ such that the subgraph induced by the vertices s, u, v, w is $C_4$. After jumping $u \cdot \overrightarrow{s} \cdot v$, we can finally solve $G_1$ with terminal peg in t.

Due to symmetry, this covers all cases.$\square$

Using the super free solvability of ladders, we can prove a fairly general result about Cartesian products. The first step in doing this is to show that Cartesian products are solvable if one of the components is the path $P_2$.

Theorem 3

$P_2 \,\square\, G$ is freely solvable for any connected graph G.

Proof

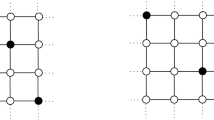
Let T be a spanning tree of G. It suffices to show that $P_2 \,\square\, T$ is solvable. If T is a path this follows from Theorem 1. So suppose that T is not a path. Choose a root vertex $v_0$ and do a depth-first-search, enumerating the vertices in the order they occur. Use this to decompose T into paths $Q_1,\ldots ,Q_m$. (cf. Fig. 2).

Start with a hole in $v_0$. Begin to solve $P_2 \,\square\, Q_1$ using Theorem 1 or Lemma 1. Let $v_k \in Q_1$ be the vertex with largest index such that $v_k$ lies in another path. A soon as the subgraph $P_2 \,\square\, \lbrace v_k \rbrace$ contains exactly one peg and one hole, stop solving $Q_1$ and start solving $Q_2$. Let $v_l \ne v_k$ be the vertex with largest index such that $v_k$ lies in another path (if such a vertex exists). Then continue in this manner (stop solving $Q_2$ and start solving $Q_3$). Keep going with this process until no such vertex $v_l$ exists. If no such $v_l$ exists in $Q_i$, solve $Q_i$ completely, ending with a hole in the subgraph $P_2 \,\square\, \lbrace v_k \rbrace$ where we started with a hole (this can be done because of Lemma 1 and Theorem 1). If $v_k$ is contained in another path $Q_j$ that has not been considered yet, continue with this path in the same way. If this is not the case, go all the way back and solve the ladders that have not been completely solved yet, always ending with a hole in the same subgraph in which we started with a hole. This process solves $P_2 \,\square\, T$. Since $v_0$ was arbitrary, we have free solvability.$\square$

Fig. 2

A tree T with decomposition into paths

Theorem 4

Let G be a graph that has an even Hamiltonian path. Then for any connected graph H, $G \,\square\, H$ is solvable.

Proof

If $H = K_1$, this is obviously true. So suppose that H has at least two vertices. Let $P = \lbrace v_1,\ldots ,v_{2m} \rbrace$ be a Hamiltonian path in G. Start with a hole in $(v_1,w)$ for some $w \in H$. Due to Theorem 3, $\lbrace v_1,v_2 \rbrace \,\square\, H$ is freely solvable. Let $\{(v_i,w')\}$ be a terminal state. If $i=1$, jump $(v_4,w') \cdot (\overrightarrow{v_3,w'}) \cdot (v_2,w'), (v_1,w') \cdot (\overrightarrow{v_2,w'}) \cdot (v_3,w')$. If $i=2$, jump $(v_3,w') \cdot (\overrightarrow{v_2,w'}) \cdot (v_2,z), (v_2,z) \cdot (\overrightarrow{v_3,z}) \cdot (v_3,w')$ for some neighbour z of $w'$. In both cases, we have a hole in the subgraph induced by $\lbrace v_3,v_4 \rbrace \,\square\, H$ and we can use this process inductively to solve $G \,\square\, H$.$\square$

3 Cartesian products of stars

Keeping in mind the results from the last section, it seems natural to take a look at Cartesian products of unsolvable graphs. Since they are particularly far away from being solvable, we consider star graphs.

Let $K_{1,n}$ denote the star (graph) on $n+1$ vertices, where we denote the central vertex by 0 and the pendant vertices by $1,2,\dots ,n$.

It is known that stars $K_{1,n}$ are not solvable for $n\ge 3$ [3]. However, the Cartesian product of any two stars on at least 2 vertices is solvable. We will prove several lemmas before turning our attention to this statement.

In Fig. 3, seven graphs (in the following often used as substructures in larger graphs) with a given (starting) state and a corresponding reachable (terminal) state are displayed. The notation $\mathrm {EP}_i$ denotes the (so called) reduction (or elimination) process that is performed by several jumps to get from the left hand state to the right hand one. The reader is invited to check that all of these reductions are in fact possible.

Fig. 3

Several intermediate states with corresponding reduced states

For the remainder of this chapter, we consider the Cartesian product $K_{1,n}\,\square\, K_{1,m}$ with $n\ge m\ge 1$. For even m (we will reduce everything to this case), we define $A=\{(g,h):g,h\in [m]\}$¹ and

$$\begin{aligned} A_i=\{(g,h)\in A:g-h\in \{-2i, -2i+1, m-2i, m-2i+1\}\} \end{aligned}$$

for $i\in \left[ 1,\frac{m}{2}-1\right]$ as well as

$$\begin{aligned} A_0=\{(g,h)\in A:g-h\in \{1-m,0,1\}\}. \end{aligned}$$

Since all possible differences are considered and appear in exactly one $A_i$, we immediately get the following result.

Lemma 2

The sets $A_0,A_1,\dots ,A_{\frac{m}{2}-1}$ form a partition of A.

This partition of A has two important properties.

Lemma 3

Let $i\in [0,\frac{m}{2}-1]$ and $A_i$ defined as before.

• (i) For every $j\in [m]$, the set $A_i$ contains exactly two elements of the form $(j,\cdot )$ and two elements of the form $(\cdot ,j)$.

• (ii) The elements of $A_i$ can be generated, starting with ${\mathfrak {x}}_0^{(i)}=\left( x_{0,1}^{(i)}, x_{0,2}^{(i)}\right) =(1,2i+1)$, using the following procedure:

  $$\begin{aligned} {\mathfrak {x}}_{k+1}^{(i)}={\left\{ \begin{array}{ll} \left( x_{k,1}^{(i)}+1, x_{k,2}^{(i)}\right) &{}\text {if }2\mid k,\\ \left( x_{k,1}^{(i)}, x_{k,2}^{(i)}+1\right) &{}\text {if }2 \,\nmid\, k, \end{array}\right. } \end{aligned}$$

  (3)

  where calculations are done modulo m with residue system [m].

Proof

For $i=0$ exactly two of the equations $j-y=a$ with $a\in \{1-m,0,1\}$ have a solution in [m], to be specific, $y=j, a=0$ and either $y=j-1, a=1$ (if $j>1$) or $y=m, a=1-m$ (if $j=1$). For $i\in [\frac{m}{2}-1]$, exactly two of the equations $j-y=a$ with $a\in \{-2i, 1-2i, m-2i, m-2i+1\}$ have a solution. We show this exemplarily for $j<m-2i$, the other (three) cases follow in the same fashion. For $a\in \{m-2i, m-2i+1\}$ apparently no solution can be found since y is positive. The other two equations have the solutions $j+2i$ and $j+2i-1$, which lie in [m] since $j<m-2i$. The arguments are similar for $(\cdot ,j)$, therefore, part (i) is true.

For part (ii), we note, that $x_{l,1}^{(i)}-x_{l,2}^{(i)}\in \{-2i, 1-2i\}$ (where the difference alternates) holds as long as $x_{l,2}^{(i)}\le m$, i.e. $l\le 2m-4i-1$. For $l_0=2m-4i-1$, we have $x_{l_0,1}^{(i)}-x_{l_0,2}^{(i)}=-2i+1$, and after changing the first second component to obtain ${\mathfrak {x}}_{k+1}^{(i)}$, we have $x_{l_0+1,1}^{(i)}-x_{l_0+1,2}^{(i)}=m-2i$. Hence, for $2m-4i\le l\le 2m-2$, we have $x_{l,1}^{(i)}-x_{l,2}^{(i)}\in \{m-2i, m-2i+1\}$ (again the difference alternates). Since ${\mathfrak {x}}_{2m-1}^{(i)}=(1,2i)$ and ${\mathfrak {x}}_{2m}^{(i)}={\mathfrak {x}}_0^{(i)}$, the set $X_i$ containing the elements generated via (3) is a subset of $A_i$. From (i) we immediately get $|A_i|=2m$. Since the construction procedure of $X_i$ is periodic of length 2m, we obtain $|X_i|=2m$. Therefore we have $X_i=A_i$, which proves statement (ii).$\square$

Let us now consider the vertex set

$$\begin{aligned} B=\{(g,h):g,h\in [0,m], (g,h)\ne (0,0), g\cdot h=0\}. \end{aligned}$$

Lemma 4

The set $A_i\cup B$ induces a cycle in $K_{1,n}\,\square\, K_{1,m}$ (with $2\mid m$) for each $i\in \left[ 0,\frac{m}{2}-1\right]$. Furthermore, in this cycle an element of B is adjacent to two elements of $A_i$ and vice versa.

Proof

We can order the elements of $A_i\cup B$ using (3) and inserting the fitting elements of B between two consecutive elements of $A_i$, in the way (again calculations are done modulo m with residue system [m])

$$\begin{aligned} (1,0),(1,2i+1),(0,2i+1),(2,2i+1),(2,0),(2,2i+2),\dots ,(m,2i),(0,2i),(1,2i), \end{aligned}$$

where consecutive elements are adjacent (note that $2i=m$ in case of $i=0$). There are no additional edges, hence the statement follows.$\square$

Lemma 5

For even m, we consider the graph induced by $A\cup B\cup \{(0,0)\}$. Starting with holes in (0, 1), (1, 1) and (i, 0), (0, i) for $i\in [2,m]$ and pegs in every other vertex, this graph is solvable with the final peg being in (0, 0).

Proof

Using Lemma 4, we eliminate all pegs in $A_i$ ($i\in \left[ \frac{m}{2}-1\right]$) with jumps along the cycle induced by $A_i\cup B$ starting in (1, 0) and ending with a peg in (1, 0). Next, we jump along the cycle induced by $A_0\cup B$, starting with $(1,0)\cdot (\overrightarrow{1,m})\cdot (0,m)$ until we have only pegs in (0, 0), (2, 1), (2, 0). The final jumps $(2,0)\cdot (\overrightarrow{0,0})\cdot (0,1)$ and $(2,1)\cdot (\overrightarrow{0,1})\cdot (0,0)$ solve the graph with final peg in (0, 0).$\square$

Lemma 6

For even m, we consider the graph induced by $A\cup B\cup \{(0,0)\}$. Starting with holes in (0, i) for $i\in [2,m]$ or in (i, 0) for $i\in [2,m]$ and pegs in every other vertex, this graph is solvable with the final peg being in (0, 0).

Proof

Due to symmetry it is sufficient to consider the case with holes in (i, 0) for $i\in [2,m]$. First, we start by removing pegs from (0, i) for $i\in [m]$ and most of the vertices from $A_0$ (except (1, 1)). This can be done by jumping

$$\begin{aligned} (0,i)\cdot (\overrightarrow{0,0})\cdot (i,0),(i,0)\cdot (\overrightarrow{i,i})\cdot (0,i),(i+1,i)\cdot (\overrightarrow{0,i})\cdot (0,0) \end{aligned}$$

for every $i\in [2,m]$ (where $m+1\equiv 1$) and $(0,1)\cdot (\overrightarrow{0,0})\cdot (2,0),(2,1)\cdot (\overrightarrow{2,0})\cdot (0,0)$. Now we can proceed as in the proof of Lemma 5 with the exception that we do not have to remove the pegs from $A_0\setminus \{(1,1)\}$.$\square$

The basic idea in proving the following theorem is first eliminating pegs from (i, 0) and (0, i) for $i\in [m]$. Next, the other pegs in the subgraph $K_{1,m}\,\square\, K_{1,m}$ will be removed. The last step is the elimination of the remaining pegs (i, j) for $i\in [m+1,n]$ (if $n>m$). If at least one of n and m is odd, we have to be particularly thorough. The occurring problems will be dealt with by reducing these cases to even n and m.

Theorem 5

The Cartesian product $K_{1,n}\,\square\, K_{1,m}$ is solvable for all $n,m\in {\mathbb {Z}}$.

Proof

If $m=1$ or $n=1$, the statement follows from Theorem 3. Thus, without loss of generality, we may assume $m,n \ge 2$ and $n\ge m$. Start with a hole in (0, 0). We distinguish four cases.

${{{\underline{\varvec{Case 1:}}}}}\, \underline{2\mid n, 2\mid m.}$ For $i\in [2,m]$, we eliminate the pegs from (i, 0) and (0, i) via the jumps

$$\begin{aligned} (i,i)\cdot (\overrightarrow{0,i})\cdot (0,0),(0,0)\cdot (\overrightarrow{i,0})\cdot (i,i). \end{aligned}$$

After the jump $(1,1)\cdot (\overrightarrow{0,1})\cdot (0,0)$, we eliminate all pegs from A and the peg in (1, 0) using Lemma 5, having pegs exactly in (0, 0) and all vertices (i, j) with $n\ge i>m\ge j\ge 0$. To eliminate these, for each $i=m+1,m+3,\dots ,n-1$, we perform the following steps.

• Use $\mathrm {EP}_1$ on the subgraph induced by the vertices

  $$\begin{aligned} (0,0), (0,1), (i,0), (i+1,0), (i,1), (i+1,1), \end{aligned}$$

  where a hole is in (0, 1) and the final peg is in (i, 0). After this process, the pegs in $(0,0),(i,1),(i+1,0)$ and $(i+1,1)$ are removed.

• For $j\in [2,m-1]$ use $\mathrm {EP}_5$ and $\mathrm {EP}_6$ alternatingly on the sugraphs induced by

  $$\begin{aligned} (0,j), (i,0), (i+1,0), (i,j), (i+1,j), \end{aligned}$$

  where the holes are in (0, j) and either in (i, 0) or $(i+1,0)$ (ending with the final peg in this one). After doing this for all j, together with the first step the pegs in $(0,0),(i,1),(i+1,0),(i+1,1)$ and all pegs in (i, j) and $(i+1,j)$ for $j\in [2,m-1]$ are removed.

• Finally, we use one of the elimination procedures $\mathrm {EP}_7$ and $\mathrm {EP}_8$ on the subgraph induced by

  $$\begin{aligned} (0,0), (0,m), (i,0), (i+1,0), (i,m), (i+1,m), \end{aligned}$$

  where the holes are in (0, 0), (0, m) and either in (i, 0) or $(i+1,0)$. Afterwards, all pegs in the vertices (i, j) and $(i+1,j)$ for $j \in [m]$ are eliminated and we can proceed with the next index i.

Case 2: $\underline{2\,\nmid\, n, 2\mid m.}$ We reduce the starting state to an intermediate state of Case 1 by eliminating all pegs from vertices (n, j) for all $j\in [0,m]$ (and some more). This can be done via jumping

$$\begin{aligned} (n,j)\cdot (\overrightarrow{n,0})\cdot (0,0),(0,j)\cdot (\overrightarrow{0,0})\cdot (n,0) \end{aligned}$$

for $j\in [2,m]$ and, finally, do $(n,1)\cdot (\overrightarrow{n,0})\cdot (0,0)$. Ignoring the vertices in question, we now have to solve $K_{1,n-1}\,\square\, K_{1,m}$ from a specific starting state. Using Lemma 6, we can eliminate all pegs from (i, 0) for $i\in [m]$ and all pegs from A, having pegs exactly in (0, 0) and all vertices (i, j) with $n-1\ge i>m\ge j\ge 0$. This situation is the same as in Case 1.

Case 3: $\underline{2\mid n, 2\,\nmid\, m.}$ We reduce the starting state to an intermediate state of Case 1 by eliminating all pegs from vertices (i, m) for all $i\in [0,n]$ (and some more). For every odd $i\in [m,n]$ we use $\mathrm {EP}_4$ on the subgraph induced by the vertices

$$\begin{aligned} (0,0), (i,0), (i+1,0), (0,m), (i,m), (i+1,m), \end{aligned}$$

where a hole is in (0, 0) and the final pegs are in (i, 0) and (0, m) (note that we also removed pegs from (i, 0) for even $i\in [m,n]$). Now we only need to take care of pegs in (i, m) for all $i\in [0,m-1]$. For every $i\in [2,m-1]$ we jump

$$\begin{aligned} (i,m)\cdot (\overrightarrow{0,m})\cdot (0,0),(i,0)\cdot (\overrightarrow{0,0})\cdot (0,m) \end{aligned}$$

and, finally, do $(1,m)\cdot (\overrightarrow{0,m})\cdot (0,0)$, obtaining a situation where all pegs in question are removed, but also pegs from (i, 0) for $i\in [2,m-1]$. This corresponds to the problem of solving $K_{1,n}\,\square\, K_{1,m-1}$ from a specific starting state. Using Lemma 6, we can eliminate all pegs from (0, i) for $i\in [m-1]$ and all pegs from A, leaving pegs exactly in (0, 0) and all vertices (i, j) with $n\ge i>m-1\ge j\ge 1$ and all vertices (i, 0) with odd $i\in [m,n]$. This situation is the same as in Case 1 except we have holes in (i, 0) for even $i\in [m,n]$. This can easily be dealt with by using $\mathrm {EP}_2$ instead of $\mathrm {EP}_1$.

Case 4: $\underline{2\,\nmid\, n, 2\,\nmid\, m.}$ We reduce the starting state to an intermediate state of Case 1 by eliminating all pegs from vertices (i, m) and (n, j) for all $i\in [0,n], j\in [0,m]$ (and some more). For each $j\in [m-1]$ we carry out the jumps

$$\begin{aligned} (n,j)\cdot (\overrightarrow{n,0})\cdot (0,0),(0,j)\cdot (\overrightarrow{0,0})\cdot (n,0). \end{aligned}$$

Next, we jump $(n,m)\cdot (\overrightarrow{0,m})\cdot (0,0)$. The second step is to remove pegs from (i, m) for $i\in [m,n]$. This can be done via the jumps

$$\begin{aligned} (i,0)\cdot (\overrightarrow{i,m})\cdot (0,m), (0,m)\cdot (\overrightarrow{0,0})\cdot (i,0), (i+1,m)\cdot (\overrightarrow{i+1,0})\cdot (0,0) \end{aligned}$$

for odd $i\in [m,n-1]$ (note that we also removed pegs from (i, 0) for even $i\in [m,n]$). We proceed with jumping $(n,0)\cdot (\overrightarrow{0,0})\cdot (0,m)$ and

$$\begin{aligned} (i,m)\cdot (\overrightarrow{0,m})\cdot (0,0), (i,0)\cdot (\overrightarrow{0,0})\cdot (0,m) \end{aligned}$$

for $i\in [2,m-1]$. After $(1,1)\cdot (\overrightarrow{1,0})\cdot (0,0), (0,m)\cdot (\overrightarrow{1,m})\cdot (1,0)$, we basically have the same situation as in Case 1 for the graph $K_{1,n-1}\,\square\, K_{1,m-1}$ before using Lemma 5 except we have holes in (i, 0) for even $i\in [m,n]$. This is dealt with as in Case 3.$\square$

Remark 1

With the ideas from above it should be possible to show that $K_{1,n}\,\square\, K_{1,m}$ is freely solvable. Since the details seem to become rather messy, we leave the verification of this conjecture as an open problem for interested researchers.

4 Open questions

We have shown that the Cartesian product of a Hamiltonian graph with even number of vertices and an arbitrary connected graph is solvable. Since Hamiltonian graphs with even number of vertices are solvable, this raises the question whether the Cartesian product of a solvable graph and an unsolvable graph (both connected) is solvable, which we believe to be true.

Conjecture 1

For any solvable graph G and any non trivial connected graph H, $G \,\square\, H$ is (freely) solvable.

In view of Theorem 5, because stars are, in a way, the most unsolvable graphs, we even believe the following much stronger statement to be true.

Conjecture 2

For any two connected non trivial graphs G and H, $G \,\square\, H$ is (freely) solvable.

We believe that this can be proven in a similar fashion as Theorem 3 via decomposing the graphs G and H into stars and paths and using the results we obtained about ladders, grids, and Cartesian products of stars. But the technical details seem very complicated.