Independent Domination Subdivision in Graphs

Abstract

A set S of vertices in a graph G is a dominating set if every vertex not in S is ad jacent to a vertex in S. If, in addition, S is an independent set, then S is an independent dominating set. The independent domination number i(G) of G is the minimum cardinality of an independent dominating set in G. The independent domination subdivision number $\hbox {sd}_{\mathrm{i}}(G)$ is the minimum number of edges that must be subdivided (each edge in G can be subdivided at most once) in order to increase the independent domination number. We show that for every connected graph G on at least three vertices, the parameter $\hbox {sd}_{\mathrm{i}}(G)$ is well defined and differs significantly from the well-studied domination subdivision number $\mathrm{sd_\gamma }(G)$. For example, if G is a block graph, then $\mathrm{sd_\gamma }(G) \le 3$, while $\hbox {sd}_{\mathrm{i}}(G)$ can be arbitrary large. Further we show that there exist connected graph G with arbitrarily large maximum degree $\Delta (G)$ such that $\hbox {sd}_{\mathrm{i}}(G) \ge 3 \Delta (G) - 2$, in contrast to the known result that $\mathrm{sd_\gamma }(G) \le 2 \Delta (G) - 1$ always holds. Among other results, we present a simple characterization of trees T with $\hbox {sd}_{\mathrm{i}}(T) = 1$.

1 Introduction

Domination subdivision in graphs is very well studied in the literature. In this paper, we study independent domination subdivisions in graphs. A set S of vertices in a graph G is a dominating set if every vertex not in S is adjacent to a vertex in S. If, in addition, S is an independent set, then S is an independent dominating set, abbreviated ID-set, of G. The domination number, denoted $\gamma (G)$, of G is the minimum cardinality of a dominating set of G, and the independent domination number, denoted i(G), of G is the minimum cardinality of an ID-set in G. An independent set of vertices in a graph G is a dominating set of G if and only if it is a maximal independent set. Thus, i(G) is equivalently the minimum cardinality of a maximal independent set of vertices in G. An ID-set of cardinality i(G) is called an i-set of G. A survey on independent domination in graphs can be found in [6].

An edge uw in a graph G is subdivided by deleting the edge uw, and adding a new vertex v and two new edges uv and vw. The added vertex v of degree 2 is called a subdivision vertex. The domination subdivision number of a connected graph G of order at least 3, denoted $\mathrm{sd_\gamma }(G)$, is the minimum number of edges that must be subdivided (where no edge in G can be subdivided more than once) in order to create a graph whose domination number exceeds that of G. The domination subdivision number of a graph G was first formally defined in the 2000 paper by Haynes, Hedetniemi and Hedetniemi [7], although the concept is attributed by the authors in [7] to Arumugan, and studied further, for example, in [1, 4, 8, 12].

The independent domination subdivision number of a connected graph G of order at least 3, denoted $\hbox {sd}_{\mathrm{i}}(G)$, is the minimum number of edges that must be subdivided (where no edge in G can be subdivided more than once) in order to create a graph whose independent domination number exceeds that of G. This parameter was introduced by Sharada and Soner at an international conference on discrete mathematics in India in 2008, and subsequently studied by them in their 2010 paper [11] in which they characterize the trees T satisfying $\hbox {sd}_{\mathrm{i}}(T) = 3$.

Although the independent domination subdivision number differs significantly from the well-studied domination subdivision number, it has not received as much attention in the literature. In this paper, we provide a more in-depth study of the independent domination subdivision number of a graph. We proceed as follows. In Sect. 1.1 we provide the necessary graph theory notation and terminology. Our main results are presented in Sect. 2, and selected known results are given in Sect. 3. In Sect. 4, we present a general upper bound on the independent domination subdivision number. In Sects. 5 and 6 we study the independent domination subdivision number of special classes of graphs such as complete bipartite graphs and block graphs. In Sect. 7, we characterize trees T with $\hbox {sd}_{\mathrm{i}}(T) = 1$.

1.1 Notation

For notation and graph theory terminology we generally follow [9]. Specifically, let G be a graph with vertex set V(G) of order $n(G) = |V(G)|$ and edge set E(G) of size $m(G) = |E(G)|$. If G is clear from the context, we simply write V and E rather than V(G) and E(G). A neighbor of a vertex v in G is a vertex adjacent to v. The open neighborhood of a vertex v in G, denoted $N_G(v)$, is the set of all neighbors of v in G, while the closed neighborhood of v is the set $N_G[v] = N_G(v) \cup \{v\}$. If the graph G is clear from the context, we write N(v) and N[v] rather than $N_G(v)$ and $N_G[v]$, respectively. We denote the degree of a vertex v in G by $d_G(v) = |N_G(v)|$. A vertex of degree 1 in G is a leaf of G, and a vertex with a leaf neighbor is a support vertex of G. A strong support vertex of G is a support vertex with at least two leaf neighbors. The minimum and maximum degrees among all vertices of G are denoted by $\delta (G)$ and $\Delta (G)$, respectively.

For a set $S \subset V(G)$ of vertices in a graph G and a vertex $v \in S$, we define the S -external private neighborhood of a vertex v, abbreviated $\mathrm{epn}_G(v,S)$, as the set of all vertices in $V(G) {\setminus } S$ that are adjacent to v but to no other vertex of S; that is, $\mathrm{epn}_G(v,S) = \{w \in V(G) {\setminus } S \mid N_G(w) \cap S = \{v\}\}$. We define an S-external private neighbor of v to be a vertex in $\mathrm{epn}_G(v,S)$.

The distance between two vertices u and v in a connected graph G, denoted $d_G(u,v)$ or simply d(u, v) if the graph G is clear from context, is the minimum length of a (u, v)-path in G. The diameter of G is the maximum distance among all pairs of vertices of G. The distance from a vertex v to the set S in G, denoted by $d_G(v,S)$, is the minimum distance from v to a vertex of S; that is, $d_G(v,S) = \min \{d(u,v) \mid u \in S\}$.

We denote the path and cycle on n vertices by $P_n$ and $C_n$, respectively. A complete graph on n vertices is denoted by $K_n$, while a complete bipartite graph with partite sets of size n and m is denoted by $K_{n,m}$. A star is the graph $K_{1,k}$, where $k \ge 1$. A double star is a tree with exactly two (adjacent) non-leaf vertices. Further if one of these vertices is adjacent to $\ell _1$ leaves and the other to $\ell _2$ leaves, then we denote the double star by $S(\ell _1,\ell _2)$. For example, the double star S(1, 1) is the path $P_4$. A block graph is a graph in which every block is a complete graph. In particular, every tree is a block graph.

A rooted tree T distinguishes one vertex r called the root. For each vertex $v \ne r$ of T, the parent of v is the neighbor of v on the unique (r, v)-path, while a child of v is any other neighbor of v. The set of children of v is denoted by C(v). A descendant of v is a vertex $u \ne v$ such that the unique (r, u)-path contains v. In particular, every child of v is a descendant of v. A grandchild of v is the descendant of v at distance 2 from v. We let D(v) denote the set of descendants of v, and we define $D[v] = D(v) \cup \{v\}$.

We use the standard notation $[k] = \{1,\ldots ,k\}$.

2 Main Result

In this paper, we continue the study of the independent domination subdivision number of a graph. We first establish a general upper bound on the independent domination subdivision number of a connected graph of order at least 3 in terms of its maximum degree and its independent domination number.

Theorem 2.1

If G is a connected graph of order at least 3, then $\hbox {sd}_{\mathrm{i}}(G) \le \Delta (G) \cdot i(G)$.

As a consequence of Theorem 2.1, the independent domination subdivision number is well defined on the class of connected graphs of order at least 3. We state this formally as follows.

Corollary 2.2

For every connected graph G of order at least 3, the parameter $\hbox {sd}_{\mathrm{i}}(G)$ is well defined.

We next determine the independent domination subdivision number of a complete regular bipartite graph.

Theorem 2.3

For $k \ge 4$, $\hbox {sd}_{\mathrm{i}}(K_{k,k}) = 3k-2$.

As a consequence of Theorem 2.3, we remark that $\hbox {sd}_{\mathrm{i}}(G)$ can be arbitrarily large, even when restricted to the class of connected bipartite graphs G.

Corollary 2.4

There exist connected graphs G with arbitrarily large maximum degree $\Delta (G)$ such that $\hbox {sd}_{\mathrm{i}}(G) \ge 3 \Delta (G) - 2$.

The following result shows that the independent domination subdivision number can be arbitrary large, even for the classes of block graphs.

Theorem 2.5

There exist block graphs G such that $\hbox {sd}_{\mathrm{i}}(G) = k$ for any arbitrary positive (fixed) integer k.

Our final aim is to give a simple characterization of trees T with $\hbox {sd}_{\mathrm{i}}(T) = 1$. For this purpose, let $\mathcal{N}(T)$ be the set of vertices in the tree T that belong to no i-set of T; that is,

$$\begin{aligned} \mathcal{N}(T) = \{ v \in V(T) \mid v \text{ is } \text{ in } \text{ no } \text{ i-set } \text{ of } T \}. \end{aligned}$$

Theorem 2.6

For a tree T of order at least 3, $\hbox {sd}_{\mathrm{i}}(T) = 1$ if and only if T has at least one of the following two properties.

$P_1$::

A leaf of T belongs to the set $\mathcal{N}(T)$.

$P_2$::

An edge of T has both its ends in $\mathcal{N}(T)$.

3 Known Results

In 2000 Haynes, Hedetniemi, and Hedetniemi [7] established the following upper bound on the domination subdivision number of a graph.

Theorem 3.1

[7] Let G be a connected graph of order $n \ge 3$. If u and v are two arbitrary adjacent vertices each having degree at least 2, then $\mathrm{sd_\gamma }(G) \le d_G(u) + d_G(v) - 1$.

As a consequence of Theorem 3.1, the domination subdivision number $\mathrm{sd_\gamma }(G)$ is defined for every connected graph G of order $n \ge 3$. As a further consequence of Theorem 3.1, we have the following upper bound on the domination subdivision number of a graph.

Corollary 3.2

[7] If G is a connected graph of order $n \ge 3$, then $\mathrm{sd_\gamma }(G) \le \delta (G) + \Delta (G) - 1$.

In 2008 Favaron et al. [5] gave a construction showing that the domination subdivision number can be made arbitrarily large.

Theorem 3.3

[5] For each pair of positive integers r and q such that $r + q \ge 4$, there exists a graph G with $\delta (G) = r$ and $\mathrm{sd_\gamma }(G) \ge r + q$.

Dettlaff [3] proved in her PhD thesis that the domination subdivision number of a block graph G is at most 3.

Theorem 3.4

[3] If G is a block graph, then $1 \le \mathrm{sd_\gamma }(G) \le 3$.

As an immediate consequence of Theorem 3.4, we have that if T is a tree, then $1 \le \mathrm{sd_\gamma }(T) \le 3$. Recall that $P_n$ denotes a path on n vertices. For $n \ge 3$, we note that $i(P_n) = \lceil n/3 \rceil$, implying the following result first observed by Sharada and Soner [11].

Observation 3.5

[11] For $n \ge 3$,

$$\begin{aligned} \hbox {sd}_{\mathrm{i}}(P_n) = \left\{ \begin{array}{lc} 1 &{} \text{ if } n \equiv 0 \, (\mathrm{mod}\, 3) \\ 3 &{} \text{ if } n \equiv 1 \, (\mathrm{mod}\, 3) \\ 2 &{} \text{ if } n \equiv 2 \, (\mathrm{mod}\, 3). \\ \end{array} \right. \end{aligned}$$

4 A General Upper Bound

We note that if $G = K_2$, then the independent domination number of G does not change when its only edge is subdivided. Further we note that it possible that the subdivision of an edge in a connected graph may decrease its independent domination number. For example, if $k \ge 2$ and G is a tree with exactly two non-leaf vertices both of which have k leaf neighbors, that is, if G is a double star S(k, k), then $i(G) = k+1$ but subdividing the edge joining the two non-leaf vertices produces a graph $G^*$ with $i(G^*) = 2 < i(G)$.

However we show that the independent domination subdivision number is well defined on the class of connected graphs of order at least 3. For each such graph, we show there always exists some set of edges that can be subdivided (where each edge can be subdivided at most once) in order to increase its independent domination number.

Theorem 4.1

If G is a connected graph of order at least 3, then there exists an i-set I of G such that the graph $G^*$ obtained from G by subdividing every edge incident with a vertex of I satisfies $i(G^*) > i(G)$.

Proof

Let G be a connected graph of order $n \ge 3$. Let I be an i-set of G with the minimum possible number of vertices of degree 1, and let ${\bar{I}}$ be the complement of the set I, and so ${\bar{I}} = V(G) {\setminus } I$. We proceed further with the following claim. $\square$

Claim 1

At least one vertex of I is not a leaf.

Proof

Suppose, to the contrary, that every vertex of I is a leaf. If two vertices of I have a common neighbor, say v, then the set $(I {\setminus } N_G(v)) \cup \{v\}$ is an ID-set of G of cardinality less than |I|, contradicting the minimality of the set I. Hence, no two vertices of I have a common neighbor. Thus, $|I| = |{\bar{I}}| = \frac{1}{2}n$ and each vertex outside I has a unique neighbor in I. Let x be an arbitrary vertex of I, and let y be its unique neighbor (in ${\bar{I}}$). Since G is a connected graph of order at least 3, we note that the vertex y has degree at least 2 in G. Thus the set $(I {\setminus } \{x\}) \cup \{y\}$ is a i-set of G that contains fewer leaves than the set I, contradicting our choice of the set I. $\square$

By Claim 1, at least one vertex in the independent set I has degree 2 or more in the graph G. Let

$$\begin{aligned} I_1 = \{v \in I \mid d_G(v) = 1\} \end{aligned}$$

and let $I_2 = I {\setminus } I_1$. By our earlier observations, $|I_2| \ge 1$. Possibly, $I_1 = \emptyset$. Let $G^*$ be the graph obtained from G by subdividing every edge incident with a vertex of I. For each vertex $v \in I$, let

$$\begin{aligned} N^*_v = N_{G^*}(v) \end{aligned}$$

be the set consisting of all neighbors of the vertex v in $G^*$. Every independent dominating set of $G^*$ must contain at least one vertex in $N_{G^*}[v] = N^*_v \cup \{v\}$ in order to dominate the vertex v for every vertex $v \in I$. Thus, $i(G^*) \ge |I| = i(G)$. We show that $i(G^*) > i(G)$. Suppose, to the contrary, that $i(G^*) = i(G)$. Let $I^*$ be an i-set of $G^*$, and so $I^*$ is an ID-set of $G^*$ and $|I^*| = i(G^*) = |I|$. In what follows we present a series of claims describing some structural properties of G which culminate in the implication of its non-existence.

Claim 2

$I_2 \subseteq I^*$.

Proof

Suppose, to the contrary, that the vertex $v \in I_2$ does not belong to the set $I^*$ for some vertex $v \in I$. By definition of the set $I_2$, we note that $d_G(v) \ge 2$. Let $v_1,v_2, \ldots , v_k$ be the neighbors of v in the graph $G^*$. We note that the set $N^*_v = \{v_1,,v_2,\ldots ,v_k\}$ of neighbors of v in $G^*$ is an independent set, and each vertex in this set is a subdivided vertex of degree 2.

By supposition, $v \notin I^*$. Renaming vertices if necessary, we may assume that $v_1 \in I^*$ in order to dominate the vertex v. We note that every vertex in I is at distance at least 4 from every other vertex of I in the graph $G^*$. In particular, for distinct vertices x and y in I, the sets $N^*_x$ and $N^*_y$ are disjoint and there is no edge joining a vertex in $N^*_x$ and a vertex in $N^*_y$. In order to dominate the vertex $v_2$, either $v_2 \in I^*$ or the (unique) neighbor of $v_2$ that belongs to the set ${\bar{I}}$ belongs to the set $I^*$. Thus, the set $I^*$ contains at least one vertex from each of the sets $N_{G^*}[w]$ for every vertex $w \in I {\setminus } \{v\}$, and contains at least two additional vertices to dominate the vertices in $N_{G^*}[v]$. Therefore, $|I^*| \ge |I| + 1$, contradicting our supposition that $|I^*| = |I|$. $\square$

By Claim 2, $I_2 \subseteq I^*$.

Claim 3

The set $I_1$ dominates the set ${\bar{I}}$ in the graph G.

Proof

Suppose, to the contrary, that there is a vertex $w \in {\bar{I}}$ that is adjacent to no vertex of $I_1$ in the graph G. Thus, no neighbor of a vertex in the set $I_1$ is adjacent to the vertex w in the graph $G^*$. Therefore, the vertex w is not dominated by any vertex in $I^*$ that belongs to one of the sets $N^*_x$ for every $x \in I_1$. By Claim 2, we have $I_2 \subseteq I^*$, implying that $I^* \cap N^*_v = \emptyset$ for every vertex $v \in I_2$. Thus, no vertex of $I^*$ belongs to one of the sets $N^*_x$ for every $x \in I_2$. Thus, in order to dominate the vertex w in $G^*$, the set $I^*$ must contain at least one vertex that belongs to the set ${\bar{I}}$, implying that $|I^*| \ge |I| + 1$, a contradiction. $\square$

By Claim 3, the set $I_1$ dominates the set ${\bar{I}}$ in the graph G. Thus, every vertex in ${\bar{I}}$ has at least one neighbor in G that belong to the set $I_1$.

Claim 4

Every vertex in ${\bar{I}}$ has at least one neighbor in G that belong to the set $I_2$.

Proof

Suppose, to the contrary, that there is a vertex $w \in {\bar{I}}$ that has no neighbor in G that belongs to the set $I_2$. Let $I_w$ be the set of neighbors of w that belong to the set I, that is, $I_w = I \cap N_G(w)$. By supposition, every neighbor of w in I belongs to the set $I_1$ noting that I is a dominating set of G. Thus, $I_w \subseteq I_1$ and $|I_w| \ge 1$. Since G is a connected graph of order at least 3, we note that the vertex w has degree at least 2 in G. The set $I^*_w = (I {\setminus } I_w) \cup \{w\}$ is an ID-set of G, implying by our earlier observations that $i(G) \le |I^*_w| = |I| - |I_w| + 1 \le |I| = i(G)$. Hence we must have equality throughout this inequality chain. In particular, this implies that $|I_w| = 1$ and the set $I^*_w$ is an i-set of G. However, the set $I^*_w$ contains fewer vertices of degree 1 that does the set I, contradicting our choice of the set I. $\square$

By Claim 3, every vertex in ${\bar{I}}$ has at least one neighbor in G that belong to the set $I_1$. By Claim 4, every vertex in ${\bar{I}}$ has at least one neighbor in G that belong to the set $I_2$. Let w be an arbitrary vertex in ${\bar{I}}$ and let $I_w$ be the set of neighbors of w in G that belong to the set I, that is,

$$\begin{aligned} I_w = I \cap N_G(w). \end{aligned}$$

Thus, $|I_w| = |I_w \cap I_1| + |I_w \cap I_2| \ge 1 + 1 = 2$. The set $I^*_w = (I {\setminus } I_w) \cup \{w\}$ is an ID-set of G of cardinality $|I^*_w| = |I| - |I_w| + 1 \le |I| - 2 + 1 < |I|$, contradicting the minimality of the set I. This completes the proof of Theorem 4.1. $\square$

Theorem 2.1 now follows as an immediate consequence of Theorem 4.1.

5 Complete Bipartite Graphs

In this section, we show that the independent domination subdivision number can be arbitrary large, even for special classes of graphs such as connected bipartite graph. We also show that the independent domination subdivision number differs significantly from the domination subdivision number. The following result determines the independent domination subdivision number of a complete bipartite graph.

Theorem 5.1

For $k \ge 2$,

$$\begin{aligned} \hbox {sd}_{\mathrm{i}}(K_{k,k}) = \left\{ \begin{array}{ll} 3k-3 &{} \text{ if } \; k \in \{2,3\} \quad \\ 3k-2 &{} \text{ if } \; k \ge 4. \\ \end{array} \right. \end{aligned}$$

Proof

For $k \ge 2$, let $G \cong K_{k,k}$ and let X and Y be the partite sets of G. If $k = 2$, then $K_{k,k} = C_4$ and $\hbox {sd}_{\mathrm{i}}(C_4) = 3 = 3(k-1)$. Hence in what follows, we may assume that $k \ge 3$. We note that $i(G) = k$ and that both X and Y are i-sets of G. We establish first a lower bound on $\hbox {sd}_{\mathrm{i}}(G)$. $\square$

Claim 5

If $k = 3$, then $\hbox {sd}_{\mathrm{i}}(G) \ge 3k-3$, while if $k \ge 4$, then $\hbox {sd}_{\mathrm{i}}(G) \ge 3k-2$.

Proof

Let $E'$ be a smallest possible set of edges of G that need to be subdivided in order to increase the independent domination number of G. Thus, $E' \subseteq E(G)$ and $\hbox {sd}_{\mathrm{i}}(G) = |E'|$. We show that $|E'| \ge 3(k-1)$. Let $G'$ be a graph obtained from G by subdividing the edges in the set $E'$. By our choice of the set $E'$, we note that $i(G') > i(G) = k$.

If the set X is a dominating set of $G'$, then since X is an independent set it is an ID-set of $G'$, implying that $i(G') \le |X| = i(G)$, a contradiction. Hence, the set X is not a dominating set of $G'$. Therefore there must exist a vertex $y \in Y$ not dominated by the set X in $G'$. This implies that every edge incident with y in G is subdivided when constructing $G'$. Analogously, reversing the roles of X and Y, we have that the set Y is not a dominating set of $G'$ and there must exist a vertex $x \in X$ such that every edge incident with x in G is subdivided when constructing $G'$. Let $E_x$ and $E_y$ be the edges of G incident with x and y, respectively. Thus, $E_x \cup E_y \subseteq E'$ and every edge of $E_x \cup E_y$ is subdivided when constructing $G'$. We note that $|E_x \cup E_y| = d_G(x) + d_G(y) - 1 = 2k - 1$. Let $X = \{x_1,x_2, \ldots , x_k\}$ and $Y = \{y_1,y_2, \ldots , y_k\}$, where $x = x_1$ and $y = y_1$. Let $Y_1 = Y {\setminus } \{y_1\}$ and let $X_1 = X {\setminus } \{x_1\}$.

Claim 5.1

If no vertex in $X_1$ dominates the set $Y_1$ or if no vertex in $Y_1$ dominates the set $X_1$, then $\hbox {sd}_{\mathrm{i}}(G) \ge 3k-2$.

Proof

Suppose that no vertex in $X_1$ dominates the set $Y_1$. This implies that at least one edge joining each vertex of $X_1$ with some vertex of $Y_1$ is subdivided when constructing the graph $G'$. Since the set $X_1$ is an independent set, at least $|X_1|$ such edges are subdivided. Further each such edge incident with a vertex of $X_1$ and a vertex of $Y_1$ does not belong to the set $E_x \cup E_y$. Hence, $|E'| \ge |E_x \cup E_y| + |X_1| = (2k-1) + (|X| - 1) = (2k-1) + (k - 1) = 3k-2$. Analogously interchanging the roles of X and Y, if no vertex in $Y_1$ dominates the set $X_1$, then $|E'| \ge 3k-2$. The desired result follows noting that $\hbox {sd}_{\mathrm{i}}(G) = |E'|$. $\square$

By Claim 5.1, we may assume that there exists a vertex $x' \in X_1$ that dominates the set $Y_1$, for otherwise $\hbox {sd}_{\mathrm{i}}(G) \ge 3k-2$ and the desired result follows. Analogously interchanging the roles of X and Y, we may assume that there exists a vertex $y' \in Y_1$ that dominates the set $X_1$. Renaming vertices if necessary, we may assume that $x' = x_2$ and $y' = y_2$. Thus, the only edge incident with $x_2$ in G that is subdivided when constructing $G'$ is the edge $x_2y_1$, and the only edge incident with $y_2$ in G that is subdivided when constructing $G'$ is the edge $x_1y_2$. We note that the vertex $x_2$ dominates the set $Y_1$ in $G'$, and the vertex $y_2$ dominates the set $X_1$ in $G'$.

Let $X_2 = X {\setminus } \{x_1,x_2\}$ and let $Y_2 = Y {\setminus } \{y_1,y_2\}$. Let $y_{1,i}$ be the subdivided vertex of $G'$ corresponding to the edge $x_iy_1$ of G for $i \in [k]$. If the set $X_2$ dominates the set $Y_2$ in $G'$, then the set $X_2 \cup \{x_1,y_{1,2}\}$, for example, is an ID-set of $G'$ noting that the set $X_2$ dominates the vertex $y_2$, implying that $i(G') \le |X_2| + |\{x_1,y_{1,2}\}| = |X_2| + 2 = |X| = i(G)$, a contradiction. Hence, the set $X_2$ does not dominates the set $Y_2$ in $G'$. Therefore there must exist a vertex $y'' \in Y_2$ not dominated by the set $X_2$ in $G'$. This implies that every edge joining $y''$ with a vertex of $X_2$ in G is subdivided when constructing $G'$. Analogously interchanging the roles of X and Y, the set $Y_2$ does not dominates the set $X_2$ in $G'$, implying that there must exist a vertex $x'' \in X_2$ not dominated by the set $Y_2$ in $G'$. This implies that every edge joining $x''$ with a vertex of $Y_2$ in G is subdivided when constructing $G'$. Renaming vertices if necessary, we may assume that $x'' = x_3$ and $y'' = y_3$.

Let $E_{x_3}$ be the set of edges of G joining $x_3$ with vertices of $Y_2$, and let $E_{y_3}$ be the set of edges of G joining $y_3$ with vertices of $X_2$. Thus, $E_{x_3} \cup E_{y_3} \subset E'$ and every edge of $E_{x_3} \cup E_{y_3}$ is subdivided when constructing $G'$. We note that $|E_{x_3} \cup E_{y_3}| = (k - 2) + (k-2) - 1 = 2k-5$. By our earlier observations, $E_x \cup E_y \cup E_{x_3} \cup E_{y_3} \subseteq E'$, and so $\hbox {sd}_{\mathrm{i}}(G) = |E'| \ge |E_x \cup E_y \cup E_{x_3} \cup E_{y_3}| = |E_x \cup E_y| + |E_{x_3} \cup E_{y_3}| = (2k-1) + (2k-5) = 4k-6$. Thus if $k = 3$, then $\hbox {sd}_{\mathrm{i}}(G) \ge 4k-6 = 3k-3$, while if $k \ge 4$, then $\hbox {sd}_{\mathrm{i}}(G) \ge 4k-6 \ge 3k-2$. This completes the proof of Claim 5. $\square$

Claim 6

If $k = 3$, then $\hbox {sd}_{\mathrm{i}}(G) \le 3k-3$.

Proof

Let $X = \{x_1,x_2,x_3\}$ and $Y = \{y_1,y_2,y_3\}$. Let $x = x_1$ and $y = y_1$, and let $E_{x}$ and $E_{y}$ be the set of edges of G incident with x and y, respectively. Let $E^* = E_x \cup E_y \cup \{x_2y_2\}$. Let $G^*$ be the graph obtained from G by subdividing the edges of G that belong to the set $E^*$. Let $y_{1,i}$ be the subdivided vertex of $G^*$ resulting from subdividing the edge $x_iy_1$ for $i \in [3]$, and let $x_{1,i}$ be the subdivided vertex of $G^*$ resulting from subdividing the edge $x_1y_i$ for $i \in [3]$. We note that $x_{1,1} = y_{1,1}$. Let w be the subdivided vertex of $G^*$ resulting from subdividing the edge $x_2y_2$. We show that $i(G^*) > i(G) = 3$. Let $I^*$ be an i-set of $G^*$.

In order to dominate the vertex $x_{1,1}$, we have that $I^* \cap \{x_1,y_1,x_{1,1}\} \ne \emptyset$. If $x_{1,1} \in I^*$, then in order to dominate the four subdivided vertices incident with x or y different from $x_{1,1}$, we need at least four additional vertices in $I^*$, and so in this case $|I^*| \ge 5$. If $\{x,y\} \subset I^*$, then we need at least two additional vertices in $I^*$ to dominate the four vertices in $\{x_2, x_3, y_2, y_3\}$, and so $|I^*| \ge 4$. Hence, we may assume that exactly one of x and y belong to the set $I^*$, for otherwise $|I^*| \ge 4$, as desired. By symmetry, we may assume that $x \in I^*$. In order to dominate the vertex y, at least one of $y_{1,2}$ and $y_{1,3}$ belongs to $I^*$. If $y_{1,2} \in I^*$, then we need at least two additional vertices in $I^*$ to dominate w and $y_3$, while if $y_{1,3} \in I^*$, then we need at least two additional vertices in $I^*$ to dominate $y_{1,2}$ and $y_2$. Thus in both cases, $|I^*| \ge 4$. Hence, $i(G^*) = |I^*| \ge 4 > i(G)$, implying that $\hbox {sd}_{\mathrm{i}}(G) \le |E^*| = 6 = 3k - 3$. $\square$

Claim 7

If $k \ge 4$, then $\hbox {sd}_{\mathrm{i}}(G) \le 3k-2$.

Proof

Let $X = \{x_1,x_2, \ldots , x_k\}$ and $Y = \{y_1,y_2, \ldots , y_k\}$. Let $x = x_1$ and $y = y_1$, and let $E_{x}$ and $E_{y}$ be the set of edges of G incident with x and y, respectively. Let $e_i = x_iy_i$ for $i \in [k]$, and let $E' = \{e_2,\ldots ,e_{k}\}$. Let $E^* = E_{x} \cup E_{y} \cup E'$. We note that $|E^*| = |E_{x} \cup E_{y}| + |E'| = (2k-1) + (k-1) = 3k-2$. Let $G^*$ be the graph obtained from G by subdividing the edges of G that belong to the set $E^*$. Let $y_{1,i}$ be the subdivided vertex of $G^*$ resulting from subdividing the edge $x_iy_1$ for $i \in [k]$, and let $x_{1,i}$ be the subdivided vertex of $G^*$ resulting from subdividing the edge $x_1y_i$ for $i \in [k]$. We note that $x_{1,1} = y_{1,1}$. The set $X \cup \{y_1\}$ is an ID-set of $G^*$ (as is the set $Y \cup \{x_1\}$), and so $i(G^*) \le |X| + 1 = k+1 = i(G) + 1$. We show that $i(G^*) = k+1 = i(G) + 1$.

Let $N_x$ and $N_y$ be the set of subdivided vertices adjacent to x and y, respectively, in $G^*$, and so $N_x=\{x_{1,i} \mid i\in [k]\}$ and $N_y=\{y_{1,i} \mid i\in [k]\}$. Let $w_i$ be the subdivided vertex in $G'$ corresponding to the edge $x_iy_i$ of G for $i \in [k]$. In particular, we note that $N_x \cap N_y = \{w_1\}$, and so $w_1 = x_{1,1} = y_{1,1}$. Let $Y_1 = Y {\setminus } \{y_1\}$ and let $X_1 = X {\setminus } \{x_1\}$. Let $I^*$ be an i-set of $G^*$. In order to dominate the vertex $w_1$, we have that $I^* \cap \{x_1,y_1,w_1\} \ne \emptyset$.

Suppose firstly that $I^* \cap \{x,y\} = \emptyset$. In this case, $w_1 \in I^*$. Since $x \notin I^*$ and $y \notin I^*$, in order to dominate the $2(k-1)$ subdivided vertices in $G^*$ that belong to the set $(N_x \cup N_y) {\setminus } \{w_1\}$, we need at least $2(k-1)$ additional vertices in $I^*$, implying that $|I^*| \ge 1 + 2(k-1) = 2k - 1 \ge k + 1$.

Suppose secondly that $|I^* \cap \{x,y\}| = 1$, and so $w_1 \notin I^*$. By symmetry, we may assume that $x \in I^*$, and so $y \notin I^*$. In order to dominate $k-1$ vertices in $N_y {\setminus } \{w_1\}$ we note that $|I^* \cap \{x_i,y_{1,i}\}| = 1$ for each $i \in [k] {\setminus } \{1\}$. Further in order to dominate the vertex y, we note that $I^* \cap (N_y {\setminus } \{w_1\}) \ne \emptyset$. Renaming vertices if necessary, we may assume that the vertex $y_{1,2} \in I^*$, and so $x_2 \notin I^*$. But then at least one additional vertex is needed in $I^*$ in order to dominate the subdivided vertex $w_2$ in $G^*$, implying that $|I^*| \ge 1 + (|N_y| - 1) + 1 = |N_y| + 1 = k + 1$.

Suppose thirdly that $\{x,y\} \subset I^*$. In this case, we need at least $k-1$ additional vertices in $I^*$ to dominate the $k-1$ vertices $w_2, w_3, \ldots , w_k$. Therefore, $|I^*| \ge 2 + (k-1) = k+1$. In all cases, we have shown that $i(G^*) = |I^*| \ge k+1 > i(G)$, implying that $\hbox {sd}_{\mathrm{i}}(G) \le |E^*| = 3k-2$. $\square$

The desired result of Theorem 5.1 now follows immediately from Claims 5, 6, and 7 . $\square$

Theorem 2.3 is a special case of Theorem 5.1 when $k \ge 4$. By Theorem 2.3, we remark that the result of Theorem 3.1 for the domination subdivision number does not hold for the independent domination subdivision number. Thus, the independent domination subdivision number differs significantly from the domination subdivision number.

6 Block Graphs

We consider next the class of block graphs, where we recall that a block graph is a graph in which every block is a complete graph. In this section we prove Theorem 2.5. Recall its statement.

Theorem 2.5. There exist block graphs G such that $\hbox {sd}_{\mathrm{i}}(G) = k$ for any arbitrary (fixed) positive integer k.

Proof

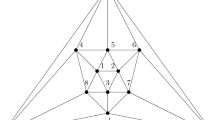
For $k = 1$, we take $G = P_n$ where $n \equiv 0 \, (\mathrm{mod}\, 3)$. For $k = 2$, we take $G = P_n$ where $n \equiv 2 \, (\mathrm{mod}\, 3)$, while for $k = 3$, we take $G = P_n$ where $n \equiv 1 \, (\mathrm{mod}\, 3)$. By Observation 3.5, we note that $\hbox {sd}_{\mathrm{i}}(G) = k$ in each of these cases. Hence, we may assume that $k \ge 4$, for otherwise the result is immediate. For $k \ge 4$, let $G_k$ be obtained from a complete graph $F \cong K_k$ on k vertices with vertex set $V(F) = \{v_1, v_2, \ldots , v_k\}$ by attaching k pendant edges to each vertex of the complete graph F. For example, when $k = 4$ the graph $G_k$ is illustrated in Fig. 1, where the darkened vertices form an i-set of $G_4$. We note that $i(G_k) = 1 + (k-1)k = k^2 - k + 1$ since every i-set of $G_k$ contains one vertex of F and all $(k-1)k$ leaves of $G_k$ not adjacent to the selected vertex of F.

Fig. 1

The graph $G_4$

We show firstly that $\hbox {sd}_{\mathrm{i}}(G) \ge k$. Let $E' \subset E(G_k)$ be an arbitrary subset of $k-1$ edges. Let $G'$ be the graph obtained from G by subdividing the $k-1$ edges in the set $E'$.

Suppose firstly that $E'$ contains at least one edge of the complete graph F. Renaming vertices if necessary, we may assume that $v_1v_2 \in E'$. Let v be the subdivided vertex in $G'$ resulting from subdividing the edge $v_1v_2$. Let W be the set of $k-2$ subdivided vertices of $G'$ different from v. Let $W_1$ be the set of subdivided vertices of $G'$ resulting from subdividing pendant edges of G incident with $v_1$ or $v_2$ (possibly, $W_1 = \emptyset$). Let $W_2$ be the set of vertices in $W {\setminus } W_1$ that have a leaf neighbor in $G'$, and let $W_3$ be the set of vertices in $W {\setminus } (W_1 \cup W_2)$ that are adjacent to neither $v_1$ nor $v_2$ in $G'$. We note that $|W_1| + |W_2| + |W_3| \le |W|$. Let $L_1$ be the set of leaves of $G'$ incident with a vertex in $W_1$, and let $L_2$ be the set of leaves in $G'$ adjacent to a vertex in $V(F) {\setminus } \{v_1,v_2\}$. We note that $|L_1| = |W_1|$, $|L_2| = (k-2)k - |W_2|$. We now consider the set

$$\begin{aligned} D = \{v_1,v_2\} \cup L_1 \cup L_2 \cup W_2 \cup W_3. \end{aligned}$$

The set D is an ID-set of $G'$, and so

$$\begin{aligned} \begin{array}{lcl} i(G') \le |D| &{} = &{} 2 + |L_1| + |L_2| + |W_2| + |W_3| \quad \\ &{} = &{} 2 + |W_1| + ((k-2)k - |W_2|) + |W_2| + |W_3| \quad \\ &{} = &{} 2 + |W_1| + (k-2)k + |W_3| \quad \\ &{} \le &{} k^2 - 2k + 2 + |W| \quad \\ &{} = &{} k^2 - 2k + 2 + (k-2) \quad \\ &{} = &{} k^2 - k \quad \\ &{} < &{} k^2 - k + 1 \quad \\ &{} = &{} i(G_k). \end{array} \end{aligned}$$

This, if $E'$ contains at least one edge of the complete graph F, then $i(G') < i(G_k)$, a contradiction. Hence, $E'$ contains no edge from the complete graph F. Thus, every edge of $E'$ is a pendant edge of G. Since $|E'| < k$, at least one vertex of F is such that none of its incident pendant edges belong to the set $E'$. Renaming vertices if necessary, we may assume that $v_1$ is such a vertex of F. In this case, we let L consist of all leaves of G that are not adjacent to $v_1$. The set $L \cup \{v_1\}$ is an ID-set of $G'$, implying that $i(G') \le |L| + 1 = (k-1)k + 1 = k^2 - k + 1 = i(G_k)$. Thus, if $E' \subset E(G_k)$ is an arbitrary subset of $k-1$ edges, then we have shown that removing the set of edges $E'$ from $G_k$ does not increase the independent domination number. This proves that $\hbox {sd}_{\mathrm{i}}(G) \ge k$, as desired.

To prove that $\hbox {sd}_{\mathrm{i}}(G) \le k$, let $u_i$ be an arbitrary leaf neighbor of the vertex $v_i$ in G for all $i \in [k]$. Let $e_i = u_iv_i$ for $i \in [k]$, and let $E^* = \{e_1,e_2, \ldots , e_k\}$. Let $G^*$ be the graph obtained from G by subdividing the k edges that belong to the set $E^*$. Let $I^*$ be an arbitrary i-set of $G^*$. By the minimality of $I^*$, the set $I^*$ contains exactly one vertex from the complete graph. Renaming vertices if necessary, we may assume that $v_1 \in I^*$, implying that $u_1 \notin I^*$. In order to dominate the leaves of $G^*$ that are not adjacent to $v_1$ in $G^*$ and are different from $u_1$, the set $I^*$ contains at least $(k-1)k$ additional vertices. Thus, $i(G^*) = |I^*| \ge 2 + (k-1)k = k^2 - k + 2 > i(G_k)$. Hence, $\hbox {sd}_{\mathrm{i}}(G_k) \le |E^*| = k$. As observed earlier, $\hbox {sd}_{\mathrm{i}}(G) \ge k$. Consequently, $\hbox {sd}_{\mathrm{i}}(G) = k$. $\square$

Recall that by Theorem 3.4, if G is a block graph, then $1 \le \mathrm{sd_\gamma }(G) \le 3$. However by Theorem 2.5, we can construct a block graph G such that $\hbox {sd}_{\mathrm{i}}(G)$ is arbitrary large. This shows once again that the independent domination subdivision number differs significantly from the domination subdivision number.

7 Trees

In this section, we present a proof of Theorem 2.6. We remark that our characterization given in Theorem 2.6 is along similar lines to that presented by Benecke and Mynhardt [2, Theorem 2] for the domination subdivision number. (In [2, Theorem 2], however, we note that the set $\mathcal{N}(T)$ is defined with respect to the domination number; that is, $\mathcal{N}(T) = \{ v \in V(T) \mid v \text{ is } \text{ in } \text{ no } \gamma \text{-set } \text{ of } T \}$.) We also remark that our proof of the necessity part of the proof of Theorem 2.6 is along similar lines to the proof presented in [2, Theorem 2].

We are now in a position to present a proof of Theorem 2.6. Recall its statement.

Theorem 2.6. For a tree T of order at least3, $\hbox {sd}_{\mathrm{i}}(T) = 1$if and only if T has at least one of the following two properties.

$P_1$::

A leaf of T belongs to the set $\mathcal{N}(T)$.

$P_2$::

An edge of T has both its ends in $\mathcal{N}(T)$.

Proof

We first prove the sufficiency. We proceed with the following two claims.

Claim 8

If the tree T has property $P_1$, then $\hbox {sd}_{\mathrm{i}}(T) = 1$.

Proof

Suppose that the tree T has property $P_1$. Let u be a leaf of T such that $u \in \mathcal{N}(T)$, and let v be its neighbor. Consider the tree $T'$ obtained from T by subdividing the edge uv and let w be the resulting subdivided vertex adjacent to u and v in $T'$. Let $I'$ be an i-set of $T'$. We note that either $u \in I'$ or $w \in I'$. Suppose firstly that $w \in I'$. In this case, the set $I = I' {\setminus } \{w\}) \cup \{u\}$ is an ID-set of T. Since $u \in \mathcal{N}(T)$, the set I is not an i-set of T, implying that $i(T') = |I'| \ge i(T) + 1$. Suppose secondly that $u \in I'$. If $v \notin I'$, then we can replace u in $I'$ with the vertex w, and obtain $i(T') \ge i(T) + 1$, as in the previous case. If $v \in I'$, then the set $I' {\setminus } \{u\}$ is an ID-set of T, implying that $i(T) \le |I'| - 1 = i(T') - 1$. Thus in all cases we have $i(T') > i(T)$. Therefore, subdividing only one edge of T, namely the edge uv, increases the independent domination number. Thus, $\hbox {sd}_{\mathrm{i}}(T) = 1$. $\square$

Claim 9

If the tree T has property $P_2$, then $\hbox {sd}_{\mathrm{i}}(T) = 1$.

Proof

Suppose that the tree T has property $P_2$. Let $e = uv$ be an edge of T such that both $u \in \mathcal{N}(T)$ and $v \in \mathcal{N}(T)$. We note that in this case neither u nor v is a leaf in T, and so $d_T(u) \ge 2$ and $d_T(v) \ge 2$. Let $T_u$ and $T_v$ be the components of the tree $T - uv$ that contain the vertex u and v, respectively. Let I be an i-set of T, and let $I_u$ and $I_v$ be the restriction of the set I to the trees $T_u$ and $T_v$, and so $I_u = I \cap V(T_u)$ and $I_v = I \cap V(T_v)$. By our earlier observations, $u \notin I_u$ and $v \notin I_v$. If $I_u$ is not an i-set of $T_u$, then $|I_u| > i(T_u)$. In this case, if $I_u^*$ is an i-set of $T_u$, then the set $I_u^* \cup I_v$ is an ID-set of T, and so $i(T) \le |I_u^*| + |I_v| < |I_u| + |I_v| = |I| = i(T)$, a contradiction. Hence, $I_u$ is an i-set of $T_u$, and so $i(T_u) = |I_u|$. Analogously, $i(T_v) = |I_v|$. If there is an i-set of $T_u$ that contains the vertex u, then such a set can be extended to an i-set of T by adding to it the set $I_v$, contradicting the supposition that $u \in \mathcal{N}(T)$. Hence, $u \in \mathcal{N}(T_u)$. Analogously, $v \in \mathcal{N}(T_v)$.

We now consider the tree $T'$ obtained from T by subdividing the edge uv and let w be the resulting subdivided vertex adjacent to u and v in $T'$. Let $I'$ be an i-set of $T'$. In order to dominate the vertex w, we note that $I' \cap \{u,v,w\} \ne \emptyset$. Let $I_u'$ and $I_v'$ be the restriction of the set $I'$ to the subtrees $T_u$ and $T_v$ of $T'$, and so $I_u' = I' \cap V(T_u)$ and $I_v' = I' \cap V(T_v)$.

Claim 9.1

If $w \notin I'$, then $\hbox {sd}_{\mathrm{i}}(T) = 1$.

Proof

Suppose that $w \notin I'$. We show that in this case, we must have $|I' \cap \{u,v\}| = 1$. Suppose, to the contrary, that $\{u,v\} \subseteq I'$. We note that $I_u'$ and $I_v'$ are ID-sets of $T_u$ and $T_v$, respectively. By supposition, $u \in I_u'$ and $v \in I_v'$. By our earlier observations, $u \in \mathcal{N}(T_u)$, implying that the set $I_u'$ is not an i-set of $T_u$, and so $|I_u'| \ge i(T_u) + 1$. Analogously since $v \in \mathcal{N}(T_v)$, we have $|I_v'| \ge i(T_v) + 1$. Thus, $i(T') = |I'| = |I_u'| + |I_v'| \ge i(T_u) + i(T_v) + 2 = i(T) + 2$. However the set $I_u \cup I_v \cup \{w\}$ is an ID-set of $T'$, implying that $i(T') \le |I_u| + |I_v| + 1 = i(T_u) + i(T_v) + 1 = i(T) + 1$. Thus we have shown that $i(T) + 2 \le i(T') \le i(T) + 1$, a contradiction.

Hence, $|I' \cap \{u,v\}| = 1$, and so exactly one of u and v belong to the set $I'$. Renaming u and v if necessary, we may assume that $u \in I'$ (and therefore that $v \notin I'$). In this case, the set $I'$ is an ID-set of T. However since $u \in \mathcal{N}(T)$, the set $I'$ is not an i-set of T, implying that $i(T') = |I'| > i(T)$. Therefore, subdividing only one edge of T, namely the edge $e = uv$, increases the independent domination number. Thus, $\hbox {sd}_{\mathrm{i}}(T) = 1$. $\square$

By Claim 9.1, we may assume that $w \in I'$, for otherwise the desired result, namely $\hbox {sd}_{\mathrm{i}}(T) = 1$, follows. Thus, $u \notin I'$ and $v \notin I'$ since the set $I'$ is an independent set. If the set $I_u'$ is not an ID-set of $T_u$, then this implies that $I_u'$ dominates all vertices of $T_u$ except for the vertex u. In this case, the set $I = (I' {\setminus } \{w\}) \cup \{u\}$ is an ID-set of T. However since $u \in \mathcal{N}(T)$, the set I is not an i-set of T, implying that $i(T') = |I'| = |I| > i(T)$. Hence we may assume that the set $I_u'$ is an ID-set of $T_u$, and analogously that the set $I_v'$ is an ID-set of $T_v$. Thus, $i(T') = |I'| = |I_u'| + |I_v'| + 1 \ge i(T_u) + i(T_v) + 1 = i(T) + 1$. Hence if $w \in I'$, then $i(T') > i(T)$. This completes the proof of Claim 9.$\square$

The proof of the sufficiency follows from Claims 8 and 9 . To prove the necessity, suppose that $\hbox {sd}_{\mathrm{i}}(T) = 1$. Thus by subdividing only one edge of T, say the edge uv, we increase the independent domination number. Let $T'$ be the tree obtained from T by subdividing the edge uv and let w be the resulting subdivided vertex adjacent to u and v in $T'$. Let $I'$ be an i-set of $T'$. By supposition, $i(T') > i(T)$.

Suppose that either u or v, say u, is a leaf of T. If the vertex u belongs to some i-set I of T, then the set $(I {\setminus } \{u\}) \cup \{w\}$ is an ID-set of $T'$, implying that $i(T') \le |I| = i(T)$, a contradiction. Hence, $u \in \mathcal{N}(T)$. Therefore we may assume that neither u nor v is a leaf of T, for otherwise the tree T has property $P_1$ as desired. Thus, $d_T(u) \ge 2$ and $d_T(v) \ge 2$. If both $u \in \mathcal{N}(T)$ and $v \in \mathcal{N}(T)$, then T has property $P_2$ as desired. Hence we may further assume that at least one of u and v, say u, belongs to some i-set of T.

Let I be an i-set of T that contains the vertex u. Let $N_T(v) {\setminus } \{u\} = \{v_1,\ldots , v_k\}$ where $k = d_T(v) - 1 \ge 1$. Let $T_i$ be the component of $T - vv_i$ that contains the vertex $v_i$ for $i \in [k]$. Let $I_i$ be the restriction of I to the tree $T_i$ for $i \in [k]$; that is, $I_i = I \cap V(T_i)$. Further, let $E_v$ be the set of k edges incident with v different from the edge uv, and let $T_v$ be the component of $T - E_v$ that contains the vertex v. Finally, let $I_v$ be the restriction of the set I to the tree $T_v$, and so $I_v = I \cap V(T_v)$. We note that

$$\begin{aligned} I = I_v \cup \left( \bigcup _{i \in [k]} I_i \right) \quad \text{ and } \quad i(T) = |I| = |I_v| + \sum _{i=1}^k |I_i|. \end{aligned}$$

We proceed further with the following series of claims.

Claim 10

The vertex u is the only neighbor of v that belongs to the set I.

Proof

Suppose, to the contrary, that the vertex $v_i \in I$ for at least one $i \in [k]$. This implies that the set I is also an ID-set in the tree $T'$, and so $i(T') \le i(T)$, a contradiction.$\square$

By Claim 10, the vertex u is the only neighbor of v that belongs to the set I; that is, $v \in \mathrm{epn}_T(u,I)$.

Claim 11

The following hold for all $i \in [k]$.

• (a) The set $I_i$ is an i-set of $T_i$.

• (b) The vertex $v_i$ does not belong to any i-set of $T_i$ for all $i \in [k]$

Proof

Since $v \notin I$, we note that the set $I_i$ is an ID-set of $T_i$. If $I_i$ is not an i-set of $T_i$ for some $i \in [k]$, then replacing the set $I_i$ in I with an i-set of $T_i$ produces an independent set of T of cardinality less than |I|, a contradiction. Hence, $I_i$ is an i-set of $T_i$ for all $i \in [k]$. This proves part (a). To prove part (b), suppose, to the contrary, that there is an i-set of $T_i$ that contains the vertex $v_i$ for some $i \in [k]$. Such an i-set can be extended to an i-set of T by adding to it the set $I_v$ and the i-sets $I_j$ of $T_j$ for $j \in [k] {\setminus } \{i\}$. However as observed in the proof of Claim 10, such an i-set of T is also an ID-set of $T'$, and so $i(T') \le i(T)$, a contradiction. Hence, vertex $v_i$ does not belong to any i-set of $T_i$ for all $i \in [k]$; that is, $v_i \in N(T_i)$ for all $i \in [k]$.$\square$

Claim 12

$v \in \mathcal{N}(T_v)$ and $v \in \mathcal{N}(T)$.

Proof

Suppose that there is an i-set, say $D_v$, of $T_v$ that contains the vertex v. In particular, we note that $i(T_v) = |I_v| = |D_v|$. In this case, the set $(I {\setminus } I_v) \cup (D_v {\setminus } \{v\}) \cup \{w\}$ is an ID-set of $T'$, implying that $i(T') \le |I| - |I_v| + |D_v| - 1 + 1 = |I| = i(T)$, a contradiction. Hence, the vertex v does not belong to any i-set of $T_v$; that is, $v \in \mathcal{N}(T_v)$.

Suppose next that there is an i-set, say S, of T that contains the vertex v. Let $S_v$ be the restriction of S to the tree $T_v$, and so $S_v = S \cap V(T_v)$. Since $v \in S_v$, we note that the set $S_v$ is an ID-set of $T_v$. However since $v \in \mathcal{N}(T_v)$, the set $S_v$ is not an i-set of $T_v$, implying that $|S_v| \ge i(T_v) + 1$. Let $S_i$ be the restriction of S to the tree $T_i$ for $i \in [k]$; that is, $S_i = S \cap V(T_i)$. If $|S_i| \ge i(T_i)$ for all $i \in [k]$, then

$$\begin{aligned} i(T) = |S| = |S_v| + \sum _{i=1}^k |S_i| \ge i(T_v) + 1 + \sum _{i=1}^k i(T_i) = i(T) + 1, \end{aligned}$$

a contradiction. Hence, $|S_i| < i(T_i)$ for at least one $i \in [k]$. For such an $i \in [k]$, the set $S_i$ is not an ID-set of $T_i$. However, $S_i$ is an ID-set of $T_i - v_i$, implying that $S_i \cup \{v_i\}$ is an ID-set of $T_i$ of cardinality $|S_i| + 1 \le i(T_i)$. Consequently, $|S_i| = i(T_i)-1$ and the set $S_i \cup \{v_i\}$ is an i-set of $T_i$ that contains the vertex $v_i$, contradicting Claim 11(b). Hence, there is no i-set of T that contains the vertex v; that is, $v \in \mathcal{N}(T)$.$\square$

By Claims 11 and 12 , for every edge $vv_i$ of T where $i \in [k]$, we have $v \in \mathcal{N}(T)$ and $v_i \in \mathcal{N}(T)$; that is, the edge $vv_i$ of T has both its ends in $\mathcal{N}(T)$ for $i \in [k]$. Hence, the tree T has property $P_2$. This completes the proof of the necessity. $\square$

As a consequence of Theorem 2.6 we present a simple proof that the independent domination subdivision number of a tree is at most 3. For this purpose, if v is a support vertex in a tree T, we denote by $L_v(T)$ the set of leaf neighbors of v in T. If the tree T is clear from context, we simply write $L_v$ rather that $L_v(T)$.

Theorem 7.1

If T is a tree of order $n \ge 3$, then $1 \le \hbox {sd}_{\mathrm{i}}(T) \le 3$.

Proof

Let T be a tree of order $n \ge 3$. If $\hbox {sd}_{\mathrm{i}}(T) = 1$, then the desired result follows. Hence we may assume that $\hbox {sd}_{\mathrm{i}}(T) \ge 2$. Thus by Theorem 2.6, the tree T has neither property $P_1$ nor $P_2$. In particular, for each leaf v of T there exists an i-set, $D_v$, of T such that $v \in D_v$, and for each edge uv of T there exists an i-set, $D_{uv}$, of T such that $|\{u,v\} \cap D_{uv}|=1$. Since T is a tree of order $n \ge 3$ satisfying $\hbox {sd}_{\mathrm{i}}(T) > 1$, we note that T not a star, and so $\mathrm{diam}(T) \ge 3$.

Suppose that $\mathrm{diam}(T) = 3$, and so T is a double star $S(\ell _1,\ell _2)$ for some integers $\ell _2 \ge \ell _1 \ge 1$. If $\ell _2 > \ell _1$, then T has property $P_1$, a contradiction. Hence, $\ell _2 = \ell _1$. If $\ell = 1$, then $T = P_4$ and $\hbox {sd}_{\mathrm{i}}(T) = 3$. If $\ell \ge 2$, then subdividing two non-adjacent edges (that have no vertex in common) results in a tree $T'$ with $i(T') = \ell _1 + 2 > \ell _1 + 1 = i(T)$, implying that $\hbox {sd}_{\mathrm{i}}(T) = 2$. Hence we may assume that $\mathrm{diam}(T) \ge 4$, for otherwise $2 \le \hbox {sd}_{\mathrm{i}}(T) \le 3$ and the desired result holds.

Among all longest paths in T, let $P :v_1v_2 \ldots v_{\mathrm{diam}(T) + 1}$ be chosen so that the degree of $v_2$ is as large as possible. We now root the tree T at the vertex $v_{\mathrm{diam}(T) + 1}$. We note that every child of $v_2$ in the rooted tree T is a leaf; that is, $L_{v_2} = C(v_2)$. Let A and B be the set of children and grandchildren, respectively, of the vertex $v_3$ in the rooted tree T. We note that each vertex of B is a leaf of T and is at distance 2 from $v_3$ in T. Further, every descendant of $v_3$ belongs to the set $A \cup B$. We proceed further with the following series of claims.

Claim 13

If $d_T(v_2) \ge 3$, then the vertex $v_3$ is a support vertex.

Proof

Let $d_T(v_2) \ge 3$ and suppose, to the contrary, that the vertex $v_3$ is not a support vertex of T. Thus each child of $v_3$ has at least one leaf neighbor. Since the child $v_2$ of $v_3$ has at least two leaf neighbors, we note therefore that $|B| \ge |A| + 1$. As observed earlier, every leaf belongs to some i-set of T. Let I be an i-set of T that contains the leaf $v_1$. We note that every child of $v_2$ is a leaf, and so, $L_{v_2} = C(v_2)$. Since $v_2 \notin I$, we note that $L_{v_2} \subset I$. If $v_3 \notin I$, then $(I {\setminus } L_{v_2}) \cup \{v_2\}$ is an ID-set of T of smaller cardinality than $|I| = i(T)$, a contradiction. Hence, $v_3 \in I$. This in turn implies that $B \subset I$. If $v_4$ has at least two neighbors in I, then let $I^* = (I {\setminus } (B \cup \{v_3\})) \cup A$. If $v_3$ is the only neighbor of $v_4$ in I, then let $I^* = (I {\setminus } (B \cup \{v_3\}) \cup (A \cup \{v_4\})$. In both cases, $I^*$ is an ID-set of T, and so $i(T) = |I^*| \le |I| - |B| + |A| < |I| = i(T)$, a contradiction.$\square$

Claim 14

If $d_T(v_2) \ge 3$, then $\hbox {sd}_{\mathrm{i}}(T) = 2$.

Proof

Let $d_T(v_2) \ge 3$. By Claim 14, the vertex $v_3$ is a support vertex. Let y be an arbitrary leaf neighbor of $v_3$, and let $T'$ be the tree obtained from T by subdividing the edges $v_1v_2$ and $v_3y$ with the new subdivided vertices $u_1$ and $u_2$, respectively. Let $I'$ be an i-set of $T'$. Suppose firstly that $v_3 \in I'$. In this case, $y \in I'$, $v_2 \notin I'$ and $|\{u_1,v_1\} \cap I'|=1$. If $u_1 \in I'$, then we can replace $u_1$ with $v_1$ in $I'$. Hence we can choose $I'$ so that $v_1 \in I'$. We now let $I^* = I' {\setminus } \{y\}$. Suppose secondly that $v_3 \notin I'$. In this case, $|\{u_2,y\} \cap I'|=1$ and $|D[v_2] \cap I'|=2$, where note that $D[v_2] = L_{v_2}(T) \cup \{v_2\}$. Hence we can choose $I'$ so that $y \in I'$ and $\{v_1,v_2\} \subset I'$. We now let $I^* = I' {\setminus } \{v_1\}$. In both cases, $|I^*| = |I'| - 1$ and the set $I^*$ is an ID-set of T, and so $i(T) \le |I^*| < |I'| = i(T')$, implying that $\hbox {sd}_{\mathrm{i}}(T) = 2$.$\square$

Claim 15

If $d_T(v_2) = 2$ and $v_3$ is a support vertex, then $\hbox {sd}_{\mathrm{i}}(T) \le 3$.

Proof

Let $d_T(v_2) = 2$ and suppose that $v_3$ is a support vertex. Let y be an arbitrary leaf neighbor of $v_3$, and let $T'$ be the tree obtained from T by subdividing the edges $v_1v_2$, $v_2v_3$ and $v_3y$ with the new subdivided vertices $u_1$, $u_2$ and $u_3$, respectively. Let $I'$ be an i-set of $T'$. Suppose firstly $v_3 \in I'$. In this case, $\{u_1,y\} \subset I'$ and we let $I^* = (I' {\setminus } \{u_1,y\}) \cup \{v_1\}$. Suppose secondly that $v_3 \notin I'$. In this case, $|\{u_1,v_1\} \cap I'|=1$, $|\{u_2,v_2\} \cap I'|=1$ and $|\{u_3,y\} \cap I'|=1$. Hence we can choose the set $I'$ so that $\{u_1,u_2,u_3\} \subseteq I'$, and we let $I^* = (I' {\setminus } \{u_1,u_2,u_3\}) \cup \{v_2,y\}$. In both cases, $|I^*| = |I'| - 1$ and the set $I^*$ is an ID-set of T, and so $i(T) \le |I^*| < |I'| = i(T')$, implying that $\hbox {sd}_{\mathrm{i}}(T) \le 3$.$\square$

Claim 16

If $d_T(v_2) = 2$ and $v_3$ is not a support vertex, then $\hbox {sd}_{\mathrm{i}}(T) \le 3$.

Proof

Let $d_T(v_2) = 2$ and suppose that $v_3$ is not a support vertex. By our choice of the vertex $v_2$, we note that each child of $v_3$ is therefore a support vertex of degree 2. Let $T'$ be the tree obtained from T by subdividing the edges $v_1v_2$, $v_2v_3$ and $v_3v_4$ with the new subdivided vertices $u_1$, $u_2$ and $u_3$, respectively. Let $I'$ be an i-set of $T'$. Suppose firstly $v_4 \in I'$. In this case, $u_3 \notin I'$, $|\{u_1,v_1\} \cap I'|=1$ and $|\{u_2,v_2,v_3\} \cap I'|=1$. Hence we can choose the set $I'$ so that $\{u_1,u_2\} \subseteq I'$, and we let $I^* = (I' {\setminus } \{u_1,u_2\}) \cup \{v_2\}$. Suppose secondly $v_4 \notin I'$ and $v_3 \in I'$. In this case, $\{u_1,v_3\} \subset I'$ and we let $I^* = (I' {\setminus } \{u_1,v_3\}) \cup \{v_2\}$. Suppose thirdly $u_3 \in I'$. In this case, $|\{u_1,v_1\} \cap I'|=1$ and $|\{u_2,v_2\} \cap I'|=1$. Hence we can choose the set $I'$ so that $\{u_1,u_2\} \subseteq I'$. Further we can choose $I'$ so that if $d_T(v_3) \ge 3$, then the set $I'$ contains all grandchildren of $v_3$ different from $v_1$. We now let $I^* = (I' {\setminus } \{u_1,u_2,u_3\}) \cup \{v_1,v_3\}$. In all three cases, $|I^*| = |I'| - 1$ and the set $I^*$ is an ID-set of T, and so $i(T) \le |I^*| < |I'| = i(T')$, implying that $\hbox {sd}_{\mathrm{i}}(T) \le 3$.$\square$

The proof of Theorem 7.1 follows from Claims 14, 15 and 16 . $\square$

8 Open Problems

We close with some open problems that we have yet to settle. By Theorem 2.1, if G is a connected graph of order at least 3, then $\hbox {sd}_{\mathrm{i}}(G) \le \Delta (G) \cdot i(G)$. A natural question is to find a general upper bound on the independent domination subdivision number of a connected graph G in terms of its maximum degree $\Delta (G)$.

Problem 1

Does there exists a constant C such that every connected graph G satisfies $\hbox {sd}_{\mathrm{i}}(G) \le C \cdot \Delta (G)$? If so, determine the smallest such constant C.

By Corollary 2.4 we know that the constant C in Problem 1, if it exists, satisfies $C \ge 3$. By Theorem 7.1, if T is a tree of order $n \ge 3$, then $1 \le \hbox {sd}_{\mathrm{i}}(T) \le 3$, and in Theorem 2.6 the trees T satisfying $\hbox {sd}_{\mathrm{i}}(T) = 1$ are characterized. It remains an open problem to characterize the trees T satisfying $\hbox {sd}_{\mathrm{i}}(T) = 2$ or $\hbox {sd}_{\mathrm{i}}(T) = 3$. We state this problem formally as follows.

By Theorem 2.5, the independent domination subdivision number of a block graph can be arbitrary large. However as remarked earlier, the independent domination subdivision number of a tree is at most 3.

Problem 2

Determine classes of graphs different from the class of trees for which the independent domination subdivision number is bounded above by a constant.