Abstract
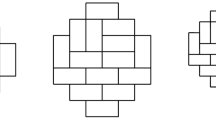
The Aztec diamond of order n is the union of lattice squares in the plane intersecting the square \(|x|+|y|<n\). The Aztec diamond theorem states that the number of domino tilings of this shape is \(2^{n(n+1)/2}\). It was first proved by Elkies et al. (J. Algebraic Comb. 1(2):111–132, 1992). We give a new simple proof of this theorem.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Notes
Note that the field of arrows is always defined on all of \(A_{n+1}\), even for a tiling of \(A_n\).
In this correspondence, the nodes in this paper correspond to odd vertices in [4].
References
Bosio, F., van Leeuwen M.A.A.: A bijection proving the Aztec diamond theorem by combing lattice paths. Electron. J. Comb. 20(4) (2004). (paper 24, 30 pp.)
Brualdi, R.A., Kirkland, S.: Aztec diamonds and digraphs, and Hankel determinants of Schröder numbers. J. Comb. Theory Ser. B 94(2), 334–351 (2005)
Elkies, N., Kuperberg, G., Larsen, M., Propp, J.: Alternating-sign matrices and domino tilings (Part I). J. Algebraic Comb. 1(2), 111–132 (1992)
Elkies, N., Kuperberg, G., Larsen, M., Propp, J.: Alternating-sign matrices and domino tilings (Part II). J. Algebraic Comb. 1(3), 219–234 (1992)
Eu, S.-P., Fu, T.-S.: A simple proof of the Aztec diamond theorem. Electron. J. Comb. 12 (2005). (research paper 18, 8 pp., electronic)
Kamioka, S.: Laurent biorthogonal polynomials, q-Naryana polynomials and domino tilings of the Aztec diamonds. J. Comb. Theory Ser. A 123, 14–29 (2014)
Kasteleyn, P.W.: The statistics of dimers on a lattice: I. The number of dimer arrangements on a quadratic lattice. Physica 27(12), 1209–1225 (1961)
Kenyon, R., Okounkov, A.: What is \(\dots \) a dimer? Not. Am. Math. Soc. 52(3), 342–343 (2005)
Kokhas, K.: Domino tilings of Aztec diamonds and squares. In: Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI), 360(Teoriya Predstavlenii, Dinamicheskie Sitemy, Kombinatornye Metody. XVI), pp. 180–230, 298 (2008)
Kuo, E.H.: Applications of graphical condensation for enumerating matchings and tilings. Theor. Comput. Sci. 319, 29–57 (2004)
Lai, T. :A generalization of Aztec diamond theorem, part I. Electron. J. Comb. 21(1) (2014). (paper 1.51, 19)
Temperley, H.N.V., Fisher, M.E.: Dimer problem in statistical mechanics—an exact result. Philos. Mag. (8) 6, 1061–1063 (1961)
Yan, W., Zhang, F.: Graphical condensation for enumerating perfect matchings. J. Comb. Theory Ser. A 110, 113–125 (2005)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Fendler, M., Grieser, D. A New Simple Proof of the Aztec Diamond Theorem. Graphs and Combinatorics 32, 1389–1395 (2016). https://doi.org/10.1007/s00373-015-1663-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00373-015-1663-x