Skip to main content
SpringerLink
Log in

Convex Pentagons for Edge-to-Edge Tiling, III

  • Original Paper
  • Published:
Graphs and Combinatorics Aims and scope Submit manuscript

Abstract

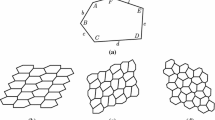
In previous papers, the cases in which there is a possibility that a convex pentagon generates an edge-to-edge tiling were sorted, and the remaining 42 cases in which there is uncertainty about whether a convex pentagon can generate an edge-to-edge tiling were shown. In this paper, the latter 42 cases are investigated using a computer. As a result, we find that convex pentagons that can generate edge-to-edge monohedral tiling of the plane can be sorted into eight types.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Notes

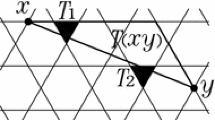
  1. DDE-2 represents the sub-cases of the tentative 3-valent node \(\{D,D,E\}\). When convex pentagons are assembled around a tentative 3-valent node, there are eight possible ways to assemble the three pentagons. As a result, some sub-cases arise for edge fitting around the 3-valent node. For example, as shown in Fig. 2, \(\{D,D,E\}\) has two sub-cases, DDE-1 and DDE-2. Notice that the equations following the colons for each label in the figure represent the conditions on edge-lengths. The convex pentagon of this example can use only DDE-2 (the two arrangement way of DDE-2) from the edge conditions. Refer to Section 4 in [8] for details.

References

  1. Bagina, O.: Tiling the plane with congruent equilateral convex pentagons. J. Comb. Theory Ser. A 105, 221–232 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bagina, O.: Tilings of the plane with convex pentagons (in Russian). Vestnik KemGU 4(48), 63–73 (2011)

    Google Scholar 

  3. Gardner, M.: On tessellating the plane with convex polygon tiles. Sci. Am. 233(1), 112–117 (1975)

  4. Grünbaum, B., Shephard, G.C.: Tilings and Patterns, pp. 15–35 (chapter 1), pp. 113–157 (chapter 3), pp. 471–487, pp. 492–497, and pp. 517–518 (chapter 9). W. H. Freeman and Company, New York (1987)

  5. Hallard, T.C., Kenneth, J.F., Richard, K.G.: Unsolved Problems in Geometry, pp. 79–80, pp. 95–96 (C14). Springer, New York (1991)

  6. Kershner, R.B.: On paving the plane. Am. Math. Mon. 75, 839–844 (1968)

    Article  MathSciNet  MATH  Google Scholar 

  7. Schattschneider, D.: Tiling the plane with congruent pentagons. Math. Mag. 51(1978), 29–44 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  8. Sugimoto, T.: Convex pentagons for edge-to-edge tiling, I. FORMA 29, 93–103 (2012)

    MathSciNet  Google Scholar 

  9. Sugimoto, T.: Convex pentagons for edge-to-edge tiling and convex polygons for aperiodic tiling (in Japanese), Ouyou suugaku goudou kenkyuu syuukai houkokusyuu (Proceeding of Applied Mathematics Joint Workshop), pp. 126–131 (2012)

  10. Sugimoto, T.: Convex pentagons for edge-to-edge tiling, II. Graphs Comb. 31, 281–298 (2015). doi:10.1007/s00373-013-1385-x

    Article  MathSciNet  MATH  Google Scholar 

  11. Sugimoto, T., Ogawa, T.: Properties of tilings by convex pentagons. FORMA 21, 113–128 (2006)

    MathSciNet  Google Scholar 

  12. Wells, D.: The Penguin Dictionary of Curious and Interesting Geometry, pp. 177–179. Penguin Books, London (1991)

Download references

Acknowledgments

The authors would like to give heartful thanks to Emeritus Professor Hiroshi Maehara, University of the Ryukyus, and Professor Shigeki Akiyama, University of Tsukuba, whose enormous support and insightful comments were invaluable. The authors would also like to thank Associate Professor Genta Ueno, The Institute of Statistical Mathematics, for a critical reading of the manuscript. The comments of the referees also helped to clarify the article.

Author information

Authors and Affiliations

  1. The Interdisciplinary Institute of Science, Technology and Art, Suzukidaini-building 211, 2-5-28 Kitahara, Asaka-shi, Saitama, 351-0036, Japan

    Teruhisa Sugimoto

Authors
  1. Teruhisa Sugimoto
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Teruhisa Sugimoto.

Appendix A.1

Appendix A.1

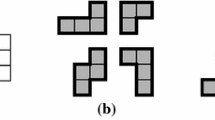
Let \(T_{x}\) be a set of convex pentagonal tiles that belongs to a type x for x = 1, 2, 4, 5, 6, 7, 8, 9. Figure 7 shows examples of the Venn diagram of \(T_{x}\). Figure 8 shows examples of the convex pentagonal tiles that are contained in each intersection of Fig. 7.

Fig. 7
figure 7

Venn diagram of \(T_{x}\)

Full size image
Fig. 8
figure 8

Convex pentagonal tiles that are contained in each intersection of Fig. 7. Representative tilings of type 2 by convex pentagonal tiles of a, i, j, m, and o are always non-edge-to-edge. Representative tilings of type 1 by convex pentagonal tiles of c, e, f, and p are always non-edge-to-edge

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sugimoto, T. Convex Pentagons for Edge-to-Edge Tiling, III. Graphs and Combinatorics 32, 785–799 (2016). https://doi.org/10.1007/s00373-015-1599-1

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00373-015-1599-1

Keywords

Search

Navigation