On Tight Components and Anti-Tight Components

Abstract

A graph $G=(V,E)$ is called factor-critical if $G\ne \emptyset$ and $G-v$ has a perfect matching for every vertex $v\in V(G)$. A factor-critical graph $G$ is tight (anti-tight, respectively) if for any $v\in V(G)$, any perfect matching $M$ in $G-v$, and any $e\in M$, $|N(v)\cap V(e)|\ne 1$ ($|N(v)\cap V(e)|\ne 2$, respectively), where $N(v)$ denotes the neighborhood of $v$ and $V(e)$ denotes the set of vertices incident with $e$. A graph $G$ is minimally anti-tight if $G$ is anti-tight but $G-e$ is not anti-tight for every $e\in E(G)$. In this paper, we prove that a connected graph is tight iff every block of the graph is an odd clique, and that every minimally anti-tight graph is triangle-free.

1 Introduction

Let $G$ be a graph and $H$ a component of $G$. For any $v\in {V(G)}$, we use $N_G(v)$ to denote the set of neighbors of $v$ in $G$. For any $e\in {E(G)}$, we use $V_G(e)$ to denote the set of vertices of $G$ incident with $e$. (If understood, we omit the reference to G.) If $G\ne \emptyset$ and $G-v$ has a perfect matching for every $v\in V(G)$, then $G$ is called factor-critical. Factor-critical graphs have been extensively studied in the past [2, 4, 5, 7, 8]. We say that $H$ is odd if $|H|$ is odd and that $H$ is a tight component (respectively, anti-tight component) if

• $H$ is factor-critical, and

• $|N(v)\cap V(e)|\ne 1$ (respectively, $|N(v)\cap V(e)|\ne 2$) for any $v\in V(H)$, any perfect matching $M$ in $H-v$, and any $e\in M$.

When $H=G$, we simply say that $G$ is tight (respectively, anti-tight).

Lee et al. [6] used tight components to solve a problem of Bollob$\acute{\mathrm{a}}$s and Scott [1, 9] about the dependence on minimum degree of bounds on judicious bisections. A block in a graph $G$ is a maximal connected subgraph that contains no cut vertex. Hence, if a block of G is not 2-connected, then it must be induced by a cut edge of $G$. A complete subgraph of a graph is usually called a clique. It is easy to see that odd cliques are tight. Lee et al. [3] observed that if every block of a connected graph $G$ is an odd clique then $G$ is tight, and mentioned that it is not clear if every tight component is of this form. In this note, we answer this question in the affirmative.

Theorem 1

A connected graph is tight iff every block of the graph is an odd clique.

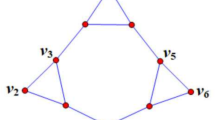
It is apparent that if a graph $G$ is factor-critical and triangle-free, then $G$ is anti-tight. But it is not true that every anti-tight graph $G$ is triangle-free (see Fig. 1). It seems difficult to characterize the anti-tight graphs. A connected graph $G$ is minimally anti-tight if $G$ is anti-tight but $G-e$ is not anti-tight for every $e\in E(G)$. Concerning the minimally anti-tight graphs, we have

Fig. 1

An anti-tight graph with a triangle

Theorem 2

Every minimally anti-tight graph $G$ is triangle-free.

Let $G$ be a graph and $M$ a matching in $G$. A vertex $v$ is called matched if it is incident with an edge in $M$, and otherwise $v$ is called unmatched. An M-alternating path is a path in which the edges belong alternatively to $E(G)\setminus M$ and $M$. An M-augmenting path is an alternating path that starts from and ends at unmatched vertices. Let $H$ be a subgraph of $G$, we use $M\Delta H$ to denote the symmetric difference of $M$ and $E(H)$. In general, we follow the terminology in [3].

2 Proof of Theorem 1

Lemma 1

Let $G_1$ and $G_2$ be subgraphs of a connected graph $G$ such that $G= G_1\cup G_2$ and $|V(G_1)\cap V(G_2)|=1$. Then $G$ is tight iff both $G_1$ and $G_2$ are tight.

Proof

Let $x\in V(G_1)\cap V(G_2)$. Suppose G is tight. Let $v\in V(G_1)$. Then $G-v$ has a perfect matching, say $M$. Note that $|V(G_1)|$ is odd and thus the edge in $M$ incident with $x$ belongs to $G_1$ when $x\ne v$; so $M\cap E(G_1)$ is a perfect matching in $G_1-v$. Now let $M_1$ be a perfect matching in $G_1-v$. Since $G-x$ has a perfect matching, $G_2-x$ has a perfect matching, say $M_2$. Then $M:=M_1\cup M_2$ is a perfect matching in $G-v$. Thus, since $G$ is tight, for any $e\in M_1$, $|N_G(v)\cap V(e)|\ne 1$; so $|N_{G_1}(v)\cap V(e)| = |N_G(v)\cap V(e)|\ne 1$. Hence, $G_1$ is tight. Similarly, we can show that $G_2$ is tight.

Now assume both $G_1$ and $G_2$ are tight. Let $v\in V(G)$. Then $v\in V(G_i)$ for some $i\in {1,2}$ and, without loss of generality, let $v\in V(G_1)$. Let $M_1$ be a perfect matching in $G_1-v$, and $M_2$ a perfect matching in $G_2-x$; so $M_1\cup M_2$ is a perfect matching in $G-v$. Now for any perfect matching $M$ in $G-v$, $M\cap E(G_1)$ is a perfect matching in $G_1-v$ while $M\cap E(G_2)$ is a perfect matching in $G_2-x$. Moreover, for any $e\in M\cap E(G_1)$, $|N_G(v)\cap V(e)| =|N_{G_1}(v)\cap V(e)|\ne 1$ (as $G_1$ is tight). Now suppose $e\in M\cap E(G_2)$. If $v\ne x$ then $|N_G(v)\cap V(e)|=0\ne 1$. So assume $v=x$. Then since $G_2$ is tight, $|N_G(v)\cap V(e)| =|N_{G_2}(v)\cap V(e)|\ne 1$. Hence, $G$ is also tight. $\square$

Lemma 2

Let $G$ be a $2$-connected tight graph. Then $G$ is a complete graph with odd order.

Proof

Suppose to the contrary that $G$ is not a complete graph. Then we can find three vertices $x,y,z$ such that $yx\in E(G)$, $yz\in E(G)$ but $xz\notin E(G)$. As $G-y$ has a perfect matching, say $M$, we let $xx_1\in M$ and $zz_1\in M$. Since $|\{x,x_1\}\cap N_G(y)|\ne 1$ and $|\{z,z_1\}\cap N_G(y)|\ne 1$, $x_1y\in E(G)$ and $z_1y\in E(G)$. Note that $G':=G-\{x,y,z\}$ has no perfect matching, otherwise, $G-\{x\}$ has a perfect matching containing $yz$ and $|N_G(x)\cap \{y,z\}|=1$, a contradiction. Then $x_1z_1\notin E(G)$. If $xz_1\in E(G)$, $G-z$ has a perfect matching $M'=(M-\{xx_1,zz_1\})\cup \{xz_1,yx_1\}$ and $|N_G(z)\cap \{x,z_1\}|=1$, a contradiction. Hence, $xz_1\notin E(G)$. Similarly, $zx_1\notin E(G)$.

Suppose $G-y$ has an $M$-alternating path $P'=xy_2\cdots y_kz$. If $xy_2\in M$ and $y_kz\in M$, then $y_2=x_1$ and $y_k=z_1$, hence, $M\Delta yxy_2\cdots y_k$ is a perfect matching in $G-z$ and $|N_G(z)\cap \{y,x\}|=1$, a contradiction. If $xy_2\in M$ and $y_kz\notin M$, then $y_2=x_1$ and $y_k\ne z_1$, clearly, $M\Delta y_2\cdots y_kzz_1y$ is a perfect matching in $G-x$ and $|N_G(x)\cap \{z_1,y\}|=1$, a contradiction. If $xy_2\notin M$ and $y_kz\in M$, then we get a similar contradiction. Thus, $xy_2\notin M$ and $y_kz\notin M$. Then $y_2\ne x_1$ and $y_k\ne z_1$. So $M\Delta xy_2\cdots y_kzz_1y$ is a perfect matching in $G-x_1$ and $|N_G(x_1)\cap \{z_1,y\}|=1$, a contradiction.

Thus, $G-y$ does not contain any $M$-alternating path from $x$ to $z$. If $x_1$ and $z$ are linked by a path $P_1$ in $G-\{x,y\}$, let $P=xx_1+P_1=xx_1v_3\cdots v_iv_{i+1}v_{i+2}\cdots z$ and assume that $xx_1v_3\cdots v_iv_{i+1}$ is an $M$-alternating path, $v_{i-1}v_i\in M$ but $v_iv_{i+1}, v_{i+1}v_{i+2} \notin M$ for some $i$. Choose $P$ so that $xx_1v_3\cdots v_iv_{i+1}$ is longest and $v_{i+1}v_{i+2}\cdots z$ is shortest. Then the matched vertex $v'_{i+1}$ with $v_{i+1}$ is not in $P$ as $xx_1, v_3v_4, \cdots$, $v_{i-1}v_i \in M$ and $v_{i+1}v_{i+2}\cdots z$ is shortest. If $v_iv'_{i+1}\notin E(G)$, then $M\Delta yxx_1v_3\cdots v_i$ is a perfect matching in $G-v_{i}$ and $|N_G(v_i)\cap \{v_{i+1},v'_{i+1}\}|=1$, a contradiction. Thus $v_iv'_{i+1}\in E(G)$. Now $xx_1v_3\cdots v_iv'_{i+1}$ $v_{i+1}v_{i+2}\cdots z$ is a path contradicts the choice of $P$, as it has a longer $M$-alternating section starting from $x$.

Hence $x_1$ and $z$ are not linked by any path in $G-\{x,y\}$. Then since $G$ is $2$-connected, there is a path $P=xv_2\cdots z$ in $G-y$ such that $x_1\notin P$. Let $P=xv_2\cdots v_iv_{i+1}v_{i+2}\cdots z$ such that $xv_2v_3\cdots v_iv_{i+1}$ is an $M$-alternating path, $v_{i-1}v_i\in M$ but $v_iv_{i+1}, v_{i+1}v_{i+2} \notin M$. Choose $P$ so that $xv_2\cdots v_iv_{i+1}$ is longest and $v_{i+1}v_{i+2}\cdots z$ is shortest. Then the matched vertex $v'_{i+1}$ with $v_{i+1}$ is not in $P$ as $v_{i+1}\ne x_1$ and $v_2v_3, \cdots , v_{i-1}v_i \in M$ and $v_{i+1}v_{i+2}\cdots z$ is shortest. If $v_iv'_{i+1}\notin E(G)$, then $M\Delta yx_1xv_2\cdots v_i$ is a perfect matching in $G-v_{i}$ and $|N_G(v_i)\cap \{v_{i+1},v'_{i+1}\}|=1$, a contradiction. Thus $v_iv'_{i+1}\in E(G)$. So $xv_2v_3\cdots v_iv'_{i+1}v_{i+1}v_{i+2}\cdots z$ is a path contradicts the choice of $P$, as it has a longer $M$-alternating section starting from $x$. $\square$

A simple corollary of Lemma 1 is the observation of Lee, Loh and Sudakov that if every block of a graph $G$ is an odd clique then $G$ is a tight component. Clearly, Lemma 1 and Lemma 2 imply Theorem 1 which says the converse.

3 Proof of Theorem 2

Assume to the contrary that $G$ is minimally anti-tight and contains a triangle $xyzx$. If $G-xz-v$ has a perfect matching for every $v\in V(G)$, every such matching $M$ is also a perfect matching in $G-v$. Since $G$ is anti-tight, $|N_{G-xz}(v)\cap V(e)|\le |N_{G}(v)\cap V(e)|\le 1$ for every $e\in M$. Hence, $G-xz$ is anti-tight, a contradiction.

Thus, there is a vertex $u\in V(G)$ such that $G-xz-u$ contains no perfect matching. $G-y$ has a perfect matching $M$ and $xz\notin M$. This implies $u\ne y$. Let $\widetilde{M}$ be a perfect matching in $G-u$. Since $G-xz-u$ contains no perfect matching, $xz\in \widetilde{M}$. Let $G'$ be the multigraph with $V(G')=V(G)$ and whose edges are edges in $M$ and $\widetilde{M}$. It is easy to see that $d_{G'}(u)=d_{G'}(y)=1$ and for any $v\in V(G)-\{u,y\}$, $d_{G'}(v)=2$. So there is a path $P=uv_1v_2\cdots v_ty$ in $G'$ between $u$ and $y$, and the length of $P$ is even. If $xz\notin P$, then $xz$ is an edge of an even cycle $C$ which is a component of $G'$, and $\widetilde{M}\Delta C$ is a perfect matching of $G-xz-u$, a contradiction. Hence, $xz\in P$, and let $\{v_i,v_{i+1}\}=\{x,z\}$. Since $v_iv_{i+1}\notin M$, the length of $uv_1\cdots v_i$ is odd and $C_1:=v_{i}\cdots v_ty+yv_i$ is an even cycle in $G$. Now $\widetilde{M}\Delta C_1$ is a perfect matching of $G-xz-u$, a contradiction. $\square$