Skip to main content
SpringerLink
Log in

The Number of Out-Pancyclic Vertices in a Strong Tournament

  • Original Paper
  • Published:
Graphs and Combinatorics Aims and scope Submit manuscript

Abstract

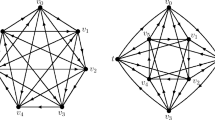
An arc in a tournament T with n ≥ 3 vertices is called pancyclic, if it belongs to a cycle of length l for all 3 ≤ l ≤ n. We call a vertex u of T an out-pancyclic vertex of T, if each out-arc of u is pancyclic in T. Yao et al. (Discrete Appl. Math. 99, 245–249, 2000) proved that every strong tournament contains an out-pancyclic vertex. For strong tournaments with minimum out-degree 1, Yao et al. found an infinite class of strong tournaments, each of which contains exactly one out-pancyclic vertex. In this paper, we prove that every strong tournament with minimum out-degree at least 2 contains three out-pancyclic vertices. Our result is best possible since there is an infinite family of strong tournaments with minimum degree at least 2 and no more than 3 out-pancyclic vertices.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bang-Jensen, J.; Gutin, G.: Digraphs: theory, algorithms and applications. Springer, London (2000)

  2. Camion P.: Chemins et circuits hamiltoniens des graphes complets. C.R. Acad. Sci. Paris. 249, 2151–2152 (1959)

    MATH  MathSciNet  Google Scholar 

  3. Feng J.: Each 3-strong tournament contains 3 vertices whose out-arcs are pancyclic. Graphs Combin. 25, 299–307 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  4. Guo Q., Li S., Guo Y., Li H.: Out-arc pancyclicity of vertices in tournaments. Discrete Appl. Math. 158, 996–1005 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  5. Havet F.: Pancyclic arcs and connectivity in tournaments. J. Graph Theory. 47, 87–110 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  6. Li, R., Li, S., Feng, J.: The number of vertices whose out-arcs are pancyclic in a 2-strong tournament. Discrete Appl. Math. 156, 88–92 (2008)

    Google Scholar 

  7. Thomassen C.: Hamiltonian-connected tournaments. J. Combin. Theory Ser. B. 28, 142–163 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  8. Yao T., Guo Y., Zhang K.: Pancyclic out-arcs of a vertex in a tournament. Discrete Appl. Math. 99, 245–249 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  9. Yeo A.: The number of pancyclic arcs in a k-strong tournament. J. Graph Theory. 50, 212–219 (2005)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Shanxi University, Taiyuan, 030006, China

    Qiaoping Guo & Hongwei Li

  2. Institute of Mathematics and Applied Mathematics, Shanxi University, Taiyuan, 030006, China

    Shengjia Li & Huiling Zhao

Authors
  1. Qiaoping Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shengjia Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hongwei Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Huiling Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qiaoping Guo.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Guo, Q., Li, S., Li, H. et al. The Number of Out-Pancyclic Vertices in a Strong Tournament. Graphs and Combinatorics 30, 1163–1173 (2014). https://doi.org/10.1007/s00373-013-1328-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00373-013-1328-6

Keywords

Search

Navigation