1 Introduction

Human color vision is achieved through a mixed response of three types of cone cells, namely the L-, M-, and S-cones, which are sensitive to long, medium, and short wavelengths of light, respectively; however, it can be impacted negatively by color vision deficiency (CVD), an eye disease caused by cone cell abnormalities—most resulting from abnormal genes—for which medical treatment has not yet been established. The most generic form of CVD is anomalous trichromacy, affecting approximately 5.71% of males and 0.39% of females, which results from the partial loss of a type of cone cell. In addition, about 2.28% of males and 0.03% of females are affected by dichromacy, which occurs when one of the three types of cone cells is completely non-functional [15, 26]. Further, protan (protanomaly) and deutan (deuteranomaly) defects refer to specific types of anomalous trichromacy in which the L-cone or M-cone presents with anomalies. Individuals with protan defects have a reduced sensitivity to red light, while those with deutan defects have a reduced sensitivity to green light. In the past decades, to address the chromatic contrast loss suffered by individuals with CVD, various recoloring methods for contrast enhancement have been proposed in existing studies[6,7,8,9,10,11,12,13, 19,20,21,22, 24, 25, 27,28,30, 32, 33]. These methods are based on CVD simulation models [23], which can be adopted to visualize CVD perceptions digitally. For contrast enhancement, some methods significantly change color appearance, rendering people with CVD as unnatural; in other words, reduced naturalness can result from significant differences between the original and recolored images. Conversely, most recoloring methods are proposed for dichromacy compensation, and there are fewer most recoloring methods are proposed for dichromacy compensation, and fewer studies consider recoloring images according to individual degrees of CVD, whereas anomalous trichromacy accounts for most cases of CVD. A state-of-the-art recoloring method for anomalous trichromacy is proposed by Zhu et al. [34] that recolors images by minimizing the objective function that is influenced by naturalness preservation and contrast enhancement constraints. Zhu et al. [34] implemented their recoloring model in the RGB color space, where the distance between two colors is not uniform when perceived by humans. As shown in Fig. 1, the two diagrams represent the RGB color space (Fig. 1a) and the CIE L*a*b* (Lab) color space (Fig. 1b), which offers perceptual uniformity, respectively. Given two colors \(c_{i}\), \(c_{j}\), along with their corresponding positions in the RGB and Lab color space, CVD simulation results are obtained using a simulation model [23], denoted as \(\widetilde{c_{1}}\) and \(\widetilde{c_{2}}\) and depicted in Fig. 1. Therein, the green line segments represent the spatial distance between colors \(c_{1}\), \(c_{2}\), and the red line segments represent the distance between \(\widetilde{c_{1}}\) and \(\widetilde{c_{2}}\). Meanwhile, in Fig. 1b, it is evident that the distance between \(c_{1}\) and \(c_{2}\) is shortened to one quarter after CVD simulation in the Lab color space, indicating significant contrast loss in CVD perception. However, Fig. 1a shows that the distance between the color pair \((c_{1}, c_{2})\) is halved after the CVD simulation in the RGB color space, which indicates that contrast loss occurs, but it is not severe. As a result, it may not reflect the contrast loss experienced by individuals with CVD when using the RGB color space.

Fig. 1
figure 1

The distance between distance of colors in different color space

Full size image

In response, we propose a personalized image-recoloring method for CVD compensation, adopting the constraint strategy proposed by Huang et al. [14]. The proposed algorithm is performed in the Lab color space. In [14], the resulting image is recolored using hues from within the gamut of dichromacy to be shown to affected individuals, as these colors are meant to be identifiable by people with CVD. However, for anomalous trichromacy, even if the image is recolored using hues from within the gamut, individuals with CVD may perceive differences from what is being shown to them. Therefore, the result of implementing a color transformation within the color gamut by utilizing the compensation range constraint and optimization model can be achieved using an intermediate image. In the end, based on the intermediate result, the final recoloring result can be obtained using a lookup table, a process deemed a back-projection procedure, as it involves mapping a color within the CVD gamut to a color in the normal color space. The contributions of this paper are summarized as follows:

  • A novel degree-adaptable image recoloring method for anomalous trichromacy compensation, simultaneously enhancing contrast and preserving naturalness.

  • Fit the color gamut of individuals with varying degrees of CVD in the Lab color space.

  • Thirteen volunteers with varying degrees of CVD were recruited to participate in a subjective evaluation experiment to compare the compensation effects of the state-of-the-art method with the proposed recoloring method.

2 Related work

2.1 CVD simulation

To visualize the color perception of individuals with CVD, Brettel et al. [2] proposed a dichromacy simulation method that models the color gamut of dichromats as two half-planes in the LMS color space. The simulation process involves a projection along the axis corresponding to abnormal cone cells. In addition, Machado et al. [23] constructed a model to simulate different degrees of CVD based on shifts in sensitivity curves and two-stage theory. In this paper, Machado et al.’s model [23] is adopted.

2.2 Image recoloring methods

Recoloring methods for improving color contrast in individuals with CVD have been proposed in the existing studies [12, 21, 22, 24, 25, 28]. For instance, in [12], a color remapping function was proposed that maps colors into the CVD gamut while maintaining the separation between each. Further, the optimization models of [22, 24, 25, 28] all include a luminance consistency constraint. In addition, for contrast enhancement, Lin et al. [21] distorted the color distribution in the opposing color space, but the changes from the original image were too significant to meet to the naturalness requirement. Image recoloring methods [6, 7, 10, 11, 13, 19, 20] all aimed to produce a recolored image as close to the original as possible for naturalness preservation. First, Hassan et al. [6, 7] increased the blue channel in proportion to the degree of perception bias, that is, the discrepancy between the real image and its CVD simulation. Yet, due to oversight of the relationship between pixels, the results showed significant contrast loss in the blue location. Further, Lau et al. [20] used k-means++ [1] to divide an image into numerous areas and enhance the contrast in nearby regions, whereas Huang et al. [13] reduced an image’s departure from the source and improved the contrast of each color pair. Meanwhile, to optimize their recoloring result, Kuhn et al. [19] utilized the mass-spring mechanism and introduced k-means for image quantization, and Huang et al. [10, 11] retrieved multiple key colors from photos or videos, which were then remapped for contrast improvement. Moreover, within the color gamut of dichromats, [32, 33] extracted and recolored a limited number of dominant colors, the former of which was achieved by thoroughly comparing candidate clusters in terms of pixel numbers and distances in both the image and color spaces, a process repeated each time. The aforementioned naturalness-preserving techniques [6, 7, 10, 11, 13, 19, 20, 32, 33] were all developed based on dichromacy simulation models [2, 23] and yielded positive results for dichromacy compensation. However, the subjective experimental results in [32, 33] also demonstrate considerable differences in perception between anomalous trichromats and dichromats. Indeed, the effect varies significantly according to the CVD color gamut. In other words, recoloring images based on the assumption of a single CVD degree makes it exceedingly difficult to obtain results appropriate to the various degrees of CVD. Wang et al. [29] proposed a fast recoloring method in which compensation is achieved by identifying a single optimal mapping route from the 3D color space to the CVD color gamut to enhance contrast and preserve naturalness simultaneously. Although the authors proposed to adjust the weight between contrast enhancement and naturalness preservation automatically according to the degree of contrast loss, the user must still set a weighting parameter. In the case of significant contrast loss, the effect on naturalness preservation of the method may be extremely limited. In response, Ebelin et al. [3] suggest an algorithm for recoloring images for dichromacy compensation while preserving luminance during recoloring. In addition, Huang et al. [14] proposed a contrast-enhanced and naturalness-preserving recoloring method that imposes hard constraints on the compensation range. Although the approach maintains a balance between contrast and naturalness, it fails to account for the varying degrees of CVD. In addition, Jiang et al. [17] proposed a personalized CVD-oriented image-generation method based on [18], but it does not allow users to specify the input image for the method. Further, Zhu et al. [34] proposed a personalized compensation algorithm that recolors images by minimizing the objective function constrained by contrast enhancement and naturalness preservation. However, this method is computationally inefficient and has complicated parameter settings. Moreover, because this method is performed in RGB space, the color gradient is poorly preserved in some images.

2.3 Color vision test

Typical clinical color vision tests include the Ishihara test [16], Farnsworth Panel D15 [5](Panel D15), Farnsworth 100 hue test [4](100-hue test), and anomaloscope test. The Ishihara test and Panel D15 are used to diagnose the type of CVD. Meanwhile, the 100-hue test and anomaloscope test can identify the degree of CVD, but their results cannot be directly applied to recoloring algorithms or used to define the color gamut of CVD.

3 Proposed method

In this paper, we proposed a novel recoloring method for anomalous trichromacy in Lab color space and its methodology was inspired by Huang et al. [14], details of whose work are presented in Sect. 3.1. The original image and its recoloring result are denoted as \(I_{i}\) and \(I_{i}^{\prime }\) and their simulations as \(\widetilde{I_{i}}\) and \(\widetilde{I^{\prime }_{i}}\), respectively. The fitting of different degrees of the CVD color gamut in Lab color space will be presented in Sect. 3.2, and Sects. 3.3–3.7 introduce the recoloring procedures of the proposed method. Finally, the discrete solver is explained in Sect. 3.8.

3.1 Background

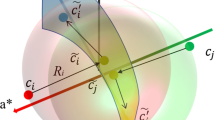
Huang et al. [14] proposed an image-recoloring method for red-green dichromacy compensation. Because the CVD color gamut modeled by Machado et al. [23] is defined in the RGB color space, Huang et al. [14] remapped the gamut from the RGB space to the Lab space. Then, a curved surface passing through the L*-axis of the Lab space was fitted using the least squares method. To maintain the naturalness of the original image, i.e., to minimize the deviation from the CVD perception of the original image, Huang et al. introduced pixel-wise compensation range (loss radius) \(R_{i}\), which is calculated as follows:

$$\begin{aligned} R_{i} = \left\| c_{i} - \widetilde{c_{i}} \right\| \end{aligned}$$
(1)

where \(c_{i}\) is a color in the original image and \(\widetilde{c_{i}}\) is the CVD simulation result for \(c_{i}\). In [14], it is assumed that naturalness of colors with smaller perception error should be preserved with a higher priority. In other words, colors whose distance to their CVD simulation result is small should be maintained preferentially. Meanwhile, each color \(c_{i}\) is constrained to find the recoloring result \(c_{i}^{\prime }\) within a sphere, which is with \(\widetilde{c_{i}}\) as the center and \(R_{i}\) as the radius. This procedure can be represented as adding a compensation vector \(\Delta c_{i}\) to \(\widetilde{c_{i}}\), \(\widetilde{c_{i}^{\prime }} = \widetilde{c_{i}} + \Delta c_{i}\), \(\left\| \Delta c_{i} \right\| \le R_{i}\). Since information loss of the a* component is severe, contrast loss probably will become severer especially when the paired colors locate on different side of the fitted curved surface. Therefore, all colors are divided into two categories according to their a* component values, and this procedure is carried out by a simplified criterion, namely, whether the value of a* component value is greater than 0. To efficiently enhance the contrast, colors in different categories will be moved in opposite directions using the following formula:

$$\begin{aligned} \widetilde{c_{i}^{\prime }} =\left\{ \begin{array}{ll} \widetilde{c_{i}}+\Delta c_{i} &{} a_{i} > 0\\ \widetilde{c_{i}} - \Delta c_{i} &{} a_{i} \le 0 \end{array}\right. \end{aligned}$$
(2)

where \(a_{i}\) denotes the a* component value of \(c_{i}\). Simultaneously, a global coefficient \(\alpha \in [-1, 1]\) is introduced to control the norm of the compensation vector \(\Delta c_{i}\), that is, \(\left\| \Delta c_{i} \right\| = \alpha R_{i}\). Therefore, determining the value of \(\alpha \) became a key task of [14]. In [14], this was achieved by minimizing the energy function to calculate the difference in contrast between the CVD simulation result of the recolored image and that of the original image. The energy function is represented as:

$$\begin{aligned} E = \sum _{\left\langle i , j \right\rangle \in P} \left( \left\| \widetilde{c_{i}^{\prime }} - \widetilde{c_{j}^{\prime }} \right\| ^{2} - \left\| c_{i} - c_{j} \right\| ^{2} \right) ^{2} \end{aligned}$$
(3)

where P is a set of pixel pairs, obtained by pairing each pixel with its adjacent pixel and global pixel, respectively, to ensure the simultaneous maintenance of local and global contrast in the result image. Finally, an energy function was adopted to find the optimal result.

Fig. 2
figure 2

Optimization procedures of the proposed method for Protan 40% in Lab color space. a Projection. b Compensation direction. c Optimization. d Result

Full size image

3.2 Color gamut

Because the projection matrix for anomalous trichromacy simulation proposed by Machado et al. [23] is defined in the RGB color space and the transformation between Lab and RGB color space is nonlinear, we propose herein to fit the CVD color gamut to the Lab color space. To construct the color gamut according to the varying degrees of CVD in Lab color space, we map the gamut defined in RGB color space by Machado et al. [23] to Lab color space. We initially sampled 262,144 color points (each of the R, G, and B channels with an interval of four) in RGB color space. For a specified combination of CVD type and degree, we utilized the simulation model of Machado et al. [23] to obtain the corresponding CVD color gamut in RGB color space. Subsequently, the gamut is transferred to Lab color space; that is, we adjust the color gamut of anomalous trichromacy to be hexagonal with six chromatic corner points in the RGB space, which are a red point (255, 0, 0), green point (0, 255, 0), blue point (0, 0, 255), yellow point (255, 255, 0), purple point (255, 0, 255), and cyan point (0, 255, 255) in RGB color space, respectively, except for black and white. As observed, the range along the b* axis is almost unaffected, while that along the a* axis is compressed gradually with an increase in degree.

3.3 Algorithm overview

As shown in Fig. 2, the whole colorized area corresponds to the gamut of normal color vision, while the gamut of CVD is delineated by a red line. Figure 2 provides an overview of the entire procedure of the proposed method. In general, for any arbitrary pixel with color \(c_{i}\) and its paired pixel with color \(g_{i}\) in the original image, the CVD simulation matrix in [23] is used to obtain the simulation results(\(\widetilde{c_{i}}\) and \(\widetilde{g_{i}}\)) within the CVD gamut. Simultaneously, the compensation range for each color is determined (Fig. 2a). Next, the compensation vector \(\Delta c_{i}\) for CVD simulated color \(\widetilde{c_{i}}\) is calculated. Specifically, calculating the compensation vector can be divided in two steps: a compensation direction calculation (Fig. 2b) and a compensation quantity calculation (Fig. 2c). Subsequently, the intermediate color result \(\widetilde{c_{i}^{\prime }}\) is obtained by adding \(\Delta c_{i}\) to \(\widetilde{c_{i}}\). Finally, to ensure the image \(\widetilde{I^{\prime }}\) is visible to individuals with CVD, the colors in \(\widetilde{I^{\prime }}\) must be mapped from the CVD gamut back to the original color space, namely, Lab color space, using a back-projection procedure (Fig. 2d). As the procedures of the proposed method, such as CVD simulation (Fig. 2a) and back-projection (Fig. 2d), can be executed independent of the image contents, except for the compensation vector calculation (Fig. 2b, c), the remaining parts of this paper aim to identify an appropriate compensation vector for each color projected onto the CVD gamut according to image contents.

3.4 Compensation range

In this study, a compensation range calculation formula similar to that in [14] is introduced. Initially, we calculate the loss radius \(R_{i}\) for color \(c_{i}\) based on Eq. (1). To facilitate naturalness and contrast adjustments, the loss radius \(R_{i}\) is then multiplied by a coefficient, referred to as the compensation range coefficient, \(\beta \) to control the scale of the compensation range. Consequently, the compensation range is calculated as follows:

$$\begin{aligned} CR_{i} = \beta * R_{i} \end{aligned}$$
(4)

where \(\beta \) (\(\beta >0\)) represents the compensation range coefficient, and the \(\beta \) value determines the compensation range for each color. A larger \(\beta \) can enhance the effect of contrast, but it may trade off naturalness preservation, while a smaller \(\beta \) has the opposite effect. In addition, the \(\beta \) value can vary with the degree of CVD. The optimal \(\beta \) value for each degree is provided in Table 1, and the procedure for obtaining these values will be explained in Sect. 4. Next, we calculate the compensation vector \(\Delta c_{i}\) for each color \(\widetilde{c_{i}}\) in \(\widetilde{I}\), within its compensation range \(CR_{i}\).

Table 1 \(\beta \) for different degrees of CVD
Full size table

3.5 Compensation vector

The compensation vector \(\Delta c_{i}\) consists of the compensation direction (\(\overrightarrow{d_{i}}\)) and compensation quantity \(q_{i}\), whereas the direction vector (\(\overrightarrow{d_{i}}\)) and compensation quantity \(q_{i}\) indicate the direction in which and distance that \(\widetilde{c_{i}}\) should move, respectively. Similar to [14], the proposed method maintains the luminance channel of colors in the image as unchanged, and after recoloring, we only make changes to the chromatic channels a* and b*; thus, the proposed method is performed on the two-dimensional (2D) a*b* plane. Consequently, compensation direction (\(\overrightarrow{d_{i}}\)) in this study is 2D, composed of a* and b* components. This contrasts with [14], whose compensation direction can be expressed as a binary, where colors move along the positive or negative direction of the b* axis. In this study, the compensation vector is calculated as follows:

$$\begin{aligned} \Delta \overrightarrow{c_{i}} = \alpha *CR_{i}*\overrightarrow{d_{i}} \end{aligned}$$
(5)

where \(\alpha \left( \alpha \in \left[ -1, 1 \right] \right) \) is the compensation coefficient utilized to enhance contrast in \(\widetilde{I^{\prime }}\). According to the above equations, the compensation vector \(\Delta \overrightarrow{c_{i}}\) can also be represented as \(\Delta \overrightarrow{c_{i}}=\left( \Delta a_{i}, \Delta b_{i} \right) \), indicating compensation quantities in the direction of the a* and b* axes, respectively. Then, we add \(\Delta a_{i}\) and \(\Delta b_{i}\) of \(\Delta \overrightarrow{c_{i}}\) to the a* and b* components of the corresponding simulation color of pixel \(\widetilde{c_{i}}\) in the simulation image, respectively, and the associated formula is as follows:

$$\begin{aligned} \widetilde{c_{i}^{\prime }}\overleftarrow{}\widetilde{c_{i}}+\Delta \overrightarrow{c_{i}} \end{aligned}$$
(6)

where \(\widetilde{c_{i}^{\prime }}\) denotes a homogeneous color in the intermediate image \(\widetilde{I^{\prime }}\). Next, we will introduce two steps to determine the compensation direction (\(\overrightarrow{d_{i}}\)) for each color \(\widetilde{c_{i}}\): the primary direction and the cluster direction.

3.5.1 Primary direction

The direction vector \(\overrightarrow{d_{i}}\) is composed of the a* component \(a_{i}\) and the b* component \(b_{i}\), which can be represented as \(\overrightarrow{d_{i}} = \left( a_{i}, b_{i} \right) \). Because the CVD gamut range in the b*-axis direction is almost the same as that of normal vision, it is necessary to enhance the contrast between colors along the b*-axis. Therefore, we calculate the compensation direction according to the degree of contrast loss between two colors concretely, the larger the contrast loss, the smaller the angle between \(\overrightarrow{d_{i}}\) and the b* axis. For each color \(c_{i}\), the compensation direction can be used to enhance its contrast with the paired color \(g_{i}\), and the a* and b* components of the direction vector \(\overrightarrow{d_{i}}\) are calculated as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} a_{i} = \frac{\sqrt{\left( \widetilde{a_{c}} - \widetilde{a_{g}}\right) ^{2}+\left( \widetilde{b_{c}} - \widetilde{b_{g}}\right) ^{2}} }{\sqrt{\left( a_{c} - a_{g}\right) ^{2}+\left( b_{c} - b_{g}\right) ^{2}}} &{}\quad e.t.0\le a_{i}\quad \textrm{and}\quad b_{i}\le 1\\ a_{i}^{2}+b_{i}^{2} = 1 &{} \end{array}\right. \end{aligned}$$
(7)

where \(a_{c}, a_{g}, b_{c}\) and \(b_{g}\) are the a* and b* component values of \(c_{i}\) and \(g_{i}\), and \(\widetilde{a_{c}}, \widetilde{a_{g}}, \widetilde{b_{c}}\), and \(\widetilde{b_{g}}\) denote a* and b* component values of CVD simulations for \(c_{i}\) and \(g_{i}\), respectively. However, such a mechanism can only produce compensation in the positive directions of the a* and b* axes. Inspired by Huang et al. [14], a portion of the compensation directions obtained by Eq. (7) are reversed according to their “color category” and paired colors, especially compensation for the contrast between colors on different sides of the b* axis should be considered. For any color \(c_{i}\) in the original image, it can be divided into distinct categories according to its a* component value, i.e., category 1: \(a \ge 0\); category 2: \(a<0\). For category 1, there is no need to change the direction on the b* axis, as shown in Fig. 3b, d, that is, \(b_{i}\). For category 2, the sign of b will be reversed as shown in Fig. 3a, c, that is \(b_{i}\rightarrow -b_{i}\).

Fig. 3
figure 3

Direction correction illustration. a \(\widetilde{g_{i}}\) is on the left of \(\widetilde{c_{i}}\) and the a* component value is bigger than 0. c \(\widetilde{g_{i}}\) is on the right of \(\widetilde{c_{i}}\) and the a* component value is less than 0. The gray arrows a, c represent the direction before correction, and the black arrows b, d represent the direction after correction

Full size image

For the a* component \(a_{i}\), we process it according to the relationship with the paired color \(g_{i}\). As shown in Fig. 3a, c, if \(\widetilde{c_{i}}\) is located to the left of \(\widetilde{g_{i}}\), it is assumed that \(\widetilde{c_{i}}\) should be moved toward the negative direction of the a* axis, i.e., \(a_{i}\rightarrow -a_{i}\); for the case shown in Fig. 3b, d, the direction is kept.

3.5.2 Cluster direction

Although the contrast of the compensated image can improve after performing the direction calculation following Sect. 3.5.1, it may cause false contrast in the local area of the image, which can be perceived as noise (Fig. 4). This issue can be caused by a color pairing being performed randomly, leading to a phenomenon in which similar colors can be assigned to extremely different compensation directions. To overcome this problem, we utilize the k-means algorithm to cluster all pixels \(p_{i}\) into k classes according to their corresponding color and to aggregate the compensation directions within each class to establish a unified compensation direction for said class. Specifically, the average of the primary direction vectors of all colors in the class is calculated and assigned to all colors in the class. At this point, all coefficients and variables related to the compensation vector have been solved, except for the compensation coefficient \(\alpha \). To determine the best alpha for the resulting image, an optimization model is introduced.

Fig. 4
figure 4

Comparison image with and without clustering, a original image, b image without clustering. c Image with clustering

Full size image

3.6 Optimization model

Because the naturalness in the recolored image is guaranteed by the loss radius of each color, an energy function is introduced to obtain the optimal contrast enhancement result. Ideally, contrast between the two colors \(\widetilde{c_{i}^{\prime }}\) and \(\widetilde{c_{j}^{\prime }}\) in the intermediate image should be the same as that between the colors \(c_{i}\) and \(c_{j}\) in the original image. Therefore, the energy function is used to calculate the difference between two kinds of contrast, and it is defined as follows:

$$\begin{aligned} E = \sum _{\left\langle i , j \right\rangle \in P} \left( \left\| \widetilde{c_{i}^{\prime }} - \widetilde{c_{j}^{\prime }} \right\| ^{2} - \eta \left\| c_{i} - c_{j} \right\| ^{2} \right) ^{2} \end{aligned}$$
(8)

where P is a set of pixel pairs obtained by pairing \(c_{i}\) on pixel \(p_{i}\) with color \(c_{j}\) on a randomly paired pixel \(p_{j}\), and \(\eta \) is the contrast enhancement coefficient, which controls the degree of contrast enhancement compared to the original image. In this paper, we set the value of \(\eta \) to 1, and in case the color \(\widetilde{c_{i}^{\prime }}\), obtained from the optimization model, is outside the color gamut, it will be pulled back to the intersection between the compensation vector and the border of the color gamut, a process depicted in Fig. 2c.

3.7 Back-projection

Finally, we use back-projection to obtain the recoloring result, as shown in Fig. 2d. CVD simulation models provide mapping approaches that project color from the original color space to the CVD gamut, whereas calculating an original color from a color in the CVD gamut is the reverse of CVD simulation. In this study, we employ a pre-built lookup table (LUT) to facilitate back-projection, and its construction involved the following procedures:

  1. (1)

    Given all colors in RGB color space, Machado et al.’s method [23] is used to generate corresponding CVD-simulated colors, and the simulated results are rounded to their closest integers;

  2. (2)

    Colors before and after CVD simulation are transferred from RGB color space to Lab color space;

  3. (3)

    A simulated color is selected as the key for the LUT, while the corresponding original color becomes its paired value.

Fig. 5
figure 5

The procedure of back-projection

Full size image
Fig. 6
figure 6

Recoloring results output by Huang [14] the state-of-the-art method [34] and the proposed method for users with Protan defects (degrees of 40, 60, 100%)

Full size image

One should note that multiple colors in the original color space may be projected to the same position in the CVD gamut; as a result, one CVD-simulated color can correspond to multiple original colors. As shown in Fig. 5, from the viewpoint of naturalness preservation, when inquiring about a simulated color \(\widetilde{c_{i}^{\prime }}\) in \(\widetilde{I^{\prime }}\), the color in LUT, which is closest to its homogeneous pixel color \(c_{i}\) in I, is selected.

Fig. 7
figure 7

Recoloring results output by Huang [14] the state-of-the-art method [34] and the proposed method for users with Deutan defects (degrees of 40, 60, 100%)

Full size image

3.8 Solver

To find the best compensation coefficient \(\alpha \), the gradient descent method can be a common solution. However, in this study, we adopted a discrete solver, similar to that in [14], and this strategy can hasten the proposed method while still producing results closest to the best solution. Given a range of values for the compensation coefficient \(\alpha \in \left[ -1, 1 \right] \) and a step size of 0.1, the solution space is discretized into 20 equal parts, and 21 candidates, that is, \(\alpha = -1.0, -0.9, \dots , 0.9, 1.0\), can be obtained. By substituting all candidates into Eq. (8), the solution that minimizes the energy function E is selected as the final result, which could clearly be more accurate if a smaller step size were set, though this will increase computation time.

4 Evaluation

In this study, qualitative and quantitative evaluation experiments were conducted, comparing the proposed method with Huang et al.’s method [14] and the state-of-the-art method [34]. Additionally, subjective experiment was conducted to compare the state-of-the-art method [34] with the proposed method.

4.1 Qualitative evaluation

Figures 6 and 7 show examples of compensation results for different degrees of the protan and deutan defects using existing methods [14, 34] and the proposed method, respectively. In Figs. 6 and 7, there are eight columns of images: the first and second columns show the original image and its simulation for different degrees of CVD; column three, column five and column seven show Huang et al.’s [14], Zhu et al.’s[34] compensation results and the proposed method’s results; and column four, column six and column eight depict the simulation results of corresponding degrees of CVD for Huang et al. [14], Zhu et al. [34] and the proposed method. In Fig. 6, people with a severe protan defect have more difficulty distinguishing between the pink rose and green leaves. Compared with the original image (Fig. 6a), the brightness of the rose in CVD perception (Fig. 6b) is significantly reduced, potentially making it difficult to identify details. In response, the image recolored using Huang et al.’s [14] (Fig. 6c) and Zhu et al.’s method [34] (Fig. 6e) enhanced the contrast between the rose and foliage. However, the methods have certain limitations: first, the rose turns blue in Huang et al.’s method [14] and the leaves turn blue in Zhu et al.’ method [34], creating an unnatural appearance for users with CVD; second, the brightness of the flower decreases compared to the original image (Fig. 6a), hindering the identification of details in Zhu et al.’s method [34]. In the recolored images produced using the proposed method (Fig. 6g, h), the color appearance of the leaves is maintained. Thus, for all degrees of CVD, the proposed method aims to preserve color as closely as possible to the simulation results in Fig. 6b. Further, it is evident that the brightness of the resulting image produced using the proposed method is much closer to that of the original image than in [34], making it easier for individuals with CVD to identify details in the flower. A similar situation can also be observed in the result of compensation for the deutan defect. In Fig. 7, with an increase in the degree of the deutan defect, the CVD simulation result demonstrated that it becomes much more difficult to distinguish the rose from the background or to identify details in the flower. Recolored images produced by [14, 34] enhanced the contrast between the flower and leaves and increased the brightness of the flower well; however, the leaves were recolored bluish in [34], that is, naturalness was not well preserved. Although Huang’s method [14] performs well at high degree of CVD, it suffers from significant losses in naturalness at medium and low degrees of CVD. The image result from the proposed method (Fig. 7g) better preserves the brightness of the original image, especially in the flower part, and the colors of the leaves appear more natural than in [34].

4.2 Quantitative evaluation

To evaluate the compensation results of the existing method [34] and the proposed method quantitatively, the color difference (CD) and local contrast error (LCE) metrics introduced in [31] are adopted to assess the preservation of naturalness and the enhancement of contrast of the 12 resulting images using each method, respectively. The CD metric calculates the color distance of homologous pixels between the test image \(I^{t}\) and the reference image \(I^{r}\). In this study, the CD metric is computed in Lab space, which can be represented as:

$$\begin{aligned} CD\left( I^{t},\ I^{r} \right) = \frac{1}{N}\sum _{i=1}^{N}\left\| c_{i}^{t} -c_{j}^{r} \right\| \end{aligned}$$
(9)

where \(c_{i}^{t}\) and \(c_{i}^{r}\) represent the colors of homologous pixels in the test and reference images, respectively, and N denotes the total number of pixels in the image. In this study, the compensation and original images are set as the test and reference images, respectively. A smaller result for the CD metric means a more natural image compensation, and as shown in Table 2, the CD scores of the proposed method are lower than those of Huang et al. [14] and Zhu et al. [34] for all degrees of CVD, indicating that the proposed method preserves naturalness better than Huang et al. [14] and Zhu et al. [34].

Table 2 CD scores for different degrees of CVD in Protan and Deutan
Full size table
Table 3 LCE scores for different degrees of CVD in Protan and Deutan
Full size table

The LCE metric calculates the difference in local contrast between two images, and it can be represented as follows:

$$\begin{aligned} LCE = \sqrt{\frac{1}{k}\sum _{j\in S}\left\{ \frac{\left\| sim\left( c_{i}^{\prime }\right) - sim\left( c_{j}^{\prime }\right) \right\| - \left\| c_{i} - c_{j} \right\| }{160} \right\} ^{2} } \end{aligned}$$
(10)

where S indicates a set of randomly selected pixels from the neighborhoods of \(c_{i}\) and k denotes the number of pixels in S. \(c_{i}\) and \(c_{j}\) are pixels in the reference image, and \(c_{i}^{\prime }\) and \(c_{j}^{\prime }\) are pixels in the test image. Further, sim denotes the simulation process, and the constant 160 regulates the output within the range of \(\left[ 0,1 \right] \). The metric used here, termed LCE, serves as a local contrast evaluator, determining the relative contrast error between the reference and test images. Here, a smaller LCE value indicates superior contrast preservation; notably, in Table 3, compared to Huang’s approach [14], results for protan are superior across all degrees, while for deutan, they are superior at low to medium degrees but are comparable at high degrees. Our method consistently demonstrates lower LCE values compared to Zhu’s [34] results across various degrees of CVD, signifying the efficacy of our approach in achieving superior contrast enhancement.

4.3 Subjective evaluation

In the subjective assessment experiment, 13 volunteers with CVD were invited to evaluate the recolored images produced using the proposed and the state-of-the-art method [34] according to naturalness preservation and contrast enhancement. The volunteers were aged 18–60 years and were tested individually for color vision, using the Ishihara test, Panel D15 and 100-hue test. The test results are shown in Table 4, of which six show a protan and seven a deutan defect. Specifically, the 100-hue test result can be considered an indicator of CVD severity, where the higher the score, the greater its acuteness; if the score is over 80, the examinee is suspected to have a specific degree of CVD. According to interviews with our volunteers, the following criteria of the 100-hue rest score, s, were empirically set to classify disease severity as “mild”, “medium”, and “high”:

  • \(Mild: 80<s \le 200\)

  • \(Medium: 200<s \le 300\)

  • \(Severe: s > 300\)

Table 4 The color vision test results of thirteen participants
Full size table

During the experiment, images were shown on an EIZO CS2400S screen, which was calibrated using an X-Rite i1Display 2. Participants in the experiment were seated 0.5 m from the screen, and a two-hour experiment involving a single subject was conducted. For the naturalness evaluation, volunteers were required to evaluate the color similarity between the original and recolored images. Because there is no effective approach to calibrate the gamut of individuals with CVD precisely, images recolored according to varying CVD degrees were shown to each participant individually. In this study, we generated compensation images for 40, 60, 80, and 100% using the proposed method and the method in [34], respectively. As the value \(\beta \) determines the compensation size, a larger \(\beta \) leads to more significant image contrast enhancement, but at the cost of decreased naturalness preservation. Therefore, we compute the optimal \(\beta \) at which the variation curves of naturalness (CD) and contrast (LCE) intersect. In Table 1, we present the selected values of \(\beta \) for different degrees of CVD, aiming to strike as even a balance between preserving naturalness and enhancing contrast as possible. Therefore, together with the original image, 12 kinds of recolored images form an image set to be shown. For each recolored image, a participant was required to rate it on a scale of 1–5, with 1 indicating completely different and 5 indicating almost identical. The higher the score, the better the natural preservation of recolored images. The average scores of each volunteer are shown in Table 5.

Table 5 Mean results of naturalness assessment for subjective experiments
Full size table
Table 6 Mean results of contrast assessment for subjective experiments
Full size table

We can see that for most results, our method achieves better scores. Thus, the compensation effect of the proposed method is comparable to Zhu et al.’s method [34] in terms of naturalness preservation. Conversely, for the contrast evaluation, volunteers were required to evaluate the contrast of recolored images in comparison with the original image. Each recolored image was rated on a scale of 1–5:

  1. 1.

    Contrast further decreased or strange information is further provided.

  2. 2.

    Contrast decreased or strange information is provided.

  3. 3.

    Almost no change from the original image.

  4. 4.

    Contrast increased.

  5. 5.

    Contrast increased more.

The contrast evaluation results are shown in Table 6, where we can see that almost all results of the proposed method are superior to those of Zhu et al.’s method [34], indicating that ours performs better in terms of contrast enhancement. In addition, we also found that the scores of our results were all greater than three, meaning our method preserves naturalness better, while also enhancing contrast.

4.4 Computation time

In this study, all compensation methods were implemented on a PC with an AMD CPU@3.80GHz and 16 GB of RAM installed. On average, our method takes less than 6 s to process images with an average of 200 K pixels, whereas [34] requires more than 20 s.

4.5 Information visualization experiment

To verify the information visualization capability of the proposed method, we conducted experiments on Ishihara Test Charts involving the 13 participants above. Because it is unnecessary to consider naturalness preservation for the Ishihara Test Charts, inspired by [23], we expanded the \(\beta \) and \(\eta \) ten-fold as compensation. The accuracy of the Ishihara compensation result and the results produced by the proposed method is more than 95%, illustrating the effectiveness of our approach in terms of information visualization capabilities.

5 Conclusion and discussion

In this paper, we proposed a personalized and hasty image recoloring method for CVD compensation. By transferring the color gamut according to varying degrees of CVD from RGB to the perceptually uniform Lab color space, we effectively enhanced color contrast while maintaining a natural image appearance. The quantitative and subjective evaluation experiments showed that our approach outperforms existing methods of contrast enhancement and is comparable to the existing method for maintaining image naturalness. Nevertheless, the proposed method requires further improvement. Considering the limitations of computational efficiency, one potential direction is to explore the possibility of real-time implementation, but the algorithmic technique should be optimized, and deep learning or machine learning should be used to replace part of the algorithmic processes. In addition, future research could focus on integrating advanced machine-learning techniques to enhance the adaptability of the algorithm for more accurate and precise CVD compensation at the individual level.