The inverse barycentric displacement problem

Abstract

In this short paper, we analyze the problem of finding the triangular barycentric coordinates of an interpolated ray hitting a given point. This task, which we term the inverse barycentric displacement problem, is general and useful in geometry processing and computer graphics. Concrete applications of the solution include the construction of displacement maps and texture baking. We derive the set of complete, closed-form solutions and discuss the number and existence of solutions. We close with a discussion of implementation-oriented optimizations and a few example applications.

1 Introduction

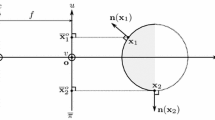
Consider a 3D embedded triangle $\mathcal {T}$ with arbitrary displacement vectors ($\textbf{d}_i$) defined at its corners ($\textbf{v}_i$) (Fig. 1, left). A ray is defined starting at a barycentrically interpolated point $\textbf{v}$ on $\mathcal {T}$, where $\textbf{v}=u \textbf{v}_0+v \textbf{v}_1+w \textbf{v}_2$, and traveling in the direction of the (corresponding) barycentrically interpolated displacement $\textbf{d}$. Traveling along this ray, a displaced point $\textbf{q}$ is defined at parametric position t:

$$\begin{aligned} \textbf{q}= \textbf{v}+ t \, \textbf{d} \end{aligned}$$

(1)

t is the scalar displacement value defined at $\textbf{v}$ and may be stored in a scalar displacement texture covering $\mathcal {T}$. In a common scenario, we are given an interpolated position $\textbf{v}$ and direction $\textbf{d}$ on $\mathcal {T}$, and we want to find $\textbf{q}$, typically on a given target surface (dotted line in Fig. 1, right). For example, $\textbf{q}$ can be found by ray casting against a high-resolution mesh. Here, we use the term direct displacement to refer to the problem of finding $\textbf{q}$ (equivalently, $t$) for specified $\textbf{v}$ and $\textbf{d}$.

Fig. 1

left - The inputs of the displacement problem (direct or inverse.) right - A 2D depiction (note that in 3D, the 3 corner rays do not meet at a point, which would otherwise make the problem trivial.)

In this work, we are interested in the inverse of the direct displacement problem, where we are given a target point $\textbf{q}$ and we want to find a position $\textbf{v}$ on $\mathcal {T}$ such that the ray defined on $\textbf{v}$ hits $\textbf{q}$. The solution is interesting, useful, and non-trivial.

Rationale: The inverse problem is useful in several contexts. For example, it makes it possible to bake or compute a displacement map, or a texture for $\mathcal {T}$ by processing positions $\textbf{q}$ directly on the target displaced surface, this sidesteps the need for ray casting, which typically requires expensive iteration over the numerous elements of a high-resolution, tessellated target surface. The design of good support meshes to be displaced can also benefit from the ability to quickly identify where on a potential $\mathcal {T}$, if anywhere, a given point $\textbf{q}$ on the target surface would be mapped.

The inverse mapping problem is not trivial, and, in spite of its potential usefulness, has never been solved in closed form (to our knowledge). The nontriviality is confirmed by the observation that the solution does not necessarily exist, nor is it necessarily unique, and certain configurations, for example when all three rays meet into $\textbf{q}$, even admit infinite solutions for $\textbf{v}$, as $\textbf{q}$ can be reached from any point on $\mathcal {T}$.

Related work: Traditionally, in contexts such as texture baking, displacement-map construction (for curved surface representations or polygonal meshes), inverse subdivision surfaces, and others, existing solutions are designed to leverage solely on the solution of the direct problem. This may be due, at least in part, to the perceived intricacy of the inverse problem, which is the subject of this work. In Sect. 5, we exemplify two scenarios where our closed-form solution to the inverse problem offers a compelling alternative to traditional solutions. The description of each scenario starts with a brief overview of the respective Related Work.

2 Problem definition

Given a target point $\textbf{q}$, we want to find a point $\textbf{v}$ on $\mathcal {T}$ such that the ray shot from $\textbf{v}$ in the interpolated direction $\textbf{d}$ hits $\textbf{q}$ (1).

Let the corners of $\mathcal {T}$ be in positions $\textbf{v}_0, \textbf{v}_1, \textbf{v}_2$, and let the three directions defined at corners be $\textbf{d}_0$, $\textbf{d}_1$, $\textbf{d}_2$. A point $\textbf{v}$ is identified by its nonnegative barycentric coordinates $\alpha _0, \alpha _1, \alpha _2$ with

$$\begin{aligned} \sum _i{\alpha _i} = 1 \end{aligned}$$

(2)

so that:

$$\begin{aligned} \textbf{v}&= \sum _i \alpha _i \, \textbf{v}_i \end{aligned}$$

(3)

$$\begin{aligned} \textbf{d}&= \sum _i \alpha _i \, \textbf{d}_i. \end{aligned}$$

(4)

Substituting (3, 4) in (1), gives

$$\begin{aligned} \textbf{q}= \sum _i \alpha _i \, \textbf{v}_i + t \sum _i \alpha _i \, \textbf{d}_i \end{aligned}$$

(5)

where the three scalars $\alpha _i$ and the scalar t are unknowns.

This seemingly simple geometric setup leads to a system, (5), of three scalar equations, quadratic with the four variables, subject to the linear constraint (2). This system is not trivial to solve directly.

3 Geometric derivation of the solution

We can rewrite Equation (5) as

$$\begin{aligned} \textbf{q}&= \sum _i \alpha _i \, ( \textbf{v}_i + t \, \textbf{d}_i) \nonumber \\&= \sum _i \alpha _i \, \textbf{a}_i \end{aligned}$$

(6)

with $\textbf{a}_{0,1,2}$ denoting the position of the vertices of $\mathcal {T}$ displaced by $t$ along the respective direction:

$$\begin{aligned} \textbf{a}_i&= \textbf{v}_i + t\, \textbf{d}_i \end{aligned}$$

(7)

Equation (6) implies that the target point $\textbf{q}$ must necessarily lie on the plane $\mathcal {P}$ passing by the three positions $\textbf{a}_i$ (see Fig. 1), irrespective of the choice of $\textbf{v}$; observe that $\mathcal {P}$ is a function solely of $t$ (and different choices of $t$ result in general in planes with different orientations). Moreover, it implies that the barycentric coordinates of $\textbf{q}$ in triangle $\textbf{a}_0, \textbf{a}_1, \textbf{a}_2$ are the same as the sought barycentric coordinates $\alpha _0,\alpha _1,\alpha _2$ of $\textbf{v}$ in $\mathcal {T}$.

Our solution is therefore to first find value(s) of $t$ so that $\textbf{q}$ lies on $\mathcal {P}$, and then simply find $\alpha _0,\alpha _1,\alpha _2$ (and thus $\textbf{v}$) with fixed t as the barycentric coordinates of $\textbf{q}$ inside triangle $\textbf{a}_0, \textbf{a}_1, \textbf{a}_2$.

The condition for $\textbf{q}$ to be on $\mathcal {P}$ can be expressed as

$$\begin{aligned} 0 = ( \textbf{a}_0 - \textbf{q}) \cdot \textbf{n}, \end{aligned}$$

(8)

that is, that the vector connecting $\textbf{q}$ to $\textbf{a}_0$ is orthogonal to $\textbf{n}$, with $\textbf{n}$ denoting a vector orthogonal to $\mathcal {P}$ ($\textbf{n}$ is, again, as a function of t):

$$\begin{aligned} \textbf{n}= ( \textbf{a}_1 - \textbf{a}_0) \times ( \textbf{a}_2 - \textbf{a}_0). \end{aligned}$$

(9)

Rewriting (8) in terms of $\textbf{v}, \textbf{d}$ and $t$ gives:

$$\begin{aligned} 0&=( \textbf{a}_0 - \textbf{q}) \cdot ( \textbf{a}_1 - \textbf{a}_0) \times ( \textbf{a}_2 - \textbf{a}_0) \nonumber \\ {}&= ( \textbf{v}_0 + t\, \textbf{d}_0 - \textbf{q})\nonumber \\&\quad \cdot ( \textbf{v}_1 + t\, \textbf{d}_1 - \textbf{v}_0 - t\, \textbf{d}_0)\nonumber \\&\quad \times ( \textbf{v}_2 + t\, \textbf{d}_2 - \textbf{v}_0 - t\, \textbf{d}_0) \nonumber \\ {}&= \left( ( \textbf{v}_0 - \textbf{q}) + t\, \textbf{d}_0 \right) \nonumber \\&\quad \cdot \left( ( \textbf{v}_1 - \textbf{v}_0) + t\, ( \textbf{d}_1 - \textbf{d}_0) \right) \nonumber \\&\quad \times \left( ( \textbf{v}_2 - \textbf{v}_0) + t\, ( \textbf{d}_2 - \textbf{d}_0) \right) \end{aligned}$$

(10)

This gives a polynomial that is cubic in $t$.

3.1 Deriving the polynomial coefficients

To ease the derivation of the coefficients of the polynomial in (10), it is convenient to group the constant sub-expressions in (10) as columns of two $3\times 3$ matrices:

$$\begin{aligned} \textbf{P}&= \left[ \, \textbf{v}_0- \textbf{q}\,|\, \textbf{v}_1- \textbf{v}_0 \,|\, \textbf{v}_2- \textbf{v}_0 \,\, \right] , \end{aligned}$$

(11)

$$\begin{aligned} \textbf{D}&= \left[ \, \,\,\,\,\,\, \textbf{d}_0 \,\,\,\,\, \,|\, \textbf{d}_1- \textbf{d}_0 \,|\, \textbf{d}_2- \textbf{d}_0 \, \right] \end{aligned}$$

(12)

We term $\textbf{P}$ the position matrix, as it depends on the positions of vertices of $\mathcal {T}$ and of target point $\textbf{q}$; we term $\textbf{D}$ the displacement matrix, as it depends on the displacement directions defined at the vertices of $\mathcal {T}$. We will refer to their columns as $\textbf{P}_0$, $\textbf{P}_1$, $\textbf{P}_2$ (and likewise for $\textbf{D}$).

Fig. 2

Construction for the geometric solution

We can now rewrite (10) as

$$\begin{aligned} 0&= (\textbf{P}_0 + t\, \textbf{D}_0) \cdot (\textbf{P}_1 + t\, \textbf{D}_1) \times (\textbf{P}_2 + t\, \textbf{D}_2) \end{aligned}$$

(13)

That is (remembering that $\det ( \textbf{a}| \textbf{b}| \textbf{c})$ is $\textbf{a} \cdot ( \textbf{b} \times \textbf{c})$):

$$\begin{aligned} 0&= \det \left( \textbf{P}+ t\, \textbf{D}\right) . \end{aligned}$$

(14)

Extracting t gives (see Appendix for a derivation):

$$\begin{aligned} 0 = A \, t^3 + B \, t^2 + C \, t + D \end{aligned}$$

(15)

with

$$\begin{aligned} A =&\det ( \textbf{D}) \nonumber \\ B =&\det ( \textbf{P}_0 | \textbf{D}_1 | \textbf{D}_2 ) +\det ( \textbf{D}_0 | \textbf{P}_1 | \textbf{D}_2 ) + \det ( \textbf{D}_0 | \textbf{D}_1 | \textbf{P}_2 ) \nonumber \\ C =&\det ( \textbf{D}_0 | \textbf{P}_1 | \textbf{P}_2 ) + \det ( \textbf{P}_0 | \textbf{D}_1 | \textbf{P}_2 ) + \det ( \textbf{P}_0 | \textbf{P}_1 | \textbf{D}_2 )\nonumber \\ D =&\det ( \textbf{P}) \end{aligned}$$

(16)

3.2 Finding all valid solutions (if any)

Solving (15) with the standard cubic formula returns up to three real solutions for $t$, which we denote as $t_0$, $t_1$, and $t_2$.

For a given choice of $t_i$, the corresponding triangle $\textbf{a}_0, \textbf{a}_1, \textbf{a}_2$ is constructed (7), then, $\alpha _i$ are trivially extracted as the barycentric coordinates of $\textbf{q}$ in that triangle:

$$\begin{aligned} \alpha _i = \frac{ \textbf{n}\cdot ( \textbf{q}- \textbf{a}_{i+2}) \times ( \textbf{a}_{i+1} - \textbf{a}_{i+2} ) }{ \textbf{n}\cdot \textbf{n}}. \end{aligned}$$

(17)

If any $\alpha _i<0$, then $\textbf{v}$ is outside the triangle $\mathcal {T}$, and the corresponding solution $t_i$ must be discarded (after [14], this can be conveniently tested prior to the division by $\textbf{n}\cdot \textbf{n}$).

This procedure fails when the triangle $\textbf{a}_0, \textbf{a}_1, \textbf{a}_2$ is degenerate, that is, when it collapses into a line or a point (meaning that the used value of $t_i$ satisfies (8) but only in the trivial sense that $\textbf{n}$ is the zero vector). This condition can be detected by checking that $\textbf{n}$ (9) vanishes. If the target point $\textbf{q}$ happens to belong to this line or point, then we have infinite solutions for $\alpha _i$ – and therefore, with (4), for $\textbf{v}$; otherwise, the solution $t_i$ must be discarded.

Depending on the context, negative values of $t_i$, or values larger than one, may also be discarded as invalid (when “backward” negative displacement, or displacements shooting “beyond $\textbf{d}$,” are to be disallowed).

Each non-discarded $t_i$, if any, results in a valid solution to the inverse projection problem. Multiple such solutions can exist. A possible strategy to employ in such cases is to consistently favor the smallest value of $|t_i|$, which has the benefit of making $\textbf{v}$ vary with continuity as $\textbf{q}$ varies (barring degenerate cases).

Special cases: It is interesting to analyze a few special cases of the general formulation above, although an implementation does not need to be aware of them.

When $\textbf{q}$ is on $\mathcal {T}$, or on the plane containing $\mathcal {T}$, then the position matrix $\textbf{P}$ is singular (its three columns are co-planar), so D is zero, and $t=0$ is always a solution of (15), as expected (observe that it is not necessarily the only solution).

When the displacement vectors $\textbf{d}_i$ are all parallel to each other (even if with different lengths), then the direction matrix $\textbf{D}$ is singular and rank 1 (as the determinant and rank of $\textbf{D}$ are the same as $[ \textbf{d}_0 | \textbf{d}_1 | \textbf{d}_2]$). This makes both A and B zero (as taking any two vectors from $\textbf{D}$ zeroes the determinant), making the polynomial (15) linear, and the solution for $t$ unique. This is also expected, from a geometric point of view (observe however that this still does not make all planes $\mathcal {P}$ parallel to each other, for all $t$: that additionally requires all displacement vectors to be the same length).

A pathological case is when all $\textbf{d}_i$ are in the same plane as $\mathcal {T}$. In that case, A, B, and C are zeroed (as each matrix is made by co-planar column vectors), making the polynomial (15) degree 0. Unless D is also 0, when $\textbf{q}$ is also on the plane of $\mathcal {T}$, there is no solution for $t$, valid or otherwise, as expected.

4 Implementation and optimizations

A reference implementation (in C++) is provided in the additional materials.

Workload: For the sake of simplicity, we will estimate the workload by counting the number of floating-point products (disregarding sums; among other reasons, because most can be absorbed by Multiply-and-Add operations). Finding the coefficients as in (,16) involves the computations of 8 determinants, that is, 8 cross products and 8 dot products, amounting to 72 products (each cross costing 6 floating-point products, and each dot costing 3).

Common sub-expressions optimization: using three temporary vectors, $\mathbf { \textbf{t}_{DD}}, \mathbf { \textbf{t}_{PD}}$ and $\mathbf { \textbf{t}_{PP}}$, allows the computation of A, B, C, D with only 4 cross products and 6 dot products (42 products in total):

$$\begin{aligned}&\mathbf { \textbf{t}_{DD}}\quad \leftarrow \textbf{D}_1 \times \textbf{D}_2 \\&\mathbf { \textbf{t}_{PD}}\quad \leftarrow \textbf{P}_1 \times \textbf{D}_2 + \textbf{D}_1 \times \textbf{P}_2 \\&\mathbf { \textbf{t}_{PP}}\quad \leftarrow \textbf{P}_1 \times \textbf{P}_2 \end{aligned}$$

(the latter is also the area vector of $\mathcal {T}$) then rewriting (16) as

$$\begin{aligned} A \leftarrow&\, \textbf{D}_0 \cdot \mathbf { \textbf{t}_{DD}}&D \leftarrow&\, \textbf{P}_0 \cdot \mathbf { \textbf{t}_{PP}}\\ B \leftarrow&\, \textbf{P}_0 \cdot \mathbf { \textbf{t}_{DD}}+ \textbf{D}_0 \cdot \mathbf { \textbf{t}_{PD}}&C \leftarrow&\, \textbf{D}_0 \cdot \mathbf { \textbf{t}_{PP}}+ \textbf{P}_0 \cdot \mathbf { \textbf{t}_{PD}}\end{aligned}$$

Caching optimization: When the inverse projection problem must be solved for multiple target points $\textbf{q}$ over the same triangle $\mathcal {T}$, only $\textbf{P}_0$ varies in each instance of the problem: The three temporary vectors, as well as three scalars A, $\textbf{D}_0 \cdot \mathbf { \textbf{t}_{PD}}$, and $\textbf{D}_0 \cdot \mathbf { \textbf{t}_{PP}}$, can be cached for a given triangle, reducing the cost of finding the four coefficients for a new $\textbf{q}$ to just three dot products (9 products in total).

5 Example applications

As we argued in Sect. 1, the presented inverse problem can find applications in several contexts in Geometry Processing. In the following, we briefly exemplify this with two use cases. A full implementation of both examples is attached in the additional material.

Fig. 3

Texture baking via inverse displacement: an example of a result. The input consists of a hi-resolution mesh $\mathcal {M}_H$ (324K faces) and a low-resolution mesh $\mathcal {M}_L$ (1000 faces), provided with per-vertex displacement directions (in blue), and a UV-map (shown). We inverse project every vertex of $\mathcal {M}_H$ into $\mathcal {M}_L$, moving it into the corresponding u, v position, and rasterize it using a normal rendering pass, obtaining the baked normal-map. Used input data: $\mathcal {M}_H$ is the Ganesa model from [11]; $\mathcal {M}_L$ is obtained by automatic simplification, using MeshLab; displacement directions on $\mathcal {M}_L$ are standard per-vertex normal directions (area-weighted average of per-face normal); the UV-map of $\mathcal {M}_L$ is constructed with [10]

5.1 Texture baking via rendering

Texture baking is a common technique, pioneered by early research such as [3, 9] and supported today by common 3D modeling suites [1, 5, 7, 12]. A baked texture (sometimes referred to as transfer map, mesh map, redetail texture, or detail-recover texture) is a synthesized texture that records data originally stored in a high-resolution mesh $\mathcal {M}_H$ into the texels of a texture image intended for a given low-resolution mesh $\mathcal {M}_L$. The texels can be filled with displacement scalars, or any information stored on $\mathcal {M}_H$, such as normals, colors, pre-lit values, or any other per-vertex attributes, per face attributes, or even an original texture; $\mathcal {M}_L$ comes with a UV-map, which for simplicity we will assume to be free from seams, and per-vertex displacement directions; the latter can be per-vertex normal directions, or can even be explicitly optimized for this specific task in preprocessing [15].

Direct approach: Traditionally, the baking is performed leveraging on the direct problem: For each texel, a ray is cast from the corresponding position on $\mathcal {M}_L$, toward the interpolated direction, and the information is extracted and stored from whichever point on $\mathcal {M}_H$ is hit.

Inverse approach (new): Using the inverse problem, we can iterate over vertices of $\mathcal {M}_H$, find a position on $\mathcal {M}_L$ by inverse projection, and reposition that vertex in the corresponding location in the 2D texture space. This way, $\mathcal {M}_H$ is morphed into the 2D parametric space of $\mathcal {M}_L$, and a simple rasterization-based rendering suffices to produce the baked texture. Alternatively, depth values t can also be rendered to bake displacement maps. The attached implementation demonstrates this process. See Fig. 3 for one example.

Vertices of $\mathcal {M}_H$ that fail to be back-projected over any face of $\mathcal {M}_L$ with a valid solution can either simply be discarded, or clamped to the boundary of the closest triangle in $\mathcal {M}_L$ (zeroing the least negative barycentric coordinate and re-normalizing the other two).

Comparison: The relative merits of the two solutions, traditional (direct) and novel (inverse), depend on the context, and a full analysis exceeds the scope of this paper; for our intents, the observation suffices that the two solutions offer a different set of advantages. In the following, we outline only a few general considerations.

Efficiency can be compared, neglecting for the sake of simplicity the impact of spatial indexing structures. A clear advantage of the inverse approach is that the final rendering pass can exploit the extremely optimized standard rasterization rendering pipeline; this is in practice extremely fast (milliseconds at most), and we can safely disregard its impact on computation time. Let $R_H$ and $R_L$ be the resolutions of $\mathcal {M}_H$ and $\mathcal {M}_L$ (number of primitives, either vertices or faces), and $R_T$ be the resolution of the baked texture (number of texels), with, typically

$$\begin{aligned} R_T> R_H\gg R_L\end{aligned}$$

(18)

(to prevent loss of information, $R_T$ needs to surpass $R_H$, e.g. by a factor 2 according to Nyquist-Shannon sampling theorem; considerably more if $\mathcal {M}_H$ comes with its own texture to be re-baked). For a given triangle, both the inverse and direct problems are solved in constant time, although direct ray casting necessitates fewer operations. In the direct method, a ray from each texel must be tested against each primitive in $\mathcal {M}_H$, leading to a $\text {O}(R_TR_H)$ complexity; in the inverse approach, all vertices of $\mathcal {M}_H$ must be inverse-projected over each triangle of $\mathcal {M}_L$, costing $\text {O}(R_HR_L)$, which is a much lower asymptotic complexity. Naturally, both approaches can be sped up considerably by employing spatial indexing structures (down to $\text {O}(R_T\log (R_H))$ and $\text {O}(R_H\log (R_L))$, respectively), which reduces the gap. Even without that non-trivial optimization, our reference implementation takes only a few seconds on consumer-level hardware for the examples in Fig. 3.

Ease of use favors the inverse-projection approach, as fragment-shaders, e.g. the same ones used in the rendering, can be directly re-used in the final pass to reproduce any complex lighting or texturing effect to bake the results in form of textures (including shadowing, wireframe, or any other mesh rendering technique).

Accuracy favors the direct approach, as in the inverse approach the linear interpolation inside the triangles of the flattened $\mathcal {M}_H$ introduces a small approximation error, which decreases with the resolution of $\mathcal {M}_H$. Also, the inverse approach requires care to work in presence of texture seams over $\mathcal {M}_L$.

5.2 Perfect reprojectability test

In the context of the construction of a displacement-mapped surface, a recurrent concern is whether or not a given base mesh, with an associated set of per-vertex displacement directions, is able to represent a given continuous target surface, often discretized as a high-resolution mesh $\textbf{M}_H$ [4, 8, 13]. A (scalar) displacement-map is limited in that it can only encode different heights for each point; in other words, it is a warped “2.5D” height-field, and, as such, it can only express a limited range of shapes. It is in general not trivial to determine if a given target surface $\textbf{M}_H$ can be represented by a displacement-map encoded over a base triangle $\mathcal {T}$.

Fig. 4

2D depiction of a case where a given surface $\mathcal {M}_H$ is not reprojectable from base triangle $\mathcal {T}$, as one interpolated ray intersects $\mathcal {M}_H$ three times, including with one with mismatching orientation (red bold line)

Direct approach: A brute force solution using the direct approach is to cast rays from a sampling of $\mathcal {T}$ and check whether or not any given ray hits multiple valid targets on $\mathcal {M}_H$, or, equivalently, whether or not it hits any back-facing face on $\mathcal {M}_H$ (see Fig. 4). This relies on the sampling to be sufficiently dense, and is work intensive, making it impractical for example in contexts where the test must be performed to inform the construction of an arrangement of $\mathcal {T}$.

Existing alternatives: In [8], the displacement is redefined as a continuous piecewise linear mapping, to make it easier to invert, making it possible to precisely test for reprojectability; while the test is exact, that framework changes the definition of the displacement map, drifting away from the traditionally intended semantics (vertices are displaced not along a single straight line, but along a broken line). In many previous works, the test is only approximated, so to make it faster. For example, in [13], the test is substituted by using a “fitmap,” which is a scalar field defined in preprocessing that describes, for each position p on $\textbf{M}_H$, the approximate maximal size of a base-triangle centered around p that can still be correctly reprojected; while this is can be an efficient way to inform the construction of an arrangement of base triangles, the test is only an approximation.

Fig. 5

Exact reprojectability test for a triangle $( \textbf{q}_0, \textbf{q}_1, \textbf{q}_2)$, over a base triangle $\mathcal {T}$. In this instance, the test fails because the projection of $( \textbf{q}_0, \textbf{q}_1, \textbf{q}_2)$ of $\mathcal {T}$ has a different orientation than $\mathcal {T}$

Inverse approach (new): to perfectly test for reprojectability, we can test if any triangle in $\mathcal {M}_H$ is mapped, by the inverse projection, into a triangle inside $\mathcal {T}$ having an orientation opposite to that of $\mathcal {T}$. Given a triangle $( \textbf{q}_0, \textbf{q}_1, \textbf{q}_2) \in \mathcal {M}_H$, we first inverse-project $\textbf{q}_0$, $\textbf{q}_1$ and $\textbf{q}_2$, obtain three sets of barycentric coordinates $\varvec{\alpha }^0$, $\varvec{\alpha }^1$ and $\varvec{\alpha }^2$ on $\mathcal {T}$, with $\varvec{\alpha }^i = (\alpha ^i_0,\alpha ^i_1,\alpha ^i_2)$ – see Fig. 5.

The consistency of orientation of the back-projected triangle on $\mathcal {T}$ is then determined by the sign the 2D cross product of the 2D triangle defined by any two barycentric coordinates:

$$\begin{aligned} (\alpha ^1_0-\alpha ^0_0) (\alpha ^1_1-\alpha ^0_1) - (\alpha ^2_0-\alpha ^0_0) (\alpha ^2_1-\alpha ^0_1) > 0 \end{aligned}$$

(19)

This test is exact; note that it does not explicitly require the 3D normal of either $\mathcal {T}$ or $( \textbf{q}_0, \textbf{q}_1, \textbf{q}_2)$.

6 Conclusions

In this work, we offer a complete solution to what we term the “inverse displacement problem,” a basic geometric sub-problem that commonly arises in contexts such as the construction or baking of scalar displacement-maps over meshes, subdivision surfaces, and other representations. Our solution is given in closed form, and can be made efficient to evaluate; while typical problem instances admit a single valid solution, our procedure also correctly identifies cases admitting no solution, infinite solutions, or a set of either two or three solutions to choose from.

We observe that the vast and long-spanning Literature on displacement-map construction, and adjacent fields, always strive to formulate their algorithms to employ the direct problem only (to the best of our knowledge). We conjecture this may be due, in some part, to the perceived intricacy of the inverse problem, which, in spite of its apparent geometric simplicity, defies at first glance straightforward solutions. The present work intends to offer an alternative and settle the question.

6.1 Problem variants

We conclude by considering the effect of a few common variations of the direct problem on the inverse problem.

In some scenario, the displacement vectors $\textbf{d}_i$ are assumed to be of the same length, or all unitary. Clearly, our solution makes no assumption about this and is directly usable. As far as we can tell, this additional assumption does not offer any opportunity to ease the inverse problem.

In some scenario, the interpolated displacement vector $\textbf{d}$ is re-normalized after interpolation, defining the ray direction as $\textbf{d}' = \textbf{d}/ || \textbf{d}||.$ This change does not affect our construction at all, provided that our final scalar displacement value $t$ is adjusted, after the computation is over, to $t'=t\, || \textbf{d}||$.

A different scenario is when the base triangle $\mathcal {T}$ is substituted by a (flat or not flat) quadrilateral $\mathcal {Q}$. For example, in many techniques, such as [2, 6, 13] a displacement map is applied over a quad-mesh rather than a triangle-mesh. The direct displacement problem is not affected much, except that $\textbf{v}$ and $\textbf{d}$ are now bilinearly interpolated between four corners, rather than being linearly interpolated between three. The inverse problem, however, becomes considerably more intricate. The presented solution is now unusable: Equations from 2 to 7 can be immediately adapted (index i now ranging from 0 to 3), but neither $\mathcal {P}$ or $\textbf{n}$ are defined any longer (as the four $\textbf{a}_i$ are not necessarily co-planar, not even when $\mathcal {Q}$ is flat and $\textbf{d}_i$ are unitary). In this variant, the inverse problem is (to our knowledge) still open.

A Derivation of (15) from (14)

For any pair of $3 \times 3$ matrices $\textbf{M}=[\textbf{M}_0|\textbf{M}_1|\textbf{M}_2]$ and $\textbf{N}=[\textbf{N}_0|\textbf{N}_1|\textbf{N}_2]$, we have

$$\begin{aligned} \det (\textbf{M}+\textbf{N})&= \det ( \textbf{M}_0 | \textbf{M}_1 | \textbf{M}_2 ) + \det ( \textbf{M}_0 | \textbf{M}_1 | \textbf{N}_2 ) \nonumber \\&+ \det ( \textbf{M}_0 | \textbf{N}_1 | \textbf{M}_2 ) + \det ( \textbf{M}_0 | \textbf{N}_1 | \textbf{N}_2 ) \nonumber \\&+\det ( \,\textbf{N}_0 | \textbf{M}_1 | \textbf{M}_2 ) + \det ( \,\textbf{N}_0 | \textbf{M}_1 | \textbf{N}_2 ) \nonumber \\&+ \det ( \,\textbf{N}_0 | \textbf{N}_1 | \textbf{M}_2 )+ \det ( \,\textbf{N}_0 | \textbf{N}_1 | \textbf{N}_2 ).\nonumber \\ \end{aligned}$$

(20)

This is an application of the general rule according to which the determinant of a sum of two $n \times n$ matrices is given by the sum of the $2^n$ determinants of the matrices obtained by any swapping of columns between the first and the second matrix; for the $n = 3$ case, this can also be immediately verified by rewriting $\det ( \textbf{a}| \textbf{b}| \textbf{c})$ as $\textbf{a} \cdot ( \textbf{b} \times \textbf{c})$.

Applying (20) to (14) with $\textbf{M}=\textbf{P}$ and $\textbf{N}= t\, \textbf{D}$, and remembering that, for any scalar k,

$$\begin{aligned} \det (k \, \textbf{a}| \textbf{b}| \textbf{c}) = \det ( \textbf{a}|k \, \textbf{b}| \textbf{c}) = \det ( \textbf{a}| \textbf{b}| k \, \textbf{c}) = k \, \det ( \textbf{a}| \textbf{b}| \textbf{c}) \end{aligned}$$

(21)

gives (15).