Road scenes segmentation across different domains by disentangling latent representations

Abstract

Deep learning models obtain impressive accuracy in road scene understanding; however, they need a large number of labeled samples for their training. Additionally, such models do not generalize well to environments where the statistical properties of data do not perfectly match those of training scenes, and this can be a significant problem for intelligent vehicles. Hence, domain adaptation approaches have been introduced to transfer knowledge acquired on a label-abundant source domain to a related label-scarce target domain. In this work, we design and carefully analyze multiple latent space-shaping regularization strategies that work together to reduce the domain shift. More in detail, we devise a feature clustering strategy to increase domain alignment, a feature perpendicularity constraint to space apart features belonging to different semantic classes, including those not present in the current batch, and a feature norm alignment strategy to separate active and inactive channels. In addition, we propose a novel evaluation metric to capture the relative performance of an adapted model with respect to supervised training. We validate our framework in driving scenarios, considering both synthetic-to-real and real-to-real adaptation, outperforming previous feature-level state-of-the-art methods on multiple road scenes benchmarks.

1 Introduction

One of the key components of a self-driving vehicle is the capability to understand the surrounding environment from sensory input data. Semantic segmentation enables accurate scene understanding, by assigning all pixels of the input images to a semantic category corresponding to key elements to be detected, such as the road, other vehicles or traffic lights and signs [1]. Nowadays, such a task is commonly tackled with deep convolutional neural networks (DCNNs), which have achieved outstanding results in image understanding tasks, provided that a sufficiently large number of labeled examples are available from the target input domain distribution. On the other side, the annotation of thousands of images of road scenes is highly expensive, time-consuming, error-prone and, possibly, worthless, since the test data can show a domain shift with respect to the training labeled samples. Therefore, recently, a new requirement has emerged for DCNN-based scene understanding systems embedded in autonomous driving vehicles, namely allowing training with a combination of labeled source samples (e.g., synthetic from ad hoc simulators or driving video games) and unlabeled target samples (e.g., real-world acquisitions from cameras mounted on cars), with the aim of getting high performance on data following the target distribution. With this strategy, the need for large quantities of labeled real-world data can be avoided by using samples from a source domain where they are abundantly available and annotations are faster and cheaper to generate.

Unfortunately, DCNNs are prone to failure when they are shown an input domain distribution other than the training one (domain shift phenomenon). In order to deal with this problem, various unsupervised domain adaptation (UDA) techniques have been developed to adapt networks at different stages (the most common are the input, feature and output levels)  [2].

Deep learning models for semantic segmentation are mostly based on encoder–decoder architectures, i.e., they build some concise latent representations of the inputs, which are highly correlated with the classifier output. As such, they are used in the subsequent classification process [3, 4] that reconstructs the full-resolution segmentation map. Nevertheless, only some UDA techniques for semantic segmentation work in the feature space because of its large dimensionality.

In this paper, we propose an approach focusing on feature space adaptation, introducing a new set of strategies working at the latent space level, built on top of our previous conference work [5]. Employing a shaping objective at that level we are able to promote class-aware feature extraction and feature invariance between source and target domains. More in detail, our target is to push the feature vectors on the boundary of an N-dimensional sphere, assigning to each class a direction orthogonal to all others. Such a shaping objective can be implemented using three major components:

Firstly, a clustering constraint groups feature vectors of each class tightly around their prototypical representation.

Secondly, a perpendicularity objective over the class prototypes promotes disjoint filter activation sets across different semantic categories.

Finally, a regularization-based norm alignment objective enforces consistent vector norms in the source and target domains, while jointly forcing progressively increasing norm values. This, in combination with the perpendicularity constraint, is able to reduce the entropy associated with feature vector channel activations.

Importantly, the proposed techniques require the generation of accurate class prototypes and the imposition of a strong correlation between feature representations and predicted segmentation maps. Hence, we also propose a novel strategy to map semantic information from the labeling maps to the low-resolution feature space (annotations downsampling).

1.1 Limitations in existing work

The major limitations of our previous approach [5] can be found in the inherent instability of pseudo-labels in the UDA setting. Since the employed architecture is trained on a different domain, the predictions and features it produces when analyzing target samples may vary significantly between batches. This leads to a loss in performance, especially when considering class-conditional clustering and feature perpendicularity. A further problem can be found in the norm alignment constraint, which enforced the same norm value for all features, regardless of the semantic content and of the specific channels’ activation profile. This strategy may introduce noise, since channels that the network may want to disable are still forced to produce a nonzero result, especially in feature vectors that correspond to pixel windows with multiple class labels (usually found along object borders) or for which there is no clear network response.

1.2 Contribution

To tackle the first problem, we focused on the computation of prototypes and feature vector extraction. The first now considers the prototype trajectory evolution for a better estimation (Sect. 3.2), while the second exploits target information to reduce the domain shift (Sect. 3.3); additionally, a class-weighting scheme is used in the source supervision (Sect. 3.1). In particular, the clustering objective was modified to be more resilient to outliers (Sect. 4.1); the perpendicularity constraint now accounts for classes not present in the current batch (Sect. 4.2); and the norm alignment now ignores low-activated channels (Sect. 4.3).

To analyze the improvements to the proposed space-shaping constraints, we report ablation studies on our approach, LSR$^+$ (Sect. 8), and for the proposed evaluation metric, mASR (Sect. 6).

Extensive experiments have been conducted on many road scenarios, expanding the set of experiments reported in [5]. The results are evaluated on 4 backbones in 6 different setups. These include not only 2 synthetic-to-real ones, commonly used in related works, but also 4 real-to-real settings addressing the critical issue of generalizing autonomous driving systems across different cities and types of roads in different regions of the world. Additional results using the unlabeled Cityscapes coarse set [6] are reported, showing significant performance gains when more unlabeled data are used (see Table 1).

Overall, our approach shows significant improvement over the conference version [5], gaining, on average, $1\%$ mIoU on all settings. Importantly, the performance gains are well spread across the classes, as is confirmed by the very high mASR score. Such achievement confirms that our space-shaping approach is able to bridge the gap between source and target domains very effectively, even when small and rare classes are considered.

2 Related works

Semantic segmentation of road scenes is a very active research field. Many semantic segmentation architectures based on the widely used encoder–decoder architecture [7,8,9,10,11,12] or more recently on vision transformers [13,14,15] have been applied to road scenes for two interconnected motivations: First, there is a large interest into the target application of self-driving vehicles, and second, there is the availability of large real world (Cityscapes [6], Mapillary [16], IDD [17], Cross-City [18], CamVid [19]) and synthetic (GTA5 [20], SYNTHIA [21], SELMA [22] and SHIFT[23]) datasets that can be employed to train deep learning architectures. These two motivations also provided a strong push for road-scenes-specific architectures [24,25,26,27,28,29], which have recently started to be proposed by the research community.

Unsupervised domain adaptation consists in transferring knowledge extracted from a label-rich source domain to a completely unlabeled target domain. The ultimate objective is to address the performance decline caused by domain shift, which negatively affects the generalization capabilities of deep neural networks. The problem was initially studied for the classification task, but recently many works dealt with the unsupervised adaptation problem in relation to semantic segmentation and in other similarly complex tasks [30]. Although several methods have been proposed to tackle the adaptation task, they all share an underlying search for a form of domain distribution alignment over some representation space. Some methods pursue distribution matching inside the input image space via style transfer [31] or image generation techniques, while others aim at bridging the statistical gap between source and target representations produced by the task model, whether manipulating some output representations or operating inside a latent feature space [2].

Input-space adaptation has been commonly addressed resorting to image-to-image translation [32,33,34,35,36,37,38,39]. By transferring visual attributes across source and target samples, domain invariance is achieved in terms of visual appearance. Source supervision can thus be safely exploited in the shared image space, retaining consistent accuracy on the source and target data.

As concerns feature and output-space adaptation, adversarial learning has been largely employed to bridge the statistical domain gap [40,41,42,43,44,45,46]. With the help of a domain discriminator, the task network is forced to provide statistically indistinguishable source and target representations, typically drawn from a latent feature space [40,41,42] or in the form of probability maps at the output of the segmentation pipeline [42,43,44,45,46]. More recently, some works focusing on feature-level regularization have been proposed [5, 47]. In [47], a class-conditional domain alignment is achieved by means of a discriminative clustering module, paired with orthogonality constraints to enhance class separability. The approach of [5] relies on conditional clustering adaptation, enhanced by a perpendicularity objective over class prototypical representations and a novel norm alignment loss to improve class separability at the latent space. As an alternative form of feature-level adaptation, dropout regularization has been explored [48,49,50]: decision boundaries are pushed away from target high-density regions in the latent space without direct supervision.

Output-space adaptation has been further pursued by resorting to self-training [51, 52], where the learning process is guided (in a self-supervised manner) by pseudo-labels extracted from target network predictions. Self-supervision has been proposed in a curriculum learning fashion as well [53,54,55]. First, simple tasks that are less sensitive to domain shift are solved, by inferring some useful properties related to the target domain. Then, the extracted information is exploited to address more complex learning tasks (e.g., semantic segmentation). Alternatively, some works introduce entropy minimization techniques [56,57,58], which force more confident network predictions over target data, thus encouraging the behavior shown in the supervised source domain.

Latent space regularization has been shown to ease the semantic segmentation tasks in different settings, such as UDA [59, 60], continual learning [61], federated learning [62] and few-shot learning [63, 64]. The idea is to embed additional constraints on feature representations during the training process, enforcing a regular semantic structure on latent spaces of the deep neural classifier. In UDA, where target semantic supervision is missing, regularization can be applied in a class-conditional manner by relying on the exclusive supervision of source samples, while indirectly propagating its effect to target representations as well. Such improved regularity has, in fact, shown to promote generalization properties, leading to statistical alignment between the source and target distributions when regularization is jointly applied over both domains [5, 47].

A multitude of feature clustering techniques based on the K-means algorithm has been proposed [59, 60, 65, 66] to address the adaptation task. Those works are mainly focused on image classification and resort to a projection to a more easily tractable lower-dimensional latent space where to perform pseudo-labeling of the original target representations extracted by the task model [60, 65, 66]. In [5, 47], the idea is further refined and applied to semantic segmentation by proposing an explicit clustering objective paired with orthogonality constraints to force feature vectors to cluster around the respective class prototypes. Feature-level orthogonality has been also explored in [67] to limit the redundancy of the information encoded in feature representations. Approaches closer to our strategy are [68, 69], where UDA is promoted via an orthogonality objective over class prototypes. Nonetheless, [67,68,69] all limit their focus to the image classification task.

3 Problem setting

In this section, we overview our setup, detailing the mathematical notation used throughout the paper. We start by identifying the input space as ${\mathcal {X} \subset \mathbb {R}^{H \times W \times 3}}$ and the corresponding label space as ${\mathcal {Y} \subset \mathcal {C}^{H \times W}}$, where H and W represent the image resolution and $\mathcal {C}$ the class set. Furthermore, we assume to have a training set ${\mathcal {T} = \mathcal {T}^s \bigcup \mathcal {T}^t}$, where ${ \mathcal {T}^s = \{ (\textbf{X}_{n}^s, \textbf{Y}_{n}^s) \}_{n=1}^{N_s} }$ contains labeled samples $(\textbf{X}_{n}^s, \textbf{Y}_{n}^s) \in \mathcal {X}^s \times \mathcal {Y}^s$ originated from a source domain, while an additional set of input samples ${ \mathcal {T}^t = \{ \textbf{X}_{n}^t \}_{n=1}^{N_t} }$ is drawn from an unlabeled target domain ($\textbf{X}_{n}^t \in \mathcal {X}^t$). We adapt the knowledge of semantic segmentation learned on the source domain to the unsupervised target domain. Superscript s identifies the source domain, while t the target.

As done by most recent approaches for semantic segmentation, we assume a model $S = D \circ E$ based on an encoder–decoder architecture, that is, made by the consecutive application of an encoder network E (referred to as backbone, which acts as feature extractor) and a decoder network D, which actually performs the classification and produces the segmentation map. We denote the features extracted from an input image $\textbf{X}$ as $E(\textbf{X}) = \textbf{F} \in \mathbb {R}^{H' \times W' \times K}_{0+}$, where K refers to the number of channels and $H' \times W'$ to the low-dimensional (feature-level) spatial resolution. Thanks to the topology of encoder–decoder DCNNs for semantic segmentation, classes are encoded into ideal latent representations, invariant with respect to the domain shift. The strategies presented in Sect. 4 enforce this goal by comparing the extracted features belonging to each class with the respective prototypical representations. In the following paragraphs, we present the techniques used to compute the prototypes and associate feature vectors with semantic classes.

3.1 Weighted histogram-aware downsampling

Given that the spatial arrangement of the pixels of an image is maintained while it is processed by an encoder–decoder dilated residual network [70] (even if at reduced resolution in the internal feature representation), we can assume a tight relationship between any feature vector (i.e., the vector of features associated with a single spatial location within the feature tensor) and the semantic labeling of the corresponding image region.

Hence, the extraction process begins with the identification of a way to propagate the labeling information to latent representations (decimation), without losing the semantic content of the window (image region) corresponding to each feature vector. Issues in the mapping typical of naïve approaches would strongly affect the whole following procedure. Our solution is a nonlinear pooling function, which instead of computing a simple subsampling (e.g., nearest neighbor) extracts a weighted frequency histogram over the labels of all the pixels in the window corresponding to a low-resolution feature location. The weights are inversely proportional to the class frequency in the source training dataset. Then, these metrics are used to select the most appropriate class for each image region, producing source feature-level label maps $\{\textbf{I}^{s}_n\}^{N_{s}}_{n=1}$. The computation of the target counterparts ($\{\textbf{I}^{t}_n\}^{N_{t}}_{n=1}$) is discussed in Sect. 3.3 and we remark that each $\textbf{I}^{s,t}_n$ belongs to the set $\mathcal {C}^{H' \times W'}$. In particular, we choose the label with the highest frequency peak in the windows, only if such a peak is relevant enough, i.e., if all other peaks are smaller than $T_h$ times it. (A similar approach is found in the orientation assignment step of the SIFT feature extractor [71].) Empirically, we set $T_h=0.5$. Finally, we remark on a useful side effect of this technique: whenever a window cannot be uniquely assigned to a class (that is, it contains multiple labels), the procedure automatically assigns it to the void class.

3.2 Prototype extraction

The feature-level label maps ${\{\textbf{I}^{s,t}_n\}^{N_{s,t}}_{n=1}}$ allow to identify the set $\mathcal {F}^{s,t}_c$ of feature vectors belonging to class $c \in \mathcal {C}$ in training batch $\mathcal {B}$:

$$\begin{aligned} \mathcal {F}^{s,t}_c = \left\{ \textbf{F}_n^{s,t}[h,w] \in \mathbb {R}^{K}_{0^+} \mid \textbf{I}^{s,t}_n[h,w] = c, \forall n \in \mathcal {B}\right\} \end{aligned}$$

(1)

where the couple [h, w] denotes the spatial location ($0 \le h < H'$ and $0 \le w < W'$). The definition is further expanded into the set of all feature vectors in batch $\mathcal {B}$ by taking their union with the set $\mathcal {F}^{s,t}_v$ of samples belonging to class void: $\mathcal {F}^{s,t} = ( \bigcup _{c} \mathcal {F}^{s,t}_c ) \cup \mathcal {F}^{s,t}_v$. From these sets, we can extract the batch-wise prototypes of each class (note that we use feature vectors exclusively from the source):

$$\begin{aligned} \textbf{p}_c[i] = \frac{1}{|\mathcal {F}^s_c|}\sum \limits _{\textbf{f} \in \mathcal {F}^s_c}{\textbf{f}[i]} \;\;\;\;\; \forall i,\;\; 1 \le i \le K \end{aligned}$$

(2)

Moreover, with the goal of obtaining more stable and reliable prototypes, and reducing estimation noise, we consider the exponentially smoothed vectors:

$$\begin{aligned} \hat{\textbf{p}}_{c,new} = (1-\eta ) \textbf{p}_c + \eta \hat{\textbf{p}}_{c,old} \end{aligned}$$

(3)

The parameters are initialized with $\hat{\textbf{p}}_c=\textbf{0}$ and $\eta =0.8$ (empirically). In our notation, $\hat{\textbf{p}}_{c,old}$ represents the smoothed estimate up to the previous optimization step, $\textbf{p}_c$ the prototypes estimated on the current batch and $\hat{\textbf{p}}_{c,new}$ the new smoothed estimate. This way, by setting $\eta >0$, we can propagate the previous estimates to the current batch, allowing to consider classes absent from $\textbf{Y}^{s}_n$ in the loss computation.

3.3 Feature pseudo-labeling

While the histogram strategy can be seamlessly extended to be used with pseudo-labels (i.e., network estimates for the unlabeled target samples, as was our strategy in the previous work [5]), this approach can introduce instability in the training procedure. To avoid such an issue, we devise a novel way of extracting the target feature-level label maps $\{\textbf{I}^{t}_n\}^{N_{t}}_{n=1}$.

Our strategy exploits the euclidean distance in the latent space, computing a clustering of the feature vectors around their prototype (see Fig. 1). More in detail, we compute an initial classification exploiting the prototypes computed over the source labeled data, which, due to the domain shift, will not be adequately representative of the target distribution:

$$\begin{aligned}{} & {} \mathcal {\widetilde{F}}_{c}^{t} = \{\textbf{F}_n^t[h,w] \; \text {if } \sigma _c(-|| \textbf{F}_n^t[h,w]- \hat{\textbf{p}}_c ||) > 0.5, \forall n \in \mathcal {B} \} \nonumber \\{} & {} \quad \textbf{p}^t_c[i] = \frac{1}{|\mathcal {\widetilde{F}}_{c}^{t}|}\sum \limits _{\textbf{f} \in \mathcal {\widetilde{F}}_{c}^{t}}{\textbf{f}[i]} \;\;\;\;\; \forall i,\;\; 1 \le i \le K \end{aligned}$$

(4)

where $\sigma _c(\cdot )$ is the softmax function computed over the classes. Then, we refine the classification keeping only those vectors that have high classification confidence according to a probability distribution attained through a softmax function:

$$\begin{aligned} \begin{aligned} \textbf{I}^t_n[h,w]&= {\left\{ \begin{array}{ll} c &{} \sigma _c(-|| \textbf{F}_n^t[h,w]-\textbf{p}^t_c ||) > 0.5 \\ \textit{void} &{} \text {otherwise} \end{array}\right. } \end{aligned} \end{aligned}$$

(5)

Fig. 1

Visual representation of our two-pass feature vector classification strategy. The initial source-based classification (in blue) can lead to erroneously classified target samples (purple-shaded areas). This problem is tackled by computing target prototypes as the centroids of the partitioned vectors (notice the shift compared to the original source prototype), these prototypes are used as new classification centers (green boundary), producing a correct segmentation

4 Methodology

Fig. 2

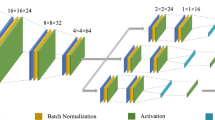
Visual summary of our strategy. Features are associated with semantic classes and prototypes are computed from them (Sect. 3). Class clustering (Sect. 4.1), prototypes perpendicularity (Sect. 4.2) and norm alignment and enhancement (Sect. 4.3) are the three proposed space-shaping constraints. Additionally, we apply on top an entropy minimization objective [56]

The proposed approach is detailed in this section, highlighting the key differences with respect to our previous work. Our investigation moves from the fact that the discriminative effect acquired by the model with the source-supervised cross-entropy objective may not be propagated to the target domain due to the distribution shift. To tackle such a problem, in [5] we proposed to use additional space-shaping objectives to increase the network generalization capability, therefore improving robustness to distribution shifts from the original source training data. In particular, we added three feature space-shaping constraints to the standard source supervision ($\mathcal {L}_{CE}^s$), whose combined effect can be expressed as:

$$\begin{aligned} \mathcal {L} = \mathcal {L}_{CE}^{s} + \lambda _C \cdot \mathcal {L}_C^{s,t} + \lambda _P \cdot \mathcal {L}_P^{s} + \lambda _N \cdot \mathcal {L}_N^{s,t} \end{aligned}$$

(6)

Here, $\mathcal {L}_C$ represents the clustering objective acting on the feature vectors (Sect. 4.1), $\mathcal {L}_P$ the perpendicularity constraint applied to class prototypes (Sect. 4.2) and $\mathcal {L}_N$ the norm alignment goal (Sect. 4.3). To simplify the notation, Eq. (6) contains each loss component with s, t superscripts to indicate the sum of the loss on source and target samples. To further improve the performance and to show how the proposed techniques can be used on top of existing strategies, we also add to the optimization target the entropy minimization loss introduced by Chen et al. [56], thus obtaining: $\mathcal {L}^+ = \mathcal {L} + \lambda _{EM} \cdot \mathcal {L}_{EM}$. By doing so, we also show that our space-shaping objectives provide a different and complementary effect on the feature vectors when compared to the entropy minimization constraint. An overview of the proposed strategy is presented in Fig. 2.

4.1 Clustering of latent representations

Due to the distribution discrepancy between source and target domains, feature vectors originating from them will be misaligned. This inevitably causes some incorrect classifications of target representations, in turn degrading the segmentation accuracy in the target domain. We introduce our first loss, a clustering objective over the latent space, to mitigate this problem, seeking class-conditional alignment of feature distribution. We do so by exploiting the prototypical representations discussed in Sect. 3 and forcing the feature vectors from source and target representations to tightly cluster around them: representations are adapted into a common class-wise distribution and the discrimination capacity of the latent space is increased.

Differently from the previous work, we define the clustering objective as the L1 distance between feature vectors and their associated class prototypes. This results in a more stable training evolution and lower error rate in clustering, thanks to the outlier-rejecting properties of the L1 norm. In particular, due to the quadratic nature of the L2 loss, outliers with distances greater than 1 have a strong push toward the clusters. On the other hand, the L1 loss is stronger than L2 for close samples, which are more representative of each class, and is significantly gentler than L2 for distant outliers. The loss can be expressed mathematically as:

$$\begin{aligned} \mathcal {L}_C^{s,t} = \frac{1}{|\mathcal {C}|} \sum \limits _{c \in \mathcal {C}} \frac{1}{|\mathcal {F}^{s,t}_c|} \sum \limits _{\textbf{f} \in \mathcal {F}^{s,t}_c} \frac{1}{K}\sum _{k=1}^{K}|\hat{\textbf{p}}_c[k]-\textbf{f}[k]| \end{aligned}$$

(7)

This loss has multiple targets: the first is the increased clustering of the latent representations thanks to label supervision, which reduces the tendency to erroneous predictions. The second one is to perform self-supervised clustering on target samples using our two-pass pseudo-labeling strategy (see Sect. 3.3). Finally, it leads to better prototype estimates, due to the fact that forcing tighter clusters will lead to more stable batch-wise centroids, which in turn will get closer to the moving-averaged prototypes.

4.2 Perpendicularity of latent representations

A prototype perpendicularity loss is further proposed to aid the latent space regularization brought by the clustering objective. Our goal is to induce compact and domain-aligned feature clusters, in order to boost the accuracy of network segmentation maps. As a direct consequence, the margin between classification boundaries and feature clusters is expanded, thus decreasing the probability that target high-density regions are traversed by such boundaries. We directly encourage a class-wise orthogonality property, not only increasing the distance among class clusters but also reducing class cross talk by discouraging shared channel activations in distinct categories.

In the loss, we encode the perpendicularity score exploiting the definition of euclidean space inner product: ${\textbf{j}\cdot \textbf{k} = ||\textbf{j}||\;||\textbf{k}|| \cos \theta }$, where $\theta$ is the angle between the two vectors $\textbf{j}$ and $\textbf{k}$. To maximize $\theta$ we just need to minimize the vectors’ normalized product (recall that $\textbf{j}, \textbf{k} \in \mathbb {R}^{K}_{0^+}$). Therefore, the cross-perpendicularity between prototypes is encoded as:

$$\begin{aligned} \mathcal {L}_P^{s} = \frac{1}{|\mathcal {C}|(|\mathcal {C}|-1)}\sum \limits _{c_i,c_j \in \mathcal {C}, i \ne j}{\frac{\hat{\textbf{p}}_{c_i}}{||\hat{\textbf{p}}_{c_i}||}\cdot \frac{\hat{\textbf{p}}_{c_j}}{||\hat{\textbf{p}}_{c_j}||}} \end{aligned}$$

(8)

Equation (8) computes the sum of the cosines over the set of all couples of non-void classes. The influence of the orthogonality objective indirectly reaches all feature vectors, as prototypical representations and single feature instances share a strong geometric bound promoted by $\mathcal {L}_C^{s,t}$. What we ultimately achieve is thus to enforce a perpendicularity constraint among instances of different clusters, with a homogeneous action over all latent representations from the same semantic class. In other words, the angular gap among distinct semantic categories in the feature space is enlarged, by inducing disjoint patterns of activated feature channels between distinct classes.

In contrast to our previous paper [5], we compute the loss on the exponentially smoothed version of the prototypes, i.e., from Eq. (3). This guarantees that the space will be more evenly occupied by the classes, since all directions are considered in the computation of the loss, instead of considering only the ones in the current batch.

4.3 Latent norm alignment constraint

This loss term is computed by exploiting source and target feature vector norms. More in detail, we enforce norm consistency between the latent representations extracted from the two domains. This has two objectives: firstly, we aim at improved classification confidence on target predictions, as done by adaptation techniques using entropy minimization in the output space [57]. Secondly, we assist the perpendicularity constraint by reducing the number of domain-specific feature channels used by the network for classification. Thirdly, we reduce the number of channels enabled only on one of the domains, which would lead to norm misalignment. Moreover, to reduce the possible decrease in norm value during the alignment process, we introduce a regularization term that promotes norm increase. Differently from [5], here the norm objective is encoded as a relative difference with a regularization term inversely proportional to the norm value. This allows obtaining a value-independent loss where norm values higher than the target are less discouraged. Moreover, we introduce a norm filtering strategy to reduce the negative effects a careless increase in norm could imply. In particular, we suppress low channel activations, stopping the gradient flow through them and preventing the norm alignment procedure to increase their value, in contrast to what source supervision indicates. Formally, we define the loss term as:

$$\begin{aligned} \mathcal {L}_N^{s,t} = \frac{1}{|\mathcal {F}^{s,t}_{*}|} \sum \limits _{\textbf{f} \in \mathcal {F}^{s,t}_{*} } \frac{{\left| (\bar{f}_s+\Delta _f) - ||\textbf{f}|| \right| }}{\bar{f}_s} \end{aligned}$$

(9)

where $\bar{f}_s$ is the average source vector norm (extracted in the previous optimization step), $\Delta _f$ dictates the regularization strength (experimentally tuned to 0.1) and $\mathcal {F}^{s,t}_{*}$ is a thresholded version of $\mathcal {F}^{s,t}$ where we set to 0 the low-activated channels of each feature vector, stopping the gradient propagation:

$$\begin{aligned} \begin{aligned} \mathcal {F}^{s,t}_{*}&= \{\phi (\textbf{f}) \;\;\; \forall \textbf{f} \in \mathcal {F}^{s,t}\} \\\phi (\textbf{f})_i&= {\left\{ \begin{array}{ll} \textbf{f}_i &{} \textbf{f}_i \ge \frac{1}{K}\sum \limits _{j=1}^{K}{\textbf{f}_i} \\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned} \end{aligned}$$

(10)

This objective is applied in a completely unsupervised manner, and the vector norms are forced to align to the same value regardless of their class. In this way, we remove the bias generated by heterogeneous pixel-class distribution in semantic labels, that, for example, lead features of the most frequent classes to have larger norms than average. The constraint of Eq. (9) forces the inter-class alignment step, i.e., it promotes gradual alignment of the norms toward a target common to all categories, while discouraging the value of such a target to decrease too rapidly. An additional benefit of rescaling the loss by the norm target is that the loss gradients will be limited in magnitude and, therefore, more stable.

5 Implementation details

5.1 Training data

We evaluated our approach (LSR$^+$, latent space regularization) on road scenes segmentation in various synthetic-to-real and real-to-real unsupervised adaptation tasks. As source domains we used the synthetic datasets GTAV [20] and SYNTHIA [21]. The first contains 24, 966 labeled images at a resolution of $1914\times 1052$ px, produced with the rendering engine of the GTAV video game, while the second contains 9, 500 labeled images at a resolution of $1280\times 760$ px, rendered with a custom software. As target domain, we selected the real-world dataset Cityscapes [6]. It contains 5, 000 labeled images at a resolution of $2048\times 1024$ px and an additional set of 20, 000 coarsely labeled samples, acquired in European cities. When considering only unlabeled samples, the two versions are equivalent and can be merged (obtaining a dataset we refer to as CS-full) improving the adaptation process (as we show in Table 1). In the real-to-real setup, we used the Cross-City benchmark, where the Cityscapes dataset takes the role of the source domain, while the Cross-City dataset [18] takes the role of target. Such dataset is comprised of 12, 800 high resolution ($2048\times 1024$ px) images taken in four major cities (Rome, Rio, Tokyo and Taipei).

We trained the model in a closed-set [2] setting, i.e., with the same source and target class sets. More in detail, we used the 19, 16 and 13 classes in common for GTAV, SYNTHIA and Cross-City, respectively. GTAV, Cityscapes and Cross-City images have been rescaled for training to $1280\times 720$ px, $1280\times 640$ px and $1280\times 640$ px, respectively, while the resolution of SYNTHIA images has not been changed.

Table 1 Comparison of adaptation strategies in terms of IoU, mIoU and mASR (Sect. 6). Best in bold, runner-up underlined. mIoU$^{1}$ and mASR$^{1}$ restricted to 13 classes, ignoring the classes with the same superscript

5.2 Segmentation network

We employed the well-known [42, 47, 56, 57, 72] DeepLabV2 network [10,11,12], with ResNet101 [73] as the backbone (using 2048 channels in the last stage of the encoder) and a stride of 8. We pre-train the network as in [5], employing the same data augmentation techniques used during adaptation.

5.3 Network training

We optimize the model with SGD (using a momentum of 0.9 and a weight decay regularization of $5 \times 10^{-4}$). The learning rate starts from $2.5 \times 10^{-4}$ and uses a polynomial decay of power 0.9 over 250k steps, as in [56]. We used for validation a subset of the original training set to tune the hyper-parameters of our loss components. To tackle overfitting, we used some data augmentation strategies: random left–right flipping; white point re-balancing $\propto \mathcal {U}([-75,75])$; and color jittering $\propto \mathcal {U}([-25,25])$ (the last two applied independently in the R, G and B channels) and random Gaussian blur [51, 56]. We perform training on an NVIDIA Titan RTX, using a batch size of 2 (1 source and 1 target samples) for 24, 750 steps (i.e., 10 epochs of the Cityscapes train set). We also exploited the validation set for early stopping.

The code developed for this work is publicly available at https://github.com/LTTM/LSR.

6 Adapted-to-supervised ratio metric

In this section, we introduce a novel measure, called mASR (mean Adapted-to-Supervised Ratio), in order to better evaluate the domain adaptation task with respect to the usual mIoU.

The idea behind the new metric sparks from realizing that the mIoU is missing a key component to evaluating an adaptation method: i.e., it does not account for the starting accuracy of the different classes in supervised training. In particular, the objective of domain adaptation is to transfer the knowledge learned on a source dataset to a target one, trying to get as close as possible to the results attainable through supervised learning on the target domain. We design mASR to capture the relative accuracy of an adapted architecture with respect to its target supervised counterpart, which we identify as a reasonable upper bound. Therefore, mASR focuses less on the absolute-term performance and more on the relative accuracy obtained by an adapted architecture when compared to traditional supervised training.

We compare the per-class IoU score of the adapted network for each $c\in \mathcal {C}$ (${{\,\textrm{IoU}\,}}^c_{adapt}$) with the results of supervised training on target data (${{\,\textrm{IoU}\,}}^c_{sup}$), and we compute mASR by:

$$\begin{aligned} {{\,\textrm{mASR}\,}}= \frac{1}{|\mathcal {C}|} \sum \limits _{c \in \mathcal {C}}{{{\,\textrm{ASR}\,}}^c}, \;\;\; {{\,\textrm{ASR}\,}}^c \overset{def}{=} \frac{{{\,\textrm{IoU}\,}}^c_{adapt}}{{{\,\textrm{IoU}\,}}^c_{sup}} \cdot 100 \end{aligned}$$

(11)

In mASR, the contribution corresponding to each semantic category is inversely proportional to the accuracy of the segmentation model on it in the supervised scenario, thus giving more relevance to the most challenging classes and producing a more class-agnostic adaptation score. Furthermore, notice how the most challenging classes in driving scenarios are typically associated with small objects like traffic lights or pedestrians and bicycles, which are very critical for autonomous navigation. In this metric, higher means better, and when the adapted network has the same performance as supervised training, the score is $100\%$.

As an example, the mASR scores reported in the last two columns of Table 1 allow identifying at a glance the algorithms that more faithfully match the target performance.

To validate the new metric, we used as a reference the supervised training on the Cityscapes dataset and compared it with the training on corrupted versions of the same dataset using the introduced mASR metric to evaluate the relative performances and so, indirectly, the domain shift introduced by the perturbations. In Fig. 3, we identified 5 types of perturbations that are likely to be encountered by an agent moving outdoors (i.e., Gaussian noise, motion blur, snow, fog, brightness) and we set 5 levels of noise intensity as defined by [74]. As expected, the higher the noise intensity, the lower the adaptation score computed by mASR. Furthermore, we can also have a hint of the most detrimental types of noise for adapting source knowledge, namely Gaussian noise, snow and motion blur. This can help us identify which set of samples we should consider more in order to obtain a reliable model capable of handling these situations. On the other hand, brightness and fog influence less the final scores.

Fig. 3

mASR score as a function of the injected noise intensity. Best viewed in color

7 Experimental evaluation

The qualitative and quantitative results achieved by the proposed approach (LSR$^+$) in various driving contexts will be presented in this section, where it will be compared with several other feature-level approaches (i.e., [42, 47, 75]), with some entropy minimization strategies (i.e., [56, 57]) that have a similar effect on feature distribution, and finally with the conference version of our work [5]. The key feature of these approaches is the training efficiency; indeed, the addition of such constraints does not increase the training computational complexity, differently from expensive adversarial approaches or modified architectures.

Our end-to-end method allows straightforward integration with other strategies, e.g., adversarial approaches at input or output level, or entropy minimization. In order to verify such compatibility, we introduce an additional entropy minimization loss [56] in our setup. We start by considering two widely used synthetic-to-real benchmarks and a standard ResNet101 as backbone architecture obtaining the results shown in Table 1. Then, a real-to-real benchmark [18] has also been used (see Table 2). To further verify the robustness of our setup, in Table 3 we report some results using different backbones (i.e., ResNet50, VGG16 and VGG13).

Table 2 Quantitative results on the Cross-City real-to-real benchmark. (r) indicates that the strategy was retrained, starting from the official code. Best in bold, runner-up underlined

Table 3 Quantitative results with different backbones, GTAV$\rightarrow$Cityscapes setup. (r) indicates that the strategy was retrained, starting from the official code

7.1 Adaptation from synthetic data to Cityscapes

When adapting source knowledge from the GTA5 dataset to the Cityscapes one, our approach (LSR$^+$) achieves a mIoU of $46.9\%$, with a gain of $10\%$ compared to the baseline and of $0.9\%$ compared to the conference version (LSR) [5], thanks to the refined space-shaping objectives. In particular, the classes which enjoyed the greatest improvements are those targeted by our approach, i.e., the less common or the ones corresponding to small objects (pole, t. light, train, etc.). Our new pipeline improves recognition of these types of classes since we actively re-weight the labels during downsampling and employ outlier-resistant strategies, differently from the previous approach. In general, our approach outperforms all compared strategies: the only techniques able to get close to its performance are the works by [47] and [56], while the other competitors see a significant score drop. The performance improvement is quite stable across per-class IoUs and is particularly noticeable in challenging classes, like terrain and t. light where our strategy shows very high accuracy gains, and on train where we significantly outperform the competitors by doubling the score of the second-best strategy.

Some qualitative results are reported in the top half of Fig. 4. From visual inspection, we can verify that our method increases the precision of edges on t. sign, t. light, pole and person classes in both images. Furthermore, our approach is the only one to correctly classify the bus on the right of the first image, which is confused as truck by the other strategies. Importantly, we can also see the effects of our two-pass labeling (see Sect.  3.3) on the left of the top image (where part of the fence is correctly classified by our strategy while being missed by all competitors) and of the second image (where LSR$^{+}$ significantly reduces the confusion between sky and the white building, and is able to correctly recognize the car, which was confused for truck by the old approach).

In the SYNTHIA to Cityscapes setup, LSR$^+$ surpasses its conference version (LSR) by about $1\%$ of mIoU in the 16-class setup and by $0.6\%$ in the 13-class one, achieving a final score of 42.6 and $48.7\%$, respectively. Again, the most noticeable improvement can be found in the difficult classes, such as wall, pole or bicycle. Such gains over the older approach confirm once again the effectiveness of our new formulation. Similarly to the GTA5-to-Cityscapes experiments, also in this setting LSR$^+$ outperforms all the other competitors, with a slight margin of $1\%$ on average with respect to [47] and a larger one (more than $3\%$) compared to all the other approaches.

Qualitative results are reported in the bottom half of Fig. 4, where the overall increase in segmentation accuracy for many classes such as car, road and sidewalk is evident. In the first image (third row of Fig. 4), we can see how LSR$^+$ is the only strategy to correctly classify both rider and bike, whereas other strategies even miss the t. sign in the foreground. Similarly, in the second image, we note improvements in the prediction of such classes and, fundamentally, of the road in the foreground (confused for car and bicycle by the competitors).

7.2 Adaptation from Cityscapes to Cross-City

Besides using synthetic data, another key requirement is the capability of adapting networks trained on road scenes coming from certain geographical areas to other regions. However, the great variability of road scenes across the world limits the wide application of locally trained models on a global scale. To investigate the capability of our approach to cope with this problem, we evaluate the performance on the Cross-City real-to-real benchmark in Table 2. This benchmark is comprised of 4 cities with a completely different type of urban setting: Rome, Rio, Tokyo and Taipei. When evaluated on those setups, our strategy reaches an mIoU score of 56.2, 52.3, 50.0 and $50.0\%$ surpassing the source-only model by 5.2, 3.4, 2.2 and $3.7\%$, respectively. Importantly, our approach achieves consistent results across the setups (LSR$^+$ is the top scorer in 3 out of 4 setups, and second in the remaining one) surpassing the average best competitor score by $0.5\%$ mIoU (52.1 versus $51.6\%$). We remark that the best competitor changes depending on the setup, being [42] for Rome and Taipei and [47] for Rio and Tokyo, underlining the unstable performances of many approaches usually associated with this benchmark.

This adaptation setup is particularly suited for evaluating approaches since it presents data with varying degrees of domain shift. The fact that our approach is able to achieve good performance in all settings highlights how the new space-shaping objectives are able to work effectively even in the presence of a significant distribution shift, thanks to the updated feature vector estimation. Looking at the per-class IoU scores, we can see how our strategy significantly outperforms the competitors in t. light and rider in the Cityscapes$\rightarrow$Rome setup (increase of $6\%$ of IoU), in person and rider in the Cityscapes$\rightarrow$Rio setup (increase of $4\%$ of IoU) and in motorbike in the Cityscapes$\rightarrow$Taipei setup (increase of $9.3\%$ of IoU). Qualitative results on this benchmark are presented in Fig. 5. From a visual inspection of the images, we can see an overall increase in the discrimination of the object borders, particularly for classes such as car, road, building, vegetation and person. In Rome, we see how LSR$^+$ is the only strategy that correctly identifies the rider behind the cars in the second image. In Rio, our architecture significantly reduces the amount of confusion regarding the building on the left of the second image. Again, in Tokyo, we note how LSR$^+$ is the only technique able to recognize the traffic sign on the right of the first image. Finally, in Taipei, we see how our approach is the only to correctly identify the person and motorcycle in the second image.

Fig. 4

Qualitative results sampled from the Cityscapes validation split. Best viewed in color

Fig. 5

Qualitative results on the Cross-City benchmark. Best viewed in color

7.3 Results with different backbones

Table 3 shows the performance of our strategy on GTAV$\rightarrow$ Cityscapes using multiple encoder–decoder backbones in order to evaluate the generalization properties of the approach to different network architectures. Here we can see how LSR$^+$ outperforms the source-only models (i.e., without adaptation) by 13.3, 12.7 and $7.8\%$ using ResNet50, VGG16 and VGG13, respectively. Even more importantly, we can see how the performance improvement is consistent across all backbones, in opposition to what happens to competing strategies. Finally, we remark on the stability of the mASR score of our strategy, hovering around a mean of $57.0\%$ with a very tight standard deviation of $1.4\%$. (The mean values of the other strategies are 48.5 and $42.2\%$, and the standard deviations are 2.5 and $31.3\%$, respectively.) We can see how the consistent performance of our approach is preserved even in the class-wise IoU scores, particularly in the train class, where we significantly outperform the competitors, gaining an average of $7\%$ of IoU across the four backbones with respect to the second-best strategy.

8 Ablation studies

In this section, we evaluate the impact of each component of the approach on the final accuracy. Quantitative results are reported in Tables 4 and 5. In the first, we evaluate our strategy by removing each constraint independently and evaluating the impact on the score, while also comparing the results with [5], highlighting the improvement over the older version of the approach. In the second, we report the performance attained when sweeping across values of each loss learning rate while keeping the optimum value for the other two losses. Several conclusions can be drawn from the tables: firstly, the removal of any of our losses incurs in a noticeable drop in performance ranging from $0.9\%$ mIoU to around $2\%$, meaning that the three objectives should always be employed together, since only when working together they can effectively shape the latent space into the desired arrangement; secondly, the novel implementation offers significantly reduced space-shaping overlap with the minimum entropy constraint, leading to a higher score when $\mathcal {L}_{EM}$ is included in the pipeline; thirdly, all three objectives offer an improvement over the baseline score regardless of the chosen weighting factor (the worst scores are 43.9, 44.6 and $45.7\%$ for $\mathcal {L}_{C}$, $\mathcal {L}_{P}$ and $\mathcal {L}_{N}$, respectively, which correspond to improvements of 1.1, 1.8 and $2.9\%$).

8.1 Analysis of the latent space regularization

For visualization purposes and for a fair comparative analysis across the classes, the plots of this section are computed on a balanced subset of feature vectors (250 vectors per class) extracted from the Cityscapes validation set.

Table 4 Ablation studies, mIoU and mASR scores comparison when removing any of the losses. Implementations of losses from [5] are compared with the new ones in this work.

Table 5 Ablation on the weighting factors of the losses, we fix the best value for two weighting coefficients and sweep values for the third one. $\lambda _{EM}$ is fixed to the best value (i.e., 0.1, according to [56])

8.1.1 Two-pass prototypes and clustering

To investigate the semantic feature representation learning produced by our approach, we computed a shared t-SNE [76] embedding of the prototypes sampled during the training procedure and of the target features produced by the final model. We remind the reader that, in order to more effectively shift target features closer to the source ones, we resort to a two-stage label assignment procedure which recovers target awareness (by averaging target-extracted features) from prototypes computed on the source domain (by centroid computation) as reported in Sect. 3.3. In the left plot of Fig. 6, we report the learned prototype trajectory embeddings and on the right the respective feature vectors. Here we can appreciate how prototypes get farther apart while training goes on and how features extracted from the target domain lie in a neighborhood of the prototype, which we recall is computed exclusively via source supervision. This underlines the effectiveness of our clustering strategy, which is able to shift the target feature distribution closer to the source one.

Fig. 6

t-SNE embedding of the target feature vectors. On the left: trajectories of prototypes sampled over 200 training steps. On the right: features produced by the final model embedded according to the shared t-SNE projection. Best viewed in color

Fig. 7

Prototypes trajectories and target feature vectors projected via PCA. Projection is three-dimensional; here, we report the three xy, xz and yz planes. Best viewed in color

To further analyze our clustering objective, we produce additional t-SNE embeddings starting from the normalized features (to remove the norm information, focusing on the angular one), which is reported in Fig. 8. Our strategy significantly improves the cluster separation in the embedded space and increases the spacing between clusters belonging to different classes, promoting features’ disentanglement. This cross-talk reduction is also reflected in the decreased probability of confusing visually similar classes (e.g., the truck class with the bus and train ones).

Finally, PCA embeddings are reported in Fig. 7 to evaluate the effect of latent-spacing techniques when projected to a lower dimension via a linear function, which confirms the findings highlighted in the t-SNE embeddings.

Fig. 8

t-SNE embeddings of the normalized feature vectors. Best viewed in color

Fig. 9

Sample image downsampled nearest (left), frequency-aware [5] (middle) or weighted frequency-aware (LSR$^+$). Best viewed in color

8.1.2 Weighted histogram-aware downsampling

In this work, we extended the scheme proposed in [5] by adding class weights inversely proportional to the class frequency in the training dataset (see Sect. 3). Our goal is to provide labeling only to spatial locations in feature maps where a clear class association can be performed, by relying on a frequency-aware scheme. By doing so, we seek the disentanglement of activations belonging to different classes, even when their feature vectors are neighbors in a given label map. This effect can be noted in Fig. 9, where our downsampling algorithms enhanced with frequency awareness are able to identify some feature locations close to class edges as unlabeled in the downsampled label map (middle and right), keeping only faithful features. As expected, class-weighting (right plot of Fig. 9) promotes rarer classes at the feature level compared to the version without it [5] (middle plot of Fig. 9): for instance, compare the traffic sign (in yellow).

Further evidence of this can be found in the class distribution of segmentation maps (computed after their downsampling to the latent space spatial resolution), which we reported in Fig. 10 for our weighted histogram-aware scheme, the previous unweighted histogram-aware scheme of the conference version [5] and the standard nearest neighbor. In particular, the schemes based on histogram awareness generally seldom preserve small object classes, promoting unlabeled classification when discrimination between classes is uncertain. Our weighted histogram-aware scheme improves uniformity across rarer or smaller semantic categories, which were over-penalized by the previous approach [5], where all classes were treated equally, regardless of their occurrence.

Fig. 10

Class frequency of the downsampled feature-level segmentation maps

Fig. 11

Mean inter-prototype angle

Fig. 12

Average channel entropy

8.1.3 Perpendicularity

is analyzed in Fig. 11 where we display the average angular distance between each prototype and all the remaining ones. Our goal is to achieve prototype perpendicularity, such that we minimize the overlap (i.e., cross-talk) among distinct semantic categories over feature activations. By the red dashed line, we highlight the upper bound to the angular distance, which is set to 90 degrees since we assume feature vectors to have nonnegative entries. From the figure, it emerges clearly that LSR-based approaches increase the inter-prototypical angle and that LSR$^+$ makes prototypes even more orthogonal with an improvement of more than 2 degrees on average.

8.1.4 Norm alignment

is analyzed in Fig. 12, where we show the mean channel entropy for each class. We observe that the entropy corresponding to feature vectors produced by LSR$^{+}$ is significantly reduced, meaning that features are characterized by more relevant peaks and fewer poorly activated channels.

9 Conclusions

In this work, we tackled domain adaptation of road scene segmentation models by introducing a set of latent space regularization strategies for unsupervised domain adaptation. We improved domain invariance using different latent space-shaping constraints (i.e., class clustering, class perpendicularity and norm alignment), to space apart features belonging to different classes while clustering together features of the same class in a consistent way on both the source and target domain. To support their computation, we introduced a novel target pseudo-labeling scheme and a weighted label decimation strategy. Results have been evaluated using both the standard mIoU and a novel metric (mASR), which captures the relative performance between an adapted model and its target supervised counterpart. We outperformed state-of-the-art methods in feature-level adaptation on two widely used synthetic-to-real road scene benchmarks and in real-to-real setups, paving the way to a new set of feature-level adaptation strategies capable to improve the discrimination ability of road scene understanding approaches.

Future work will focus on designing novel feature-level techniques and on evaluating their capability of generalizing to various tasks in driving scenarios. The adaptation from multiple source domains to multiple target ones will also be considered together with the application also to multimodal data (e.g., LIDARs or depth cameras) mounted on cars.