Abstract
In many applications, visual analytics (VA) has developed into a standard tool to ease data access and knowledge generation. VA describes a holistic cycle transforming data into hypothesis and visualization to generate insights that enhance the data. Unfortunately, many data sources used in the VA process are affected by uncertainty. In addition, the VA cycle itself can introduce uncertainty to the knowledge generation process but does not provide a mechanism to handle these sources of uncertainty. In this manuscript, we aim to provide an extended VA cycle that is capable of handling uncertainty by quantification, propagation, and visualization, defined as uncertainty-aware visual analytics (UAVA). Here, a recap of uncertainty definition and description is used as a starting point to insert novel components in the visual analytics cycle. These components assist in capturing uncertainty throughout the VA cycle. Further, different data types, hypothesis generation approaches, and uncertainty-aware visualization approaches are discussed that fit in the defined UAVA cycle. In addition, application scenarios that can be handled by such a cycle, examples, and a list of open challenges in the area of UAVA are provided.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Huge amounts of data are created every day that need to be properly analyzed. This need drove the development of a new data processing concept, called visual analytics (VA) [21]. It states that analytic reasoning should be supported by interactive visual interfaces that allow users to explore datasets according to their needs and perform decision-making tasks.
Keim et al. [65] described the VA process as a graph consisting of four major components (dataset, hypothesis, visualization, and insight). These components are connected by functions that allow to transform and analyze given input datasets while creating new insights, as shown in Fig. 1. In many applications, VA is applied as a standard tool to find novel insights and perform decision making [69].
VA cycle introduced by Keim et al. [65]. The cycle consists of four major components (dataset, hypothesis, visualization, and insight) that are connected, including a feedback loop that inserts insights back into the VA process
The role of uncertainty in the VA process has been described by Sacha et al. [96]. It mainly states that uncertainty has to be properly communicated, allowing decision makers to perform their tasks properly. The term VA has been constantly refined throughout the last two decades while including the human in the loop and refining knowledge generation [2, 97, 109]. These definitions are all valid, providing different levels of detail and emphasis in the description of VA, while the description by Keim et al. provides a compact and prominent mapping of the VA process.
Keim et al. [64] stated that the integration of uncertainty is one of the major challenges in VA. By now, many applications have started incorporating uncertainty analysis in their VA tools, summarized in Sect. 2.
The data, models, and the proper interaction of users in real-world applications are often affected by uncertainty due to a variety of effects such as data incompleteness, imprecise measurements, reconstruction artifacts, or model imprecision [43], as shown in Sect. 3. Each component in the VA cycle can be affected by uncertainty that needs to be quantified, propagated, and communicated throughout the VA cycle. Although a variety of approaches in different applications for uncertainty-aware VA (UAVA) exist, there is a lack of a unified description that defines the necessary steps to achieve this goal.
This forms the motivation for the presented work. We aim to provide a general description of a UAVA cycle (see Sect. 4) by revisiting the VA definition of Keim et al. [65], extending it to provide uncertainty-aware quantification and transformation approaches along the VA cycle. Furthermore, we added novel connections and steps in the VA process, when required, to achieve uncertainty awareness. In its entirety, this formulates an uncertainty-aware description of the VA process. The description of this cycle is assisted by a hands-on example originating from the medical domain. Here, each step is explained and correlated with the generalized description of the UAVA process.
In Sect. 5, we show the applicability of the presented approach by offering a summary of potential uncertainty-aware solutions of specific components in the VA cycle. Based on the presented description of a UAVA cycle, Sect. 6 identifies components and connections that require further research to be properly defined.
In summary, our manuscript allows a starting point for researchers in the area of VA that face the challenge of uncertainty while creating VA solutions. The manuscript is intended to provide a guide to understanding sources of uncertainty, how they interfere with the VA cycle, and shows potential solutions. Although we do not provide a state-of-the-art analysis, we aim to summarize potential sources for further reading in specific subtasks of the VA cycle.
Therefore, in this work, we contribute:
-
A comparative analysis of existing UAVA approaches, framing the need of an unified approach (see Sect. 2)
-
A quick guide to uncertainty analysis allowing researchers to identify the existing sources of uncertainty in a VA cycle (see Sect. 3)
-
An uncertainty-aware extension of the VA cycle defined by Keim et al. [65], building a unified framework to handle uncertainty in VA (see Sect. 4)
-
A summary of potential solutions of UAVA that builds a starting point for selecting potential solutions in UAVA (see Sect. 5)
-
A summary of open problems in UAVA, building the research agenda in the presented area (see Sect. 6)
2 Related work
In Sect. 2.1, we aim to summarize the most important definitions in VA and show why these approaches are not able to handle uncertainty systematically. Then, the uncertainty-aware visualization approaches essential in UAVA are examined in Sect. 2.2. Based on these findings, Sect. 2.3 aims to summarize approaches that target the challenge of including UAVA for specific scenarios. In addition, a variety of works in related disciplines, such as sensitivity analysis, are examined in Sect. 2.4. Here, we aim to summarize the most related work in the context of the given approach. The approaches have been selected according to the keywords of the presented work (VA, uncertainty analysis, and uncertainty-aware visualization). If an article contains a minimum of two of these keywords, it was considered in this analysis. The work found in this section will be summarized and compared in Sect. 2.5 to define the target and scope of the presented work.
2.1 Definition of visual analytics
The definition of VA has been constantly developed throughout the years. Thomas and Cook [109] developed the term VA and highlighted the need for systematic development in this area. Keim et al. [65] developed a systematic description of the VA cycle while defining four components that transform data into hypothesis and visualization to create insight. This insight can be fed back into the cycle as novel data. The feedback loop has been further separated and examined by Sacha et al. [97]. This resulted in the knowledge generation model in VA. Further, Andrienko et al. [2] interpreted the term VA as model building, refining the original definition of Keim et al. Unfortunately, all these definitions do not include uncertainty in their considerations. Still, they provide a systematic description of the VA cycle, which forms the motivation of the presented work.
MacEachren [82] stated that a classic visualization approach is not sufficient to deal with uncertainty. They proposed that UAVA is required as it provides the user with an approach to tackle data not restricted to visualization. We use this statement as a starting point for the presented description of UAVA. This statement is also evaluated for a specific use case, showing that the visual communication of uncertainty is necessary [73].
2.2 Uncertainty-aware visualization
The VA process is highly dependent on the contained component visualization, as it can be seen as a key component.
Surveys on uncertainty visualization are manifold but do not have a relation to UAVA. Potter et al. [88] achieved a taxonomy of uncertainty visualization. Brodlie et al. [14] followed a similar classification scheme to provide a general taxonomy. Based on previous work, Bonneau et al. [9] presented a STAR on uncertainty visualization which forms a basis for Jena et al. [56] to build an online browsing tool to explore several uncertainty-aware visualization approaches. Here, uncertainty visualization approaches were classified based on the underlying data. Olston et al. [85] presented a STAR report regarding the visualization of bounded uncertainty, whereas Hullman et al. [54] presented a STAR report targeting the evaluation of uncertainty visualization.
Kamal et al. [59] provided a summary of recent challenges in uncertainty visualization. The challenges are presented in a structured manner, leading to a summary of open challenges that are mainly centered around the inclusion of the user in the visualization process.
Bhatt et al. [8] provided guidelines that aim to suggest the use of uncertainty visualization. Still, these findings need to be transferred to VA.
Although these taxonomies are a useful starting point for the presented research area, it solely covers the visualization component in VA. We, therefore, aim to extend these approaches to the entire VA process.
2.3 Uncertainty-aware visual analytics
UAVA approaches have been designed for multiple data types and computational models such as: multi-variate time-series [10], principal component analysis [42], merge-trees [124], moving object detection [50], or tensor analysis [35].
Based on the classic definition of the VA cycle by Keim et al. [65], a massive amount of VA applications have been developed and applied. Still, the field of VA holds a set of open problems. One is the proper quantification, communication, and visualization of uncertainty in the VA cycle [65].
Sacha et al. [96] formulated requirements that need to be fulfilled to obtain an uncertainty-aware visualization. Their suggestions include uncertainty quantification, uncertainty propagation, visualization of uncertainty in each component, and suitable interaction with uncertainty-aware visualization. These requirements will be used to adapt the classic VA cycle in this work.
Correa et al. [19] showed how the requirements by Sacha et al. could be described mathematically. Although this gives first hints on the requirements needed to implement a UAVA cycle, it does not clearly state where this information comes from and how it can be applied. In contrast to the presented work, we aim to provide an adapted and extended VA cycle that incorporates the suggestion by Sacha et al.
Karami [60] provided a UAVA cycle that allows the processing of big datasets. Their work includes precise descriptions of each component in the VA cycle when considering big data. This limitation neglects further flavors of data that will be targeted in the presented work by a description of UAVA.
Senaratne [100] described the role of uncertainty for spatiotemporal data and presented solutions for uncertainty-aware image-based volunteered graphic information, exploration of location-based mobile communication data, and bi-dimensional numerical data. We use these approaches as a starting point for available techniques.
Although the problem of uncertainty in VA is quite known, a generalized uncertainty-aware description of the VA cycle does not exist. As parts of the VA cycle highly depend on the underlying dataset, we aim to include uncertainty-aware descriptions of different data types.
UAVA plays an important role in a variety of applications. These include medicine [37,38,39], biochemestry [80], environmental sciences [91], urban planning [31], mechanical engineering [70], and digital humanities [58, 67]. Unfortunately, although the issue of including uncertainty in the VA process is quite known in these disciplines, the existing solutions are highly specialized and cannot be applied to further use cases right away. Therefore, we aim to provide a general description of UAVA that allows targeting all applications.
2.4 Uncertainty-awareness in related disciplines
Uncertainty awareness is highly related to a set of other disciplines including sensitivity analysis or VA of ensembles. We aim to shed light on these approaches and define starting points for our research. To find these approaches, we searched terms that are considered related to uncertainty as shown in the taxonomy by Rocha et al. [95].
VA in the context of ensemble datasets is highly related to the presented topic, as ensemble data can be transformed into uncertainty data (including loss of knowledge) and vice versa. Wang et al. [117] provided a state-of-the-art analysis for VA of ensembles and showed that a suitable communication of variability in an ensemble can be achieved by VA approaches. We would like to derive important knowledge from this work to achieve a UAVA cycle.
Liu et al. [78] showed that the quality of data is an important aspect that needs to be monitored in the VA cycle. In their work, they provided a mechanism that extends the VA cycle to enhance data quality and create awareness of data flaws. The quality of data is highly affected by data uncertainty. Resulting from this, we will include the data quality defined by Liu et al. in this proposed approach.
Sensitivity analysis [98] is highly related to uncertainty analysis as this discipline examines the effect of changing input variables to the output variable(s). Especially in machine learning, VA approaches are derived to conduct sensitivity analysis [107]. This also highly relates to uncertainty analysis as uncertainty expresses the variability of parameters in a system. We will include sensitivity analysis in the presented work if it is applicable. Although we found several related disciplines to uncertainty analysis and visualization, these sciences cannot build a UAVA cycle right away. This is based on two reasons. First, the related disciplines are themselves not solved and second uncertainty cannot be transformed into another problem without loss. Therefore, this work aims to provide a UAVA cycle.
2.5 Summary and implications
We showed that there exist a variety of approaches that deal with uncertainty in relation to VA. Table 1 provides a summary of the examined approaches. It shows which of the considered approaches provide a theoretic approach in the area of VA, which of them allow a systematic approach in the respective area independent from the application, and which approaches consider uncertainty awareness (UA).
There does not exist an approach that provides a theory that describes a systematic approach for UAVA. This results in a clear research gap that we aim to tackle in this work.
3 Definitions
This section defines the mathematical basics of uncertainty. Here, we describe how to define, quantify, propagate, and accumulate uncertainty as a reference for the remaining manuscript.
3.1 Definition of uncertainty
Independent of the data source, task, and user, datasets are usually acquired by measuring or simulating a phenomenon creating data points. As this work is dedicated to incorporate uncertainty into the visual analytics cycle, we will not discuss the influence of tasks and users in general, as a variety of approaches have been tackling these effects [65].
Measurements can be distorted by a variety of effects leading to measurement errors and uncertainty. Error and uncertainty are referring to two different aspects when considering measurements.
Let \(a \in (-\infty , \infty )\) be a measurand and \(a^{*}\) be the true value of this measurand. When performing the measurement, the result will be \(a{'}\). \(a^{*}\) and \(a{'}\) may be the same value, but in reality, their values differ due to a variety of effects. The error e of the performed measurement can be defined as the difference between the measured value and the true value of the measurand [12]. This means: \(e = \Vert a^{*} - a' \Vert \). As a consequence, the quantification of an error requires a ground truth that clearly shows the difference between the actual value and the measured value. Naturally, as there is no unique definition of uncertainty, errors can be communicated using a variety of visualization techniques in the VA cycle. Further, computations of data points that are affected by an error can be performed right away.
The uncertainty of a measurement is a quantification of the doubt about the measurement result [46]. If this uncertainty is known, the measurand is defined to be uncertainty-aware. In contrast, if this uncertainty is unknown, a measurand is called uncertain. As there is no unique description of uncertainty, it has a massive affect to the VA process. In particular, a variety of uncertainty events can occur at different stages in the process, which can lead to wrong decision making. We will list these sources in discussion of this manuscript.
Unfortunately, there is no unique definition of how to compute uncertainty. Arbitrary functions can be considered to achieve uncertainty quantification. In many cases, uncertainty is described as a boundary around the measurand [85]. It defines an interval around the measurand that can be defined as: \( u_{B}(a) = [a{'} - u, a{'} + u ]\). This description of uncertainty is chosen when the distribution of the occurrences is not important. Instead, it is important to know the limits in this variation [7].
Another popular definition of uncertainty utilizes probabilistic distribution functions [79] \(u_{\text {PDB}}(a)\). These functions allow describing the probability density of a measurand to be located at an arbitrary point in some space. Here, the measurand usually defines the most probable location of the true value that was captured. A prominent choice of probabilistic distribution functions are Gaussian distribution functions. [47].
3.2 Quantification of uncertainty
To achieve an uncertainty definition, proper uncertainty quantification is required. The most important methodologies can be roughly separated into four categories: forward uncertainty quantification, sensitivity analysis methods, response surface methods, and dimension reduction methods [76]. We will explain each category briefly in the following.
Most of the uncertainty forward propagation techniques aim to assign a statistical distribution for each of the model parameters considered to be uncertain. A summary of these techniques can be found in [72] and these techniques are referred to as forward uncertainty quantification (FUQ).
Sensitivity analysis methods (SAM) can be used for uncertainty quantification. Here, the idea is to provide a measure of the variability of input parameters in a system. As a result, the effect of variability of input parameters on the output of a system can be described [4].
Response surface method (RSM) approximation techniques aim to build a mathematical model by providing a simplified meta-model mostly using linear or quadratic functions [41]. These methods are used to reduce the computational effort in large and complex systems.
As parameter analysis can be computationally expensive, dimension reduction methods (DRM) can be utilized for uncertainty quantification [17]. These techniques aim to reduce the set of input parameters to facilitate uncertainty quantification. A summary of dimension reduction approaches can be found in [103].
As there exist a variety of uncertainty quantification approaches, a proper approach fitting the current application has to be chosen. Unfortunately, there is no clear way to choose the right approach, as this decision is always depending on the use case, the underlying data, and the goal. Still, Skyu et al. [101] proposed guidelines that should be considered when selecting an uncertainty quantification, which will be summarized in the following.
-
Uncertainty quantification should be invariant to data transformation and parameterization of the model
-
Uncertainty quantification should reflect the informativeness of the observed data for the underlying process
-
Uncertainty quantification should be amenable to be probed empirically for possible violations
-
If an uncertainty quantification is not sufficiently accurate, it should be possible to diagnose potential problems in the model and ways to correct them
3.3 Propagation of uncertainty
The propagation of uncertainty is an important issue when data (including their uncertainty) is transformed. Although there is an explicit component that is in charge of handling the incoming data in the VA cycle, all other components of the VA cycle produce data in some manner. While piping data through the VA cycle, this data gets manipulated by the hypothesis, visualization, and insights component.
Pathways of uncertainty propagation. When an operation O is applied to an attribute a at an arbitrary point in the VA cycle, an adapted function \(\overline{O}\) needs to be applied to the uncertainty of the attribute. Note that these attributes can be arbitrary point in the VA cycle and are not limited to the data component. The uncertainty of the attribute influences the function O. In addition, uncertain values need to be adapted by a damping factor d
Data is mostly propagated through mathematical operations O. This is not limited to the data component itself, but can also express data points inherent in the hypothesis, visualization, and insights component. These operations do not solely affect the data, but also the attached uncertainty. Besides, mathematical operations are affected by the uncertainty of their operands. This results in the need to adjust mathematical operations to be able to handle uncertainty, as shown in Fig. 2.
In order to extend mathematical operations, an operation O is modified to \(\overline{O}\), where \(\overline{O} : \overline{a} \rightarrow \overline{a}^{*}\). This means that in addition to the attribute a itself, an uncertainty quantification u(a) is required. To accomplish a manipulation of \(\overline{a}^{*}\), three computational paths are required: first, the manipulation of the attribute itself (O(a)). Second, the manipulation of the uncertainty quantification of the attribute (\(\overline{O}(u(a))\)), and third, a damping factor that manipulates the influence of an attribute according to its uncertainty d(u(a)).
An uncertainty-aware formulation of O can be achieved by:
where d(a) is the damping factor of each attribute. d(a) can be defined as:
This means that every time an attribute is utilized in a mathematical operation, the attribute value will be damped when the respective uncertainty is high. When uncertainty is zero, the attribute value will be fully considered. Furthermore, all mathematical operations that are applied to an attribute will be applied to the uncertainty quantification of this attribute. Here, the function \(\overline{O}\) is dependent on the mathematical function O and can be derived considering the uncertainty propagation rules summarized by Gillmann et al. [36].
3.4 Accumulation of uncertainty
As shown above, uncertainty can be introduced into the VA cycle at all components, or multiple sources of uncertainty can affect one component. This results in the need for a mechanism that allows the accumulation of uncertainty.
The accumulation of uncertainty can, in principle, be achieved by arbitrary accumulation functions. Cai et al. [16] presented a survey of aggregation functions. In the VA process, a proper aggregation function needs to be able to aggregate all sources of uncertainty in the VA cycle in an orderly manner, also allowing the user to adjust the importance of all sources of uncertainty in the VA cycle. This is required, as users may need to determine which sources of uncertainty are more important than others or even discard specific sources.
3.5 The role of uncertainty in visual analytics
Keim et al. [64] proposed that the inclusion of uncertainty into the VA cycle is a non-trivial task. This is due to a variety of sources of uncertainty in this cycle. This section aims to summarize these sources to create a basis for the required adaptations in the VA cycle to make it uncertainty-aware.
In fact, each main component of the VA cycle can introduce uncertainty, as shown in Fig. 3. The sources of uncertainty can have different origins: uncertainty based on the underlying model (epistemic uncertainty), statistical uncertainty resulting from variations in the measurement result when running an experiment multiple times (aleatoric uncertainty), and subjective uncertainty resulting from humans interacting with the VA system.
Data Starting from the input dataset, uncertainty can be introduced into the VA cycle by data incompleteness, finite instrument resolution, non-representative sampling, variations in observations, and incomplete knowledge about the measurand [11]. An example would be medical measurements of blood sugar over time, where patients miss to perform the measurement on a regular basis. By definition, these sources of uncertainty are aleatoric. In this area, forward uncertainty quantification can be used to tackle all mentioned sources.
Hypothesis When considering hypothesis, uncertainty can be introduced by parameter uncertainty. This means that computational models often require parameters, which can be hard to find in many cases or it is hard to determine if a chosen parameter is optimal [83]. By model, we refer to the computational theory that is used to transform the input data. Furthermore, the computational model itself introduces uncertainty into the VA cycle. Models are incomplete or approximate physical behavior of natural phenomena by definition. As our knowledge of the world and computational power is limited, hypothesis forming is affected by uncertainty [33]. An example would be a simulation of stiffness in a particular material where boundary conditions need to be set, as not all physical behavior in the world can be modeled.
Visualization In terms of visualization, uncertainty can be introduced by the mapping of visual variables of the visualization algorithm, as well as the resolution of the display device [84]. Also, users reviewing the shown visualization can introduce uncertainty into the VA process that stems from perceptual uncertainty, memory uncertainty, and thinking uncertainty [28]. Here, an example would be that users might fail to perceive depth in a volume rendering due to inappropriate visualization approaches.
Insight At last, uncertainty can be introduced into the VA cycle while creating a hypothesis. Here, users can introduce uncertainty through a decision-making bias. This means that users may tend to ignore VA results, as they might be biased by previous results. The experience and knowledge of domain experts can also introduce uncertainty into the VA cycle [114]. This also relates to further disciplines as cognition theory and psychology, as uncertainty in the human component is hard to handle [29]. Enke and Graeber provided a theoretical framework to address this issue and performed experiments on how humans deal with uncertainty. Their findings indicate that uncertainty is perceived very differently depending on the decision maker. Still, the authors indicate that uncertainty needs to be communicated and discussed to allow a secure decision making.
Please note that not all mentioned sources of uncertainty are present in each scenario where VA is applied. Also, cases exist where a specific source of uncertainty may be present, but is neglected as its influence is too small. This decision is highly dependent on the use case, data source, and user. Still, one or even multiple sources of uncertainty are likely introduced into a specific implementation of the VA cycle.
UAVA. Starting from an input dataset, a U-Dataset can be created. This U-Dataset can be utilized to create an uncertainty-aware hypothesis or an uncertainty-aware visualization. Based on these analysis techniques, an uncertainty-aware insight can be generated through user interaction and provenance creation. The uncertainty-aware insight can be fed back into the Dataset or U-Dataset component
4 Uncertainty-aware visual analytics
In this work, we aim to provide a description of UAVA that allows visualization researchers to get a quick overview of the necessary steps that need to be accomplished when being confronted with an application affected by uncertainty.
This includes two important adaptations to the traditional VA cycle. First, all existing components and connections in the VA cycle need to be extended or adapted to incorporate uncertainty information. Second, the existing traditional VA cycle does not hold mechanisms to insert uncertainty knowledge into the VA cycle and keep track of them, which means that there are missing components and connections in the classic VA cycle that need to be added.
To make this process more understandable, we would like to use a hands-on example that shows how the different steps and components that are defined in the following can be implemented explicitly. Therefore, we use a real-world example from the domain of medicine [36]. Here, a keyhole surgery is planned to remove a brain tumor. Therefore, a secure way through the patient’s brain is required under uncertain conditions.
At first, we will follow the definition of the VA cycle by Keim et al. [65], as shown in Fig. 1. The adapted cycle is shown in Fig. 4, where all components and connections are listed in Table 2. In this work, the VA cycle is composed of four components:
-
Dataset

-
Hypothesis

-
Visualization

-
Insight

The components are connected by operations required in the VA process. These operations are encoded as connections between components and are defined as functions that transform one component into another. We sort these operations into the four main components according to where they fit best.
Please note that all connections originating from the classic VA process will be marked by a box (\(\blacksquare \)) in the respective color of the category they belong to.
To describe a complete UAVA cycle, we need to introduce two novel components and several connections to already existing components. Namely, the novel components are:
-
U-Dataset

-
Provenance

The novel connections include uncertainty quantification and provenance generation concerning the existing components and connections of the VA cycle. Please note that all novel components will be marked by a triangle (\(\blacktriangle \)) in the respective color throughout the entire manuscript for smooth reading. The presented description will be structured along with the six components we defined.
4.1

A dataset S is a very general concept that consists of n records \((r_1, r_2, \ldots , r_n)\), where each record \(r_i\), consists of m observations, variables, or attributes \((a_1, a_2, ..a_n)\). An attribute \(a_i\) is a single entity such as a number or symbol. A dataset holds a structure that can be syntactic or semantic [118]. They can be generally defined as a function t. These relations are normally used to differentiate various types of data, e.g., attributes that are aligned on a grid are usually referred to as image data.
Based on the respective problem description, a dataset S is generated to be analyzed in the VA cycle. In contrast to the classic definition of the VA cycle, an UAVA cycle requires mechanisms that allow extending the dataset into an uncertainty-aware U-Dataset. The required steps in this process will be explained in the following.
4.1.1 Preprocessing \(D_W\)

The classic VA cycle allows processing of the input dataset by four different operations: data transformation \(D_T\), data cleaning \(D_C\), data selection \(D_S\), and data integration \(D_I\). Up to the point, where no uncertainty definition or quantification has been performed, these operations can be applied as defined in the classic VA cycle. Although data preprocessing is an important or even indispensable step in the VA cycle, it is not recommended to apply it before uncertainty definition and quantification have been achieved [15].
4.1.2 Uncertainty quantification \(Q_{\overline{S}}\)

Depending on the data format, application, and task that the user needs to fulfill, proper uncertainty quantification is required. In this scenario, aleatoric uncertainty is of interest. This holds for each record (and its attributes) in a dataset, as well as for the relations defined in the dataset. There exist a variety of datasets that are acquired in conjunction with an uncertainty quantification such as molecular data. In this case, uncertainty quantification of the input dataset can be neglected if the provided uncertainty quantification expresses the uncertainty of the input dataset well enough.
Hands-On Example In our hands-on example, the dataset consists of magnetic resonance imaging of the patients’ brain that shows the tumor. Therefore, forward uncertainty quantification can be used to provide an understanding of which areas in the medical record are more trustworthy than others. As a result, each pixel of the image obtains an uncertainty quantification.
4.2

Resulting from the input dataset S in conjunction with the extracted uncertainty quantification \(Q_{\bar{S}}\), we aim to achieve an uncertainty-aware dataset (U-Dataset) \(\overline{S}\).
As a first definition, we require the uncertainty of an attribute. Let a be an attribute, and A be the set of all possible values for a, then \(\overline{a} = (a, u(a)))\) is the uncertainty-aware description of the attribute a. Here, u(a) describes aleatoric uncertainty, and \(\overline{A}\) holds all possible uncertainty-aware descriptions of the set of attributes a. Attributes can be single measurands, but in the following, they can also contain entire datasets (large and complex data). This means that dataset combinations such as multi-field data or ensemble datasets are explicitly possible.
The uncertainty quantification of a dataset can also affect the function t, expressing the relation within the dataset. Resulting from this, uncertainty quantification can result in a novel function \(\overline{t} = (s, u(t))\) that allows to express uncertainty within the relation function. One example is the connection between points within a graph. Here, the function that defines the relationship between data points can be adapted to capture the degree of certainty that the respective points are connected.
4.2.1 Uncertainty-aware data preprocessing \(\overline{D_W}\)

Once an uncertainty-aware dataset is achieved, preprocessing operations can be applied to transform the dataset into a format that allows the creation of hypotheses or apply visualization approaches. Here, data transformation \(\overline{D_{T}}\), data cleaning \(\overline{D_{C}}\), data selection \(\overline{D_{S}}\), and data integration \(\overline{D_{I}}\) are available, as defined in the original VA cycle. Still, they need to be adapted to be uncertainty-aware.
The transformation of data is concerned with an application of mathematical functions to describe the transformation. As we consider U-Datasets in the UAVA cycle in the form \(\overline{S} = (S, u(s))\), we require mathematical operations that can be applied in this setting. Here, three different pathways have to be followed, as shown in Fig. 2.
In the classic VA cycle as well as in most other data analysis scenarios, datasets are cleaned, selected, and integrated into each other to provide a stable dataset that can be processed. When considering data cleaning, we propose two important adaptations in this process: Do not eliminate any captured data point and merged data points, including their uncertainty.
When eliminating a data point, the information, no matter how uncertain it is, is neglected in the VA cycle. No matter how well selected these points are, the selection is based on a hypothesis or metric that could be wrong or incomplete. To avoid this, we propose to find a suitable uncertainty quantification that assigns very high uncertainty to the selected data point.
The merging of data points arises when a phenomenon is captured in the data multiple times. Here, data points are merged to avoid multiple occurrences of the same phenomena in the dataset. In this case, one must not only merge the data points. In addition, the uncertainty of the data points needs to be merged as well, resulting in an accumulation of uncertainty. This accumulation can be computed based on the suggestion in Sect. 3.4.
Hands-On Example As usual, the images generated in medicine require further processing. Histogram equalization is to enhance the underlying image. In this example, the histogram equalization is not solely manipulating the image itself, but also the underlying uncertainty quantification. The result is a contrast enhanced MRI with an included uncertainty quantification.
4.3

A hypothesis is a supposition or proposed explanation made based on limited evidence as a starting point for further investigation. To achieve this, the null hypothesis is usually utilized. In this case, a hypothesis is formed and tested. Then, the hypothesis can be either rejected or fail to be rejected.
In the classic VA cycle, the component hypothesis H is described as a general tool to create insight or knowledge based on statistical analysis. When considering hypotheses that are based on uncertainty-aware datasets, we need to define an uncertainty-aware Hypothesis \(\overline{H} = (H, u(H))\). Here, u(H) describes epistemic uncertainty. As shown in the UAVA cycle, the hypothesis can be further built from visualization. Still, the visualization can be considered as an input dataset that allows creating hypothesis. Here, u(H) describes a confidence value for the formulated Hypothesis. This means that whatever the output of a statistical analysis method is, a result is composed of the derived Hypothesis H and an uncertainty quantification u(H) of the generated hypothesis. The generation of an uncertainty-aware hypothesis and possible interaction methods will be shown in the following.
4.3.1 Uncertainty quantification in hypothesis \(Q_{\overline{H}}\)

As shown in Sect. 3.5, uncertainty can be introduced by a hypothesis itself, namely through parameter uncertainty, incompleteness, and approximation of models. For input parameter uncertainty, we suggest utilizing sensitivity analysis uncertainty quantification approaches [101], or for a high number of input parameters dimension reduction uncertainty quantification approaches should be used.
The incompleteness and approximation approach in a model can be described using model reliability approaches. A summary, including an evaluation of these approaches, can be found in [93].
The quantified uncertainties need to be combined with the uncertainty quantification that is attached to the input dataset or the visualization using an uncertainty accumulation approach as described in Sect. 3.2.
4.3.2 Generation from U-datasets 
The generation of an uncertainty-aware hypothesis \(\overline{H}\) can be described by a function starting from two sources: an uncertainty-aware dataset (\(\overline{H_S}: \overline{S} \rightarrow \overline{H}\)) and an uncertainty-aware visualization (\(\overline{H_V}: \overline{V} \rightarrow \overline{H}\)). The latter is part of the hypothesis/visualization subcycle of VA that will be discussed in Sect. 4.5.
In the classic VA cycle, the generation of hypothesis H can be based on a dataset utilizing a set of statistical analysis tools \(\{f_{S1}, f_{S2}, \ldots , f_{Sq}\}\). These statistical operations need to be redefined to provide an uncertainty-aware creation of a hypothesis. Fortunately, physicians and engineers are concerned with this issue for decades and massive literature is available that summarizes the hypothesis generation based on statistical analysis. Devore [24] summarized uncertainty-aware descriptions of all standard statistical tests for uncertainty-aware datasets. It includes average, variance, standard deviation, the sum of squares, root sum of squares, pooled variance, linear interpolation, linear regression, sensitivity coefficient, covariance, and correlation. For statistical approaches that have not been described yet, we suggest the uncertainty propagation rules described in Sect. 3.3.
During the last decades, machine learning approaches became increasingly important in the generation of hypotheses and are a standard tool by now. In this context, clustering approaches are a popular form of machine learning. A survey on uncertainty-aware clustering approaches was presented by Aggarwal and Reddy [1]. These algorithms are capable of transforming uncertainty throughout their computational model and provide an uncertainty-aware hypothesis forming. Neural networks are increasingly popular in providing hypotheses, as well. Here, Gal provided a state-of-the-art analysis of uncertainty-aware approaches [34]. Most popular in this context are deep learning approaches that utilize Bayesian theory [116] to output an uncertainty-aware hypothesis.
4.3.3 User interaction with hypothesis 
User interaction with a hypothesis usually concerns operations such as selecting a proper hypothesis generation algorithm or adapting previous choices. In this context, the interaction is only allowed to select uncertainty-aware hypothesis forming operations. In addition, a user may be enabled to adapt input parameters required for computing uncertainty-aware hypothesis forming. Here, users need to be able to not solely set the input parameter J. In addition, the input parameter needs to be expressed with an uncertainty quantification u(J) as well. Thus, the user should be enabled to manipulate this uncertainty quantification. The resulting uncertainty-aware input parameter \(\overline{J} = (J, u(J))\) needs to be considered in the uncertainty-aware computation based on the propagation rules defined in Sect. 3.3. Here, sensitivity analysis can be utilized to quantify this uncertainty.
Hands-On Example In the hand-on example, the goal is to understand surgery paths that are planned to remove a brain tumor. As the choice of these surgery paths massively affects the patients’ health, depending on the areas that will be intersected, the goal is to identify different areas in the patient’s brain. This results in a clear segmentation task for the given MRI dataset. Therefore, a fuzzy segmentation approach is selected that assigns a probability to each pixel to be contained in a specific area. The chosen approach is highly interactive guiding the user through the segmentation process. Here, users can review their segmentation results and adjust the settings of the segmentation algorithm.
Based on the segmentation of the patient’s brain, a probing is applied that samples different surgery paths according to their intersection with the identified brain regions. To create a hypothesis about what surgery paths are more suitable than others, a query procedure is provided that allows sorting the tested surgery paths based on user-defined criteria such as the exclusion of specific areas.
4.4

Visualization is a key component in the VA cycle. It allows users to gain valuable insight into the dataset and provide a natural understanding of the underlying uncertainty [53]. In the UAVA cycle, an uncertainty-aware visualization is defined as \(\overline{V} = (V, u(V))\), where u(V) can describe all types of uncertainty.
4.4.1 Uncertainty quantification \(Q_{\overline{V}}\)

The visualization process itself introduces uncertainty into the VA process, namely mapping, perceptual, memory, and thinking uncertainty, as shown in Sect. 3.5. Dasgupta and Kosara [23] summarized the need for quality metrics in visualization that can quantify uncertainty such as mapping uncertainty. Diamond [25] provided a survey on perceptual uncertainty and how it can be expressed. Coutinho et al. [20] described the role of memory and thinking uncertainty when reviewing a visualization. They propose that the description of these uncertainties is hard to achieve as human cognition is very complex and parts of its functionality is still unknown.
4.4.2 Generation from U-datasets 
The generation of an uncertainty-aware hypothesis \(\overline{V}\) can be described by a function starting from two sources: an uncertainty-aware dataset (\(\overline{V_S}: \overline{S} \rightarrow \overline{V}\)) and an uncertainty-aware visualization (\(\overline{V_H}: \overline{H} \rightarrow \overline{V}\)). The latter is part of the hypothesis/visualization subcycle of VA that will be discussed in Sect. 4.5.
Uncertainty-aware visualization is a very active field that has been researched for decades resulting in a variety of visualization approaches. Still, it only represents one component of the VA process. Therefore, visualization can be seen as one computational step in the pipeline.
In general, the utilized visual variables that are considered to express uncertainty in visualization can be listed as follows: comparison techniques, attribute modification, glyphs, and image discontinuity [88]. The choice of uncertainty visualization and the visual variable expressing the uncertainty is highly dependent on the underlying dataset and the use case, the VA cycle is designed for.
4.4.3 User interaction with visualization 
User interaction with visualizations can be quite manifold. A summary of available interaction techniques was given by Brodbeck et al. [13]. In terms of interaction with uncertainty visualization, Sacha et al. [96] proposed a suitable user interaction with uncertainty-aware visualization approaches as a fundamental requirement to provide a suitable UAVA cycle. Still, a summary of all necessary interaction metaphors is not available. In this context, we would like to suggest the following considerations when designing uncertainty-aware interactions for visualization.
First, there needs to be specific selection or zooming operations that are based on the data uncertainty, not on the data itself. Second, the result of the current interaction methodology needs to provide information about the currently shown uncertainty and overall uncertainty captured in the dataset.
Hands-On Example The hypothesis generation in the presented case is highly connected to visualization. First, the segmentation of different brain regions is achieved via an interactive visualization. Users are enabled to define and review brain regions individually to control the result of the fuzzy segmentation approach. Second, the selection of surgery paths is assisted with visualization as well. Here, the surgery paths are mapped and color-coded to provide an understanding of which brain areas will be affected by the surgery paths. This also includes the visualization of the underlying fuzzy segmentation result. The visualization also provides an interactive backend to control the surgery path selection.
4.5 The interplay of 
Hypothesis and visualization together form a subcycle in the VA cycle defined by Keim et al. This connection forms the core of the VA cycle and needs to be preserved in the UAVA cycle that we construct. This cycle can be run arbitrarily often, which requires specific handling for the uncertainty accumulated along with these runs.
As shown in Sect. 3.3, there exist propagation rules for uncertainty. These rules can technically be applied in the hypothesis/visualization subcycle. Still, the question arises what knowledge can be extracted from uncertainty-aware hypothesis and visualization if the amount of captured uncertainty constantly increases. Here, we suggest setting a user-selected threshold that allows indicating data points containing a higher uncertainty quantification as this threshold. As a result, the user would interact with the uncertainty-aware hypothesis and visualization and in each step, increasing the uncertainty attached to this process. When the user-defined threshold is exceeded for specific data points, they will be highlighted and the user can adapt the selections.
The interplay of an uncertainty-aware hypothesis \(\overline{H}\) and an uncertainty-aware visualization uncertainty-aware hypothesis \(\overline{V}\) happens in both directions, which will be explained in the following.
4.5.1 Generation from hypothesis 
The process of generating an uncertainty-aware visualization based on an uncertainty-aware hypothesis can be described as \(\overline{V_H}: \overline{H}\rightarrow \overline{V}\). Here, we assume that an uncertainty-aware statistical analysis has been conducted requiring a proper visualization. Depending on the output of the statistical analysis, a U-dataset can be created. The specific data type depends on the underlying statistical analysis approach and requires a sophisticated visualization approach. Here, the same rules apply as in Sect. 4.4.2.
4.5.2 Generation from visualization 
Building uncertainty-aware hypothesis from uncertainty-aware visualizations is defined as the function \(\overline{H_V}: \overline{V} \rightarrow \overline{H}\). Unfortunately, this process cannot be determined analytically in its entirety, as it involves the subjective impression of a user to refine a hypothesis when regarding the available visualization. What can be determined is the user input that leads to a hypothesis. Here, we suggest letting the user quantify how certain his selections are to express the uncertainty of the hypothesis generation at least partially.
In these considerations, user bias are an important aspect to consider. Szafir [105] provided five suggestions to deal with this bias:
-
Use diverging colors instead of rainbow color tables
-
Avoid animation in the visualization, instead encode movement statically
-
Instead of truncating axes, show relative between values
-
Avoid 3D visualization if possible
-
Provide a transparent description of the visualization process
Hands-On Example In the presented example, the interplay between visualization and hypothesis is a crucial component. Here, uncertainty-aware segmentation results (hypothesis) are visualized. In addition, the computation of intersections of surgery tunnels and different areas in the brain are computed and mapped into a visualization. On the other hand, the visualization is used as an indicator to capture if parameters need to be adjusted. In this example, this can be adaptations of the segmentation approach input or the selection of desired areas in the human brain. Here, the description of the subcycle is clearly visible, as this process can be repeated arbitrarily often.
4.6

The term insight I can be defined as knowledge that is gained during analysis and has to be internalized, synthesized, and related to prior knowledge [96]. In terms of uncertainty, an uncertainty-aware insight \(\overline{I} = (I, u(I))\) is composed of the insight generated from the UAVA cycle and quantification of the credibility of the derived result u(I). Here, u(I) describes subjective uncertainty. In reality, insight cannot be defined mathematically in many cases, as it is a subjective impression of the user, often affected by personal bias that runs the VA cycle. Based on this problem, it might not be possible to describe the respective uncertainty quantification.
4.6.1 Uncertainty quantification \(Q_{\overline{I}}\)

Insight generated in the VA cycle can be affected by uncertainty due to decision-making bias or experience and knowledge that may keep a user from accepting novel findings. Lewandowsky et al. [74] stated that knowledge is always affected by uncertainty. Unfortunately, insights are subjective, such that uncertainty quantification is hard to achieve. Most considerations are philosophical rather than computational [22]. For evaluation purposes, benchmark tasks have shown to be useful for identifying and assessing analytic findings. Still they are not sufficient in most cases [87]. Here, a clear strategy of uncertainty quantification is missing.
4.6.2 User interaction to create insights from hypothesis \(\overline{U_{CH}}\)

Uncertainty-aware insight generated from an uncertainty-aware Hypothesis can luckily be quantified mathematically (to the point where analysis results are interpreted). Here, uncertainty-aware hypothesis directly implies the uncertainty of the derived uncertainty-aware insight. In fact, they are identical, which means \(u(I) = u(H)\).
4.6.3 User interaction to create insights from visualization \(\overline{U_{CV}}\)

Throughout the interaction of the user with uncertainty-aware visualization, insight is generated. This insight can usually not be described mathematically as it is depending on a subjective user experience. Here, visualization evaluation approaches come into play, as they offer metrics and approaches to quantify the amount of insight generated by a visualization.
In terms of uncertainty visualization, Hullmann et al. [54] presented a state-of-the-art report that summarizes uncertainty visualization evaluation approaches. These approaches can be used to at least approximate the insight generated by an uncertainty-aware visualization approach.
4.6.4 Feedback loop F(S)  and uncertainty-aware feedback loop \(\overline{F(S)}\)
and uncertainty-aware feedback loop \(\overline{F(S)}\)

As indicated by the classic VA approach, VA is designed to be a cycle F(S). When generating new knowledge, this knowledge can act as further data input. As already shown, generated insight from the UAVA cycle can be of two types: insight, with uncertainty quantification, and insight without uncertainty quantification. These types of insight need to be treated differently. Insights without uncertainty quantification that need to be reinserted into the VA cycle are fed back into the dataset component. This is the reason why an UAVA cycle still requires the dataset. Starting from here, a suitable uncertainty quantification needs to be found according to the data structure of the insight. As the uncertainty of insight cannot be computed directly in many cases, insight can be modeled as a normal dataset and then be transferred into a U-Dataset through a suitable uncertainty quantification as described in Sect. 3.2.
On the other hand, insights that have an uncertainty quantification need to be inserted in the U-Dataset component, as there is no uncertainty definition or quantification required.
Hands-On Example In the presented example, uncertainty-aware insights can be made in various ways. Here, users can use the hypothesis to understand different regions in the patients’ brain as well as obtain an impression of how safe the selection of a specific surgery path is. This results in the creation of the mentioned feedback loop. First, the segmentation and surgery path analysis result in novel insight into the structure and composition of the human brain and the uncertainty inherent in this computation. As shown, this knowledge can be directly fed back into the VA cycle. On the other hand, subjective considerations on trust in the visualization and computation techniques cannot be quantified in terms of uncertainty and need to be fed back into the original data component.
4.7 Provenance generation 
When running an UAVA cycle, uncertainty will be propagated and accumulated along with the performed operations of the VA cycle. The importance of provenance analysis and visualization has been described by Varga et al. [111]. This implies the tracking of uncertainty throughout each computational step of the VA cycle, referred to as provenance. Therefore, each time an uncertainty-aware dataset, a hypothesis, or a visualization is created, the current uncertainty quantification and the respective operation need to be stored and are subject to further analysis.
We encourage to provide a visualization and interaction tool to let users follow the development of uncertainty throughout the VA process. This can give users important hints on which operations caused a drastic increase of uncertainty or at which point the accumulated uncertainty exceeds a threshold that is known to be the highest amount of uncertainty that still allows for interpretation. Herschel et al. [49] provided a survey on provenance creation.
4.7.1 Provenance generation for U-datasets \(P_{\overline{S}}\)
 and uncertainty-aware hypothesis \(P_{\overline{H}}\)
and uncertainty-aware hypothesis \(P_{\overline{H}}\)

The provenance of data focuses on the history of changes and movement of data. Data provenance is often heavily emphasized in computational simulations and scientific visualization, in which significant data processing is conducted. The history of data changes can include subsetting, data merging, formatting, transformations, or execution of a simulation to ingest or generate new data [90]. This can be directly transferred to the uncertainty of a U-Dataset and the uncertainty of a hypothesis.
4.7.2 Provenance generation for uncertainty-aware visualization \(P_{\overline{V}}\)

As Ragan et al. [90] stated, visualization provenance is concerned with the history of graphical views and visualization states. This process is tightly coupled with data transformation and the interactions used to produce the visualization. These concepts need to be adapted to provide a provenance generation for the uncertainty in uncertainty-aware visualization. A survey on available methods in provenance visualization and user interaction was conducted by Xu et al. [122].
4.7.3 Provenance generation for uncertainty-aware insight \(P_{\overline{I}}\)

The provenance of uncertainty-aware insights needs to include the component of uncertainty as well. Unlike data computations, insights are not directly observable in all cases and so their uncertainty is not observable directly, as shown in Sect. 4.6. Here, solely quantifiable insights can be included in the provenance generation of uncertainty.
Hands-On Example In the described example, there exist a variety of computational steps as well as a variety of potential user interactions. To implement the principle of provenance, all computational steps, their intermediate computational results, and the attached uncertainty to each of these results are stored and visually communicated in a story graph. This allows users to understand each computational step in the UAVA cycle.
5 Opportunities of uncertainty-aware visual analytics
Based on the proposed UAVA cycle, we aim to provide prominent approaches that fit in this scope and that can be considered when designing an UAVA cycle. Here, we structure the approaches along the components of the UAVA cycle: (U-)Data (Sect. 5.1), hypothesis (Sect. 5.2), and visualization (Sect. 5.3). As already mentioned, the component insight cannot be expressed properly; therefore, a clear research gap is visible and does not obtain a dedicated section here.
5.1 (U)-data
To apply the provided definition of uncertainty to different data types, the characteristics of each data type has to be considered. Table 3 shows the most prominent data types occurring in the context of VA. It holds a short description of the dataset characteristics as well as a list of different types of uncertainties occurring in specific data types.
Geospatial data \(\textbf{S}_\textbf{1}\) uses geospatial locations or trajectories L. Here, various attributes A are assigned to such a domain L by a function \(f:L \rightarrow A\). Therefore, two types of uncertainty, namely spatial uncertainty and attribute uncertainty [75], are found in such datasets. Spatial uncertainty origins from the underlying areas or trajectories that can be displaced or shifted in shape, deviating from the stored data. Attribute uncertainty, on the other hand, describes the uncertainty of data attributes themselves. Both types of uncertainty are illustrated in Fig. 5a by showing positional and attribute uncertainty. Li et al. [75] described how analytic models can be utilized to achieve uncertainty quantification.
Graph data \(\textbf{S}_\textbf{2}\) connects a set of nodes V via links E creating a network called graph. These nodes and links can hold various attributes, provided by functions \(f:V \rightarrow A\) and \(g:E \rightarrow A\). Graph data can hold three different types of uncertainty [61]. First, the presence of a node can be uncertain. Second, a link between nodes can be uncertain, and third, the attributes contained in nodes or links can be uncertain. It should be noted that the position of visualized nodes is not a fundamental uncertainty, as it is derived from the graph description or some graph-drawing algorithm. Engel et al. [27] provided an uncertainty quantification for graph data. A visual indication of these types of uncertainty can be found in Fig. 5b.
Field data \(\textbf{S}_\textbf{3}\) can contain scalars, vectors, and tensors (attributes A), often arranged on some grid. This grid is defined by a set of positions and neighborhood relations on those given positions. The result are cells or positions with neighborhood information about their adjoined cells or positions, while each cell holds its attribute L. They are connected by a function \(f:P \rightarrow A\) where P is the set of positions or set of cells. Here, two types of uncertainty can occur, as depicted in Fig. 5c. Both positions, as well as the attributes defined over P can be uncertain [45]. It is important to note that each attribute value may be affected by uncertainty to differing extents. This means, for example, that vector entries can have varying uncertainty depending on their dimension. Potter et al. [88] provided a summary on uncertainty quantification for field data.
High-dimensional data \(\textbf{S}_\textbf{4}\) is defined by a dimension N that determines the number of attributes A contained in one entry. N is a larger number, usually higher than 10, even though some authors talk about high-dimensional data if \(N>3\). Here, only attribute uncertainty needs to be considered, as shown in Fig. 5d.
Temporal data \(\textbf{S}_\textbf{5}\) contains attributes A that are sorted along a time line T utilizing a function \(f: T \rightarrow A\). These attributes can be manifold and may be of any type of data that was mentioned before. Here, two types of uncertainty arise: time uncertainty and attribute uncertainty [18], as shown in Fig. 5e. Each point in time can be affected by uncertainty as well as the attribute attached to this point in time. Zhen et al. [52] demonstrated the quantification of uncertainty in temporal data.
Text/Document data \(\textbf{S}_\textbf{6}\) is data in the form of text or documents that hold attributes A at a specific character position P. This connection is given by the function \(f:P \rightarrow A\). Here, two types of uncertainty can arise, as shown in Fig. 5f: Document uncertainty and attribute uncertainty [66]. Each document can have an overall uncertainty and all of its entries can be affected by uncertainty. Quantification of uncertainty in textual data was given by Kerdjoudj et al. [66].
5.2 Hypothesis
In the area of hypothesis, Keim et al. [63] described five different types of data analysis approaches for hypothesis forming: statistical analysis, supervised learning, cluster analysis, rule mining, and dimension reduction.
In general, each computation that is made based on U-Data needs a propagation of uncertainty. Here, error and uncertainty propagation approaches can be used [71]. These computations provide rules that can transform uncertainty attached to data points, according to the underlying transformation of these points. Alternatively, these computations can be accomplished by Bayesian error propagation [92].
Supervised learning aims to learn a function that maps an input to an output based on example input-output pairs. Here, machine learning, especially using neural networks, plays an important role. Naturally, models, such as machine learning, hold a high potential for epistemic uncertainty. The work that has been accomplished targeting epistemic uncertainty in supervised learning was summarized by Zhou et al. [126].
Cluster analysis is a common approach for hypothesis generation. It defines a broad field where a variety of approaches have been developed [123]. A subgroup of these approaches is well suited for UAVA, defined as fuzzy cluster analysis [125]. Here, data points are not strictly distributed into different classes. Instead, fuzzy clustering aims to compute a probability that a data point can be contained in a class.
Rule mining is a rule-based machine learning method for discovering interesting relations between variables in large databases [62]. Due to the nature of these rules, they are often not able to express and handle uncertainty. Still, there exist approaches that aim to extend these computations such that the determined rules can cover uncertainty information [101].
Dimension reduction approaches aim to minimize the dimensionality of data points to find important dimensions and ease the understanding of the data. The approaches are manifold [32]. Unfortunately, there does not exist a structured summary of dimension reduction approaches that can handle uncertainty. Still, there exist examples of prominent dimension reduction approaches such as the uncertainty-aware principal component analysis [42].
5.3 Visualization
Visualization plays a crucial role when uncertainty-aware data or a hypothesis is generated. The chosen visualization is highly related to the underlying data (or the dataformat of the hypothesis). In the following, we aim to summarize visualization approaches that can be used to visualize the data categories in Sect. 5.1.
Visualizations of uncertainty-aware spatial data include earth, space, and environmental sciences [119], urban science [104, 106], terrain visualization , [110], and geographic/geospatial visualization [81]. An example is shown in Fig. 6a, providing the uncertainty in predicting wildfires, color-coding a map of terrain at risk.
Uncertainty-aware graph-based data, occurring in applications like business and finance [44, 113], social and information sciences [6], sensor networks [26, 102], bioinformatics [112], and cybersecurity [3], can be visualized by a variety of approaches. These approaches are usually based on uncertainty-aware graph-drawing algorithms. An example where edge and node attributes that contain uncertainty are visually encoded by areas of varying sizes is given in Fig. 6b.
Uncertainty-aware field data visualizations can be found in mathematics, physical sciences and engineering [77], multimedia(image/video/music) [120], biomedical and medical [45, 68, 94] applications. Here, the visualization highly depends on the attributes that are encoded in the respective field and can be seen as tables containing a variety of values. An example of uncertainty-aware visualization using diffusion tensors is shown in Fig. 6c. The surrounding transparent surfaces indicate the varying visual appearance of the visualized tensor.
Uncertainty-aware high-dimensional data can be found in a variety of applications. Hoffmann et al. [51] provided a survey of potential visualization approaches. An example of uncertainty-aware parallel coordinates visualization is given by Fig. 6d. Instead of visualizing lines between axes, the images visually indicate areas with varying occurrences of connecting lines.
Uncertainty-aware time-dependent data often occurs in digital humanities [108], as well as robotics [86]. A timeline visualization utilizing different glyphs to indicate the uncertainty of specific time steps is shown in Fig. 6e.
Uncertainty-aware text/document data can occur in nearly all kinds of applications. Prominent examples are digital humanities [108] and software visualization [5].
The visualization strongly depends on the underlying text that is visualized. A visualization of a tag cloud that is adapted according to the uncertainty of the underlying words is provided by Fig. 6f. Uncertain words are shown with a lower opacity compared to certain words.
6 Open challenges
Although we described an UAVA cycle and show how it can be applied to a variety of cases, there remain open problems that need further investigation. They separate into two groups: open problems that result from the VA cycle (see Sect. 6.1) itself and open problems that result from the inclusion of uncertainty (see Sect. 6.2).
6.1 Open problems that result from the visual analytics cycle
Generalization In this paper, we showed that the VA cycle can be extended to include uncertainty. Although this is a suitable extension for many real-world problems, there exist further cases that cannot be treated with the classic VA cycle. These cases include ensemble datasets or multi-modal datasets. Here, proper extensions of the VA cycles are required.
Proper description of the insight As shown in this manuscript, the insight that can be generated using a VA cycle, regardless of whether it incorporated uncertainty or not, cannot be quantified properly. This is because the insight is mainly depending on the user of the provided cycle. Here, proper quantification approaches of the insight are required that may drive the development of VA cycles.
Approximation of the amount of knowledge that is generated by a visualization As shown in Sect. 4, the amount of insight that can be generated based on visualization cannot be quantified so far. Based on this problem, the uncertainty of the insight also lacks proper quantification. Although the amount of knowledge that can be created by visualization is a highly subjective process depending on the user, at least an approximation of the knowledge would be beneficial. This would contribute to classic VA as well as UAVA.
6.2 Open problems that result from the inclusion of uncertainty
Selection of proper scenarios A further open problem is the question whether UAVA is required in a specific scenario. Naturally, the extension of the classic VA cycle requires further resources. There might exist cases where the effect of uncertainty can be neglected or where the effort in extending an UAVA cycle might be too big in comparison with the insight that is generated.
Survey of existing techniques We showed that there exists a variety of work that deals with UAVA in many applications and for many data types. Still, a holistic state-of-the-art report in this area is missing. Such a report may be a good starting point for researchers that start in the field and need to understand what possibilities they have. In addition, further open problems in the field could be identified.
Construction of UAVA cycles In this work, we showed that an UAVA cycle can be described. A logical next step would be to determine a standardized way to construct such a cycle. A good starting point might be the use of a classic VA cycle, then deriving rules on how to provide uncertainty awareness. There exist several approaches to construct a VA cycle that may assist as a starting point [30, 121].
Frameworks/libraries with ready-to-use UAVA approaches In this work, we identified multiple steps in the UAVA pipeline that can be accomplished by existing methodologies. Examples are the determination and description of uncertainty-aware datasets, adaptation of preprocessing and hypothesis generation approaches, and provenance generation. In this context, frameworks or libraries that provide at least the uncertainty-aware visual analytic steps that can be standardized would be a massive contribution to the VA community. Gillmann et al. [40] provided a survey on uncertainty awareness in open-source visualization solutions, which can be a great starting point for the creation of an UAVA framework. To the best of our knowledge, the implementation of such a framework was not conducted so far.
Teaching of uncertainty-aware principles Although uncertainty is an effect that is occurring in nearly all data acquisition processes, the application of uncertainty-aware analysis techniques, in general, is often a neglected point. This can be due to a variety of reasons. One major reason is that uncertainty-aware analysis principles are rarely taught to students. Here, lectures on UAVA would help new visualization researchers to understand the problems of data that is affected by uncertainty, giving them the awareness of principles that have to be kept in mind when dealing with uncertainty in datasets.
Approximation of knowledge uncertainty As mentioned before, the amount of uncertainty in insight can only be quantified in the case that the extracted knowledge is based on an uncertainty-aware hypothesis. This is an important open problem for UAVA as this distorts the feedback loop in the analysis cycle. Although we proposed two feedback cycle connections, the right one has to be picked. Here, suitable approaches to quantify insight and its uncertainty are highly requested.
The missing link between ensemble visualization and uncertainty visualization In contrast to uncertainty visualization, an ensemble visualization is concerned with visualizing multiple datasets representing the same captured scenario. Still, these disciplines are closely related. There are approaches available, where uncertainties can be generated from ensembles or ensembles that can be generated from an uncertainty distribution. Ensemble visualization is a highly active research field [117], providing a massive amount of VA solutions. Unfortunately, the link between these two disciplines is not defined properly. If one could arbitrarily transform ensemble datasets into uncertainty datasets, both disciplines could benefit from each other.
7 Conclusion
In this work, we described an UAVA cycle. Here, the original VA cycle is extended such that uncertainty can be quantified, propagated, and communicated in each component of the VA cycle. This results in a holistic mechanism to tackle uncertainty originating from data, models, and humans in VA approaches. We showed how to use this concept to tackle different types of input data as well as various use cases. As a result, we were able to formulate a variety of open problems originating from the VA cycle and the incorporation of uncertainty.
References
Aggarwal, C.C., Reddy, C.K.: Data Clustering: Algorithms and Applications, 1st edn. Chapman & Hall, Boca Raton (2013)
Andrienko, N., Lammarsch, T., Andrienko, G., Fuchs, G., Keim, D., Miksch, S., Rind, A.: Viewing visual analytics as model building. In: Computer Graphics Forum (2018)
Angelini, M., Santucci, G.: Visual cyber situational awareness for critical infrastructures. In: Proceedings of the 8th International Symposium on Visual Information Communication and Interaction (New York, NY, USA), VINCI ’15, pp. 83–92. ACM (2015)
Arriola, L., Hyman, J.M.: Sensitivity Analysis for Uncertainty Quantification in Mathematical Models, Mathematical and Statistical Estimation Approaches in Epidemiology, pp. 195–247. Springer, Cham (2009)
Bassil, S., Keller, R.K: Software visualization tools: survey and analysis. In: Proceedings 9th International Workshop on Program Comprehension. IWPC 2001, pp. 7–17. IEEE (2001)
Beck, F., Burch, M., Diehl, S., Weiskopf, D.: The state of the art in visualizing dynamic graphs. In: EuroVis (STARs) (2014)
Belforte, G., Bona, B., Cerone, V.: Bounded measurement error estimates: their properties and their use for small sets of data. Measurement 5(4), 167–175 (1987)
Bhatt, U., Antorán, J., Zhang, Y., Liao, Q.V., Sattigeri, P., Fogliato, R., Melançon, G., Krishnan, R., Stanley, J., Tickoo, O. et al.: Uncertainty as a form of transparency: measuring, communicating, and using uncertainty. In: Proceedings of the 2021 AAAI/ACM Conference on AI, Ethics, and Society, pp. 401–413 (2021)
Bonneau, G.-P., Hege, H.-C., Johnson, C.R., Oliveira, M.M., Potter, K., Rheingans, P., Schultz, T.: Overview and state-of-the-art of uncertainty visualization. In: Scientific Visualization, pp. 3–27. Springer (2014)
Bors, C., Bernard, J., Bögl, M., Gschwandtner, T., Kohlhammer, J., Miksch, S.: Quantifying uncertainty in multivariate time series pre-processing. In: von Landesberger, T., Turkay, C. (Eds.) EuroVis Workshop on Visual Analytics (EuroVA). The Eurographics Association (2019)
Boumans, M., Hon, G., Petersen, A.C.: Error and Uncertainty in Scientific Practice. Routledge, New York (2015)
Boyat, A.K., Joshi, B.K.: A review paper: noise models in digital image processing. arXiv (2015)
Brodbeck, D., Mazza, R., Lalanne, D.: Interactive Visualization-A Survey, Human Machine Interaction, pp. 27–46. Springer, Berlin (2009)
Brodlie, K., Osorio, R.A., Lopes, A.: A review of uncertainty in data visualization. In: Expanding the Frontiers of Visual Analytics and Visualization, pp. 81–109 (2012)
Cai, G., Mahadevan, S.: Big data analytics in uncertainty quantification: application to structural diagnosis and prognosis. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 4(1), 04018003 (2018)
Cai, S., Gallina, B., Nyström, D., Seceleanu, C.: Data aggregation processes: a survey, a taxonomy, and design guidelines. Computing 101(10), 1397–1429 (2019)
Chen, P., Quarteroni, A.: A new algorithm for high-dimensional uncertainty quantification based on dimension-adaptive sparse grid approximation and reduced basis methods. J. Comput. Phys. 298, 176–193 (2015)
Cheng, R., Emrich, T., Kriegel, H.-P., Mamoulis, N., Renz, M., Trajcevski, G., Züfle, A.: Managing uncertainty in spatial and spatio-temporal data. In: 2014 IEEE 30th International Conference on Data Engineering, pp. 1302–1305. IEEE (2014)
Correa, C.D., Chan, Y.-H., Ma, K.-L.: A framework for uncertainty-aware visual analytics. In: 2009 IEEE Symposium on Visual Analytics Science and Technology, pp. 51–58. IEEE (2009)
Coutinho, M.V.C., Redford, J.S., Church, B.A., Zakrzewski, A.C., Couchman, J.J., Smith, J.D.: The interplay between uncertainty monitoring and working memory: Can metacognition become automatic? Mem. Cogn. 43(7), 990–1006 (2015)
Cui, W.: Visual analytics: a comprehensive overview. IEEE Access 7, 81555–81573 (2019)
D’ Argens, M.: Philosophical Dissertations on the Uncertainty of Human Knowledge. With Some Remarks on the Theology of the Grecian Philosophers, vol. 04. Gale Ecco, Farmington Hills (2018)
Dasgupta, A., Kosara, R.: The need for information loss metrics in visualization. In: Workshop on the Role of Theory in Information Visualization (2010)
Devore, J.L.: Probability and Statistics for Engineering and the Sciences. Cengage Learning, Boston (2011)
Diamond, M.E.: Perceptual uncertainty. PLoS Biol. 17(8), e3000430 (2019)
Dogan, G., Brown, T.: Uncertainty modeling in wireless sensor networks. In: Proceedings of the International Conference on Big Data and Internet of Thing (New York, NY, USA), BDIOT2017, pp. 200–204. ACM (2017)
Engel, D.W., Jarman, K.D., Xu, Z., Zheng, B., Tartakovsky, A.M., Yang, X., Tipireddy, R., Lei, H., Yin, J.: Uq methods for hpda and cybersecurity models, data, and use cases. Technical report, Pacific Northwest National Lab. (PNNL), Richland, WA (United States) (2015)
Enke, B., Graeber, T.: Cognitive uncertainty. Technical report, National Bureau of Economic Research (2019)
Enke, B., Graeber, T.: Cognitive uncertainty. Microeconomics: Decision-Making Under Risk & Uncertainty eJournal (2019)
Federico, P., Amor-Amorós, A., Miksch, S.: A nested workflow model for visual analytics design and validation. In: Proceedings of the Sixth Workshop on Beyond Time and Errors on Novel Evaluation Methods for Visualization, pp. 104–111 (2016)
Güell, J.M.F.: How to approach urban complexity, diversity and uncertainty when involving stakeholders into the planning process (2017)
Fodor, I.K.: A survey of dimension reduction techniques. Technical report, Lawrence Livermore National Lab., CA (US) (2002)
Frank, A.U.: Incompleteness, error, approximation, and uncertainty: an ontological approach to data quality. In: Geographic Uncertainty in Environmental Security, pp. 107–131. Springer (2007)
Gal, Y.: Uncertainty in deep learning. Ph.D. thesis, University of Cambridge (2016)
Gerrits, T., Rössl, C., Theisel, H.: Towards glyphs for uncertain symmetric second-order tensors. In: Computer Graphics Forum, vol. 38, pp. 325–336. Wiley Online Library (2019)
Gillmann, C., Arbelaez, P., Hernandez, J.T., Hagen, H., Wischgoll, T.: An uncertainty-aware visual system for image pre-processing. J. Imaging 4(9), 109 (2018)
Gillmann, C., Peter, L., Schmidt, C., Saur, D., Scheuermann, G.: Visualizing multimodal deep learning for lesion prediction. IEEE Comput. Graph. Appl. 41(5), 90–98 (2021)
Gillmann, C., Saur, D., Wischgoll, T., Scheuermann, G.: Uncertainty-aware visualization in medical imaging-a survey. In: Computer Graphics Forum, vol. 40, pp. 665–689. Wiley Online Library (2021)
Gillmann, C., Smit, N.N., Gröller, E., Preim, B., Vilanova, A., Wischgoll, T.: Ten open challenges in medical visualization. IEEE Comput. Graph. Appl. 41(5), 7–15 (2021)
Gillmann, C., Wischgoll, T., Hagen, H.: Uncertainty-awareness in open source visualization solutions (2016)
Giunta, A.A., Eldred, M.S., Castro, J.P.: Uncertainty quantification using response surface approximations. In: 9th ASCE Specialty Conference on Probabilistic Mechanics and Structural Reliability, Citeseer, pp. 26–28 (2004)
Görtler, J., Spinner, T., Streeb, D., Weiskopf, D., Deussen, O.: Uncertainty-aware principal component analysis. IEEE Trans. Visu. Comput. Graph. 26(1), 822–831 (2019)
Griethe, H., Schumann, H., et al.: The visualization of uncertain data: methods and problems. In: SimVis, pp. 143–156 (2006)
Guo, S., Du, F., Malik, S., Koh, E., Kim, S., Liu, Z., Kim, D., Zha, H., Cao, N.: Visualizing uncertainty and alternatives in event sequence predictions. In: Proceedings of the 2019 CHI Conference on Human Factors in Computing Systems, pp. 1–12 (2019)
Hansen, C.D., Chen, M., Johnson, C.R., Kaufman, A.E., Hagen, H.: Scientific Visualization: Uncertainty, Multifield, Biomedical, and Scalable Visualization. Springer, Cham (2014)
Hasinoff, S.W., Durand, F., Freeman, W.T.: Noise-optimal capture for high dynamic range photography. In: 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, pp. 553–560. IEEE (2010)
Hegel, T.M., Cushman, S.A., Evans, J., Huettmann, F.: Current state of the art for statistical modelling of species distributions. In: Spatial Complexity, Informatics, and Wildlife Conservation, pp. 273–311. Springer (2010)
Heinrich, J., Weiskopf, D.: State of the art of parallel coordinates. In: Sbert, M., Szirmay-Kalos, L. (Eds.) Eurographics 2013—State of the Art Reports. The Eurographics Association (2013)
Herschel, M., Diestelkämper, R., Lahmar, H.B.: A survey on provenance: What for? what form? what from? VLDB J. 26(6), 881–906 (2017)
Höferlin, M., Höferlin, B., Weiskopf, D., Heidemann, G.: Uncertainty-aware video visual analytics of tracked moving objects. J. Spat. Inf. Sci. 2011(2), 87–117 (2011)
Hoffman, P.E., Grinstein, G.G.: A survey of visualizations for high-dimensional data mining. In: Information visualization in data mining and knowledge discovery, pp. 47–82 (2001)
Hu, Z., Mahadevan, S., Du, X.: Uncertainty quantification in time-dependent reliability analysis. In: International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, vol. 57083, p. V02BT03A062. American Society of Mechanical Engineers (2015)
Hullman, J.: Why authors don’t visualize uncertainty. IEEE Trans. Vis. Comput. Graph. 26(1), 130–139 (2019)
Hullman, J., Qiao, X., Correll, M., Kale, A., Kay, M.: In pursuit of error: a survey of uncertainty visualization evaluation. IEEE Trans. Vis. Comput. Graph. 25(1), 903–913 (2018)
Jänicke, S., Focht, J., Scheuermann, G.: Interactive visual profiling of musicians. IEEE Trans. Vis. Comput. Graph. 22(1), 200–209 (2015)
Jena, A., Engelke, U., Dwyer, T., Raiamanickam, V., Paris, C.: Uncertainty visualisation: an interactive visual survey. In: 2020 IEEE Pacific Visualization Symposium (PacificVis), pp. 201–205. IEEE (2020)
Jiao, F., Phillips, J.M, Stinstra, J., Krger, J., Varma, R., Hsu, E., Korenberg, J., Johnson, C.R.: Metrics for uncertainty analysis and visualization of diffusion tensor images. In: International Workshop on Medical Imaging and Virtual Reality, pp. 179–190. Springer (2010)
Jänicke, S., Geßner, A., Büchler, M., Scheuermann, G.: Visualizations for text re-use. In: International Conference on Information Visualization Theory and Applications (IVAPP), 2014, pp. 59–70 (2014)
Kamal, A., Dhakal, P., Javaid, A.Y., Devabhaktuni, V.K., Kaur, D., Zaientz, J., Marinier, R.: Recent advances and challenges in uncertainty visualization: a survey. J. Vis. 24(5), 861–890 (2021)
Karami, A.: A framework for uncertainty-aware visual analytics in big data. In: CEUR Workshop Proceedings, vol. 1510, pp. 146–155 (2015)
Kassiano, V., Gounaris, A., Papadopoulos, A.N., Tsichlas, K.: Mining uncertain graphs: an overview. In: International Workshop of Algorithmic Aspects of Cloud Computing, pp. 87–116. Springer (2016)
Kaur, J., Madan, N.: Association rule mining: a survey. Int. J. Hybrid Inf. Technol. 8, 239–242 (2015)
Keim, D., Andrienko, G., Fekete, J.-D., Görg, C., Kohlhammer, J., Melançon, G.: Visual analytics: definition, process, and challenges. In: Information Visualization, pp. 154–175. Springer (2008)
Keim, D., Zhang, L.: Solving problems with visual analytics: challenges and applications. In: Proceedings of the 11th International Conference on Knowledge Management and Knowledge Technologies, pp. 1–4 (2011)
Keim, D.A., Mansmann, F., Schneidewind, J., Thomas, J., Ziegler, H.: Visual analytics: scope and challenges. In: Visual Data Mining, pp. 76–90. Springer (2008)
Kerdjoudj, F., Curé, O.: Evaluating Uncertainty in Textual Document. URSW at ISWC (Bethlehem, United States) (2015)
Khulusi, R., Kusnick, J., Meinecke, C., Gillmann, C., Focht, J., Jänicke, S.: A survey on visualizations for musical data. In: Computer Graphics Forum, vol. 39, pp. 82–110. Wiley Online Library (2020)
Kniss, J.M.: Managing uncertainty in visualization and analysis of medical data. In: 2008 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, pp. 832–835. IEEE (2008)
Kohlhammer, J., May, T., Hoffmann, M.: Visual analytics for the strategic decision making process. In: Geospatial Visual Analytics, pp. 299–310. Springer (2009)
Kretzschmar, V., Gillmann, C., Günther, F., Stommel, M., Scheuermann, G.: Visualization framework for assisting interface optimization of hybrid component design. In: VMV, pp. 57–67 (2020)
Ku, H.H.: Notes on the use of propagation of error formulas. J. Res. Natl. Bur. Stand. 70(4), 263–273 (1966)
Lee, G., Kim, W., Hyunseok, O., Youn, B.D., Kim, N.H.: Review of statistical model calibration and validation-from the perspective of uncertainty structures. Struct. Multidiscip. Optim. 60(4), 1619–1644 (2019)
Leffrang, D., Müller, O.: Should i follow this model? the effect of uncertainty visualization on the acceptance of time series forecasts. In: 2021 IEEE Workshop on TRust and EXpertise in Visual Analytics (TREX), pp. 20–26. IEEE (2021)
Lewandowsky, S., Ballard, T., Pancost, R.D: Uncertainty as knowledge, p. 20140462 (2015)
Li, L., Ban, H., Wechsler, S., Xu, B.: Spatial Data Uncertainty, vol. 1, pp. 313–340. Elsevier, Amsterdam (2017)
Lin, G., Engel, D.W, Eslinger, P.W.: Survey and evaluate uncertainty quantification methodologies. Technical report, Pacific Northwest National Lab. (PNNL), Richland, WA (United States) (2012)
Lipşa, D.R., Laramee, R.S., Cox, S.J., Roberts, J.C., Walker, R., Borkin, M.A., Pfister, H.: Visualization for the physical sciences. In: Computer Graphics Forum, vol. 31, pp. 2317–2347. Wiley Online Library (2012)
Liu, S., Andrienko, G., Yingcai, W., Cao, N., Jiang, L., Shi, C., Wang, Y.-S., Hong, S.: Steering data quality with visual analytics: the complexity challenge. Vis. Inform. 2(4), 191–197 (2018)
Loucks, D.P., van Beek, E.: An introduction to probability, statistics, and uncertainty. In: Water Resource Systems Planning and Management, pp. 213–300. Springer (2017)
Maack, R.G.C., Raymer, M.L., Wischgoll, T., Hagen, H., Gillmann, C.: A framework for uncertainty-aware visual analytics of proteins. Comput. Graph. 98, 293–305 (2021)
MacEachren, A., Robinson, A., Hopper, S., Gardner, S., Murray, R., Gahegan, M., Hetzler, E.: Visualizing geospatial information uncertainty: What we know and what we need to know. Cartogr. Geogr. Inf. Sci. 32, 139–160 (2005)
MacEachren, A.M: Visual analytics and uncertainty: its not about the data (2015)
Maier, H., Tolson, B.: Sensitivity and Uncertainity. Elsevier, Amsterdam (2008)
Mastrandrea, M.D., Mach, K.J., Plattner, G.-K., Edenhofer, O., Stocker, T.F., Field, C.B., Ebi, K.L., Matschoss, P.R.: The ipcc ar5 guidance note on consistent treatment of uncertainties: a common approach across the working groups. Clim. Change 108(40), 675–691 (2011)
Olston, C., Mackinlay, J.D.: Visualizing data with bounded uncertainty. In: IEEE Symposium on Information Visualization, 2002. INFOVIS 2002, pp. 37–40. IEEE (2002)
Pfeiffer, J.J: Using brightness and saturation to visualize belief and uncertainty. In: International Conference on Theory and Application of Diagrams, pp. 279–289. Springer (2002)
Plaisant, C.: The challenge of information visualization evaluation. In: Proceedings of the Working Conference on Advanced Visual Interfaces (New York, NY, USA), AVI ’04, pp. 109–116. Association for Computing Machinery (2004)
Potter, K., Rosen, P., Johnson, C.R.: From quantification to visualization: a taxonomy of uncertainty visualization approaches. In: IFIP Working Conference on Uncertainty Quantification, pp. 226–249. Springer (2011)
Preston, A., Gomov, M., Ma, K.-L.: Uncertainty-aware visualization for analyzing heterogeneous wildfire detections. IEEE Comput. Graph. Appl. 39(5), 72–82 (2019)
Ragan, E.D., Endert, A., Sanyal, J., Chen, J.: Characterizing provenance in visualization and data analysis: an organizational framework of provenance types and purposes. IEEE Trans. Visu. Comput. Graph. 22(1), 31–40 (2015)
Raith, F., Scheuermann, G., Gillmann, C.: Uncertainty-aware detection and visualization of ocean eddies in ensemble flow fields—a case study of the Red Sea. In: Proceedings of the Workshop on Visualisation in Environmental Sciences (2021)
Ranftl, S., von der Linden, W., MaxEnt 2021 Scientific Committee: Bayesian surrogate analysis and uncertainty propagation. In: Physical Sciences Forum, vol. 3, MDPI, p. 6 (2021)
Rebba, R., Mahadevan, S.: Computational methods for model reliability assessment. Reliab. Eng. Syst. Saf. 93(8), 1197–1207 (2008)
Ristovski, G., Preusser, T., Hahn, H.K., Linsen, L.: Uncertainty in medical visualization: towards a taxonomy. Comput. Graph. 39, 60–73 (2014)
Souza, R.R., Dorn, A., Piringer, B., Wandl-Vogt, E.: Towards a taxonomy of uncertainties: analysing sources of spatio-temporal uncertainty on the example of non-standard German corpora. In: Informatics, vol. 6, p. 34. Multidisciplinary Digital Publishing Institute (2019)
Sacha, D., Senaratne, H., Kwon, B.C., Ellis, G., Keim, D.A.: The role of uncertainty, awareness, and trust in visual analytics. IEEE Trans. Vis. Comput. Graph. 22(1), 240–249 (2015)
Sacha, D., Stoffel, A., Stoffel, F., Kwon, B.C., Ellis, G., Keim, D.A.: Knowledge generation model for visual analytics. IEEE Trans. Vis. Comput. Graph. 20(12), 1604–1613 (2014)
Saltelli, A., Tarantola, S., Campolongo, F., Ratto, M.: Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models. Halsted Press, New York (2004)
Schulz, C., Nocaj, A., Goertler, J., Deussen, O., Brandes, U., Weiskopf, D.: Probabilistic graph layout for uncertain network visualization. IEEE Trans. Vis. Comput. Graph. 23(1), 531–540 (2016)
Senaratne, H.V.: Uncertainty-aware visual analytics for spatio-temporal data exploration. Ph.D. thesis, Universität Konstanz, Konstanz (2017)
Shyu, M.-L., Haruechaiyasak, C., Chen, S.-C., Premaratne, K.: Mining association rules with uncertain item relationships. Comput. Ind. Eng. 34(1), 3–20 (1998)
Sodergren, T., Hair, J., Phillips, J.M., Wang, B.: Visualizing sensor network coverage with location uncertainty. In: 2017 IEEE Visualization in Data Science (VDS), pp. 52–59. IEEE (2017)
Sorzano, C.O.S., Vargas, J., Montano, A.P.: A survey of dimensionality reduction techniques. arXiv (2014)
Su, X., Talmaki, S., Cai, H., Kamat, V.R.: Uncertainty-aware visualization and proximity monitoring in urban excavation: a geospatial augmented reality approach. Vis. Eng. 1(1), 1–13 (2013)
Szafir, D.A.: The good, the bad, and the biased: five ways visualizations can mislead (and how to fix them). Interactions 25(4), 26–33 (2018)
Taylor, P., Derudder, B.: World City Network: A Global Urban Analysis. Routledge, New York (2015)
Therón, R., De Paz, J.F.: Visual sensitivity analysis for artificial neural networks. In: International Conference on Intelligent Data Engineering and Automated Learning, pp. 191–198. Springer (2006)
Sánchez, R.T., Santos, A.B., Vicente, R.S., Gómez, A.L.:Towards an uncertainty-aware visualization in the digital humanities. In: Informatics, vol. 6, p. 31. Multidisciplinary Digital Publishing Institute (2019)
Thomas, J.J., Cook, K.A: Illuminating the path: the research and development agenda for visual analytics. Technical report, Pacific Northwest National Lab. (PNNL), Richland, WA (United States) (2005)
Timpf, S., Laube, P.: Advances in Spatial Data Handling: Geospatial Dynamics, Geosimulation and Exploratory Visualization. Springer, Berlin (2012)
Varga, M., Varga, C.: Visual analytics: data, analytical and reasoning provenance. In: Building Trust in Information, pp. 141–150. Springer (2016)
Vehlow, C., Hasenauer, J., Kramer, A., Raue, A., Hug, S., Timmer, J., Radde, N., Theis, F.J., Weiskopf, D.: IVUN: interactive visualization of uncertain biochemical reaction networks. BMC Bioinform. 14(19), 1–14 (2013)
Vosough, Z., Kammer, D., Keck, M., Groh, R.: Visualizing uncertainty in flow diagrams: a case study in product costing. In: Proceedings of the 10th International Symposium on Visual Information Communication and Interaction, pp. 1–8 (2017)
Wall, E., Blaha, L.M., Paul, C.L., Cook, K., Endert, A.: Four perspectives on human bias in visual analytics. In: Cognitive Biases in Visualizations, pp. 29–42. Springer (2018)
Wallace, M., Platis, N.: The uncertain tag cloud. In: 2015 10th International Workshop on Semantic and Social Media Adaptation and Personalization (SMAP), pp. 1–5 (2015)
Wang, H., Yeung, D.-Y.: A survey on Bayesian deep learning. ACM Comput. Surv. (CSUR) 53(5), 1–37 (2020)
Wang, J., Hazarika, S., Li, C., Shen, H.-W.: Visualization and visual analysis of ensemble data: a survey. IEEE Trans. Vis. Comput. Graph. PP, 1–1 (2018)
Ward, M., Grinstein, G., Keim, D.: Interactive Data Visualization: Foundations, Techniques, and Applications. A. K. Peters Ltd, Natick (2010)
Watanabe, N., Wang, W., McDermott, C.I., Taniguchi, T., Kolditz, O.: Uncertainty analysis of thermo-hydro-mechanical coupled processes in heterogeneous porous media. Comput. Mech. 45(4), 263–280 (2010)
Wilson, R., Granlund, G.H.: The uncertainty principle in image processing. IEEE Trans. Pattern Anal. Mach. Intell. (6), 758–767 (1984)
Wu, D.T.Y., Chen, A.T., Manning, J.D., Levy-Fix, G., Backonja, U., Borland, D., Caban, J.J., Dowding, D.W., Hochheiser, H., Kagan, V., et al.: Evaluating visual analytics for health informatics applications: a systematic review from the American Medical Informatics Association visual analytics working group task force on evaluation. J. Am. Med. Inform. Assoc. 26(4), 314–323 (2019)
Xu, K., Ottley, A., Walchshofer, C., Streit, M., Chang, R., Wenskovitch, J.: Survey on the analysis of user interactions and visualization provenance. In: Computer Graphics Forum, vol. 39, pp. 757–783. Wiley Online Library (2020)
Rui, X., Wunsch, D.: Survey of clustering algorithms. IEEE Trans. Neural Netw. 16(3), 645–678 (2005)
Yan, L., Wang, Y., Munch, E., Gasparovic, E., Wang, B.: A structural average of labeled merge trees for uncertainty visualization. IEEE Trans. Vis. Comput. Graph. 26(1), 832–842 (2019)
Yang, M.-S.: A survey of fuzzy clustering. Math. Comput. Model. 18(11), 1–16 (1993)
Zhou, X., Liu, H., Pourpanah, F., Zeng, T., Wang, X.: A survey on epistemic (model) uncertainty in supervised learning: recent advances and applications. Neurocomputing (2021)
Acknowledgements
The authors acknowledge the financial support by the Federal Ministry of Education and Research of Germany and by the Sächsische Staatsministerium für Wissenschaft Kultur und Tourismus in the program Center of Excellence for AI-research “Center for Scalable Data Analytics and Artificial Intelligence Dresden/Leipzig,” Project Identification Number: ScaDS.AI.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts of interests to declare.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Maack, R.G.C., Scheuermann, G., Hagen, H. et al. Uncertainty-aware visual analytics: scope, opportunities, and challenges. Vis Comput 39, 6345–6366 (2023). https://doi.org/10.1007/s00371-022-02733-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00371-022-02733-6


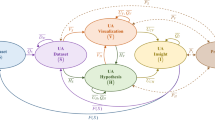
































 and uncertainty-aware feedback loop
and uncertainty-aware feedback loop 

 and uncertainty-aware hypothesis
and uncertainty-aware hypothesis 



