1 Introduction

Many crucial robot tasks such as obstacle detection, mapping or autonomous navigation require accurate pose estimates. Apart from many other sensor types such as laser scanners, GPS and inertial measurement units, optical camera systems have been proven successful for ego motion estimation. They are comparatively cheap and due to their high information density not only restricted to localization tasks.

This paper deals with estimating a mobile robot's ego motion driving on a planar surface, as it is the case in many industrial applications. The image stream of a downward looking camera is used to compute the relative transformation between consecutive camera frames (visual odometry). Knowing the initial pose at the beginning, the robot's path can be fully recovered by concatenating all relative transformations. For an overview over current state-of-the-art visual odometry (VO) systems, we refer to the work of [1]. A more fundamental introduction to the subject can be found in [2]. Generally speaking, images of a planar scene, e.g. a ground plane, are related by a homography transformation. Constraining the motion of the camera, e.g. forcing it downward with constant height above the ground, eliminates degrees of freedom (DoF) in the homography transformation and yields an Euclidean transformation which is defined up to a scale factor by 3 DoF.

We propose a novel, deep learning based, approach to infer the transformation parameters \(\left( {\theta , t_{x} ,t_{y} } \right)\) directly as outputs from a convolutional neural network. The two proposed network architectures, in the following referred to as EarlyBird and SlowBird, are inspired by the work of [3] and do not require any ground truth labelling as they are trained in an unsupervised manner. Unlike the proposed homography estimator in [3], we exploit the fact that in our simpler Euclidean case, there is no ambiguity between translational and [2] rotational parameters. This allows us to estimate the parameters of the Euclidean transformation matrix directly from the regression network, no detour via point correspondences and Direct Linear Transform algorithm [3, 4] is needed.

In order to improve our estimation accuracy and obtain a smoother output, we adapt the Slow Fusion design principle presented in [5]. Considering ego motion estimation with 6 DoF, [5] has shown the potential in learning temporal information over multiple image frames instead of relying solely on consecutive image pairs. However, their networks are trained in a supervised manner. We present an unsupervised version of their Slow Fusion architecture modified to retrieve the relative transformation between every consecutive image frame pair and will investigate if our approach benefits of the spatio-temporal feature extraction as well.

The contribution of this work can be summarized as followed: We present two neural networks architectures called EarlyBird and SlowBird for the general planar incremental ego-motion estimation with a downward facing camera. In contrast to other related work in the field, we do not assume any kind of steering model. Our proposed method can be applied to any vehicle type, e.g. ackermann-steering, differential-drive or omnidirectional. We demonstrate that by constraining the camera motion to face the ground, it is possible to train the networks in an unsupervised manner with unlabeled synthetic and real world data. Both network architectures are evaluated on synthetic data and on a real-world commercial robot system.

2 Related work

Estimating a mobile ground robot's ego motion via a downward facing camera is a rich area of research. Prior work has demonstrated the value of exploiting constrained camera motion introduced simplifications of the homography estimation. The work in this field can be subdivided in systems relying purely on relative transformations between consecutive frames (odometry) and map-based localization approaches. Methods for absolute localization are not prone to drift but need a preceding map building. Closer examination of these methods is out of the scope of this work, and for the interested reader, we refer to the extensive related work section of [6].

Saurer et al. [7] propose different minimal solutions based on point correspondences for the relative pose estimation between two camera frames depending on the prior knowledge about the 3D scene. Qifa and Kanade [8] virtually rotate the camera downward and estimate the ego motion of the camera by minimizing the sum of squared differences of pixel intensities with respect to motion parameters. Kitt et al. [9] use homographies of a virtually downward facing camera to recover the scale of the motion in their visual odometry pipeline. Yu et al. [10] propose a rotated template matching algorithm to compute the translation and rotation between consecutive images.

Other works constrain the problem to car-like vehicles [11,12,13]. By assuming the Ackermann steering model, the general planar motion can be restricted to 2DoF. Gao et al. [11] propose a keypoint-less method to recover the ego motion of car-like steering models using an optimal image registration technique based on global branch-and-bound optimization. Peng et al. [12] use an event-based camera system to overcome the downsides of a frame-based camera such as latency, motion blur and low dynamic range. In [13], template matching is applied for calculating the image displacement between consecutive frames. While the assumption of an Ackermann-like steering model greatly simplifies the registration problem, it is at the expense of generalization and not suitable for our presented use case.

In [14,15,16], the image registration problem is transformed into the frequency domain. Ri and Fujimoto [14] use phase-only correlation based on fast Fourier transforms (FFT) to estimate the Euclidean transformation parameters between image pairs. Goecke et al. [15] use the Fourier-Mellin transform to solve for the rotation and translation parameters simultaneously. In order to speed up the estimation process, [16] tackles the ego motion estimation problem by only solving for translational shift between image pairs. They apply FFT to multiple regions on each frame and recover the rotation from the shift between corresponding regions of consecutive image frames.

Downward facing cameras also play an important role in the field of micro aerial vehicles [17, 18]. In [17], an optical flow based approach based on a sparse feature set is applied for estimating the two dimensional pose of the micro aerial vehicles. The height above the ground is measured with an ultrasound sensor. Fu et al. [18] imply a direct approach for estimating the homography between consecutive image frames. An inertial measurement unit and a single beam laser rangefinder are used to make the ego motion estimation of the micro aerial vehicle more salient.

3 Problem formulation

Images taken from different viewpoints \({}_{{}}^{0} {\varvec{C}}\) and \({}_{{}}^{1} {\varvec{C}}\) of the same plane are related by a (planar) homography \({\varvec{H}}\) (Fig. 1, left). The warping between corresponding points \({}_{{}}^{0} {\varvec{x}}\) and \({}_{{}}^{1} {\varvec{x}}\) is defined as:

$$ {}_{{}}^{0} {\varvec{x}} = {\varvec{H}} {}_{{}}^{1} {\varvec{x}} $$
(1)
Fig. 1
figure 1

Two images of a planar scene taken at different viewpoints \({}_{{}}^{0} C\) and \({}_{{}}^{1} C\) are related by a homography matrix. The left scene describes the general case, whereas the right scene illustrates the downward looking case. Introducing motion constraints simplifies the homography estimation

Full size image

Knowing the rotation \({}_{0}^{1} {\varvec{R}}\) and translation \({}_{0}^{1} {\varvec{t}}\) from camera frame \({}_{{}}^{1} {\varvec{C}}\) to \({}_{{}}^{0} {\varvec{C}}\), the homography matrix \({\varvec{H}}\) can be expressed as

$$ {\varvec{H}} = {}_{0}^{1} {\varvec{R}} - \frac{1}{d} {}_{0}^{1} \user2{t n}^{T} $$
(2)

where \(d\) is the distance between \({}_{{}}^{1} {\varvec{C}}\) and the observed plane described by the normal vector \({\varvec{n}}\) [7]. For the special case of a downward looking camera (Fig. 1, right) with constant height \(d\) above the ground, Eq. 2 can be expressed as:

$$ \begin{aligned} \user2{H} & = ~{}_{0}^{1} \user2{R}_{z} - \left[ {\begin{array}{*{20}c} {\frac{{t_{x} }}{d}} \\ {\frac{{t_{y} }}{d}} \\ 0 \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } \right]^{T} \\ & = ~\left[ {\begin{array}{*{20}c} {\cos \theta } & { - \sin \theta } & {t_{x}^{\prime} } \\ {\sin \theta } & {\cos \theta } & {t_{y}^{\prime} } \\ 0 & 0 & 1 \\ \end{array} } \right] \\ \end{aligned} $$
(3)

Equation 3 shows that in this particular case, the image warping from frame \({}_{{}}^{1} {\varvec{C}}\) to \({}_{{}}^{0} {\varvec{C}}\) is described by an Euclidean transformation and there is no ambiguity between rotational and translational parameters [8]. The rotation \({}_{1}^{0} {\varvec{R}}\) and translation \({}_{1}^{0} {\varvec{t}}\) can be retrieved by estimating the warping matrix \({\varvec{H}}\) between those images and knowing the scale.

The complete robot's path can be recovered by concatenating all relative transformations \({}_{k}^{k - 1} {\varvec{T}}\) for \(k = 1 \ldots n\) with \({}_{0}^{w} {\varvec{C}}\) being the initial camera pose at the start [2]:

$$ {}_{n}^{w} {\varvec{C}} = {}_{0}^{w} {\varvec{C}} \cdot {}_{1}^{0} {\varvec{T}} \cdot \cdots \cdot {}_{n - 1}^{n - 2} {\varvec{T}} \cdot {}_{n}^{n - 1} {\varvec{T}} $$
(4)

4 Neural network architecture

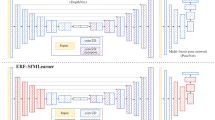
The proposed networks EarlyBird and SlowBird are both trained in the same way, only their respective regression network's input and architecture differ (see Fig. 3). In both cases, consecutive image frames with spatial dimensions of 200 × 200 pixels are fed into the regression network and the estimated parameters \(\left( {\theta , t_{x} ,t_{y} } \right)\) are relative to the previous image \({\varvec{I}}_{n - 1}\). They describe the transformation from image \({\varvec{I}}_{n - 1}\) taken at a previous point in time \(t = n - 1\) to the current image in time \({\varvec{I}}_{n}\).

In order to train the regression network without any provided ground truth, the error signal is computed by warping an image \({\varvec{I}}_{n - 1}\) taken at a previous point in time \(t = n - 1\) accordingly to the network's estimation for \(\left( {\theta , t_{x} ,t_{y} } \right)\) and by analyzing how similar the warped image \({\varvec{I}}_{n - 1} \left( {\theta ,t_{x} ,t_{y} } \right)\) and the target image \({\varvec{I}}_{n}\) are (see Fig. 2). The warping is done via a layer called Spatial Transformer (STL) [19]. It consists of a sampling grid generator and a bilinear sampler. Both entities are differentiable, so that the regression network can be trained in an end-to-end manner.

Fig. 2
figure 2

The unsupervised training of the networks is done via comparing on how similar the warped image \({\varvec{I}}_{n - 1} \left( {\theta ,t_{x} ,t_{y} } \right)\) and the target image \({\varvec{I}}_{n}\) are. In order to remove the black areas introduced by the warping procedure, both images are centrally cropped \(\tilde{\user2{I}}_{n - 1} \left( {\theta ,t_{x} ,t_{y} } \right)\) and \(\tilde{\user2{I}}_{n}\). The white box indicates the central crop with \(\alpha_{c} = 0.6\)

Full size image

Our loss function is based on the structural similarity index (SSIM) [20]. The SSIM function takes the warped and the target image as inputs and returns a value between \(\in \left( { - 1 ,1} \right)\). The return value is close to 1 if both images are similar. We modify it by adding a constant of value one and inverting the sign of the SSIM. As a result, our proposed loss function returns a value between \(\in \left( {0, 2} \right)\). Since the robot is moving, consecutive image frames \({\varvec{I}}_{n - 1}\) and \({\varvec{I}}_{n}\) generally do not contain the same real world scene. Depending on the camera's focus length, the distance to the floor, the frame rate, and the robot's velocity successive frames overlap more or less and black borders are introduced in the warped image. To compensate these artefacts, the warped image \({\varvec{I}}_{n - 1} \left( {\theta ,t_{x} ,t_{y} } \right)\) and the target image \({\varvec{I}}_{n}\) are centrally cropped by a factor \(\alpha_{c} \in \left( {0, 1} \right)\). The hyperparameter \(\alpha_{c}\) has to be chosen so that the cropped image patches \(\tilde{\user2{I}}_{n - 1} \left( {\theta ,t_{x} ,t_{y} } \right)\) and \(\tilde{\user2{I}}_{n}\) theoretically show the same real world scenery.

The resulting loss function is defined as:

$$ L = 1 - {\text{SSIM}}\left( {\tilde{\user2{I}}_{n - 1} \left( {\theta ,t_{x} ,t_{y} } \right), \tilde{\user2{I}}_{n} } \right) $$
(5)

In the work of [3], the \(l1\) loss function is used; however, in the course of our work, we experienced the SSIM loss function to be easier to train and encourage to experiment with both.

In the following, the two proposed regression network architectures for EarlyBird and SlowBird will be further described, as well as the subsequent warping procedure in the STL.

4.1 EarlyBird

The EarlyBird network (see Fig. 3) takes as input two consecutive grey level images \({\varvec{I}}_{n - 1}\) and \({\varvec{I}}_{n}\). They are stacked channel wise (200, 200, 2) and forwarded into the net following the Early Fusion design principle of [21]. The net layout is inspired by the VGGNet architecture of [3]. It has five convolutional blocks, each one consisting of two 2D convolutional layer and a max pooling layer. The filter sizes of the convolutional layers become greater going deeper into the network: 8, 16, 32, 64, and 64. The quadratic kernel size remains the same with (3, 3). The pooling kernel remains (2, 2) throughout the net. The second last fully connected layer has 512 neurons. The final layer consists of three neurons, one for each transformation parameter. Between those two layers there is dropout.

Fig. 3
figure 3

Overview over proposed neural network architectures: EarlyBird (top) and SlowBird (bottom). Except for the input and the regression part both networks share the same structure. The training is done via warping the previous image in time accordingly to the estimated transformation parameters \({\varvec{I}}_{n - 1} \left( {\theta ,t_{x} ,t_{y} } \right)\) and comparing it against the current image in time \({\varvec{I}}_{n}\)

Full size image

4.2 SlowBird

The SlowBird network (see Fig. 3) has as input five consecutive grey level images \({\varvec{I}}_{n - 4} \ldots I_{n}\) and follows the Slow Fusion design principle of [5, 21]. Instead of being stacked up channel wise (EarlyBird) and fed as a whole into the net, they are ordered in a 4-dimensional way (200, 200, 5, 1) and convoluted over the spatial dimensions (1st and 2nd dimension) as well as the time (3rd dimension). In order to deal with the four-dimensional shape of the input, 3D convolutional layers [22] are used with the following kernel sizes: (3, 3, 3), (3, 3, 2), (3, 3, 1), and (3, 3, 1). Since the convolutional operation is not only performed over the spatial dimension of the feature map as it is the case with 2D convolutions, the temporal information of the image frames is preserved in its output signals. With every 3D convolutional operation, the time dimension vanishes until it finally disappears in the third 3D convolution. The following 3D convolutional operations can be seen as standard 2D convolutions. After every second convolutional operation, max pooling is applied. This downsampling step only affects the spatial dimension of the feature map, the time dimension is not involved. Just as in the EarlyBird network, high-level reasoning is done via two fully connected layers. They have the same structure and number of neurons as the fully connected neural network in the EarlyBird approach.

4.3 Spatial transformer network

The STL introduced in [19] performs an inverse affine warping of the pixel coordinates of image \({\varvec{I}}_{n - 1}\). It is differentiable and allows backpropagation of the error gradient through the STL into the regression network. First, the regression network's output \(\left( {\theta ,t_{x} ,t_{y} } \right)\) is converted into an affine transformation matrix \(A\):

$$ {\varvec{A}} = \left[ {\begin{array}{*{20}c} {\theta_{11} } & {\theta_{12} } & {\theta_{13} } \\ {\theta_{21} } & {\theta_{22} } & {\theta_{21} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos \theta } & { - \sin \theta } & {t_{x} } \\ {\sin \theta } & {\cos \theta } & {t_{y} } \\ \end{array} } \right] $$
(6)

The following inverse warping of the STL can be subdivided into two steps: 1. generation of the sampling grid and 2. bilinear sampling. The sampling grid generator applies an inverse warping of the regular and normalized target grid \({\varvec{G}}\). For every target pixel \({\varvec{G}}_{i} = \left( {x_{i}^{t} , y_{i}^{t} } \right)^{T}\) of our target grid \({\varvec{G}} = \left\{ {{\varvec{G}}_{i} } \right\}\) a source coordinate \({\varvec{S}}_{i} = \left( {x_{i}^{s} , y_{i}^{s} } \right)^{T}\) is defined.

$$ \left( {\begin{array}{*{20}c} {x_{i}^{s} } \\ {y_{i}^{s} } \\ \end{array} } \right) = {\varvec{A}}\left( {\begin{array}{*{20}c} {x_{i}^{t} } \\ {y_{i}^{t} } \\ 1 \\ \end{array} } \right) = \left[ {\begin{array}{*{20}c} {\theta_{11} } & {\theta_{12} } & {\theta_{13} } \\ {\theta_{21} } & {\theta_{22} } & {\theta_{23} } \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {x_{i}^{t} } \\ {y_{i}^{t} } \\ 1 \\ \end{array} } \right) $$
(7)

To perform the warping of the input image, a differentiable sampler takes the set of source coordinates \({\varvec{S}} = \left\{ {{\varvec{S}}_{i} } \right\}\), along with the input image \({\varvec{I}}_{n - 1}\) and produces the sampled output image \({\varvec{I}}_{n - 1} \left( {\theta ,t_{x} ,t_{y} } \right)\). Since the source coordinates \({\varvec{S}}_{i}\) are in general not aligned with the grid-like structure of the input image \({\varvec{I}}_{n - 1}\), the STL makes use of a differentiable bilinear interpolation kernel. For every source pixel \({\varvec{S}}_{i} = \left( {x_{i}^{s} , y_{i}^{s} } \right)^{T}\), the interpolation is described via

$$ V_{i} = \mathop \sum \limits_{n}^{H} \mathop \sum \limits_{m}^{W} I_{n - 1} \left( {n,m} \right)\max \left( {0, 1 - \left| {x_{i}^{s} - m} \right|} \right)\max \left( {0, 1 - \left| {y_{i}^{s} - n} \right|} \right) $$
(8)

where \(V_{i}\) is the sampled pixel value belonging to the target pixel \({\varvec{G}}_{i}\) and \(I_{n - 1} \left( {n, m} \right)\) stands for the pixel value of image \({\varvec{I}}_{n - 1}\) at position (n,m). Height and width normalised coordinates are used, such that \(- 1 \le x_{i}^{t} , y_{i}^{t} ,x_{i}^{s} ,y_{i}^{s} \le 1\), when within the spatial bounds of the input or output image.

5 System setup

Images are recorded with a frame rate of 90 fps. The camera is mounted in front of a differential drive mobile robot and facing downward with an approximately distance to the ground of 0.11 m. To eliminate shadows when driving around and to realize higher shutter speeds, two LED spotlights are illuminating the ground. For later use cases, it would be also possible to mount the camera underneath the robot. In order to accomplish an exact bird's eye vision system, each camera image is warped accordingly to a homography estimated in advance with a calibration chessboard pattern laying on the ground (see Fig. 4). This warping procedure allows us to set the scale arbitrary. It is however to be considered to choose the desired resolution accordingly to the original camera image to minimize interpolation error. In our case, we set the resolution to 8 \(\frac{{{\text{px}}}}{{{\text{mm}}}}.\)

Fig. 4
figure 4

In order to compensate for mounting inaccuracies of the camera the raw image is warped by a precalibrated homography \({\varvec{H}}_{bird}\). The warped image is cropped to 200 × 200 pixels and fed into the network

Full size image

The average inference times are 18.31 ms (\(\sim\) 54 fps) for the SlowBird network and 19.51 ms (\(\sim\) 51 fps) for the EarlyBird network and 14.75 ms (\(\sim\) 67 fps) for the FFT method (GeForce GTX 1080 Ti, i7-8700 @3.20 GHz).

6 Training

The two networks EarlyBird and SlowBird are pretrained on synthetic datasets and then fine-tuned for the surface texture of the real world testing area.

6.1 Synthetic dataset

The synthetic dataset is generated by laying hand designed trajectories based on Bézier curves upon multiple high resolution images acting as different ground surfaces. A virtual robot is travelling along these trajectories and taking snapshots of the ground images. Its velocity is randomized in order to cover a broader range of relative transformations between consecutive image frames. Though ground truth is available for our synthetic dataset, we do not use it for training. In total, the synthetic dataset consists of 50 trajectories and 25 different ground images resulting in one million training samples.

6.2 Real world dataset

Transfer learning [23] is used to transfer the knowledge gained with the synthetic dataset to the real world domain. Our experience has shown that without pretraining on the synthetic dataset finding the proper hyperparameters to minimize the loss on the real world dataset might become very exhaustive in some cases. Although it is still possible without, we recommend to begin training on the synthetically pretrained models. The real world dataset consists of 730 k training samples. Since no labelling is required, it can be obtained in under 2.5 h of driving around with the robot in our testing area (max. translational velocity of 0.1 \(\frac{{\text{m}}}{{\text{s}}}\) and max. angular velocity of 10 \(\frac{{{\text{deg}}}}{{\text{s}}}\)). The networks are trained with data augmentation on a single consumer grade GPU (GTX 1080 Ti) for about one day (including the synthetic dataset). Data augmentation is done by randomly skipping image frames and by feeding them backwards into the net. This simulates different inter frames velocities and generates more reverse training samples. Adam [24] was used for optimization. Our experiments showed that beneath setting the learning rate to \(\alpha = 0.0001\), modifying the value of the numerical stability constant \(\hat{\varepsilon } = 0.0001\) (default value \(\hat{\varepsilon } = 1 \times 10^{ - 8}\)) yielded to good results. To avoid overfitting, the network is evaluated on a separate validation dataset after every 3000 training iterations and the model with the best performance (minimal loss value) is kept.

7 Results and discussion

We evaluated our proposed neural network architectures by comparing them against a state-of-the-art image registration techniqueFootnote 1 based on FFT [14]. Although it is already well known that feature-based methods have difficulties with the fast moving, texture less images of a downward facing camera, we added an ORB feature based approach to our evaluation as a conservative baseline. Experiments are conducted on synthetic and on real world data.

7.1 Synthetic data experiments

The synthetic test dataset consists of eight unseen trajectories on nine different surfaces each. As proposed in [25], we used the root mean square relative pose error (RMS-RPE) and root mean square absolute trajectory error (RMS-ATE) as evaluation metrics. As we are evaluating a visual odometry system based on incremental motion estimation between consecutive frames, we choose for the time parameter \(\Delta = 1\). The RMS-RPE accounts for the drift per frame and can be divided in translational (trans) and rotational (rot) components, whereas the RMS-ATE relates to the global consistency of the predicted and the ground truth trajectory. For an in-depth discussion of the used metrics, please refer to [25].

Evaluation on the whole synthetic data (Table 1) shows that EarlyBird has the lowest translational (RMS-RPE trans) as well as rotational relative pose error (RMS-RPE rot), followed by FFT and SlowBird. In terms of ATE SlowBird performed best, followed by EarlyBird and FFT.

Table 1 RPE and ATE for given models evaluated on the synthetic test dataset for different models
Full size table

In “Fig. 8 in Appendix”, the RPE was put in relation to the amount of overlap between image pairs by sorting and dividing the error into three groups of same size and computing the RMS-RPE separately for each tertile. The results show that, independent of the chosen method, the amount of overlap between consecutive image frames has a strong impact on the accuracy of the registration problem and is not distributed equally over all three performance tertiles. This illustrates a short-coming for the usage in incremental motion estimation methods where consistent performance is desired.

An important requirement for a visual odometry system is its functionality on a wide variety of different floor surfaces. Therefore, we analyzed the statistical distribution of RMS-RPE and RMS-ATE according to the different surface images of our test dataset (see Table 2). It can be seen that FFT has the smallest standard deviation (STD) for the translational component of FFT while still performing worse than EarlyBird which has the lowest STD for RMS rot and ATE. An extensive overview over all trajectories can be found in “Table 7 in the Appendix”. Looking at the ATE value for the ORB method, it becomes clear that its performance is not very consistent over different surfaces. For feature rich, highly textured surfaces it performs well, but fails when encountering highly illuminated, featureless images (see “Fig. 7 in Appendix” for an overview over the chosen test surface images).

Table 2 Statistical error distribution for RMS-RPE and RMS-ATE divided according to different surface images
Full size table

In order to test the sensitivity of our models regarding illumination changes or noise in between consecutive image frames, we augmented each image in the test dataset by a random pixel intensity value of \(\beta \in \left( { - 10, 10} \right)\) or added Gaussian distributed white noise (\(\mu = 0\)) for each pixel with \(\sigma^{2} = 4\). From Table 3, it can be seen that FFT and EarlyBird performed best when encountering changing illumination in the video stream. On the dataset with added noise, SlowBird had the lowest RPE and ATE, though having an increased error of 54.6%, 207.4% and 111.8% with regard to the original dataset (see Table 4).

Table 3 RMS-RPE and RMS-ATE evaluated on test dataset with augmented illumination changes
Full size table
Table 4 RMS-RPE and RMS-ATE evaluated on test dataset with added Gaussian distributed noise
Full size table

7.2 Real world experiments

We recorded 19 test trajectories with a differential drive robot going straight, taking turns, moving backward, driving arbitrary loops or circles (see “Table 8 in Appendix” for more details about the chosen trajectories). The recording of the test dataset has been completely independent from our train and evaluation dataset drive. The ground truth trajectory is recorded with a Valve Index VR kit. In a predefined testing area, the controller is globally tracked and therefore not vulnerable to drift. This makes it to a well suited ground truth sensor for odometry systems. For our real world experiments, we are comparing the translational and rotational ATE at the end of each drive ATE(tend). See Fig. 5 for a visualization over a subset of the test trajectories.

Fig. 5
figure 5

Visualization over a subset (12 out of 19 trajectories are shown) of all test trajectories for the real world robot. As it is common with all incremental motion estimation methods, rotational errors generally grow unbounded in lateral position. That is why these methods have such a high demand on rotational accuracy

Full size image

The results on the real world test data (see Table 5) show that SlowBird outperforms FFT, EarlyBird and ORB when considering the ATE(tend) over all test trajectories. The fact that RMSE is very sensitive to outliers suggests that SlowBird is the most consistent method for this dataset. Looking at the high error for the ORB based approach, the results once again confirm the general consent that feature-based methods are not suitable for this use-case.

Table 5 The translational and rotational ATE over all test trajectories
Full size table

Comparing both network architectures, it can be said that our proposed model based on the Early Fusion design principle had the smallest RPE on the synthetic dataset, and our model based on the Slow Fusion design principle performed best considering the absolute trajectory error on synthetic as well as real world data (see Tables 2, 5). Looking at the paths in Fig. 5 and the results in Table 9, it can be observed that FFT is able to predict the correct trajectory very well on a subset of trajectories but does not perform as consistently as SlowBird (higher RMSE) over all trajectories.

Although our proposed networks EarlyBird and SlowBird had the best performance on the synthetic and real world dataset and there is a positive correlation between loss function error and relative pose error (\(\rho_{{{\text{RPEtrans}} - {\text{SSIM}}}} = 0.33 \) and \(\rho_{{{\text{RPErot}} - {\text{SSIM}}}} = 0.42\) evaluated on the synthetic test dataset), it can be observed that very small orientation estimation errors, as they appear in Fig. 6 when driving straight, seem to pass unnoticed by the signal noise (Fig. 6, right) of our proposed SSIM loss function. This may be explained by the weak correlation between rotation error and SSIM value for the first and second tertile. Therefore, for very small rotational errors (mean RPE rot of 1st tertile is 0.0003 rad), it can be assumed that the error cannot be minimized by minimizing the objective function (see Table 6). Since VO systems are in general prone to drift, this illustrates a shortcoming of our currently used loss function.

Fig. 6
figure 6

Estimated SlowBird trajectory for Path 1 (left) and corresponding loss values (right). The crosses illustrate loss outliers of the \(3\sigma\)-intervall. Drift does not necessarily correspond to outliers in the loss signal (e.g. outlier at x = 800 mm in left image)

Full size image
Table 6 The correlation between RPE and SSIM loss value divided into three error tertiles evaluated on our synthetic dataset
Full size table

8 Conclusion

In this work a novel, deep learning based approach to estimate the ego motion of a camera facing the ground is presented. In contrast to many other work, it is independent of the chosen drive type as long as the camera is moving parallel with constant distance to the ground plane. Both proposed network architectures achieved similar and partially better results than the performance of a state-of-the-art FFT image registration method evaluated on synthetic and real world scenarios for a differential drive robot. Especially our proposed SlowBird approach represents a promising alternative to existing methods regarding its performance consistency on both datasets.

Though, in this work, the network weights were fine-tuned for a wooden floor, results on synthetic data demonstrate that both networks can generalize to different floor materials, sudden illumination changes and image noise. With the proposed unsupervised learning strategy, the model weights can be easily and cheaply adapted to alternative ground surfaces and even drive types, no expensive labels are required. We are aware that the currently used SSIM loss function does have its limitations when it comes to rotational accuracy for small errors. Future work should concentrate on alternative loss functions or additional sensors such as IMUs and compasses to compensate for that. Also for future work, it would be interesting to investigate how an online learning approach would be applicable since no ground truth data is required for training.

Despite the aforementioned limitations, our experiments have shown that a deep learning based image registration method, trained completely unsupervised, is over a long series of images accurate enough to become a viable alternative to existing methods. We are aware that our solution is not yet practically and economically feasible, but with current progress in Edge AI, estimating ego motion unsupervised with downward facing cameras might become an interesting use case.