Abstract
Color vision deficiency (CVD) is caused by anomalies in the cone cells of the human retina. It affects approximately 200 million individuals throughout the world. Although previous studies have proposed compensation methods, contrast and naturalness preservation have not been adequately and simultaneously addressed in the state-of-the-art studies. This paper focuses on red–green dichromats’ compensation and proposes a recoloring algorithm that combines contrast enhancement and naturalness preservation in a unified optimization model. In this implementation, representative color extraction and edit propagation methods are introduced to maintain global and local information in the recolored image. The quantitative evaluation results showed that the proposed method is competitive with state-of-the-art methods. A subjective experiment was also conducted and the evaluation results revealed that the proposed method obtained the best scores in preserving both naturalness and information for individuals with severe red–green CVD.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
The human retina contains two kinds of photoreceptors: rod cells and cone cells. The rod cells are sensitive to low-intensity light. In comparison, there are three kinds of cone cells (L, M, and S), which are sensitive to long, medium, and short spectral ranges of visible light, respectively. Cone cells play a crucial role in the formation of color vision. Anomalies occurring in these cells cause color vision deficiency (CVD) and impair the ability of affected individuals to perceive colors. Such disorders prevent people from engaging in some color-related work.
CVD is hereditary, and it cannot currently be treated [1]. It is suggested that CVD can be classified as anomalous trichromacy, dichromacy, and monochromacy, according to alterations of photopigments. Anomalous trichromacy and dichromacy involve one type of altered photopigment and can be divided into protan (L cone), deutan (M cone), and tritan (S cone) deficiencies. Research [1, 2] reports that approximately 200 million individuals suffer from CVD and approximately 99.38% of them are anomalous trichromacy and dichromacy. Both the individuals with protan deficiency and those with deutan deficiency have difficulty distinguishing red and green; therefore, such disorders are typically called red–green CVD. The incidences of red–green CVD for male and female are approximately 5–8% and 0.8%, respectively. Tritan deficiency is rare and only affects approximately 0.003% of the population.
CVD decreases the color gamut of individuals and causes contrast loss in their visual perception. The disorder additionally affects the formation of human cognition to acquired environments. CVD has been reported to influence behaviors, leading to the tendency to ignore low-contrast information. In the digital image research field, contrast is the difference between and inside objects and is considered as the source from which information, such as edges and textures, is generated. Therefore, individuals with CVD are at risk of missing such information. Moreover, the identification of colors contributes to absolute color information recognition. Although the color gamut of CVD is decreased, individuals with protan or deutan deficiencies can identify some colors such as blue and yellow as well as achromatic colors, the same as with the normal. It is essential to maintain these colors if a compensation method is applied.
Through the observation of the natural world, both individuals with normal color vision (trichromats) and those with CVD have cognition to the world and the ability to judge the naturalness, which is also understood as comfortability. Because the original image, especially photograph of natural scene, is supposed to be a copy of the world (considered as natural), deviation from the original image should generally be minimized in recoloring image for CVD compensation. However, the contrast of an image plays a role in constructing global structural information and local information (such as texture). The loss of contrast leads to the loss of such information. To compensate for the contrast loss caused by CVD, a recolored image should preserve contrast information; therefore, it requires a careful balance to enhance contrast and maintain naturalness.
Image recoloring algorithms [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27] have been proposed to compensate for CVD and its resulting loss of contrast. Some of these studies concentrated on contrast enhancing [9,10,11,12,13,14,15,16,17], while others directed more attention to issues of naturalness preservation [18,19,20,21]. Although several studies took both issues into consideration, the existing approaches have limitations, such as relying on user input and limited applicability to some image types [19], loss of contrast and naturalness [17, 20, 21], and being trapped by the local minimum during optimization [18].
In this paper, a new recoloring algorithm that recolors images for red–green dichromats is proposed. Because the two targets (naturalness preservation and contrast enhancement) are contradictory, an optimization model driven by an energy function consisting of error items for both targets is put forward. Objective evaluation metrics were applied to assess the performance of the proposed method. Subjects with red–green CVD simultaneously evaluated the effectiveness of the proposed technique. The objective evaluation results demonstrated that the proposed method is competitive with the state-of-the-art studies and the results of the subjective experiment showed that the proposed method outperforms the state-of-the-art methods in preserving both naturalness and information preservation for individuals with severe red–green CVD.
2 Related works
2.1 Color vision deficiency simulation
Both Meyer et al. [3] and Brettel et al. [4] refer to studies on unilateral dichromats (one eye with trichromacy but the other with dichromacy) [5, 6] and propose dichromacy simulation algorithms by projecting colors perceived by trichromats to the color gamut within the CIE 1960 color space and the LMS color space, respectively. Specifically, the LMS color space is composed of three axes: L, M, and S axes, which represent the responses of the L, M, and S cones. The color gamut of dichromats is modeled as two half-planes by [4] and the simulation result is synthesized by projecting the color in three-dimensional space to the half-plane, along the anomalous axis. Inspired by spectral sensitivity function shift theory [1], Machado et al. [7] adopt a two-stage model [8] and refer to the dichromacy simulation results generated by [4] to simulate trichromacy, anomalous trichromacy, and dichromacy in a unified model. Because it is difficult to accurately calibrate deficiency levels of anomalous trichromacy, this study focuses on compensation for dichromats and adopts the method in [4] for dichromacy simulation.
Along with the widespread use of digital display devices, image processing techniques [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27] for CVD assistance are attracting significant attention. Mainstream research has been conducted to enhance color contrast for users with CVD [9,10,11,12,13,14,15,16,17], and some researchers [22,23,24,25,26,27] have also taken the communication between normal color vision users and CVD users into consideration and proposed methods that enable the sharing of the same contents between normal and CVD users.
2.2 Image recoloring for CVD users
For contrast enhancement, customized parameters have been required by previous work for recoloring webpages [9]. Parameter adjustment interfaces are developed by [10] and [11]. However, user skill affects the quality of the recoloring results of these algorithms. To solve such problems, automatic algorithms have been developed for color discrimination improvement [12] and color distribution adjustment [13]. The effects of compensation are further improved by optimization approaches [14,15,16,17]. Machado et al. [17] enhances the contrast between color pairs and maintains luminance consistency by projecting all colors of an image in the CIE L*a*b* color space to a flat plane, which is obtained by principal component analysis, and then rotating projected colors to dichromatic planes, which are proposed by [18]. Nevertheless, maintaining naturalness has not been taken into account by contrast enhancement algorithms, and loss of naturalness is significant in the results of these works.
For naturalness preservation, the difference between the colors perceived by normal color vision users and those of CVD simulation result is introduced by [18,19,20,21]. Color quantization methods and the mass-spring system are adopted by [18]. They attempt to maintain those colors, which have small difference between the original value and simulation result, by enlarging the mass of them in the mass-spring system. However, the algorithm is easily trapped by the local minimum; the selection principle of method and level of color quantization, which has important influence on results, are not suggested in [18]. Key colors are extracted by [19] from the original image. Besides, those colors are selected as anchor colors if their differences to CVD simulation results are lower than threshold. However, the threshold may filter all key colors out from anchor while at least one anchor color is necessary for the algorithm. Hassan et al. [20, 21] simply add the difference to the blue channel of each pixel without considering the original level of the blue channel as well as the relationship between neighboring pixels. Therefore, the blue channel of pixels with original high values can become saturated and severe contrast loss can occur in area with such pixels.
Despite these problems, [17] and [20] have confirmed their effectiveness in enhancing contrast and preserving naturalness, respectively, compared to [18]. Therefore, this study conducted evaluation experiment involving subjects with red–green CVD to compare the proposed method to [17] and [20].
2.3 Image recoloring for visual sharing
When considering the sharing of visual contents between normal color vision users and CVD users, it is important to avoid visible changes to original images while processing images for better perception by CVD users. Among studies [22,23,24,25] that generate single recolored image from the original one, Huang et al. [22, 23] introduce an error function to mitigate bias, although bias remained significant among normal color vision audiences. In [24] and [25], textures are added to different areas in original images to improve contrast without changing colors; however, both normal color vision audiences and CVD audiences are confused whether the textures are imported one or belong to the original image. The aforementioned issues in visual sharing are well handled by subsequent research using stereo display [26, 27]. Chua et al. [26] and Shen et al. [27] utilize two different experiences of stereo display, namely wearing and not wearing stereo glasses. Their methods synthesize a pair of images from an original one. Normal color vision audiences who do not wear stereo glasses perceive the blending of the paired images, while CVD audiences wearing the glasses are presented with different contrast-enhanced images for left and right eyes.
2.4 Compensating using augmented reality
With the development of augmented reality (AR) technology, approaches in [28] and [29] aim to assist CVD users by mixing the field of view with compensation overlays computed from captured scenes of the real world. Such research mainly focuses on how to reproduce the results of previous CVD compensation algorithms on head-mounted displays rather than putting forward new recoloring methods.
In this paper, a new recoloring algorithm based on [4] for dichromats compensation is proposed. The recoloring procedure is performed on the color gamut of dichromats in the LMS color space. Recoloring procedure is formulated as an optimization problem that takes into consideration both naturalness preservation and contrast enhancement.
3 Proposed method
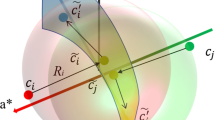
Dichromacy simulation method [4] is adopted to simulate the color perception of dichromats and the color gamut of red–green dichromats is modeled as two half-planes which are illustrated in Fig. 1a. Both protanopes and deuteranopes identify blue and yellow well, and these colors correspond to two types of visible light, namely wavelengths 475 nm (blue) and 575 nm (yellow). These colors are referred as vectors B and Y in the LMS color space, respectively, and are used to construct the half-planes. In addition, responses to achromatic light are introduced as vector W and then the color gamut of red–green dichromats is defined. This allows a color perceived by trichromats to be projected to the two half-planes for simulations of protanopia (along the L axis) and deuteranopia (along the M axis). In other words, except for the anomalous component, the values of the two normal components of color perceived by trichromats remained unchanged after projection. In three-dimensional space, if two colors contain similar values of two normal components, they are projected to nearby positions on the half-planes. As Fig. 1a illustrates, colors \( c_{i} \) and \( c_{j} \) are far from each other in the color space, but in the results of the protanopia simulation, the distance between \( c_{i}^{s} \) and \( c_{j}^{s} \) is very short. Contrast loss occurs in such situation.
Simulation results of two images are illustrated in Fig. 2. Figure 2a, b shows the lotus flowers of different colors. Protanope and deuteranope simulation results of Fig. 2a, b are shown in Fig. 2c–f, respectively. Figure 2 shows the perception difference between protanope and deuteranope. Individuals with protanopia regard the color of lotus flower in image 1 (Fig. 2a) is darker than that of image 2 (Fig. 2b). However, individuals with deuteranopia regard that of image 2 (Fig. 2b) is darker. We utilized such kind of difference to classify protan and deutan deficiencies in Sect. 5.2.
In this paper, all procedures concerning the proposed optimization model are performed in LMS color space and the colors in this space can be represented as three-dimensional vector \( \left( {l,m,s} \right)^{T} \). To compensate contrast loss, image \( I^{c} \) is synthesized from the original image \( I \) via optimization. The dichromacy simulation image of \( I^{c} \) is defined as \( I^{sc} \). The contrast perceived from \( I^{c} \) by dichromats, namely contrast of \( I^{sc} \), is hoped to be as strong as that perceived from \( I \) by trichromats. The optimization procedure for protanopes is illustrated in Fig. 1a, and the view along the anomalous axis (L axis) is shown in Fig. 1b. In Fig. 1, colors \( c_{i}^{s} \) (\( \left( {l_{i}^{s} ,m_{i}^{s} ,s_{i}^{s} } \right)^{T} \)) and \( c_{j}^{s} \) are protanopia simulation results of colors \( c_{i} \)\( \left(\left( {l_{i} ,m_{i} ,s_{i} } \right)^{T}\right) \) and \( c_{j} \). They are moved from their original positions via optimization under the constraints of naturalness preservation and contrast enhancement. \( c_{i}^{sc} \)\( \left( ({l_{i}^{sc} ,m_{i}^{sc} ,s_{i}^{sc} })^{T}\right) \) and \( c_{j}^{sc} \) are simulation results of \( c_{i}^{c} \)\( \left(( {l_{i}^{c} ,m_{i}^{c} ,s_{i}^{c} } )^{T}\right) \) and \( c_{j}^{c} \) in the recolored image. For enhancing global contrast, each color is compared to all other colors in the image. The optimization of contrast enhancement is realized by minimizing the energy function \( E_{\text{cont}} \) below
where \( N \) denotes the number of colors in \( I \), and \( \delta_{ij} \) stands for the modified contrast between colors \( c_{i} \) and \( c_{j} \) in \( I \). \( E_{\text{cont}} \) requires the contrast strength in \( I^{sc} \) to be consistent with that in \( I \). The lost contrast of anomalous component a can only be compensated by modifying the two normal components represented as k. In other words, distributing the lost contrast of a to components k is necessary. In this study, the lost contrast is equally distributed to two normal components: for protanope, \( a = l \), \( k = \{ m,s\} \); for deuteranope, \( a = m \), \( k = \{ l,s\} \); and for tritanope, though it is not implemented in this paper, \( a = s \), \( k = \{ l,m\} \). Components k of the modified contrast, \( \delta_{ij}^{k} \), are thus represented as
where \( v_{i}^{k} \), \( v_{j}^{k} \), \( v_{i}^{a} \), and \( v_{j}^{a} \) denote values of normal and anomalous components of colors \( c_{i} \) and \( c_{j} \) (for protanope, \( v_{i}^{k} \) refers to \( m_{i} \), \( s_{i} \) of \( c_{i} \) and \( v_{i}^{a} \) refers to \( l_{i} \) of \( c_{i} \); for deuteranope, \( v_{i}^{k} \) refers to \( l_{i} \), \( s_{i} \) of \( c_{i} \) and \( v_{i}^{a} \) refers to \( m_{i} \) of \( c_{i} \)) in \( I \), respectively, and \( \alpha_{ij}^{k} \) determines the sign of the components k of contrast \( \delta_{ij}^{k} \) as
In this way, the magnitude consistency of two colors can be preserved after optimization. In other words, given the values of k components, \( v_{i}^{k} \) and \( v_{j}^{k} \), of colors \( c_{i} \) and \( c_{j} \), and those of corresponding components, \( y_{i}^{k} \) and \( y_{j}^{k} \), for colors \( c_{i}^{sc} \) and \( c_{j}^{sc} \) in \( I^{sc} \), if \( v_{i}^{k} \) is smaller than \( v_{j}^{k} \), then \( y_{i}^{k} \) is also smaller than \( y_{j}^{k} \) and vice versa. In the case that \( v_{i}^{k} \) is identical to \( v_{j}^{k} \), the magnitude relation of \( v_{i}^{a} \), \( v_{j}^{a} \) is referred to. Coefficient μ controls the contrast strength of the recolored image. If μ is set to 0.5, contrast strength of the recolored image is identical to that of the original image because the square sum of the normal components k of \( \delta_{ij} \) is identical to that of the three components of \( c_{i} - c_{j} \). To enhance contrast, \( \mu \) can be enlarged, if necessary.
The difference between the result of dichromacy simulation of the original image \( I \) and that of the recolored image \( I^{c} \) is minimized for naturalness preservation. Therefore, image \( I^{sc} \) of the dichromacy simulation for \( I^{c} \) is constrained by image \( I^{s} \) of dichromacy simulation to \( I \). The energy function is represented as
where \( c_{i}^{s} \) denotes the result of the dichromacy simulation of \( c_{i} \). The energy function of contrast pushes \( c_{i}^{sc} \) away from \( c_{i}^{s} \), while naturalness pulls it back (Fig. 1b). Then, two contradictory constraints are put in a unified optimization model by combining two energy functions. The combined energy function of the optimization model is represented as
In this implementation, the weight \( \lambda \) of the naturalness term is set to 1. Setting the partial derivations of \( y_{i}^{k} \) in \( E \) to 0 results in the simultaneous linear equations system below
Bi-Conjugate Gradient (BiCG) iterative method of [30] is adopted to solve the linear equations system. In fact, the values of anomalous component a of the simulation image \( I^{sc} \) are not updated because component a depends on two normal components and can be obtained using the projection method in [4]. Though the contrast of the anomalous component between colors in \( I^{sc} \) is not counted, it does not benefit global contrast enhancement. To obtain the recolored image \( I^{c} \) from the simulation image \( I^{sc} \) and to minimize deviations from the original image \( I \), the values of the anomalous component a of \( I^{sc} \) are moved to the same levels as those of \( I \). In this way, the distance between \( I^{c} \) and \( I \) was shortened as much as possible. Nevertheless, \( I^{c} \) can still be perceived as \( I^{sc} \) by dichromats.
4 Implementation
Because of the requirement of global contrast enhancement, each color is compared with all colors in an image. However, this makes the coefficients matrix of the simultaneous linear equations system non-sparse and memory occupying. For example, if N = 100,000, the coefficient matrix needs 74.5 GB memory space. In fact, an area that looks having uniform color to human may actually consist of a lot of different colors. For example, in Fig. 3, a patch with size 24 × 17 captures a part of flower petal (Fig. 3a). In the patch, there are 216 different values in RGB, but the patch is likely to be perceived to have uniform color pink (Fig. 3b). Although these small color differences are important for representing shading and local texture, more distinct color differences, such as the differences between red and green or between yellow and purple, are usually important for representing global structures. Thus, the size of the coefficients matrix is reduced by grouping similar colors together and selecting a representative color from each group. This procedure is called representative color extraction. Then, after recoloring the representative colors with the proposed optimization procedure, the local information is recovered via the edit propagation method proposed by [31].
K-means clustering [32] and Mean-shift [33] are usually used to divide samples into several clusters, and the centers of the clusters are selected as the representative. Based on k-means clustering, Chang et al. [34] selects color palette from the original image. However, these methods may produce fake representative colors that do not exist in the image. The affinity propagation [35] algorithm extracts existing sample from each cluster but requires users to set the preference parameter.
The dominant color-extracting technique used in Liu et al.’s [36] color to gray algorithm produces a more satisfying result of color feature extraction. In this implementation, a representative color extraction method similar to that of [36] was used to reduce the number of colors for global contrast enhancement.
4.1 Representative color extraction
Representative color extraction reduces the number of color clusters while inhibiting noise. The extraction procedure is illustrated in Fig. 4. As the three channels of the RGB color space [0, 255]3 have homogenous value ranges and are independent from each other, the extraction is performed within this space. It starts with obtaining local peak clusters from the \( I \), referring to the Euclidean distance in the RGB color space (Fig. 4a); the number of clusters is then further reduced via neighboring clusters comparison, which refers to both the color space and image space (Fig. 4b, c). The final process is to compare each cluster to all other clusters, referring to the number of pixels, to reject noise (Fig. 4d).
An extent \( \varPhi_{c}^{r} \) that is centered on color c with a radius r in the RGB color space is used for the local peak cluster extraction. If the color c has the largest number of pixels among the colors within \( \varPhi_{c}^{r} \), then a local peak cluster p centered on c is obtained. All colors are classified to the nearest peak cluster and each peak cluster p contains not only the center color but also its neighboring colors. The center of a cluster never shifts and the number of pixels in p is defined as \( NP_{p} \) and counted as
where c is a color belonging to cluster p, and \( NP_{c} \) denotes the number of pixels with c in the image. Local peak cluster extraction reduces similarities. The distance between colors in the color space is adopted as the extraction principle. However, it is difficult or even impossible to complete extraction for diverse images relying on a constant extent radius. Therefore, the extent radius is continuously enlarged to adapt to various images, until the termination condition is satisfied.
For further cluster reduction, each cluster \( p_{i} \) must be compared to neighboring clusters, such as cluster \( p_{j} \), which is within the enlarged extent of \( p_{i} \). In the comparison of \( p_{i} \) and \( p_{j} \), cluster \( p_{i} \) that is assumed to hold larger pixel number must be reserved and cluster \( p_{j} \) with smaller pixel number is decomposed unless it holds both a certain scale of number of pixels and a certain distance to \( p_{i} \) in pixel distribution. Detailed conditions of the scale and distance are defined as the ratio of pixel numbers of two clusters, \( R_{ij}^{NP} \), and the ratio of distribution distance to the diagonal line \( d = \sqrt {d_{h}^{2} + d_{v}^{2} } \) (\( d_{h} \), \( d_{v} \) denote the width, height of the image, respectively) of the image, \( R_{ij}^{D} \), respectively. Consideration that more is the number of pixels in \( p_{j} \) and farther is the distribution distance, more possible is the \( p_{j} \) reserved, makes both as numerators of the ratios. Thus, two ratios are computed as
where \( NP_{pi} \), \( NP_{pj} \) denote the numbers of pixels of \( p_{i} \), \( p_{j} \), and \( H_{pi} \), \( H_{pj} \) stand for the average coordinates of pixels in \( p_{i} \), \( p_{j} \), which are computed as
where \( q^{co} \)\( \left( {{\mathbf{x}}_{p} ,{\mathbf{y}}_{p} } \right) \) denotes the coordinates (\( {\mathbf{x}}_{p} \): horizontal, \( {\mathbf{y}}_{p} \): vertical) of a pixel with color c in cluster p in the image space. Two ratios are combined by multiplication. With the dilating of the extent of cluster, similarity between clusters diminishes and the reservation condition of cluster \( p_{j} \) decreases as consequence. Therefore, the reciprocal of difference between center colors \( c_{i} \), \( c_{j} \) of clusters \( p_{i} \), \( p_{j} \) is set as the border of abandon and reservation. In other words, if
then \( p_{j} \) is also reserved; otherwise, colors that are originally classified into cluster \( p_{j} \) are assimilated to the nearest reserved clusters. In this implementation, \( \alpha \) was set to 1.
Extent radius r used for local peak cluster extraction starts from 10 and is increased by 10 each round during cluster reduction. For some iterative solution methods of simultaneous linear equations system, such as BiCG method adopted above, difference between two solutions before and after and the maximal iteration number are set as the terminations condition of the iteration. Similar to such iterative method, the dilation of the extent radius is terminated if the numbers of clusters are the same as that of the previous round. At the same time, the upper limit of the extent radius is also adopted. Heckbert et al. [37] considered a difference at approximate 80 in the RGB color space as large enough to discriminate two colors. Therefore, a larger value of 100 is selected as the upper limit of the extent radius.
The last issue concerning representative color extraction is noise rejection. Clusters with very small scales may be reserved as being far from others, but no color feature representative ability. Therefore, a cluster with very small number of pixels less than 1% of that of the largest cluster is treated as noise and rejected. Finally, center colors of reserved peak clusters are chosen as representative colors, RC, of the original image. For the extraction example in Fig. 4, finally, four representative colors were extracted.
Figure 5 illustrates two extraction results of the proposed method and k-means. Figure 5b, g shows the results of k-means and Fig. 5d, i shows those of the proposed method. Figure 5c, e, h, j shows the RC map of Fig. 5b, d, g, i, respectively, where RC map is generated through exchanging the color of each pixel in the original image by its nearest RC. In Fig. 5c, the yellow color was not preserved at the center of the lotus flower, and in Fig. 5h the black boat disappeared, while those are well preserved in Fig. 5e, j.
4.2 Representative color recoloring
With the extracted representative colors, the optimization model in Sect. 3 is revised as
Each representative color is viewed as an important color feature of the original image, and hence uniform weight is assigned to them, though the number of pixels may be different from each other. The simultaneous linear equations system is consequently revised as
The BiCG iterative method is then adopted to solve the revised equations system, and recolored representative colors (RRC) are obtained.
4.3 Representative color diffusion
After the representative colors are recolored in the LMS color space, they are then transformed into CIE L*a*b* color space and are diffused throughout the whole image via edit propagation model in [32].
Chen et al. [32] collects user edits and specifies these edits as diffusion sources. In this paper, user edits are exchanged by RRC. Then, the specified source is propagated via a locally linear embedding (LLE) model [38].
According to the LLE model, a color \( c_{i} \) can be represented by the weighted sum of a set of nearest neighboring colors, \( \Omega _{i} \). The weights are obtained by minimizing the formula below
where \( w_{ij} \) denotes the weight of the jth neighbor color of \( c_{i} \) and is constrained by the formula
Then, obtained weights are used to maintain the local linear structures of neighboring colors while propagating the specified colors via the optimizing model. The energy function of the propagation model is represented as
where \( z_{i} \), \( z_{j} \) denote the results of recoloring colors \( c_{i} \), \( c_{j} \); \( g_{i} \) stands for the recolored representative colors and is specified as the diffusion source. Similar to [32], the propagating optimizing model is also rewritten in a matrix form
where Z denotes the colors after propagation, and I, W are identity and weight matrices, respectively. Diffusion source related matrices \( \varLambda \) and G are defined as
To complete the propagation optimization, the partial derivation of Z is taken to 0 and the equation below is obtained
5 Results and evaluations
5.1 Results
Figures 6 and 7 show two sets of recolored image examples. Each example occupied two rows. The first row of each example showed the original image, results of [17] and [20], and the proposed method, from (a) to (d), respectively. Perceptions to these images by dichromats were simulated by [4] and are shown below to demonstrate the effectiveness of the corresponding methods.
In Fig. 6, the red sun in the original image in Exam. 1 was considered an important feature of the image; however, this feature became very weak in protanopes’ perception (Fig. 6a) because of contrast loss while was almost unperceivable from results of [20] (Fig. 6c). Though the result of the proposed method (Fig. 6d) appears strange to normal color vision viewers, the simulation of the recolored image demonstrated a more brilliant and contrast-enhanced result and the subjects with severe protan deficiency voted it as the most natural among all the four images in the evaluation experiment, which is to be described in 5.2. In Exam. 2, “gray sky” in Fig. 6b led to both naturalness and information loss; the tulips in Fig. 6c were decolorized; for the result of the proposed method (Fig. 6d), the “blue sky” was preserved and the tulips were not decolorized.
In Fig. 7, color difference the lotus and the leaves in Exam. 1 became difficult to be distinguished by deuteranopes (Fig. 7a) and was improved to some extent in the result of [20] (Fig. 7c). Machado et al. [17] (Fig. 7b) enhanced contrast; however, the yellow bud which was perceivable to deuteranopes was recolored to blue. The color difference between the lotus and leaves was more significant and the bud remained yellow in the result of the proposed method (Fig. 7d). Two of the three subjects with severe deutan deficiency voted the result of the proposed method as the most natural. In Exam. 2, though the color of the flower perceived by deuteranopes was different from that perceived by trichromats, the texture of the flower was identifiable to them (Fig. 7a). However, because of the overflow of the blue channel, some areas became homogeneous and texture loss occurred in [20] (Fig. 7c). The proposed method (Fig. 7d) preserved the information well.
5.2 Evaluation experiment
To verify the effectiveness of the proposed method, its results were compared to those of state-of-the-art methods [17, 20] in terms of objective and subjective evaluation experiments.
Objective experiments were performed to measure the naturalness and information preservation in the dichromacy simulation images of the results. Since human’s visual system is more sensitive to the difference, rather than the absolute level of intensity and color, contrast is regarded as an important index of information amount. In [17], a relative contrast metric, root-mean-square (RMS), was proposed; it calculates the contrast difference between the test image and the reference image. However, such a metric may regard an enhanced contrast as a contrast loss. Another contrast metric, the average gradient norm (AGN) proposed in [39], can measure the absolute strength of contrast; it is formulated as follows:
where \( G_{h} (i) \) and \( G_{v} (i) \) denote horizontal and vertical Sobel gradient operators, respectively. The larger the AGN value, the stronger the contrast. The AGN values of both the two state-of-the-art methods and the proposed method are shown in Table 1. The dichromacy simulation results of 10 images, including natural scenes and artificial objects, were used to compute AGN. A portion of the images were selected from the contrast preservation benchmark used in recoloring studies such as color-to-gray [40, 41] and edit propagation [32]. Some images were selected because they are supposed to contain information which is unperceivable based on dichromacy simulation [4]. The average AGN values of the 10 simulated images are also shown in Table 1. The values of the proposed method are higher than those of the existing methods for both protanope and deuteranope.
As discussed in Sect. 1, because the individuals with CVD have perceived the natural world since birth, the original images, especially the photographs of natural scenes (supposed to be copies of the world), are considered as natural; therefore, deviation from the original image should be minimized in recoloring images for CVD compensation. Hassan et al. [20] used a naturalness evaluation metric, which summed \( \parallel c_{i} - c_{i}^{'} \parallel^{2} \) where \( c_{i} \), \( c_{i}^{'} \) denote the colors in the original image and recolored image, respectively, and \( i \) is ith color in the image. A shortcoming of this naturalness evaluation metric is that it does not take the fact that a change to the original image may not lead to a change to the perceptions of individuals with CVD into consideration. For example, deuteranope cannot perceive the change from “purple” to “blue” because both colors are perceived as “blue”. Consequently, for the evaluation of naturalness preservation, the chromatic difference between CVD simulated image of the original image and that of the recolored image are considered.
The results of the naturalness evaluation for the three methods are shown in Table 2. The proposed method obtained the best score for protanope. For deuteranope, the quantitative evaluation results indicate that images synthesized by [20] have a lower naturalness error than those of the proposed method. Subjects with a severe deutan deficiency scored the images recolored by the proposed method as slightly better than those by [20], which will be described subsequently in this section.
A subjective evaluation experiment involving 12 subjects (ages 20 to 50) with red–green CVD (5 protan, 7 deutan) were conducted to evaluate the naturalness and information preservation. Subjects were divided into protan and deutan groups according to the Ishihara Test [42] results and the instance illustrated in Fig. 2. Depending on the results of interviews with subjects regarding how CVD influenced their quality of life, 2 of 5 subjects with protan deficiency and 3 of 7 subjects with deutan deficiency were further classified as severe protan and deutan deficiencies, respectively. They reported that it was difficult to distinguish the colors of traffic lights, which contain red and green. Since their perceptions are comparable to those of dichromats, particular attention was directed to their feedback.
This experiment consisted of two parts. The first evaluated naturalness. The subjects were presented with one set of examples at a time (as with the examples shown in Figs. 6 and 7), but without dichromacy simulation images or method labels; 10 sets of examples were shown. The images were sorted in random order in one set of examples. Both absolute and relative evaluations were performed during the naturalness evaluation. For the absolute naturalness evaluation, subjects determined whether the image was natural or not. For the relative naturalness evaluation, subjects needed to sort the images in order (from the most natural as “1” to the least natural as “4”), including the original image, which was also anonymous to the subjects.
The results of the absolute naturalness evaluation are presented in Tables 3 and 4. The results of the relative naturalness evaluation are presented in Tables 5 and 6.
The average results of the 10 examples evaluated by the subjects with severe CVD for absolute naturalness are shown in Table 3. With the exception of the original images, the average number of times that the proposed method received the label “natural” was the highest for both the protan and the deutan deficiencies. This indicates that the images synthesized by the proposed method were more natural to them than those of the previous studies. The results for the subjects with mild CVD are shown in Table 4. Because the image synthesized by the proposed method can be unnatural to trichromats, these images were likely to receive a less “natural” label from them. The important reason for this is that the subjects with mild CVD reserved a much greater extent of the ability to identify colors like trichromats do. This phenomenon is discussed further in Sect. 6. Among the three methods, the results of [20] were more comparable to the original images and Table 4 shows that they were likely to be evaluated as natural by mild subjects. In those cases, the proposed method’s performance was slightly inferior to that of [20]. For the relative naturalness evaluation results, the average ranks of the three methods are presented in Table 5 (severe CVD) and Table 6 (mild CVD). The lower the number, the better the performance of the method. According to the evaluation by the severe subjects, the proposed method obtained the best scores for both protan and deutan deficiencies among the three methods. The results of the relative naturalness evaluation by the mild subjects were similar to those for the absolute naturalness evaluation.
The results of both the absolute and the relative naturalness evaluations demonstrate that the proposed method performed better than previous studies [17] and [20] for subjects with severe CVD.
The second part of the experiment was the evaluation of the information preservation. Both contrast enhancement and CVD-identifiable information preservation were evaluated. As with the naturalness evaluation, 10 sets of examples were displayed set-by-set to the subjects. In contrast to the naturalness evaluation, the original image of each example in the information evaluation was marked out and the subjects were asked to label the images with tags (“information increased,” “not changed,” and “information decreased”) after comparing the recolored images to the original image. Before the experiment began, the meaning of the tags was explained to the subjects, using examples such as “increased: contrast is enhanced while no incorrect information (for example, blue is recolored to other colors) is induced,” “not changed: almost no change from the original image,” or “decreased: texture on flower petal disappeared.”
The average number of times that each of the three methods received the labels from the severe and mild CVD subjects is listed in Tables 7 and 8. The larger the number of the “increased” label, and the lower the number of the “decreased” label, the better the method performed for increasing information. Among the three methods, the numbers for the “increased” label of the proposed method were largest and the numbers for the “decreased” label were smallest for both severe protan and deutan deficiencies, as shown in Table 7. Because of the contrast enhancement constraint in this optimization model, the proposed method received the largest number of “increased” labels for mild protan and deutan deficiencies (Table 8). From both the naturalness and the information evaluations, the proposed method worked best for severe CVD subjects.
During the experiment, the naturalness preservation evaluation was performed first and the answer sheets for the naturalness preservation evaluation were withdrawn before the information evaluation began. In Tables 1–8, the best scores of the three methods are in bold.
6 Discussion
The subjective experiment results showed inconsistency between severe and mild CVD, especially for naturalness evaluation. For instance, as the example shown in Fig. 8, mild anomalous trichromats or trichromats tended to regard the result synthesized by the proposed method (Fig. 8d) as unnatural. However, when it was presented to the two severe protan deficiency subjects, both of them regarded it as the most natural among four images without any hesitation, and the original image (Fig. 8a) ranked second. Color gamut of dichromats varies from that of trichromats or anomalous trichromats. And color gamut of severe CVD individuals is more approximate to that of dichromats than those of mild ones. This study recolored images within the color gamut of dichromats, and it performed better for subjects with severe CVD. Therefore, it is assumed that if deficiency level or color gamut of anomalous trichromats is calibrated, then the CVD simulation projection method can be exchanged and better compensation results can be provided to them.
In this implementation, the attention is focused on synthesizing optimal recolored result with algorithm trade-off being time efficiency for accuracy. Extracting representative colors from a 640 × 480 image may take approximately 40 s, but it could be accelerated by parallel computation optimization. For the simultaneous linear equation for recoloring representative colors, we can solve it in real time. The edit propagation method adopted in this implementation was not optimal from the view point of speed. Faster method such as [43] has been proposed. However, this method cannot produce deterministic result because it downsizes the user edits by random sampling. What is more, [32] has shown that their method outperformed [43] in propagation accuracy. Therefore, method in [32] is chosen for achieving better recoloring accuracy. Since we could confirm the effectiveness of the proposed method, reducing the processing time, such as by replacing the current edit propagation by faster one, will be our next step.
7 Conclusion
In this paper, a recoloring algorithm for dichromats compensation was proposed and the result of the proposed method was compared with the state-of-the-art works [17, 20] by objective and subjective evaluations. The results of the experiment showed that the proposed method performs the best in naturalness preservation and contrast enhancement for severe red–green CVD and is comparable to the state-of-the-art methods for subjects with mild red–green CVD.
In particular, feedbacks from subjects with anomalous trichromacy showed the necessity of extending the proposed method for individual assistance. For practical application, accelerating the algorithm is also an important future work.
References
Sharpe, L., Stockman, A., Jägle, H., Nathans, J.: Opsin genes, cone photopigments, color vision, and color blindness. In: Gegenfurtner, K.R., Sharpe, L.T. (eds.) Color Vision: From Genes to Perception. Cambridge University Press, Cambridge (1999)
Rigden, C.: The eye of the beholder—designing for colour-blind users. Br. Telecommun. Eng. 17, 2–6 (1999)
Meyer, G.W., Greenberg, D.P.: Color-defective vision and computer graphics displays. IEEE Comput. Graph. Appl. 8(5), 28–40 (1988)
Brettel, H., Viénot, F., Mollon, J.D.: Computerized simulation of color appearance for dichromats. J. Opt. Soc. Am. 14(10), 2647–2655 (1997)
Judd, D.B.: Color perceptions of deuteranopic and protanopic observers. J. Res. Natl. Bur. Stand. 41, 247–271 (1948)
Graham, C.H., Hsia, Y.: Studies of color blindness: a unilaterally dichromatic subject. PNAS 45(1), 96–99 (1959)
Machado, G.M., Oliveira, M.M., Fernandes, L.A.F.: A physiologically-based model for simulation of color vision deficiency. IEEE TVCG 15(6), 1291–1298 (2009)
Judd, D.B.: Fundamental studies of color vision from 1860 to 1960. PNAS 55(6), 1313–1330 (1966)
Iaccarino, G., Malandrino, D., Del Percio, M., Scarano, V.: Efficient edge-services for colorblind users. In: Proceedings of 15th International Conference on World Wide Web, pp. 919–920 (2006)
Jefferson, L., Harvey, R.: Accommodating color blind computer users. In: ACM SIGACCESS Conference on Computers and Accessibility, pp. 40–47 (2006)
Jefferson, L., Harvey, R.: An interface to support color blind computer users. In: SIGCHI Conference on Human Factors in Computer Systems, pp. 1535–1538 (2007)
Ichikawa, M., Tanaka, K., Kondo, S., Hiroshima, K., Ichikawa, K., Tanabe, S., Fukami, K.: Preliminary study on color modification for still images to realize barrier-free color vision. Proc. IEEE Int. Conf. Syst., Man Cybern. 1, 36–41 (2004)
Lau, C., Heidrich, W., Mantiuk, R.: Cluster-based color space optimizations. In: Proceedings of IEEE ICCV, pp. 1172–1179 (2011)
Wakita, K., Shimamura, K.: SmartColor: disambiguation framework for the colorblind. In: ACM Assets, pp. 158–165 (2005)
Rasche, K., Geist, R., Westall, J.: Detail preserving reproduction of color images for monochromats and dichromats. IEEE CGA 25(3), 22–30 (2005)
Rasche, K., Geist, R., Westall, J.: Re-coloring images for gamuts of lower dimension. Eurographics 24, 423–432 (2005)
Machado, G.M., Oliveira, M.M.: Real-time temporal-coherent color contrast enhancement for dichromats. Comput. Graph. Forum 29(3), 933–942. In: Proceedings of EuroVis 2010
Kuhn, G.R., Oliveira, M.M., Fernandes, L.A.F.: An efficient naturalness-preserving image-recoloring method for dichromats. IEEE TVCG 14(6), 1747–1757 (2008)
Huang, C.R., Chiu, K.C., Chen, C.S.: Key color priority based image recoloring for dichromats. In: Proceedings of Pacific-Rim Conference on Multimedia, pp. 637–647 (2010)
Hassan, M.F., Paramesran, R.: Naturalness preserving image recoloring method for people with red–green deficiency. Signal Process. Image Commun. 57, 126–133 (2017)
Hassan, M.F.: Flexible color contrast enhancement method for red–green deficiency. Multidimens. Syst. Signal Process. (2019). https://doi.org/10.1007/s11045-019-00638-7
Huang, J.B., Tseng, Y.C., Wu, S.I., Wang, S.J.: Information preserving color transformation for protanopia and deuteranopia. IEEE Signal Process. Lett. 14(10), 711–714 (2007)
Huang, J.B., Chen, C.S., Jen, T.C., Wang, S.J.: Image recolorization for the colorblind. In: IEEE International Conference on Acoustics, Speech, and Signal Processing, pp. 1161–1164 (2009)
Hung, P., Hiramatsu, N.: A colour conversion method which allows colourblind and normal-vision people share documents with colour content. Technical Report Konica Minolta Tech. Report, Marunouchi (2013)
Sajadi, B., Majumder, A., Oliveira, M.M., Schneider, R.G., Raskar, R.: Using patterns to encode color information for dichromats. IEEE TVCG 19(1), 118–129 (2013)
Chua, S.H., Zhang, H., Hammad, M., Zhao, S., Goyal, S., Singh, K.: Colorbless: augmenting visual information for color-blind people with binocular luster effect. ACM TOCHI 21(6), 32 (2015)
Shen, W., Mao, X., Hu, X., Wong, T.T.: Seamless visual sharing with color vision deficiencies. ACM TOG 35(4), 70 (2016)
Tanuwidjaja, E., Huynh, D., Koa, K., Nguyen, C., Shao, C., Torbett, P., Emmenegger, C., Weibel, N.: Chroma: a wearable augmented-reality solution for color blindness. In: Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing, pp. 799–810 (2014)
Langlotz, T., Sutton, J., Zollmann, S., Itoh, Y., Regenbrecht, H.: ChromaGlasses: computational glasses for compensating colour blindness. In: Proceedings of the 2018 CHI Conference on Human Factors in Computing Systems, p. 390 (2018)
Barrett, R., Berry, M.W., Chan, T.F., Demmel, J., Donato, J., Dongarra, J., Van der Vorst, H.: Templates for the solution of linear systems: building blocks for iterative methods. SIAM, Philadelphia (1994)
Chen, X., Zou, D., Zhao, Q., Tan, P.: Manifold preserving edit propagation. ACM TOG 31(6), 132 (2012)
Lloyd, S.: Least squares quantization in PCM. IEEE Trans. Inf. Theory 28(2), 129–137 (1982)
Chang, H., Fried, O., Liu, Y., DiVerdi, S., Finkelstein, A.: Palette-based photo recoloring. ACM TOG 34(4), 139 (2015)
Cheng, Y.: Mean shift, mode seeking, and clustering. IEEE TPAMI 17(8), 790–799 (1995)
Frey, B.J., Dueck, D.: Clustering by passing messages between data points. Science 315(5814), 972–976 (2007)
Liu, C., Zhu, Z., Wu, M., Zhao, J.: Dominant color detection and grayscale propagation based color2gray method. J. Comput.-Aided Des. Comput. Graph. 28(3), 433–442 (2016)
Heckbert, P.: Color image quantization for frame buffer display. ACM 16(3), 297–307 (1982)
Roweis, S.T., Saul, L.K.: Nonlinear dimensionality reduction by locally linear embedding. Science 290(5500), 2323–2326 (2000)
Gibson, K.B., Nguyen, T.Q.: A no-reference perceptual based contrast enhancement metric for ocean scenes in fog. IEEE TIP 22(10), 3982–3993 (2013)
Gooch, A.A., Olsen, S.C., Tumblin, J., Gooch, B.: Color2gray: salience-preserving color removal. ACM TOG 24(3), 634–639 (2005)
Lu, C., Xu, L., Jia, J.: Contrast preserving decolorization. In: IEEE ICCP, pp. 1–7 (2012)
Ishihara, S.: Tests for colour-blindness. Kanehara Shuppan Co., Tokio (1979)
Li, Y., Ju, T., Hu, S.M.: Instant propagation of sparse edits on images and videos. Comput. Graph. Forum 29(7), 2049–2054 (2010)
Acknowledgements
We thank all the volunteers who helped with the evaluation and for their valuable comments which contributed the improvements of the proposed method. In addition, we are grateful to all reviewers and the editor for their valuable comments.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. This work is supported by JSPS Grants-in-Aid for Scientific Research (Grant No. 17H00738).
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhu, Z., Toyoura, M., Go, K. et al. Processing images for red–green dichromats compensation via naturalness and information-preservation considered recoloring. Vis Comput 35, 1053–1066 (2019). https://doi.org/10.1007/s00371-019-01689-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00371-019-01689-4