Abstract
Non-isometric surface registration, aiming to align two surfaces with different sizes and details, has been widely used in computer animation industry. Various existing surface registration approaches have been proposed for accurate template fitting; nevertheless, two challenges remain. One is how to avoid the mesh distortion and fold over of surfaces during transformation. The other is how to reduce the amount of landmarks that have to be specified manually. To tackle these challenges simultaneously, we propose a consistent as-similar-as-possible (CASAP) surface registration approach. With a novel defined energy, it not only achieves the consistent discretization for the surfaces to produce accurate result, but also requires a small number of landmarks with little user effort only. Besides, CASAP is constrained as-similar-as-possible so that angles of triangle meshes are preserved and local scales are allowed to change. Extensive experimental results have demonstrated the effectiveness of CASAP in comparison with the state-of-the-art approaches.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
With the development of 3D geometry acquisition technology, 3D scanning allows us to capture high-resolution and highly detailed 3D geometries. However, the scanned data are often incomplete or noisy and cannot be used directly. Therefore, plenty of manual efforts are required to create usable and high-fidelity 3D models from scanning data. To deal with this problem, one typical solution is to deform an existing highly crafted character model (template) to fit the scanned data (target). Surface registration as an essential technique to do so has been arousing intensive attentions. The goal of the surface registration is to find a deformation mapping f that transforms the template surface \({\mathcal {S}}\) to the target \({\mathcal {T}}\). The classes of mappings [8] and their corresponding geometrical properties are listed in Table 1.
It can be seen that surface registration is roughly divided into two categories: rigid and non-rigid. Rigid registration is to find a global transformation between two surfaces; however, it cannot handle local transformations. Non-rigid registration is then divided into isometric and non-isometric. Isometric registration aims at finding a set of local rigid transformations but lacks local scalability due to its length-preserving property. Non-isometric registration can be further classified into: equiareal, smooth and similar. Specifically, equiareal registration has scale-preserving property but is unable to address size difference between the template and the target. In contrast, smooth registration based on smoothness regularization is robust to size difference. However, it allows piecewise stretching transformation, which can result in shear distortion and losing template details. Similar registration fits the deformation gradient into a similarity matrix, which is an isotropic scale factor s times a rotation matrix \({\mathbf {R}}\). The scale factor is able to handle size difference, while the rotation matrix part prevents local stretch and distortion. Thus, it has been widely used in methods [21, 30, 32] to align surfaces with different sizes and details. However, the energies they adopt to constrain the local deformation similarity are not consistent. This may tend to produce fold over and self-intersection during transformation. Here, consistent indicates that the discrete energy should converge to the continuous case as the discretization refined.
To our best knowledge, there is no such a surface registration method which takes all the factors mentioned above into consideration. In this paper, we propose a consistent as-similar-as-possible (CASAP) surface registration approach. Given a small number of feature points, CASAP not only is capable of fitting the template to the target with different size and poses, but also preserves the structure of the template well.
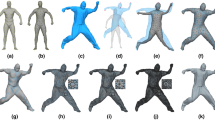
Consistent as-similar-as-possible (CASAP) non-isometric registration. Given a small number of feature correspondences (seven for the head registration and nine for the whole-body registration) only, CASAP not only is capable of fitting the template toward the target with different size (revealed in the whole-body registration example), but also captures the details well (shown in the face registration example) and preserves the structure of the template (seen from the colored wireframe shading mode)
The main contributions of this work are summarized as follows:
-
Introducing local scaling to the rotation in the prior SR-ARAP energy, we propose a novel consistent energy called CASAP energy, which is used to deform surface meshes in an as-similar-as-possible manner. It results in consistent discretization for surfaces and improves the quality of the surface deformation and registration.
-
With CASAP energy as regularization, we further propose a non-isometric surface registration approach. It not only produces more accurate fitting results with requiring little user effort only, but also preserves angles of triangle meshes and allows local scales to change. Furthermore, a coarse-to-fine strategy is proposed to further improve the robustness and efficiency of our approach.
-
Taking local geometrical feature descriptors into account, we propose a matching energy to choose more reasonable correspondent pairs between template and target models.
2 Related works
Over the last two decades, non-rigid registration has been an active research topic [29]. In this paper, we only focus on registration techniques related to our work: isometric registration, smooth registration and similar registration. As the deformation technique is quite essential and critical during registration, influencing the overall geometry quality directly, we will provide a brief summary of these registration methods and their underlying deformation techniques.
Isometric registration approaches aim to preserve the local rigidity of surfaces. Techniques in this class are based on minimizing as-rigid-as-possible (ARAP) energy. The ARAP energy measures the local deviation of the differential of a mapping between two shapes from rigidity. In order to apply this scheme to discretization cases, rigid regularization needs to be enforced on each discrete cell. There are four typical kinds of discrete cell introduced in [14]: triangle, tetrahedron, spokes, and spokes and rims. Apart from all of these cells above, Muller et al. [19] provided a meshless deformation technique, in which the discrete cell is defined as a cluster. The discrete cell adopted in as-rigid-as-possible deformation technique [23] is spokes; however, this method requires the use of a positive weighting scheme to guarantee the correct minimization of the energy. Chao et al. [7] took into account all the opposite edges in the triangles incident to a vertex, and the discrete cell in their work is spokes and rims. Compared with ARAP deformation, this technique is guaranteed to always correctly minimize the energy even if the weights are negative. However, the discretization of [7] is only consistent for volumetric case with tetrahedron cells in 3D or parameterization with triangle cells in 2D, and it is not consistent for the surface case with spokes and rims cells in 3D. In order to come up with a consistent discretization for surface in 3D, Levi et at. [14] introduced a new ARAP-type energy, named SR-ARAP (ARAP with smooth rotations); they add a bending term onto the ARAP energy to enable the discretization consistent. Li et al. [15] achieved isometric registration using the deformation model of [26]. Huang et al. [22] constrained transformations locally as rigid as possible. However, these approaches are incapable of handling surfaces with different sizes since they try to reserve the local rigidity.
Smooth registration techniques are based on harmonic mappings or other smoothness regularizations. Jacobson [10] introduced that the harmonic, biharmonic, triharmonic equations w.r.t. surface displacement fields correspond to minimizers of the Dirichlet, Laplacian, Laplacian gradient energies. Jacobson [10] offered a detailed derivation to obtain a linear system to solve this second-order elliptic partial differential equation. Jacobson et al. [12] used mixed finite elements to provide a discretization for biharmonic and triharmonic equations on meshes. Bounded biharmonic weights are proposed in [11] to minimize the Laplacian energy subject to bound constraints. There are some works [1, 2] based on other smoothness regularization whose purpose are to make the deformation between neighbors as smooth as possible; this idea is similar to the bending term added in [14]. Although these techniques are robust to different sizes, they are too weak to preserve mesh structures against shear distortions because they allow stretch transformations. They require a great number of landmarks to avoid distortion and achieve a desirable result.
Similar registration method is to preserve the local similarity of surfaces; it remains the angle of intersection of every pair of the intersecting arcs unchanged during deformation process. Sorkine et al. [24] offer a linear approximation of similarity matrix to make deformed Laplacian coordinates consistent. However, this method only works well under small rotations as the approximation removes the quadratic term. Thus, it cannot handle large rotation. Yamazaki et al. [30] extended ARAP energy to as-similar-as-possible (ASAP) energy with spokes discrete cells. The work in [21] is a variation of shape matching [19] called similarity shape matching. Although these techniques utilize similar mapping to enable them to address size difference and shear distortion, they do not consider the smoothness regularization, which shows that they are incapable of handling large changes in pose or shape. Yoshiyasu et al. [32] incorporated smooth regularization into the total energy; however, it is a unweighted energy, which does not take into account the impact of the length of edges. Moreover, the discrete cell they adopt is spokes, which leads to an inconsistent energy.
In this paper, we employ spokes and rims discrete cells and incorporate a bending term to produce consistent ASAP energy, allowing us to address large deformation desirably. The experiments demonstrate that the results obtained by our method outperform existing methods.
3 Registration
Given a template surface \({\mathcal {S}}\) and a target one \({\mathcal {T}}\), the goal of surface registration is to deform the surface \({\mathcal {S}}\) into \( {\mathcal {S}}'\) so that \(\mathcal {S'}\) can be sufficiently close to surface \({\mathcal {T}}\) with structure preserved and less distortion. With that purpose in mind, we enforce consistent as-similar-as-possible (ASAP) regularization on the template surface when we are attracting it to the target. Let \(\mathbf {p}, \mathbf {p}',\mathbf {q}\) denote the vertex positions on surface \({\mathcal {S}},{\mathcal {S}}',{\mathcal {T}}\) respectively; we define the cost function as
where \(E_{d}\) constrains deformation ASAP consistently, \(E_c\) penalizes distances between the points of template and their correspondences on the target, and \(E_f\) penalizes distances between the feature points of template and target surface. The weights before these energy terms adjust the influence they account for in total energy. In the next subsections, we introduce each energy term, respectively.
3.1 Consistent ASAP Energy
Assuming we are deforming a mesh \({\mathcal {S}}\) into \({\mathcal {S}}'\) with the same connectivity as similar as possible, the piecewise linear geometric embedding of \({\mathcal {S}}\) is defined by the vertex positions \(\mathbf {p}_i \in {\mathbf {R}}^3\), which is deformed into a different geometric embedding \(\mathbf {p}'_i\). Given the cell \({\mathcal {C}}_i\) on mesh \({\mathcal {S}}\) corresponding to vertex i, and its deformed version \({\mathcal {C}}'_i\) on mesh \({\mathcal {S}}'\), we define the approximate similar transformation between the two cells. Unlike [23, 30, 32] regarding spokes as the cell, the cell chosen in our paper is spokes and rims (denoted as \(\mathcal {E}_i\)) in order to arrive at an analyzable energy [7]. If the deformation \({\mathcal {C}}_i \rightarrow {\mathcal {C}}'_i\) is similar, then there exists a scale factor \(s_i > 0\) and a rotation matrix \({\mathbf {R}}_i\) such that
where \(\mathcal {E}_i\) consists of the set of edges incident to vertex i (the spokes) and the set of edges in the link (the rims) of vertex i in the surface mesh \({\mathcal {S}}\). When the deformation is not similar, we can still find the best approximating scale factor \(s_i\) and rotation \({\mathbf {R}}_i\) by minimizing a weighted cost function
where \(w_{jk}\) are edge weighting coefficients. We chose the cotangent weights for \(w_{jk}\) as they make our deformation energy mesh-independent [17].
In order to measure the similarity of a deformation of the whole mesh, we sum up over the deviations from similarity per cell which yields us following ASAP energy functional:
However, according to [7], the analyzable ASAP energy we obtained so far is not consistent yet. In fact, the resulting ASAP energy differs from the continuous one by a bending term. Inspired by [14], we incorporate the smooth regularization into (4) leading us to a consistent ASAP energy:
where \({\mathcal {N}}({\mathcal {E}}_i)\) are the neighboring cells of \({\mathcal {E}}_i\); \(\alpha \) is a weighting coefficient; A is the area of the whole mesh surface, which is used to make the energy scale invariant; \(w_{il}\) are scalar weights; and \(\Vert \cdot \Vert _F\) denotes the Frobenius norm. Although using 1 for \(w_{il}\) usually gets compelling results, we still chose cotangent weights for \(w_{il}\) for constructing consistent energy. The second term \(E_b\) we add is the bending energy [14], which penalizes the similarity difference between a cell and its neighboring cells. In this way, we have made up the missing bending energy in ASAP energy to form a consistent one (Fig. 2).
3.2 Correspondence constraints
In order to attract points on the template toward the target, we need to find their correspondent vertices on the target surface. Many works [9, 30, 32] regard the closest points as goal positions; however, correspondences chosen by these approaches are not quite appropriate as they only consider distances between the closest points of template and target surface. Inspired by [21, 22], we concern feature descriptors and smooth factor additionally. Starting from the closest points on the target, we then flood over their neighbors to find out the smallest matching energy points until converge. We define matching energy \(E_m\) between points of the template and the target as
where \(\mathbf {p}_i\) is vertex i on template surface and \(\mathbf {q}_j\) is vertex j on target surface; the feature descriptors distance is defined as \(d_f(\mathbf {p}_i, \mathbf {q}_j)=f(\mathbf {p}_i)-f(\mathbf {q}_j)\), where f(v) is the feature vector for vertex v, we concatenate all feature descriptors into a single feature vector; the mean value distance \(\overline{d_f(\mathbf {p}_i, \mathbf {q}_j)} = \frac{1}{|{\mathcal {N}}(j)|+1}\sum _{k \in {\mathcal {N}}(j)\cup j}d_f(\mathbf {p}_i, \mathbf {q}_k)\), where \({\mathcal {N}}(j)\) is the 1-ring neighbors of vertex j on the target surface.
There is a great number of feature descriptors that characterize the geometric properties of the point or of its neighborhood, often in a multi-scale way, for example various notions of curvature (Gaussian, mean) [17], diffusion-based descriptors, such as the heat or wave kernel signatures [3, 27], or more classical descriptors such as spin images or shape contexts [4, 13]. In our experiment we concatenate vertex position, vertex normal, multi-scale mean curvatures [20], wave kernel signatures [3] and scale-invariant heat kernel signatures [6] to form a feature vector.
In order to prevent unnecessary matchings, we filter out the pairs if the distance between them exceeds D or if the angle between their normals exceeds a threshold \(\varTheta \). Thus, the algorithm of finding correspondence \(\mathbf {q}_{\text {idx}(i)}\) on the target surface for each point on the template can be summarized as Algorithm 2, where \(\text {idx}(i)\) is the index of the target point that is matched with template vertex i.

After given the correspondence of template vertices, the template surface can be attracted toward the target according to the matching pairs. However, in order to avoid extreme distortion in tangential space, rather than attracting the template points to their correspondences directly, we attract them to the projections of their correspondences on their normals denoted by \(Proj(\mathbf {q}_{\text {idx}(i)})\) (Fig. 3). Now the correspondent constraint energy in (1) can be expressed as
where \(\mathbf {p}', \mathbf {q}\) are the vertex positions on surface \({\mathcal {S}}',{\mathcal {T}}\), respectively, and \({\mathbf {C}}_c, {\mathbf {D}}_c\) are the sparse matrices that define the filtered matching correspondences between \({\mathcal {S}}'\) and \({\mathcal {T}}\). Assuming the mth correspondence is \(\mathbf {p}_i\) on \({\mathcal {S}}'\) and \(\mathbf {q}_{\text {idx}(i)}\) on \({\mathcal {T}}\), then
\(\mathbf {q}_j\) is the closest vertex on the target to \(\mathbf {p}_i\); \(\mathbf {q}_{\text {idx}(i)}\) is the correspondent vertex found by minimizing the matching energy; \(\mathbf {n}\) is the normal vector of \(\mathbf {p}_i\); \(Proj(\mathbf {q}_{\text {idx}(i)})\) is the projection of \(\mathbf {q}_{\text {idx}(i)}\) onto normal vector \(\mathbf {n}\)
3.3 Feature point constraints
For the fitting of the template’s pose and size to the target, several feature correspondences are required to be established. Feature point constrains are designed to drag feature points on the template toward corresponding target ones. This constraint energy can be represented as
where \({\mathbf {C}}_f, {\mathbf {D}}_f\) are the sparse matrices that define the feature point pairs between \({\mathcal {S}}'\) and \({\mathcal {T}}\).
3.4 Optimization
In this subsection, we introduce the optimization algorithm to minimize the total energy in (1). There are two loops in the optimization: the outer loop searches for the correspondent vertices to construct \(E_c\), the inner loop optimizes the deformed vertex positions by minimizing \(E(\mathbf {p}')\). Once the inner loop is converged, weights are adjusted and a new outer iteration starts again. Note that in the inner loop except the vertex positions \(\mathbf {p}_i\) are unknown, \(s_i\) and \({\mathbf {R}}_i\) in (5) are also unknown for each vertex. We employ the alternating optimization scheme following [14, 23, 30] to solve them, respectively. Each inner iteration consists of a local step followed by a global step. In local step, we optimize \(s_i\) and \({\mathbf {R}}_i\) with \(\mathbf {p}'_i\) fixed. By contrast, \(\mathbf {p}'_i\) are optimized with \(s_i\) and \({\mathbf {R}}_i\) fixed in global step.
\(\mathbf{Local }\) \(\mathbf{ step }\) In this step, \(\mathbf {p}'_i\) are fixed, and then, we solve \({\mathbf {R}}_i\), \(s_i\) in sequence to construct consistent ASAP energy (5). For convenience, let us denote the edge \(\mathbf {e}_{jk}:=\mathbf {p}_j-\mathbf {p}_k\) and \(\mathbf {e}'_{jk}:=\mathbf {p}'_j-\mathbf {p}'_k\). Then, we can change the formula (5) for cell i as
First we solve for optimal rotation \({\mathbf {R}}_i\). Extending the equation (9) and dropping the terms that do not contain \({\mathbf {R}}_i\), we are remained with
where \({\mathbf {S}}_i\) is defined as
Following [23], we derive the optimal rotation \({\mathbf {R}}_i\) from the singular value decomposition of \({\mathbf {S}}_i = {\mathbf {U}}_i\mathbf \Sigma _i{\mathbf {V}}_i^T\):
If \(\det ({\mathbf {R}}_i)<0\), then the sign of the column of \({\mathbf {U}}_i\) corresponding to the smallest singular value will be changed.
Then, we compute scale factor \(s_i\). Since the second term in (9) is independent of \(s_i\), we only extend the first term and divide extended terms by \(s_i\)
Taking derivative (12) w.r.t. \(s_i\) and letting the derivative to be zero yields
\(\mathbf{Global }\) \(\mathbf{ step }\) In this step, vertex positions \(\mathbf {p}'_i\) are optimized from \(s_i, {\mathbf {R}}_i\) obtained by the local step. We first introduce the optimization of consistent ASAP energy (5) as it is a part of total energy and the only part dependent on \(s_i, {\mathbf {R}}_i\). After minimizing this energy, the optimization of total energy will be obvious.
Taking partial derivative of (5) w.r.t. the position \(\mathbf {p}'_i\) (note that the second term has nothing to do with \(\mathbf {p}'_i\)), we arrive at
where \({\mathcal {N}}(i)\) is one-ring neighbors of vertex \(\mathbf {p}'_i\); \(s_m, s_n\) and \({\mathbf {R}}_m, {\mathbf {R}}_n\) are the scalar factors and rotation matrices of the vertices \(\mathbf {p}_m, \mathbf {p}_n\) which are the opposite vertices of the edge \(\mathbf {e}_{ij}\). Setting partial derivative (14) to zero gives the following sparse linear system of equations:
Notice that the linear combination on the left-hand side is the discrete Laplace–Beltrami operator applied to \(\mathbf {p}'\). Now the system of equations can be reduced as \({\mathbf {L}}\mathbf {p}' = \mathbf {d}\), where \({\mathbf {L}}\) represents the discrete Laplace–Beltrami operator, which only depends on the initial mesh; thus, it can be pre-factored for efficiency; \(\mathbf {d}\) is given by the right-hand side of (15).
Now let us take back to the total energy (1); taking derivative of it w.r.t. \(\mathbf {p}'\) gives us a linear system:
where
Up to now, the routine of consistent ASAP surface registration can be summarized as Algorithm 2.

4 Coarse-to-fine fitting strategy
In this section, we discuss the details of fitting the template. To improve the efficiency and robustness of registration, we take a coarse-to-fine fitting strategy. Instead of fitting overall template surface from the beginning, a coarse mesh is extracted from the original template mesh and then fitted to several feature points to roughly adjust the overall size of the template. In this way, approximated goal positions are obtained which is a better initial guess of fine fitting leading to fast converge and it also reduces the fold over occurrence. Afterward, a dense mesh is rebuilt from the deformed coarse mesh, and fine fitting step is performed to produce the final result.
Surface registration algorithm overview: a Sampled points (marked as yellow dots) via farthest point sampling technique; b remeshing from the sampled points as embedded coarse mesh; c input of target surface; d the feature points specified by users (red dots for target and cyan dots for template); e coarse fitting; f mid-scale fitting; g reconstructed through embedded deformation; h fine fitting
4.1 Fitting steps
There are four fitting steps: initialization, coarse fitting, mid-scale fitting and fine fitting:
\(\mathbf{Initialization }\) In this step, a coarse mesh is extracted from the template first. We employ the farthest point sampling approach [18] to sample certain number of vertices to represent the shape of objects approximately (Fig. 4a). Note that all of the sampled vertices are the subset of the original vertex set. Then, the geodesic remeshing technique [28] is used to generate the coarse mesh from the sampled points (Fig. 4b).
\(\mathbf{Coarse }\) \(\mathbf{ fitting }\) We utilize the similarity constraints and feature point constraints to fit the coarse mesh to several feature points on the target so that the size and post of the template are roughly adjusted to the target (Fig. 4e).
\(\mathbf{Mid-scale }\) \(\mathbf{ fitting }\) After fitting the template roughly to the target using feature points, the coarse mesh is deformed gradually toward the target. Apart from the two constraints adopted in the first step, correspondence constraints are also applied to achieve template attraction (Fig. 4f).
\(\mathbf{Fine }\) \(\mathbf{ fitting }\) In this stage, a dense mesh is first reconstructed from the deformed coarse mesh by embedded deformation [26] (Fig. 4g). The extracted coarse mesh is considered as deformation graph laid under the dense mesh. From formulas (13) and (11), we associate an affine transformation with each vertex in the coarse graph. The deformed positions of vertices in the dense mesh can be calculated from the transformations of the deformation graph. We use the same approach as [32] to rebuild the dense mesh. Again, all the constraints are performed to fit the dense mesh to the target (Fig. 4h).
4.2 Weights and parameters
In the initialization step, we regard the feature point constraints as boundary condition to induce deformation. In next two steps, we set \(D = 0.02r_{box}\) and \(\varTheta = 90^\circ \), where \(r_{box}\) is the bounding box diagonal. As for the weights in the linear system (16), we use \(w_{d} = 1000\), \(w_{c} = 5\), \(w_{f} = 10^5\) in the coarse fitting stage and divide \(w_{d}\) by 1.1 after every iteration until it is less than 1. In the fine fitting, we take the same procedure with \(w_f = 1\).
5 Experiments and results
We tested our algorithm on various surfaces. For surface deformation, the data (cylinder and bar) in [5] are adopted. We show twist and translation deformation on these meshes in Fig. 5. For surface registration, we use the human head mesh, 3D face scanning, the human body and animal models which are from SCAPE, TOSCA data sets. All the algorithms are implemented in MATLAB, and all the statistics are measured on an Intel Xeon E5 3.4 GHz 64-bit workstation with 16GB of RAM.
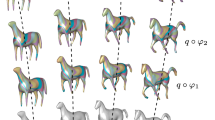
Generic models We apply CASAP registration technique to register from one human head with holes to a face scanning from another human (Fig. 1); from a human body to a gorilla (Fig. 1, 4); and from a pig to a horse (Fig. 6). Each pair has large difference on size or details. CASAP not only is able to handle size difference as shown in whole-body registration example in Fig. 4, but also can capture geometrical details such as the human expression (Fig. 1) and preserve the connectivity of the template well, thus reducing the risk of producing fold over (Figs. 1, 6).
\(\mathbf{Comparisons }\) We first compare our consistent as-similar-as-possible (CASAP) deformation approach with other three deformation methods (ARAP [23], SR-ARAP [14] and ASAP [30]) in Fig. 5. The result of ARAP is not satisfying because its energy is not consistent. SR-ARAP overcomes the weakness of ARAP, offering a consistent discretization. However, it cannot handle local scalability. ASAP allows piecewise scale, but its energy is not consistent, which may lead to undesirable results such as fold over and self-intersection. CASAP combines the benefits of ASAP with the advantages of the SR-ARAP approach such that it can not only handle local scale but also guarantees the deformation smoothness. It produces consistent discretization for surfaces, which enables it to generate competitive results as SR-ARAP does when processing isometric deformation (seen from the twisted bars). Figure 2 shows the advantages of our consistent energy.
We then compare our registration technique to other state-of-the-art algorithms: as-conformal-as-possible surface registration (ACAP) [32], similarity-invariant shape registration (ASAP) [30], the embedded deformation technique (ED) [26], the shape matching-based registration technique that minimizes the as-similar-as-possible energy (SM-ASAP) [21], the Laplacian surface editing technique (LSE) [24] and the registration technique that utilizes the point-based deformation smoothness regularization (PDS) [2] in Fig. 6. ACAP employs nonlinear conformal stiffness and regularization terms in registration process, which produces the closest results to CASAP. However, since the regularization energy it adopts is not consistent, fold overs still occur around the left wrist of gorilla and the neck of horse. ASAP and SM-ASAP do not require specifying feature points, but they are only able to handle surfaces with close initial alignment and similar poses. ED is an isometric counterpart of ACAP. As it cannot adjust local scale, ED may produce poor initial shape estimation, which makes parts of surface converge to inaccurate places as shown at the right leg of gorilla. LSE cannot handle large deformation as it use a linear approximation of similar transformation. PDS is based on smoothness regularization, but it is too weak against shear distortions. Only CASAP exhibits no fold over and almost no distortion in the examples, which produce quite pleasant visual results.
From the perspective of quantitative evaluation, following the same criterion as in [32], we measure 1) distance error, which is the average distance from the vertices of the deformed template to the corresponding points of the target relative to the bounding box diagonal, 2) angle error, which is the average angle deviation from the template, 3) bending error, which is the average deviation in dihedral angles from the template, 4) intersection error, which is the number of self-intersecting faces. These statistics can be found in Table 2. All the errors of CASAP are the smallest among all the techniques except the bending error in horse example, which is because of the LSE’s disability of handling large rotations. The number of self-intersecting faces is zero, which reveals the ability of CASAP to reduce the change in fold over and shear distortion appearance.
The number of iteration steps and timings are shown in Table 3. The time required for a single inner iteration of CASAP is minimum. Although it requires more iteration steps than ACAP to converge, the total registration time it spends is less than ACAP.
Number of feature points required Previous methods [25, 31] require specifying 20–70 feature points, whereas our technique requires less than 20 points: 7 for the face registration (Fig. 1), 9 for the whole-body registration(Figs. 1, 4), 15 for registration from pig to horse (Fig. 6)). That is because CASAP provides a good initial shape approximation, and the consistent energy preserves the template structure and angles well.
\(\mathbf{Limitation }\) Although our consistent ASAP deformation technique and the coarse-to-fine strategy can efficiently reduce the chance of fold over, it cannot solve this issue, especially for model with large curvature. An easy solution is to add more feature points around the fold overs and adjust the position of them to achieve better result. Other methods such as fold over removing technique [31] or bounded distortion mapping [16] can also be utilized to solve this issue.
Another limitation is that we cannot achieve automatic registration. Therefore, the quality of the feature points specified by users will directly influence the registration result.
6 Conclusion
We have presented a novel surface registration approach (CASAP) that constrains deformations locally as similar as possible. With the proposed consistent regularization energy, CASAP not only results in consistent discretization for surface but also reduces the occurrence of fold over and shear distortion. Experiments have shown that CASAP produced more accurate fitting results and preserved angles better than previous methods.
In the future, we will attempt to avoid the occurrence of fold over completely during transformation to make the registration procedure more robust. In addition, if the feature points are detected accurately between the template and the target on different size, automatic registration will be achieved without any user intervention. These would also be a quite appealing research direction.
References
Allen, B., Curless, B., Popović, Z.: The space of human body shapes: reconstruction and parameterization from range scans. In: ACM Transactions on Graphics (TOG), 22, pp. 587–594. ACM (2003)
Amberg, B., Romdhani, S., Vetter, T.: Optimal step nonrigid icp algorithms for surface registration. In: 2007 IEEE Conference on Computer Vision and Pattern Recognition, pp. 1–8. IEEE (2007)
Aubry, M., Schlickewei, U., Cremers, D.: The wave kernel signature: a quantum mechanical approach to shape analysis. In: Computer Vision Workshops (ICCV Workshops), 2011 IEEE International Conference on, pp. 1626–1633. IEEE (2011)
Belongie, S., Malik, J., Puzicha, J.: Shape matching and object recognition using shape contexts. IEEE Trans. Pattern Anal. Mach. Intell. 24(4), 509–522 (2002)
Botsch, M., Sorkine, O.: On linear variational surface deformation methods. IEEE Trans. Vis. Comput. Gr. 14(1), 213–230 (2008)
Bronstein, M.M., Kokkinos, I.: Scale-invariant heat kernel signatures for non-rigid shape recognition. In: Computer Vision and Pattern Recognition (CVPR), 2010 IEEE Conference on, pp. 1704–1711. IEEE (2010)
Chao, I., Pinkall, U., Sanan, P., Schröder, P.: A simple geometric model for elastic deformations. ACM Trans. Gr. (TOG) 29(4), 38 (2010)
Floater, M.S., Hormann, K.: Surface parameterization: a tutorial and survey. In: Advances in Multiresolution for Geometric Modelling, pp. 157–186. Springer (2005)
Gilles, B., Reveret, L., Pai, D.: Creating and animating subject-specific anatomical models. In: Computer Graphics Forum, vol. 29, pp. 2340–2351. Wiley Online Library (2010)
Jacobson, A.: Algorithms and interfaces for real-time deformation of 2d and 3d shapes. Ph.D. thesis (2013)
Jacobson, A., Baran, I., Popovic, J., Sorkine, O.: Bounded biharmonic weights for real-time deformation. ACM Trans. Graph. 30(4), 78 (2011)
Jacobson, A., Tosun, E., Sorkine, O., Zorin, D.: Mixed finite elements for variational surface modeling. In: Computer Graphics Forum, 29, pp. 1565–1574. Wiley Online Library (2010)
Johnson, A.E., Hebert, M.: Using spin images for efficient object recognition in cluttered 3d scenes. IEEE Trans. Pattern Anal. Mach. intell. 21(5), 433–449 (1999)
Levi, Z., Gotsman, C.: Smooth rotation enhanced as-rigid-as-possible mesh animation. IEEE Trans. Vis. Comput. Gr. 21(2), 264–277 (2015)
Li, H., Sumner, R.W., Pauly, M.: Global correspondence optimization for non-rigid registration of depth scans. In: Computer Graphics Forum, 27, pp. 1421–1430. Wiley Online Library (2008)
Lipman, Y.: Bounded distortion mapping spaces for triangular meshes. ACM Trans. Gr. (TOG) 31(4), 108 (2012)
Meyer, M., Desbrun, M., Schröder, P., Barr, A.H.: Discrete differential-geometry operators for triangulated 2-manifolds. In: Visualization and Mathematics III, pp. 35–57. Springer (2003)
Moenning, C., Dodgson, N.A.: Fast marching farthest point sampling (2003)
Müller, M., Heidelberger, B., Teschner, M., Gross, M.: Meshless deformations based on shape matching. ACM Trans. Gr. (TOG) 24(3), 471–478 (2005)
Panozzo, D., Puppo, E., Rocca, L.: Efficient multiscale curvature and crease estimation. In: Proceedings of Computer Graphics, Computer Vision and Mathematics (Brno, Czech Rapubic 1(6) (2010)
Papazov, C., Burschka, D.: Deformable 3d shape registration based on local similarity transforms. In: Computer Graphics Forum, vol. 30, pp. 1493–1502. Wiley Online Library (2011)
Qixing, H., Adams, B., Wicke, M., Guibas, L.: Non-rigid registration under isometric deformations. In: Computer Graphics Forum, 5 North Holland (2008)
Sorkine, O., Alexa, M.: As-rigid-as-possible surface modeling. In: Symposium on Geometry processing, vol. 4 (2007)
Sorkine, O., Cohen-Or, D., Lipman, Y., Alexa, M., Rössl, C., Seidel, H.P.: Laplacian surface editing. In: Proceedings of the 2004 Eurographics/ACM SIGGRAPH symposium on Geometry processing, pp. 175–184. ACM (2004)
Sumner, R.W., Popović, J.: Deformation transfer for triangle meshes. ACM Trans. Gr. (TOG) 23(3), 399–405 (2004)
Sumner, R.W., Schmid, J., Pauly, M.: Embedded deformation for shape manipulation. In: ACM Transactions on Graphics (TOG), 26, p. 80. ACM (2007)
Sun, J., Ovsjanikov, M., Guibas, L.: A concise and provably informative multi-scale signature based on heat diffusion. In: Computer graphics forum, 28, pp. 1383–1392. Wiley Online Library (2009)
Surazhsky, V., Surazhsky, T., Kirsanov, D., Gortler, S.J., Hoppe, H.: Fast exact and approximate geodesics on meshes. In: ACM Transactions on Graphics (TOG), 24, pp. 553–560. ACM (2005)
Van Kaick, O., Zhang, H., Hamarneh, G., Cohen-Or, D.: A survey on shape correspondence. In: Computer Graphics Forum, 30, pp. 1681–1707. Wiley Online Library (2011)
Yamazaki, S., Kagami, S., Mochimaru, M.: Non-rigid shape registration using similarity-invariant differential coordinates. In: 2013 International Conference on 3D Vision-3DV 2013, pp. 191–198. IEEE (2013)
Yeh, I.C., Lin, C.H., Sorkine, O., Lee, T.Y.: Template-based 3d model fitting using dual-domain relaxation. IEEE Trans. Vis. Comput. Gr. 17(8), 1178–1190 (2011)
Yoshiyasu, Y., Ma, W.C., Yoshida, E., Kanehiro, F.: As-conformal-as-possible surface registration. In: Computer Graphics Forum, 33, pp. 257–267. Wiley Online Library (2014)
Acknowledgements
Open access funding provided by Bournemouth University.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Jiang, T., Qian, K., Liu, S. et al. Consistent as-similar-as-possible non-isometric surface registration. Vis Comput 33, 891–901 (2017). https://doi.org/10.1007/s00371-017-1390-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00371-017-1390-9