NeuFENet: neural finite element solutions with theoretical bounds for parametric PDEs

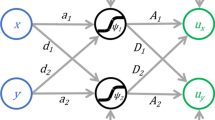
Abstract

We consider a mesh-based approach for training a neural network to produce field predictions of solutions to parametric partial differential equations (PDEs). This approach contrasts current approaches for “neural PDE solvers” that employ collocation-based methods to make pointwise predictions of solutions to PDEs. This approach has the advantage of naturally enforcing different boundary conditions as well as ease of invoking well-developed PDE theory—including analysis of numerical stability and convergence—to obtain capacity bounds for our proposed neural networks in discretized domains. We explore our mesh-based strategy, called NeuFENet, using a weighted Galerkin loss function based on the Finite Element Method (FEM) on a parametric elliptic PDE. The weighted Galerkin loss (FEM loss) is similar to an energy functional that produces improved solutions, satisfies a priori mesh convergence, and can model Dirichlet and Neumann boundary conditions. We prove theoretically, and illustrate with experiments, convergence results analogous to mesh convergence analysis deployed in finite element solutions to PDEs. These results suggest that a mesh-based neural network approach serves as a promising approach for solving parametric PDEs with theoretical bounds.

Appendices

Appendix 1: Representation of random diffusivity

With $\omega$ taken from the sample space $\Omega$, the diffusivity/permeability $\nu$ can be written as an exponential of a random quantity Z

$$\begin{aligned} \nu = \exp \left( Z({\textbf{x}}; \omega ) \right) . \end{aligned}$$

(46)

We assume that Z is square integrable, i.e., $\mathbb {E}\left[ |Z({\textbf{x}}; \omega )|^2 \right] < \infty$. Then, we can write Z using the Karhunen–Loeve expansion [68], as

$$\begin{aligned} Z({\textbf{x}}; \omega ) = {\bar{Z}}({\textbf{x}}) + \sum _{i = 1}^{\infty } \sqrt{\lambda _i}\phi _i({\textbf{x}})\psi _i(\omega ), \end{aligned}$$

(47)

where ${\bar{Z}}({\textbf{x}}) = \mathbb {E}(Z({\textbf{x}}, \omega ))$, and $\psi _i(\omega )$ are independent random variables with zero mean and unit variance. $\lambda _i$ and $\phi _i({\textbf{x}})$ are the eigenvalues and eigenvectors corresponding to the Fredholm equation

$$\begin{aligned} \int _D C_Z({\textbf{s}},{\textbf{t}})\phi (s)\textrm{d}s = \lambda \phi ({\textbf{t}}), \end{aligned}$$

(48)

where $C_Z(s,t)$ is the covariance kernel given by,

$$\begin{aligned} C_Z({\textbf{s}}, {\textbf{t}}) = \sigma _z^2 \exp \left( -\left[ \frac{s_1-t_1}{\eta _1}+\frac{s_2-t_2}{\eta _2}+\frac{s_3-t_3}{\eta _3} \right] \right) , \end{aligned}$$

(49)

where $\eta _i$ is the correlation length in the $x_i$ coordinate. This particular form of the covariance kernel is separable in the three coordinates, thus the eigenvalues and the eigenfunctions of the multi-dimensional case can be obtained by combining the eigenvalues and eigenfunctions of the one-dimensional covariance kernel given by:

$$\begin{aligned} C_Z(s,t) = \sigma _Z^2\exp \left( -\frac{s-t}{\eta }\right) , \end{aligned}$$

(50)

where $\sigma _Z$ is the variance and $\eta$ is the correlation length in one-dimension.

Equation 46 can then be written as

$$\begin{aligned} {\tilde{\nu }}({\textbf{x}}; \omega )&= \exp \left( \sum _{i = 1}^{m} a_i \sqrt{\lambda _{xi}\lambda _{yi}} \phi _i(x)\psi _i(y) \right) , \end{aligned}$$

(51)

where $a_i$ is an m-dimensional parameter, $\lambda _x$ and $\lambda _y$ are vectors of real numbers arranged in the order of monotonically decreasing values; and $\phi$ and $\psi$ are functions of x and y, respectively. $\lambda _{xi}$ is calculated as

$$\begin{aligned} \lambda _{xi} = \frac{2\eta \sigma _x}{(1+\eta ^2 \omega _x^2)}, \end{aligned}$$

(52)

where $\omega _x$ is the solution to the system of transcendental equations obtained after differentiating Eq. 48 with respect to ${\textbf{t}}$. $\lambda _{yi}$ are calculated similarly. $\phi _i(x)$ are given by

$$\begin{aligned} \phi _i(x) = \frac{a_i}{2}\cos (a_i x) + \sin (a_i x), \end{aligned}$$

(53)

and $\psi _i(y)$ are calculated similarly. We take $m = 6$ and assume that each $a_i$ is uniformly distributed in $[-\sqrt{3},\sqrt{3}]$, and thus, ${\textbf{a}} \in [-\sqrt{3},\sqrt{3}]^6$. The input diffusivity $\nu$ in all the examples in Sects. 6.3 and 6.4 are calculated by choosing the 6-dimensional coefficient ${\textbf{a}}$ from $[-\sqrt{3},\sqrt{3}]^6$.

Appendix 2: Further discussion on convergence studies

1.1 Discussion on the role of keeping $e_{\mathcal {H}}$ and $e_{\theta }$ low

If we choose a fixed network architecture and use it to solve Eq. 35 across different h-levels, then the errors do not necessarily decrease with decreasing h. As shown in Fig. 13, the errors actually increase when $h>2^{-5}$. This reason for this behavior is that, when h becomes low, the number of discrete unknowns in the mesh (i.e., $U_i$’s in Eq. 14) increases. In fact, in this case, the number of basis functions/unknowns, N is exactly equal to $\frac{1}{h^2}$. As h decreases, the size of the space $V^h$ increases. However, since the network remains the same, the discrete function space $V^h$ does not remain a subspace of $V^h_\theta$ anymore. This network function class also needs to get bigger to accommodate all the possible functions at the lower values of h. Figure 13 also shows the errors obtained when the network is indeed enhanced to make $V^h_\theta \supset V$ (this is a clone of the errors plotted in Fig. 7).

Fig. 13

Convergence of the error in $L^2$ norm for the Poisson equation with analytical solution $u =\sin {(\pi x)}\sin {(\pi y}$)

Appendix 3: Solutions to the parametric Poisson’s equation

1.1 Randomly selected examples

See Figs. 14, 15.

Table 2 Norm of solution fields for a few randomly selected

Fig. 14

Contours for the randomly selected examples presented in Table 2: (left) $\ln (\nu )$, (mid-left) $u_{\theta }$, (mid-right) $u^h$ and (right) $(u_{\theta }-u^h)$

1.2 Mean and standard-deviation fields

See Table 3.

Table 3 Norm of the mean and standard-deviation fields

Fig. 15

(top) Mean and (bottom) standard-deviation fields: (left) NeuFENet ($u_{\theta }$), (mid) Conventional FEM ($u^h$, (right) pointwise difference ($u_{\theta }-u^h$)