1 Introduction

Adequate modeling of 3D geometries is usually a cumbersome process in computational mechanics while dealing with real and practical applications. One of the most recent solutions to this problem is isogeometric analysis (IGA) [1], where exact conic sections and complex geometries can be adopted. The strength of IGA arises from its ability of using high order approximations. The nature of IGA allows linking the computer-aided design (CAD) model of the geometry with the numerical model used for the analysis, in which both models are approximated using the same basis functions. In the previous decade, Non-Uniform Rational B-Splines, or briefly NURBS, are considered as the most common and used IGA basis functions. NURBS are able to reduce the pollution errors produced by other numerical methods. Finer meshes can be obtained by applying an easy knot insertion refinement to NURBS. A different refinement by degree elevation can be applied to NURBS increasing the spline order. In both refinement cases, IGA is able to reduce the computational cost by employing less degrees of freedom (DOFs) compared to other numerical methods, such as standard finite element method (FEM) [2]. IGA was utilized in several engineering applications, showing the foregoing features. Among these applications are: shells [3], wave propagation problems [4], biomedical engineering [5, 6], piezoelectric materials [7], etc. Moreover, IGA is coupled with boundary element method (BEM) yielding IGABEM with the same nature of BEM of parameterizing only the boundaries without any domain discretization [8]. This reduces the problem dimensionality by one. The performance of IGABEM was checked in many applications, in which it was found out that, it surpasses standard BEM [9]. Various applications benefit from the characteristics of IGABEM, such as: elasto-static problems [10], acoustics [11], fluids [12], etc.

This paper is devoted for the acoustic wave propagation problem based on the time harmonic equation of Helmholtz in the frequency domain. This can be applied to practical engineering fields or research aspects, such as: communication systems, ultrasonic devices, noise control, biomedical applications, seismology, damage control, etc. However, only simple cases can be treated by closed form solutions [13]. Therefore, the proper technique for real advanced cases is to approximate the solution by other numerical methods. The most suitable methods to approximate the wave propagation problems are those that belong to the boundary-type approaches, such as: standard BEM [14], IGABEM [15], extended IGABEM [16], method of fundamental solutions (MFS) [17] and isogeometric indirect BEM [18]. These approaches are preferable since they do not need any domain discretization. Furthermore, they fulfill the Sommerfeld radiation condition [19] directly without any approximation to the truncation boundary at the far-field essential to capture the infinite domain of exterior acoustic problems. Nevertheless, domain-type approaches have also considerable contributions in the acoustic field, such as: FEM [20], Galerkin/least-squares FEM [21] and IGA [4].

BEM is introduced in different forms. The most famous forms are the direct formulations, such as: the conventional BEM [22], extended BEM [16], dual BEM [23] and Burton-Miller method [24], where the main equation contains both physical variables creating two coefficient matrices. Another efficient solution is that one related to the family of indirect BEM approaches, where the collocation is executed based on the available known physical variable (boundary condition) creating a single coefficient matrix used directly to initiate the linear system of equations. One of these methods is the method of fundamental solutions (MFS) [25,26,27,28,29], in which a linear combination of the effect of virtual discrete point sources is considered based on the governing fundamental solution with no integration efforts. The virtual sources are distributed outside the computational domain in order to cancel the free-terms and avoid the singularities corresponding to coinciding the collocation points with the virtual point sources. Nevertheless, MFS suffers from a non-uniqueness problem and needs intensive investigations in order to discover the best position and distribution of the point sources producing stable results [17, 30, 31]. Another research work utilized virtual continuous line sources placed as a circle outside the domain instead of the discrete point sources, but with no solution to the non-uniqueness problem [32]. Many research works tried to achieve the unique solution by placing the sources on the boundaries [33,34,35,36,37,38]. However, they could deal only with simple geometries where they could cancel the singularity. Another work could avoid the singularity problem by converting the point sources to area-distributed sources integrated analytically for 2D problems [39]. This can be extended for 3D problems by using volume-distributed sources. The most complete work that produces robust results for general 2D geometries and avoids singularities is that one adopting virtual continuous line sources discretized by NURBS [18].

This manuscript aims to solve 3D Helmholtz time harmonic problems using indirect boundary element method (indirect BEM) coupled with isogeometric analysis (IGA), forming isogeometric indirect BEM (IGAinBEM). IGAinBEM is based on placing virtual surface sources directly on scatterer boundaries with the same shape of the scatterer. These virtual sources are approximated using the same NURBS basis function used to parameterize the scatterer CAD model. The boundary value problem of the Helmholtz equation is approximated by employing a collocation scheme with offsets at \(C^0\)-continuities. The performance of IGAinBEM is discussed using different exterior acoustic problems in addition to the practical muffler problem with extended internal thin tubes, in which the obtained results are compared against other numerical methods.

A remark to be highlighted here is that, the proposed solution is an extension work to the 2D isogeometric solution in [18] based on the original indirect BEM in [14], which uses virtual sources governed by the fundamental solution. This method is entirely different from another method with a close name "Variational Indirect BEM" [40,41,42,43,44], which creates two opposite spaces and adds the two corresponding integral equations together in order to solve then the variational forms with a symmetric system of equations.

The manuscript is organized as follows: a brief description for the Helmholtz equation is presented in Sect. 2. Then, the solution of the Helmholtz equation using the indirect boundary element method is explained in Sect. 3. This solution is coupled with isogeometric analysis in Sect. 4. Section 5 includes the numerical examples verifying the proposed solution. Finally, the derived conclusions are written in Sect. 6.

2 The boundary value problem of Helmholtz time harmonic equation

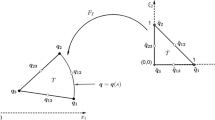
The wave propagation problem of Helmholtz is explained by Fig. 1, where an incident wave is scattered by a sound scatterer embedded in an isotropic homogeneous acoustic domain \(\Omega\). The boundary of the scatterer \(\Gamma\) is designated in most cases by three non-intersecting boundary conditions (BCs): Dirichlet \(\Gamma _p\), Neumann \(\Gamma _v\) and Robin \(\Gamma _r\) boundary conditions, while \(\Gamma = \Gamma _p \cup \Gamma _v \cup \Gamma _r\). The Helmholtz equation as a time harmonic equation is written in the form of a boundary value problem (BVP) that aims to find out the acoustic pressure u as follows [15]:

$$\begin{aligned} \begin{aligned}&\triangle u + k^2u = f \;\;\;\; \;\; \;\text { in } \;\; \Omega \\&u = g_1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\; \;\; \;\; \; \; \; \text {on} \; \Gamma _p \\&\frac{ \partial u}{ \partial \textbf{n}} = g_2 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\; \;\; \; \; \; \text {on} \; \Gamma _v \\&\frac{ \partial u}{ \partial \textbf{n}} - iku = g_3 \;\;\;\;\;\;\;\; \;\; \; \; \; \text {on} \; \Gamma _r \end{aligned} \end{aligned}$$
(1)

where \(\triangle\) denotes to the Laplace operator. k refers to the wavenumber. k is written in a relation to the wavelength \(\lambda\) as \(\lambda =2\pi /k\). i is the imaginary unit. f, \(g_1\), \(g_2\) and \(g_3\) are prescribed functions, in which f is associated with the sound source term, while \(g_1\), \(g_2\) and \(g_3\) correspond to the defined boundaries. \(\textbf{n}\) refers to the unit normal pointing outside the domain \(\Omega\).

Fig. 1
figure 1

Helmholtz acoustic problem

Full size image

Another condition is defined at infinity in the case of exterior acoustic problems to capture the unbounded domains, which is the Sommerfeld radiation condition [19]. This condition truncates all potential reflections related to spurious acoustic waves transferring from the far-field (\(\Gamma _{\infty }\)). It is written for 3D problems as follows:

$$\begin{aligned} \lim \limits _{r \rightarrow \infty } {r} \left( \frac{ \partial u}{ \partial r}-iku\right) =0 \end{aligned}$$
(2)

where the distance r is taken from the origin.

3 Indirect BEM solution depending on virtual surface sources

The basic idea of this solution is inspired from the method of fundamental solutions (MFS) described in [28]. In that method, virtual discrete point sources \(\textbf{q}\) are distributed outside the domain and the BVP is weakened by collocating on the scatterer boundary at points \(\textbf{p}\) using the available BCs: the acoustic pressure u or its normal derivative \(\frac{ \partial u}{ \partial \textbf{n}}\) written with the following linear combinations:

$$\begin{aligned} \begin{aligned}&u(\textbf{p})= \sum \limits _{s=1}^{N_s} U^*(\textbf{p},\textbf{q}) X_s(\textbf{q}) \\&\frac{ \partial u}{ \partial \textbf{n}}(\textbf{p})= \sum \limits _{s=1}^{N_s} \frac{ \partial U^*(\textbf{p},\textbf{q})}{ \partial \textbf{n}(\textbf{p})} X_s(\textbf{q}) \end{aligned} \end{aligned}$$
(3)

in which \(N_s\) denotes the number of the discrete point sources. \(X_s(\textbf{q})\) refers to the unknown amplitude associated with each point source \(\textbf{q}\). \(U^*(\textbf{p},\textbf{q})\) is the fundamental solution for the 3D Helmholtz acoustic governing equation, taking into account the influence of the point sources \(\textbf{q}\) on the boundary points \(\textbf{p}\). Both the fundamental solution and its normal derivative at the point of interest \(\textbf{p}\) are formulated as follows:

$$\begin{aligned} \begin{aligned}&U^*(\textbf{p},\textbf{q})= \frac{e^{ikr}}{4 \pi r } \\&\frac{ \partial U^* (\textbf{p},\textbf{q})}{ \partial \textbf{n} (\textbf{p})}= - \frac{e^{ikr}}{4 \pi r^2 } (1-ikr) \frac{ \partial r}{ \partial \textbf{n}(\textbf{p})} \end{aligned} \end{aligned}$$
(4)

in which \(r=|\textbf{p}-\textbf{q}|\), and

$$\begin{aligned}{} & {} \frac{\partial r}{ \partial \textbf{n} (\textbf{p})} = - \frac{ \textbf{x}(\textbf{q}) - \textbf{x}(\textbf{p})}{ r} \textbf{n}(\textbf{p}) \end{aligned}$$
(5)

where \(\textbf{x}=\{x,y,z\}\) refers to the point coordinates. Equation (3) can be applied also at any field point (\(\textbf{p})\).

In this solution, the virtual point sources \(\textbf{q}\) are positioned outside the acoustic domain to avoid all singularity problems associated with collocating on or near the point sources \(\textbf{q}\). Nevertheless, another problem appears, which is the non-uniqueness solution due to the positioning of the virtual point sources, and this requires extensive investigations to find out the optimal positions producing the correct results.

In order to overcome these problems, a solution was proposed in [18] for 2D acoustic problems extending MFS by using virtual continuous line sources discretized by NURBS and positioned directly on the scatterer boundary. Placing the sources on the boundary could achieve the uniqueness solution and produce robust results, while using continuous sources discretized by NURBS could handle the singularity problems. The final form of the acoustic pressure u and its normal derivative \(\frac{ \partial u}{ \partial \textbf{n}}\) were written in [18] following the general case in [14] as follows:

$$\begin{aligned} \begin{aligned}&u(\textbf{p})= \int _{\Gamma } U^*(\textbf{p},\textbf{q}) X_s(\textbf{q}) d\Gamma (\textbf{q}), \; \;\; \; \; \; \textbf{p},\textbf{q} \in \Gamma \\&\frac{ \partial u}{ \partial \textbf{n}}(\textbf{p})= \int _{\Gamma } \frac{ \partial U^*(\textbf{p},\textbf{q})}{ \partial \textbf{n}(\textbf{p})} X_s(\textbf{q}) d\Gamma (\textbf{q}) + c(\textbf{p}) X_s(\textbf{p}), \; \;\; \; \; \; \textbf{p},\textbf{q} \in \Gamma \end{aligned} \end{aligned}$$
(6)

where the discretized unknown amplitude \(X_s(\textbf{q})\) (by total number \(N_{\phi }\) of shape functions \(\phi _l(\textbf{q})\) and corresponding nodal unknowns \(x_l\)) is written as follows:

$$\begin{aligned} X_s(\textbf{q}) = \sum \limits _{l=1}^{N_{\phi }} \phi _l(\textbf{q}) {x}_l \end{aligned}$$
(7)

Some remarks are summarized for this solution as follows:

  1. 1.

    This solution can be considered for 3D problems with the same expression of Eq. (6), where the boundary \(\Gamma\) is considered as the surface of the scatterer.

  2. 2.

    The normal direction is predicted only at the collocation point \(\textbf{p}\).

  3. 3.

    Since the virtual surface sources are placed on the boundary \(\Gamma\), the free term \(c(\textbf{p})\) associated with the normal derivative \(\frac{ \partial u}{ \partial \textbf{n}}\) appears due to the Cauchy Principal Value when collocating on the boundary \(\Gamma\) as explained in [45]. In this work, \(c(\textbf{p})\) equals 0.5 as a standard value according to [14, 45], since the collocation is performed on smooth surfaces as will be clarified in the next section.

  4. 4.

    The collocation scheme in the next section could avoid the singularity of order \(\mathcal {O} (1/r)\) existing in the fundamental solution of Eq. (4) and turn it into weakly singular integrals, which can be treated by applying the integration in polar coordinates reducing the order of singularity by one as described in [46], by a standard technique such as Telles transformation method [47] as suggested in [48] or by more Gauss quadrature points as proposed in [49]. The normal derivative of the fundamental solution has a singularity of order \(\mathcal {O} (1/r^2)\) multiplied by \(\frac{ \partial r}{ \partial \textbf{n}}\). This leads to a reduced singularity of order \(\mathcal {O} (1/r)\).

  5. 5.

    The Sommerfeld radiation condition mentioned in Eq. (2) is in content with the proposed solution without modeling any truncation boundaries at \(\Gamma _{\infty }\), similar to other boundary element methods.

4 IGAinBEM mathematical expression

In following subsections, a brief description is presented for indirect BEM coupled with isogeometric analysis (IGA), forming isogeometric indirect BEM (IGAinBEM). The mathematical expression of Eq. (6) is considered here as well, while the unknown amplitude \(X_s\) is discretized by NURBS.

4.1 NURBS

In BEM, 2D problems are modeled in a 1D parametric space \(\xi \in [0,1]\), where NURBS are defined using a knot vector: \(\Xi =\{\xi _1=0,\ldots , \xi _i, \ldots ,\xi _{n+p+1} =1 \}\) with number of basis functions n, knot index i and polynomial degree p. The knot vector is arranged with a non-decreasing set of real numbers. The ith B-spline function of pth-degree \(N_{i, p}(\xi )\) assigned for the knot vector is written as a recursive formula as follows [1, 50]:

$$\begin{aligned} N_{i,0}(\xi ) = \Bigg \{ \begin{array}{lcl} 1, \;\;\;\;\;\;\;\;\;\; \xi _i\le \xi <\xi _{i+1} \\ 0, \;\;\;\;\;\;\;\;\;\; \text{ otherwise } \end{array} \end{aligned}$$
(8)

and for \(p\ge 1\)

$$\begin{aligned}{} & {} N_{i,p}(\xi )=\frac{\xi -\xi _i}{\xi _{i+p}-\xi _i} N_{i,p-1}(\xi )+\frac{\xi _{i+p+1}-\xi }{\xi _{i+p+1}-\xi _{i+1}} N_{i+1,p-1}(\xi ) \end{aligned}$$
(9)

For 3D problems, the definitions explained above are extended to the 2D parametric space \((\xi ,\eta ) \in [0,1]\times [0,1]\), introducing two knot vectors: \(\Xi =\{\xi _1=0,\ldots , \xi _i,\ldots ,\xi _{n+p+1} =1 \}\) and \(\Upsilon =\{\eta _1=0,\ldots , \eta _j,\ldots ,\eta _{m+q+1} =1 \}\). Thus, NURBS are defined by the tensor product of two B-spline functions \(N_{i, p}(\xi )\) and \(N_{j, q}(\eta )\) as the following:

$$\begin{aligned}{} & {} R_{ij}(\xi ,\eta )=\frac{N_{i,p}(\xi ) N_{j,q}(\eta ) w_{ij}}{\sum \limits _{\overline{i}=1}^{n} \sum \limits _{\overline{j}=1}^{m} N_{\overline{i},p}(\xi ) N_{\overline{j},q}(\eta ) w_{\overline{i} \overline{j}}} \end{aligned}$$
(10)

in which \(w_{ij}\) refers to the weight coincided with the control point \(P_{ij}\). The NURBS surface is parameterized using the following form:

$$\begin{aligned} S(\xi ,\eta )=\sum \limits _{i=1}^{n} \sum \limits _{j=1}^{m} R_{ij} (\xi ,\eta )P_{ij} \end{aligned}$$
(11)

Similarly, the unknown amplitude \(X_s(\xi ,\eta )\) is discretized using NURBS according to the following formula:

$$\begin{aligned} X_s(\xi ,\eta )=\sum \limits _{i=1}^{n} \sum \limits _{j=1}^{m} R_{ij} (\xi ,\eta )x_{ij} \end{aligned}$$
(12)

in which \(x_{ij}\) refers to the associated control variable.

4.2 Collocation scheme with offset at \(C^0\)-continuities

The collocation is performed in this work based on the Greville abscissae with offsets at \(C^0\)-continuities following [49, 51]. First, the following \(n \times m\) total collocation points \({\widehat{\xi }}_a\) and \({\widehat{\eta }}_b\) are generated:

$$\begin{aligned} \begin{aligned}&{\widehat{\xi }}_a= \frac{\xi _{a+1}+\xi _{a+2}+\cdots +\xi _{a+p}}{p},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; a=1,2,\ldots ,n \\&{\widehat{\eta }}_b= \frac{\eta _{b+1}+\eta _{b+2}+\cdots +\eta _{b+q}}{q},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; b=1,2,\ldots ,m \end{aligned} \end{aligned}$$
(13)

Hence, the number of collocation points equals the number of unknown control variables.

Then, collocation on sharp corners (\(C^0\)-continuities) is avoided by introducing discontinuous NURBS and corresponding discontinuous amplitudes (\(C^{-1}\)-discontinuities). This is achieved by increasing the corresponding knot multiplicity in the knot vector. Consequently, the attached control points are repeated. Another step is associated with these procedures, which is increasing the number of collocation points as well. Applying Eq. (13) on the updated knot vectors leads to repeated collocation points at \(C^{-1}\)-discontinuity. After that, the following equations are used to separate those points by introducing an offset \(\alpha\):

$$\begin{aligned} \begin{array} {l} {\widehat{\xi }}_a = {\widehat{\xi }}_a + \alpha ({\widehat{\xi }}_{a+1} - {\widehat{\xi }}_{a} ), \; \; \; \; \; \;\text {and} \\ {\widehat{\xi }}_a = {\widehat{\xi }}_a - \alpha ({\widehat{\xi }}_{a} - {\widehat{\xi }}_{a-1} ), \; \; \; \; \; \; 0< \alpha < 1 \\ \end{array} \end{aligned}$$
(14)

Moreover, Eq. (14) is used to shift both the first and last collocation points in each knot vector.

An example in Fig. 2 is clarifying the proposed collocation scheme. The example is written with the two knot vectors: \(\Xi =\{ 0, 0, 0, 1/3, 2/3, 2/3, 1, 1, 1 \}\) and \(\Upsilon = \{ 0, 0, 0, 1/3, 2/3, 2/3, 1, 1, 1 \}\) in the original continuous form (\(C^0\)-continuity). Then, the two knot vectors are modified to achieve the \(C^{-1}\)-discontinuity as follows: \(\Xi =\{ 0, 0, 0, 1/3, 2/3, 2/3, 2/3, 1, 1, 1 \}\) and \(\Upsilon = \{ 0, 0, 0, 1/3, 2/3, 2/3, 2/3, 1, 1, 1 \}\), in which NURBS are defined with polynomials degree 2.

Fig. 2
figure 2

An example illustrating the collocation scheme with offsets. The original collocation points are in orange while the shifted collocation points are in green

Full size image

The free-term \(c(\textbf{p})\) in Eq. (6) is calculated in general depending on the geometry and corner angles, which is very complicated while collocating at sharp corners (\(C^0\)-continuities). The strength of the proposed collocation scheme is to avoid any collocation point at corners by shifting these points with an offset \(\alpha\), so that the collocation is performed on smooth surfaces and thus \(c(\textbf{p})\) equals only the standard value (0.5) without any calculations. It provides also easy prediction for the normal direction at the collocation point \(\textbf{p}\) of the same equation.

Furthermore, the collocation scheme can overcome the singularity of order \(\mathcal {O} (1/r)\) existing in the fundamental solution of Eq. (4), since the collocation points are shifted away from \(\xi _i\) and \(\xi _{i+1}\). This converts these singular integrals into weakly singular integrals. A further discussion is illustrated in the numerical examples in Sect. 5.1 for the methods which can treat this weakly-singular integrals, such as: Telles transformation method [47] and the integration in polar coordinates [46].

The offset \(\alpha\) is taken as 0.05 in all examples. This value is chosen not so small that would produce a near singularity while integrating over the neighbor elements, and not so large that would reduce the accuracy.

4.3 IGAinBEM

NURBS surface \(S(\xi ,\eta )\) and the unknown amplitude of Eq. (11) and Eq. (12), respectively, are re-written after being mapped from the global indices ij to a local index A for each element discretized by total number \(N=(p+1) \times (q+1)\) of NURBS basis functions as follows:

$$\begin{aligned} \begin{aligned} S(\xi ,\eta )= \sum \limits _{A=1}^{N} R_{A} (\xi ,\eta )P_{A} \\ X_s(\xi ,\eta )=\sum \limits _{A=1}^{N} R_{A} (\xi ,\eta )x_{A} \end{aligned} \end{aligned}$$
(15)

in which \(P_{A}\) and \(x_{A}\) refer to the associated mapped control variables.

In the framework of isogeometric analysis, the virtual surface sources are placed-directly and identically—on the scatterer surface, where they are discretized into \(N_e\) non-overlapping elements. Each element e is written in a knot span/interval \([\xi _{e_1}, \xi _{{e_1}+1}] \times [\eta _{e_2}, \eta _{{e_2}+1}]\) in the parametric space. The acoustic pressure u and its normal derivative \(\frac{ \partial u}{ \partial \textbf{n}}\) are updated by substituting Eq. (15) into Eq. (6). Then, \(n \times m\) total equations are evaluated using the available BCs on the collocation points \((\xi _c,\eta _c)\) defined on the discretized elements as follows:

$$\begin{aligned} \begin{aligned}&u(\textbf{p}(\xi _c,\eta _c))= \sum _{e=1}^{Ne} \sum _{A=1}^{N} \Big [ \int _{\xi _{e_1}}^{\xi _{{e_1}+1}} \\&\int _{\eta _{e_2}}^{\eta _{{e_2}+1}} U^*(\textbf{p}(\xi _c,\eta _c),\textbf{q} (\xi ,\eta ) ) R_{A}(\xi ,\eta )|J^e (\xi ,\eta )| d\xi d\eta \Big ] x_A \\&\frac{ \partial u}{ \partial \textbf{n}}(\textbf{p}(\xi _c,\eta _c))= \sum _{e=1}^{Ne} \sum _{A=1}^{N} \Big [ \int _{\xi _{e_1}}^{\xi _{{e_1}+1}}\\&\int _{\eta _{e_2}}^{\eta _{{e_2}+1}} \dfrac{ \partial U^*(\textbf{p}(\xi _c,\eta _c),\textbf{q} (\xi ,\eta ) )}{ \partial \textbf{n} (\textbf{p}(\xi _c,\eta _c)) } R_{A}(\xi ,\eta )|J^e (\xi ,\eta )| d\xi d\eta \Big ] x_A \\ & \quad + c(\xi _c,\eta _c)\sum _{A=1}^{N} R_{A}(\xi _c,\eta _c) x_{A} \end{aligned} \end{aligned}$$
(16)

where \(|J^e(\xi ,\eta )|\) denotes the Jacobian used in integration purposes to transform the physical space to a parametric space. The knot indices \(e_1\) and \(e_2\) correspond to the first and second knot vectors, respectively, for each element e.

The implementation of the proposed method is simpler compared to other BEM methods. At each collocation point \((\xi _c,\eta _c)\), an equation is written based on the two equations in Eq. (16) and fulfilling the available BC at this point. In most cases, the known BC (the left hand side of Eq. (16)) is the acoustic pressure u, its normal derivative \(\frac{ \partial u}{ \partial \textbf{n}}\) or a mixed function. NURBS, Jacobians, normals and other kernels under the integration in Eq. (16) are calculated directly based on the source and collocation points, and the distance between these two points, while only the amplitudes \(x_A\) are set as the unknowns. A total of \(n \times m\) equations are written and then are arranged straightforwardly to the following linear system of equations:

$$\begin{aligned} \textbf{A}\textbf{x}=\textbf{b} \end{aligned}$$
(17)

in which \(\textbf{A}\) refers to the coefficient matrix including the integrations associated to the unknown amplitudes \(x_A\) ordered in the vector \(\textbf{x}\). The vector \(\textbf{b}\) includes the known BCs. IGAinBEM shows an advantage, as it constructs the linear system of equations directly using a single coefficient matrix, rather than using two matrices and then re-arranging them to the final form in Eq. (17) as implemented in conventional BEM. After evaluating the unknown amplitudes in the vector \(\textbf{x}\), the acoustic pressure values at any point inside the acoustic domain can be computed easily using again Eq. (16).

In each numerical example in Sect. 5, the equation which constructs the system matrix is written based on the corresponding available BC. Please refer to Eq. (20) and Eq. (28).

The integration in this work is performed according to the following steps:

  1. 1.

    Each knot span/interval, extracted from the two knot vectors and written as: \([\xi _{e_1}, \xi _{{e_1}+1}]\) or \([\eta _{e_2}, \eta _{{e_2}+1}]\), is divided to 4 sub-divisions. This yields 16 sub-divisions in each \([\xi _{e_1}, \xi _{{e_1}+1}] \times [\eta _{e_2}, \eta _{{e_2}+1}]\).

  2. 2.

    The integration is implemented on each sub-division employing 6 \(\times\) 6 Gauss quadrature points.

5 Numerical results

The following numerical examples discuss the performance of IGAinBEM in solving 3D acoustic problems. First, a convergence analysis is implemented on the plane wave scattering problem by a rigid sphere with a comparison against other boundary element methods: the conventional boundary integral equation (CBIE) and Burton-Miller method (BM) [49]. Then, the results of two irregular rigid shapes are examined. Finally, the muffler problem as a practical interior acoustic problem is checked and compared against different numerical methods in addition to experimental data.

5.1 Convergence analysis on the plane wave scattering problem by a rigid sphere

The convergence analysis is conducted on a rigid sphere with a radius \(a=1.0\) m as an exterior plane wave scattering acoustic problem. The impedance medium is air with density \(\rho =1.2\) kg/m\(^3\) and sound speed \(c=343\) m/s. The sphere is subject to an incident wave governed by the following equation:

$$\begin{aligned}{} & {} u_{inc}(\textbf{p}) = A e^{i k \; \textbf{d} \cdot \mathbf {\textbf{p} }} \end{aligned}$$
(18)

in which A denotes the wave amplitude, which is taken in this example as 1.0. \(\mathbf {|d|}=1\) refers to propagation direction in a vector form. In this example, the direction is considered in the x-axis (\(\textbf{d}=\{1,0,0\}\)). The total acoustic pressure in an exact form is written according to the following equation [52]:

$$\begin{aligned} u^\textrm{ex} (r,\theta ) & = A e^{i k \; \textbf{d} \cdot \mathbf {\textbf{p} }} - \sum _{m=0}^{\infty } i^m (2m+1) \nonumber \\ & {\frac{j_m^{'}(k a) }{ h_m^{'}(k a) }} h_m(k r) P_m(cos \theta ) \;\;\;\;\;, r\ge a \end{aligned}$$
(19)

where r refers to the distance to the concerned point \(\textbf{P}\) from the origin. The angle \(\theta\) is defined between the axis drawn from the origin to the point \(\textbf{P}\) and the incident wave direction as illustrated in Fig. 3. \(h_m\) and \(j_m\) refer to the spherical Hankel and Bessel functions of the first kind, respectively. \(P_m\) denotes the Legendre polynomial. Functions and polynomials are defined of order m, which is set in this example as 10 to adequately perform the convergence analysis for the discussed frequencies. \((')\) is written for all derivatives with respect to their concerned arguments.

Fig. 3
figure 3

Plane wave scattering problem by a rigid sphere

Full size image
Fig. 4
figure 4

The rigid sphere

Full size image
Fig. 5
figure 5

NURBS model and control points grid for the rigid sphere

Full size image

The numerical model of the sphere shown in Fig. 4 is approximated using NURBS polynomial degree 2 for each knot direction for the two knot vectors: \(\Xi =\{ 0, 0, 0, 0.5, 0.5, 1, 1, 1 \}\) and \(\Upsilon = \{ 0, 0, 0, 0.25, 0.25, 0.5, 0.5, 0.75, 0.75, 1, 1, 1 \}\). The corresponding control points are presented in Fig. 5.

IGAinBEM numerical solution in this example is executed as follows:

  1. 1.

    Since the sphere is rigid, the linear system of equation is constructed based on the normal derivative \(\frac{ \partial u}{ \partial \textbf{n}}\) at all collocation points \(\mathbf {p(\xi _c,\eta _c)}\) on the sphere boundary/surface as an available boundary condition according to the following equation:

    $$\begin{aligned} \begin{aligned}&\frac{ \partial u}{ \partial \textbf{n}}(\textbf{p}(\xi _c,\eta _c))= \sum _{e=1}^{Ne} \sum _{A=1}^{N} \Big [ \int _{\xi _{e_1}}^{\xi _{{e_1}+1}}\\&\int _{\eta _{e_2}}^{\eta _{{e_2}+1}} \dfrac{ \partial U^*(\textbf{p}(\xi _c,\eta _c),\textbf{q} (\xi ,\eta ) )}{ \partial \textbf{n} (\textbf{p}(\xi _c,\eta _c)) } R_{A}(\xi ,\eta )|J^e (\xi ,\eta )| d\xi d\eta \Big ] x_A \\ {}&+ c(\xi _c,\eta _c)\sum _{A=1}^{N} R_{A}(\xi _c,\eta _c) x_{A} = - i k \textbf{d} \cdot \textbf{n} (\textbf{p}) A \, e^{i k \textbf{d} \cdot \textbf{p}} \end{aligned} \end{aligned}$$
    (20)

    in which the solution of this system matrix is to find out the unknowns \(x_A\) as clarified in Sect. 4.3.

  2. 2.

    The total acoustic pressure at any point \(\textbf{p}\) is computed as the aggregate of the incident and scattered waves as follows:

    $$\begin{aligned}{} & {} u(\textbf{p})= A e^{i k \; \textbf{d} \cdot \textbf{p}} + \sum _{e=1}^{Ne} \sum _{A=1}^{N} \Big [ \int _{\xi _{e_1}}^{\xi _{{e_1}+1}} \nonumber \\{} & {} \int _{\eta _{e_2}}^{\eta _{{e_2}+1}} U^*(\textbf{p},\textbf{q} (\xi ,\eta ) ) R_{A}(\xi ,\eta )|J^e (\xi ,\eta )| d\xi d\eta \Big ] x_A \end{aligned}$$
    (21)

For the convergence analysis, two relative errors are evaluated:

1- On-Surface Relative \(L_2\) Error Norm (\(e_{L_2}\))

The relative \(L_2\) error norm (\(e_{L_2}\)) is verified on the sphere surface as follows:

$$\begin{aligned} e_{L_2} \equiv \frac{||u^\textrm{ex}-u^\textrm{num}||}{||u^\textrm{ex}||} = \sqrt{ \frac{\int _\Gamma {(u^\textrm{num}-u^\textrm{ex})^T(u^\textrm{num}-u^\textrm{ex})d\Gamma }}{\int _\Gamma {u^\textrm{ex}}^T u^\textrm{ex}d\Gamma }} \end{aligned}$$
(22)

where \(u^\textrm{num}\) refers to the numerical solution of IGAinBEM obtained from Eq. (21) while \(u^\textrm{ex}\) is the exact solution in Eq. (19). Only six Gauss quadrature points are required for each knot span to perform the integration in Eq. (22). Note that, Telles transformation method [47] is proposed in this scheme to overcome the weakly singularities which appear when any integration point of Eq. (22) coincides with the integration points of Eq. (21).

2- Off-Surface Relative Error (\(e_D\))

Another relative error \(e_D\) is checked on \(N=200\) discrete points inside the acoustic domain. The points are uniformly distributed on a circle with a radius of 1.50 m and centered at the sphere origin in the X–Y plane where \(Z=0\). \(e_D\) is written as follows:

$$\begin{aligned}{} & {} e_D \equiv \frac{||u^\textrm{ex}-u^\textrm{num}||}{||u^\textrm{ex}||} = \sqrt{ \frac{\sum \limits _{i=1}^{N}{(u^\textrm{num}_i - u^\textrm{ex}_i)^T(u^\textrm{num}_i-u^\textrm{ex}_i)}}{\sum \limits _{i=1}^{N} {u^\textrm{ex}_i}^T u^\textrm{ex}_i }} \end{aligned}$$
(23)

It is worth mentioning that, the integration is performed smoothly in the Off-Surface scheme apart from the collocation points. Therefore, the obtained errors from this scheme is less than those obtained from the On-Surface scheme.

Another remark that needs to be highlighted in this example is that, the proposed solution does not include hyper-singular integrals. Thus, the implementation is simpler compared to other research works utilizing IGABEM, which carry out a special treatment on NURBS distorted triangle elements containing the sphere poles when the collocation is performed on the pole point [46, 53]. Other research works need to implement this treatment in order to overcome the the nearly singular integral through \(\theta\)-direction corresponding to singularity subtraction technique (SST), which is not the case in the proposed solution.

Fig. 6
figure 6

Relative error in terms of total DOFs for different frequencies

Full size image
Fig. 7
figure 7

On-Surface errors (\(e_{L_2}\)) for the case in Fig. 6b while performing Telles transformation and polar integration

Full size image
Fig. 8
figure 8

Compiled on-surface errors (\(e_{L_2}\))

Full size image
Fig. 9
figure 9

Compiled off-surface errors (\(e_D\))

Full size image
Fig. 10
figure 10

Relative error in terms of DOFs per wavelength in each coordinate direction for different frequencies

Full size image
Fig. 11
figure 11

On-Surface relative error (\(e_{L_2}\)) for different frequencies

Full size image
Fig. 12
figure 12

Off-Surface relative error (\(e_D\)) for different frequencies

Full size image
Fig. 13
figure 13

Condition number of the system matrices for different frequencies

Full size image

The variation of the two proposed relative errors (\(e_{L_2}\) and \(e_D\)) computed by IGAinBEM is explained in Fig. 6 in terms of total DOFs. The plots are presented in a comparison with previously published results in [49] obtained by isogeometric Burton-Miller method (IGABM) and isogeometric conventional boundary integral equation (IGACBIE). The studied frequencies are: 50, 100, 150, 200, 250 and 300 Hz corresponding to wavenumbers k = 0.92, 1.83, 2.75, 3.66, 4.58 and 5.50, respectively. It can be seen that, Off-Surface errors are less than those related to On-Surface scheme for all methods. Moreover, IGAinBEM produces more accurate results for all frequencies in the case of Off-Surface scheme. Meanwhile, IGAinBEM shows also more accurate results in the case of On-Surface scheme, but only when the comparison is performed using moderate DOFs. Then, the more DOFs are used, the less accuracy is obtained (compared to other methods) in which the results take the shape of a plateau curve due to the rapid increase of the weakly singularity corresponding to the collocation on the boundary.

The treatment of the weakly singular integrals is discussed in Fig. 7 for the frequency case shown in Fig. 6b, where the On-Surface errors (\(e_{L_2}\)) obtained by IGAinBEM are computed while performing two alternatives: Telles transformation method [47] and the integration in polar coordinates which reduces the order of singularity by one [46]. The same number of Gauss points are used for both alternatives. It can be seen that, both alternatives produce close results where the problem of rapid increase of the weakly-singularity exists, with some preferences to Telles transformation. Thus, all other examples in this manuscript showing the On-Surface errors (\(e_{L_2}\)) or any surface values are treated by Telles transformation.

All On-Surface results obtained by IGAinBEM are compiled in Fig. 8, while the Off-Surface results are compiled in Fig. 9, showing the effect of increasing the frequency on the gained accuracy.

Another comparison is demonstrated in Fig. 10 for both \(e_{L_2}\) and \(e_D\) in terms of total DOFs per wavelength in each coordinate direction related to each knot vector. This comparison includes the methods and frequencies discussed in the previous plots in Fig. 6. The same conclusion is noticed here as well, as IGAinBEM produces the least errors in the case of Off-Surface scheme and also in the case of On-Surface scheme while using only moderate DOFs (5 DOFs/wavelength).

Although IGAinBEM shows very good performance compared to other BEM methods, it could not overcome the fictitious eigenfrequency problem in exterior acoustic problem, showing the same behavior of IGACBIE. Only IGABM could handle this problem. This can be seen from the instabilities corresponding to the two frequencies 171.5 and 343 Hz corresponding to wavenumbers k = \(\pi\) and \(2 \pi\), respectively, which appear in Figs. 11 and 12, where both \(e_{L_2}\) and \(e_D\) are plotted against different frequencies using 16 DOFs/wavelength for each direction.

The condition number of IGAinBEM system matrix is studied in Fig. 13 and compared against other BEM methods. IGA is performed for all methods using 10 DOFs/wavelength for each direction. It can be seen that, IGACBIE shows the least condition number which is about 10, similar to what was recorded in [54]. The condition number of IGAinBEM is in the range of 36–50 which is not much higher than that of IGACBIE. IGABM has the biggest condition number in this comparison. However, all condition numbers in this comparison are low and the system matrices are considered well conditioned which are solved efficiently without any special solvers. This is different from the cases discussed in [15, 55] related to extended IGABEM (XIBEM) for 2D problems, where the condition number reached \(10^{16}\) and the system matrix was solved by a more efficient solver such as the singular value decomposition (SVD). Similar to the comparison in Figs. 11 and 12, it can be seen here as well that, IGABM shows stable results while IGAinBEM and IGACBIE suffer from the fictitious eigenfrequency problem at frequencies 171.5 and 343 Hz corresponding to wavenumbers k=\(\pi\) and \(2 \pi\), respectively.

Fig. 14
figure 14

Surface values for frequency of 50 Hz

Full size image
Fig. 15
figure 15

Domain values in x–y plane where \(z=0\) for frequency of 50 Hz

Full size image
Fig. 16
figure 16

Surface values for frequency of 100 Hz

Full size image
Fig. 17
figure 17

Domain values in x–y plane where \(z=0\) for frequency of 100 Hz

Full size image
Fig. 18
figure 18

Surface values for frequency of 150 Hz

Full size image
Fig. 19
figure 19

Domain values in x–y plane where \(z=0\) for frequency of 150 Hz

Full size image
Fig. 20
figure 20

Surface values for frequency of 200 Hz

Full size image
Fig. 21
figure 21

Domain values in x–y plane where \(z=0\) for frequency of 200 Hz

Full size image
Fig. 22
figure 22

Surface values for frequency of 250 Hz

Full size image
Fig. 23
figure 23

Domain values in x–y plane where \(z=0\) for frequency of 250 Hz

Full size image
Fig. 24
figure 24

Surface values for frequency of 300 Hz

Full size image
Fig. 25
figure 25

Domain values in x–y plane where \(z=0\) for frequency of 300 Hz

Full size image

Figures 14,15, 16, 17, 18, 19, 20, 21, 22, 23, 2425 demonstrate the real and imaginary parts as well as the absolute errors w.r.t the exact solution for the acoustic pressure values obtained by IGAinBEM. These values are plotted on the sphere surface and inside the acoustic domain in the x–y plane where \(z=0\). The studied frequencies are 50, 100, 150, 200, 250 and 300 Hz, where the sphere is modeled with 128, 200, 288, 392, 512 and 648 DOFs, respectively. It is shown that, IGAinBEM produces very low errors.

Fig. 26
figure 26

CPU time for the relative error \(e_{D}\)

Full size image

The CPU time is computed for the relative error \(e_D\) obtained by IGAinBEM, IGABM and IGACBIE in Fig. 26 versus the total DOFs. All numerical models are compiled using Intel Fortran Compiler (Beta) supporting Fortran 95 and getting benefit from OpenMP 4.5 parallelization features. It can be noticed that, both IGAinBEM and IGACBIE require less CPU time than IGABM because of their less integration efforts. It is shown also that, IGAinBEM has an advantage over IGACBIE as it is slightly faster due to constructing the system matrix directly with only one coefficient matrix. Furthermore, it is clear from Fig. 26 that, in the three compared methods, the runtime scaling with the problem size \(N_\textrm{DOF}\) follows the quadratic complexity nature of BEM of order \(\mathcal {O} (N_\textrm{DOF}^2\)) due to their dense system matrices.

It is concluded that, IGAinBEM is a fast alternative with accurate results, but it needs some experience to avoid the frequencies causing the eigenfrequency problem.

5.2 Plane wave scattering problems by rigid irregular shapes

In this section, two rigid irregular shapes produced by the optimization analysis performed in Ref.[49] are tested to calculate the total acoustic pressure using IGAinBEM and the results are compared against those obtained from IGABM and IGACBIE, in order to show the ability of the proposed method to handle general 3D geometries.

5.2.1 An optimized rigid sphere

The problem explained in Sect. 5.1 is discussed in this section as well with the same incident wave direction, but for the optimized irregular sphere produced by ref.[49] and shown in Fig. 27. This shape is modeled using NURBS polynomial degree 2 and the corresponding control points illustrated in Fig. 28. The two knot vectors are written similar to the previous example. The total real and imaginary parts of the acoustic pressure values are computed on the surface of the irregular shape. The used frequency is 100 Hz \((k=1.83)\). The surface values are presented in Fig. 29 for all comparative methods: IGAinBEM, IGABM and IGACBIE using total 288 DOFs. It can be seen that, all methods give similar results.

Fig. 27
figure 27

The rigid irregular sphere produced by ref.[49]

Full size image
Fig. 28
figure 28

NURBS model and control points grid for the rigid irregular sphere

Full size image
Fig. 29
figure 29

Surface values for the irregular sphere shape produced by Ref. [49] for a frequency of 100 Hz

Full size image

5.2.2 An optimized rigid vase

The optimized rigid vase produced by Ref. [49], see Fig. 30, is considered in this example following the features and medium explained in Sect. 5.1, but with an incident wave in the y-axis (\(\textbf{d}=\{0,1,0\}\)). The irregular vase shape is modeled with NURBS polynomial degree 2 and two knot vectors written as follows: \(\Xi =\{ 0, 0, 0, 1/12, 2/12, 3/12, 4/12, 5/12, 6/12, 7/12, 8/12, 9/12, 10/12, 11/12, 1, 1, 1 \}\) and \(\Upsilon = \{ 0, 0, 0, 0.25, 0.25, 0.5, 0.5, 0.75, 0.75, 1, 1, 1 \}\). Figure 31 shows the NURBS model with its corresponding control points. Figure 32 displays the domain values in x–y plane where \(z=6\) m in terms of the total real and imaginary parts for all comparative methods using 1736 total DOFs. The studied frequency is 200 Hz \((k=3.66)\). As shown, the three methods produce the same values.

Fig. 30
figure 30

The rigid irregular vase produced by Ref. [49]

Full size image
Fig. 31
figure 31

NURBS model and control points grid for the rigid irregular vase

Full size image
Fig. 32
figure 32

Domain values in the x–y plane at \(z=6\) m for the irregular vase produced by Ref. [49] for a frequency of 200 Hz

Full size image

5.3 Muffler with extended inlet/outlet thin tubes

The muffler problem with extended inlet/outlet thin tubes is considered in this section as a practical acoustic problem. The problem is defined as shown in Fig. 33, where the sound waves go through the muffler inlet \(\Gamma _\textrm{in}\) into the acoustic domain surrounded by the muffler rigid body \(\Gamma _\textrm{rigid}\). Then, these waves exit the acoustic domain through the muffler outlet \(\Gamma _\textrm{out}\). The muffler is divided to a main chamber with a length L and diameter D, and two smaller internal extended tubes with lengths \(L_1 \; \& \; L_2\) and diameters \(D_1 \; \& \; D_2\). The thickness t of these thin tubes is clarified separately in a small detail in Fig. 34. The muffler is an interior acoustic problem, where the unit normal vector \(\textbf{n}\) points outside the muffler domain.

Fig. 33
figure 33

The Muffler problem with extended inlet/outlet thin tubes

Full size image
Fig. 34
figure 34

Detail: internal tube thickness

Full size image

The BVP in Eq. (1) is written for the muffler problem as follows [56]:

$$\begin{aligned} \triangle u + k^2u = 0 \;\;\;\; \;\; \;\text { in } \;\; \Omega \end{aligned}$$
(24)

The muffler efficiency is measured by computing the Transmission Loss (TL), which is the ratio of the incident to the transmitted sound powers. Several methods were proposed in the literature to calculate TL, such as: the three-point method [57], the four-pole transfer matrix [56] or the improved four-pole transfer matrix [58]. In this work, the improved four-pole transfer matrix is chosen as a fast method that could obtain the physical variables entering and exiting the muffler easily when it is coupled with BEM [49], following the linear acoustic four-pole network:

$$\begin{aligned} \bigg [ \begin{array}{c} u_\textrm{in} \\ u_\textrm{out} \end{array} \bigg ] = \bigg [ \begin{array}{c} A^* \, \, \, B^* \\ C^* \, \, \, D^* \end{array} \bigg ] \bigg [ \begin{array}{c} v_\textrm{in} \\ -v_\textrm{out} \end{array} \bigg ] \end{aligned}$$
(25)

in which u refers to the acoustic sound pressure of Eq. (24). v denotes the normal particle velocity. u and v are indexed with in and out to get along with the inlet and outlet (\(\Gamma _\textrm{in}\) and \(\Gamma _\textrm{out}\)), respectively. A negative sign appears in Eq. (25) as it is added to \(v_\textrm{out}\) to consider the opposite normal directions on the muffler inlet and outlet. The parameters \(A^*\), \(B^*\), \(C^*\) and \(D^*\) are computed using two BCs:

  1. 1.

    \(v_\textrm{in}\)=1 and \(v_\textrm{out}\)=0, so that, \(A^*=u_\textrm{in}\) and \(C^*=u_\textrm{out}\).

  2. 2.

    \(v_\textrm{in}\)=0 and \(v_\textrm{out}\)=-1, so that, \(B^*=u_\textrm{in}\) and \(D^*=u_\textrm{out}\).

Consequently, the four-pole parameters are produced as follows:

$$\begin{aligned} A &=A^*/C^* \\ B &= B^* - A^* D^*/C^*\\ C& = 1/C^* \\ D &=-D^*/C^* \end{aligned}$$
(26)

yielding the TL in (dB):

$$\begin{aligned} TL= 20 \log _{10} \bigg [ \frac{ 1}{ 2} |A + B/(\rho c) + C \rho c + D | \bigg ] + 10 \log _{10} S_\textrm{in}/S_\textrm{out} \end{aligned}$$
(27)

where \(S_\textrm{in}/S_\textrm{out}\) refers to the ratio of the inlet tube to the outlet tube areas. This term is neglected in this work since the two tubes are taken the same.

In this example, the linear system of equation considering the two explained BCs on the inlet and outlet tubes in addition to the rigid muffler body is constructed based on the normal derivative \(\frac{ \partial u}{ \partial \textbf{n}}\) at the collocation points \(\mathbf {p(\xi _c,\eta _c)}\). This can be written as a function of the normal particle velocity (v) as follows:

$$\begin{aligned} \begin{aligned}&\frac{ \partial u}{ \partial \textbf{n}}(\textbf{p}(\xi _c,\eta _c))= \sum _{e=1}^{Ne} \sum _{A=1}^{N} \Big [ \int _{\xi _{e_1}}^{\xi _{{e_1}+1}} \\&\int _{\eta _{e_2}}^{\eta _{{e_2}+1}} \dfrac{ \partial U^*(\textbf{p}(\xi _c,\eta _c),\textbf{q} (\xi ,\eta ) )}{ \partial \textbf{n} (\textbf{p}(\xi _c,\eta _c)) } R_{A}(\xi ,\eta )|J^e (\xi ,\eta )| d\xi d\eta \Big ] x_A \\ {}&+ c(\xi _c,\eta _c)\sum _{A=1}^{N} R_{A}(\xi _c,\eta _c) x_{A} = - i \rho \omega v \end{aligned} \end{aligned}$$
(28)

where \(\omega\) denotes the angular frequency and is computed as \(\omega =kc\). The sound speed c is considered in this example as 346.1 m/s in the medium of air of density \(\rho\) = 1.1839 kg/m\(^3\). v equals 0 on all rigid parts of the muffler. Equation (28) is solved twice fulfilling the two explained BCs while keeping the same coefficient matrix (the summation of the two terms in the left hand side of Eq. (28)). This gives the improved four-pole transfer matrix a preference in reducing the computational cost. The first stage of the problem is accomplished after obtaining two vectors of the unknowns \(x_A\) corresponding to the two BCs. Then, the acoustic pressure values required for the four-pole parameters are evaluated at the points \(\textbf{p}\) on the muffler inlet and outlet according to:

$$\begin{aligned}{} & {} u(\textbf{p})= \sum _{e=1}^{Ne} \sum _{A=1}^{N} \Big [ \int _{\xi _{e_1}}^{\xi _{{e_1}+1}} \nonumber \\{} & {} \int _{\eta _{e_2}}^{\eta _{{e_2}+1}} U^*(\textbf{p},\textbf{q} (\xi ,\eta ) ) R_{A}(\xi ,\eta )|J^e (\xi ,\eta )| \textrm{d}\xi \textrm{d}\eta \Big ] x_A \end{aligned}$$
(29)

The muffler in Fig. 35 is studied, where the length of the main chamber is \(L=\) 28.23 cm and its diameter is \(D=\) 15.32 cm. Inlet and outlet tubes are taken the same with diameter \(D_1=D_2=\) 4.86 cm, small thickness \(t=\) 0.2 cm and outside length 8.0 cm, while the internal extended lengths are taken differently: \(L_1=\) 13.1 cm and \(L_2=\) 6.1 cm. The muffler is modeled with NURBS polynomial degree 2 with two knot vectors: \(\Xi =\{ 0, 0, 0, 1/13, 1/13, 2/13, 2/13, 3/13, 3/13, 4/13, 4/13, 5/13, 5/13, 6/13, 6/13, 7/13, 7/13, 8/13, 8/13, 9/13, 9/13, 10/13, 10/13, 11/13, 11/13, 12/13, 12/13, 1, 1, 1 \}\) and \(\Upsilon = \{ 0, 0, 0, 0.25, 0.25, 0.5, 0.5, 0.75, 0.75, 1, 1, 1 \}\). The NURBS model is presented in Fig. 36.

The TL is evaluated by IGAinBEM and plotted in Fig. 37 as a spectrum in terms of different frequencies and compared against the values obtained by the different following methods:

  1. 1.

    IGABM with the improved four-pole transfer matrix [24].

  2. 2.

    Galerkin-FEM (GFEM) employing quadratic axi-symmetric analysis with triangular elements and the improved four-pole transfer matrix [59].

  3. 3.

    IGA with 3D models utilizing NURBS polynomial degree 3 and a mathematical formulation for the TL [60].

  4. 4.

    Standard BEM with quadratic shape functions and the four-pole transfer matrix [61].

  5. 5.

    Experimental data [61].

It can be seen that, IGAinBEM is in excellent agreement with IGABM and IGA, while there are some differences in the resonance zone in the cases of higher frequencies with comparison to GFEM. The experimental data are in agreement with the fore-mentioned methods as the noticed differences are related to the measurement errors. Standard BEM, which neglected the small thickness of the extended tubes, could not achieve the same accuracy for the cases of higher frequencies. This proves the capability of IGAinBEM and IGABM in treating such problems with small thicknesses due to the presence of the normal direction in the system matrix for collocation points at the opposite sides of any thin tube/wall, which is not the case in standard BEM. This appears also in fracture mechanics while handling crack surfaces with dual BEM [23].

Fig. 35
figure 35

Outer and internal views for a muffler with extended inlet/outlet thin tubes

Full size image
Fig. 36
figure 36

NURBS model and the corresponding control points grid for a muffler with extended inlet/outlet thin tubes

Full size image
Fig. 37
figure 37

Comparison between TL values obtained by different methods for a muffler with extended inlet/outlet thin tubes

Full size image

6 Conclusions

An indirect boundary element solution coupled with isogeometric analysis—forming isogeometric indirect BEM (IGAinBEM)—is proposed in this paper to solve 3D Helmholtz acoustic problems. The solution extends the method of fundamental solutions (MFS)—that utilizes discrete point sources—and introduces instead virtual surface sources placed directly on the scatterer boundary taking identically the scatterer geometry. This produces robust results and avoids the non-uniqueness problems associated with MFS that employs extensive investigation to detect the best positions for the point sources outside the domain giving stable results. The virtual surface sources are approximated with the same NURBS parameterizing the scatterer CAD model. IGAinBEM can handle general 3D geometries properly giving comparable results to other numerical methods. IGAinBEM requires less computational cost, since it constructs only one coefficient matrix arranged directly for the linear system of equations. This reduces the consumed time compared to other boundary element methods, such as the conventional BEM that constructs two coefficient matrices.

Similar to common boundary element methods, IGAinBEM does not need any domain discretization. Moreover, it can satisfy the Sommerfeld radiation condition directly with no far-field truncation boundaries. These two features support IGAinBEM over other domain-type methods such as finite element method.

The collocation scheme followed in this work is the famous Greville abscissae but with offsets at \(C^0\)-continuities. This scheme turns all singular integrals of order \(\mathcal {O} (1/r)\) into weakly singular integrals treated easily by more Gauss quadrature points, polar integration or Telles transformation method. It allows also the collocation points to be positioned in smooth surface. This leads to easy prediction of the normals at these collocation points without any complex calculations. Furthermore, all free-terms could be considered directly as 0.5. Most boundary element methods coupled with isogeometric analysis perform special treatment when they deal with highly distorted elements, such as the NURBS triangle elements containing the sphere poles. Nevertheless, this is not the case in this work, as the proposed collocation scheme could avoid this problem.

3D general geometries are studied by IGAinBEM, where comparisons are conducted against other BEM methods showing comparable results. Another practical example concerning the muffler problem with extended internal thin tubes is discussed and the results are plotted against other numerical methods and the experimental data as well, where the validity of the proposed technique is presented to handle such thin-walled geometries. It can be concluded that, IGAinBEM is a fast and convenient alternative but with some concerns about the non-uniqueness behavior at frequencies causing the eigenfrequency problem, which can be avoided by experience.