THB-Diff: a GPU-accelerated differentiable programming framework for THB-splines

Abstract

We have developed a differentiable programming framework for truncated hierarchical B-splines (THB-splines), which can be used for several applications in geometry modeling, such as surface fitting and deformable image registration, and can be easily integrated with geometric deep learning frameworks. Differentiable programming is a novel paradigm that enables an algorithm to be differentiated via automatic differentiation, i.e., using automatic differentiation to compute the derivatives of its outputs with respect to its inputs or parameters. Differentiable programming has been used extensively in machine learning for obtaining gradients required in optimization algorithms such as stochastic gradient descent (SGD). While incorporating differentiable programming with traditional functions is straightforward, it is challenging when the functions are complex, such as splines. In this work, we extend the differentiable programming paradigm to THB-splines. THB-splines offer an efficient approach for complex surface fitting by utilizing a hierarchical tensor structure of B-splines, enabling local adaptive refinement. However, this approach brings challenges, such as a larger computational overhead and the non-trivial implementation of automatic differentiation and parallel evaluation algorithms. We use custom kernel functions for GPU acceleration in forward and backward evaluation that are necessary for differentiable programming of THB-splines. Our approach not only improves computational efficiency but also significantly enhances the speed of surface evaluation compared to previous methods. Our differentiable THB-splines framework facilitates faster and more accurate surface modeling with local refinement, with several applications in CAD and isogeometric analysis.

1 Introduction

The standard representation used in computer-aided design (CAD) is a boundary representation (B-Rep), where the surfaces of the geometry are represented through single or multi-patch B-splines or Non-Uniform Rational B-splines (NURBS) [1]. NURBS surfaces are known for their smoothness, enabling complex shapes to be represented with fewer degrees of freedom. The flexibility of modifying a localized region of the surface without drastically altering the overall structure makes B-splines and NURBS highly effective. They can easily represent surfaces with high curvature due to their smooth and continuous characteristics, and their smoothness and continuity can be finely controlled by altering the degree of the basis function. Due to their ubiquitous nature, NURBS have also been directly used in analysis with the development of isogeometric analysis (IGA) [2]. While NURBS are ubiquitous in CAD and IGA, one of their main limitations is that NURBS do not offer adaptive local refinement due to their inherent tensor structure of the control points [3]. Consequently, several additional splines have been proposed to address this limitation. These include T-Splines [4,5,6], hierarchical B-splines (HB-splines) [3, 7], PHT-Splines [8], truncated hierarchical B-splines (THB-splines) [9,10,11], and locally refined (LR) B-splines [12]. Some of the more recent works include a new blended B-spline method tailored for unstructured meshes, ensuring consistency and optimal convergence [13]. Truncated T-splines were further developed to demonstrate superior performance in localized refinement for complex geometries [14]. Furthermore, a novel truncated hierarchical tri cubic spline construction (TH-spline3D) was recently proposed, which improved efficiency and adaptability on unstructured hexahedral meshes [15]. Collectively, these studies represent pivotal progress in improving the local refinement property of traditional NURBS or B-splines. Among these different representations, THB-splines are an ideal choice for refining B-splines for complex geometric shapes, utilizing a hierarchical tensor structure to perform adaptive and local refinement. Some of the key advantages of THB-splines over other spline representations are that they have reduced overlap of B-splines at different refinement levels and satisfy the partition of unity property.

To leverage the properties of THB-splines, several open source software such as GISMO have implemented THB-splines for different applications. Open source softwares such as DTHB3D_Reg [16], JISR [17], and NeuronSeg_BACH [18], employ THB-splines in the context of image analysis [19, 20]. In this paper, we will build a framework for evaluating THB-splines that is fast and useful for several downstream tasks (including tasks such as surface fitting in CAD, isogeometric analysis, or geometric deep learning).

Fig. 1

Overview of our THB-Diff module. The module uses GPU-accelerated evaluation of THB-splines. The local error metric is then used to generate adaptive refinement of the parametric space to enable the fitting of surfaces. The derivative of the surface evaluation points with respect to the input parameters is used to perform optimization using gradient descent

Building a differentiable framework for THB-splines requires a GPU-enabled approach due to the computational cost of forward and backward evaluation and compatibility with existing deep learning frameworks. However, the hierarchical tensor structure inherent in THB-splines creates unique computational challenges. Adaptive refinement and the management of reduced overlap of B-splines at different refinement levels require intricate dependencies between computations and a level of parallelism that is not easily achieved through traditional CPU-based methods. Graphics Processing Units (GPUs), with their data parallel architecture, can be adapted to handle multiple levels and localized refinements with reduced overlap. Unlike multicore CPUs, GPUs are designed to manage large-scale data parallelism, facilitating faster data processing and the precise manipulation of splines essential for modern CAD, IGA, and deep learning applications. There has been prior work on using GPUs to parallelize NURBS evaluation and modeling operations [21,22,23]. However, to the best knowledge of the authors, there are no GPU-accelerated frameworks for THB-spline evaluations. Our paper delves into GPU-accelerated THB-spline evaluations.

Alongside the growing need for parallelism in THB-spline evaluations, a critical dimension to explore is the integration of differentiable programming with splines. Differentiable programming is a paradigm that uses automatically computed derivatives or gradients of a function with respect to the input parameters to perform downstream operations in deep learning, such as gradient descent for training using the backpropagation algorithm. This key idea can be integrated with B-spline or NURBS evaluation, enabling a bridge between CAD modeling and deep learning methods. Deep learning methods have become prominent and efficient tools in geometry processing, such as automatically generating 3D models from point clouds and imaging data. There have been some prominent work to effectively segment point cloud data for 3D shape representation and object classification [24, 25]. Deep learning methods have also been integrated with meshes to perform mesh processing tasks efficiently [26]. While there has been some good progress in this field, the research into integrating CAD modeling with deep learning is not yet well explored. Some of the recent work includes SplineCNN [27], where a geometric deep-learning method is implemented using B-spline kernels. Building upon this foundation, using B-spline kernels to perform convolution operators on point cloud data and meshes has enhanced traditional deep learning methods like convolutional neural networks (CNNs) to handle point cloud and meshes to perform different geometry tasks.

Previous work on implementing differentiable programming frameworks with NURBS has explored imposing constraints in various optimization problems, with some notable examples being the two works utilizing differentiable programming for optimization using adjoint-based design optimization [28, 29] on applications in deep learning and CAD. These contributions have led to more advanced integrations between differentiable programming and geometric modeling. However, applying differentiable programming to NURBS presents intrinsic challenges. Evaluating partial derivatives with respect to control points, knots, and weights is a complex task. Evaluating basis functions, such as through the Cox de Boor recursive algorithm, adds further difficulty. There has been prior work, NURBS-Diff [30], for computing the derivatives of NURBS surfaces more accessible for differentiable programming. Yet, these solutions do not directly translate to THB-splines, where the hierarchical tensor structure adds layers of complexity, making it a non-trivial extension. THB-splines offer unique advantages, particularly for deep learning and other optimization applications. Their structure allows for more refined control and adaptability. Extending the concept of differentiable programming to THB-splines could unlock new potentials in complex surface modeling tasks, isogeometric analysis, and geometric deep learning. In this context, our work aims to pioneer a path in this exciting intersection of disciplines.

In this paper, we extend the differentiable programming framework to truncated hierarchical B-splines (THB-splines). We have proposed a new differentiable programming module, “THB-Diff”, which is the extension of the “NURBS-Diff” package (see Fig. 1). With the benefits of using fewer degrees of freedom with highly localized and adaptive support, THB-splines can now be integrated with deep learning methods for CAD modeling applications. Specifically,

• 1. We create a differentiable THB-splines evaluation that can be seamlessly integrated into deep learning modules, thereby extending the applicability of THB-splines in contemporary CAD modeling.

• 2. We enhance the computational efficiency of the THB-Diff package with GPU computing, providing a robust and adaptive solution for large-scale data processing in various surface modeling tasks.

• 3. We demonstrate the computational benefits of the THB-Diff package in the application of point cloud reconstruction through a detailed comparison with uniform refinement in terms of memory usage, computational efficiency, and accuracy.

The rest of the article is organized as follows. In Sect. 2, we provide a brief overview of THB-splines. We then introduce the differentiable programming for THB-splines in Sect. 3. In Sect. 4, we provide the algorithm and details for using the THB-Diff module for surface fitting. We provide benchmark examples and validation of the THB-Diff for surface fitting in Sect. 5. We demonstrate the results on real-world CAD geometries and point clouds in Sect. 6. Finally, we conclude in Sect. 7 with a discussion of the future work and potential applications of the module.

2 Mathematical formulation of THB-splines

In this section, we will briefly review the definition and construction of THB-splines. The process of constructing HB-splines follows a hierarchical subdivision system, where local refinement is carried out by overlapping B-splines from different refinement levels of spline spaces. HB-splines utilize the tensor product structure inherent in B-splines [31] and exhibit the advantageous characteristics of uniform B-splines, such as linear independence, local support, and non-negativity. Nevertheless, HB-splines exhibit a growing degree of overlap as refinement levels increase and fail to satisfy the partition of unity principle, which holds significant importance in their applicability for analysis, particularly in the context of isogeometric analysis. THB-splines were introduced as a modification of HB-splines, aiming to add a truncation approach that guarantees the satisfaction of the partition of unity. Moreover, the extent of overlapping among B-splines at various levels is reduced compared to HB-splines, improving matrix sparsity for numerical computations.

We first describe the mathematical formulation of HB-splines and then explain the truncation mechanism for constructing THB-splines. We will consider bivariate B-splines basis functions, although this mathematical formulation can be extended for multivariate splines. We start by defining a hierarchy of L nested spline spaces $S^1 \subset S^2 \subset \cdots \subset S^{L}$ over the corresponding nested hierarchy of parametric domains $\Omega ^{L} \subset \Omega ^{L-1} \subset \cdots \subset \Omega ^1$. At a particular refinement level l, we can define the parametric domain $\Omega ^{l}$ as

$$\begin{aligned} \Omega ^{l} = \mathcal{U}^l \times \mathcal{V}^l, \end{aligned}$$

(1)

where $\mathcal{U}^l = [u^l_1, u^l_2, \ldots , u^{l}_{m^l}]$ and $\mathcal{V}^l = [v^l_1, v^l_2, \ldots , v^{l}_{n^l}]$ are the knot spans with $m^l$ and $n^l$ as the number of knots in each parametric direction u and v at refinement level l.

Fig. 2

Schematic diagram of the construction of hierarchical basis $B^{l}_{{\textbf {k}}} \in \mathcal{H}^{l}$ (a) and the construction of the THB-spline basis $B^{l}_{{\textbf {k}}} \in \mathcal{T}^{l}$ (b). The B-splines marked active are shown in blue whereas the B-splines marked passive are shown in red

The bivariate B-spline basis function $B^{l}_{\textbf{k}}$, $\textbf{k} = [i, j]$ is the global index, is evaluated as the tensor product of univariate basis functions defined on the knot spans $\mathcal{U} = \{u_i, {u_{i+1}}, \cdots u_{i+p +1}\}$ and $\mathcal{V} = \{v_j, v_{j+1}, \cdots v_{j+q+1}\}$, where p and q are the spline degrees along the corresponding directions. The local support of each basis function $B^l_{{\textbf {k}}}$ is defined as $supp(B^l_{{\textbf {k}}}) = [u_i, u_{i+p+1}] \times [v_j, v_{j+q+1}]$. At a particular refinement level l, each bivariate basis function $B^{l}_{\textbf{k}} = \{ B^l_{\textbf{k}}|supp(B^l_{\textbf{k}})\subset \Omega ^l \wedge B^l_{\textbf{k}}\in S^l\}$ can be evaluated as a linear combination of a subset of bivariate basis functions at the refinement level $l+1$, defined as the children basis functions, such that

$$\begin{aligned} B^l_{{\textbf {k}}} = \sum _{{\textbf {r}}=1}^{n_c} c_{{\textbf {r}}} B^{l+1}_{{\textbf {r}}},\; \text {supp}(B_{{\textbf {r}}}^{l+1})\subseteq \text {supp}(B^l_{{\textbf {k}}}) . \end{aligned}$$

(2)

The number of children basis functions $n_c$ varies according to the degree of the B splines and the position of the basis functions on the open knot vector. For a univariate basis function of degree p, which is not at the boundary, the number of children basis functions is $p+2$. For a basis function at the boundary of the parametric domain, there are fewer children basis functions compared to interior basis functions because of the reduced support in open knot vectors at the boundary. The coefficients $c_{\textbf {r}}$ are computed using the Oslo knot insertion algorithm [32]. The construction of hierarchical basis $\mathcal{H}^l$ for two refinement levels l and $l+1$ (shown in Fig. 2a) is as follows:

• 1. At a particular coarse refinement level l, we identify a set of B-splines that are to be refined using certain refinability criteria. These B-splines are marked passive, while the corresponding spline space is denoted as $\mathcal{P}^l$. The remaining B-splines that are not refined form the active spline space $\mathcal{A}^l$.

• 2. The children basis functions at level $l+1$ of the refined B-splines are set as active, and are part of the spline space $\mathcal{A}^{l+1}$.

• 3. The hierarchical basis is constructed by collecting only the active splines at levels l and $l+1$, thus constructing the hierarchical spline space. Thus,

  $$\begin{aligned} \mathcal{H}^{l+1} = \mathcal{A}^{l} \cup \mathcal{A}^{l+1}. \end{aligned}$$

  (3)

We perform the above steps recursively to extend to several refinement levels.

Fig. 3

Schematic representation of truncation of basis functions at level 0 to create $\mathcal {T}^{1}$

The truncated hierarchical basis $\mathcal{T}^{l+1}$ is constructed in the same manner as HB-splines (Fig. 2b) but modifies certain active B-splines to satisfy the partition of unity property. As can be seen in the hierarchical basis shown in Fig. 3a, we identify active B-splines at the refinement level l that have partial support in $\mathcal{A}^{l+1}$ (shown in Fig. 3c) and truncate the B-splines by removing this partial support in the subdivision equation (Eq. 2). Thus,

$$\begin{aligned} \text {trunc} (B_{{\textbf {k}}}^{l}) = \sum _{\text {supp }(B_{{\textbf {k}}}^{l}) \not \subset \Omega ^{l+1}} c_{{\textbf {r}}} B^{l+1}_{{\textbf {r}}}. \end{aligned}$$

(4)

The THB-spline surface can be written as

$$\begin{aligned} {\textbf {S}}(u,v) = \sum _{l=1}^{L}\sum _{k=1}^{n_{b}} {\textbf {P}}^l_{{\textbf {k}}}\,{B}^l_{{\textbf {k}}}(u,v), \end{aligned}$$

(5)

where ${\textbf {P}}^l_{{\textbf {k}}}$ are the control points and $B^l_{{\textbf {k}}}(u,v)$ are the THB-spline basis functions defined over the parametric domain $[u, v] \in [0,1]\times [0,1]$. $n_b$ are the number of active basis functions at each refinement level and L are the maximum number of refinement levels.

3 Differentiable programming

For the efficient utility of THB-Diff for different applications, the evaluation of THB-splines must be GPU-accelerated and amenable to differentiable programming. Several recent works have been proposed to harness different programming paradigms to approximate function gradients. Authors such as [33, 34] propose differentiable operators for sorting-based tasks, while [35] compute gradients for various optimization problems by constructing linear approximations to discrete-valued functions. Furthermore, some methods incorporate structured priors as modules in deep learning frameworks, similar to [36,37,38]. In the context of surface modeling, [28] have performed automatic differentiation for surface derivatives in adjoint-based sensitivity analysis and [29] have used gradient-based optimization in aerodynamic shape optimization. Furthermore, [30] built a GPU-accelerated differentiable NURBS module, particularly for deep learning-based geometry applications. Our THB-Diff extends this paradigm by creating an adaptable and efficient framework for THB-splines, to leverage THB-splines for shape optimization and constraint imposition. The implementation process in THB-Diff involves two specific tasks: forward and backward evaluations.

In the $R^{3}$ space, let ${\textbf {P}}$ represent the control points of the THB-spline surface and let ${\textbf {S}}$ be the points obtained from the evaluation of the THB-spline surface. The total number of evaluation points on the THB-spline surface is $n_{\text {eval}}$. During the forward evaluation, the objective is to calculate ${\textbf {S}} = f_{\textsc {THB-Diff}}({\textbf {P}})$, where $f_{\textsc {THB-Diff}}$ represents the function to evaluate the THB-spline surface. For differentiable programming, given the gradient ${\partial \mathcal {L}}/{\partial \textbf{S}}$, we would like to obtain ${\partial \mathcal {L}}/{\partial \textbf{P}}$. Here, $\mathcal {L}$ represents a quantity of interest evaluated on $\textbf{S}$, which could be either some physical quantity, such as stress, or a loss function evaluated on the surface $\textbf{S}$ based on a target surface $\textbf{T}$. In the backward evaluation, THB-Diff evaluates ${\partial \mathcal {L}}/{\partial \textbf{P}} = b_{\textsc {THB-Diff}} ( {\partial \mathcal {L}}/{\partial \textbf{S}})$. In Sects. 3.1 and  3.2, we discuss the implementation of forward and backward evaluation in detail. In addition, we also discuss the GPU implementation for the acceleration of both forward and backward evaluations.

3.1 Forward evaluation

During forward evaluation, the basis functions corresponding to each evaluation point are precomputed and stored in an array. This approach is implemented to enhance the computational efficiency of evaluating the THB-spline surface during the optimization process, where many iterative steps are carried out, commonly found in surface fitting and geometric deep learning frameworks. These precomputed arrays must be updated after every adaptive refinement step, as adaptive refinement modifies the hierarchical spline space and, thereby, the nonzero basis functions associated with each evaluation point. The execution of a THB-spline surface evaluation on a GPU presents a significantly higher level of difficulty. This is due to the variable number of non-zero THB-spline basis functions at multiple refinement levels at every knot span, which deviates from the data parallelization framework ideal for GPU evaluation. This variability increases further when adaptive refinement is performed for a large number of refinement levels. Thus, the precomputation of basis functions is necessary to reduce the computational overhead. Another reason to precompute and store the basis functions is their utility during the backward evaluation.

Given a grid of parametric coordinates $\mathcal {G} = [u_{g}, v_{g}]$, $g \in [1, n_{\text {eval}}]$, we use forward evaluation to evaluate the THB-spline surface points at these parametric coordinates. The basis functions for each point in $\mathcal {G}$ are precomputed as described in Algorithm 1. The size of the array storing the precomputed basis functions $\mathbf {\Phi _{\text {NURBS}}}$ at all evaluation points for a NURBS surface of degree p is $[n_{\text {eval}} \times (p+1)^2]$. Unlike NURBS, where the number of nonzero basis functions at each evaluation point is the same ($(p+1)^2$), there is a variable number of nonzero B-splines from different refinement levels at each parametric coordinate for a THB-spline surface. The variable number of nonzero B-splines at each evaluation point results in an array of basis functions of non-uniform size $\mathbf {\Phi _{\text {THB}}}$, which cannot be directly used for GPU implementation. To integrate the THB-spline evaluation with the GPU implementation instead of a 2D array of variable size, we flatten the tensor product array and concatenate the basis function values at each evaluation point to create a single 1D array storing the basis function values for all the evaluation points. We also store the indices of the nonzero basis functions in B in a single 1D array and the number of non-zero basis functions for each evaluation point in the array $\mathrm {N_{\text {supp}}}$. Using $\mathrm {N_{\text {supp}}}$, we can split the array to evaluate the nonzero basis functions at each evaluation point. For each parametric coordinate $(u_g, v_g)$, we find the corresponding active knot indices at the current refinement level l and store the active knot index values for each evaluation point in $\mathcal {K}$. Next, associated with each knot index, we find the global indices of the nonzero B-splines that have support in the knot span $(u_{idx}, u_{idx+1}) \times (v_{idx}, v_{idx+1})$. The bivariate basis functions are evaluated as the tensor product of the univariate B-splines and multiplied by the subdivision coefficient matrix D [39]. These basis functions are stored in a 1D array $\mathbf {\Phi _{\text {THB}}}$ along with $\mathrm {N_{\text {supp}}}$.

Algorithm 1

Pre-computation of basis functions

Algorithm 2

Forward Evaluation CUDA kernel

In the forward evaluation, we compute the THB-spline surface points $\textbf{S}$ for each parametric coordinate in $\mathcal {G}$ as given in Eq. 5. The detailed algorithm for forward evaluation is given in Algorithm 2. As explained in [30], the forward evaluation is performed for all the parametric coordinates in $\mathcal {G}$. The hierarchical basis $\mathcal {T}$ poses a challenge for rapid evaluation, especially when computing over an extensive number of parameter coordinates. To improve the computational efficiency of the forward evaluation, we implement the parallelization of the forward evaluation at every point $(u_g,v_g)$ in the parametric space. For a given set of parametric coordinates $\mathcal {G}$, each GPU thread computes the THB-spline surface at one point $(u_g, v_g)$. We utilize the precomputed basis functions and knot spans during forward evaluation. This parallel evaluation can be extended for deep learning applications through an additional batch size parameter during parallelization.

For efficient memory management and computational cost, we precompute the basis functions on the CPU and then transfer them to the GPU at the beginning of the evaluation. These basis functions remain on the GPU until the end of the computation, as they are used in both forward and backward evaluations. This memory management strategy is designed to be lightweight, minimizing CPU-GPU memory transfer. Our approach seamlessly integrates with the PyTorch library through a custom THB-spline layer developed in PyTorch. The main evaluation code within this layer invokes our custom CUDA kernel, which is bound to PyTorch using Pybind11 [40]. This kernel is designed to be highly configurable; Users can set the total thread size (up to 1024 in our implementation) and partition the data into different blocks, effectively utilizing the GPU’s parallel processing capabilities. Users can also choose the block and thread sizes based on their GPU configurations, offering flexibility and adaptability. While we have developed this GPU-accelerated THB-spline evaluation method primarily for integration into deep learning frameworks, it is designed to be sufficiently modular to be used as a standalone component in a broader CAD modeling pipeline or in various optimization tasks.

3.2 Backward evaluation

In the backward evaluation, our aim is to compute the partial derivatives of the loss function $\mathcal {L}$ with respect to every parameter, in this case each control point in the active basis ${\textbf {P}}^{l}_{{\textbf {k}}}$ as ${\partial \mathcal {L}}/{\partial {\textbf {P}}^{l}_{{\textbf {k}}}}$, given the known gradient ${\partial \mathcal {L}}/{\partial {\textbf {S}}}$. Utilizing the chain rule, we express this as:

$$\begin{aligned} \frac{\partial \mathcal {L}}{\partial {\textbf {P}}^{l}_{{\textbf {k}}}} = \frac{\partial \mathcal {L}}{\partial \textbf{S}} \times \frac{\partial \textbf{S}}{\partial {\textbf {P}}^{l}_{{\textbf {k}}}}, \end{aligned}$$

(6)

where ${\partial {\textbf {S}}}/{\partial \textbf{P}}^l_{{\textbf {k}}}$ is given as $B^{l}_{{\textbf {k}}}(u,v)$.

For efficient computation, our implementation retrieves pre-computed basis functions and knot spans directly from GPU memory, where they are stored following their computation during the forward evaluation. This strategy is adopted to avoid frequent CPU-GPU data transfers, which can become a significant bottleneck. Our GPU parallel implementation in the backward evaluation is executed over evaluation points. For each evaluation point, a parallel thread is assigned to calculate the relevant components of $\frac{\partial \mathcal {L}}{\partial \textbf{P}^l_{{\textbf {k}}}}$. There is a subsequent reduction phase, in which the gradients contributed from different evaluation points to the same control point are summed. This summation uses atomic additions to ensure thread safety during parallel execution. Despite the intricate nature of surfaces, the memory footprint on the GPU remains modest. Moreover, the cost of retaining precomputed basis functions in GPU memory is easily outweighed by the computational time saved from reduced data transfers between CPU and GPU. To exploit the sparsity of the Jacobian matrix $\frac{\partial \mathcal {L}}{\partial \textbf{S}} \times \frac{\partial \textbf{S}}{\partial {\textbf {P}}^{l}_{{\textbf {k}}}}$, we adopt an efficient strategy that only evaluates nonzero basis functions within the support of a particular control point, made possible due to the local support property of the B-spline basis functions. Our backward function is part of a custom THB-spline layer in PyTorch. This PyTorch layer is therefore fully compatible with existing deep learning workflows and allows seamless integration into various neural network architectures. Our implementation supports batch processing in both forward and backward evaluations for deep learning applications. This capability allows the THB-spline layers to be used effectively within a mini-batch gradient descent optimization process, a standard in training deep neural networks. The user configures the thread size and partition into different blocks for GPU processing, similar to forward evaluation. This flexibility allows users to optimize the computation for their specific GPU. Algorithm 3 shows the brief overview of the algorithm proposed for backward evaluation.

Algorithm 3

Backward Evaluation CUDA kernel

3.3 Adaptive refinement

Adaptive refinement based on THB-splines is performed using a tolerance error-based refinement strategy. At each parametric coordinate $(u_g, v_g) \in \mathcal {G}$, we compute the error, which is problem-specific, defined as $\mathcal {E}(g)$. At certain parametric coordinates where the error exceeds the threshold error ($\mathcal {E}(g)\ge \delta _{e}$), the corresponding active B-spline basis functions in $\mathcal {T}$ which have non-zero support at these parametric coordinates are then marked as to be refined. These basis functions are accordingly set as passive and replaced with the corresponding children basis functions from the next level, which are set as active. The active basis functions, which have partial support of the children basis functions, are truncated as shown in Eq. 4. Besides refining the hierarchical space, the refinement procedure also involves updating the subdivision coefficient matrix and evaluating new control points in the refined regions. The detailed algorithm is shown in Algorithm 4. Utilizing an error metric to guide adaptive refinement enables the automated execution of refinement procedures throughout the optimization process. Furthermore, using a pre-established threshold limit ensures convergence within the specified error limit while minimizing the introduction of too many control points.

Algorithm 4

Refinement Procedure

4 Surface fitting framework

We present a surface fitting framework using our THB-Diff module, which leverages the principles of differentiable programming to effectively fit THB-spline surfaces to various geometric representations such as point clouds, triangle meshes, and NURBS surfaces. We initialize the truncated hierarchical basis ($\mathcal {T}$) of degree (p, q) on a parametric domain $(u,v) \in [0,1] \times [0,1]$ and specify the maximum number of refinement levels as L. At the first refinement level ($l_{0}$), we initialize a uniform mesh using control points ${\textbf {P}}^{0}$. The initialization of the control point positions is carried out so that the THB spline surface ${\textbf {S}}$ is a good initial approximation of the target surface ${\textbf {T}}$. Some additional parameters set at the beginning of the surface fitting process are the maximum number of iterations at each refinement level $n_{\text {iter}}$, the tolerance error value for refinement $\delta _e$, and the refinement scheduler $R_m$, which is a list of iteration indices where we check for refinement. $R_m$ is based on the convergence rate of the loss function; an ideal place to check for refinement is when the minimization of loss reaches a plateau.

Algorithm 5

Surface Fitting

We provide the overall algorithm for our surface fitting framework in Algorithm 5. We evaluate the surface using the GPU-accelerated forward evaluation function, starting from an initial guess of control points and coarse $\mathcal {T}^0$. We use a gradient-based optimization method (Adam optimizer [41]) to minimize a loss function $\mathcal {L}$ based on the mismatch error between the THB-spline surface and the target geometry. The gradient of the loss function with respect to the control points, which are the parameters for our surface fitting framework, is evaluated through backward propagation. We check for refinement and mark certain basis functions for refinement ($\mathcal {M}$) based on the threshold error limit at specific iteration indices specified in the array $R_{m}$. If no basis functions are marked for refinement (i.e., $\mathcal {M}$ is empty) when the refinement check was performed based on error tolerance, the algorithm terminates since we reached the required tolerance limit.

For fitting analytical surfaces (as shown in Figs. 4 and  5) and NURBS target representations (shown in Fig. 8), we used normalized mean squared error ($\mathcal {L}_{\textrm{NMSE}}$) as the loss metric. The loss function $\mathcal {L}_{\textrm{NMSE}}$ is summed over all evaluation points $\textbf{S}_i$, and is given as

$$\begin{aligned} \mathcal {L}_{\textrm{NMSE}}=\sum _{\mathbf {S_i}\in \textbf{S}}{n_{\textrm{PC}}\frac{||\textbf{S}_i-\textbf{T}_i||^2_2}{\sum _i^{n_{\textrm{PC}}}{\textbf{S}_i}}}. \end{aligned}$$

(7)

The normalized mean squared error metric is only applicable when there is a corresponding point in the target point cloud for every evaluation point on the THB-spline surface. Therefore, we only use this loss metric for fitting analytical surfaces and CAD models where we can establish a one-to-one correspondence between the THB-spline surface and the target surface. For fitting unstructured point clouds (Fig. 9), we use the one-sided Chamfer distance between the target point cloud ${\textbf {T}}$ and the surface points ${\textbf {S}}$. The $\mathcal {L}_{\text {CD}}$ is defined as

$$\begin{aligned} \mathcal {L}_{\textrm{CD}} = \sum _{\mathbf {T_i}\in \textbf{T}} \underset{\mathbf {S_j}\in \textbf{S}}{\min } ||\mathbf {T_i-S_j}||_2. \end{aligned}$$

(8)

However, relying solely on the chamfer distance loss metric will not result in a smooth-fitted surface since chamfer distance does not account for the topology of the underlying surface. Therefore, we add regularization terms to the loss function $\mathcal {L}$ and apply boundary conditions to enforce continuity. For the case of a point cloud representing a cylindrical shape, we have to enforce the seam boundary condition to preserve continuity. This is given as

$$\begin{aligned} \mathcal {L}_{\textrm{seam}} = \sum _{i}||\textbf{S}_i(0,v)-\textbf{S}_i(1,v)||^2_2. \end{aligned}$$

(9)

In addition, we employ a term that minimizes the maximum curvature of the surface to obtain a smoother surface. The loss function associated with curvature regularization is given as

$$\begin{aligned} \mathcal {L}_{\textrm{curv}} = \underset{\mathbf {S_i \in S}}{\text {max}}\;\left| \frac{\partial ^2\mathbf {S_i}}{\partial u^2}\right| + \underset{\mathbf {S_i \in S}}{\text {max}}\;\left| \frac{\partial ^2\mathbf {S_i}}{\partial u \partial v}\right| + \underset{\mathbf {S_i \in S}}{\text {max}}\;\left| \frac{\partial ^2\mathbf {S_i}}{\partial v \partial u}\right| + \underset{\mathbf {S_i \in S}}{\text {max}}\;\left| \frac{\partial ^2\mathbf {S_i}}{\partial v^2}\right| . \end{aligned}$$

(10)

The final loss function is a suitably weighted combination of all of these individual loss functions.

$$\begin{aligned} \mathcal {L} = \mathcal {L}_{CD} + \lambda _1\mathcal {L}_{\textrm{seam}} +\lambda _2\mathcal {L}_{\textrm{curv}}. \end{aligned}$$

(11)

We set the values of the weights $\lambda _1$ and $\lambda _2$ initially to match the scale of the chamfer distance. After that, we adjust the values of the weights empirically based on the accuracy of the fitting result.

The error indicators for marking refinement regions depend on target representation. It is the squared distance between corresponding points in the target and source for analytical surfaces or NURBS surfaces. In the case of fitting unstructured point clouds, we use the nearest neighbor distance for each surface point in the target point cloud.

$$\begin{aligned} \mathcal {E}_i = {\left\{ \begin{array}{ll} {n_{\textrm{PC}}\frac{||\textbf{S}_i-\textbf{T}_i||^2_2}{\sum _i^{n_{\textrm{PC}}}{\textbf{S}_i}}} &{} \text {for analytical surfaces, NURBS}\\ \underset{\mathbf {T_j}\in \textbf{T}}{\min } ||\mathbf {S_i-T_j}||_2 &{} \text {for unstructured point clouds} \end{array}\right. }. \end{aligned}$$

(12)

5 Surface fitting benchmarks and validation

In this section, the surface fitting framework is initially evaluated using the THB-Diff module on analytical surfaces for validation. We present a comparative analysis of the performance of the THB-Diff module with B-splines with uniform refinement. Additionally, we do a performance comparison between the GPU and CPU implementation. The analytical surface, depicted in Fig. 4b, is represented by the function

$$\begin{aligned} f(x,y) = x\,y\,{\text {sin}}(x)\,{\text {cos}}(y) \; | \;-5<x<5, -5<y<5. \end{aligned}$$

(13)

The B-spline surface at the first refinement level consists of uniformly distributed control points arranged in a $15 \times 15$ grid whose positions are randomly initialized as shown in Fig. 4a. We use the Adam optimizer to perform gradient descent for 300 iterations at each refinement level. The surface fitting result at the end of the first refinement level is shown in Fig. 4c. The normalized squared pointwise $L^2$ norm is evaluated between the fitted THB-spline surface and the target analytical surface and is used to perform the adaptive refinement. We use the normalized error metric shown in Eq. 12 and plot it in Fig. 4e. We set a predefined tolerance error based on the required fitting accuracy. The tolerance error is decided mainly based on the learning and convergence rate of the loss function. In Fig. 4, at iterations 300 and 600, refinement is carried out if the tolerance value is not reached.

As expected, the error is greater in regions characterized by more surface fluctuations or steeper gradients, such as the corners, in contrast to the comparatively smoother inner regions. Local refinement is carried out for basis functions whose local support the error crosses the tolerance value $\delta _{e} = 1.5\times 10^{-5}$. After two levels, we reach the target tolerance value. The final fitting result at the end of the second refinement level is shown in Fig. 4d. We can also see the corresponding error distribution in Fig. 4f, which shows the error is now within the established tolerance limit.

Fig. 4

Surface fitting with THB-Diff module for analytical surface $f(x,y)=x\,y\,\text{sin}(x)\,\text{cos}(y)$. The initialized THB-spline surface and the target surface are shown in (a) and (b), respectively. The predicted surfaces at the first and second refinement levels are shown in (c) and (d), respectively. The NMSE heatmaps for the first and second refinement levels are shown in (e) and (f), respectively

Fig. 5

Comparison of the predicted THB-spline surfaces and error distributions for different tolerance values $\delta _{e}$

5.1 Effect of tolerance limit

Within THB-Diff surface fitting framework, it is possible to establish an initial tolerance limit ($\delta _{e}$)at the start of the fitting procedure. Subsequently, the framework can automatically locally refine regions where the error exceeds the predetermined threshold limit. Therefore, control points are selectively added only where necessary, enhancing the precision and effectiveness of the fitting process. In Fig. 5, we provide the results of surface fitting for an analytical surface with respect to different initial tolerance values and show the associated locally refined grids. The analytical surface [9] for this study is given as

$$\begin{aligned}f(x,y)&= \frac{2}{3\,{\text {exp}}(\sqrt{(10\,x-3)^2+(10\,y-3)^2})}\\&+\frac{2}{3\,{\text {exp}}(\sqrt{(10\,x+3)^2 +(10\,y+3)^2})}\\&+\frac{2}{3\,{\text {exp}}(\sqrt{(10\,x)^2+(10\,y)^2})} \; |\\&-1<x<1, -1<y<1. \end{aligned}$$

(14)

We start with an initial grid of $15 \times 15$ control points and set the maximum refinement level to be 5. The initial THB-spline surface is also generated by randomly initializing the positions of the control points, similar to Fig. 4. This means that we are able to achieve a high fitting accuracy using a randomized surface. The sole requirement is that the initial surface matches the topology of the target surface. An initial surface that is closer to the target surface will generate a better fitting result. In Fig. 5, we provide the results of the surface fitting process together with the adaptively refined meshes for specified tolerance thresholds of $10^{-1}$, $10^{-2}$, $10^{-3}$, $10^{-4}$, and $10^{-5}$. With the tolerance value of 0.1, we can capture the fitting result at the first refinement level, seen in Fig. 5b. As the tolerance value is decreased, the grid undergoes adaptive refinement. Control points are automatically inserted in regions exhibiting high error, specifically near the three distinct peaks within the domain as seen in Fig. 5c–f. The refinement process is performed until the predetermined tolerance threshold limit or maximum refinement level is attained. Table 1 presents the degrees of freedom, maximum error ($\mathcal {E}$) value, and the maximum refinement levels for each tolerance value. The strategic placement of control points by the refinement algorithm allows for a higher concentration in areas characterized by sharper features in the target surface. This approach increases the geometric accuracy associated with the fitting process, achieving the same result with fewer control points than a uniformly refined mesh.

Table 1 Number of control points, maximum error and maximum refinement levels for different tolerance values $\delta _{e}$

5.2 Comparison with uniform refinement

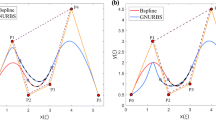
For the example shown in Figs. 4 and  5, we also compare the results obtained by the THB-Diff module with uniform refinement in Figs. 6 and  7, respectively. We perform adaptive mesh and uniform refinement for the error tolerance value $\delta _{e} = 1.5\times 10^{-5}$. We show the fitted surfaces and error distribution plots for adaptive and uniform refinement in Figs. 6 and  7. For the error distribution plots for the first analytical surface Fig. 6c and d, we notice slightly higher maximum $\mathcal {E}$ of $8.701 \times 10^{-6}$ with THB-Diff module as compared to the error of $1.21 \times 10^{-6}$ with the uniformly refined NURBS-Diff module. Similarly, for the second analytical surface Fig. 7c and d, we notice higher maximum $\mathcal {E}$ of $1.77 \times 10^{-4}$ with THB-Diff module as compared to the error of $9.51 \times 10^{-5}$ with the uniformly refined NURBS-Diff module. However, both examples show that the maximum error is within the tolerance limit (Table 2).

Table 2 Comparison of maximum $\mathcal {E}$, number of control points, and maximum refinement levels between the THB-Diff and uniform refinement

With the same tolerance limit, the degrees of freedom used by THB-Diff are lower than the uniformly refined mesh. Even at two levels of refinement, we can show a good reduction of the number of control points used to reach a certain tolerance limit as seen in Fig. 6b, while a significant reduction can be seen after five refinement levels in Fig. 7a. As the refinement levels increase or the tolerance limit decreases, the number of control points used by THB-Diff module will be significantly lower than the uniformly refined mesh.

Fig. 6

Comparison of the surface fitting result of the proposed THB-Diff module with uniform refinement with respect to accuracy and efficiency

Fig. 7

Comparison of the surface fitting result of the proposed THB-Diff module with uniform refinement with respect to accuracy and efficiency

5.3 Comparison of GPU versus CPU implementation

We compare the time per iteration of the GPU implementation of our THB-Diff module with the CPU implementation. Each iteration involves computing forward evaluation, loss, gradient, backward evaluation, and optimization steps. All tests were run on a workstation powered by an Intel i7 12700K with 32GB system memory and Nvidia Quadro T1000 with 4GB device memory. In Table 3, we show the speedup of our GPU code for different evaluation points while keeping the total number of control points fixed as $15 \times 15$. A significant acceleration of around 546-fold is observed in our GPU implementation for evaluation points of size $64 \times 64$. As the number of evaluation points increases to $1024 \times 1024$, the GPU implementation becomes significantly faster.

Table 3 Comparison of the GPU versus CPU surface fitting framework with $15 \times 15$ control points shown for different evaluation points

In Table 4, we fix the size of the evaluation points to $256 \times 256$ and test the speed-up of the GPU with respect to the CPU implementation for different control point sizes. However, it can be seen that the evaluation time mainly depends on the number of evaluation points and is independent of the number of control points. This is because the most compute-intensive step of the THB-spline evaluation is the control point multiplication step.

Table 4 Comparison of the GPU versus CPU surface fitting framework with $256 \times 256$ evaluation points shown for different control points

We notice a significant speed-up of our GPU version compared to the CPU version. The GPU version uses pybind11 to incorporate forward and backward evaluation kernels programmed in C++ and CUDA into the THB-Diff framework. Each point evaluation runs parallel in the GPU version, taking advantage of massively parallel hardware architecture. The CPU version runs sequentially in Python entirely with some PyTorch extensions. Additionally, the CPU version has longer processing times than the GPU version due to slower Python for loop performance while iterating through active basis functions. C++ loops outperform Python loops because C++ is a compiled and statically typed language with low-level access and efficient memory management, unlike Python, which is interpreted. This results in per-point evaluation being more computationally expensive in the CPU version compared to the GPU version while using the same algorithm. The performance boost mainly stems from GPU parallelism, with a minor contribution from using C++ and CUDA in forward and backward evaluations. Similar to all GPU-accelerated algorithms, our implementation uses many cores to execute tasks concurrently.

6 CAD applications

In this section, we demonstrate the performance of our module on two numerical examples: a closed-surface CAD model (NURBS surface) and a point-cloud dataset of an artery model. We now look at some numerical examples of surface fitting with the THB-Diff module.

6.1 NURBS surface fitting

Fig. 8

Using the THB-Diff module to fit a THB-spline surface to a Ducky NURBS surface. The highlighted region on the parametric domain shown in (g) corresponds to the highlighted region on the surface shown in (d)

In Fig. 8, we demonstrate the fitting of a THB-spline surface to a single patch NURBS surface representing a complex CAD model of a Ducky. The THB-spline fitting with three levels of refinement enables a closer fit using local refinement. The need for local refinement arises in regions with high curvature; for the Ducky model, these regions are predominantly located around the head and tail regions. Local refinement helps reduce error in these regions, leading to a more accurate representation of the actual model. The fitting process starts with an initial grid of randomly placed control points $15\times 15$, evaluation points $512\times 512$, and the error tolerance limit $10^{-5}$. After initial fitting with coarse mesh, the error is high in all regions, exceeding the tolerance limit as seen in Fig. 8e. The parametric mesh is uniformly refined due to fewer degrees of freedom offered by the coarse initial mesh. After uniform refinement, the error is significantly higher around the neck region (see Fig. 8f). The next level of refinement is carried out in the upper part of the parametric grid to reduce the fitting error near the neck region (see Fig. 8g).

The correspondence between parametric grid refinement and the corresponding region in the model can be identified by the relative increase in the density of the control points. The fitting algorithm terminates here since the error has reached below the tolerance limit. This result demonstrates the ability of our THB-Diffframework to fit a THB-spline surface to an existing NURBS model with high accuracy.

Fig. 9

Using the THB-Diff module to fit a THB-spline surface to a point cloud of a patient-specific aorta. The top and bottom edges of the parametric domain form the seam highlighted in Fig. 9b

6.2 Point cloud fitting

We also demonstrate the capability of THB-Diff to fit a THB-spline surface to an unstructured point cloud. Unlike analytical surfaces and CAD models, fitting point clouds is not as straightforward due to the lack of underlying connectivity information. This means that there is no one-to-one correspondence between the evaluated points of the THB-spline and the points of the point cloud; hence, NMSE is undefined. To overcome this challenge, we used a combination of nearest-neighbor-based loss metric, such as the chamfer distance, coupled with boundary conditions as explained in Sect. 4.

We chose a point cloud representing a patient-specific aorta from the open-access vascular database [42]. The target point cloud shown in Fig. 9a has 10,533 points. The fitting procedure was initialized using an initial cubic B-spline surface of $11\times 11$ control points and $100\times 100$ evaluation points. The initial THB-spline surface is shown in Fig. 9b. Here we also construct a cylinder whose axis is bent in the middle to make the fitting process easier to achieve a good accuracy. We ran our surface fitting framework using the loss shown in Eq. 11. The error tolerance for refinement was 0.001. The initial fitting after 5000 iterations (Fig. 9c) is a good approximation of the point cloud, but has some high error regions in the interior and on the right side, which corresponds to the annulus of the aorta (Fig. 9f). The algorithm then identifies the basis functions for refinement based on the nearest-neighbor distance between the surface and the point cloud (Eq. 12). Figure 9d and g show the refined surface and the error map after 10,000 iterations. It can be seen that the refinement reduced the high error regions observed in the previous level. We refined the surface to reach a tolerance limit 0.001 in Fig. 9e. These results demonstrate that THB-spline surfaces can be effectively fitted to unstructured point clouds using the chamfer distance, regularization loss terms, and boundary conditions.

7 Conclusions

Using the differentiable programming paradigm, we have developed a differentiable THB-spline module for surface fitting and deep-learning applications. Our THB-Diff module is accelerated by GPU data-parallel algorithms, which provide a significant speed-up over CPU implementations. We benchmark our THB-Diff module using analytical surfaces. We show the applicability of our THB-Diff to surface fitting applications with examples of fitting to a complex NURBS surface and an unstructured point cloud. In all cases, we show that the adaptive refinement of THB-splines enables the representation of complex surfaces with fewer degrees of freedom.

There are still a few avenues for future research. Our THB-Diff module can be further enhanced by supporting the surface fit of the noisy point cloud, creating a robust point cloud to the THB-spline pipeline. In addition, currently, the basis function refinement is processed on the CPU because of the complex bookkeeping involved with THB-spline data structures. Therefore, refining a dense set of control grids is relatively slow. Further work is required to develop a GPU-accelerated concurrent refinement algorithm for data-parallel execution.

In general, our THB-Diff module utilizing the state-of-the-art differentiable programming paradigm will enable a better integration of CAD with deep learning applications. We will release our THB-Diff module as an open source software along with this paper, enabling the wide adoption of this approach for diverse machine learning applications.