1 Introduction

Modern high-fidelity, nonlinear computational analysis is mostly computationally intensive in terms of time and memory. In particular, many multiphysics analyses adopt a partitioned method in which the solvers regarding each type of physics are executed separately. Such an approach also requires computation for the data interpolation among different types of discretization and executes iterative computation within a single time step, demanding even more intensive computation. Consequently, model order reduction (MOR) has been suggested to alleviate the computational time and memory consumption. Two types of MOR frameworks exist: intrusive and non-intrusive. Intrusive MOR depends upon the governing equation to construct the reduced bases. The Galerkin projection is one of the most widely used approaches for projecting an ensemble of the full-order model (FOM) results into the governing equation [1, 2]. However, a parametric analysis may become extremely challenging when the algorithm is not explicitly established as it manipulates the governing equation directly [3]. Instead, an approach that is completely data-driven, non-intrusive MOR (NIMOR) may be considered. NIMOR aims to discover the embedded pattern in the FOM dataset and rescale those to a much smaller dimensionality. Unlike intrusive MOR, NIMOR is independent of the governing equation, thereby making it extremely versatile.

Among the various MOR methods, linear subspace MOR (LS-MOR) has been widely considered as it is mathematically rigorous and efficient. LS-MOR has been successfully employed in fluid dynamics, flow control, structural dynamics, aeroelasticity, and fluid–structure interaction (FSI) [4,5,6,7,8,9,10,11]. However, LS-MOR may require an excessive number of subspaces to accurately represent a nonlinear, complex FOM. For example, in complex turbulent fluid flows, proper orthogonal decomposition (POD) extracts its modes with respect to the energy ratio and the details are filtered out [12]. These details are usually excluded, because they are very low energy and the corresponding coefficients are quite random. LS-MOR methods are generally known to be less effective on systems with a slowly decaying Kolmogorov n-width, such as advection-dominated, sharp-gradient, and multiphysics systems [12,13,14,15].

Recent exponential development in the field of machine learning has enabled neural networks to be used for MOR. Specifically, the autoencoder has become a viable nonlinear MOR method where a shallow, well-trained autoencoder with a linear activation function is known to behave similarly to POD [16,17,18]. Instead of the linear activation functions, many autoencoders adopt nonlinear activation functions, using them to generate nonlinear subspace [17, 18]. Such an autoencoder-based method has been implemented widely to reduce the dimensionality of various engineering problems, including fluid dynamics, convection problems, and structural dynamics [14, 19,20,21,22,23,24]. However, the performance of an autoencoder as a generative neural network is known to be quite limited [25]. The deterministic aspect of its loss function, which was designed to only reconstruct the input, limits autoencoders to generate diverse outputs. Attempts to enhance the generative capability have led to the development of the variational autoencoder (VAE) and generative adversarial network (GAN) [26, 27]. These methods implement probabilistic loss functions that construct a dense and smooth latent space. Between the two alternatives, VAE was selected for use in this study owing to its stable training property [10]. VAE has been widely studied for use in the field of computer vision, but it has also been used to interpolate dynamic systems [10, 11].

VAE in its simplest form, vanilla VAE, is capable of generating data of significantly superior quality compared with the autoencoder. However, VAE commonly experiences a phenomenon known as posterior collapse, where the generative model learns to ignore a subset of the latent variables [28]. The posterior collapse was easily alleviated by applying a technique known as Kullback–Leibler divergence (KL divergence) annealing, or \(\beta \)-VAE [29,30,31,32,33,34]. Another problem with vanilla VAE is that it is restricted to a shallow network, limiting its expressiveness. Vanilla VAE tends to perform worse as the network becomes deeper due to the loss of long-range correlation and its performance was found to be insufficient when processing complex data [10, 32]. Deep hierarchical VAEs, such as the LVAE, IAF-VAE, and NVAE, have been developed to enhance the performance of vanilla VAE [30, 32, 35]. These VAEs mainly adopt a type of residual cells that connect the encoder and decoder directly without passing through the latent space. Similar to U-nets, the skip connections allow bidirectional information sharing between the encoder and decoder, thereby preventing the loss of long-range correlation.

Recently, various types of VAEs have been adopted as a nonlinear MOR method owing to their superior generative capability compared to conventional autoencoders. VAEs have been adopted for flow problems [36,37,38,39], transonic flow [40, 41], numerics [42], biology [43], brain MRI images [44], and anomaly detection [45, 46]. While earlier studies adopted the simplest convolutional VAE, many recent studies consider \(\beta \)-VAE due to its near-orthogonal latent space [33, 34]. Although previous studies showed that \(\beta \)-VAE may successfully construct nonlinear subspace, the majority of networks used in those studies were quite shallow. The use of shallow networks may result in insufficient expressiveness if the input data have a large number of degrees of freedom (DOFs) and exhibit a complex response.

Instead, a deep hierarchical VAE, least-squares hierarchical VAE (LSH-VAE), is proposed for nonlinear MOR of a dynamic system. LSH-VAE is a deep hierarchical network that incorporates a modified loss function similar to that of \(\beta \)-VAE. The deep hierarchical structure comprises a very deep, stable network (>100 layers) with highly expressive and accurate interpolation results. The modified loss function consists of a hybrid weighted least-squares and Kullback–Leibler divergence function that alleviates posterior collapse and enhances the orthogonality of the latent space [33, 34, 47]. The least-squares error in the loss function is also known to enhance the accuracy when used on a continuous dataset [11].

A very deep VAE (>100 layers) implemented for nonlinear MOR has not yet been reported. The present framework is validated by solving the following three problems. First, a standard two-dimensional FSI benchmark problem developed by Turek and Hron is exemplified [48]. Then, the highly nonlinear aeroelastic phenomenon of limit cycle oscillation (LCO) is considered to examine the accuracy of the proposed framework under nonlinearity. Finally, the flow surrounding a three-dimensional cylinder is analyzed to establish the capability of the current framework to accommodate a system with significantly many DOFs. The computational efficiency and accuracy is assessed and compared with those of existing nonlinear MOR methods.

2 Machine-learning methods

This section provides the theoretical background pertaining to the machine-learning methods. The formulation of the proposed network, LSH-VAE, is presented on the basis of the existing convolutional autoencoder and \(\beta \)-VAE.

2.1 Convolutional autoencoder (CAE)

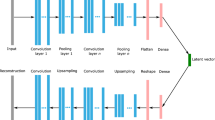
A convolutional autoencoder (CAE) is a neural network that is trained to output data that are similar to its input. The typical architecture of the CAE, shown in Fig. 1, enables the encoder to compress the input data into a smaller latent dimensionality. The decoder then expands the latent variable back to its original dimensionality. By training both the encoder and decoder, CAE learns to extract important features of the input dataset. The latent variable contains the embedded features recognized by the CAE that can be used as the reduced bases in the ROM. The interpolation of data using CAE is conducted by interpolating the latent variables. The interpolated latent variable contains the interpolated features, which leads to the interpolation of the input data.

Fig. 1
figure 1

Architecture of a typical convolutional autoencoder

Full size image
Fig. 2
figure 2

Architecture of a typical VAE

Full size image

The loss function of the CAE is quite intuitive. CAE takes the input, x, and passes it through the encoder, \(\Phi \), to obtain the latent vector, z. Then, the decoder, \(\Psi \), receives the latent vector and generates the output, y. The output, y, is compared against the input, x, using the mean-squared error (MSE) loss function. In this way, the CAE is trained, such that the difference between y and x is reduced, aiming for a more accurate reconstruction of the input. The equations for the encoder and decoder network are presented in Eq. (1), where the loss function is shown in Eq. (2)

$$\begin{aligned} z= & {} \Phi (x), \quad y = \Psi (z) \end{aligned}$$
(1)
$$\begin{aligned} L= & {} \textrm{MSE}(\Psi (\Phi (x))-x). \end{aligned}$$
(2)

The simplest form of CAE, known as the vanilla CAE, has been shown to produce unsatisfactory interpolation outcomes [25]. Hence, derivatives thereof, such as VAE and GAN, may be utilized to enhance the performance.

2.2 Variational autoencoder (VAE)

VAE and autoencoder share a similar architecture. The largest difference lies therein that the encoder of VAE utilizes probabilistic latent variables instead of discrete ones. The probabilistic encoder models the latent feature probability distribution. The resultant latent space is continuous and smooth, enabling higher quality outcomes to be generated. Several methods have been developed to model the probability distribution of latent codes. VAEs, including Dirichlet, von Mises–Fisher, Bernoulli, Gaussian mixture, and Gaussian normal distributions, have been developed [26, 49,50,51,52]. Here, a Gaussian normal VAE is considered as it is one of the most widely used VAEs for real-valued data. The encoder of a Gaussian VAE extracts the mean, \(\mu \), and the variance, \(\sigma \), which are used to generate the latent variable, z. A typical VAE structure can be observed in Fig. 2.

VAE aims to efficiently infer the intractable posterior distribution, \(p(z \vert x)\). It is performed by adopting an approximate posterior, \(q(z \vert x)\), because determining the true posterior is quite challenging. Here, the encoder or inference network is represented by \(q(z \vert x)\), whereas the decoder network is denoted as \(p(x \vert z)\).

Kullback–Leibler (KL) divergence is the expectation of the difference between two distributions, which always has a positive value. The KL divergence between the approximate and the real posterior is written as Eq. (3)

$$\begin{aligned} D_{KL}(q(z \vert x) \vert \vert p(z \vert x))=-\int q(z \vert x)\log (\frac{p(z \vert x)}{q(z \vert x)})\textrm{d}z\ge 0.\nonumber \\ \end{aligned}$$
(3)

Applying Bayes’ theorem to Eq. (3) yields Eq. (4)

$$\begin{aligned}{} & {} D_{KL}(q(z \vert x) \vert \vert p(z \vert x)) = -\int q(z \vert x) \log (\frac{p(x \vert z)p(z)}{q(z \vert x)p(x)}) \textrm{d}z \nonumber \\= & {} \quad -\int q(z \vert x) \log (\frac{p(x \vert z)p(z)}{q(z \vert x)}) \textrm{d}z + \log p(x)\ge 0. \end{aligned}$$
(4)

Equation (4) can be rewritten as Eq. (5). The application of logarithmic rules to Eq. (5) yields Eq. (6)

$$\begin{aligned} \begin{aligned} \log p(x) \ge \int q(z \vert x)\log \frac{p(x \vert z)p(z)}{q(z \vert x)}\textrm{d}z \end{aligned} \end{aligned}$$
(5)
$$\begin{aligned} \log p(x){} & {} \ge \int q(z \vert x) \log (\frac{p(z)}{q(z \vert x)})\textrm{d}z \nonumber \\{} & {} +\int q(z \vert x)\log p(x \vert z) \textrm{d}z\nonumber \\{} & {} \ge {\mathbb {E}}_{q(z \vert x)}[\log p(x \vert z)]-D_{KL}(q(z \vert x) \vert \vert p(z)). \end{aligned}$$
(6)

The right-hand side of Eq. (6) is the evidence lower bound (ELBO). VAE aims to maximize ELBO which maximizes the logarithmic probability of the data by proxy. Following the convention of minimizing the loss function, the right-hand side of Eq. (6) is converted to Eq. (7), which is the goal of VAE

$$\begin{aligned} \min [ -{\mathbb {E}}_{q(z \vert x)}[\log p(x \vert z)]+ D_{KL}(q(z \vert x) \vert \vert p(z)) ]. \end{aligned}$$
(7)

The goal of VAE is to minimize both the reconstruction and KL divergence loss. In Eq. (7), the first and second terms correspond to the reconstruction loss and the KL divergence (KLD) loss, respectively. The KL divergence loss enforces the decoder (approximate posterior) to become similar to the inverse of the encoder.

The loss function in Eq. (7) has to be differentiable to minimize it during the training. Usually, the KLD term can be integrated analytically [26]; however, the reconstruction loss is not directly differentiable. To enforce the reconstruction loss to be differentiable, the reparameterization technique is adopted [26].

First, Gaussian sampled random noise, \(\varepsilon \), is introduced. The latent variable z is formulated, as shown in Eq. (8), to introduce the mean and standard deviation to the equation

$$\begin{aligned} z=\mu +(\sigma \times \varepsilon ),~ \varepsilon \sim {\mathcal {N}}(0,1). \end{aligned}$$
(8)

Because the latent variable is formulated as in Eq. (8), the KL divergence in Eq. (7) is rewritten as Eq. (9), assuming the posterior and prior follow a Gaussian distribution:

$$\begin{aligned} D_{KL}(q(z\vert x)\vert \vert p(z)) \approx \frac{1}{2}\sum (\sigma ^2+\mu ^2-(\log (\sigma ^2)+1)). \end{aligned}$$
(9)

The latent variable with the reparameterization technique enforces the latent space to be stochastically determined. The reparameterization enables the reconstruction loss to be differentiable by the Monte Carlo method. Further details and the step-by-step derivation of the VAE loss function can be found in reports by Kingma and Odaibo [26, 53].

2.3 Least-squares hierarchical variational autoencoder (LSH-VAE)

Conventional vanilla VAE is limited to shallow networks due to the vanishing gradient and the loss of long-range correlation. However, shallow networks may lack expressiveness on complex systems with a significant number of DOFs. In this study, a deep VAE with a hierarchical structure is proposed to enhance the performance specifically to alleviate the loss of long-range correlation and stabilize the training process of a very deep network. The hierarchical structure creates direct passages between the earlier layers of the encoder and the latter layers of the decoder to circumvent the middle layers. These direct passages enable bidirectional information sharing between the encoder and decoder network. The bidirectional information enables the earlier layers of the VAE to greatly affect the outcome, thus, alleviating the loss of long-range correlation. The diagram in Fig. 3 shows the hierarchical structure of LSH-VAE.

Fig. 3
figure 3

Hierarchical structure of LSH-VAE

Full size image

In the hierarchical VAE, the latent variables are divided into L groups, where the ith latent variable is denoted as \(z_i, i=1,\ldots , L\). By dividing by the latent dimension, the prior, p(z) and approximate posterior distribution, \(q(z\vert x)\) are expressed as Eq. (10)

$$\begin{aligned} p(z)= & {} p\left( z_{L}\right) \prod _{i=1}^{L-1} p\left( z_{i} \vert z_{i+1}\right) \nonumber \\ q(z \vert x)= & {} q\left( z_{1} \vert x\right) \prod _{i=2}^{L} q\left( z_{i} \vert z_{i-1}\right) . \end{aligned}$$
(10)

\(p\left( z_{i} \vert z_{i+1}\right) \) and \(q\left( z_{i} \vert z_{i-1}\right) \) of Eq. (10) can be expressed as Eq. (11). In the equation, \({\mathcal {N}}(z|\mu ,\sigma ^2)\) denotes the Gaussian probability density function of z, \(\mu \) denotes the mean, and \(\sigma ^2\) denotes the variance. Equation (11) shows that the distribution of each latent group follows the Gaussian normal:

$$\begin{aligned} \begin{aligned} p(z_{i} \vert z_{i+1})&={\mathcal {N}}(z_{i} \vert \mu (z_{i+1}), \sigma ^{2}(z_{i+1}))\\ p(z_{L})&={\mathcal {N}}(z_{L} \vert 0, I)\\ q(z_{i} \vert z_{i-1})&= {\mathcal {N}}(z_{i} \vert \mu (z_{i-1}), \sigma ^{2}(z_{i-1}))\\ q(z_{1} \vert x)&={\mathcal {N}}(z_{1} \vert \mu (x), \sigma ^{2}(x)), \end{aligned} \end{aligned}$$
(11)

The loss function for hierarchical VAE is shown in Eq. (12). The loss function is obtained by computing the KL divergence separately for each group from Eq. (7)

$$\begin{aligned} \begin{aligned} \min [ -{\mathbb {E}}_{q(z \vert x)}[\log p(x \vert z)]+ D_\textrm{K L}(q(z_L \vert x) \ \vert p(z_L))\\ +\sum _{i=1}^{L-1} {\mathbb {E}}_{q(z_{<i} \vert x)}[D_\textrm{K L}(q(z_{i} \vert z_{<i}, x) \ \vert p(z_{i} \vert z_{>i}))]]. \end{aligned} \end{aligned}$$
(12)
Fig. 4
figure 4

Detailed architecture of the encoder and decoder blocks of LSH-VAE

Full size image

By breaking down the KL divergence into groups, bidirectional information flows are created between the inference and generative network. Detailed descriptions and the derivation of the deep hierarchical structure of VAE can be found in [30].

The present LSH-VAE adopts hierarchical structures inspired by LVAE, IAF-VAE, and NVAE [30, 32, 35]. The latent variables in the hierarchical VAE are formed by both bottom–up and top–down information. The latent variables that are output by each of the groups share information (from the encoder and decoder) to the next decoder block. Because the information of the encoder and decoder network is shared via latent variables, the network delivers higher performance.

In the hierarchical structure, LSH-VAE implements a hybrid weighted loss function. The loss function consists of the mean-squared error (MSE) and KL divergence instead of conventional binary cross entropy. The use of the MSE as a reconstruction error has been known to be successful for continuous datasets [11].

From Eq. (12), the reconstruction portion, \(-{\mathbb {E}}_{q(z \vert x)}\)\([\log p(x \vert z)]\), is considered. \(\log p(x \vert z)\) of the reconstruction loss can be expressed as Eq. (13), where the output of the decoder (\(p(x\vert z)\)) is expressed with its mean, \(\mu _{\theta }(z)\) and variance, \(\sigma ^2_{\theta }(z)\)

$$\begin{aligned} \begin{aligned} \log p(x \vert z)&= \log \left( \frac{1}{\sqrt{(2\pi \sigma ^2_{\theta }(z))}}e^{-\frac{(x-\mu _{\theta }(z))^2}{2 \sigma ^2_{\theta }(z)}}\right) \\&=\frac{1}{2}\log 2\pi \sigma ^2_{\theta }(z) + \frac{(x-\mu _{\theta }(z))^2}{2\sigma ^2_{\theta }(z).} \end{aligned} \end{aligned}$$
(13)

Considering that VAE aims to maximize ELBO, \(\log p(x \vert z)\) should be minimized. The right-hand side of Eq. (13) should be minimized by reducing both \(\sigma ^2_{\theta }(z)\) and \((x-\mu _{\theta }(z))^2\). In the case of the real-valued data, it is a common practice to assume that the output follows a Gaussian normal distribution [26]. Thus, \(\sigma ^2_{\theta }(z)\) becomes \(\sigma ^2_{\theta }1\), and Eq. (13) is written as Eq. (14)

$$\begin{aligned} \frac{1}{2}\log 2\pi \sigma ^2_{\theta }(z){} & {} + \frac{(x-\mu _{\theta }(z))^2}{2\sigma ^2_{\theta }(z)}=\frac{1}{2}\log 2\pi \sigma ^2_{\theta }\nonumber \\{} & {} + \frac{(x-\mu _{\theta }(z))^2}{2\sigma ^2_{\theta }}. \end{aligned}$$
(14)

The first term in Eq. (14) is a constant. Only the second term needs to be minimized. By assigning the output of the decoder to \({\hat{x}}\), minimizing \(\log p(x|z)\) becomes equivalent to minimizing the MSE loss between x and \({\hat{x}}\).

Adopting the MSE loss, the loss function of LSH-VAE is shown in Eq. (15), where the coefficients \(\alpha \) and \(\beta \) denote the weights of the MSE and KL divergence, respectively

$$\begin{aligned} \begin{aligned}&\min _{\phi , \theta } [\alpha \textrm{MSE}(x, {\tilde{x}})+ \beta D_\textrm{K L}(q(z \vert x) \ \vert p(z))\\&\quad +\sum _{i=1}^{L-1}{\mathbb {E}}_{q(z_{<i} \vert x)}[\beta D_\textrm{K L}(q(z_{i} \vert z_{<i}, x) \ \vert p(z_{i} \vert z_{>i}))]]. \end{aligned} \end{aligned}$$
(15)

Usually, the weights \(\alpha \) and \(\beta \) are set to be \(\alpha / \beta _{target}\approx 10^6\). During the training, \(\alpha \) is a fixed value, whereas \(\beta \) is a variable that varies with respect to the epochs. The variable \(\beta \) is implemented to prevent posterior collapse in which some latent variables become inactive. This method is known as KL-annealing or \(\beta \)-VAE, where \(\beta \) is formulated as Eq. (16) [29]

$$\begin{aligned} \beta = {\left\{ \begin{array}{ll} 1\times 10^{-4}\beta _\textrm{target} &{}\text {if epoch} <0.3n_\textrm{epochs}\\ \beta _\textrm{target}\frac{\textrm{epoch}}{n_\textrm{epochs}}&{}\text {if epoch} >0.3n_\textrm{epochs}. \end{array}\right. } \end{aligned}$$
(16)

During the training, \(\beta \) is initially assigned a low value, such that LSH-VAE behaves as an autoencoder. During the first few epochs, the input data are mapped on the latent space. Beyond a few epochs, \(\beta \) is gradually ramped up to a prescribed constant, \(\beta _\textrm{target}\), such that LSH-VAE may behave as a VAE to generate smooth latent space. Ideally, a large \(\beta _\textrm{target}\) is desirable. A large \(\beta _\textrm{target}\) enables the construction of a compact and well-organized latent space. However, a large \(\beta _\textrm{target}\) degrades the reconstruction loss. In practice, the largest \(\beta _\textrm{target}\) that minimally degrades the reconstruction loss is desired.

3 Present framework

3.1 Architecture of the least-squares hierarchical VAE (LSH-VAE)

LSH-VAE adopts a one-dimensional (1D) convolutional layer to accommodate the transient response of the unstructured grids. The use of a 1D convolutional layer enables the temporal continuity of the physical variables to be considered. The encoder and decoder of the LSH-VAE consist of the blocks discussed in the previous section, where a detailed schematic of these blocks is shown in Fig. 4.

Being a deep neural network (DNN), LSH-VAE encoder and decoder blocks are composed of stacks of multiple layers. These layers consist of the following layers: spectral normalization (SN), 1D convolution, dense, exponential linear unit (ELU), Swish, and batch normalization (BN). Swish, and ELU nonlinear activation functions are chosen as their continuous derivatives enhance the stability of a DNN [54]. The LSH-VAE implements a normalization-activation sequence instead of the conventional activation-normalization sequence. Such a sequence is known to deliver benign performance empirically when used before the convolutional computation [32]. The output of the encoder block is branched in three ways. The first branch connects to the input of the next block and the remaining two branches form \(\mu \), and \(\sigma \). The encoder latent variable is formulated by reparameterizing \(\mu \), and \(\sigma \). The reparameterized latent variable and ELU layer infer bottom–up information transfer, shown in green in Fig. 4.

In the current configuration, the decoder network is significantly deeper and more complex than the encoder network. The deep decoder network enables an expressive output when accompanied by a system with many DOFs. The decoder network receives two inputs: top–down information from the predecessor decoder block and encoder–decoder shared information from the latent variable. Through a series of layers, the decoder outputs top–down information, shown in blue. The decoder block generates the decoder latent variable and input for the next block. The i-th encoder latent variable and the i-th decoder latent variable are added to generate the i-th shared latent variable, \(z_i\), as shown in Fig. 4. The shared latent variable contains both top–down and bottom–up information, enabling bidirectional information sharing.

3.2 Preprocessing dataset

Acquiring many FOM samples may be quite cumbersome. In particular, many-queried FOM computations are extremely time-consuming if the FOM is highly nonlinear, includes multiphysics, and involves a significant number of DOFs. Acquiring those FOM data through experiments and simulations is considered prohibitive for computational and financial reasons. Instead, data augmentation is considered to sample sparsely and expand the amount of training data. A larger amount of training data improves the generalization of a neural network and thus enhances the accuracy. Similar to the data augmentation typically performed on images, the pre-acquired FOM results are processed using the following three methods. First, temporal data are resampled by shortening the time step, i.e., frequency elongation. Then, the training data are augmented by changing the amplitude and adding a random number within the bound of \(\pm 30\%\) for every epoch. Training the neural network using the augmented data ensures that the neural network is effectively trained against a very large dataset, resulting in a high-performance network.

3.3 LSH-VAE training and interpolation

The current framework performs MOR directly on FOM results. The LSH-VAE employs 1D convolutional layers which requires three-dimensional input in the format (batch, sequence, and channel). In the current configuration, the temporal continuity of the FOM results is considered in the convolutional dimension. The resultant input composition of LSH-VAE becomes \(\left( \textrm{batch}, N_t, N_\textrm{DOF}\right) \), where \(N_t\) denotes the number of time steps and \(N_\textrm{DOF}\) denotes the number of DOFs in the dynamic system. LSH-VAE receives this input and compresses it into latent vectors via the encoder. The dimensionality change throughout LSH-VAE is expressed in Eq. 17, where \(N_i\) represents the latent dimension in the i-th latent group. The total latent dimension, \(\sum N_i\), is much smaller than the FOM dimension, thereby achieving MOR

$$\begin{aligned} \left( , N_t, N_\textrm{DOF}\right) \xrightarrow {\text {encoder}} \left( , \sum N_{i}\right) \xrightarrow {\text {decoder}}\left( , N_t, N_\textrm{DOF}\right) . \end{aligned}$$
(17)

Before the algorithm is trained, the physical variables of interest are normalized. The variable, \(v^i(t,p)\), is a function of the time step, t and parameter, p, normalized to the range of [\(-0.7, 0.7\)] for each DOF. The normalizing function, N() and the denormalizing function, \(N^{-1}()\) is defined as Algorithm 1.

Algorithm 1
figure a

Normalize FOM variables

Full size image

The training algorithm for LSH-VAE is shown in Algorithm 2. The normalized variable is then augmented by resampling for \(N_A\) instances. Then, the training dataset, \(x_\textrm{train}\), is constructed by concatenating the original normalized variable with the augmented ones. The training dataset of the network becomes, \(x_\textrm{train} = [x, R(x)_1, R(x)_2,\ldots , R(x)_{N_A}]\), where \(R(x)_n\) denotes the resampled normalized variable of interest.

Algorithm 2
figure b

Training of LSH-VAE

Full size image

The training dataset is further augmented for amplitude and offset. The amplitude and offset augmentation is performed using random values for every epoch. The network receives a different input in every epoch, enabling the network to be trained against a very large dataset. After the data augmentation is completed, the encoder and decoder networks are trained. After the decoder is trained, the loss function can be obtained by Eq. 15. The training of LSH-VAE is optimized by the Adamax optimizer, which has delivered good performance compared with the conventional Adam and SGD optimizers.

Generative neural networks usually require latent vectors to be sought. This is required owing to the probabilistic formulation that is used to parameterize the latent vector. However, we empirically found that sufficient epochs and a small number of parameters obviate the need for latent searching. In this study, rather than attempting latent searching, the latent vectors are directly calculated using the mean value from the encoder network.

Upon acquiring the latent vectors, slerp interpolation is performed to collect the targeted latent vector. The latent space created by VAEs is in the form of a well-structured, multi-dimensional hypersphere, which enables complex operation by vector arithmetic [55]. This is possible, because the reparameterization trick introduces a Gaussian random number, which is attributed to the vector length and angle in the latent hypersphere. The slerp interpolation shown in Algorithm 3 not only interpolates the rotation angle of vectors, but it also interpolates the arc length. This slerp interpolation enables the latent vectors to be interpolated following the path of the complex latent manifold. The use of slerp interpolation for performing latent interpolation has been widely accepted [56, 57].

Algorithm 3
figure c

Interpolation of latent variables

Full size image

4 Numerical results

This section presents the numerical results obtained by the proposed framework. First, the framework is applied to solve an FSI benchmark problem previously developed by Turek and Hron [48]. The accuracy of the current method is evaluated and compared against that obtained by the conventional nonlinear MOR, CAE. Then, the proposed framework is examined on a wing section that undergoes limit cycle oscillation (LCO). LCO analysis is performed to evaluate the accuracy of the proposed framework on the nonlinear multiphysics phenomenon. Finally, the applicability of LSH-VAE to a system with many DOFs is demonstrated by analyzing a three-dimensional fluid flow.

The numerical results presented in this paper were obtained by intentionally sampling a small number of initial FOM results. Sparse sampling is performed, because the replication of its own training data by a neural network often produces sufficiently accurate results; in fact, it is as accurate as the use of dense sampling would have been. The other reason for attempting sparse sampling is that dense and iterative computations on a nonlinear system with many DOFs are rather unrealistic.

For all of the results, the same LSH-VAE network is used for each variable of interest. The hyperparameters used for training are listed in Table 1, in which the first value for the latent dimension criterion denotes the latent dimension in which the interpolation is performed. The latter value denotes the latent dimension used for information sharing between the encoder and decoder networks. LSH-VAE used for the following numerical results consists of 7 encoder and decoder blocks, with a total of 107 layers. Although detailed optimization of the hyperparameters would improve the accuracy, this procedure is not performed to emphasize the generability of the framework. However, different batch sizes are used considering the number of DOFs, and this is limited by the VRAM capacity of the GPU.

Table 1 Hyperparameters of LSH-VAE
Full size table

All of the results presented in this paper were computed on an AMD 3950X CPU to obtain the FOM results. The neural networks were trained using an NVIDIA GeForce GTX 3090 GPU.

4.1 Turek–Hron FSI benchmark

4.1.1 Description of the analysis

The widely accepted FSI benchmark developed by Turek and Hron is described in this section [48]. The benchmark problem consists of a rigid cylinder with a diameter of 0.1 m and a highly flexible tail. The fluid flowed from the inlet to the outlet with laminar separation occurring behind the cylinder. Von Kàrmàn vortex street created by the flow separation excites the tail, which exhibits a large deflection. A hyperbolic inlet profile is used to consider the no-slip initial wall boundary condition at the upper and lower computational domain. A detailed schematic regarding the analysis is shown in Fig. 5.

The current framework requires a few parametric initial FOM samples to extract the embedded patterns. For the Turek–Hron FSI benchmark problem, seven initial FOM results were collected. The inflow speed was selected as a parameter and speeds ranging from 0.7 to 1.3 m/s, in 0.1 m/s intervals were sampled. The FOM samples are analyzed using Navier–Stokes computational fluid dynamics (CFD) and finite-element method (FEM) two-way FSI analysis provided in the commercial software, ANSYS. The flow field is discretized by 29,788 CFD nodes and the flexible body is discretized by 954 FEM nodes.

Fig. 5
figure 5

Analysis setup of the Turek–Hron FSI problem

Full size image
Fig. 6
figure 6

Original and interpolated FSI field for the Turek–Hron FSI problem at \(t=2\) s

Full size image

The ensemble of FOM results is constructed by collecting 2 s of the fully converged response in intervals of 0.01 s. The pre-acquired FOM ensemble is then subjected to interpolation by LSH-VAE (Table 1). After the training of LSH-VAE was completed, the latent variable was interpolated. In the present case, the unseen inflow speed of 0.95 m/s was selected as the target parameter. The latent variable corresponding to 0.95 m/s was acquired by the slerp interpolation shown in Algorithm 3. The interpolated latent variable was then decoded by the decoder network where the resultant interpolated variables were generated.

4.1.2 Accuracy and efficiency

The accuracy of the current framework was assessed by comparing the results of the ROM against those obtained with the FOM. Five physical variables, dX, dY, u, v, and p were considered for interpolation in this case. More specifically, dX denotes the x-directional CFD grid deformation, dY denotes the y-directional CFD grid deformation, u denotes the x-directional velocity, v denotes the y-directional velocity, and p denotes the pressure. Among them, the first two variables denote the grid deformation in the x- and y-direction. The interpolated variables were used to construct the interpolated FSI field. The interpolated FSI field and FOM are shown in Fig. 6.

An evaluation of the results shown in Fig. 6 verified that the proposed framework is reasonably accurate. Subsequently, the accuracy of LSH-VAE is compared against that of CAE and \(\beta \)-VAE. For comparison, the CAE and \(\beta \)-VAE networks were constructed using the same hyperparameters that were used for LSH-VAE. The CAE, \(\beta \)-VAE, and LSH-VAE were compared by comparing the coefficient of determination (\(R^2\)). The coefficient of determination will be obtained by Eq. 18, where y denotes the ground truth, \({\bar{y}}\) denotes the average of y, and \({\hat{y}}\) denotes the prediction. \(R^2\) commonly has a value between zero and one, where a higher value suggests a smaller discrepancy

$$\begin{aligned} \begin{aligned} {R^2 = 1-\frac{\Sigma (y-{\hat{y}})^2}{\Sigma (y-{\bar{y}})^2.}} \end{aligned} \end{aligned}$$
(18)

Here, the results of the reduced order model were used for \({\hat{y}}\). In Eq. 18, y is a vector with a length of \(N_\textrm{DOF}\) and \(R^2\) is acquired for each time step. For comparison, the time-averaged \(R^2\) values with respect to various networks are presented in Table 2. Overall, LSH-VAE has the largest \(R^2\) value, whereas \(\beta \)-VAE performed the worst. These results suggest that the inability of CAE and \(\beta \)-VAE to generate an expressive output degrades the accuracy of the interpolated FSI field. The accuracy of LSH-VAE proved to be acceptable as the \(R^2\) values of LSH-VAE are 0.99 except for that of the v-velocity.

Subsequently, the efficiency of the proposed framework was assessed. The computational procedures for the proposed framework comprise four stages and the computational time required for each stage is listed in Table 3. For the Turek–Hron FSI problem, each FOM query requires 109.0 h, whereas the online stage consumes 0.11 h. The proposed framework, therefore, exhibits a speed-up factor of 990 for each unseen parametric estimation. The expected computational time in terms of the number of computations is shown in Fig. 7.

4.2 Limit cycle oscillations

4.2.1 Description of the analysis

Table 2 Time-averaged \(R^2\) value of the interpolated Turek–Hron FSI field using LSH-VAE, CAE, and \(\beta -\)VAE
Full size table
Table 3 Computational time requirements for the Turek–Hron FSI problem
Full size table

Limit cycle oscillation (LCO) is a nonlinear periodic oscillation with limited amplitude on an aerodynamic surface. LCO of an aircraft is a highly nonlinear FSI phenomenon that is caused by nonlinearities in both the fluid and structure. Typical causes of LCO include flow separation, transonic shock, geometric nonlinearity, and nonlinear stiffness of the control surface. For an aircraft, LCO may result in structural fatigue in the wings, thus requiring high-fidelity analysis for safety. During the design stage of an aircraft, iterative LCO analysis is performed to satisfy the vibration criterion. Such parametric LCO analysis is considered to be quite cumbersome and tedious as it is highly nonlinear and involves many DOFs. In this section, the proposed framework is used to conduct a simplified nonlinear parametric LCO analysis of a wing section.

Fig. 7
figure 7

Computational time in terms of the parametric queries for the Turek–Hron FSI problem

Full size image

The wing section considered in this analysis is derived from that reported by O’Neil et al. [58]. In it, a two-dimensional wing section was constrained by the pitch and heave springs, as shown in Fig. 8. The pitch and heave stiffnesses are nonlinear in their cubic terms, which are expressed in Eq. 19. LCO is caused by the cubic stiffness in the structure and LCO is observed at the inflow stream speed of 15.5–50 m/s

$$\begin{aligned}{} & {} K_{\alpha } = 2.57(\alpha +500\alpha ^3)\nonumber \\{} & {} K_{h} = 0.09(h+2860h^3)). \end{aligned}$$
(19)
Fig. 8
figure 8

Analysis setup of the LCO

Full size image
Fig. 9
figure 9

Original and interpolated FSI field for the LCO at \(t=2\) s

Full size image

The inflow speed was chosen as the parameter in this analysis. The initial FOM samples were collected by adjusting the inflow speed from 20 to 45 m/s in increments of 5 m/s. The relevant flow field was discretized by 19,381 nodes and solved using the commercial Navier–Stokes solver, ANSYS. The initial FOM samples were obtained by collecting 2 s of the fully converged response in intervals of 0.01 s. The FOM ensemble was subjected to MOR and interpolation by LSH-VAE.

After LSH-VAE was trained, the latent variable for the desired parameter was acquired via slerp interpolation. The target parameter was an unseen inflow speed of 32.5 m/s, and the corresponding latent variable was interpolated using Algorithm 3. The interpolated latent variable was then decoded by the decoder and the interpolated FSI field was generated.

4.2.2 Evaluation of accuracy and efficiency

The accuracy of LSH-VAE was assessed by comparing the ROM results against those produced by FOM. In this case, the five physical variables discussed in the previous section were considered. The interpolated variables were used to generate the FSI field, and the interpolated FSI field and FOM are shown in Fig. 9.

The interpolated FSI field constructed by LSH-VAE (Fig. 9) is shown to be accurate. Then, the accuracy of LSH-VAE is compared against that of CAE and \(\beta \)-VAE. The \(R^2\) values of the interpolated physical variables generated by LSH-VAE, CAE, and \(\beta \)-VAE are presented in Table 4. Similar to the Turek–Hron problem, LSH-VAE exhibited the smallest discrepancy. However, in this case, \(\beta \)-VAE outperformed CAE. In the case of LCO, the accuracy of LSH-VAE proved to be exceptional as it exhibited \(R^2\) values higher than 0.99 for all the variables.

The efficiency of the proposed framework was also assessed. The computational time required for each stage is summarized in Table 5. The offline FOM computation required 280.1 h including the computation of six initial FOM samples. LSH-VAE training required 3.52 h for the five variables of interest, resulting in a total offline stage of 283.6 h. For the online stage, FSI field reconstruction and saving to disk requires the most time as it requires 0.06 h. The present framework exhibits a speed-up factor of 660 for each unseen parametric estimation. The expected computational time in terms of the unseen parametric queries is shown in Fig. 10.

4.3 Three-dimensional fluid flow

4.3.1 Description of the analysis

Finally, the fluid flow surrounding a simple stationary three-dimensional (3D) cylinder was analyzed. The analysis of the 3D fluid serves to demonstrate the use of the proposed framework to analyze a system with a significant number of DOFs. A 3D cylinder with a diameter of 1 m was subjected to a uniform inflow, as shown in Fig. 11. Similar to the Turek–Hron FSI benchmark, a von Kàrmàn vortex is formed behind the cylinder. For CFD analysis, a cuboid computational domain of 20 m \(\times \) 10 m \(\times \) 10 m was discretized into 1,121,000 tetrahedral elements. The Reynolds number of the inflow was varied from 100 to 160 in intervals of 10.

The initial FOM samples were obtained using the ANSYS Navier–Stokes solver and 2s of FOM data were collected in intervals of 0.01 s. Then, the LSH-VAE was trained against the FOM ensemble and interpolated with respect to the parameter.

After LSH-VAE was trained, the latent variable representing the targeted parameter was acquired. The target parameter was selected as the unseen inflow Reynolds number of Re = 125. The latent variable corresponding to Re = 125 was acquired by the interpolation shown in Algorithm 3. The interpolated latent variable was then decoded and the resultant interpolated flow field was generated.

Table 4 Time-averaged \(R^2\) values of the interpolated LCO FSI field using LSH-VAE, CAE, and \(\beta -\)VAE
Full size table
Table 5 Computational time requirements for the LCO
Full size table
Fig. 10
figure 10

Computational time in terms of the parametric queries for the LCO

Full size image
Fig. 11
figure 11

Analysis setup of the 3D fluid flow

Full size image
Fig. 12
figure 12

Original and interpolated FSI field for the 3D fluid flow at \(t=2\) s

Full size image

4.3.2 Evaluation of the accuracy and efficiency

The accuracy of LSH-VAE was assessed by comparing the results of ROM with those obtained using FOM. In this case, four physical variables, u, v, w, and p, were considered for the interpolation, where w denotes the z-directional velocity. Using the interpolated variables, the interpolated flow field was generated. The interpolated and original flow fields are displayed in Fig. 12.

The interpolated flow field constructed by LSH-VAE proved to be reasonably accurate. The \(R^2\) values of the interpolated physical variables generated by LSH-VAE are listed in Table 6. The \(R^2\) values are quite high, except for the velocity in the z-direction, the w-velocity. This low value is observed, because the flow is approximately laminar. The near-randomness of the w-velocity degrades the accuracy of parametric interpolation. Except for the w-velocity, other \(R^2\) values are quite high even with the large number of DOFs that was interpolated.

As the initial physical variables were interpolated well, the relationship between the variables was inspected. In this case, the results computed by LSH-VAE were not compared with those of CAE and \(\beta \)-VAE as the large number of DOFs destabilized the networks. Instead, the normalized Q-criterion was considered to assess whether the interpolated flow field preserved its vorticity. The normalized Q-criterion shown in Fig. 13 was obtained using the interpolated variables shown in Fig. 12. Figure 13 shows the iso-surface generated on the basis of the normalized Q-criterion. The iso-surface is colored by the u-velocity and pressure for visualization.

Table 6 Time-averaged \(R^2\) value of the interpolated 3D cylinder flow field
Full size table

The good agreement in terms of the Q-criterion indicates that LSH-VAE interpolates the direct variables sufficiently well, such that the relationship between variables may be well preserved.

Finally, the efficiency of the present framework was assessed. The computational time required for each stage is listed in Table 7. The offline FOM computation requires 193.7 h including the seven initial FOM samples. LSH-VAE training requires 11.3 h resulting in a total offline stage of 205.0 h. For the online stage, variable reconstruction and writing to disk requires the most time (2.02 h). The proposed framework exhibits a speed-up factor of 14 for each unseen parametric estimation. The expected computational time in terms of queries is plotted in Fig. 14.

5 Conclusions

This paper proposes a nonlinear data-driven parametric MOR framework based on a neural network. The present framework adopts a novel neural network, LSH-VAE, to perform parametric MOR and interpolation. The validations presented here demonstrated that the LSH-VAE is capable of the parametric interpolation of a dynamic system while significantly reducing the computational time. This study made the following contributions:

  • A novel machine-learning method, LSH-VAE, was developed for nonlinear MOR and the parametric interpolation of nonlinear, dynamic systems.

  • LSH-VAE was assessed on three nonlinear and multiphysics dynamic systems with many DOFs. The proposed framework was proved to be accurate and to significantly reduce the computational time.

  • Compared against existing nonlinear MOR methods, the convolutional autoencoder and \(\beta \)-VAE, LSH-VAE demonstrated significantly higher accuracy.

The performance of LSH-VAE was assessed on three nonlinear dynamic systems: an FSI benchmark, LCO, and three-dimensional flow. For all of the systems, LSH-VAE was shown capable of constructing an accurate parametric ROM. Particularly, LSH-VAE exhibited significantly enhanced accuracy compared to CAE and \(\beta \)-VAE. In addition, the effectiveness of LSH-VAE was not only limited to the accurate interpolation of the variables, but LSH-VAE also interpolated the vorticity with high accuracy, which is embedded in the patterns of variables. For accurate parametric MOR, LSH-VAE exhibited speed-up factors of 990, 660, and 14, respectively.

Fig. 13
figure 13

Original and interpolated flow fields: iso-surface of the 3D fluid flow at \(t=1.5\) s

Full size image
Table 7 Computational time requirements for the 3D fluid flow
Full size table
Fig. 14
figure 14

Computational time in terms of the parametric queries for the 3D fluid flow

Full size image

These results were possible owing to the improvements in the LSH-VAE. First, a hierarchical structure was adopted for LSH-VAE that enables a much deeper and more stable network. Second, a hybrid weighted loss function consisting of mean-squared error and KL divergence was adopted for LSH-VAE. The use of the mean-squared error improved the performance against continuous datasets, while the hybrid weights reduced posterior collapse. Finally, the use of slerp interpolation instead of linear interpolation in the latent space significantly enhanced the interpolation quality following the complex latent manifolds.

However, a few challenges still need to be overcome. First, LSH-VAE may require a significant amount of video random access memory (VRAM) if it is incorporated with an extensive number of DOFs. The excessive VRAM requirement stems from its deep structure. By adopting a deep structure, LSH-VAE is capable of generating an expressive result at the cost of training an extensive number of learnable nodes. The excessive VRAM requirements necessitate limiting the batch size for the 3D fluid flow example. Yet, the VRAM limitations may be alleviated by adopting parallel computing and utilizing many GPUs. Splitting the DOFs into several groups and merging them after interpolation may also be considered as a solution. Second, extrapolation is limited in the proposed framework. Accurate extrapolation would require dense sampling in the parametric space. However, the construction of ROM with sufficiently dense sampling accompanied by an effective latent manifold tracking method would make reasonable extrapolation viable. Finally, the effectiveness of the proposed framework decreases as the FOM becomes simpler and increasing DOFs are involved. An example of this tendency is demonstrated in the 3D fluid flow example where the speed-up factor diminished to 14 compared to 990 and 660 in the previous cases.

In the future, the plan is to extend the evaluation of the proposed framework to various multiphysics problems such as the analysis of heat-structure systems. Considering that the present framework is purely data-driven, LSH-VAE is expected to be used in its current form. In addition, multi-parametric analysis coupled with sampling algorithms such as Latin hypercube will be attempted by adopting conditional tokens in the latent space.