1 Introduction

Corrosion is widely recognized as one of the most common yet destructive failure mechanisms of engineering components and structures, carrying a cost of about 3.1% of the gross domestic product (GDP) in industrialized countries [1]. Corrosion can be classified into two categories: general corrosion and localized corrosion. The first one refers to uniform metal dissolution and can be prevented by physical and electrochemical measures, e.g., through the use of coatings and cathodic protection. However, localized corrosion, such as pitting corrosion, is more difficult to prevent and detect in engineering practice. Moreover, by interacting with mechanical loads, localized corrosion can often lead to catastrophic structural failures through phenomena such as mechanically-assisted corrosion and stress corrosion cracking (SCC). Thus, there is a need for developing physically-based models capable of predicting localized corrosion failures.

Mechanistic predictions of localized corrosion require resolving the underlying physical processes, which has long been considered a remarkably complex task [2]. Two main challenges exist. First, predicting localized corrosion requires resolving a strongly coupled electro-chemo-mechanical problem involving, at the very least, the transport of ionic species, interface reactions, changes in electrolyte conductivity and mechanical behaviour of the metal, as well as their interactions. Secondly, localized corrosion is a complex interfacial problem; the electrolyte-metal interface exhibits a highly irregular morphology and its evolution depends on the local chemistry and mechanics, which are themselves dependent on the interface morphology [3]. Promising progress has been achieved, independently, in the modeling of these two key challenges. New mathematical models describing mass transport, homogeneous chemical reactions and charge balance have been proposed to better understand the electro-diffusive mass transport of multiple species and its effects on corrosion evolution (see, e.g., [4,5,6] and Refs. therein). However, these works are limited by the assumption of a stationary electrolyte-metal interface. On the other hand, a number of computational schemes have been recently presented to track the evolution of the corrosion front [7,8,9,10,11,12,13,14]. Among these, the phase field model stands out for its thermodynamics roots and its ability to efficiently capture corrosion morphologies of arbitrary complexity. In addition, it can be readily integrated into existing finite element schemes. Instead of explicitly tracking a moving boundary (and the associated boundary conditions), the phase field paradigm describes the evolution of the interface by means of an auxiliary order parameter \(\phi \) that varies smoothly between the two phases (metal and electrolyte, in the case of corrosion) and evolves based on a suitable governing equation [15,16,17]. The application of the phase field paradigm to corrosion was first shown by Stahle and Hansen [18] and Abubakar et al. [19]. Mai and co-workers extended these works to present a phase field corrosion framework that accounts for the diffusion of dissolved species and reactants in the electrolyte [8, 20]. Later, Cui et al. [12] incorporated the role of mechanics in the corrosion process, capturing both the enhancement of corrosion rates due to mechanical fields [21] and the process of passive film formation, rupture and subsequent repassivation [22]. More recently, mechanics-enhanced phase field corrosion models have been extended to include mechanical fracture [23, 24], which could be assisted by the ingress of aggressive species such as hydrogen [24]. However, these models do not fully resolve the electrochemistry of the system; there is a need to develop electro-chemo-mechanical phase field formulations for localized corrosion that can capture the sensitivity to the applied potential and the concentration of species in the environment.

In this work, we present a new electro-chemo-mechanical phase field-based formulation for predicting localized corrosion in elastic–plastic solids. The model combines, for the first time, an electrochemical description of ionic species transport and electrostatic potential distribution in the electrolyte with a mechanics-dependent interface kinetics law built upon mechanochemical theory [21] and the film rupture–dissolution–repassivation (FRDR) mechanism [22]. The theoretical framework is numerically implemented in the finite element package COMSOL MULTIPHYSICS and numerical experiments are conducted to showcase the ability of the model in capturing the main experimental trends. Focus is also placed on the details of the COMSOL implementation, making the model freely available and providing details that enable reproducibility and facilitate usage. The remainder of this paper is organised as follows. In Sect. 2 we present our theoretical framework. Then, the COMSOL implementation is described in Sect. 3. The results of the numerical experiments conducted are presented and discussed in Sect. 4. Finally, concluding remarks end the manuscript in Sect. 5.

2 Theory

2.1 General considerations

The process of localized corrosion is usually initiated by the rupture of the passivation film that protects the metal from corroding. Following the local failure of the passive film, the metallic surface is exposed to the corrosive environment, triggering the dissolution process and releasing cations into the electrolyte, i.e.

$$\begin{aligned} \textrm{M} \rightarrow \textrm{M}^{n_\textrm{M}^+} + n_\textrm{M}e^- \end{aligned}$$
(1)

where M is the corroded metal and \(n_\textrm{M}\) is the charge number of metal M. The present theory aims at encapsulating the electrochemical and mechanical mechanisms involved in this process.

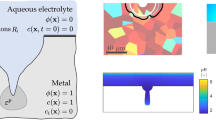
An overview of the elements of our theory is provided in Fig. 1. There, it can be seen that the evolution of the corrosion front is described by a so-called phase field order parameter \(\phi \), which varies from 0 (electrolyte) to 1 (intact metal) within a diffuse region. The interplay between activation-controlled corrosion and diffusion-controlled corrosion is captured by simulating the transport of metal ions. To this end, a normalized concentration \(c_\textrm{M}=c_\textrm{M}^0/c_\textrm{solid}\) is defined, where \(c_\textrm{M}^0\) is the metal ion concentration and \(c_\textrm{solid}\) is the concentration of atoms in the metal. Accordingly, \(c_\textrm{M}=1\) inside the metal while \(c_\textrm{M}=0\) in regions of the electrolyte that are far away from the electrolyte-electrode interface. Following our previous work [12], we characterize the mechanical behaviour of the metal using an elastic–plastic constitutive model and capture as well the interplay between mechanics and corrosion (mechanochemistry, FRDR mechanism). Unlike our previous work [12], the current model also resolves the electrochemistry of the electrolyte. This is achieved by solving for the concentration of multiple ionic species \(c_i\) (where i equals, e.g., \(\textrm{Na}^+, \textrm{Cl}^-, \textrm{H}^+, \textrm{OH}^-\), etc.), and the electrolyte potential \(\varphi _{\text {l}}\). Accordingly, the primary variables of the theory are the phase field order parameter \(\phi \), the normalized metal ion concentration \(c_\textrm{M}\), the electrostatic potential \(\varphi _{\text {l}}\), the concentration of multiple ionic species \(c_i\) and the metal displacement vector \({\textbf {u}}\). Based on these preliminaries, we shall first define the energy functions (Sect. 2.2), then derive the balance equations of the primal fields (Sect. 2.3), introduce the main corrosion-mechanics coupling relations in the electro-chemo-mechanical system (Sect. 2.4), particularize the electrochemistry of the electrolyte (Sect. 2.5) and, finally, summarize the governing equations of our theory (Sect. 2.6).

Fig. 1
figure 1

Schematic illustration of the main variables involved in the electro-chemo-mechanical phase field-based formulation presented for predicting localized corrosion as a function of the environment, material and loading conditions. The illustration showcases a domain \(\Omega \) that encompasses the metal (\(\phi =1\)) and electrolyte (\(\phi =0\)) phases, and the diffuse interface in-between

Full size image

2.2 Free energy

Consistent with our prior research [12], we consider two distinct systems, namely the electrochemical system and the mechanical system. These two systems possess their respective free energies, denoted by \(\Pi ^\textrm{E}\) and \(\Pi ^\textrm{M}\), which will be formulated in Sects. 2.2.1 and 2.2.2, respectively. The coupling of these two systems will be addressed in Sect. 2.4.

2.2.1 Electrochemical system

In this section, we introduce a general expression for the energy function in corrosion problems. Consider first the free energy of the electrochemical system, denoted by \(\Pi ^\textrm{E}\), which is an integral of the electrochemical energy density \(\psi ^\textrm{E}\) over the domain \(\Omega \), such that

$$\begin{aligned} \Pi ^\textrm{E} = \int _\Omega \psi ^\textrm{E} \textrm{d}V = \int _\Omega \left( \psi ^\textrm{ch}+\psi ^\textrm{i}+\psi ^\textrm{el}\right) \textrm{d}V \end{aligned}$$
(2)

where \(\psi ^\textrm{ch}, \psi ^\textrm{i}\), and \(\psi ^\textrm{el}\) denote the chemical, interfacial, and electrostatic free energy densities, respectively. These are defined below.

Chemical free energy density \(\psi ^\textrm{ch}\). The chemical free energy density \(\psi ^\textrm{ch}\) can be further decomposed into the energy for metal dissolution \(\psi ^\textrm{ch,d}\) and the energy stored in the dilute solution \(\psi ^\textrm{ch,s}\),

$$\begin{aligned} \psi ^\textrm{ch} = \psi ^\textrm{ch,d} + \psi ^\textrm{ch,s} \end{aligned}$$
(3)

We follow the KKS model [25] to define \(\psi ^\textrm{ch,d}\). Accordingly, each material point is a mixture of both solid and liquid phases with different concentrations but equal chemical potentials. Thus, \(\psi ^\textrm{ch,d}\) is given by

$$\begin{aligned} \psi ^\textrm{ch,d} = h \left( \phi \right) \psi _\textrm{S}^\textrm{ch,d} + \left[ 1- h (\phi ) \right] \psi _\textrm{L}^\textrm{ch,d} \end{aligned}$$
(4)

where \(h\left( \phi \right) =-2\phi ^3+3\phi ^2\) is a degradation function intrinsic to the phase field model. Here we define \(h(\phi =1)=1\) as intact metal and \(h(\phi =0)=0\) as fully corroded region to describe the phase transition due to metal dissolution. Also, \(h'(\phi =0)=h'(\phi =1)=0\) must be satisfied to ensure that the energy converges to a finite value where the domain is locally intact/fully damaged. \(\psi _\textrm{S}^\textrm{ch,d}\) and \(\psi _\textrm{L}^\textrm{ch,d}\) are the chemical free energy density terms respectively associated with the concentrations of the solid phase \(c_\textrm{S}\) and the liquid phase \(c_\textrm{L}\). Accordingly,

$$\begin{aligned} \frac{\partial \psi _\textrm{S}^\textrm{ch,d} \left( c_\textrm{S} \right) }{\partial c_\textrm{S}} = \frac{\partial \psi _\textrm{L}^\textrm{ch,d} \left( c_\textrm{L} \right) }{\partial c_\textrm{L}} \end{aligned}$$
(5)

and,

$$\begin{aligned} c_\textrm{M} = h \left( \phi \right) c_\textrm{S} + \left[ 1 - h \left( \phi \right) \right] c_\textrm{L} \end{aligned}$$
(6)

Consistent with the KKS model, \(\psi _\textrm{S}^\textrm{ch,d}\) and \(\psi _\textrm{L}^\textrm{ch,d}\) are given by

$$\begin{aligned} \psi _\textrm{S}^\textrm{ch,d} = A (c_\textrm{S} - c_\textrm{Se})^2 \,\,\,\,\,\,\,\, \text {and} \,\,\,\,\,\,\,\, \psi _\textrm{L}^\textrm{ch,d} = A (c_\textrm{L} - c_\textrm{Le})^2 \end{aligned}$$
(7)

where \(c_\textrm{Se}=c_\textrm{solid}/c_\textrm{solid}=1\) and \(c_\textrm{Le}=c_\textrm{sat}/c_\textrm{solid}\) are the normalized equilibrium concentrations for the solid and liquid phases. Also, A is the free energy density parameter, which is assumed to be equal for the solid and liquid phases and can be determined by benchmarking the chemical free energies obtained from KKS model with those obtained from thermodynamic databases [19, 23].

Combining Eqs. (4)–(7), one reaches

$$\begin{aligned} \psi ^\textrm{ch,d} = A \left[ c_\textrm{M} - h (\phi )(c_\textrm{Se} - c_\textrm{Le}) - c_\textrm{Le} \right] ^2 \end{aligned}$$
(8)

The second element of \(\psi ^\textrm{ch}\), the energy stored in the dilute solution, \(\psi ^\textrm{ch,s}\), is defined as follows:

$$\begin{aligned} \psi ^\textrm{ch,s} = \sum _{i=1}^n c_i\,R_{\text {g}} T \left( \ln c_i-1\right) + c_i\,\mu _i^0 \end{aligned}$$
(9)

where i is the associated ionic species (e.g., \(\textrm{Na}^+, \textrm{Cl}^-, \textrm{H}^+, \textrm{OH}^-\)), \(R_{\text {g}}\) is the gas constant, T is the temperature, and \(\mu _i^0\) is the reference chemical potential. Here, one should note that the chemical energy associated with the metallic ions \(\textrm{M}^{n_\textrm{M}^+}\) is already accounted for through the KKS model.

Interfacial free energy density \(\psi ^i\). The interfacial strain energy density \(\psi _i\) is defined as the sum of double-well potential energy and the energy corresponding to the phase field gradient, reading

$$\begin{aligned} \psi ^i = g \left( \phi \right) w + \frac{\alpha }{2} |\nabla \phi |^2 \end{aligned}$$
(10)

where \(\alpha \) is the gradient energy coefficient and w is the height of the double-well potential \(g(\phi )\), which is chosen here as \(g \left( \phi \right) =\phi ^2 (1 - \phi )^2\). As discussed and derived in Appendix A, the height w and the gradient energy coefficient \(\alpha \) in Eq. (10) can be related to the interface energy per area \(\gamma \) and its thickness \(\ell \) as:

$$\begin{aligned} \gamma = \sqrt{\frac{\alpha w}{18}} \,\,\,\,\,\,\,\, \text {and} \,\,\,\,\,\,\,\, \ell = \sqrt{\frac{8 \alpha }{w}} \end{aligned}$$
(11)

Electrostatic free energy density \(\psi ^\textrm{el}\) Finally, the electrostatic energy density \(\psi ^\textrm{el}\) is defined as a function of the charge density as follows

$$\begin{aligned} \psi ^\textrm{el} = F\varphi _{\text {l}} \left( n_\textrm{M}c_\textrm{M}c_\textrm{solid} + \sum _{i=1}^n n_i c_i \right) \end{aligned}$$
(12)

where F is Faraday’s constant, and \(n_i\) is the charge number of the ith ionic species.

2.2.2 Mechanical system

We proceed to define the mechanical strain energy \(\Pi ^\textrm{M}\). We consider an elastic–plastic solid with a strain energy density \(\psi ^\textrm{M}\) that can be additively decomposed into its elastic (\(\psi ^\textrm{e}\)) and plastic (\(\psi ^\textrm{p}\)) parts, such that

$$\begin{aligned} \Pi ^\textrm{M} = \int _\Omega \psi ^\textrm{M} \textrm{d}V = \int _\Omega h \left( \phi \right) \left( \psi ^\textrm{e}+\psi ^\textrm{p}\right) \textrm{d}V \end{aligned}$$
(13)

where the corrosion degradation function \(h \left( \phi \right) \) captures the reduction of material stiffness due to metal dissolution. The elastic strain energy density is given as

$$\begin{aligned} \psi ^\textrm{e} = \frac{1}{2} {\varvec{\varepsilon }}^\textrm{e} : {\varvec{C}}^\textrm{e} : {\varvec{\varepsilon }}^\textrm{e} \end{aligned}$$
(14)

where \({\varvec{C}}^\textrm{e}\) is the linear elastic stiffness matrix and \({\varvec{\varepsilon }}^\textrm{e}\) is the elastic strain tensor. The plastic behaviour of the solid is characterized in this work by means of von Mises J2 plasticity theory. Accordingly, for a plastic strain tensor \({\varvec{\varepsilon }}^\textrm{p}\), the plastic component of the strain energy density reads,

$$\begin{aligned} \psi ^\textrm{p} = \int _0^t {\varvec{\sigma }}_0 : \dot{{\varvec{\varepsilon }}}^\textrm{p} \, \text {d}t \end{aligned}$$
(15)

where \({\varvec{\sigma }}_0\) is the so-called undamaged or effective Cauchy stress tensor.

2.3 Balance equations

Consistent with the free energy defined in Sect. 2.2, we shall now formulate the governing equations of the electro-chemo-mechanical phase field corrosion theory.

2.3.1 Phase field evolution

As in previous phase field corrosion models [8, 12], the phase field evolves based on the following Allen–Cahn equation:

$$\begin{aligned} \frac{\partial \phi }{\partial t} = -L \left( \frac{\partial \psi ^\textrm{E}}{\partial \phi } - \alpha \nabla ^2 \phi \right) \end{aligned}$$
(16)

with

$$\begin{aligned} \frac{\partial \psi ^\textrm{E}}{\partial \phi } = - 2 A \left[ c_\textrm{M} - h \left( \phi \right) (c_\textrm{Se} - c_\textrm{Le}) - c_\textrm{Le} \right] (c_\textrm{Se} - c_\textrm{Le}) h '\left( \phi \right) + w g' \left( \phi \right) \end{aligned}$$
(17)

Here, L is the interface kinetics coefficient, which can be related to the corrosion current density [24, 26] or the overpotential [27]. Following Ref. [12], we shall enrich the definition of L to incorporate the role of mechanics in enhancing corrosion rates and breaking the passivation film—see Sect. 2.4. For the moment, let us assume that L is constant and denote \(L \equiv L_{\text {a}}\) for the case where mechanical fields are absent. Then, as discussed in Ref. [24], \(L_{\text {a}}\) is proportional to the corrosion current density \(i_{\text {a}}\) when corrosion is activation-controlled. Accordingly,

$$\begin{aligned} \xi = \frac{L_{\text {a}}}{i_{\text {a}}}= \frac{L_0}{i_0} \end{aligned}$$
(18)

where \(i_0\) is the exchange current density and \(L_0\) is the interface kinetics coefficient when the overpotential \(\eta \) is zero. Thus, as shown in Sect. 4.2, the proportionality constant \(\xi \) can be determined by conducting a numerical experiment under activation corrosion conditions (small \(L_{\text {a}}\)).

The corrosion current density \(i_{\text {a}}\) can usually be estimated by using the so-called Butler–Volmer equation:

$$\begin{aligned} i_{\text {a}}=i_0 \left[ \text {exp}\left( \frac{a_{\text {a}} n_\textrm{M} F\eta }{R_{\text {g}} T}\right) -\text {exp}\left( -\frac{(1-a_{\text {a}}) n_\textrm{M} F\eta }{R_{\text {g}} T}\right) \right] \end{aligned}$$
(19)

where \(a_{\text {a}}\) is the anodic charge transfer coefficient. Consistent with Eqs. (18)–(19), \(L_{\text {a}}\) can also be estimated by a Butler–Volmer-type equation:

$$\begin{aligned} L_{\text {a}}=L_0 \left[ \text {exp}\left( \frac{a_{\text {a}} n_\textrm{M} F\eta }{R_{\text {g}} T}\right) -\text {exp}\left( -\frac{(1-a_{\text {a}}) n_\textrm{M} F\eta }{R_{\text {g}} T}\right) \right] \end{aligned}$$
(20)

And Eq. (20) can be further simplified as a Tafel-type equation if only the anodic reaction is relevant at the dissolution surface; i.e.,

$$\begin{aligned} L_{\text {a}}=L_0\,\text {exp}\left( \frac{a_{\text {a}} n_\textrm{M} F\eta }{R_{\text {g}} T}\right) \end{aligned}$$
(21)

Finally, the overpotential is expressed as:

$$\begin{aligned} \eta =\varphi _{\text {s}} - \varphi _{\text {l}} - E_\text {eq} \end{aligned}$$
(22)

where \(\varphi _{\text {s}}\) is the solid (applied) potential and \(E_\text {eq}\) is the equilibrium potential. In this work, we assume \(E_\text {eq}=0\) for convenience.

2.3.2 Transport of species

The transport of ionic species is governed by mass conservation. Accordingly, the rate of change in time of any of the species must be equal to the sum of its concentration flux through the boundary \(\partial \Omega \) and the reactants/products due to chemical reactions in \(\Omega \), such that

$$\begin{aligned} \int _\Omega \frac{\partial c}{\partial t}\,\text {d}V = - \int _{\partial \Omega } {\textbf {J}} \cdot {\textbf {n}}\,\text {d}S + \int _\Omega R\,\text {d}V \end{aligned}$$
(23)

where \({\textbf {J}}\) is the concentration flux and R is the chemical reaction term. Here, one should note that Eq. (23) is valid for both \(c_\textrm{M}^0\) and \(c_i\). Since Eq. (23) must hold for any arbitrary volume, recalling that \(c_\textrm{M}^0=c_\textrm{M}c_\textrm{solid}\) and using Gauss’ divergence theorem one reaches

$$\begin{aligned} \frac{\partial c_\textrm{M}c_\textrm{solid}}{\partial t}+\nabla \cdot \textbf{J}_\textrm{M}=R_\textrm{M} \end{aligned}$$
(24)

and

$$\begin{aligned} \frac{\partial c_i}{\partial t}+\nabla \cdot \textbf{J}_i=R_i \end{aligned}$$
(25)

The transport process is driven by the chemical potential \(\mu \). For the metal ions, \(\mu _\textrm{M}\) can be further decomposed into two terms, one associated with the KKS-based phase field formulation, \(\mu _{M1}\), and another one related to the migration process, \(\mu _{M2}\), such that

$$\begin{aligned} \mu _\textrm{M} = \frac{\partial \psi ^\textrm{E}}{\partial c_\textrm{M}c_\textrm{solid}} = \underbrace{2A\left[ c_\textrm{M} - h \left( \phi \right) (c_\textrm{Se} - c_\textrm{Le}) - c_\textrm{Le} \right] /c_\textrm{solid}}_{\mu _\textrm{M1}} + \underbrace{F\varphi _{\text {l}} n_\textrm{M}}_{\mu _\textrm{M2}} \end{aligned}$$
(26)

Where we emphasise that \(c_\textrm{solid}\) is a constant used for normalising the metal ion concentration.

Accordingly, the flux \(\textbf{J}_\textrm{M}\) can be calculated by a Fick law-type relation,

$$\begin{aligned} \begin{aligned} \textbf{J}_\textrm{M}&= \textbf{J}_\textrm{M1} + \textbf{J}_\textrm{M2} = - \frac{D_\textrm{M}}{2A} c_\textrm{solid}^2 \nabla \mu _\textrm{M1} - \frac{[1-h\left( \phi \right) ] D_\textrm{M} c_\textrm{M}c_\textrm{solid}}{R_{\text {g}} T} \nabla \mu _\textrm{M2}\\&=- D_\textrm{M} c_\textrm{solid} \nabla \left[ c_\textrm{M} - h \left( \phi \right) (c_\textrm{Se} - c_\textrm{Le}) - c_\textrm{Le} \right] - \frac{[1-h\left( \phi \right) ] D_\textrm{M} c_\textrm{M}c_\textrm{solid}}{R_{\text {g}} T} F n_\textrm{M} \nabla \varphi _{\text {l}} \end{aligned} \end{aligned}$$
(27)

Note that the term \([1-h\left( \phi \right) ]\) is present in \(\textbf{J}_\textrm{M2}\) to ensure the transport of species is only valid in the electrolyte and along the interface (\(\phi <1\)). However, this term is not necessary for \(\textbf{J}_\textrm{M1}\), given that \(c_\textrm{M}\) and \(\phi \) are naturally coupled by the KKS model. Also, note that we use the real metal ion concentration \(c_\textrm{M}^0=c_\textrm{M} c_\textrm{solid}\) in (27) to maintain the dimensional consistency of \(\textbf{J}_\textrm{M}\) and \(\textbf{J}_i\). Now, inserting (27) into the mass conservation equation (24), the transport of metal ions is formulated as

$$\begin{aligned} \begin{aligned}&\frac{\partial c_\textrm{M}}{\partial t} - \nabla \cdot D_\textrm{M} \nabla \left[ c_\textrm{M} - h \left( \phi \right) (c_\textrm{Se} - c_\textrm{Le})- c_\textrm{Le} \right] \\&\quad - \nabla \cdot \left\{ \frac{[1-h\left( \phi \right) ] D_\textrm{M} c_\textrm{M} }{R_{\text {g}} T} F n_\textrm{M} \nabla \varphi _{\text {l}}\right\} = \frac{R_\textrm{M}}{c_\textrm{solid}} \end{aligned} \end{aligned}$$
(28)

Similarly, the driving force for other species, \(\mu _i\), is given by,

$$\begin{aligned} \mu _i = \frac{\partial \psi ^\textrm{E}}{\partial c_i} = R_{\text {g}} T\textrm{ln}c_i + \mu _i^0 + F\varphi _{\text {l}} n_i \end{aligned}$$
(29)

and the flux \({\textbf {J}}_i\) is defined as,

$$\begin{aligned} {\textbf {J}}_i = - \frac{[1-h\left( \phi \right) ] D_i c_i}{R_{\text {g}} T} \nabla \mu _i = - [1-h\left( \phi \right) ] D_i \nabla c_i - \frac{[1-h\left( \phi \right) ] D_i c_i}{R_{\text {g}} T} F n_i \nabla \varphi _{\text {l}} \end{aligned}$$
(30)

The resulting mass transport equation can be obtained by inserting Eq. (30) into the balance Eq. (25), rendering a phase field-dependent form of the Nernst-Planck equation:

$$\begin{aligned} \frac{\partial c_i}{\partial t}- \nabla \cdot \left\{ [1-h\left( \phi \right) ] D_i \nabla c_i \right\} - \nabla \cdot \left\{ \frac{ [1-h\left( \phi \right) ] D_i c_i}{R_{\text {g}} T} F n_i \nabla \varphi _{\text {l}} \right\} = R_i \end{aligned}$$
(31)

Finally, for both \(R_\textrm{M}\) and \(R_i\), we introduce a generalized form of the reaction term, which is given by

$$\begin{aligned} R_j=\sum _{m=1}^{m_t} \left\{ k_{mp} \prod _{v_{jm}>0} c_j^{v_{jm}}-k_{mr} \prod _{v_{jm}<0} c_j^{-v_{jm}}\right\} \end{aligned}$$
(32)

where \(m_t\) is the total number of chemical equations, \(v_{jm}\) is the stoichiometric coefficient for species j in the chemical reaction m, and \(k_{mp}\) and \(k_{mr}\) respectively denote the rate constant of products and reactants in reaction m. Note that we define \(v_{jm}>0\) for products and \(v_{jm}<0\) for reactants. Also, we emphasize that when the metal ion is involved, the actual concentration \(c_\textrm{M}^0=c_\textrm{M} c_\textrm{solid}\) must be adopted in Eq. (32).

2.3.3 Electrostatic potential

The distribution of electrostatic potential \(\varphi _{\text {l}}\) can be estimated by the following Poisson-type equation [28, 29],

$$\begin{aligned} \nabla \cdot (\kappa \nabla \varphi _{\text {l}})= n_\textrm{M} F c_\textrm{solid} \frac{\partial \phi }{\partial t} \end{aligned}$$
(33)

In Eq. (33), the variation of charge density due to the chemical reaction shown in Eq. (1) is accounted for by defining an additional term on the right-hand side, with the term \(c_\textrm{solid} \partial \phi / \partial t\) capturing the creation of electrons due to the dissolution of the metal electrode. Also, \(\kappa \) is the electric conductivity, which is defined as

$$\begin{aligned} \kappa = h\left( \phi \right) \kappa _{\text {s}} + \left[ 1- h\left( \phi \right) \right] \kappa _{\text {l}} \end{aligned}$$
(34)

where \(\kappa _{\text {s}}\) and \(\kappa _{\text {l}}\) are the conductivity in solid and liquid phases, respectively. The magnitude of the solid conductivity is chosen to be a sufficiently large value (\(\kappa _{\text {s}}=1\times 10^{7}\) S/m), so as to ensure a uniform distribution of \(\varphi _{\text {l}}\) in the solid phase. Thus, \(\varphi _{\text {l}}\), which is indistinctly referred to as electrolyte or electrostratic potential, is solved for in the entire domain but its magnitude is only relevant within the electrolyte and at the electrolyte-electrode interface. Then, upon the assumption of a dilute solution [30], \(\kappa _{\text {l}}\) is given by the following concentration-dependent function

$$\begin{aligned} \kappa _{\text {l}}= \frac{F^2}{R_{\text {g}} T} \left( c_\textrm{M} c_\textrm{solid} D_\textrm{M} n_\textrm{M}^2 + \sum _i c_i D_i n_i^2\right) \end{aligned}$$
(35)

2.3.4 Mechanical deformation

The governing equation of the mechanical system is derived by minimizing the strain energy density \(\delta \Pi ^\textrm{M}=0\). Let us neglect for simplicity body loads and external tractions. Accordingly, see Eqs. (13)–(15), one reaches:

$$\begin{aligned} \int _{\Omega } h (\phi ) \, \varvec{\sigma }_0: \delta \varvec{\varepsilon }\,\, \textrm{d} V={\varvec{0}} \end{aligned}$$
(36)

with \(\varvec{\varepsilon }=\varvec{\varepsilon }^\textrm{e} + \varvec{\varepsilon }^\textrm{p}\) being the total strain tensor. By application of the Gauss divergence theorem and considering that Eq. (36) must hold for any arbitrary variations, we obtain the following balance:

$$\begin{aligned} \nabla \cdot \left[ h (\phi ) {\varvec{\sigma }}_0 \right] ={\varvec{0}} \end{aligned}$$
(37)

where \({\varvec{\sigma }}_0\) is the undamaged or effective stress tensor, which is given by

$$\begin{aligned} {\varvec{\sigma }}_0={\varvec{C^{\textrm{ep}}}} : \left( {\varvec{\varepsilon }}^\textrm{e} + {\varvec{\varepsilon }}^\textrm{p} \right) = {\varvec{C^{\textrm{e}}}}: {\varvec{\varepsilon }}^\textrm{e} \end{aligned}$$
(38)

with \({\varvec{C^{\textrm{ep}}}}\) being the elastic–plastic consistent material Jacobian. It follows that the homogenized or damaged Cauchy stress tensor is given by \({\varvec{\sigma }}=\partial _{\varepsilon } \psi ^\textrm{M}= h (\phi ) {\varvec{\sigma }}_0 \).

The solid is assumed to exhibit isotropic strain hardening, which is characterized by means of the following power law relationship between the flow stress \(\sigma \) and the equivalent plastic strain \(\varepsilon ^\textrm{p}\):

$$\begin{aligned} \sigma =\sigma _{y}\left( 1+\frac{E \varepsilon ^\textrm{p}}{\sigma _{y}}\right) ^\textrm{N} \end{aligned}$$
(39)

where E is the Young’s modulus, \(\sigma _{y}\) is the initial yield stress and N is the strain hardening exponent (\(0 \leqslant N \leqslant 1\)).

2.4 Dissolution-mechanics interactions

Two important physical couplings are relevant to our theory. Firstly, the evolution of localized corrosion will result in material damage and redistribution of mechanical fields, see Eq. (37). Secondly, the mechanical deformation of the solid will impact metallic dissolution by enhancing corrosion rates (mechanochemical theory [21]) and by fracturing the passivation layer (FRDR mechanism [22]). The latter is captured by enhancing the phase field mobility coefficient, as proposed by Cui et al. [12]. Thus, the mechanical work required to fracture the passivation film is characterised using the equivalent plastic strain \(\varepsilon ^\textrm{p}\), such that film rupture will occur when \(\varepsilon ^\textrm{p}\) reaches a critical value \(\varepsilon _f\). After a film rupture event, passivation will result in the deposition of an initially unstressed oxide layer on the newly exposed metallic surface. Thus, corrosion rates are the result of a competition between the kinetics of passivation and straining. Accordingly, the relevant time scale over which strains accumulate is the time that it takes for the new passivation layer to rupture, since its deposition. This rupture-dissolution-repassivation cycle time interval is here denoted \(t_i\) and accordingly,

$$\begin{aligned} \varepsilon _i^\textrm{p} = \varepsilon _f \,\,\,\,\,\,\,\, \text {with} \,\,\,\,\,\,\,\, \varepsilon _i^\textrm{p} = \int _0^{t_i} \dot{\varepsilon }^\textrm{p} \, \text {d}t \end{aligned}$$
(40)

Once film rupture occurs, the bare metal interface kinetics coefficient \(L_{\text {a}}\) is immediately recovered. Bare metal interface kinetics are sustained for a certain period \(t_0\), as it takes time for the passive film to be sufficiently stable to impact corrosion kinetics. Once the film is sufficiently stable, dissolution rates are gradually reduced, with the decay process being dependent on the environment-material system, and captured here by means of a stability parameter k. After a time \(t_f\) since the decay starts, film rupture occurs again, \(\varepsilon _i^\textrm{p} = \varepsilon _f\), and a new FRDR cycle begins. Thus, the time interval for each rupture–dissolution–repassivation cycle equals \(t_i=t_0+t_f\), with \(t_f\) being determined by the mechanical fields. Accordingly, in terms of the corrosion current density, each rupture–dissolution–repassivation cycle is given by,

$$\begin{aligned} i_f(t_i)=\left\{ \begin{aligned} i_{\text {a}}&, \,\,\,\,\,\,\,\,\text {if} \,\,\, \ 0< t_i \leqslant t_0 \\ i_{\text {a}} \ \textrm{exp} \left[ -k \left( t_i-t_0 \right) \right]&, \, \,\,\,\,\,\,\,\,\text {if} \,\,\, t_0 < t_i \leqslant t_0+t_f \\ \end{aligned}\right. \end{aligned}$$
(41)

In addition, and independently of the FRDR process, corrosion kinetics are accelerated by mechanical fields [21]. Following Gutman’s mechanochemical theory [31], we introduce an additional term \(k_{\text {m}}\) to describe this phenomenon. Thus the corrosion current density reads,

$$\begin{aligned} i (t) =k_\textrm{m} \left( \varepsilon ^\textrm{p}, \sigma _{\text {h}} \right) i_f(t_i) = \left( \frac{\varepsilon ^\textrm{p}}{\varepsilon _y} + 1 \right) \textrm{exp}\left( \frac{\sigma _{\text {h}} V_{\text {m}}}{R_{\text {g}} T}\right) i_f(t_i) \end{aligned}$$
(42)

where \(\sigma _{\text {h}}\) is the hydrostatic stress and \(V_{\text {m}}\) is the molar volume. The latter is defined as \(V_{\text {m}}=M_{\text {m}}/\rho _{\text {m}}\), such that for a stainless steel with density \(\rho _{\text {m}}=7930\) \(\mathrm {kg/m^3}\) and molar mass \(M_{\text {m}}=0.056\) kg/mol, the molar volume equals \(V_{\text {m}}=7.1\times 10^{-6}\) \(\mathrm {m^3/mol}\).

Accordingly, building upon the connection between the mobility coefficient L and the corrosion current density i, a generalized L can be defined that incorporates: (i) the FRDR mechanism, via (41); (ii) the sensivity of corrosion kinetics to mechanical fields, via (42); and (iii) the impact of the overpotential \(\eta \) on the corrosion current, via (19)–(21). Hence,

$$\begin{aligned} L=L\left( \varepsilon ^\textrm{p} , \sigma _{\text {h}}, \eta \right) =\left\{ \begin{aligned} k_\textrm{m} \left( \varepsilon ^\textrm{p} , \sigma _{\text {h}} \right) \, L_{\text {a}} (\eta )&, \,\,\,\,\,\,\,\,\text {if} \,\,\, 0< t_i \leqslant t_0 \\ k_\textrm{m} \left( \varepsilon ^\textrm{p} , \sigma _{\text {h}} \right) \, L_{\text {a}} (\eta ) \ \textrm{exp} \left[ -k \left( t_i-t_0 \right) \right]&, \,\,\,\,\,\,\,\,\text {if} \,\,\, t_0 < t_i \leqslant t_0+t_f \\ \end{aligned} \right. \end{aligned}$$
(43)

2.5 Species and reactions in the electrolyte

The transport of ionic species and the homogeneous chemical reactions in the electrolyte have an impact on localized corrosion. Here, we assume that the electrolyte is a NaCl-based solution containing the following six ionic species: \(\textrm{M}^{n_\textrm{M}^+}\), \(\mathrm {M(OH)}^{(n_\textrm{M}-1)^+}\), \(\textrm{H}^{+}\), \(\textrm{OH}^{-}\), \(\textrm{Na}^{+}\) and \(\textrm{Cl}^{-}\). These result in the following chemical reactions:

$$\begin{aligned}{} & {} \text {M}^{{n}_{\textrm{M}}^+} + \text {H}_2\text {O}\, {\mathop {\rightleftharpoons }\limits _{k_{f1}}^{k_{b1}}} \,\text {M(OH)}^{(n_\textrm{M}-1)^+} + \text {H}^+ \end{aligned}$$
(44)
$$\begin{aligned}{} & {} \text {H}_2\text {O}\, {\mathop {\rightleftharpoons }\limits _{k_{f2}}^{k_{b2}}} \, \text {H}^+ + \text {OH}^- \end{aligned}$$
(45)

Thus, the reaction term for each ionic species in Eq. (32) can be re-written as:

$$\begin{aligned} \begin{aligned} R_\textrm{M}&= -k_{f1}\,c_{\textrm{M}} c_\textrm{solid} + k_{b1}\,c_{\textrm{H}} c_{\textrm{MOH}}\\ R_\mathrm {M(OH)}&= k_{f1}\,c_{\textrm{M}} c_\textrm{solid} - k_{b1}\,c_{\textrm{H}} c_{\textrm{MOH}}\\ R_\textrm{H}&= k_{f1}\,c_{\textrm{M}} c_\textrm{solid} - k_{b1}\,c_{\textrm{H}} c_{\textrm{MOH}} + k_{f2} - k_{b2}\,c_{\textrm{H}} c_{\textrm{OH}} \\ R_\textrm{OH}&=k_{f2} - k_{b2}\,c_{\textrm{H}} c_{\textrm{OH}} \end{aligned} \end{aligned}$$
(46)

where \(k_f\) and \(k_b\) respectively denote the rate constants for the forward and backward reactions, with the subscripts 1 and 2 being employed to distinguish between the reactions (44) and (45), respectively. Chemical reactions typically occur over much shorter times scales than mass transport and, as a result, the reactions are typically assumed to be in equilibrium. Under equilibrium conditions, the concentrations involved must remain proportional to each other and consequently an equilibrium constant can be defined for each of the reactions being considered; i.e., here one findsFootnote 1

$$\begin{aligned} \begin{aligned} K_1= \frac{k_{f1}}{k_{b1}} = \frac{c_{\textrm{H}} c_{\textrm{MOH}}}{c_{\textrm{M}} c_\textrm{solid}},\,\,\,\,\,\,\,\,\,\,K_2= \frac{k_{f2}}{k_{b2}}= c_{\textrm{H}} c_{\textrm{OH}} \end{aligned} \end{aligned}$$
(47)

Two approaches are typically followed to introduce the equilibrium assumption in the Nernst–Planck equations (31) [32]. One can solve for some of the ionic species assuming \(R_i=0\) and then estimate the remaining concentrations via their equilibrium relationships. For example, focusing on reaction (45), a numerical solution for \(c_{\textrm{H}}\) can be obtained by solving Eq. (31) with \(R_\textrm{H}=0\), and then Eq. (47b) can be used to estimate \(c_{\textrm{OH}}\), as the magnitude of \(K_2\) is known. Alternatively, the magnitude of \(R_i\), the source term in Eq. (31), can be adequately chosen so as to ensure that the equilibrium conditions are fulfilled. I.e., for the case of reaction (45), the magnitudes of \(R_\textrm{H}\) and \(R_\textrm{OH}\) are chosen such that the numerical estimates for \(c_{\textrm{H}}\) and \(c_{\textrm{OH}}\) always satisfy \(c_{\textrm{H}} c_{\textrm{OH}} = K_2\). Here, the latter approach is adopted. Thus, following Eq. (47), the expressions for the reaction terms (46) can be re-formulated as

$$\begin{aligned} \begin{aligned} R_\textrm{M}&= k_{b1} \left( -K_1\,c_{\textrm{M}} c_\textrm{solid} + c_{\textrm{H}} c_{\textrm{MOH}}\right) \\ R_\textrm{MOH}&= k_{b1}\left( K_1\,c_{\textrm{M}} c_\textrm{solid} - c_{\textrm{H}} c_{\textrm{MOH}}\right) \\ R_\textrm{H}&= k_{b1}\left( K_1\,c_{\textrm{M}} c_\textrm{solid} - c_{\textrm{H}} c_{\textrm{MOH}}\right) + k_{b2} \left( K_2 - c_{\textrm{H}} c_{\textrm{OH}}\right) \\ R_\textrm{OH}&=k_{b2} \left( K_2 - c_{\textrm{H}} c_{\textrm{OH}}\right) \end{aligned} \end{aligned}$$
(48)

and by inserting (48) into (28) and (31), the governing equations for all concerned species are obtained. Here, it is important to note that the local equilibrium assumption for the chemical reactions implies that one does not need to know the magnitude of the backward and forward reaction rates (\(k_{fi}\) and \(k_{bi}\)), it suffices to know the value of the equilibrium constants \(K_i\). Consider for example Eq. (48)d, the term \(k_{b2}\) acts as a penalty term as increasing its magnitude will constraint the solution to ensure that \(c_{\textrm{H}} c_{\textrm{OH}} = K_2\) is met. Accordingly, the choice of \(k_{bi}\) is purely numerical, with the equilibrium condition been enforced for \(k_{bi} \rightarrow \infty \). As discussed in Sect. 4.1, the magnitude of \(k_{bi}\) is chosen to be sufficiently large to approximate equilibrium conditions but not so large so as to induce convergence problems.

2.6 Summary of governing equations

Table 1 Summary of the governing equations of the electro-chemo-mechanical phase field corrosion model presented
Full size table

The balance equations can be particularized upon the consideration of the constitutive choices made in Sects. 2.3, 2.4 and 2.5. A summary of the governing equations is provided in Table 1. This overview emphasises the couplings between the different elements of our theory. First, it can be observed that mechanics plays a role in the evolution of the corrosion front, via the term \(L(\varepsilon ^\textrm{p}, \sigma _{\text {h}}, \eta )\) in the phase field evolution equation (T.1). Secondly, the evolution of the corrosion front leads in turn to a degradation of the material stiffness and a re-distribution of the mechanical fields, see (T.5). Thirdly, the phase field evolution equation is impacted by the electrostatic potential via the dependency of the mobility coefficient on the overpotential (\(L(\varepsilon ^\textrm{p}, \sigma _{\text {h}}, \eta )\)), with the overpotential \(\eta \) being related to the electrostatic potential \(\varphi _{\text {l}}\) through Eq. (22). Due to electromigration, the electrostatic potential also has an impact on the transport of solid phase ions, see (T.2), and on the transport of the electrolyte ionic species, see (T.3). These transport equations for ionic species also contain a phase field dependent term, to ensure that transport is limited to the electrolyte. Finally, the calculation of the electrostatic potential is influenced by both the phase field, as (T.4) accounts for the creation of electrons, and the concentration of ionic species (T.2)–(T.3), due to the influence of those on the electrolyte conductivity, as shown in (T.8). Thus, the electro-chemo-mechanical system is fully coupled through these interactions.

3 COMSOL implementation

The electro-chemo-mechanical phase field formulation presented in Sect. 2 is implemented in the finite element package COMSOL MULTIPHYSICS. The primal fields and nodal degrees-of-freedom (DOFs) are the phase field order parameter \(\phi \), the displacement components \({\textbf {u}}\), the concentration of metal ions \(c_\textrm{M}\), the concentrations of the ionic species involved \(c_i\), and the electrostatic potential \(\varphi _{\text {l}}\). In COMSOL, as a result of its symbolic differentiation capabilities, the governing equations of the model can be formulated in either the weak or the strong form, without the need to provide explicit expressions for the residuals and tangent stiffness matrices. As described below, five COMSOL physics interfaces are used in the implementation, two in-built ones (Solid Mechanics and Transport of Diluted Species), and three user-defined interfaces that exploit the Mathematics module to simulate the evolution of the phase field, the transport of metal ions, and the distribution of electrostatic potential. So-called State Variables are used to capture the film rupture-dissolution-repassivation mechanism. The COMSOL implementation is made freely available at http://www.empaneda.com/codes.

3.1 Module setup

Phase field (T.1) We use the Coefficient Form PDE interface to define the evolution of the phase field order parameter \(\phi \). When using this interface, COMSOL provides the following generic form to define PDEs that contain derivatives up to second order in both time and space,

$$\begin{aligned} \begin{aligned} e_{\text {a}} \frac{\partial ^2 \phi }{\partial t^2} + d_{\text {a}} \frac{\partial \phi }{\partial t} + \nabla \cdot \left( -c\nabla \phi -{\varvec{\alpha }}\phi +{\varvec{\gamma }}\right) + {\varvec{\beta }} \cdot \nabla \phi + a\phi =f \end{aligned} \end{aligned}$$
(49)

To mimic (T.1), the PDE coefficients are chosen as \(d_{\text {a}}=1/L\), \(c=\alpha \), \(f=-\frac{\partial \psi ^\textrm{E}}{\partial \phi }\), \(e_{\text {a}}=a=0\), and \({\varvec{\alpha }}={\varvec{\beta }}={\varvec{\gamma }}={\varvec{0}}\).

Transport of metal ions (T.2) We use the General Form PDE interface to define the transport of solid phase ions. This interface enables defining differential equations of the following form:

$$\begin{aligned} \begin{aligned} {e_{\text {a}} \frac{\partial ^2 c_\textrm{M}}{\partial t^2} + d_{\text {a}} \frac{\partial c_\textrm{M}}{\partial t} + \nabla \cdot {\varvec{\Gamma }} =f} \end{aligned} \end{aligned}$$
(50)

Accordingly, Eq. (50) can be particularised to (T.2) upon the following choices: \(d_{\text {a}}=1\), \(e_{\text {a}}=0\), \(f=R_\textrm{M}\)/\(c_\textrm{solid}\) and

$$\begin{aligned} \begin{aligned} \Gamma _{x_i}=-D_\textrm{M} \frac{\partial c_\textrm{M}}{\partial \textbf{x}}+D_\textrm{M}(c_\text {Se}-c_\text {Le})\frac{\partial h(\phi )}{\partial \textbf{x}} - \frac{[1-h\left( \phi \right) ] D_\textrm{M} c_\textrm{M}}{R_{\text {g}} T} F n_\textrm{M}\frac{\partial \varphi _{\text {l}}}{\partial \textbf{x}} \end{aligned} \end{aligned}$$
(51)

The source term of Eq. (50) contains the reaction variable \(R_\textrm{M}\), whose evolution is described by the algebraic equation (48), which is defined as a COMSOL Variable.

Transport of ionic species (T.3) The Nernst-Planck equations are implemented using the Transport of Diluted Species interface, which is part of the Chemical Species Transport module. Diffusion and migration in electric field are considered to be the main transport mechanisms (i.e., neglecting convection) and we particularise the implementation to five species (Dependent Variables) with concentrations \(c_{\textrm{H}}\), \(c_{\textrm{Cl}}\), \(c_{\textrm{OH}}\), \(c_{\textrm{MOH}}\), and \(c_{\textrm{Na}}\). As per Eqs. (48)b–d, three associated reactions are defined: \(R_\textrm{H}\), \(R_\textrm{OH}\), and \(R_\mathrm {M(OH)}\). The coupling term \([1-h(\phi )]\) is incorporated via the definition of the diffusion coefficients and the electric potential is defined to be the electrolyte potential \(\varphi _{\text {l}}\).

Electrostratic potential distribution (T.4) We use the Poisson’s Equation interface to define the distribution of electrostratic potential \(\varphi _{\text {l}}\). The Poisson’s equation is written as: \(\nabla \cdot \left( -c \nabla \varphi _{\text {l}} \right) =f\). Thus, we define \(c=-\kappa \) and \(f=n_\textrm{M} F c_\textrm{solid} \partial \phi /\partial t\) to mimic (T.4).

Mechanical balance (T.5) The Solid Mechanics interface is used to implement the governing equation of the mechanical problem (T.5). The degradation of the material stiffness associated with the evolution of the corrosion front (\(\phi \)) is captured at the weak form level by editing the Weak expression. If the body is assumed to be linear elastic, then one can attain the same effect by degrading only the Young’s modulus. However, in the case of an elastic–plastic material, such a strategy would imply that the degree of plastic flow is estimated using the homogenized (degraded) stress, whereas it is more common to use the effective (undegraded) stress [33, 34], as it corresponds to the actual stress acting on the undegraded area.

Finally, two State Variables are used to implement the FRDR mechanism, (T.7). To this end, two history-dependent variables are defined that respectively store the last values of equivalent plastic strain and time at which the last film rupture event took place:

$$\begin{aligned} \varepsilon _c=\left\{ \begin{aligned} \varepsilon ^\textrm{p}&, \,\,\,\,\,\,\,\,\text {if} \,\,\, \left( \varepsilon ^\textrm{p}-\varepsilon _c \right) > \varepsilon _f \\ \varepsilon _c&, \,\,\,\,\,\,\,\,\text {otherwise} \\ \end{aligned} \right. \end{aligned}$$
(52)

and

$$\begin{aligned} t_c=\left\{ \begin{aligned} t&, \,\,\,\,\,\,\,\,\text {if} \,\,\, \left( \varepsilon ^\textrm{p}-\varepsilon _c \right) > \varepsilon _f \\ t_c&, \,\,\,\,\,\,\,\,\text {otherwise} \\ \end{aligned} \right. \end{aligned}$$
(53)

Hence, \(\varepsilon ^\textrm{p}-\varepsilon _c\) is a measure of the accumulated equivalent plastic strain since the last film rupture occurrence, and the time \(t_i\) in (T.7) equals to \(t-t_c\) in this definition. Note that \(t_c\) is updated at the end of each FRDR cycle, such that \(t_i\) becomes zero at the beginning time each FRDR cycle. Also, at the beginning of the calculation, we define \(\varepsilon _c (t=0)=t_c(t=0)=0\). Thus, storing \(\varepsilon _c\) enables determining when the film rupture event occurs (\(\varepsilon ^\textrm{p}-\varepsilon _c=\varepsilon _f\)) and, using \(t_c\), this information is used to identify what stage of the FRDR cycle corresponds to the current time t. Accordingly, the interface mobility is defined in COMSOL as

$$\begin{aligned} \begin{aligned} L\left( \varepsilon ^\textrm{p}, \sigma _{\text {h}}, \eta \right) = k_\textrm{m} \left( \varepsilon ^\textrm{p} , \sigma _{\text {h}} \right) \, L_0 \cdot \text {exp}\left( \frac{a_{\text {a}}nF\eta }{R_{\text {g}} T}\right) \cdot \textrm{min} \left\{ 1, \textrm{exp} \left[ -k \left( t-t_c-t_0 \right) \right] \right\} \end{aligned} \end{aligned}$$
(54)

such that L corresponds to the mobility coefficient of the bare metal if the time since the last rupture event (\(t-t_c\)) is smaller than the time that it takes for the film to stabilise (\(t_0\)), and is degraded otherwise.

3.2 Solution strategies

The time-dependent solution step is used. COMSOL provides both monolithic and staggered solution algorithms, respectively termed Fully Coupled and Segregated. While monolithic approaches are appealing due to their unconditional stability, they generally lead to a poor performance convergence-wise, unless quasi-Newton methods such as BFGS are used [35,36,37], which are currently not available in COMSOL. Thus, a staggered approach is adopted here. First, the charge balance problem (T.4) is solved to obtain the distribution of electrostatic potential \(\varphi _{\text {l}}\). Then, the Nernst–Planck equations (T.3) are evaluated and the concentrations of \(\mathrm {M(OH)}^{(n_\textrm{M}-1)^+}\), \(\textrm{H}^{+}\), \(\textrm{OH}^{-}\), \(\textrm{Na}^{+}\), and \(\textrm{Cl}^{-}\) are obtained. Then, the deformation of the solid is estimated by solving the balance of linear momentum, (T.5). Finally, solutions are obtained for the phase field evolution equation (T.1) and the transport of solid phase ions (T.2). Converge is assessed for all fields in what is usually referred to as a Jacobi-type multi-pass solution approach. This is defined by specifying a number of iterations in the Segregated node settings.

4 Results

4.1 Pencil electrode test with electrochemistry

We shall first employ the proposed electro-chemo-mechanical phase field formulation to simulate the so-called pencil electrode test, a paradigmatic benchmark in corrosion science. As shown in Fig. 2, a stainless steel wire with a height of \(\textrm{H}_{\text {s}}=150\) \(\mu \)m and a diameter of \(d=25\) \(\mu \)m, is mounted into an epoxy coating, leaving only the top edge of the sample exposed to the corrosive solution. This boundary value problem has been investigated using multiple computational techniques, including phase field [8, 12, 27, 38], but without incorporating the electrochemical behaviour of the electrolyte. Here, we explore the impact of the electrochemical process on the pencil electrode test by considering the electrochemical parameters listed in Table 2 (unless otherwise stated).

Fig. 2
figure 2

Schematic description of the pencil electrode test, including the boundary conditions adopted at the top edge

Full size image
Table 2 Electrochemical parameters for the pencil electrode test, values taken from Refs. [4, 12, 28]
Full size table

In previous phase field corrosion analyses of this benchmark test (see, e.g., Refs. [12, 38, 39]), only the stainless steel wire was modeled, with the Dirichlet boundary conditions \(\phi =c_\textrm{M}=0\) being applied at the top edge. This scenario corresponds to assuming that the environment near the corrosion front is completely isolated [40]. It is unclear whether this simplification is sensible, even for the case of occluded environments such as cracks. A less restrictive and more realistic approach is to simulate the electrolyte and enforce the boundary conditions \(\phi =c_\textrm{M}=0\) at the edge of the electrolyte. We shall explore the outputs from both approaches here and in the context of a corrosion pit (Sect. 4.2). In this case study, we take advantage of our electro-chemo-mechanical model and simulate the electrochemical behaviour of the electrolyte, applying the Dirichlet boundary conditions \(\phi =c_\textrm{M}=0\) at the top edge of the electrolyte domain and varying its height \(H_{\text {l}}\) to assess its influence. Regarding the initial conditions, we set \(\phi (t=0)=c_\textrm{M}(t=0)=1\) for the metal and \(\phi (t=0)=c_\textrm{M}(t=0)=0\) for the electrolyte, such that the dissolution will naturally initiate from the interface. In the absence of electrolyte (the case \(\textrm{H}_{\text {l}}=0\)) the Dirichlet boundary conditions \(\phi =c_\textrm{M}=0\) are prescribed at the top edge, and the initial conditions are defined as \(\phi (t=0)=c_\textrm{M}(t=0)=1\) for the entire domain. Following Ref. [12], the interface mobility coefficient is chosen to be \(L_0=2\times 10^6\) \(\mathrm {mm^2/(N \cdot s)}\), and one should note that neither film rupture nor mechanical effects are relevant in this case study. The element length in the expected corroded region is made to be at least 3 times smaller the interface thickness \(\ell \), to ensure mesh objective results.

Fig. 3
figure 3

Pencil electrode test with electrochemistry: predictions of pit depth versus time t as a function of the electrolyte height \(\textrm{H}_{\text {l}}\) (for a fixed metal height \(\textrm{H}_{\text {s}}=150\) \(\mu \)m)

Full size image

First, we investigate the interplay between the transport of solid phase ions and corrosion by neglecting the role of the electrolyte potential and the transport of the remaining ionic species (\(\varphi _{\text {l}}=c_i=0 \, \forall \, \textbf{x}\)). The results obtained are shown in Fig. 3, in terms of the pith depth (in \(\mu \)m) versus time (in s). The pit depth is defined as the distance between the initial metal/electrolyte interface to the current corrosion interface. It can be observed that corrosion rates decrease when the initial electrolyte height \(\textrm{H}_{\text {l}}\) increases. In the limit case, \(\textrm{H}_{\text {l}}=0\), corrosion is clearly in the diffusion-controlled regime, and thus the rate-limiting step is the transport of metal ions away from the pit boundary. These results can be rationalized based on the impact of \(\textrm{H}_{\text {l}}\) on the gradient of the normalized concentration of metal ions \(c_{\text {m}}\). Decreasing \(H_{\text {l}}\) leads to a reduction in the magnitude of \(\nabla c_\textrm{M}\), as well as in the corrosion rates. This is shown in Fig. 4, where the distribution of the normalized concentration of metal ions \(c_\textrm{M}\) is given along the vertical axis for two \(\textrm{H}_{\text {l}}\) choices. The concentration of metal ions equals the concentration of atoms in the metal \(c_\textrm{solid}\) for low \(y/\textrm{H}_{\text {s}}\) values, until the interface is reached (\(\phi \approx 0.5\)), where the concentration of metal ions drops until reaching the interface saturation value \(c_\textrm{sat}\). Then, \(c_\textrm{M}\) progressively diminishes until becoming zero at the far end of the electrolyte. Hence, the larger the electrolyte, the smaller the gradient of \(c_\textrm{M}\). This is readily seen in the figure, with the slope of the last stage being more pronounced for the case of \(\textrm{H}_{\text {l}}=0\), relative to the \(\textrm{H}_{\text {l}}=200\) \(\upmu \)m result. This leads to a reduction of the corrosion rates through Eqs. (T.2), (16) and (17). This can also be readily seen in the figure, as the corrosion front is closer to the bottom edge of the metal (\(y=0\)) for the case of \(\textrm{H}_{\text {l}}=0\).

Fig. 4
figure 4

Pencil electrode test with electrochemistry: normalized metal concentration \(c_\textrm{M}\) distribution along the vertical direction (\(y/\textrm{H}_{\text {s}}\)). Results are obtained for a time of \(t=100\) s for two selected values of the electrolyte height (\(\textrm{H}_{\text {l}}=0\) and \(\textrm{H}_{\text {l}}=200\) \(\mu \)m)

Full size image

We shall now turn our attention to the role of the applied potential and the concentration of ionic species in governing corrosion kinetics. As shown in Table 2, we consider a solution with pH = 7 and molarity 0.001 M NaCl; i.e., a bulk NaCl concentration of 0.001 mol/L (1 mol/m\(^3\)). Thus, the initial values of \(c_i\) at \(t=0\) can be determined as follows. First, the concentrations \(c_\textrm{M}\) and \(c_\textrm{MOH}\) are chosen to be zero, given that no dissolution occurs at \(t=0\). Secondly, the concentration \(c_{\textrm{H}}\) is determined from the initial pH using the standard relation pH\( = -\textrm{log}_{10} \,c_{\textrm{H}}\). From \(c_{\textrm{H}}\), one can readily estimate the initial value of \(c_{\textrm{OH}}\) using the equilibrium condition (47)b. Finally, \(c_\textrm{Cl}\) and \(c_\textrm{Na}\) are same as the initial NaCl concentration (i.e., 1 \(\mathrm {mol/m^3}\) in this case). These choices automatically satisfy the electroneutrality condition: \(n_{\textrm{M}} c_{\textrm{M}} c_{\textrm{solid}} + \sum _i n_i c_i=0\). These initial values of \(c_i\) are also prescribed at the top edge of the electrolyte domain through Dirichlet boundary conditions. In what follows, the results are computed using a reference interface kinetics coefficient of \(L_0=0.001\) \(\mathrm {mm^2/(N \cdot s)}\) and an electrolyte height of \(\textrm{H}_{\text {l}}=200\) \(\mu \)m. As discussed in Sect. 2.5, the equilibrium conditions (44)–(45) can be automatically satisfied when \(k_{b1}\) and \(k_{b2}\) are large enough. However, one shall note that high values of \(k_{b1}\) and \(k_{b2}\) can also worsen numerical convergence. After a sensitivity study, we find that \(k_{b1}=5\times 10^2\) \(\mathrm {m^3/(mol \cdot s)}\) and \(k_{b2}=5\times 10^3\) \(\mathrm {m^3/(mol \cdot s)}\) are sufficiently large to effectively satisfy the equilibrium conditions without hindering convergence.

Fig. 5
figure 5

Pencil electrode test with electrochemistry: predictions of pit depth versus time t as a function of applied potential \(\varphi _{\text {s}}\)

Full size image

The results obtained for a varying applied potential \(\varphi _{\text {s}}\) are shown in Fig. 5, where \(\varphi _{\text {s}}\) spans the range 0.1 to 0.3 V. In agreement with expectations, corrosion occurs faster with increasing \(\varphi _{\text {s}}\), as a result of the enhancement of the overpotential \(\eta \), see Eqs. (21) and (22). For all cases, corrosion is activation-controlled with a linear relation between pit depth and time, revealing that the electrostatic potential \(\varphi _{\text {l}}\) does not change significantly in time. Figure 6 further compares the distributions of \(\varphi _{\text {l}}\) with two typical applied potentials, 0.1 V and 0.3 V. Results show that the electrostatic potential \(\varphi _{\text {l}}\) remains constant in the solid phase and then drops as we move away from the interface in the electrolyte region. We emphasize that all electrolyte-related variables are solved for in the entire domain, with the phase field being used to track the location of the electrode-electrolyte interface. Thus, the distribution of \(\varphi _{\text {l}}\) in the solid phase (\(\phi =1\)) has no practical interest. Another interesting observation from Fig. 6 is the increase in magnitude of \(\varphi _{\text {l}}\) with increasing \(\varphi _{\text {s}}\), as readily observed when comparing legends. This can be understood by considering the dual role that the applied potential plays. On the one hand, corrosion kinetics are accelerated for larger values of the applied potential, as shown in Fig. 5 and discussed above. On the other hand, see (T.4), the increased dissolution rate (\({\text {d}}\phi /{\text {d}}t\)) resulting from higher applied potentials translates into a higher gradient of \(\varphi _{\text {l}}\) and, given that \(\phi _{\text {l}}=0\) at the top edge, in a higher value of the electrolyte potential.

Fig. 6
figure 6

Pencil electrode test with electrochemistry: contours of electrostatic potential \(\varphi _{\text {l}}\) after \(t=200\) s for two selected values of the applied potential \(\varphi _{\text {s}}\)

Full size image

We conclude this benchmark test by assessing the influence of initial NaCl concentration. As evident from (T.4) and (T.8), changing the initial concentration of solvent species would affect the distribution of electrostatic potential \(\varphi _{\text {l}}\) by changing the electrolyte conductivity, and this has an impact on the overpotential, via Eq. (22), and on the interface mobility coefficient (T.7). To examine the role of solute concentration, we fix the applied potential to be \(\varphi _{\text {s}}=0.2\) V and consider four selected values of the NaCl content: 0.001 M, 0.05 M, 0.1 M, and 0.5 M. The results obtained are shown in Fig. 7, in terms of pit depth versus time. In agreement with experimental observations [41], simulations predict an increase in corrosion rate with bulk NaCl concentration. The results shown in Figs. 5 and 7 demonstrate that the present electro-chemo-mechanical phase field formulation can capture the sensitivity of corrosion rates to the applied potential and the solute concentration, respectively.

Fig. 7
figure 7

Pencil electrode test with electrochemistry: predictions of pit depth versus time t as a function of the initial NaCl concentration

Full size image

4.2 Mechanically-assisted corrosion from a semi-circular pit: electro-chemo-mechanical analysis

We now turn our attention to the interplay between electrochemistry and mechanics. A rectangular plate of width \(W=0.3\) mm and height \(H_{\text {s}}=0.15\) mm is considered. Plane strain conditions are assumed. The plate contains a circular pit of radius 10 \(\upmu \)m and is exposed to a NaCl-based electrolyte solution that extends over a domain with height \(H_{\text {l}}=0.3\) mm. The geometry of the metal-electrolyte system is shown in Fig. 8, together with the initial and boundary conditions. As shown in Fig. 8, we assume that the pit has nucleated as a result of the localised rupture of the passive film, and therefore consider the presence of a passive film along all regions of the metal-electrolyte interface outside the pit region. Within the void region (\(R=10\) \(\upmu \)m), we assume the passive film is less stable, allowing the FRDR process described by (T.7) to be applicable. Conversely, the passive film outside of the void region is assumed to be stable enough to preclude corrosion and the transport of ionic species. This is implemented by separating the electrolyte and the metal over those protected regions with an impenetrable and non-corroding 1 \(\upmu \)m layer, as indicated by the bold line in Fig. 8.

Fig. 8
figure 8

Mechanically-assisted corrosion from a semi-circular pit: geometric setup, initial and boundary conditions

Full size image

For simplicity, the same electrochemical parameters used in the pencil electrode test case study are adopted (Table 2), unless otherwise stated. The applied potential is chosen to be \(\varphi _{\text {s}}=0.4\) V. The Dirichlet boundary conditions \(\phi =c_\textrm{M}=0\) and \(\varphi _{\text {l}}=0\) are prescribed at the top edge. The initial values of \(c_i\) and the associated Dirichlet boundary conditions at the top edge of the electrolyte are same as those in the pencil electrode test. As in Ref. [24], the constitutive behaviour of the stainless steel is characterized by a Young’s modulus of \(E=190\) GPa, a Poisson’s ratio of \(\nu =0.3\), a yield stress of \(\sigma _y=400\) MPa, and a strain hardening exponent of \(N=0.1\). Film rupture, dissolution and repassivation is assumed to take place along the pit surface, and is characterized by the following FRDR parameters \(k=0.0001\), \(t_0=50\) s, and \(\varepsilon _f=0.003\) [24]. A constant mechanical load is applied by constraining the left side of the metallic sample and prescribing a constant horizontal displacement of \(u^{\infty }=0.8\) \(\upmu \)m in its right edge. The entire metal-electrolyte system is discretized by means of approximately 20,000 triangular linear finite elements, with the mesh being particularly refined in the expected corrosion region, where the characteristic element length is at least three times smaller than the interface thickness \(\ell \).

Let us now estimate the reference mobility coefficient \(L_0\) by exploiting Eq. (18) to establish a connection with the experimentally-measured value of exchange current density \(i_0\). To this end, we conduct a simulation considering only phase field corrosion (T.1) and the transport of metal ions (T.2), such that L is a constant independent of the mechanical fields and the overpotential. By choosing a sufficiently small value of L we make sure to be under activation-controlled corrosion conditions and proceed to measure the velocity at which the corrosion front evolves, \(v_n\). For the choice of \(L= 1\times 10^{-3}\) \(\mathrm {mm^2/(N s)}\), the finite element model predicts a corrosion velocity of \(v_n=0.0032\) \(\upmu \)m/s. The corresponding corrosion current density i can then be estimated using Faraday’s second law:

$$\begin{aligned} v_{n}=\varvec{v} \cdot \textbf{n}=\frac{i}{n_\textrm{M} F c_{\textrm{solid}}} \end{aligned}$$
(55)

and this leads to a proportionality constant of \(\xi =1.08\times 10^{-11}\) in (18). Using the experimentally measured exchange current density \(i_0=1.422\) \(\mathrm {mA/cm^2}\) reported in Ref. [42], the reference interface mobility parameter is found to be \(L_0=1.5\times 10^{-10}\) \(\mathrm {mm^2/(N s)}\).

Fig. 9
figure 9

Mechanically-assisted corrosion from a semi-circular pit: phase field contours illustrating the pit evolution over three selected time stages: a \(t=1800\) s, b \(t=3600\) s and c \(t=5400\) s

Full size image

The results obtained are shown in Fig. 9, in terms of the phase field contours, which illustrate the evolution of the corrosion front. A more quantitative description of the corrosion pit is shown in Fig. 10, where the pit growth along the depth and width directions is shown. Here, pit depth refers to the growth along the vertical direction (or \(\theta =90^\circ \) for a polar coordinate system centred at the pit mouth), while pit width refers to the growth along the horizontal direction (\(\theta =0^\circ \)). The results show that pitting is not symmetric, with corrosion rates being faster along the depth direction due to the role of mechanical fields in enhancing corrosion kinetics—see Eqs. (42) and (43). Differences are notable, with the pit extending along the vertical direction more than twice the pit width after 5400 s.

Fig. 10
figure 10

Mechanically-assisted corrosion from a semi-circular pit: predictions of pit extension along the depth (vertical) and width (horizontal) directions. For a polar coordinate system (\(r,\theta \)) centred at the pit mouth, the depth direction corresponds to \(r, \, \theta =90^\circ \) while the width direction corresponds to \(r, \, \theta =0^\circ \)

Full size image

Moreover, results reveal that corrosion rates reduce with time, deviating from the linear behaviour reported in the results obtained for the pencil electrode test (Figs. 5 and 7). This is despite \(L_0\) being much smaller in the present case study; \(L= 1.5\times 10^{-10}\) \(\mathrm {mm^2/(N s)}\) vs \(L=0.001\) \(\mathrm {mm^2/(N \cdot s)}\) for Figs. 5 and 7. It is of interest to investigate the source of this drop in corrosion rates, which can be potentially caused by three factors: (i) the role of film passivation, (ii) a shift from activation-controlled corrosion to diffusion-controlled corrosion, and (iii) a raise in electrolyte potential \(\varphi _{\text {l}}\). Inspection of the \(c_\text {M}\) distribution shows that the concentration of metal ions at the interface is below the saturation concentration \(c_\text {sat}\); hence, we proceed to disregard (ii). Then, the role of the electrostatic potential is investigated by plotting the contours of \(\varphi _{\text {l}}\) for relevant time intervals. The results are shown in Fig. 11 for times \(t=1800\) s, \(t=3600\) s, and \(t=5400\) s, with the solid domain (\(\phi =1\)) marked with a grey colour. It can be seen that, while \(\varphi _{\text {l}}\) evolves with time, the change in magnitude is very small, of roughly 0.001 V from 1800 s to 5400 s. Moreover, the electrolyte potential decreases with time, which should lead to a higher dissolution rate, as per (T.7) and (22).

Fig. 11
figure 11

Mechanically-assisted corrosion from a semi-circular pit: contours of electrostatic potential \(\varphi _{\text {l}}\) at times: a 1800 s, b 3600 s, and c 5400 s

Full size image

It remains to assess the role of film repassivation. To this end, we vary the magnitude of the stability parameter k, considering three selected values: \(k=0.0001\), \(k=0.0002\) and \(k=0.0003\). The results obtained are shown in Fig. 12 in terms of pit depth (i.e., growth along the vertical direction) versus time. In agreement with expectations, the more stable the film (larger k), the smaller the corrosion rates. Results reveal significant sensitivity to changes in k, suggesting that film repassivation is the largest contributor to the observed reduction in corrosion kinetics with time.

Fig. 12
figure 12

Mechanically-assisted corrosion from a semi-circular pit: pit depth versus time t predictions as a function of the film stability parameter k

Full size image

Next, we examine the distribution of the ionic species in the electrolyte. Figure 13 shows the contours of \(c_\textrm{M} c_\textrm{solid}\), pH, and \(c_\textrm{Cl}\) for a time of \(t=5400\) s. The contours show how metal ions accumulate close the corrosion front, how the pH remains relatively constant but changes significantly when approaching the electrolyte edge, and how the concentration of chloride ions decreases progressively from the pitting interface to the bulk solution. It is also worth noting that the concentration of metal ions \(c_\textrm{M}\cdot c_\textrm{solid}\) remains well below the saturation concentration (\(c_\textrm{sat}\), see Table 2), indicative of activation-controlled corrosion conditions. Overall, it is clear that the concentrations of ionic species near the pit mouth are significantly different from those at the top edge of the electrolyte (the bulk solution). A more quantitative insight into the distribution of the various ionic species is shown in Fig. 14, where the natural logarithm of the concentration of relevant ionic species is shown as a function of their position along the vertical axis, going from the bottom of the pit to the top edge of the electrolyte. The results show how the concentration of metal ions is highest near the corrosion front, due to metal dissolution, and then decreases as we move deep into the electrolyte. The accumulation of metal ions results in lower pH values (increasing \(c_\textrm{H}\)) inside the pit due to the hydrolysis reaction (44). Consequently, as per reaction (45), the magnitude of \(c_\textrm{OH}\) inside the pit becomes relatively small and increases as we approach the edge of the electrolyte. In addition, changes in \(c_\textrm{Cl}\) are shown to be of secondary nature, but a higher \(\textrm{Cl}^-\) concentration is attained near the corrosion front to maintain the solution charge balance. It is important to note that the accumulation of \(\textrm{H}^+\) at the pit surface may favour hydrogen uptake into the metal and thus hydrogen embrittlement damage mechanisms [43, 44].

Fig. 13
figure 13

Mechanically-assisted corrosion from a semi-circular pit: Contours of a \(c_\textrm{M} \cdot c_\textrm{solid}\), b pH, and c \(c_\textrm{Cl}\). The results are shown for a time \(t=5400\) s

Full size image
Fig. 14
figure 14

Mechanically-assisted corrosion from a semi-circular pit: predictions of ionic concentrations along the y-axis, starting from the pit base and going all the way until the top edge of the electrolyte (as characterized by the distance to the bottom edge of the metal domain). The results are shown for a time \(t=5400\) s

Full size image

Finally, we investigate the differences between the present modeling strategy, where the electrolyte domain is resolved, and the simpler, commonly used approach of neglecting the electrolyte and prescribing on the pit mouth the concentrations of ionic species in the bulk solution (see, e.g., [12, 20]). The differences between the predicted values of \(c_i\) and \(\varphi _{\text {l}}\) at the pit surface and the top of the electrolyte (see Figs. 11 and 13) suggest that results will be sensitive to this choice of modeling approach. Figure 15 shows the extension of pit depth along the vertical direction predicted both by accounting for the electrolyte domain (“electrolyte simulation” curve) and by replacing the electrolyte by Dirichlet boundary conditions for the concentrations and electrolyte potential at the pit mouth (“Pit mouth Dirichlet BCs” curve). The results show that accounting for the role of the electrolyte domain is important not only to rigorously predict the pit chemistry but also to accurately estimate the resulting pitting. In particular, the simplistic approach of prescribing electrochemical boundary conditions at the pit mouth results in a sharper pit morphology that translates into an earlier pit-to-crack transition at the pit base. The slower corrosion rates predicted for the model resolving the electrolyte are likely associated with the drop in ionic concentration (as transport is enhanced), which results in a reduction in conductivity \(\kappa \) through (T.8) and, accordingly, to a slower corrosion rate.

Fig. 15
figure 15

Mechanically-assisted corrosion from a semi-circular pit: Comparison of pit growth along the vertical direction considering two modelling strategies: (i) resolving the electrolyte domain (“electrolyte simulation” curve), and (ii) neglecting the electrolyte and prescribing the concentrations of the bulk solution on the pit mouth (“Pit mouth Dirichlet BCs” curve)

Full size image

5 Conclusions

We have presented an electro-chemo-mechanical phase field framework for predicting localized corrosion. Its main ingredients are: (i) a phase field description of the evolution of the corrosion front, (ii) the modeling of mechanics phenomena such as the enhancement of corrosion kinetics with mechanical fields and the film rupture-dissolution-repassivation (FRDR) process, and (iii) the characterization of electrochemical electrolyte behaviour, including the transport of multiple ionic species and the distribution of electrostatic potential. These three components are fully coupled and impact corrosion kinetics by means of a mechanics- and electrochemistry-dependent interface mobility parameter \(L\left( \varepsilon ^\textrm{p}, \sigma _{\text {h}}, \eta \right) \). The model is implemented in COMSOL MULTIPHYSICS, with the numerical implementation being described and made freely available to the reader at http://www.empaneda.com/codes. Numerical experiments were conducted on two case studies of particular interest to investigate the interplay between electrolyte behaviour and localized corrosion; key findings include:

  • The size of the electrolyte domain plays an important role on the corrosion process. If the electrolyte domain is chosen to be very small, then the transport of metal ions is hindered and, as a result, corrosion shifts from activation-controlled to diffusion-controlled.

  • Increasing the applied potential and the initial bulk solution concentration leads to a rise in dissolution rates. On the other hand, faster corrosion kinetics can potentially increase the electrolyte potential, reducing the overpotential and the magnitude of the mobility coefficient.

  • There are significant differences between the bulk and local pit electrochemical behaviours. Among other, due to the hydrolysis reaction, an increase in the concentration of hydrogen ions is observed inside the pit, which can enhance hydrogen ingress into the metal and embrittlement.

  • The simplistic yet widely used modeling approach of replacing the simulation of the electrolyte by prescribing the bulk concentration and electrolyte potential at the pit mouth overpredicts corrosion rates and underpredicts the time required for the pit-to-crack transition to occur.