Skip to main content
SpringerLink
Log in

Hybrid kernel approach to improving the numerical stability of machine learning for parametric equations with Gaussian processes in the noisy and noise-free data assumptions

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

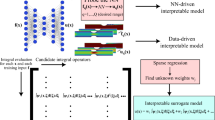
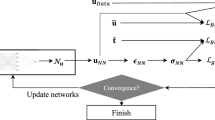
In many applied sciences, the main aim is to learn the parameters of parametric operators which best fit the observed data. Raissi et al. (J Comput Phys 348(1):683–693, 2017) provide an innovative method to resolve such problems by employing Gaussian process (GP) within a Bayesian framework. In this methodology, GP priors are modified based on the particular form of operators and are employed to infer hyperparameters by the maximum likelihood estimation (MLE). However, MLE-based and Bayesian inference usually involves setting up a covariance matrix that can be ill-conditioned. In this paper, the numerical stability of the methodology is investigated during training and prediction in two different assumptions: noisy and noise-free data. Based on the numerical simulations, for noisy data observations, by increasing noise in the data, the uncertainty in the predictions increases, and the accuracy of estimating the parameters decreases. However, the likelihood computation and model prediction will be significantly stable. While in the noise-free data observations, by increasing the number of data, the uncertainty quantification encoded in the posterior variances is significantly reduced, and the accuracy of the estimates is increased. But, the conditioning of the problem will be seriously distorted and we will face a very ill-condition problem. Therefore, in this paper, an approach is provided to manage the problem conditioning in the best possible way and consequently to improve the method performance in the noise-free data assumption using the hybrid kernels technique.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30
Fig. 31
Fig. 32
Fig. 33
Fig. 34
Fig. 35

Similar content being viewed by others

Data Availability

The datasets used for this study are partially available on request to the corresponding author.

References

  1. Raissi M, Perdikaris P, Em Karniadakis G (2017) Machine learning of linear differential equations using Gaussian processes. J Comput Phys 348(1):683–693

    Article  MathSciNet  Google Scholar 

  2. Bender EA (1978) An introduction to mathematical modeling. Dover Publications Inc., Mineola

    Google Scholar 

  3. Bouhlel MA, Martins JRRA (2019) Gradient-enhanced kriging for high-dimensional problems. Eng Comput 35:157–173

    Article  Google Scholar 

  4. Shao W, Deng H, Ma Y et al (2012) Extended Gaussian Kriging for computer experiments in engineering design. Eng Comput 28:161–178

    Article  Google Scholar 

  5. Arthur CK, Temeng VA, Ziggah YY (2020) Novel approach to predicting blast-induced ground vibration using Gaussian process regression. Eng Comput 36:29–42

    Article  Google Scholar 

  6. Narayan A, Yan L, Zhou T (2021) Optimal design for kernel interpolation: applications to uncertainty quantification. J Comput Phys 430:1–20

    Article  MathSciNet  Google Scholar 

  7. Qin T, Chen Z, Jakeman JD, Xiu D (2021) Deep learning of parameterized equations with applications to uncertanity quantification. Int J Uncert Quantif 11(2):63–82

    Article  Google Scholar 

  8. Mueller JL, Siltanen S (2012) Linear and nonlinear inverse problems with practical applications, computational science and engineering, vol 10. SIAM, Philadelphia

    Book  Google Scholar 

  9. Neto FDM (2013) An introduction to inverse problems with applications. Springer, Berlin

    Book  Google Scholar 

  10. Dass SC, Lee J, Lee K et al (2017) Laplace based approximate posterior inference for differential equation models. Stat Comput 27:679–698

    Article  MathSciNet  Google Scholar 

  11. Williams CK, Rasmussen CE (2006) Gaussian processes for machine learning. The MIT Press, Cambridge

    Google Scholar 

  12. Murphy KP (2012) Machine learning: a probabilistic perspective. MIT Press, Cambridge

    Google Scholar 

  13. Raissi M, Perdikaris P, Em Karniadakis G (2018) Numerical Gaussian processes for time-dependent and nonlinear partial differential equations. SIAM J Sci Comput 40(1):172–198

    Article  MathSciNet  Google Scholar 

  14. Vapnik V (2013) The nature of statistical learning theory. Springer, New York

    Google Scholar 

  15. Cavoretto R, De Rossi A, Perracchione E (2023) Learning with partition of unity-based Kriging estimators. Appl Math Comput 448:127938

    MathSciNet  Google Scholar 

  16. Tikhonov A (1963) Solution of incorrectly formulated problems and the regularization method. Soviet Math. Dokl. 5:1035–1038

    Google Scholar 

  17. Poggio T, Girosi F (1990) Networks for approximation and learning. Proc IEEE 78:1481–1497

    Article  Google Scholar 

  18. Fasshauer GE (2007) Meshfree approximation methods with Matlab, interdisciplinary mathematical sciences, vol 6. World Scientific Publishing, Singapore

    Google Scholar 

  19. Fasshauer GE, McCourt M (2015) Kernel-based approximation methods using MATLAB, interdisciplinary mathematical sciences. World Scientific Publishing, Singapore

    Google Scholar 

  20. Kohn R, Ansley CF, Tharm D (1991) The performance of cross-validation and maximum likelihood estimators of spline smoothing parameters. J Am Stat Assoc 86(416):1042–1050

    Article  MathSciNet  Google Scholar 

  21. Sacks J, Welch WJ, Mitchell TJ, Wynn HP (1989) Design and Analysis of Computer Experiments. Stat Sci 4(4):409–435

    MathSciNet  Google Scholar 

  22. Rasmussen CE, Ghahramani Z (2001) Occam’s razor. Adv Neural Inform Process Syst 294–300

  23. Perkins TJ, Jaeger J, Reinitz J, Glass L (2006) Reverse engineering the gap gene network of Drosophila melanogaster. PLoS Comput Biol 2(5):e51

    Article  Google Scholar 

  24. Alvarez MA, Luengo D, Lawrence ND (2023) Linear latent force models using Gaussian processes. IEEE Trans Pattern Anal Mach Intell 35(11):2693–2705

  25. Poustelnikova E, Pisarev A, Blagov M, Samsonova M, Reinitz J (2004) A database for management of gene expression data in situ. Bioinformatics 20(14):2212–2221

    Article  Google Scholar 

  26. Chatrabgoun O, Esmaeilbeigi M, Cheraghi M (2022) Stable likelihood computation for machine learning of linear differential operators with Gaussian processes. Int J Uncertain Quantif 12(3):75–99

    Article  MathSciNet  Google Scholar 

  27. Wendland H (2000) Scattered data approximation. Cambridge University Press, Cambridge

    Google Scholar 

  28. Esmaeilbeigi M, Chatrabgoun O, Daneshkhah A et al (2022) On the impact of prior distributions on efficiency of sparse Gaussian process regression. Eng Comput. https://doi.org/10.1007/s00366-022-01686-7

  29. Hussain M (2021) Hybrid radial basis function methods of lines for the numerical solution of viscous Burgers’ equation. Comput Appl Math 40:107

    Article  MathSciNet  Google Scholar 

  30. Hussain M, Haq S (2020) A hybrid radial basis functions collocation technique to numerically solve fractional advection diffusion models. Numer Methods Partial Differ Equ 36:1254–1279

    Article  MathSciNet  Google Scholar 

  31. Mishra PK, Fasshauer GE, Sen MK, Ling L (2019) A stabilized radial basis-finite difference (RBF-FD) method with hybrid kernels. Comput Math Appl 77:2354–2368

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the Iran National Science Foundation (INSF) for support of this work under project No. 99014278. The authors sincerely thank the two anonymous referees for their valuable comments and suggestions, which enabled to significantly improve the quality of this paper.

Author information

Authors and Affiliations

  1. Faculty of Mathematical Sciences and Statistics, Malayer University, Malayer, Iran

    Mohsen Esmaeilbeigi & Meysam Cheraghi

Authors
  1. Mohsen Esmaeilbeigi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Meysam Cheraghi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mohsen Esmaeilbeigi.

Ethics declarations

Conflict of interest

The authors declare that they have no any competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Esmaeilbeigi, M., Cheraghi, M. Hybrid kernel approach to improving the numerical stability of machine learning for parametric equations with Gaussian processes in the noisy and noise-free data assumptions. Engineering with Computers 40, 761–794 (2024). https://doi.org/10.1007/s00366-023-01818-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-023-01818-7

Keywords

Search

Navigation