Hybrid modeling of hetero-agglomeration processes: a framework for model selection and arrangement

Abstract

Modeling of hetero-agglomeration processes is invaluable for a variety of applications in particle technology. Traditionally, population balance equations (PBE) are employed; however, calculation of kinetic rates is challenging due to heterogeneous surface properties and insufficient material data. This study investigates how the integration of machine learning (ML) techniques—resulting in so-called hybrid models (HM)—can help to integrate experimental data and close this gap. A variety of ML algorithms can either be used to estimate kinetic rates for the PBE (serial HM) or to correct the PBE’s output (parallel HM). As the optimal choice of the HM architecture is highly problem-dependent, we propose a general and objective framework for model selection and arrangement. A repeated nested cross-validation with integrated hyper-parameter optimization ensures a fair and meaningful comparison between different HMs. This framework was subsequently applied to experimental data of magnetic seeded filtration, where prediction errors of the pure PBE were reduced by applying the hybrid modeling approach. The framework helped to identify that for the given data set, serial outperforms parallel arrangement and that more advanced ML algorithms provide better interpolation ability. Additionally, it enables to draw inferences to general properties of the underlying PBE model and a statistical investigation of hyper-parameter optimization that paves the way for further improvements.

1 Introduction

Agglomeration refers to the assembly of particles into larger clusters (the agglomerates). It is a unit operation of mechanical process engineering and thus relevant for almost all processes in particle technology. Homo-agglomeration of a single particle system is well understood and mainly used to either formulate products from powders (tablets) or to improve separation properties in suspensions (flocculation). Hetero-agglomeration refers to agglomeration processes between different materials and results in multi-substance compounds. These hetero-agglomerates often combine desired properties of the individual materials and therefore exhibit a wide range of applications: In cathode materials for lithium-ion batteries, carbon black is agglomerated with the active material to enhance conductivity. The hetero-agglomeration process further defines the micro-structure of these cathode materials and significantly impacts the final product properties [44]. Throughout this work, magnetic seeded filtration (MSF) [62,63,64] is used as application example, where the separation behavior of suspensions is drastically changed by hetero-agglomeration: Non-magnetic target particles are selectively agglomerated with magnetic seed particles and the formed hetero-agglomerates are subsequently magnetically separated due to their newly gained magnetic properties.

On an experimental level, a “simple” measurement of the agglomerate size is often not sufficient, since many product properties only arise from the micro-structure of the hetero-agglomerates. Meanwhile, only limited analytical capabilities exist to determine sought-after properties, such as the material-specific agglomerate composition, most of which are laborious and offline. This motivates the search for models that provide insight into the micro-processes and kinetics. Usually, population balance equations (PBE) with different numerical solution techniques are employed; however, calculations are challenging, because all interactions between all components must be taken into account and formed hetero-agglomerates have locally heterogeneous surface properties. Generally, the accurate calculation of agglomeration rates or so-called kernels pose the limiting factor. Mechanistic equations exist, which, however, are subject to specific assumptions. Furthermore, the quality and quantity of underlying material and process data is unsatisfactory: literature values of Hamaker constants are off by orders of magnitude due to surface roughness, and experimentally determined zeta potentials are by definition only a makeshift for the sought surface potentials. This multitude of uncertainties makes a predictive and reliable calculation of hetero-agglomeration processes highly challenging [55].

Machine learning (ML) methods are a promising pathway for introducing experimental data into the calculations. They have gained significant traction over the last decade and are becoming a standard modeling technique in chemical engineering [86]. ML methods generally map any given input space on a desired output space and are referred to as black-box models (BBM) throughout this work due to being empirical in nature. This already poses the major limitation for a direct application in hetero-agglomeration processes: As the name suggests, they do not give any insights into the physical micro-processes and generally possess poor extrapolation qualities. A promising solution are the so-called hybrid models (HM) that employ a mechanistic or white-box model (WBM), as e.g., the PBE mentioned above and utilize BBMs to perform certain sub-tasks [87]. HMs can be arranged in various ways: BBM and WBM may be operated in parallel, where the BBM corrects the output of the WBM, or in serial, where typically the BBM calculates and passes necessary kinetic parameters to the WBM [87]. Furthermore, there is a variety of ML algorithms that can be used to realize the BBM, resulting in a wide range of resulting HM structures.

Early examples for the application of HM in chemical engineering date back to the 1990 s [56, 78], while current applications are summarized in von Stosch et al. [87], Sansana et al. [65], Sharma and Liu [72], Mowbray et al. [49], McBride et al. [45]; Zendehboudi et al. [93], and Thon et al. [79] and include general process modeling [2, 35, 58], process control [22, 66, 91], process optimization [5, 54, 94], the development of soft sensors [24, 31, 90], and scale-up [46, 47, 73]. HMs have also been used in combination with PBE to model agglomeration processes: Georgieva et al. [21] employed a series connection of ANN and PBE to model batch crystallization. Similarly, Hornik et al. [27] modeled batch crystallization of cobalt oxalate with a parallel arrangement. Recently, Dosta and Chan [15] combined micro-scale DEM simulations for retrieving mechanical properties with a hybrid ANN/PBE model, ultimately realizing a multi-scale technique. Nazemzadeh et al. [50] and Nielsen et al. [51] applied an HM for modeling a flocculation process and the development of a soft sensor.

The generalization and extrapolation capabilities of a HM are directly linked to its structure. This encompasses both the used ML algorithm as well as the arrangement of BBM and WBM in serial or parallel [87]. Several studies are concerned with a comparison between the general model structure, without varying the ML algorithm: They compare serial to parallel arrangement [6, 13, 40], multiple more elaborate arrangements [7, 43], or different HMs to both the pure WBM and BBM [83]. Other studies focus on the comparison of different ML algorithms in either a pure BBM [60], a parallel [41], or serial [34, 48, 89] hybrid arrangement. There are only very few studies that focus on a combined investigation of ML algorithm and HM structure. Chen and Ierapetritou [11] investigate the pure WBM, pure BBM, and HMs in serial and parallel while varying the ML algorithm between an artificial neural network (ANN) and a support vector machine (SVM). As the optimal combination is generally problem-dependent, there is no best or one size fits all HM model [87], which at first glance makes comparing different HM structures redundant. However, this emphasizes the necessity for a general framework that enables a problem-specific comparison, optimization, and selection.

The aforementioned points give rise to three distinct goals that we address in this study:

• 1. Present a general approach for hybrid modeling of hetero-agglomeration processes with PBE.

• 2. Present a general framework that allows for a fair and problem-specific comparison of various HMs that includes both the HM structure (serial or parallel) and the used ML algorithm.

• 3. Apply this framework to magnetic seeded filtration and discuss how it can be generalized to enhance hybrid model performance in a variety of chemical engineering problems.

2 Models

2.1 White-box model: discrete 2-D population balance

Population balance equations (PBE) are the standard technique for calculating the time-dependent number concentrations n(x, y, t) of agglomerates with properties x and y (2-D case). As this work is focused on MSF as application example, x vividly describes the partial volume of the non-magnetic component (NM) and y the partial volume of the magnetic component (M), so that every conceivable hetero-agglomerate build from these materials can be fully characterized with a pair of values (x, y). It should be emphasized that the presented framework can readily be generalized to higher dimensional problems and that the 2-D case is merely a working example. By defining x and y as volumes, the additivity is directly given by mass conservation and the general form of the continuous PBE is given by Ramkrishna [57]

$$\begin{aligned} \frac{\partial n(x,y,t)}{\partial t}&= \underbrace{\frac{1}{2}\int _{0}^{x}\int _{0}^{y}k(x-x',y-y',x',y')n(x-x',y-y',t)n(x',y',t)\textrm{d}x'\textrm{d}y'}_{\mathrm {(A)}} \nonumber \\&\quad -\underbrace{\int _{0}^{\infty }\int _{0}^{\infty }k(x,y,x',y')n(x,y,t)n(x',y',t)\textrm{d}x'\textrm{d}y'}_{\mathrm {(B)}} \quad . \end{aligned}$$

(1)

Note that Eq. 1 neglects both breakage and convective transport effects. Term (A) describes the formation rate of (x, y) from agglomeration processes of smaller classes. Since the internal coordinates (volumes) are additive, (x, y) results from the agglomeration of any class $(x',y')$ (with $x'<x$ and $y'<y$) and its associated partner $(x-x',y-y')$. The kinetic rates or agglomeration kernels k are elaborated in Eqs. 4 and 5. Term (B) has a negative sign and describes the loss of (x, y) due to further agglomeration. Since (x, y) is in principle capable of agglomerating with all possible classes $(x',y')$, integration is performed over the entire range of values.

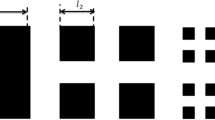
Equation 1 is an integro-differential equation and can only be solved analytically for simplified cases, which is why a numerical consideration of the problem is necessary. One way of doing so, is to transfer the problem from the continuous space (x, y) to the discrete space (i, j), which transforms Eq. 1 into a set of ODEs. This work employs the so-called geometric discretization scheme, where the agglomerate volume along a coordinate increases by a constant factor s and which is schematically shown in Fig. 1 for $s=2$. Starting from primary particles $(i,j)=(1,0)$ for NM and $(i,j)=(0,1)$ for M, all conceivable agglomerate combinations up to a critical agglomerate size defined by the lattice parameter $N_\textrm{S}$ are defined according to

$$\begin{aligned} V(i,j)= & {} V_{\textrm{NM}}(i,j)+V_{\textrm{M}}(i,j) \end{aligned}$$

(2)

$$\begin{aligned} V_{\textrm{NM}}(i,j)= & {} s^{i-1}V(1,0) \quad \vert \quad V_{\textrm{M}}(i,j)=s^{j-1}V(0,1). \end{aligned}$$

(3)

This type of discretization makes calculations manageable for poly-disperse particle systems which would require orders of magnitude more grid points in equidistant grids. However, since the spatial discretization is based on a factor s, not all formed agglomerates fall on exactly one grid point. As a consequence, agglomerate birth [Term (A) in Eq. 1] cannot always be accounted for directly, but must first be distributed in some way among the surrounding grid points. Figure 1 illustrates this effect for the agglomerate of (1, 2) with (2, 1). Kumar et al. [38] developed the cell average technique, which performs said distribution while ensuring mass conservation in the system. Due to their lengthy and engineer-deterring form, the modified birth term and resulting ODEs are given in Appendix 1.

Fig. 1

Discretization with geometric grid. $N_{\textrm{S}}=3$ and $s=2$. The agglomerate of (1, 2) and (2, 1) has to be distributed between neighboring grid points

Fig. 2

Definition of possible collision cases A–D between two hetero-agglomerates (i, j) and (l, m)

The agglomeration kernels k are required between each of the investigated agglomerate classes. They are defined as the product of collision frequency $\beta$ and collision efficiency $\alpha$ ($k=\beta \alpha$) and are calculated depending on the applied model assumptions which are reviewed, e.g., by Jeldres et al. [32], Taboada-Serrano et al. [76] or Elimelech [16]. In the orthokinetic (flow-controlled) case, the collision frequency is calculated according to Eq. 4 and is proportional to the agglomerate volume (radius $r^3$) and mean shear rate $\bar{G}$ [12, 16]

$$\begin{aligned} \beta _{12}=\frac{4}{3}\left( r_1+r_2\right) ^3\bar{G}. \end{aligned}$$

(4)

Defining the probability of agglomeration upon collision, the collision efficiency generally requires an analysis of particle trajectories in the orthokinetic case. However, Selomulya et al. [68] presented an empirical factor that corrects the perikinetic $\alpha ^*$-values obtained by the modified Fuchs approach [20, 26]. This integrates size effects into the PBE while drastically reducing computational effort. The definition and incorporation of this factor is shown in Eq. 12. The perikinetic collision efficiency is calculated according to

$$\begin{aligned} \alpha ^*_{12}= \left[ 2\int \limits _{0}^{\infty }\frac{6u^2+13u+2}{6u^2+4u}\, \textrm{exp}\left( \frac{E_{\textrm{el,12}}+E_{\textrm{vdW,12}}}{k_{\textrm{B}}T}\right) \frac{\textrm{d}u}{\left( u+2\right) ^2}\right] ^{-1}, \end{aligned}$$

(5)

with u being the dimensionless form of surface-to-surface distance h according to

$$\begin{aligned} u(h)=\frac{2h}{r_1+r_2} \quad . \end{aligned}$$

(6)

The collision efficiency is governed by the interplay between attractive and repulsive particle–particle interactions. This work is only concerned with electrostatic and van der Waals (DLVO) interactions, while other applications might require the integration of, e.g., hydrophobic interaction energies. The electrostatic interaction energy $E_{{\text {el}},12}$ is defined as [23]

$$\begin{aligned} E_{\textrm{el,12}}\left( h\right)= & {} \frac{128\pi r_1r_2N_{\textrm{A}}k_{\textrm{B}}T}{\left( r_1+r_2\right) \kappa ^2}\gamma _1\gamma _2\,\textrm{exp}\left( -\kappa h\right) \end{aligned}$$

(7)

$$\begin{aligned} \kappa ^{-1}= & {} \sqrt{\frac{\varepsilon k_{\textrm{B}}T}{2e^2IN_{\textrm{A}}}} \quad \Big \vert \quad \gamma _{\textrm{i}}=\textrm{tanh} \left( \frac{e\zeta _{\textrm{i}}}{4k_{\textrm{B}}T}\right) \end{aligned}$$

(8)

with reciprocal Debye length $\kappa$, permittivity $\varepsilon$, electron charge e, and ionic strength I. The van der Waals interaction energy $E_{\textrm{vdW,12}}$ is given by [25]

$$\begin{aligned} E_{\textrm{vdW,12}}\left( h\right)&=-\frac{A_{\textrm{H,12}}}{6}\left[ \frac{2r_1r_1}{h^2+2r_1h+2r_2h}\right. \nonumber \\&\quad +\frac{2r_1r_2}{h^2+2r_1h+2r_2h+4r_1r_2} \nonumber \\&\quad + \left. \textrm{ln}\left( \frac{h^2+2r_1h+2r_2h}{h^2+2r_1h+2r_2h+4r_1r_2}\right) \right] \quad . \end{aligned}$$

(9)

Calculating the interaction energies in Eqs. 7 and 9 requires knowledge of material-specific surface properties in form of the zeta potential $\zeta$ and the Hamaker constant $A_{\textrm{H}}$. This poses a problem in the case of hetero-agglomerates: How is the integral property of a heterogeneous surface defined? A previous publication solved this issue by introducing the so-called collision case model [61] that is briefly elaborated in the following. Figure 2 shows the collision of two hetero-agglomerates (i, j) and (l, m). Depending on the surface property with which each agglomerate collides, four collision cases A) to D) can be differentiated. Vividly, in case A), (i, j) collides with its magnetic and (l, m) collides with its non-magnetic side. Since the material properties in the collision plane are defined, a collision efficiency $\alpha ^*_{\mathrm {A-D}}$ can be calculated according to Eq. 5 for each case. Subsequently, the probabilities of each case are required. They are defined as the product of the individual probabilities of the agglomerates colliding with the respective material. The latter are estimated according to Eq. 10 under the assumption that the partial volumes are perfectly distributed and that no preferred orientation is present

$$\begin{aligned} P_{ij\textrm{,M}}=1-P_{ij\textrm{,NM}}=X_{\textrm{M}}(i,j)= {\left\{ \begin{array}{ll} \displaystyle \frac{s^{j-1}V(0,1)}{V(i,j)} &{} \quad j>0 \\ \displaystyle 0 &{} \quad j=0. \end{array}\right. } \end{aligned}$$

(10)

It is apparent that the required probabilities are merely a function of the agglomerate volume composition, which is pre-defined by the implemented discretization scheme. Combining all cases, the collision efficiency of the overall collision is calculated according to

$$\begin{aligned} \alpha ^*(i,j,l,m)= \begin{pmatrix} \alpha ^*_{\textrm{A}} \\ \alpha ^*_{\textrm{B}} \\ \alpha ^*_{\textrm{C}} \\ \alpha ^*_{\textrm{D}} \end{pmatrix} \cdot \begin{pmatrix} P_{\textrm{A}} \\ P_{\textrm{B}} \\ P_{\textrm{C}} \\ P_{\textrm{D}} \end{pmatrix} \approx \begin{pmatrix} \alpha ^*(0,1,1,0) \\ \alpha ^*(0,1,0,1) \\ \alpha ^*(1,0,1,0) \\ \alpha ^*(0,1,1,0) \end{pmatrix} \cdot \begin{pmatrix} P_{ij\textrm{,M}}P_{lm\textrm{,NM}} \\ P_{ij\textrm{,M}}P_{lm\textrm{,M}} \\ P_{ij\textrm{,NM}}P_{lm\textrm{,NM}} \\ P_{ij\textrm{,NM}}P_{lm\textrm{,M}} \end{pmatrix} =\varvec{\alpha }_{\textrm{p}}\cdot \varvec{P}. \end{aligned}$$

(11)

Note that all probabilities add up to one, viz., $\varvec{1}\cdot \varvec{P}=1$. Further, Eq. 11 assumes that the effect of surface properties outweighs the effect of agglomerate size and that, therefore, the collision efficiencies of primary particles $\varvec{\alpha }_{\textrm{p}}$ are sufficient. This simplification is supported by theoretical and experimental studies [42] and reduces computational effort, as the numerical integration of Eq. 5 is not required for all class combinations. Furthermore, this allows for a promising integration of the PBE into a hybrid model as discussed in Sect. 2.3. Further justification arises from the fact that the resulting collision efficiencies are corrected by the aforementioned empirical factor given by Selomulya et al. [68] as shown in the following:

$$\begin{aligned} \alpha _{12}=\alpha ^*_{12}\frac{\textrm{exp}\left( -x_{\textrm{S}} \left( 1-\frac{r_1}{r_2}\right) \right) }{\left( r_1r_2\right) ^{y_{\textrm{S}}}} \end{aligned}$$

(12)

with model parameters $x_{\textrm{S}}$ and $y_{\textrm{S}}$. The key take-away and main benefit of the collision case model is that every collision efficiency between any two given agglomerates is readily calculated based on the known agglomerate volume composition and the un-corrected collision efficiencies between primary particles $\varvec{\alpha }_{\textrm{p}}$, as discussed in [55, 61]. With this, all required equations are given to solve the PBE and to obtain the discrete, time-dependent agglomerate composition distribution n(i, j, t).

Experimental studies on MSF, however, do not yield such detailed information but only offer integral knowledge about the amount of totally separated non-magnetic material. Thus, to close the gap between PBE and experiment, the magnetic separation step needs to be modeled. Note that this is specific to the investigated MSF-process and is not required in the general case of hetero-agglomerating systems. The class-specific separation efficiency is calculated according to

$$\begin{aligned} T(i,j)=\left[ 1+\textrm{exp}\left( -C_{1}\left( r^2(i,j)X_{\textrm{M}}(i,j)-C_{2}\right) \right) \right] ^{-1}, \end{aligned}$$

(13)

and is generally dependent on the cross-sectional area of an agglomerate and its magnetic volume fraction. Both $C_1$ and $C_2$ are empirical parameters. Applying Eq. 13 to the entire distribution before and after agglomeration yields the overall separation efficiency of non-magnetic particles

$$\begin{aligned} A_{\textrm{NM}}=\frac{\sum \nolimits _{i=0}^{N_{\textrm{S}}}\sum \nolimits _{j=0}^{N_{\textrm{S}}}n(i,j,\textrm{end})V(i,j)\left( 1-X_{\textrm{M}}(i,j)\right) T(i,j)}{\sum \nolimits _{i=0}^{N_{\textrm{S}}}\sum \nolimits _{j=0}^{N_{\textrm{S}}}n(i,j,0)V(i,j)\left( 1-X_{\textrm{M}}(i,j)\right) } \quad . \end{aligned}$$

(14)

The separation efficiency states what proportion of the originally present non-magnetic particles are separated. $A_{\textrm{NM}}=1$ means that all of the material was separated, while for $A_{\textrm{NM}}=0$, no separation took place. A more in-depth look and derivation of Eq. 13 are given in the supplementary information (SI.1).

2.2 Black-box models

BBMs are universal non-linear function approximators [27] and map any given input space on a desired output space. In the scope of this work, various ML algorithms are used as BBM, all of which belong to the group of supervised learning algorithms. In supervised learning, the available data set is commonly split into a train and a test sub-set. The train set is used to build the ML model by learning a relationship between its input and target variables. The model quality is then evaluated by comparing its predictions with the test data. All investigated algorithms are briefly described below in terms of their structure, application to regression problems, and relevant hyper-parameters (HP). An overview of the relevant HPs is given in Table 2 and an optimization framework is discussed in Sect. 2.4. All algorithms were implemented using the Pyhton library Scikit-learn [53] (KNeighborsRegressor, DecisionTreeRegressor, RandomForestRegressor, MLPRegressor, and SVR). It is important to note that an ever-increasing number of other ML algorithms exists in the literature and practice that may be better suited for any given dataset. The presented models should, therefore, be seen as an exemplary selection and other ML algorithms can readily be implemented in the presented framework.

2.2.1 k-Nearest neighbor algorithm

Applied to regression problems, the k-nearest neighbor algorithm (kNN) calculates the target value of a test sample by averaging the corresponding target value of the k-nearest train samples in feature space, which are determined by different distance metrics (norms). Distance weighting can be applied to emphasize the influence of neighbors closer to the test set sample. For a more time-efficient search for the k-nearest neighbors, a pre-organization of the data, e.g., by means of tree-based methods, can be useful for larger data sets.

2.2.2 Tree-based methods

Tree-based ML methods include the Classification and Regression Tree (CART) algorithm and its extension, the Random Forest (RF) algorithm. The CART algorithm builds a binary decision tree that divides the feature space of the train set into J distinct segments (leaves) based on certain decision criteria (nodes) while minimizing a particular error function such as the mean squared error. This decision tree assigns the objects or samples of the train set to the different segments. To prevent an overly complex tree and thus overfitting, the maximum complexity of the tree can be defined before training by certain criteria (pre-pruning), such as specifying the maximum tree depth, the minimum number of samples required to be in a segment or leaf, and/or the minimum number of samples required to split a node. The principle of the RF algorithm is to generate multiple decision trees on the same train set and then average the predictions of each tree on the test set. Bootstrap aggregating (bagging) and randomly selecting a certain number of candidates from all possible features to be considered when splitting a node generate different decision trees on the same train set.

2.2.3 Artificial neural networks

Artificial neural networks (ANN) with their most commonly used class, the multilayer perceptron (MLP), mimic the neural structures of living organisms. An MLP consists of at least three different layers, an input, an output, and one or more hidden layers. The input variables of the data set form the input layer, which is connected to the target variables in the output layer via a certain number of artificial neurons. The output signal of each neuron results from the sum of its weighted input signals and subsequent conversion by a so-called activation function. Backpropagation is used to optimize the weights (i.e., train the model) while minimizing an error function composed of model deviation and complexity, thus creating an optimal functional relationship. This optimization is iterated multiple times, while the step size with which the weights are adjusted is determined by the learning rate. During training, high model complexity is punished via a regularization term. In the scope of this work, only a single hidden layer was used due to the small data set.

2.2.4 Support vector machines

Support vector machines are a statistical machine learning algorithm, and referred to as Support Vector Regression (SVR), when applied to regression tasks. In $\varepsilon$-SVR [84], an $\varepsilon$-insensitive region, the so-called $\varepsilon$-tube, is introduced symmetrically around the target function to be approximated, whereby the width of the $\varepsilon$-tube is determined by $\varepsilon$. This region, and thus the objective function, is optimized to contain as much training data as possible within the $\varepsilon$-tube (small prediction error) while being as flat as possible (prevention of overfitting). In this optimization problem, the regularization parameter C controls the trade-off between the flatness of the objective function and the amount up to which training data outside the $\varepsilon$-tube, the so-called Support Vectors (SV), are punished [74]. To approximate non-linear functions, various so-called kernels are used. These transform the feature space into a higher dimensional kernel space and are composed of different kernel-internal parameters ($\gamma$, p, c) depending on the kernel type.

2.3 Hybrid models

Hybrid models (HM) represent a combination of purely mechanistic models (WBM) and purely data-driven models (BBM). The hybrid approach makes it possible to combine the advantages as well as attenuate the disadvantages of its components, allowing, e.g., more accurate predictions on unseen data, improved extrapolation properties, more efficient model development, and increased transparency [87]. The WBM and BBM can be arranged in parallel or serial mode within the HM, while the serial arrangement possesses two sub-categories: (A) BBM $\rightarrow$ WBM or (B) WBM $\rightarrow$ BBM. Each arrangement has its individual benefits and drawbacks as well as preferred application areas. The parallel arrangement is mainly used when a WBM is available, but its accuracy is limited, e.g., due to un-modeled effects, non-linearity, or dynamic behavior [87]. In this case, the BBM compensates for the WBM’s inaccuracy by correcting its predictions. There are multiple ways of combining both sub-models, but the most frequently used is pure superposition, i.e., summation of the models outputs. Arranging the HM in serial structure (B) can be applied as an alternative to the parallel arrangement, but is scarcely used in chemical and biochemical engineering [87] and therefore neglected in all further considerations. Serial arrangement (A) (further referred to as just serial arrangement), on the other hand, is frequently applied, especially in cases, where the WBM is based on conservation laws such as mass (e.g., PBE), energy, or momentum balances [87] and is therefore inherently correct. Here, the BBM represents the parts of the equations for which no reliable model exists (e.g., kinetic rates) or which is generally extracted from experimental data (e.g., material parameters).

Figure 3 shows both HM structures as well as a pure BBM applied to MSF (viz., our working example for hetero-agglomeration processes). For the case of a pure BBM, the process parameters, which will be discussed more thoroughly in Sect. 3, serve as input and the BBM directly estimates the separation efficiency $A_{\textrm{NM,mod}}$. For parallel arrangement, the BBM estimates a correction term $\Delta A_{\textrm{NM}}$ that is added to the output of the WBM to yield the final result. In serial arrangement, the purpose of the BBM is to estimate the collision efficiency vector between primary particles $\varvec{\alpha }_{\textrm{p}}$ (see Eq. 11) that is further processed by the WBM to calculate $A_{\textrm{NM,mod}}$. When generalizing to other hetero-agglomeration processes, it is important to remember that any data-driven model, i.e., any hybrid model, requires data to be trained on. As trivial as this might seem, it has crucial implications on the achievable information content: A pure BBM, as shown in Fig. 3 (a), will never be able to predict anything that is not directly measurable, as, e.g., the time-dependent agglomerate size and composition distribution n. A serial HM, on the other hand, is able to estimate non-measurable variables thanks to the integrated WBM. However, any form of measurable variable (as in this case separation efficiency) is required to infer information on kinetic rates and ultimately the agglomerate population. The achievable information content of all presented models is further discussed in Sect. 3.7.

Fig. 3

Pure BBM (a), parallel HM (b), and serial HM (c) applied to MSF with corresponding input, intermediate, and output variables

The performance of a HM is strongly dependent on the WBM’s structure and accuracy: When the WBM does not include all effects (structural mismatch), parallel HMs can compensate for that and perform better. In turn, a serial connection is not expected to perform well in this case [6, 40, 87]. If the underlying WBM is accurate, however, serial arrangement is expected to perform better and further improve extrapolation properties [6, 13, 14, 82, 83, 87].

Besides the performance of the HM, the way its parameters are determined also depends on the choice of model arrangement. For the parallel model structure, parameter identification, also known as training, can be performed via direct approach. Here, priority is given to the identification of the WBM’s parameters [65]. Once determined, the BBM’s parameters are identified by a straightforward training with the known deviations from the experimental values (supervised learning). Training is more difficult in serial arrangement, as the necessary training data, namely the kinetic rates, are not directly measurable [52, 87]. Determination of the kinetic rates, e.g., via optimization of the WBM and subsequent parameter extraction, makes training via the direct approach possible. In this work, WBM optimization is necessary for comparing its performance to the hybrid structures, hence allowing for extraction of the kinetic rates ($\varvec{\alpha }_{\textrm{p}}$) and application of the direct approach. Other examples for the application of this approach are found in Tholudur and Ramirez [77], Schubert et al. [67]. Parameter identification can also be performed via incremental approach, where the identification problem is decomposed into smaller parts that are solved sequentially [33]. Alternatively, the indirect or sensitivity approach adapts the backpropagation technique to the entire hybrid model. Here, the gradient of the HM’s output is estimated with respect to the BBM’s output and is used as error signal for parameter identification of the BBM [1, 21, 39, 52, 56]. However, this approach is often limited by the complexity of the WBM with regard to computation time in practice [1].

2.4 Hybrid model optimization framework: realizing a meaningful comparison

The optimal arrangement of the HM (serial or parallel) as well as the optimal ML algorithm used as BBM is highly problem-dependent and relies, e.g., on the WBM’s structure, the quantity and quality of the data and the application area it will be used for. Consequently, one cannot know a priori which HM combination is best for a given problem. Therefore, it is necessary to develop a general framework that compares different ML algorithms in different HM arrangements. However, there are several requirements that have to be met to realize a meaningful and reliable comparison. Said requirements are summarized in Table 1 together with individual solution strategies. Combining all these strategies into one single framework results in a powerful tool that allows a systematic model comparison independently of application area and data quantity and quality. Note that integration is incremental in the sense that, e.g., repeated nested cross-validation (requirement 5) extends the idea of a nested cross-validation (requirement 4).

Table 1 Requirements for a meaningful and reliable model comparison and corresponding solution strategies

1. Supervised learning requires a split of the data set into training and test data. This is problematic, as model performance (i.e., the basis of comparison) is therefore only evaluated on a sub-set of the data. To evaluate a model on the entire data set, a k-fold cross-validation (CV) is used. Here, the data set containing n samples is divided into k different train and test sets (with $n-n/k$ and n/k samples, respectively), whereby each sample is exactly once part of the test set. Each train set is used to train a model that is validated with the corresponding test set, thus leading to k different prediction errors. The root-mean-square error (RMSE) between experimental and calculated separation efficiency is used as measure for accuracy and defined for $N_{\textrm{test}}=n/k$ test samples according to

$$\begin{aligned} \textrm{RMSE}=\sqrt{\frac{1}{N_{\textrm{test}}}\sum \limits _{\textrm{i}=1}^{N_{\textrm{test}}} \left( A_{\textrm{NM,exp}}(i)-A_{\textrm{NM,mod}}(i)\right) ^2} \quad . \end{aligned}$$

(15)

The averaged prediction error of the cross-validation

$$\begin{aligned} \mathrm {RMSE_{CV}}=\frac{1}{k}\sum \limits _{\textrm{i}=1}^{k}\textrm{RMSE}(i) \end{aligned}$$

(16)

allows for an evaluation of model quality on the entire data set.

2. To meaningfully compare HMs with respect to model structure and ML algorithm, all models have to be optimized. Otherwise, simpler HMs (with less HP) have an advantage in the sense that more complex HMs are less likely to be in an optimal state. Using the direct approach for HM training, optimization of the entire model means optimizing the HP of its BBM, as the WBM and its parameters are fixed. HP are, in contrast to model parameters (e.g., weights of the ANN), defined before training. As, again, the ideal choice of HP is problem-specific, an automated HP optimization (HPO) is required before the actual training. Depending on the model structure, training of the BBM is performed on different input and output variables (see Fig. 3). Furthermore, different ML algorithms vary in the number and type of HPs (continuous, discrete, categorical, and conditional) and hence in complexity. This results in varying optimization environments depending on the model structure and ML algorithm.

Widely used HP optimization algorithms include grid search, where the HP search space is uniformly sampled and evaluated or random search, where the HP search space is explored (semi-) randomly until a pre-defined “fitness” is reached [3, 29]. Bayesian optimization (BO) is an example for a more sophisticated method, one of the most efficient optimization methods in terms of required iterations [8] and therefore well suited for expensive objective functions as is the case in the present study. Broadly speaking, it initially evaluates a fixed amount of randomly chosen HP combinations and builds a surrogate model based on these data that estimate the objective function. Subsequently, the BO selects the next HP combination for evaluation based on an acquisition function (e.g., the optimum of the surrogate model), essentially considering all previously acquired knowledge of the optimization problem. A commonly used surrogate model is Gaussian processes (GP) as they are easy to compute and deliver uncertainty estimates. However, GP scale poorly in higher dimensions and are unable to handle categorical and conditional HP spaces well [29]. Random forests (RF) are an alternative to GP: They allow searching over any kind of HP space (categorical, discrete, continuous, and conditional) [69, 92] and exhibit shorter computation times compared to GP, especially in higher dimensional problems [29, 69]. BO-RF does not provide an uncertainty estimate per se, although empirical methods have been shown to work well in practice [28]. Furthermore, BO-RF possesses poor extrapolation abilities and requires additional work when maximizing the acquisition function [69]. Nevertheless, BO-RF was applied in this study, as the efficiency and universal applicability of BO-RF allows for the optimization of any ML algorithm in any HM arrangement in a wide HP search space. It should be noted though that the applied surrogate model of the BO or optimization algorithm in general may easily be altered in the HPO framework to account for individual properties of the investigated data and models. The HP considered in this work with respective value ranges are shown in Table 2 for each ML algorithm. Note that the HP search spaces are data-set-specific and were pre-selected for the given problem. However, as shown in Sect. 3.8, the proposed framework allows to re-evaluate the search space at a later time. Due to the compatibility to the methods from Scikit-learn the implementation of the BO was done with the BayesSearchCV method from the Python library Scikit-Optimize.

Table 2 Considered HPs with corresponding search ranges for HPO of all implemented ML algorithms

3. An ML model is considered overfit, when it achieves high accuracy on train data, but low accuracy on (unseen) test data, i.e., low extrapolation ability. On the other hand, a model is underfit, when no sufficient accuracy is achieved at all. Overfitting should generally be avoided and is especially dangerous when comparing different HMs, as some structures may be more or less prone to it. Overfitting can be reduced through HPO on an appropriate search space (e.g., integration of regularization terms in ANN and SVR or maximum tree depth in CART) and by employing an appropriate optimization criterion. Here, the prediction error on the test set is suitable, since it indicates both over- and underfitting. To identify an optimal HP combination representative for the entire data set, HPO was based on k-fold CV. Therefore, the cross-validation error $\text {RMSE}_\text {CV}$ (see Eq. 16) is used as optimization criterion.

4. If both HPO and model evaluation are performed on the basis of k-fold CV, dual use of the data set can lead to overoptimistic model performances (overfitting) [85]. The extent of overfitting is greater the smaller the data set [80]. In Shaikhina and Khovanova [70], a data set with fewer than ten samples per feature is referred to as small. Moreover, this type of overfitting depends on the number of HP considered in the HPO [10] and thus on the ML algorithm. Since the data set used in this work is small (see Sect. 3.2) and the number of HP varies depending on the ML algorithm used (see Table 2), this type of overfitting has to be addressed. This is done using a procedure called double or nested CV. Here, the (inner) k-fold CV of the HPO is embedded into the (outer) k-fold CV of the model evaluation. HPO thus only operates on the train data of the respective fold. The concept of nested CV dates back on an early study of Stone [75] and is also described in more recent works, as, e.g., by Rendall and Reis [60].

5. Since the test/train split during k-fold CV is a stochastic process, both HPO and model evaluation will exhibit variance for repeated calculations. This variance is stronger in smaller data sets [71]. To minimize these deviations, each k-fold CV (both for HPO and model evaluation) is repeated multiple times, with different train and test sets selected in each repetition, which is referred to as repeated nested CV [18, 36].

The final framework of repeated nested CV is given in Algorithm 1 and contains all aspects described above. It therefore allows for a meaningful and fair model comparison.

3 Case study: magnetic seeded filtration

3.1 Experimental procedure and parameters

Fig. 4

Schematic representation of the MSF experiment and relevant variables

This study uses data from MSF experiments that are performed similarly to Rhein et al. [63] and are shown schematically in Fig. 4 together with the relevant variables. Two individual studies (A and B) were performed with their respective parameters given in Table 3. A mono-disperse silica–magnetite composite ($\hbox {SiO}_2$-MAG) was used as seed material, while the non-magnetic particle system was varied between a poly-disperse $\hbox {SiO}_2$ and poly-disperse ZnO powder. More information on these particle systems is given in Appendix 2. Stock suspensions of the dry particle systems were prepared by sonification with the Digital Sonifier 450 from Branson Ultrasonics Co. (conditioning). A sample of the stock suspension $P_0$ was taken and its actual concentration determined, taking deviations in preparation into account. Subsequently, the respective volumes of the stock suspensions to achieve the desired volume concentrations $c_{\textrm{v},i}$ were transferred into a snap-on lid vial. The suspension parameters ionic strength I and pH were adjusted by addition of $2\,\textrm{M}$ NaCl solution, and $0.5\,\textrm{M}$ HCl or NaOH solution, respectively. Finally, the experimental volume was filled to $V_{\textrm{L}}=30\,\textrm{mL}$ with ultrapure water. The suspension was agitated for the agglomeration time $t_{\textrm{A}}$ in the laboratory shaker Vortex Genius 3 from IKA GmbH. After agglomeration, a ferromagnetic separation matrix was immersed in the suspension and the vial was positioned next to a permanent magnet. Magnetic separation was performed for $t_{\textrm{S}}=2\,\textrm{min}$. A representative sample $P_{\textrm{E}}$ was taken from the non-separated suspension and sonified again achieve comparable levels of dispersity. Samples $P_0$ and $P_{\textrm{E}}$ were analyzed via UV–Vis spectroscopy and the volume concentrations were determined through previously performed, substance- and system-specific calibrations. Separation success is quantified via the separation efficiency of the non-magnetic component

$$\begin{aligned} A_{\textrm{NM}}=1-\frac{c_{\textrm{v,NM,E}}}{c_{\textrm{v,NM,0}}} \quad . \end{aligned}$$

(17)

Table 3 Varied experimental parameters

3.2 Experimental results and data analysis

Figure 5 shows the experimentally determined separation efficiencies for $\hbox {SiO}_2$ (left) and ZnO (right) for various values of pH and ionic strength I. The experimental separation efficiency data is published here https://doi.org/10.5445/IR/1000154994. Regarding the separation of $\hbox {SiO}_2$, a decrease in pH results in an increase in $A_{\textrm{NM}}$. This is explained by the zeta potentials shown in Fig. 12: At pH = 12, both $\hbox {SiO}_2$ and $\hbox {SiO}_2$-MAG have a high, negative charge that results in a strong electrostatic repulsion, low hetero-agglomeration, and ultimately low separation efficiency. The zeta potential decreases with decreasing pH and both particle systems are even oppositely charged at pH = 3, resulting in high separation efficiencies. Generally, ZnO is separated more efficiently than $\hbox {SiO}_2$ for any given pH. Again, this is retraced to lower surface charge of ZnO (see Fig. 12) and therefore lower electrostatic repulsion. An increase in ionic strength leads to an increased separation efficiency for equally charged particles. This is due to a decreased Debye length (see Eq. 8), leading to a shorter range in the repulsive electrostatic interactions, enhanced agglomeration, and separation.

When comparing results from both studies, the separation efficiencies of A are generally slightly above the corresponding results of B. This is explained by a lower relative concentration of magnetic to non-magnetic particles in study B (see Table 3). However, the experimental datapoint for ZnO at pH = 12 and $I=0.01\,\textrm{M}$ in study A is noteworthy: No separation was achieved, although the corresponding datapoint in study B showed high separation in the range of 40–60%. This is clearly an inconsistency that might be retraced to experimental error. Said datapoint is marked in Fig. 5 and henceforth referred to as outlier, as it will again be important for comparing model prediction ability in Sect. 3.5.

Fig. 5

Results of the MSF experiments. Left: experiments with $\hbox {SiO}_2$; right: experiments with ZnO. Two different studies (A and B, see Table 3) were performed which is indicated through coloring. The variation of the pH value is indicated by different markers

3.3 Performance and challenges white-box model

As stated by Praetorius et al. [55], calculating the agglomeration efficiencies $\alpha$ ab initio remains very challenging, despite having theoretical descriptions given in Eqs. 5, 11, and 12. The main reason lies both in the availability and the accuracy of process and material-specific data. In the presented case, especially $\bar{G}$, $A_{\textrm{H}}$ and $\zeta$ are prone to error and require adjustment to experimental data. $\bar{G}$ is adjusted directly, while correction factors are introduced that scale $\zeta$ and $A_{\textrm{H}}$ according to

$$\begin{aligned} \zeta _{\textrm{i}}^*= & {} C_{\zeta }\zeta _{\textrm{i}} \end{aligned}$$

(18)

$$\begin{aligned} A_{\textrm{H},ii}^*= & {} C_{\textrm{A},i}A_{\textrm{H},ii}. \end{aligned}$$

(19)

As all zeta potentials are measured identically, the error is assumed to be independent of the particle system and $C_{\zeta }$ is used globally. However, Hamaker constants depend drastically on the particle surface properties [81] and are therefore scaled with material-specific correction factors. This results in five model parameters that are optimized with algorithms of the Python toolkit SciPy with varying starting and boundary conditions. The global optimizers basinhopping [88] and shgo [17] are used to identify temporary minima in a widely scattered search field, which are further improved with the local optimizer minimize [9]. The RMSE between experimental and calculated separation efficiency, defined in Eq. 15, is used as minimization criterion. The discretization scheme of the WBM was validated beforehand by comparison with analytical solutions, which is discussed in the supplementary information (SI.2). Furthermore, a preliminary grid study elaborated in the supplementary information (SI.3) ensured that the results are independent of chosen grid parameters for $N_{\textrm{S}}=12$ and $s=2.5$. Table 4 lists the number of experimental data points $N_{\textrm{E}}$ (each measured in triplicate), the optimal model parameters and the associated RMSE. Each material system of every data set is optimized individually, and additionally, all experimental data points are optimized together. The first procedure naturally yields the lowest RMSE and, therefore, best agreement between WBM and experiment. These results are used to extract the agglomeration efficiencies $\varvec{\alpha }_{\textrm{p}}$ that are necessary for training the BBM in the serial HM arrangement (direct approach, see Fig. 3). Optimizing all data points at once is bound to yield higher RMSE values due to the inconsistency of the underlying data set (outlier) discussed in Sect. 3.2. However, as all other models also operate on the entire data set, these WBM results are considered more appropriate for comparison and subsequently used.

Table 4 Results of the WBM parameter optimization with corresponding RMSE values

3.4 Study structure for model comparison

The framework from Sect. 2.4 was used to optimize and compare five different ML algorithms (kNN, CART, RF, ANN, and SVM) in two different HM arrangements (parallel and serial) and as pure BBMs. Furthermore, these models are compared to the pure WBM, optimized on the entire data set (see Sect. 3.3). This results in a comparison of 16 different models, which are visualized in Fig. 6. A model-structure-internal comparison (1) provides information about the influence of the ML algorithm on model performance, whereas a ML-algorithm-internal comparison (2) allows conclusions about the influence of model structure. Comparing different HMs with the pure WBM (3) allows the quantification of a possible model improvement by applying hybrid modeling. It should be emphasized that the results of this study are case-specific in nature. It does not aim to draw universal conclusions on model performance, but to show the potential of the methodological framework to reliably and comprehensively compare different models on any given data set.

Fig. 6

Visual representation of all 16 compared model structures. Five different ML algorithms (kNN, CART, RF, ANN, and SVM) are used in two different HM arrangements (parallel and serial) and as pure BBMs. The results are further compared to the standalone WBM

For a comprehensive coverage of the models’ advantages and disadvantages, the comparison was carried out on the basis of several criteria: The prediction quality (a) refers to the accuracy of predicting the separation efficiencies $A_{\textrm{NM}}$ from the process parameters and is quantified by the $\mathrm {RMSE_{HM}}$, i.e., the mean $\mathrm {RMSE_{CV}}$ of the outer repetitions (see Algorithm 1). The ability of the model to interpolate between the existing data points is described by the interpolation quality (b), which provides information about the applicability of the model to new, unseen data and indicates overfitting. Finally, model transparency (c) is investigated and shows whether and how reliably the hetero-agglomeration process is represented by the respective model.

Calculations were performed using $k_\textrm{outer} = 10$ folds for the outer CV (model evaluation) and $k_\textrm{inner} = 5$ folds for the inner CV (HPO) (see Algorithm 1). It is common to set $k_\textrm{inner} < k_\textrm{outer}$ and this choice of k-values has been shown empirically to deliver a good balance between bias and variance (bias–variance trade-off) of the test set errors [30]. The number of used experimental datapoints for training each model in the outer k-folds is therefore given as $N_{\textrm{train},k}=(1-k_{\textrm{outer}}^{-1})N_{\textrm{E}}=26$ (see Table 4). Each k-fold CV was repeated 10 times (reps$_\textrm{inner} = {\text {reps}}_\textrm{outer} = 10$) for further reduction of variance. Seeds were kept constant or chosen deterministically during repeated CV, to obtain reproducible results. A critical parameter is the number of iterations $n_\textrm{iter}$ of the BO. The optimization was initially computed with $n_\textrm{iter} = 50$ and subsequently increased to $n_\textrm{iter} = 100$. Since no significant improvement in prediction quality (i.e., $\mathrm {RMSE_{HM}}$) was found between 50 and 100 iterations, regardless of the HM, the results for $n_\textrm{iter} = 50$ are given. To provide good starting conditions for BO, the number of randomly chosen HP-starting combinations was set to 20, which proved sufficient in preliminary studies.

3.5 Comparing prediction ability

This section compares the ability of the models to predict MSF separation efficiencies from corresponding process parameters using the $\textrm{RMSE}$ as measure of accuracy. By means of this metric, it is possible to compare the prediction quality on the basis of one single value, which is advantageous with regard to clarity and interpretability. Figure 7 shows the averaged $\textrm{RMSE}$ of all implemented models with corresponding standard deviations from the ten outer CV repetitions (see Eq. 16). As mentioned in Sect. 3.2, one experimental data-point is considered an outlier and drastically influences RMSE values. Although all models were trained including the outlier, Fig. 7 shows two graphs, one including (a) and one excluding (b) the experimental outlier in the final calculation of the RMSE. For comparison, the RMSE of the pure WBM is drawn as a horizontal line. Due to the extensive information content of this plot and the exemplary character of this study, only the most important aspects are discussed. As stated in Sect. 3.4, model comparison is performed both in a model-structure-internal and ML-algorithm-internal way.

Fig. 7

Mean RMSE of all implemented models: a including the outlier and b excluding the outlier in the final calculations of RMSE. All models were trained including the outlier. The models inside the gray-shaded area (ANN) are further investigated in Fig. 8

When looking at the model structure internally, it is striking that, independent of the used ML algorithm and whether outlier exclusion is performed or not, the parallel HM and the pure WBM show very similar prediction errors. Hence, the parallel HM is not able to correct the predictions of the WBM, and may even worsen the results on average (CART and RF). Since no ML algorithm leads to a significant improvement, the cause for this probably lies in insufficient data quality and quantity. In essence, the experimental data do not appear to contain a physically based connection between process parameters and deviation of the WBM [82]. Both the serial HM and pure BBM exhibit a strong dependence on outlier exclusion, which is apparent in the large decrease in $\text {RMSE}$ for all ML algorithms when moving from Fig. 7a to 7b. This emphasizes the importance of data analysis and outlier detection prior to applying HMs, to avoid misinterpretations of prediction ability. If no outlier exclusion is performed (a), both model structures, without exception, have higher $\text {RMSE}$ values than the pure WBM. However, if the outlier is excluded (b), serial HMs show lower prediction errors as the pure WBM for nearly all ML algorithms and pure BBMs for the more complex algorithms RF, ANN, and SVM. Extending the WBM by an appropriate BBM for taking over the error-prone part of determining the collision efficiencies, therefore, leads to a significant improvement in prediction accuracy. This can be considered a worst-case estimate, as exclusion of the outlier before training will naturally further enhance model performance. Additionally, the serial HM shows generally lower prediction errors for all ML algorithms compared to the parallel arrangement, which infers that the WBM does not have severe un-modeled effects or structural mismatch (see Sect. 2.3). Both points indicate that the calculation of kinetic rates is indeed the limiting factor for WBM accuracy and that an appropriate BBM can attenuate this effect.

While the choice of ML algorithm has no significant impact on RMSE in serial arrangement, it is crucial for pure BBMs: kNN and CART show significantly higher prediction errors compared to the other implemented algorithms. Both algorithms predict the target variables in a similar way, i.e., by averaging target variables of training samples with similar features to predict the test samples. The small size of the data set and the associated sparse distribution of samples in the feature space therefore limit the prediction quality. As mentioned in Sect. 2.2, other ML algorithms that are not tested in this study (as, e.g., multiple linear regression and it’s variations) might be able to further decrease prediction errors.

It is striking that although a variety of model architectures were trained multiple times, none was able to achieve near perfect prediction accuracy. All models (including the pure WBM) appear to be offset by a minimum RMSE of about 0.1. Again, this may be attributed to inconsistencies and experimental errors in the underlying data set and emphasizes the robustness of the framework against overfitting.

Fig. 8

Predicted vs. experimentally determined separation efficiencies for a pure WBM, b pure BBM (ANN), c parallel HM (ANN), and d serial HM (ANN). The gray-shaded rectangle shows the range of physical results ($A_{\textrm{NM}}\in [0,1]$), while a linear regression visualizes performance. The outlier is framed and marked with an arrow

As already mentioned, misinterpretations can occur when solely looking at the the single $\text {RMSE}$-value. This is due to the significant influence of outliers on this metric. To detect these outliers, it is helpful to plot the separation efficiencies predicted by the model $A_\text {NM,mod}$ against the experimentally determined values $A_\text {NM,exp}$. This enables outlier detection via a data-point-specific evaluation of prediction accuracy. Figure 8 shows these plots for the pure WBM (a), the pure BBM (b), and both parallel (c) and serial (d) hybrid model using ANN as ML algorithm. For reference, the respective models are indicated by a gray-shaded rectangle in Fig. 7. These plots are exemplary and all 16 plots for the investigated model architectures are given in the supplementary information (SI.4). These plots clearly show that the outlier is poorly predicted by both the serial HM and pure BBM (top left corner). This phenomenon is observable for all other ML algorithms and explains the large decrease in $\text {RMSE}$ for these model structures when the outlier is excluded. Both the serial HM and pure BBM not being able to predict the outlier regardless of repeated calculations seems bizarre at first glance. However, this can be interpreted as proof for a well-functioning overfitting prevention of the methodological framework. Figure 8 further shows that the pure WBM performs poorly in the intermediate range of separation efficiency ($0.2<A_{\textrm{NM}}<0.8$) and that the parallel HM is not able to compensate for this effect. Qualitatively, the performance of the serial HM and the pure BBM is better in this area, again emphasizing why only looking at RMSE is insufficient for a holistic model evaluation. Figure 8 indicates the range of physical results ($A_{\textrm{NM}}\in [0,1]$) by gray-shaded rectangles. Both pure WBM and serial HM are strictly bound to this area, while the pure BBM an parallel HM produce non-physical results on both ends of the spectrum. For the pure BBM with ANN as ML algorithm, this might be remedied by choosing a more appropriate activation function in the output layer. Nevertheless, this underlines the benefits of having a mechanistic and therefore physically based model produces the final results.

3.6 Comparing interpolation ability

This chapter investigates the models’ predictive performance on new, unseen data, in between the existing data points in feature space (interpolation) to identify potential overfitting. An overfitted model generally exhibits low training error paired with high prediction errors. Strong overfitting is especially apparent in cases where a monotonous function or relationship is mapped in a highly non-monotonous way. As can be seen in Fig. 5 and is explained in Sect. 2.1, the seperation efficiency is monotonically increasing with ionic strength and therefore a good test case for overfitting. Thus, a new input data set with varying ionic strength between $0.01\,\textrm{M}$ and $1\,\textrm{M}$ (32 logarithmically spaced points) was generated and estimated with each previously—i.e., during the optimization procedure described in algorithm 1—trained model. All other input parameters were kept constant at their respective values from data set A ($\hbox {SiO}_2$, pH = 7). It should be emphasized that this only represents a small part of feature space and the subsequently discussed statements should therefore not be generalized. The resulting 100 predictions ($k_\text {outer} \times {\text {reps}}_\text {outer}$) are averaged and shown in Fig. 9 for all model structures with kNN (a) and ANN (b) as ML algorithm. These two algorithms were chosen as examples, since ANN is a representative for a generalizing and kNN for a non-generalizing algorithm. The plots for all other ML algorithms are given in the supplementary material (SI.5).

Fig. 9

Averaged curves of predicted separation efficiencies over ionic strength for pure WBM, pure BBM, and each HM model structure for a kNN and b ANN as ML algorithm. The experimentally determined separation efficiencies (data set A: $\hbox {SiO}_2$, pH 7; see Fig. 5) are also shown

As data set A ($\hbox {SiO}_2$, pH = 7) is part of the above mentioned intermediate range in separation efficiency, Fig. 9 illustrates once more that the pure WBM has difficulties describing the real process behavior. The experimental datapoints for $I=0.01\,\textrm{M}$ and $I=1\,\textrm{M}$ are not reproduced well by the WBM, although they were used during training and the WBM can therefore be considered underfit rather than overfit. As the underlying PBE and their implementation were validated beforehand (SI.2), the low performance of the WBM is either due to inaccuracy of the model equations (Eqs. 4, 5, 11, 12) or of the correction parameters (see Sect. 3.3) used for estimating the agglomeration kernels. Inaccurate model equations can be replaced or adjusted by resolved numerical simulation methods [19, 59], which, however, require additional material data and significantly increase the complexity and computation time of the PBE. Similarly, applying more detailed (viz. a larger number of) correction parameters for unknown material parameters may increase model accuracy but will also increase the complexity of both the PBE and the optimization procedure. This emphasizes a major benefit of serial HMs: The uncertainties regarding model equations and material parameters are all wrapped inside the BBM and therefore drastically reduce model complexity of the WBM, while simultaneously increase the overall prediction accuracy (see Sect. 3.5).

Similarly to the results discussed in Sect. 3.5, the parallel arrangement did not yield a significant improvement, neither for kNN nor ANN. Using kNN as ML algorithm (a), a correction of the separation efficiencies closer to the discrete experimental values is observed, but the representation of the dynamic behavior in between those reference points remains poor. A decrease of separation efficiency with increasing ionic strength represents non-physical behavior, which also occurs for pure BBM or serial HM with kNN as ML algorithm. Using ANN as ML algorithm (b), the interpolated curves appear smooth, which better represents the physical behavior. This smoothness is explained by the fact that generalizing ML algorithms, unlike kNN, CART, or RF, learn a functional relationship between process parameters and separation efficiency during model training.

Generally, pure BBM and serial HM are in better accordance to the expected slowly and monotonically increasing dynamic compared to pure WBM and parallel HM, thus indicating better interpolation ability. This trend is apparent for both ML algorithms, while the pure BBM is slightly closer to the experimental data points.

3.7 Comparing transparency

The model comparison with regard to prediction and interpolation ability showed similar performances for the pure BBM and the serial HM, when one of the more profound ML algorithms (RF, ANN, or SVM) is employed. Therefore, the question arises if all the additional effort for realizing a WBM and combining it into HMs is even justified. An argument can be made that if one is solely interested in predicting separation efficiency from a given set of process parameters, pure BBMs perform best and are both easier and faster to set up, as they do not require any physical knowledge on the problem. However, only models with incorporated WBMs provide insights into the micro-processes, i.e., give information on the time-dependent agglomerate distribution n. The pure BBM, being empirical in nature, does not provide any insights in this regard. Since the serial HM, generally exhibits lower prediction errors as the pure WBM as well as the parallel HM (with outlier exclusion), it can be stated that the hetero-agglomeration processes are most reliably described by this type of model structure. Even for well-performing parallel HM (e.g., on other data sets), this argument holds: As a parallel HM only provides a correction of the separation efficiency predicted by the WBM, its insight into the micro-processes, namely the calculation of the PBE, remains unchanged. This is a crucial aspect for various applications, as, e.g., model predictive control and process optimization, as one of the incentives for process modeling to begin with is to allow access to non or hard to measure phenomena.

3.8 A closer look on hyper-parameter optimization

Besides providing the basis for a reliable and meaningful model comparison, the methodological framework presented in Sect. 2.4 also allows for a statistical evaluation of the optimal HP combinations. By applying repeated nested CV, 100 (${\text {reps}}_\text {outer} \times k_\text {outer}$) HPOs were performed on different parts of the data set. Figure 10 shows the exemplary histograms of the resulting, optimal HP combinations for the serial HM with ANN as ML algorithm. Since it is impossible to a priori state which HP settings will provide an optimal adaption to the data set, a subsequent HP evaluation is even more decisive: This information can, e.g., be used to narrow down the HP search space after an initially broad definition. As a result, a more precisely defined search space is expected to both reduce the number of necessary iterations and—in some cases—even produce a better optimum value.

Figure 10 shows that the number of neurons was mostly distributed in the lower range of around 10–20, and therefore, the upper limit of HP search space could be limited to, e.g., 40. Furthermore, as the linear activation function was never considered optimal, it might be removed from the HP search space. The results further indicate that one-hot encoding of the categorical input variable NM and no pre-processing of the ionic strength generally increased prediction accuracy.

Fig. 10

Histograms of the resulting HPs for ANN in serial HM. Pre-processing of NM and I, the activation function, and number of neurons are considered

4 Conclusions

Hybrid modeling is a promising technique for describing hetero-agglomeration processes as it is an elegant way of introducing experimental data into mechanistic models, while simultaneously attenuating major limitations of purely data-driven approaches. The presented general framework alleviates one major difficulty in applying hybrid models, namely that the optimal model architecture and ML algorithm cannot be know beforehand, as they are highly problem-dependent. By implementing a repeated nested cross validation with integrated hyper-parameter optimization, any HM combination can be compared for any given data set in a fair and objective manner to select the best-suited architecture. Additionally, the framework allows for a statistical evaluation of the selected hyper-parameters, which paves the way for further enhancement of model accuracy.

The capabilities of this approach were portrayed by a case study on magnetic seeded filtration: 16 different model architectures—including the pure WBM as well as pure BBMs, serial and parallel HMs for different ML algorithms—were compared with respect to multiple criteria. Both the serial HM and pure BBM were able to achieve a significant increase in prediction accuracy compared to the pure WBM. They also proved to enhance interpolation ability between experimental data points, especially when more elaborate ML algorithms like the ANN are used. However, as serial HMs further allow for a more accurate depiction of the ongoing micro-processes, while pure BBMs do not provide any insight, it is concluded that serial HMs are best-suited for describing hetero-agglomeration during MSF.

Appendices

Appendix 1: Geometric discretization scheme

The following section briefly summarizes the necessary equations to realize the 2-D geometric discretization scheme. For more in-depth explanations and derivations, it is referred to Kumar et al. [37, 38]. The general form of the ODE is given by

$$\begin{aligned} \frac{\textrm{d}n(i,j,t)}{\textrm{d}t}=B_{i,j}+D_{i,j}\quad . \end{aligned}$$

(20)

The death term $D_{\textrm{i,j}}$ describes the loss of (i, j) due to further agglomeration with (l, m) and is calculated according to

$$\begin{aligned} D_{i,j}=-\sum \limits _{l=0}^{N_{\textrm{S}}}\sum \limits _{m=0}^{N_{\textrm{S}}}k(i,j,l,m)n(i,j,t)n(l,m,t)\quad . \end{aligned}$$

(21)

For easier notation, define $X_{\textrm{i}}$ as partial volume of the non-magnetic component and $Y_{\textrm{j}}$ as the partial volume of the magnetic component of agglomerate (i, j) according to

$$\begin{aligned} X_{i}=V_{\textrm{NM}}(i,j)=s^{i-1}V(1,0) \quad |\quad Y_{j}=V_{\textrm{M}}(i,j)=s^{j-1}V(0,1) \quad . \end{aligned}$$

(22)

The unmodified birth term is given by

$$\begin{aligned} B^*_{i,j}= \underset{Y_{j-1}\le Y_{m}+Y_{b}< Y_{j+1}}{\underset{ X_{i-1}\le X_{l}+X_{a}< X_{i+1}}{\sum \limits _{l=1}^{i}\,\sum \limits _{a=1}^{i}\, \sum \limits _{m=1}^{j}\,\sum \limits _{b=1}^{j}}} \frac{1}{2}\gamma k(l,m,a,b)n(l,m,t)n(a,b,t) \end{aligned}$$

(23)

with

$$\begin{aligned} \gamma ={\left\{ \begin{array}{ll} 1 &{} \quad V(i,j)=V(l,m)+V(a,b) \\ \frac{1}{2} &{} \quad V(i,j)\ne V(l,m)+V(a,b) \end{array}\right. } \quad . \end{aligned}$$

(24)

Note that the indices of $\gamma (i,j,l,m,a,b)$ are not written out to improve visibility. Further, the net flux of non-magnetic volume $x_{\textrm{i,j}}$ and magnetic volume $y_{\textrm{i,j}}$ into cell (i, j) are defined by

$$\begin{aligned} x_{i,j}=&\underset{Y_{j-1}\le Y_{m}+Y_{b}< Y_{j+1}}{\underset{ X_{i-1}\le X_{l}+X_{a}< X_{i+1}}{\sum \limits _{l=1}^{i}\,\sum \limits _{a=1}^{i}\, \sum \limits _{m=1}^{j}\,\sum \limits _{b=1}^{j}}} \frac{1}{2}\gamma k(l,m,a,b)n(l,m,t)n(a,b,t)\left( X_{l}+X_{a}\right) \end{aligned}$$

(25)

$$\begin{aligned} y_{i,j}=&\underset{Y_{j-1}\le Y_{m}+Y_{b}< Y_{j+1}}{\underset{ X_{i-1}\le X_{l}+X_{a}< X_{i+1}}{\sum \limits _{l=1}^{i}\,\sum \limits _{a=1}^{i}\, \sum \limits _{m=1}^{j}\,\sum \limits _{b=1}^{j}}} \frac{1}{2}\gamma k(l,m,a,b)n(l,m,t)n(a,b,t)\left( Y_{m}+Y_{b}\right) . \end{aligned}$$

(26)

The average properties of newly formed agglomerates in cell (i, j) are calculated as

$$\begin{aligned} \bar{X}_{i,j}=\frac{x_{i,j}}{B_{i,j}} \quad |\quad \bar{Y}_{i,j}=\frac{y_{i,j}}{B_{i,j}}, \end{aligned}$$

(27)

and finally, the modified birth term is calculated as

$$\begin{aligned} B_{{ij}}&= \sum \limits _{{p}=0}^1\sum \limits _{{q}=0}^1 B^{*}_{{i-p,j-q}} \lambda ^{-,-}_{{i,j}}\left( X_{{i-p}},Y_{{j-q}}\right) \nonumber \\&\quad \times {H}\left[ \left( -1\right) ^{p}\left( X_{{i-p}}-\bar{X}_{{i-p,j-q}}\right) \right] {H}\left[ \left( -1\right) ^{q}\left( Y_{{j-q}}-\bar{Y}_{{i-p,j-q}}\right) \right] \nonumber \\&\quad + \sum \limits _{{p}=0}^1\sum \limits _{{q}=0}^1 B^*_{{i-p,j+q}} \lambda ^{-,+}_{{i,j}}\left( X_{{i-p}},Y_{{j+q}}\right) \nonumber \\&\quad \times {H}\left[ \left( -1\right) ^{p}\left( X_{{i-p}}-\bar{X}_{{i-p,j+q}}\right) \right] {H}\left[ \left( -1\right) ^{q+1}\left( Y_{{j+q}}-\bar{Y}_{{i-p,j+q}}\right) \right] \nonumber \\&\quad + \sum \limits _{{p}=0}^1\sum \limits _{{q}=0}^1 B^*_{{i+p,j-q}} \lambda ^{+,-}_{{i,j}}\left( X_{{i+p}},Y_{{j-q}}\right) \nonumber \\&\quad \times {H}\left[ \left( -1\right) ^{p+1}\left( X_{{i+p}}-\bar{X}_{{i+p,j-q}}\right) \right] {H}\left[ \left( -1\right) ^{q}\left( Y_{{j-q}}-\bar{Y}_{{i+p,j-q}}\right) \right] \nonumber \\&\quad + \sum \limits _{{p}=0}^1\sum \limits _{{q}=0}^1 B^*_{{i+p,j+q}} \lambda ^{+,+}_{{i,j}}\left( X_{{i+p}},Y_{{j+q}}\right) \nonumber \\&\quad \times {H}\left[ \left( -1\right) ^{p+1}\left( X_{{i+p}}-\bar{X}_{{i+p,j+q}}\right) \right] {H}\left[ \left( -1\right) ^{q+1}\left( Y_{{j+q}}-\bar{Y}_{{i+p,j+q}}\right) \right] \end{aligned}$$

(28)

with

$$\begin{aligned} \lambda _{i,j}^{\pm ,\pm }\left( X,Y\right) = \frac{\left( X-X_{i\pm 1}\right) \left( Y-Y_{j\pm 1}\right) }{\left( X_{i}-X_{i\pm 1}\right) \left( Y_{j}-Y_{j\pm 1}\right) }, \end{aligned}$$

(29)

and the Heaviside function H defined as

$$\begin{aligned} {H}\left( x\right) ={\left\{ \begin{array}{ll} 1 &{} \quad x>0\\ \frac{1}{2} &{} \quad x=0\\ 0 &{} \quad x<0 \end{array}\right. }\quad . \end{aligned}$$

(30)

Appendix 2: Material data

Figure 11 shows the cumulative particle-size distribution of the used particle systems. For $\hbox {SiO}_2$-MAG, the distribution was measured with an analytical disc centrifuge (CPS Instruments), while ZnO and $\hbox {SiO}_2$ were measured by laser diffraction (Helos, Sympatec). The pH-dependent zeta potentials are shown in Fig. 12 and were fitted with a polynomial function of degree three for continuous integration into the PBE. All zeta potentials were measured at constant ionic strength $I=0.1\,\textrm{M}$ and constant particle concentration $c_{\textrm{v}}=3.75\times 10^{-3}\,\textrm{vol}\%$. Further information about the particle systems is given in Table 5. Zeta potential and size distribution data is published here https://doi.org/10.5445/IR/1000154994.

Fig. 11

Cumulative particle-size distributions of the used particle systems

Fig. 12

Zeta potentials of the used particle systems and their respective polynomial fit of third degree for usage in the PBE

Table 5 Relevant properties of used particle systems