1 Introduction

Diffuse interface descriptions, such as phase-field models, are widely used within the framework of integrated computational materials engineering, and more specifically for the microscopic modeling of solidification [1,2,3]. Quantitative simulations require a proper numerical resolution of the diffuse solid/liquid interface, i.e., the diffuse interface profile has to be resolved by a certain minimal amount of grid points. In case of numerical under-resolution, the simulation is subjected to spurious grid anisotropy as well as grid friction, which in the worst case leads to the “pinning” of the diffuse interface on the computational grid. We define the dimensionless profile resolution number \(\tilde{\lambda }=\lambda /\Delta {x}\) as the ratio of the half profile width \(\lambda\) to the spacing \(\Delta {x}\) between next neighboring grid points. The half profile width \(\lambda\) refers to the equilibrium phase-field profile function \(\phi _{\mathbf {n}}(x)=\{1-\tanh (2x/\lambda )\}/2\), which is received upon a cut through the diffuse interface in normal direction. In conventional phase-field models, the minimal number of grid points used to resolve the profile is about 4 [4],which corresponds to the dimensionless profile resolution number \(\tilde{\lambda }=2\). However, depending on the accuracy demands of the simulation, the double, triple or even quadruple profile resolution numbers can be required.

Recently, Finel et al. found a striking new way to eliminate grid friction and pinning in one dimension, called the sharp phase-field model [5]. This method is conceptually related to other techniques to improve the performance of phase-field models based on the phase-field profile function, such as the nonlinear preconditioning of the phase-field equation [6,7,8,9,10,11,12]. The 1D sharp phase-field model operates at one-grid-point profile resolutions (\(\tilde{\lambda }=0.5\)) and below without the occurrence of grid pinning!

However, besides the profile resolution, there is one other important aspect that limits the spatial resolution efficiency of phase-field models in general: They cannot operate at arbitrarily small interface energy densities \(\Gamma\). Consider an interface between two phases at different bulk free energy density levels. The latter, also called the driving force \({\mu }\), induces an interface motion lowering the total free energy of the system. For too small interface energies or too large driving forces, either the high energy phase turns unstable (phase stability limit) or the phase-field profile is spuriously altered. The alternation is accompanied by strong grid friction effects. We define the dimensionless driving force \({\tilde{\mu }}={\mu }\Delta {x}/\Gamma\), which relates to the spatial resolution of the simulation via the grid spacing \(\Delta {x}\). Imposing constant driving forces, we consider the simulation of stationary interface motion in 1D at different dimensionless spatial resolution numbers \(\tilde{\lambda },{\tilde{\mu }}\). Reasonable model operation at the resolution \(\tilde{\lambda },{\tilde{\mu }}\) is said to require phase stability as well as less than \(10\%\) relative deviations from the theoretically expected interface velocity. Further information on this study is given in Sect. 3.1. In Fig. 1, we compare the resulting parameter windows of reasonable model operation for the most frequently used conventional phase-field model (blue) and the sharp phase-field model (green). The elimination of spurious grid friction in the sharp phase-field model allows for orders of magnitude more efficient simulations, than possible with the conventional phase-field model.

Fig. 1
figure 1

Evaluation of the principle capability of phase-field models to operate at different dimensionless spatial resolutions \(\tilde{\lambda }\) and \({\tilde{\mu }}\) (Criteria: phase stability and stationary interface motion with relative errors \(<0.1\)). The different possible resolution ranges are compared for two different models: The most frequently used conventional model (blue area) and the sharp phase-field model (green area)

Full size image

During diffusion-limited solidification, the complex evolution of the solid/liquid interface undergoes a branching instability [13]. In a fully isotropic system, this leads to the self-organized formation of so-called isotropic dense branching or seaweed microstructures [14], as visible in the inset of Fig. 1. The structure shows a characteristic distance between branches, which nontrivially relates to the atomistically small capillary length \({d}_{0}\), that is proportional to the interface energy density \(\Gamma\) [1]. A fundamental challenge in solidification modeling is the fact that the microscopic distance between branches is typically several orders of magnitude larger than a central aspect of its cause, i.e., the atomistically small capillary length. If, however, the phase-field model is able to stably operate at a certain small interface energy or, in other words, a certain large dimensionless driving force, then the grid spacing \(\Delta {x}\) can exceed \({d}_{0}\) in a respective proportion [15].

Here, we propose a new sharp phase-field model, which captures the 3D formation of isotropic dense branching even at one-grid-point profile resolutions (\(\tilde{\lambda }=0.5\)), see Fig. 1. The absence of any spurious dendritic selection by the computational grid indicates quite high degrees of isotropy [16, 17]. This denotes remarkable methodological progress in the modeling of microscopic solidification. Before, the phase-field method was understood to be substantially less efficient than respective cellular automata models, where the transformation from the liquid to the solid phase is carried by single cells. The advantage of the phase-field method is that the inefficient, diffuse interfaces of large widths naturally provide enormously high degrees of isotropy in the description, which can hardy be reached by the cellular automata [1, 18]. Now, with one-grid-point interface resolutions, the sharp phase-field model is able to reach fully isotropic solidification conditions at the efficiency scale of respective cellular automata models!

During simulations of diffusion-limited solidification, as for instance shown in Fig. 1, the driving forces are largely inhomogeneous. We visualize the respective driving force distribution by a boxplot with whiskers to the maximal and minimal value. In this work, we show that the sharp phase-field model provides quantitative interface velocities within the full range of different driving forces! To achieve a comparable accuracy over a similarly wide range of driving forces, the conventional phase-field model would require profile resolutions of \(\tilde{\lambda }=5\), as shown in Fig. 1. In this regard, the new sharp phase-field model allows for 3D simulations of isotropic solidification with a \(10^{3}\times\)more efficient spatial resolution.

The article is structured as follows: The derivation of different models based on the sharp phase-field method is presented in Sect. 2, where the central new aspects are the locally adaptive restoration of Translational Invariance (TI), as discussed in Sect. 2.1, and the newly proposed regularization of the latent heat release at the solid/liquid interface, discussed in Sect. 2.2. Detailed information on the calibration of the different models is given in Sect. 2.3, and an overview on the construction of the different models is presented in Sect. 2.4. This is followed by the results and discussion Sect. 3. First, we discuss the constantly driven stationary motion of planar interfaces, in Sect.. 3.1, which provides the basic operational frame of the different models. The simulations of quantitative stationary solidification with inhomogeneous driving forces are discussed in Sect. 3.2. Finally, in Sect. 3.3, we discuss the application of different models to the case of isotropic diffusion-limited solidification.

2 Sharp phase-field modeling

The derivation of the different models is started from a discrete Helmholtz free energy functional \(F\left[ \phi _{{\mathbf {p}}}\right] =\sum _{{\mathbf {p}}}f_{{\mathbf {p}}}\Delta {x}^{3}\), where \({\mathbf {p}}\) denotes the locations of the grid points within the simple cubic 3D numerical lattice with a grid spacing \(\Delta {x}\). In the following, we describe orientations and directions relative to our simple cubic computational grid using a Miller index notation system, where the principle \(\left\langle 100\right\rangle\)-vectors correspond to the basis vectors of the grid. The discrete Helmholtz free energy density \(f_{{\mathbf {p}}}\) associated with the grid point \({\mathbf {p}}\) is

$$\begin{aligned} f_{{\mathbf {p}}}\!=&\frac{\Gamma }{C_{\Gamma }\lambda }\sum _{j,k}\!\gamma _{j}\nu _{j}\Big (\frac{\lambda ^{2}}{2}(\partial _{k}^{+}\phi _{{\mathbf {p}}})^{2}\!+\!g_{k}(\phi _{{\mathbf {p}}})\Big )\!+\!{\mu }_{{\mathbf {p}}}h(\phi _{{\mathbf {p}}}). \end{aligned}$$
(1)

We restrict the formulation to grid point interactions up to the first three neighboring shells \(j\!=\!1,2,3\), with \(\left| \mathbf {r}_{k}\right |_{j}\!=\!\sqrt{j}\Delta {x}\) and \(\mathbf {r}_{k}\) being a numerical lattice vector that connects two neighboring grid points along the direction \(k\). \(\partial _{k}^{+}\phi _{{\mathbf {p}}}\) denotes the discrete directional derivative, which is approximated by the forward finite difference expression \(\partial _{k}^{+}\phi _{{\mathbf {p}}}\!\equiv \!(\phi _{{\mathbf {p}}+\mathbf {r}_{k}}\!-\!\phi _{{\mathbf {p}}})/\left | \mathbf {r}_{k}\right |\). For a given neighboring shell with \(m_{j}\) neighboring nodes, the coefficients \(\nu _{j}\!=\!3/m_{j}\) correct for the multiplicity of the shell. Similar to [5], the ponderation coefficients \(\gamma _{j}\) are chosen to get best possible energetic equality of differently oriented ideal interfaces.

The equilibrium potentials \(g_{k}(\phi )\) are minimal at \(\phi \!=\!0\) and \(\phi \!=\!1\), which corresponds to the two distinct phases of the system. \(\lambda\) denotes the width of the diffuse interface, \(\Gamma\) is the interface energy density, and \(C_{\Gamma }\) is the interface energy calibration parameter. A positive bulk free energy density difference \({\mu }_{{\mathbf {p}}}\) favors the growth of phase \(\phi \!=\!0\) on the expanse of phase \(\phi \!=\!1\). Concerning the interpolation function \(h(\phi )\), we focus on the natural interpolation \(h_{3}\!=\!\phi ^{2}(3\!-\!2\phi )\) [5] and the most frequently used polynomial \(h_{\mathrm {5}}\!=\!\phi ^{3}(10\!-\!15\phi \!+\!6\phi ^{2})\) [19,20,21,22,23,24].

The functional derivative of the discrete Helmholtz free energy is given by \(\delta _{\phi }F\!=\!\partial _{\phi }f_{{\mathbf {p}}}\!-\!\sum _{j,k}\partial _{k}^{-}(\partial _{\left( \partial _{k}\phi \right) }^{+}f_{{\mathbf {p}}}),\) where the second directional derivative \(\partial _{k}^{-}\) is approximated by \(\partial _{k}^{-}\left( \partial f_{{\mathbf {p}}}\right) \!\equiv \!\left( \partial f_{{\mathbf {p}}}\!-\!\partial f_{{\mathbf {p}}-\mathbf {r}_{k}}\right) /\left |\mathbf {r}_{k}\right |\). The phase-field evolution equation demands that the time derivative \(\partial _{t}\phi _{{\mathbf {p}}}\) is proportional to \(-\delta _{\phi }F\). We write, \(3\lambda \Gamma \partial _{t}\phi _{{\mathbf {p}}}\!=\!-2M\delta _{\phi }F\), where \(M\) is a kinetic coefficient with the dimension \(\left[ M\right] \!=\!\mathrm {m}^{2}\mathrm {s}^{-1}\)[25]. Then, the phase-field equation is given as

$$\begin{aligned} \partial _{t}\phi _{{\mathbf {p}}}=&\frac{2M}{3C_{\Gamma }}\sum _{j,k}\gamma _{j}\nu _{j}\left( \partial _{k}^{-}\left( \partial _{k}^{+}\phi _{{\mathbf {p}}}\right) -\frac{1}{\lambda ^{2}}\partial _{\phi }g_{k}(\phi _{{\mathbf {p}}})\right) \nonumber \\&-\frac{2M}{3\lambda \Gamma }{\mu }_{{\mathbf {p}}}\;\partial _{\phi }h(\phi _{{\mathbf {p}}}), \end{aligned}$$
(2)

where \(\partial _{\phi }\!=\!\partial /\partial \phi\) denotes the partial phase-field derivative. A constant driving force \({\mu }\) results in stationary interface motion, whereas total energy conservation demands the velocity to be \(\upsilon_{\mathrm {th}}\!=\!-M{\mu }/\Gamma\). The phase-field equation promotes solutions of the form

$$\begin{aligned} \phi _{\mathrm {{\mathbf {p}}}}&=\left( 1-\tanh 2\left( {\mathbf {p}}\cdot \mathbf {n}-c_{n}\right) /\lambda \right) /2, \end{aligned}$$
(3)

where \(\mathbf {n}\) is the unit normal interface vector and \(c_{n}\!=\!\upsilon_{\mathrm {th}}t\) denotes the central interface position moving with the velocity \(\upsilon_{\mathrm {th}}\). It can be shown, that this function is an analytic solution of the non-equilibrium, continuum phase-field Eq. (2), if \(g(\phi )\!=\!\sum _{j,k}g_{k}\!\equiv \!8\phi ^{2}\left( 1\!-\!\phi \right) ^{2}\) and \(h(\phi )\!=\!h_{3}\!=\!\phi ^{2}(3\!-\!2\phi )\). Within the distance \(2\lambda\) the phase-field value undergoes \(96.4\%\) of its total transition from \(\phi \!=\!0\) to \(\phi \!=\!1\) (\(\tanh 2\!\simeq \!0.964\)) [26]. The hyperbolic tangent function provides the following addition property,

$$\begin{aligned} \tanh \left( p\pm q\right)&=\frac{\tanh \left( p\right) \pm \tanh \left( q\right) }{1\pm \tanh \left( p\right) \tanh \left( q\right) }, \end{aligned}$$
(4)

which can be reformulated in terms of the phase-field profile function (3)

$$\begin{aligned} \phi _{{\mathbf {p}}\pm \mathbf {r}_{k}}&=\frac{\left( 1\pm a_{k}\right) \phi _{{\mathbf {p}}}}{1\pm \left( 2\phi _{{\mathbf {p}}}-1\right) a_{k}}, \end{aligned}$$
(5)

where we introduce the grid coupling parameters \(a_{k}\!\left( \mathbf {n}\right) =\!\tanh \left( 2\mathbf {r}_{k}\!\cdot \!\mathbf {n}/\lambda \right)\), which depend on the interface normal vector. For vanishing driving forces \({\mu }\!=\!0\) and no phase-field motion \(\partial _{t}\phi \!=\!0\), the phase-field equation (2) reduces to

$$\begin{aligned} {\textstyle \sum _{j,k}}\gamma _{j}\nu _{j}\{\lambda ^{2}(\phi _{{\mathbf {p}}+\mathbf {r}_{k}}\!\!-\!2\phi _{{\mathbf {p}}}\!+\!\phi _{{\mathbf {p}}-\mathbf {r}_{k}})/\mathbf {r}_{k}^{2}-\partial _{\phi }g_{k}\}&=0, \end{aligned}$$
(6)

This discrete force density equilibrium condition (6) holds, if all 1D \(k\)-components are simultaneously satisfied. The individual \(k\)-component can be satisfied at any real time during the propagation of the interface using the addition property of the hyperbolic tangent profile. Inserting (5) into the \(k\)-th component of the equilibrium condition (6) yields

$$\begin{aligned} \partial _{\phi }g_{k}(\phi )&=a_{k}^{2}\frac{\lambda ^{2}}{\mathbf {r}_{k}^{2}}\frac{4\phi \left( 1-\phi \right) \left( 1-2\phi \right) }{1-a_{k}^{2}\left( 1-2\phi \right) ^{2}}. \end{aligned}$$
(7)

After integration, we obtain the \(k\)-th component of the modified equilibrium potential

$$\begin{aligned} g_{k}(\phi )\frac{\mathbf {r}_{k}^{2}}{\lambda ^{2}}=\phi (1\!-\!\phi )\,+\,&\frac{1\!-\!a_{k}^{2}}{4a_{k}^{2}}\ln \bigg (\frac{1\!-\!a_{k}^{2}}{1\!-\!a_{k}^{2}\left( 1\!-\!2\phi \right) ^{2}}\bigg ), \end{aligned}$$
(8)

which further satisfies \(g_{k}(\phi \!=\!0,\!1)\!=\!0\), to allow an easy calculation of the system’s total interface energy by \(F_{\mathrm {int}}(\phi _{{\mathbf {p}}})\!=\!\sum _{{\mathbf {p}}}f_{{\mu }=0}\) for an arbitrary phase-field [27, 28]. In the continuum limit \(\left |\mathbf {r}_{k}\right |\!\rightarrow \!0\), Eq. (8) converges to the conventional Continuum Field (CF) potential \(g_{k}^{\infty }\!=\!8\phi ^{2}\left( 1\!-\!\phi \right) ^{2}\).

The grid coupling parameters as well as the modified equilibrium potential (8) depend on the a priorily unknown interface orientation. To get a globally determined modified equilibrium potential (8), Finel et al. proposed to concentrate on interface orientations, which usefully relate to certain lattice plane families of the computational grid [5]. In our notation, this corresponds to replacing the a priorily unknown interface normal vector \(\mathbf {n}\) by a globally constant unit vector \(\mathbf {u}\), which is pointing in the direction normal to the lattice plane \(\left( hkl\right)\). Then, a 3D sharp phase-field model can be constructed based on the globally constant set of grid coupling parameters \(a_{k}(\mathbf {u})=\tanh \left( 2\mathbf {r}_{k}\!\cdot \!\mathbf {u}/\lambda \right) .\) Finel et al. have shown, that the resulting model provides the Translational Invariance (TI) for planar interfaces with an orientation normal to all the equivalent directions \(\left\langle hkl\right\rangle\) [5]. The maximal possible number of different equivalent directions can be 24, if \(h\ne k\ne l\). We refer to the class of globally constant sharp phase-field models as the TI\(_{\left\langle hkl\right\rangle }\)-models, where the index indicates the constant directions of restored translational invariance.

2.1 Locally adaptive translational invariance

Here, we propose a new sharp phase-field model. It uses a locally adaptive modified equilibrium potential (8) based on locally determined grid coupling parameters \(a_{k}\!\left( \mathbf {n}\right)\). This is difficult in two respects: First, usual finite difference expressions for the calculation of the unit normal vector \(\mathbf {n}\) can not be applied. Those expressions do not provide a sufficiently accurate determination of the normal direction in case of small profile resolution numbers \(\tilde{\lambda }\). To provide the necessary accuracy, we calculate preliminary grid coupling parameters by \(\hat{a}_{k}\!=\!(\hat{a}_{k}^{+}\!+\!\hat{a}_{k}^{-})/2\), with

$$\begin{aligned} \hat{a}_{k}^{\pm }&=\frac{\pm \left( \phi _{{\mathbf {p}}\pm \mathbf {r}_{k}}-\phi _{{\mathbf {p}}}\right) }{\phi _{{\mathbf {p}}}-2\phi _{{\mathbf {p}}\pm \mathbf {r}_{k}}\phi _{{\mathbf {p}}}+\phi _{{\mathbf {p}}\pm \mathbf {r}_{k}}}, \end{aligned}$$
(9)

which is a reformulation of Eq. (5).

The second difficulty arises from the necessary interaction between the different directions \(k\) within the formulation: Using the modified equilibrium potentials the explicit dependence of the phase-field equation on the profile width \(\lambda\) cancels out. Then, \(\lambda\) is solely controlled by the preliminary grid coupling parameters, which at the same time contain the a priori unknown interface normal vector \(\hat{\mathbf {n}}\). Thus, without length control of \(\hat{\mathbf {n}}\) the profile width \(\lambda\) would not be defined in the model. Therefore, we locally calculate all components of the preliminary interface normal vector by, \(\hat{n}_{k}\!=\!\lambda \:\mathrm {arctanh}(\hat{a}_{k})/\left |2\mathbf {r}_{k}\right |\), restore unit length via \(\mathbf {n}\!=\!\hat{\mathbf {n}}/\left |\hat{\mathbf {n}}\right |\), calculate the corrected grid coupling parameters as

$$\begin{aligned} a_{k}\!\left( \mathbf {n}\right)&=\!\tanh \left( \frac{2\mathbf {r}_{k}\!\cdot \!\mathbf {n}}{\lambda }\right) , \end{aligned}$$
(10)

and finally insert those into the derivative of the modified equilibrium potential (7) to solve the phase-field equation in the current time step. In the following, we refer to this model as the TI\(_{\mathbf {n}}\)-model, which provides the local restoration of TI in the direction of the local interface normal \(\mathbf {n}\).

Fig. 2
figure 2

Model comparison with respect to the theoretic ability to restore Translational Invariance (TI). For each model, we plot the oscillation amplitude A of the total discrete interface force (i.e. the system integral over Eq. (6)) using the moving, ideal profile function (3) for different interface orientation angles \(\vartheta _{[001]}\) and \(\vartheta _{[011]}\). The black solid curve shows the Continuum Field (CF) model, where no TI is restored. The different TI\(_{\left\langle hkl\right\rangle }\) models use global equilibrium potentials (8), that restore TI for interfaces oriented normal to the \(\left\langle hkl\right\rangle\)-directions. The TI\(_{\mathbf {n}}\)-model (green curve) provides TI locally in the interface normal direction \(\mathbf {n}\). The profile resolution number is \(\tilde{\lambda }\!=\!\lambda /\Delta {x}\!=\!0.5\); system size \(300\!\times \!1\!\times \!1\)

Full size image

Next, we evaluate the theoretic ability of the different models to restore Translational Invariance (TI) of the profile function (3) within discrete the phase-field equation. Therefore, we consider a discrete 3D system with a phase-field as represented by an array of floating point numbers, each associated with a grid point within the simple cubic numerical lattice of size \(300\times 1\times 1\) (excluding the one stencil boundary halo). The phase-field values are initialized according to the ideal profile function (3), such that the interface is sitting in the middle of the system. The total force acting on the interface in equilibrium is given by the system integral over (6). While the continuum force integral clearly vanishes in equilibrium, the discrete force integral can oscillate, when the ideal profile is moved on the computational grid. In Fig. 2, we plot the oscillation amplitude A of the discrete interface force as a function of the interface orientation for different models. Without restoration of TI, the system integral over Eq. (6) oscillates, when the ideal profile (3) is moved in such a way that the interface center \(c_{n}\) passes several grid points. The conventional Continuum Field (CF) model (black curve) provides the largest equilibrium force oscillations, which indicates fully broken TI.

Finel et al. proposed to restore TI using globally constant grid coupling parameters \(a_{k}\!\left( \mathbf {u}\right)\) based on a unit vector \(\mathbf {u}\), pointing in the direction normal to the lattice plane \(\left( hkl\right)\) [5]. This provides vanishing force oscillations only for those interface orientations, that match with one of the equivalent numerical lattice directions \(\left\langle hkl\right\rangle\): When the grid coupling parameters are, for instance, calculated from a unit lattice vector \(\mathbf {u}\) parallel to the \(\left[ 110\right]\)-direction (TI\(_{\left\langle 110\right\rangle }\): dark blue curve in Fig. 2), then vanishing force oscillations are found for interface normal vectors pointing in all the \(\left\langle 110\right\rangle\)-directions. This study denotes an independent confirmation of the statements and derivatives given in [5]. However, it is further visible in Fig. 2, that for a profile resolution of \(\tilde{\lambda }\!=\!0.5\) the TI\(_{\left\langle hkl\right\rangle }\)-models provide quite narrow interface orientation windows, in which the force oscillation amplitudes are found to be below \(10^{-4}\). This highlights the sensitivity of the TI restoration method with respect to interface orientations. The newly proposed TI\(_{\mathbf {n}}\)-model (green curve) uses grid coupling parameters calculated from accurately determined local interface normal directions. This model provides very small equilibrium force oscillations regardless of the interface orientation, which indicates that the TI\(_{\mathbf {n}}\)-model successfully restores TI for arbitrary planar interfaces in 3D.

2.2 Latent heat release

Here, we discuss the solidification specific aspects of the models. The advancing solidification is accompanied by a release of latent heat at the solid/liquid interface [29]. Thus, the dimensionless temperature field \(U_{{\mathbf {p}}}\!=\!C(T_{{\mathbf {p}}}\!-\!T_{M})/L\) is introduced, where \(T_{M}\), L and C denote the melting temperature, latent heat and heat capacity, respectively [30]. The driving force for solidification is given by \({\mu }_{{\mathbf {p}}}\!=\!-U_{{\mathbf {p}}}\Gamma /{d}_{0}\), where \({d}_{0}\!=\!\Gamma T_{M}C/L^{2}\) denotes the capillary length. The temperature obeys a diffusion equation,

$$\begin{aligned} \partial _{t}U_{{\mathbf {p}}}\!&=\!D\nabla ^{2}U_{{\mathbf {p}}}\!+\!R(\phi _{{\mathbf {p}}})\partial _{\phi }h\partial _{t}\phi _{{\mathbf {p}}}, \end{aligned}$$
(11)

with the assumption of equal diffusion coefficients D in the solid and liquid phases. For small profile resolutions, \(\lambda /\Delta {x}\!\le \!2\), and \(R\!=\!1\), we observe spuriously inhomogeneous releases of latent heat, whenever the progressing interface center passes a grid point. The spurious heat release provides oscillations in the solidification velocity as well as some degree of kinetic anisotropy. Therefore, we propose the regularization \(R(\phi _{{\mathbf {p}}})\) in the diffusion equation

$$\begin{aligned} R(\phi _{{\mathbf {p}}})&=\frac{3C_{R}}{4}\frac{a_{\left[ 100\right] }\lambda }{\Delta {x}}\left( 1-a_{\left[ 100\right] }^{2}\left( 1-2\phi _{{\mathbf {p}}}\right) ^{2}\right) ^{-2}, \end{aligned}$$
(12)

where the grid coupling parameter is \(a_{\left[ 100\right] }\!=\!\tanh 2\Delta {x}/\lambda\) and \(C_{R}\) denotes a calibration constant, which is required to maintain total energy conservation during solidification. The numerical description of the Laplace operator in the thermal diffusion equation includes interactions with the second to next nearest neighboring grid points, in order to obtain an increased degree of isotropy. More specifically, we implement the 19-point finite difference formula for the Laplace operator provided by Kassner et al. (see appendix on page 17 in [29]).

Fig. 3
figure 3

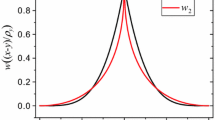
Comparison of the heat release range of the source term \(S(\phi )\!=\!\partial _{\phi }h\partial _{t}\phi \!\sim \!\partial _{\phi }h^{2}(\phi )\) with (\(\tilde{\lambda }\!=\!0.4\)) and without (\(\tilde{\lambda }\!=\!2\)) the regularization factor \(R(\phi )\) Eq. (12). The comparison is based on the ideal phase-field profile function (3)

Full size image

The idea behind the source term regularization \(R(\phi )\) Eq. (12) is to distribute the latent heat release over a slightly enlarged range, involving more than just a single grid point. The different heat release ranges of different source term variants are compared in Fig. 3. The regularization requires a profile resolution dependent calibration procedure. For a given profile resolution, the calibration parameter \(C_{R}\) has to take a specific value to ensure the conservation of the total energy in the system. Using some arbitrary starting value for \(C_{R}\), we perform long-term simulations of solidification until quasi two phase equilibrium in a small, thermally isolated, one-dimensional system with an initially homogeneous undercooling temperature of \(U_{0}\!=\!-0.7\). Then, based on the deviation of the measured solid-phase fraction from the expected outcome of 0.7, we successively optimize the \(C_{R}\) value.

2.3 Model calibration

The interface energy calibration \(C_{\Gamma }\) is calculated via \(C_{\Gamma }\!=\!\sum _{{\mathbf {p}}_{[100]}}\!\mathbf {e}_{[100]}\!\cdot \!\mathbf {n}f(\phi _{{\mathbf {p}}}(\mathbf {n}))_{{\mu }=0}/\Gamma\), where \(\mathbf {e}_{[100]}\) denotes a unit vector pointing in the [100]-direction of the computational grid, \(\sum _{{\mathbf {p}}_{[100]}}\) denotes the sum in the [100]-direction, \(\mathbf {n}\) is again the direction normal to the interface, and the phase-field values \(\phi _{{\mathbf {p}}}(\mathbf {n})\) are given by the ideal profile (3) with interface orientation \(\mathbf {n}\). For the determination of \(C_{\Gamma }\), we chose the [100]-direction as interface orientation. The determination of the energy calibration factor is independent from the choice of the ponderation coefficients. Figure 4 shows the profile resolution dependence of the different calibration factors. The continuum limit for the calibration factor, \(C_{\Gamma }^{\infty }\!=\!2/3\), is indicated by the solid black line in Fig. 4. For sharp diffuse interfaces with a profile resolution below \(\tilde{\lambda }\!<\!2\), we obtain substantially smaller values for the calibration line integral as compared to the limiting value.

Fig. 4
figure 4

Plot of the different calibration parameters \(C_{\Gamma }\) (solid green), \(C_{\Gamma }^{\mathrm {CF}}\) (dashed green), \(C_{R}\) (red) and the ponderation coefficients \(\gamma _{2}\) (violet) and \(\gamma _{3}\) (blue) as a function of the dimensionless profile resolution \(\tilde{\lambda }\). \(\gamma _{1}\!=\!1\!-\!\gamma _{2}\!-\!\gamma _{3}\)

Full size image

For the determination of the ponderation coefficients an optimization procedure similar to the one proposed by Finel et al. [5] has been developed. The ponderation coefficients \(\gamma _{j}\) should be chosen such that the interface energy becomes as isotropic as possible, i.e., the discrete interface energy integral \(\Gamma (\mathbf {n})\!=\!\big <\sum _{{\mathbf {p}}_{[100]}}\!\mathbf {e}_{[100]}\!\cdot \!\mathbf {n}f(\phi _{{\mathbf {p}}}(\mathbf {n}))_{{\mu }=0}\big >_{c_{n}}\) should dependent on the interface orientation \(\mathbf {n}\) as little as possible. Since at least some of these line integrals may not be Translationally Invariant, we further average over a number of different values obtained for different positions \(c_{n}\) of the interface center, as denoted by the angle brackets with index \(c_{n}\). Given a starting set for the ponderation coefficients \(\gamma _{j}\), we calculate the following three different interface energy densities: \(\Gamma ([100])\!=\!\Gamma _{j=1}\), \(\Gamma ([110])\!=\!\Gamma _{j=2}\) and \(\Gamma ([111])\!=\!\Gamma _{j=3}\). As a measure for interface energy isotropy and as the minimization target, the square root of the sum of the deviations from the average interface energy value in square of these three energy densities is chosen. i.e., 

$$\begin{aligned} \left\{ \gamma _{j}\right\} :&\min \sqrt{{\textstyle \sum _{j}}(\overline{\Gamma }-\Gamma _{j})^{2}}, \end{aligned}$$
(13)

with \(\overline{\Gamma }\!=\!\sum _{j}\Gamma _{j}/3\). The optimal choice for the ponderation coefficients \(\left\{ \gamma _{j}\right\}\), with respect to this minimization target and under the constraint \(\sum _{j}\gamma _{j}\!=\!1\), has been calculated by a simple steepest decent algorithm. In Fig. 4, the optimal ponderation coefficients are plotted as function of the profile resolution for the TI\(_{\mathbf {n} }\)-model (solid curves) as well as for the TI\(_{\left\langle 100\right\rangle }\)-model (dashed curves). The ponderation coefficients obtained for the CF-model are nearly identical to those of the TI\(_{\left\langle 100\right\rangle }\)-model.

2.4 Construction of the different models

Here, we explain how the different models are constructed from the given finite difference equations. An overview over all the different models is given in Tab. 1. The models differ by different choices for the equilibrium potentials \(g_{k}(\phi )\) and for the interpolation function \(h(\phi )\). Further, the source term regularization factor \(R(\phi )\) can be either imposed or otherwise set to unity. All models are separately calibrated. Thus, the imposed calibration parameters, \(C_{\Gamma }\), \(\gamma _{j}\), can be different for the different models. The Continuum Field (CF) model is obtained in the limit \(\lim _{\left |\mathbf {u}_{k}\right |\rightarrow 0}\). In this limit the equilibrium potentials (8) converge to the classical quartic double-well potential. For the CF-model, we impose the equilibrium potentials \(g_{k}^{\infty }\!=\!\bar{\nu }8\phi ^{2}(1\!-\!\phi )^{2}\), where the multiplicity correction \(\bar{\nu }\!=\!1/3\) equilibrates for the overweighting by the sum in the equilibrium potentials within each neighboring shell \(j\). Further, the most frequently used interpolation function \(h_{5}\!=\!\phi ^{3}(10\!-\!15\phi \!+\!6\phi ^{2})\) is applied, which provides phase stability for infinitely large driving forces.

Table 1 Overview over the different models constructed from the sharp phase-field formulation
Full size table

Translational Invariance (TI) is obtained when the new equilibrium potentials Eqs. (8) are imposed in conjunction with the natural interpolation function \(h_{3}\). When all the grid coupling parameters \(a_{k}\) in the equilibrium potentials are set as fixed, based on the globally fixed lattice vector \(\mathbf {u}\!=\!\left[ 100\right]\), then TI is restored for all equivalent \(\left\langle 100\right\rangle\)-directions of the computational grid. This model is denoted as TI\(_{\left\langle 100\right\rangle }+h_{3}\). A combination of the new equilibrium potentials with the other interpolation function is not useful, because the nonequilibrium phase-field profile alternation destroys the carefully restored TI again. In case of the TI\(_{\mathbf {n}}\)-models, the locally calculated and length corrected grid coupling parameters \(a_{k}\left( \mathbf {n}\right)\) (see Eq. (9) ff.) are used in the equilibrium potentials \(g_{k}(\phi )\) Eq. (8).

3 Results and discussion

3.1 Stationary interface motion

Here, we consider the simulation of planar interface motion in one dimension driven be a constant chemical potential \({\mu }\). After some transient period of time a stationary state of motion is reached. In this case, the interface velocity is exactly know from energy conservation principles, and is given as

$$\begin{aligned} \upsilon_{\mathrm {th}}&=\!-M{\mu }/\Gamma . \end{aligned}$$
(14)

If further the natural interpolation function \(h_{3}\!=\!\phi ^{2}(3\!-\!2\phi )\) is imposed, then the phase-field profile function (3), with \(c_{n}\!=\!\upsilon_{\mathrm {th}}t\), turns out to be an analytic solution of the nonlinear, nonequilibrium phase-field Eq. (2). The stationary interface velocity as well as the interface profile, as received from the different simulations, are compared to these analytic predictions.

Fig. 5
figure 5

Evaluation of the parameter window of reasonable model operation based on error plots of the stationary interface velocity (top row) and the fitted interface width (middle row) as a function of the dimensionless driving force \({\tilde{\mu }}={\mu }\Delta {x}/\Gamma\), for different profile resolutions: \(\tilde{\lambda }=\lambda /\Delta {x}=4.0,\;3.0,\;2.5,\;0.5\). Two models are compared: (i) Continuum Field (CF) model with \(h_{5}\) (blue) and (ii) the sharp phase-field model with Translational Invariance (TI\(+h_{3}\)) (green). Solid lines denote the mean relative errors and the oscillations are indicated as transparently colored areas. The time resolution is \(M{\mu }\Delta {t}/(\Gamma \Delta {x})=1.6\cdot 10^{-7}\)

Full size image

In Fig. 5, we compare mean errors in the interface velocities and widths (solid lines) as well as their relative oscillation amplitudes (colored areas) for different models. The colored areas start from the relative value of the oscillation amplitude and end at the mean value. When the colored area is found above the mean value, we have the “healthy” situation that the measured value oscillates around the theoretic expectation. In contrast, colored areas below the mean value denote the “unhealthy” case, when the theoretic expectation is located outside the oscillation interval. While the conventional Continuum Field (CF) model is subjected to pinning, the sharp phase-field model allows for arbitrarily small driving forces.

The condition of phase stability demands the driving force to be small enough to guarantee meta-stability of the high energy phase: The two local minima of the potential energy density at \(\phi =0,1\) have to be separated by a maximum. The TI\(+h_{3}\)-model provides a profile resolution dependent stability limit, which can be surprisingly high. For instance, imposing the profile resolution \(\tilde{\lambda }=0.4\), then the limiting driving force is \(\tilde{\left |{\mu }\right |}_{\tilde{\lambda }=0.4}\lesssim 7200\)! The theoretic stability limits for the different profile resolutions \(\tilde{\lambda }=\lambda /\Delta {x}=4.0,\;3.0,\;2.5,\;0.5\) have been indicated by the vertical dashed green lines in Fig. 5. These theoretical limits nicely reflect the behavior of the sharp phase-field model.

Switching the interpolation function changes the phase stability limits. The most common choice for the interpolation function is \(h_{\mathrm {5}}=\phi ^{3}(10-15\phi +6\phi ^{2})\). The CF\(+h_{5}\)-model provides phase stability for infinitely large driving forces! However, using interpolation functions other than the natural one leads to altered nonequilibrium phase-field profiles. The resulting deviation of the fitted profile width \(\lambda _{\mathrm {fit}}\) from the theoretic expectation \(\lambda\) is plotted in the middle row of Fig. 5. The profile alternation increases with increasing driving force. Increasingly stronger alternations lead to increasingly stronger grid friction effects. Consider the resolution numbers \(\tilde{\lambda }=3.0\) and \(\tilde{\mu }=100\), then the diffuse interface is compressed down to \(22\%\) of its original width. Grid friction drops the interface velocity down to about \(5\%\) of the theoretic expectation. Thus, for large dimensionless driving forces, the CF-model \(h_{5}\) is effectively limited by spurious grid friction. The study reveals an unexpected limited applicability at large dimensionless driving forces also for the CF\(+h_{5}\)-model, which provides theoretic phase stability for infinite driving forces. Therefore, this serious restriction applies to a surprisingly broad class of different phase-field models. The operational limits of other types of phase-field models, such as, for instance, the models with a section-wise defined double obstacle potential, providing a sinusoidal interface profile [31], will be subject of future investigations. Also interesting, in this regard, is the behavior of the recently rediscovered class of nonlinear-preconditioned phase-field models [6,7,8,9,10,11,12]. This technique to improve the numerical capabilities of phase-field models has conceptional relations to the sharp phase-field method, as both formulations are based on the nonlinear interface profile function.

In the lower part of Fig. 5, we plot the parameter window of reasonable model operation. The range of reasonable operation is defined to end when the relative velocity error exceeds 0.1. The evaluation of the principle capability of the two different phase-field models to operate at different dimensionless spatial resolutions \(\tilde{\lambda }\) and \({\tilde{\mu }}\), as shown in Fig. 1, is based on this evaluation of the parameter window of reasonable model operation.

3.2 Quantitative stationary solidification

Fig. 6
figure 6

Stationary solidification using (i) the Continuum Field model (CF\(+h_{5}\)) for \(\tilde{\lambda }\!=\!2\) in blue, (ii) the Translationally Invariant model (TI\(+h_{3}\)) for \(\tilde{\lambda }\!=\!0.4\) in red and (iii) the TI-model with regularization (TI\(+h_{3}\!+\!R\)) in green. (a) Exemplary simulation results and a plot of the velocity as function of the interface center (\({\tilde{\mu }}_{\mathrm {int}}\!=\!100\)). The temperature \(U\) is given by colored lines and the phase-field values by black full symbols. (b) Plot of the interface velocity error as function of the dimensionless driving force \({\tilde{\mu }}_{\mathrm {int}}\!=\!{\mu }_{\mathrm {int}}\Delta {x}/\Gamma\)

Full size image

In Fig. 6a), the configuration of stationary solidification is shown. An animation of this figure is provided in the supplementary material. Far in front of the solid/liquid interface, the temperature is \(U(L)\!=\!-2.0\). When the system reaches a stationary state, the solid phase is found at the minimal undercooling temperature of \(U_{\mathrm {int}}\!=\!-1.0\). Then, the theoretically expected stationary solidification velocity is given by

$$\begin{aligned} \upsilon_{\mathrm {th}}\!&=\!-MU_{\mathrm {int}}/{d}_{0}, \end{aligned}$$
(15)

where \(M\) denotes the kinetic coefficient, and \({d}_{0}\) is the capillary length [32]. We restrict to the comparison with the sharp interface equation and omit more sophisticated thin interface corrections [33]. The ratio between the total system length and the theoretic stationary diffusion length \(l_{D}\!=\!2D/\upsilon_{\mathrm {th}}\) is chosen to be \(L/l_{D}\!=\!5\). The system is resolved by 200 grid points, i.e. \(L/\Delta {x}\!=\!200\), with a solid-phase fraction of \(12\%\). The fraction is kept constant by incremental shifting of the whole system [34].

In Fig. 6b) the relative error in the solidification velocity is plotted as function of the dimensionless driving force \({\tilde{\mu }}_{\mathrm {int}}\!=\!{\mu }_{\mathrm {int}}\Delta {x}/\Gamma\). The CF\(+h_{5}\)-model (blue color) is subjected to strong spurious grid friction for both small as well as large dimensionless driving forces. In case of \({\tilde{\mu }}_{\mathrm {int}}\!=\!100\), the observed solidification velocity is \(90\,\%\) smaller than the expectation. The TI-models are limited by phase stability only. This limit is indicated by the vertical dashed line in Fig. 6b). The TI\(+h_{3}\)-model (red curve) provides large oscillations in the interface velocity. These result from spuriously inhomogeneous heat release at the solid/liquid interface, as visible in Fig. 6a). It can be avoided by employing the newly proposed source term regularization \(R\) Eq. (12), see the green curves in Fig. 6.

3.3 Diffusion-limited solidification

For dimensionless undercooling temperatures \(U\) smaller than unity, we obtain diffusion-limited solidification. In this case, more latent heat is released at the progressing solid/liquid interface, than needed for the heating up of the material from the undercooling temperature up to the melting point. Then, an increasing heat accumulation at the solid/liquid interface must be transported away, before a further progression of the solidification is possible. The two coupled governing equations are the phase-field equation (2), with a driving force proportional to the negative of the dimensionless temperature field, \(\mu _{{\mathbf {p}}}=-U_{{\mathbf {p}}}\Gamma /{d}_{0}\), as well as the diffusion equation (11). The latter equation couples back to the phase-field via the source term, which is responsible for the latent heat release during the progressing solidification.

Fig. 7
figure 7

Time series of phase-field simulations of diffusion-limited solidification using four different models: The TI\(_{\mathbf {n}}\!+\!h_{3}\) model (i) with and (ii) without regularization \(R\), (iii) the TI\(_{\left\langle 100\right\rangle }\!+\!h_{3}\) model each with \(\tilde{\lambda }\!=\!0.5\), and (iv) the CF\(+h_{5}\)-model with \(\tilde{\lambda }\!=\!2.0\). The temperature \(U\) is visualized by the coloring and the phase-field is represented by the \(\phi \!=\!1/2\)-contour. Further parameters: \({d}_{0}/\Delta {x}\!=\!2\cdot 10^{-3}\), \(D/M\!=\!5\!\cdot \!10^{-3}\), domain size \(120\!\times \!60\!\times \!60\)

Full size image

Four comparable simulations are performed using four different phase-field models, as shown in Fig. 7. An animation showing the full courses of all four simulations is provided in the supplementary material. The simulations are started from the same initial state at \(U=-0.3\). All boundaries are thermally insulating, except for the boundary at the \(\left[ 100\right]\)-end of the simulation domain on the right hand side, which is held at \(U_{\mathrm {max}}=-0.3\). The initial quasi planar solid/liquid interface has small bumps at regular intervals of \(10\Delta {x}\). In the beginning, the interface develops the Mullins–Sekerka instability [13], since the dimensionless capillary length is chosen to be sufficiently small \(\tilde{{d}_{0}}\!=\!0.002\) (\(\tilde{\mu }_{\mathrm {max}}\!=\!U_{\mathrm {max}}/\tilde{{d}_{0}}\!=\!150\)). As soon as the most advanced point of the solid/liquid interface exceeds the fraction of 0.7 of the simulation domain along the \(\left[ 100\right]\)-direction, the whole system is shifted back by one grid point [34].

In later stages, the disordered seaweed or dense-branching morphology develops [14, 35, 36], if the residual grid anisotropy is sufficiently small. For super efficient one-grid-point profile resolutions of \(\tilde{\lambda }\!=\!0.5\), this requires the local restoration of TI in the local interface normal direction as well as the inclusion of the source term regularization Eq. (12), as shown in first row in Fig. 7. Without regularization the simulation shows a spurious dendritic selection in the \(\left\langle 110\right\rangle\)-directions of the computational grid, which originates from the inhomogeneous temperature release via the source term in the diffusion equation. The simulations using the TI\(_{\left\langle 100\right\rangle }\)- and CF- model show spurious dendritic selection in the \(\left\langle 100\right\rangle\)-directions. For the TI\(_{\left\langle 100\right\rangle }\) model, the selection originates from anisotropic interface kinetics [16, 17], which result from residual grid friction for interface orientations that differ from the \(\left\langle 100\right\rangle\)-directions. In case of the CF-model, it results from strong grid friction due to the alternation of the nonequilibrium phase-field profile at large dimensionless driving forces.

4 Conclusion

A new sharp phase-field model is proposed: Instead of using global grid dependent equilibrium potentials (8), that restore the Translational Invariance (TI) for a finite amount of fixed interface orientations, the newly proposed model restores TI locally for the local interface normal direction \(\mathbf {n}\). Furthermore, we propose a source term regularization Eq. (12) to effectively suppress spurious inhomogeneous temperature releases by diffuse interfaces as sharp as \(\tilde{\lambda }\!=\!0.4\), see Fig. 6. Compared to the conventional phase-field model with the resolution limits \(\tilde{\lambda }\!>\!2.0\) and \(\left|\tilde{\mu }\right|\!<\!1.0\), the sharp phase-field model allows for super efficient quantitative simulations of stationary solidification with phase-field profile resolutions of \(\tilde{\lambda }\!=\!0.4\) and dimensionless driving forces up to \(\tilde{\mu }\!=\!7200\)! The new sharp phase-field model with source term regularization (TI\(_{\mathbf {n}}\!+\!h_{3}\!+\!R\)) provides extremely high degrees of isotropy. Considering diffusion-limited solidification, it provides the expected isotropic seaweed or dense-branching morphology with an extraordinary efficient spatial resolution: \(\tilde{\lambda }\!=\!0.5\) and \(\tilde{\mu }_{\mathrm {max}}\! =\!U_{\mathrm {max}}/\tilde{{d}_{0}}\!=\!150\)! The absence of spurious dendritic selection at such an efficient spatial resolution, provides the basis for quantitative phase-field modeling of microscopic solidification of the next generation.