Accurate computation of partial volumes in 3D peridynamics

Abstract

The peridynamic theory is a nonlocal formulation of continuum mechanics based on integro-differential equations, devised to deal with fracture in solid bodies. In particular, the forces acting on each material point are evaluated as the integral of the nonlocal interactions with all the neighboring points within a spherical region, called “neighborhood”. Peridynamic bodies are commonly discretized by means of a meshfree method into a uniform grid of cubic cells. The numerical integration of the nonlocal interactions over the neighborhood strongly affects the accuracy and the convergence behavior of the results. However, near the boundary of the neighborhood, some cells are only partially within the sphere. Therefore, the quadrature weights related to those cells are computed as the fraction of cell volume which actually lies inside the neighborhood. This leads to the complex computation of the volume of several cube–sphere intersections for different positions of the cells. We developed an innovative algorithm able to accurately compute the quadrature weights in 3D peridynamics for any value of the grid spacing (when considering fixed the radius of the neighborhood). Several examples have been presented to show the capabilities of the proposed algorithm. With respect to the most common algorithm to date, the new algorithm provides an evident improvement in the accuracy of the results and a smoother convergence behavior as the grid spacing decreases.

1 Introduction

The peridynamic theory provides a nonlocal reformulation of classical continuum mechanics: the internal forces are evaluated with integral equations, which are valid regardless of the presence of discontinuities in the displacement field. Hence, peridynamics can naturally model crack initiation, propagation and branching in solids. The first formulation of the peridynamic theory was the bond-based version [1], in which the Poisson’s ratio is restricted to a fixed value. Subsequently, state-based peridynamics was developed [2], introducing the possibility of varying the Poisson’s ratio. In the literature, there are many examples of applications [3, 4], ranging from complex crack patterns, such as spontaneous branching [5], to multi-physics problems involving fracture [6, 7].

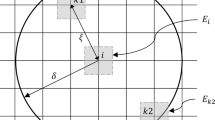
Peridynamic points interact with each other up to a finite distance $\delta$, called “horizon”. The “neighborhood” of a point is the set of all the points interacting with that point. Therefore, the neighborhood has a circular shape in 2D problems and a spherical shape in 3D problems. The peridynamic equation of motion is based on the spatial integration over the neighborhood of the internal forces, which are generated by the interactions between neighboring points. In practice, the integration of the peridynamic equation of motion is carried out by means of numerical tools. The body can be discretized by a uniform or non-uniform grid (see for instance [8,9,10]). Various methods have been utilized to integrate numerically peridynamic equations: meshfree method with composite midpoint quadrature [11,12,13,14], Gauss-Hermite quadrature [12], finite element method [12, 15, 16], collocation method [17, 18] and an adaptive integration method with error control [19]. Thanks to its simplicity of implementation and relatively low computational cost compared to other approaches, the meshfree method with a uniform grid is the most commonly used for peridynamic simulations. In this method, the body is discretized in volume cells with a square shape in 2D problems and cubic in 3D, and the nodes lie at the center of the corresponding cells. The spatial integration over the neighborhood is transformed into a summation of integrals over cells and the midpoint quadrature rule is then applied in each cell, in which the nodes are employed as quadrature points.

However, near the boundary of the neighborhood, some cells are only partially within the neighborhood itself. Therefore, the quadrature weights related to those cells are computed as the fraction of cell volume which actually lies inside the neighborhood. The intersection area or volume of those cells with the neighborhood is also referred to as “partial area” in 2D and “partial volume” in 3D. The accuracy and convergence of the peridynamic results depend on the algorithm to compute the quadrature weights, i.e., the partial areas or volumes [13, 14, 20].

The first algorithm proposed in [11] considers the nodes within the neighborhood with their entire cell (even if a part of the volume is partially outside the neighborhood) and neglects the nodes outside the neighborhood (even if their cell is partially inside the neighborhood). This approach, under grid refinement, leads to an oscillatory convergence behavior in which the fluctuations seem rather random [13]. Many other algorithms to approximate the partial volumes have been proposed since then. An approximation based on the distance between neighboring nodes is proposed in [21], which improves the computation of the partial volumes of nodes within the neighborhood. A similar approximation is used in [22, 23] to include the previously neglected partial volumes of nodes outside the neighborhood but with a part of the cell inside it. These algorithms reduce, but never eliminate, the seemingly random fluctuations of the convergence behavior. Subsequently, the algorithm to compute analytically the partial areas has been developed in [13]: the types of intersection between the neighborhood and the cells are rigorously categorized and then subdivided into domains of basic geometry (triangles, rectangles and circular segments), for which the analytical computation of the area is straightforward. Using this algorithm, the convergence behavior is smoothly oscillatory and the simulations yield results affected by a smaller error, on average, compared to the previously mentioned algorithms. In [13], it is also suggested to use the centroids of the partial areas as quadrature points, but this significantly increases the complexity of the computational model. The analytical computation of the partial volumes in 3D problems is much more complex and no algorithm is currently available for such purpose. The partial volumes can be computed numerically by two proposed algorithms, one based on the trapezoidal rule [19] and one based on a process of recursive subdivisions and sampling [14]. However, to reach the desired accuracy the computational cost may be very high. Other algorithms, specialized for non-uniform grids, are presented in [9, 22, 24, 25].

The aim of this paper is to simplify the implementation of the algorithm to compute analytically the partial areas presented in [13] by skipping the step of subdivision of the intersection area in basic geometries, and to develop an algorithm for the analytical computation of the partial volumes. In order to achieve this, we solve directly the integrals which describe all the possible intersection areas or volumes. Actually, some integrals involved in the computation of the partial volumes are not explicitly solvable. Hence, we perform a Taylor series expansion of those functions and integrate the polynomials. The computation of the partial volumes converges to the analytical solution if the sum of infinite terms is not truncated. This, clearly, is not possible in a numerical model, but we will show that the algorithm is able to reach values of the error very close to machine precision with little computational effort. The numerical results obtained with the new algorithm show an evident improvement in the accuracy and in the convergence behavior when compared to the results obtained by the algorithm based on the approximation proposed by [22], which is arguably the most commonly used in engineering applications. We compared the numerical results by using the ordinary state-based version of the peridynamic theory, but the algorithm can be used with the bond-based version as well.

The paper is divided as follows. Section 2 reviews the basics of the state-based peridynamic theory and its discretized formulation. Section 3 presents the innovative algorithms for the computation of the partial areas and partial volumes. Section 4 contains several numerical examples that show the improvements provided by the proposed algorithm for the computation of the partial volumes with respect to the most commonly used algorithm. Section 5 draws the conclusions of the work.

2 Peridynamic theory

The peridynamic theory is a continuum theory based on nonlocal interactions between material points [1]. The derived numerical formulation is a very useful tool for simulating crack propagation in solid bodies. In the following, we present the fundamentals of the ordinary state-based peridynamics and the discretized formulae which could be implemented in a computational code.

2.1 Continuum model

The nonlocal interaction between two points, ${\mathbf {x}}$ and ${\mathbf {x}}'$, in a peridynamic body $\mathcal {B}$ is described by a quantity named “bond”:

$$\begin{aligned} {\varvec{\xi }} := {\mathbf {x}}' - {\mathbf {x}} \, , \end{aligned}$$

(1)

where the point ${\mathbf {x}}'$ is contained in the neighborhood $\mathcal {H}_{{\mathbf {x}}} := \big \{ \, {\mathbf {x}}' \in \mathcal {B}: \Vert {\varvec{\xi }}\Vert \le \delta \, \big \}$. The relative displacement vector ${\varvec{\eta }}$ is defined as

$$\begin{aligned} {\varvec{\eta }} := {\mathbf {u}}({\mathbf {x}}',t) - {\mathbf {u}}({\mathbf {x}},t) \, , \end{aligned}$$

(2)

where ${\mathbf {u}}$ is the displacement field. Note that ${\varvec{\xi }} + {\varvec{\eta }}$ is the relative position of points ${\mathbf {x}}$ and ${\mathbf {x}}'$ after the deformation occurred.

The state-based peridynamic equation of motion of a point ${\mathbf {x}}$ within the body $\mathcal {B}$ is given by [2]

$$\begin{aligned} \rho ({\mathbf {x}}) \, \ddot{{\mathbf {u}}}({\mathbf {x}},t) = \int _{\mathcal {H}_{{\mathbf {x}}}} \big ( \, \underline{{\mathbf {T}}} [{\mathbf {x}},t] \langle {\varvec{\xi }} \rangle - \underline{{\mathbf {T}}} [{\mathbf {x}}',t] \langle -{\varvec{\xi }} \rangle \, \big ) {\mathrm {d}} {V}_{{\mathbf {x}}'} + {\mathbf {b}}({\mathbf {x}},t) \, , \end{aligned}$$

(3)

where $\rho$ is the material density, $\ddot{{\mathbf {u}}}$ is the acceleration field, $\underline{{\mathbf {T}}}$ is the force state, ${\mathrm {d}} {V}_{{\mathbf {x}}'}$ is the differential volume of a point ${\mathbf {x}}'$ within the neighborhood $\mathcal {H}_{{\mathbf {x}}}$ and ${\mathbf {b}}$ is the external force density field. The notation $\underline{{\mathbf {T}}} [{\mathbf {x}},t] \langle {\varvec{\xi }} \rangle$ means that the state $\underline{{\mathbf {T}}}$ depends on the position of the point ${\mathbf {x}}$ and on the time t, and operates on the bond ${\varvec{\xi }}$. In an ordinary state-based peridynamic model, the force state is aligned with the corresponding bond for any deformation, as depicted in Fig. 1. For the purposes of the paper, it suffices to limit the study to quasi-static problems [26,27,28]. Hence, the peridynamic equilibrium equation is derived from Eq. (3) by dropping the dependence on time:

$$\begin{aligned} - \int _{\mathcal {H}_{{\mathbf {x}}}} \big ( \, \underline{{\mathbf {T}}} [{\mathbf {x}}] \langle {\varvec{\xi }} \rangle - \underline{{\mathbf {T}}} [{\mathbf {x}}'] \langle -{\varvec{\xi }} \rangle \, \big ) {\mathrm {d}} {V}_{{\mathbf {x}}'} = {\mathbf {b}} ({\mathbf {x}}) \, . \end{aligned}$$

(4)

Fig. 1

Body $\mathcal {B}$ modelled with ordinary state-based peridynamics: the force states $\underline{{\mathbf {T}}} [{\mathbf {x}}] \langle {\varvec{\xi }} \rangle$ and $\underline{{\mathbf {T}}} [{\mathbf {x}}'] \langle -{\varvec{\xi }} \rangle$ arise in the bond ${\varvec{\xi }}$ due to the deformation of the body

The reference position scalar state $\underline{x}$, representing the bond length, the extension scalar state $\underline{e}$, describing the elongation (or contraction) of the bond in the deformed body, and the deformed direction vector state $\underline{{\mathbf {M}}}$, the unit vector in the direction of $\underline{{\mathbf {T}}}$, are, respectively, defined as

$$\begin{aligned} \underline{x} \langle {\varvec{\xi }} \rangle&:= \Vert {\varvec{\xi }} \Vert \, , \end{aligned}$$

(5)

$$\begin{aligned} \underline{e} \langle {\varvec{\xi }} \rangle&:= \Vert {\varvec{\xi }} + {\varvec{\eta }} \Vert - \Vert {\varvec{\xi }} \Vert \, , \end{aligned}$$

(6)

$$\begin{aligned} \underline{{\mathbf {M}}} \langle {\varvec{\xi }} \rangle&:= \frac{{\varvec{\xi }} + {\varvec{\eta }}}{\Vert {\varvec{\xi }} + {\varvec{\eta }} \Vert } \, . \end{aligned}$$

(7)

The weighted volume m and the dilatation $\theta$ of a point ${\mathbf {x}}$ are defined as

$$\begin{aligned} m_{{\mathbf {x}}}&:= \int _{\mathcal {H}_{{\mathbf {x}}}} \underline{\omega } \langle {\varvec{\xi }} \rangle \left( \underline{x} \langle {\varvec{\xi }} \rangle \right) ^2 {\mathrm {d}} {V}_{{\mathbf {x}}'} \, , \end{aligned}$$

(8)

$$\begin{aligned} \theta _{{\mathbf {x}}}&:= \frac{3}{m_{{\mathbf {x}}}} \int _{\mathcal {H}_{{\mathbf {x}}}} \underline{\omega } \langle {\varvec{\xi }} \rangle \, \underline{x} \langle {\varvec{\xi }} \rangle \, \underline{e} \langle {\varvec{\xi }} \rangle {\mathrm {d}} {V}_{{\mathbf {x}}'} \, , \end{aligned}$$

(9)

where $\underline{\omega }$ is a prescribed spherical influence function [29]. We adopt the Gaussian influence function

$$\begin{aligned} \underline{\omega } \langle {\varvec{\xi }} \rangle := \exp \left( -\frac{\Vert {\varvec{\xi }} \Vert ^2}{\delta ^2} \right) \, . \end{aligned}$$

(10)

Adopting the linear peridynamic solid model [2], the force state is computed as

$$\begin{aligned} \underline{{\mathbf {T}}} [{\mathbf {x}}] \langle {\varvec{\xi }} \rangle = \left[ \left( 3K - 5 \mu \right) \, \frac{\underline{\omega } \langle {\varvec{\xi }} \rangle \, \underline{x} \langle {\varvec{\xi }} \rangle }{m_{{\mathbf {x}}}} \, \theta _{{\mathbf {x}}} + 15 \mu \, \frac{\underline{\omega } \langle {\varvec{\xi }} \rangle \, \underline{e} \langle {\varvec{\xi }} \rangle }{m_{{\mathbf {x}}}} \right] \underline{{\mathbf {M}}} \langle {\varvec{\xi }} \rangle \, , \end{aligned}$$

(11)

where K is the bulk modulus and $\mu$ is the shear modulus. Since $\underline{{\mathbf {M}}} \langle {\varvec{\xi }} \rangle = -\underline{{\mathbf {M}}} \langle -{\varvec{\xi }} \rangle$, the ordinary state-based peridynamic equilibrium equation becomes [2, 30, 31]

$$\begin{aligned} \begin{aligned}&- \int _{\mathcal {H}_{{\mathbf {x}}}} \left[ \left( 3K - 5 \mu \right) \left( \frac{\theta _{{\mathbf {x}}}}{m_{{\mathbf {x}}}} + \frac{\theta _{{\mathbf {x}}'}}{m_{{\mathbf {x}}'}} \right) \underline{\omega } \langle {\varvec{\xi }} \rangle \, \underline{x} \langle {\varvec{\xi }} \rangle \right. \\&\quad \left. + 15 \mu \left( \frac{1}{m_{{\mathbf {x}}}} + \frac{1}{m_{{\mathbf {x}}'}} \right) \underline{\omega } \langle {\varvec{\xi }} \rangle \, \underline{e} \langle {\varvec{\xi }} \rangle \right] \underline{{\mathbf {M}}} \langle {\varvec{\xi }} \rangle {\mathrm {d}} {V}_{{\mathbf {x}}'} = {\mathbf {b}} ({\mathbf {x}}) \, . \end{aligned} \end{aligned}$$

(12)

Equation (12) relates the external forces to the displacement field, which might be a discontinuous function with respect to the spatial coordinates.

2.2 Discretized model

We adopt a meshfree method with a uniform grid spacing h to discretize the body domain (see, for instance, the discretization of a neighborhood in Fig. 2). Therefore, the cells surrounding each node are squares in 2D and cubes in 3D, respectively, with an area $A=h^2$ and a volume $V=h^3$.

Fig. 2

In the continuum model of the neighborhood $\mathcal {H}_{{\mathbf {x}}}$ of a given point ${\mathbf {x}}$, some points (as point ${\mathbf {x}}'$) lie inside the neighborhood and some other (as point ${\mathbf {x}}''$) lie outside. Similarly, in the discretized model of the neighborhood $\mathcal {H}_{i}$ of a given node i, there are some nodes (solid circles) whose cell lies completely or partially inside the neighborhood and other nodes (empty circles) whose cell lies completely outside the neighborhood

Consider a node i as the node at which the peridynamic equilibrium equation should be computed and a node j with a portion of its cell inside the neighborhood $\mathcal {H}_i$ of node i. The bond connecting node i to node j is described by

$$\begin{aligned} {\varvec{\xi }}_{ij} = {\mathbf {x}}_j - {\mathbf {x}}_i \, . \end{aligned}$$

(13)

Analogously, the relative displacement vector after the deformation of the body is defined as

$$\begin{aligned} {\varvec{\eta }}_{ij} = {\mathbf {u}}_j - {\mathbf {u}}_i \, , \end{aligned}$$

(14)

where ${\mathbf {u}}_i$ and ${\mathbf {u}}_j$ are the displacement vectors of nodes i and j, respectively.

Hence, the reference position scalar state and the influence function of bond ij can be computed as follows:

$$\begin{aligned} \underline{x}_{ij}= & {} \Vert {\varvec{\xi }}_{ij} \Vert \, , \end{aligned}$$

(15)

$$\begin{aligned} \underline{\omega }_{ij}= & {} \exp \left( -\frac{\Vert {\varvec{\xi }}_{ij} \Vert ^2}{\delta ^2} \right) \, . \end{aligned}$$

(16)

Under the assumption of small displacements, the extension scalar state of bond ij is given as

$$\begin{aligned} \begin{aligned} \underline{e}_{ij}&= \Vert {\varvec{\xi }}_{ij} + {\varvec{\eta }}_{ij} \Vert - \Vert {\varvec{\xi }}_{ij} \Vert \\&{\mathop {\approx }\limits ^{ \Vert {\varvec{\eta }}_{ij} \Vert \ll \Vert {\varvec{\xi }}_{ij} \Vert }} {\varvec{\eta }}_{ij} \cdot \frac{{\varvec{\xi }}_{ij}}{\Vert {\varvec{\xi }}_{ij} \Vert } \, . \end{aligned} \end{aligned}$$

(17)

The non-local properties of node i, i.e., the weighted volume $m_i$ and the dilatation $\theta _i$, are determined numerically by transforming the integrals in Eqs. (8) and (9) into a summation of integrals over cells and applying a midpoint quadrature rule in each cell:

$$\begin{aligned} m_i= & {} \sum _{j \in \mathcal {H}_i} \underline{\omega }_{ij} \, \underline{x}_{ij}^2 \, \beta _{ij} \, V \, , \end{aligned}$$

(18)

$$\begin{aligned} \theta _i= & {} \frac{c_{\theta }}{m_i} \sum _{j \in \mathcal {H}_i} \underline{\omega }_{ij} \, \underline{x}_{ij} \, \underline{e}_{ij} \, \beta _{ij} \, V \, , \end{aligned}$$

(19)

where $\beta _{ij} V$ represents the quadrature weight of the contribution of node j in the integral over the neighborhood of node i. The accurate computation of coefficients $\beta _{ij}$ is the main result of the paper, which is presented in Sect. 3. In 2D problems under plane stress conditions, the volume of the cell is given as $V=A \, t$, where t is the constant thickness of the plate.

Under the assumption of small displacements ($\underline{{\mathbf {M}}} \langle {\varvec{\xi }}_{ij} \rangle \approx {\varvec{\xi }}_{ij} / \Vert {\varvec{\xi }}_{ij} \Vert$), the peridynamic equilibrium equation in the discretized form is computed by using the quadrature scheme previously described as

$$\begin{aligned}&- \sum _{j \in \mathcal {H}_i} \left[ \left( 3K - 5 \mu \right) \left( \frac{\theta _i}{m_i} + \frac{\theta _j}{m_j} \right) \underline{\omega }_{ij} \, \underline{x}_{ij} \right. \nonumber \\&\quad \left. + 15 \mu \left( \frac{1}{m_i} + \frac{1}{m_j} \right) \underline{\omega }_{ij} \, \underline{e}_{ij} \right] \frac{{\varvec{\xi }}_{ij}}{\Vert {\varvec{\xi }}_{ij} \Vert } \, \beta _{ij} \, V = {\mathbf {b}}_i \, , \end{aligned}$$

(20)

where $m_j$ and $\theta _j$ are, respectively, the weighted volume and the dilatation of node j computed with Eqs. (18) and (19), and ${\mathbf {b}}_i$ is the external force density vector applied to node i.

3 Algorithms for the computation of the quadrature weights

The quadrature coefficient $\beta _{ij}$ is the dimensionless factor defined as

$$\begin{aligned} \beta _{ij} := {\left\{ \begin{array}{ll} \frac{\, \widetilde{V} \,}{V} &{} \text {in 3D,} \\ \frac{\, \widetilde{A} \,}{A} &{} \text {in 2D,} \\ \end{array}\right. } \end{aligned}$$

(21)

where $\widetilde{V}$ and $\widetilde{A}$ are, respectively, the partial volume and partial area of the cell, which should be computed from the intersection between the neighborhood $\mathcal {H}_i$ and the cell itself. In particular, $\beta _{ij}=1$ if the cell is completely inside $\mathcal {H}_i$, $\beta _{ij}=0$ if the cell is completely outside $\mathcal {H}_i$ and $0< \beta _{ij} < 1$ if the cell is partially inside $\mathcal {H}_i$. The set of nodes which constitutes $\mathcal {H}_i := \big \{ \, j \in \mathcal {B}: \beta _{ij} > 0 \, \big \}$ depends on the algorithm used to compute $\beta _{ij}$.

We present one of the algorithms based on the approximation of the partial volume [22], used as a reference to compare our results. To compute analitycally $\beta _{ij}$ in a convenient framework, we define a new reference system and exploit the cell–neighborhood symmetries. Then, we improve the algorithm for the analytical computation of partial areas by employing a simpler scheme and we use the same scheme to compute quasi-analytically the partial volumes. We utilize the expression “quasi-analytical” because the algorithm includes the truncation of the Taylor series expansions, but it is able to attain accurate results with a relatively small truncation order.

3.1 Approximated computation of partial areas or volumes

In the literature there are many algorithms that compute the partial areas or volumes as an approximation based on the distance between neighboring nodes [13]. The algorithm presented in [22] (see Algorithm 1) is arguably the most commonly used to date. This algorithm is based on the analytical computation of partial lengths in 1D problems, as shown in Fig. 3. If the distance between node i and the farthest side of the cell of node j is smaller than the horizon size, namely $\Vert {\varvec{\xi }}_{ij} \Vert +\frac{h}{2} < \delta$ where h is the grid spacing, then $\beta _{ij}=1$ (see Fig. 3a). If the distance between node i and the closest side of the cell of node j is greater than the horizon size, namely $\Vert {\varvec{\xi }}_{ij} \Vert -\frac{h}{2} > \delta$, then $\beta _{ij}=0$ (see Fig. 3c). Otherwise, $\beta _{ij}$ is computed as the difference between the horizon size and the distance of the closest side of the cell of node j from node i, divided by the grid spacing h (see Fig. 3b).

Fig. 3

Possible cases of intersections between neighborhood and cell considered by Algorithm 1: the gray area represents the quadrature weight of the corresponding cell

Algorithm 1 is applied without modifications to 2D and 3D problems. If the direction of ${\varvec{\xi }}_{ij}$ lies along one of the axis, as for instance in Fig. 3b, the approximation is quite accurate. However, Fig. 4 shows other examples in which the computation of the quadrature weights with Algorithm 1 can be rather inaccurate. As a result, even if this algorithm is very simple, it leads to convergence issues [13, 14]: for small variations of the grid spacing (considering fixed the horizon size) there are considerable variations of the computed mechanical properties, as the numerical results of Sects. 4.2 and 4.3 show.

Fig. 4

Some examples in which the quadrature weights computed with Algorithm 1 are rather different from their analytical values: the gray area represents the quadrature weight of the corresponding cell computed with Algorithm 1

3.2 Change of reference system

For simplicity sake, the concepts are hereinafter explained in the 2D case, but the generalization to a 3D case is straightforward. Since the focus is on the neighborhood of a node i, we adopt a new system of reference $(\overline{x},\overline{y})$ with the origin at $(x_i,y_i)$ and the distances scaled by a factor 1/h, as shown in Fig. 5. Note that, since the quadrature coefficient $\beta _{ij}$ is normalized with the area or volume of the cell (see Eq. 21), its value is not affected by the scaling of the distances. The coordinates of a node j in the new reference system are given as

$$\begin{aligned} \left( \overline{x}_j, \overline{y}_j \right) = \left( \frac{x_j-x_i}{h} , \frac{y_j-y_i}{h} \right) . \end{aligned}$$

(22)

Since the grid is uniform, $\overline{x}_j$ and $\overline{y}_j$ are integer numbers.

Fig. 5

a $\mathcal {H}_i$ is the neighborhood of node i in a general reference system and b $\overline{\mathcal {H}}_i$ in the scaled reference system: the origin of the new reference system is centered at node i and the distances are scaled by a uniform factor 1/h in all directions, where h is the grid spacing. The coordinates of a node j in the new reference system are given as $\overline{x}_j = (x_j-x_i)/h$ and $\overline{y}_j = (y_j-y_i)/h$, and the horizon size of the neighborhood becomes $\overline{m} = \delta /h$

As shown in Fig. 5b, the grid spacing in the new reference system is equal to 1, so that the area or the volume of each cell are $A=1$ and $V=1$, respectively. Therefore, $\beta _{ij}$ is simply computed as the area or volume of the intersection between the neighborhood of node i and the cell of node j: $\beta _{ij} = \widetilde{A}/A = \widetilde{A}$ or $\beta _{ij} = \widetilde{V}/V = \widetilde{V}$. Furthermore, the only parameter which can change the values of the quadrature coefficients is the $\overline{m}$-ratio, given as

$$\begin{aligned} \overline{m} := \frac{\delta }{h} \, . \end{aligned}$$

(23)

If $\overline{m}$ is unique for the whole peridynamic body (as it is often the case), then the values of $\beta _{ij}$ can be computed only once and used for the neighborhoods of all the nodes.

3.3 Cell–neighborhood symmetries

The symmetries of the neighborhood with respect to the nodal grid, named “cell–neighborhood symmetries”, can be exploited to reduce the number of cases to be considered. In [13] the symmetries with respect to the axes were used to compute the quadrature weights only in the first quadrant. On the other hand, we use four lines of symmetry for a 2D neighborhood (both the axes and the bisectors of the quadrants), as shown in Fig. 6. Therefore, the computation of the partial area can be carried out only for the nodes satisfying the following conditions: $M \ge \overline{y}_j \ge \overline{x}_j \ge 0$, where $M:=\lfloor \overline{m}+0.5 \rfloor$ ($\lfloor \cdot \rfloor$ stands for the floor function and finds the greatest integer smaller than or equal to the input), and $\overline{y}_j \ne 0$. The latter condition is given by the fact that the central node does not interact with itself. On the other hand, the value M is used to provide an upper limit to the search for possible nodes inside the neighborhood. These nodes are enclosed by a red line in Fig. 6. Thanks to the cell–neighborhood symmetries, $\beta _{ij}$ of the other nodes have the same values. For instance, the computation of the partial area for the node $(\overline{x}_j=2, \overline{y}_j=3)$ is the same for nodes (3, 2), $(3,-2)$, $(2,-3)$, $(-2,-3)$, $(-3,-2)$, $(-3,2)$ and $(-2,3)$.

Fig. 6

Dashed lines represent the lines of the cell–neighborhood symmetries and the nodes enclosed by the red line are the only ones that are considered by the proposed algorithm

Analogously, we exploit six planes of symmetry for a neighborhood in a 3D model (planes containing two axes or one axis and one bisector of the octants). Therefore, in this case, we consider only nodes that satisfy the following conditions: $M \ge \overline{z}_j \ge \overline{y}_j \ge \overline{x}_j \ge 0$ and $\overline{z}_j \ne 0$. The nodes considered in the proposed algorithm for the computation of the partial volumes for $\overline{m} = 3.2$ are represented in Fig. 7.

Fig. 7

Thanks to the cell–neighborhood symmetries, the nodes enclosed by the surfaces represented by red lines are the only ones that are considered by the proposed algorithm. The six planes of symmetry are not represented for image clarity

Cell–neighborhood symmetries come into play also during the computation of some partial areas and volumes, as shown in Fig. 8. In 2D problems, the intersections between the neighborhood and cells of nodes with $\overline{x}_j = 0$ (see Fig. 8a) are symmetric with respect to the $\overline{y}$-axis. Similarly, in 3D problems, the intersections between the neighborhood and cells of nodes with $\overline{x}_j = 0$ and $\overline{y}_j \ne 0$ or $\overline{x}_j = \overline{y}_j = 0$ (see Fig. 8b, c) are symmetric with respect to the planes perpendicular, respectively, to the $\overline{x}$-axis or both the $\overline{x}$- and $\overline{y}$-axis. These symmetries will be exploited in Appendix A and Sect. 3.5.

Fig. 8

Examples of nodes for which the cell–neighborhood symmetry can be exploited within the cell in the computation of the partial areas or volumes

3.4 Computation of partial areas

The first algorithm proposing the analytical computation of partial areas can be found in [13]: the area of intersection between the neighborhood and the cells is subdivided into domains of basic geometry (triangles, rectangles and circular segments), for which the analytical computation of the area is straightforward. Reference [13] proposes 8 different cases of cell–neighborhood intersection. In Appendix A, we propose a novel approach to compute analytically the partial areas, which is based on the definition of the quadrature coefficient in an integral form. The integrals are then solved by distinguishing only 5 possible cases of cell–neighborhood intersections, for each of which an explicit analytical expression for the value of the quadrature coefficient is obtained.

Algorithm 2 shows how to compute analytically the quadrature coefficients in 2D with the proposed approach. Function 1 is used to solve the only non-trivial integral derived from the computation of the quadrature coefficient. Please refer to Appendix A for the details of the analytical derivation, which is also very useful to better understand the extension of the formulae from 2D to 3D for the computation of the partial volumes shown in the next section.

3.5 Computation of partial volumes

We show hereinafter how to compute quasi-analytically the quadrature weights in 3D problems. The partial volumes are computed with the same approach explained in Appendix A for the partial areas. Therefore, the quadrature coefficients are computed as

$$\begin{aligned} \beta _{ij}= & {} 2^s \int _{a_x}^{b_x} \int _{a_y}^{\min \left( \overline{y}_2, \sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_1^{\, 2}} \right) }\nonumber \times \int _{\overline{z}_1}^{\min \left( \overline{z}_2, \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}^2} \right) } {\mathrm {d}} {\overline{z}} {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \, , \end{aligned}$$

(24)

where $\overline{x}_1=\overline{x}_j-0.5$, $\overline{x}_2=\overline{x}_j+0.5$, $\overline{y}_1=\overline{y}_j-0.5$, $\overline{y}_2=\overline{y}_j+0.5$, $\overline{z}_1=\overline{z}_j-0.5$ and $\overline{z}_2=\overline{z}_j+0.5$ are the coordinates of the faces of the cubic cell and s is the number of symmetries of the cell with respect to the neighborhood ($s=2$ if $\overline{y}_j=\overline{x}_j=0$, $s=1$ if $\overline{x}_j=0$ and $\overline{y}_j\ne 0$ and $s=0$ if $\overline{x}_j\ne 0$ and $\overline{y}_j\ne 0$, see Fig. 8b, c). The integration limits $a_x$, $b_x$ and $a_y$ are scalar values that can be computed at the beginning of the algorithm. Similarly to what described in Appendix A, the lower limits are defined to exploit the cell–neighborhood symmetry, or symmetries, shown in Fig. 8b or c:

$$\begin{aligned} a_x = \max \left( 0,\overline{x}_1 \right) , \qquad a_y = \max \left( 0,\overline{y}_1 \right) . \end{aligned}$$

(25)

Figure 9 shows all the possible cases of intersection between the spherical neighborhood and a cubic cell. Note that in Fig. 9 only cells with no symmetries are illustrated, but the portions of the symmetric cell–neighborhood intersections that are used in the computation of the quadrature weights, i.e., the portions in the first octant of Fig. 8b, c, belong to one of those cases. The upper limit of the integral in $\overline{x}$ direction of Eq. (24) is the greatest $\overline{x}$ coordinate of the cell–neighborhood intersection, and it can be computed as

$$\begin{aligned} b_x = \min \left( \overline{x}_2, \sqrt{\overline{m}^2-a_y^{\, 2}-\overline{z}_1^{\, 2}} \right) . \end{aligned}$$

(26)

Therefore, $b_x$ is equal to $\overline{x}_2$ from case-2 to case-8, and to $\sqrt{\overline{m}^2-a_y^{\, 2}-\overline{z}_1^{\, 2}}$ in case-9. The computation of Eq. (26) at the beginning of the algorithm allows to compute case-8 and case-9 with the same formulae.

Fig. 9

Possible cases of intersections between neighborhood and cell in 3D. Symmetric cell–neighborhood intersections are not shown here, but the unsymmetric portions of those intersections belong to one of the shown cases. Since the true origin of the reference system lies outside the images, it has been translated to one of the vertices of the cube for visualization clarity

Similarly to Eq. (A1) in Appendix A, Eq. (24) can be solved for each case by splitting the integrals in correspondence of the intersections between the boundary of the neighborhood and the edges parallel to the $\overline{x}$-axis and the faces parallel to the $\overline{x}$-$\overline{y}$ plane (for details refer to Appendix B). There are 3 types of non-trivial integrals that derive from the previous step:

$$\begin{aligned}&\int \sqrt{\overline{m}^2-\overline{x}^2-k_1^{\, 2}} {\mathrm {d}} {\overline{x}} \nonumber \\&\quad = \frac{1}{2} \, \left( \overline{m}^2 - k_1^{\, 2} \right) \, \arcsin \left( \frac{\overline{x}}{\sqrt{\overline{m}^2-k_1^{\, 2}}} \right) \nonumber \\&\qquad + \frac{1}{2} \, \overline{x} \, \sqrt{\overline{m}^2-\overline{x}^2-k_1^{\, 2}} + \text {const.} \, , \end{aligned}$$

(27)

$$\begin{aligned}&\int \left( \overline{m}^2-\overline{x}^2 \right) \arcsin \left( \frac{k_2}{ \sqrt{ \overline{m}^2-\overline{x}^2 } } \right) {\mathrm {d}} {\overline{x}} \, , \end{aligned}$$

(28)

$$\begin{aligned}&\int \left( \overline{m}^2-\overline{x}^2 \right) \arcsin \left( \frac{ \sqrt{ \overline{m}^2-\overline{x}^2-k_3^{\, 2} } }{ \sqrt{ \overline{m}^2-\overline{x}^2 } } \right) {\mathrm {d}} {\overline{x}} \, , \end{aligned}$$

(29)

where $k_1$ can be equal to $a_y$, $\overline{y}_2$, $\overline{z}_1$ or $\overline{z}_2$, $k_2$ to $a_y$ or $\overline{y}_2$, and $k_3$ to $\overline{z}_1$ or $\overline{z}_2$. The parameters $k_1$, $k_2$ and $k_3$ are defined in these ways to group the same types of integrals derived from Eq. (24). The explicit solution given in Eq. (27) is used in Function 2 to compute the integral in a general interval [a, b].

On the other hand, integrals in Eqs. (28) and (29) do not have an explicit solution. Therefore, we perform a Taylor series expansion centered at $\overline{x}_0$ of the following functions:

$$\begin{aligned}&\arcsin \left( \frac{k_2}{ \sqrt{ \overline{m}^2-\overline{x}^2 } } \right) \nonumber \\&\quad = \arcsin \left( \frac{k_2}{ \sqrt{ \overline{m}^2-\overline{x}_0^{\, 2} } }\right) \nonumber \\&\qquad + \sum _{n=1}^{N} \frac{ \sum \nolimits _{p=1}^{\lfloor 3n/2 \rfloor } \left( \sum \nolimits _{q=1}^{p} c(n,p,q) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q-1} \right) \overline{x}_0^{\, 3n-2p} }{ \left( \overline{m}^2 - \overline{x}_0^{\, 2} \right) ^n \left( \overline{m}^2 - \overline{x}_0^{\, 2} - k_2^{\, 2} \right) ^{n-1/2} }\nonumber \\&\qquad \cdot \frac{ \left( \overline{x}-\overline{x}_0 \right) ^n }{n!} \, , \end{aligned}$$

(30)

$$\begin{aligned}&\arcsin \left( \frac{ \sqrt{ \overline{m}^2-\overline{x}^2-k_3^{\, 2} } }{ \sqrt{ \overline{m}^2-\overline{x}^2 } } \right) \nonumber \\&\quad = \arcsin \left( \frac{ \sqrt{ \overline{m}^2-\overline{x}_0^{\, 2}-k_3^{\, 2} } }{ \sqrt{ \overline{m}^2-\overline{x}_0^{\, 2} } } \right) \nonumber \\&\qquad - \sum _{n=1}^{N} \frac{ \sum \limits _{p=1}^{\lfloor 3n/2 \rfloor } \left( \sum \limits _{q=1}^{p} c(n,p,q) \, \overline{m}^{2(p-q)} \, k_3^{\, 2q-1} \right) \overline{x}_0^{\, 3n-2p} }{ \left( \overline{m}^2 - \overline{x}_0^{\, 2} \right) ^n \left( \overline{m}^2 - \overline{x}_0^{\, 2} - k_3^{\, 2} \right) ^{n-1/2} } \nonumber \\&\qquad \cdot \frac{ \left( \overline{x}-\overline{x}_0 \right) ^n }{n!} \, , \end{aligned}$$

(31)

where c is a coefficient depending on the order n of the corresponding derivative and the indices p and q. For more details about the computation of the derivatives of a general order n (and the corresponding coefficients c(n, p, q)), please refer to Appendix C. The matrix ${\mathbf {c}}$ containing all the coefficients c is obtained with Algorithm 3. If the order N of truncation of the Taylor series expansion tends to infinity ($N \rightarrow \infty$), then the solution of the integral is exact. Clearly, in a numerical algorithm N must be a finite number, but we will show that our approach is able to attain accurate results with little computational effort (i.e., with N relatively low). Hence, we substitute Eqs. (30) and (31), respectively, in Eqs. (28) and (29) and solve the indefinite integrals:

$$\begin{aligned}&\int \left( \overline{m}^2-\overline{x}^2 \right) f (\overline{x}) {\mathrm {d}} {\overline{x}} \nonumber \\&\quad = \int \left( \overline{m}^2-\overline{x}^2 \right) \left[ f (\overline{x}_0) + \sum _{n=1}^{N} \frac{ f^{(n)} (\overline{x}_0) }{n!} \left( \overline{x}-\overline{x}_0 \right) ^n \right] {\mathrm {d}} {\overline{x}} \nonumber \\&\quad = f (\overline{x}_0) \left( \overline{m}^2 \, \overline{x} - \frac{\overline{x}^3}{3} \right) \nonumber \\&\qquad + \sum _{n=1}^{N} \frac{ f^{(n)} (\overline{x}_0) }{n!} \left[ \frac{\overline{m}^2 - \overline{x}_0^{\, 2}}{n+1} \left( \overline{x}-\overline{x}_0\right) ^{n+1} \right. \nonumber \\&\qquad \left. - \frac{2 \overline{x}_0}{n+2} \left( \overline{x} - \overline{x}_0 \right) ^{n+2} - \frac{1}{n+3} \left( \overline{x}-\overline{x}_0\right) ^{n+3} \right] \nonumber \\&\qquad + \text {const.} \, , \end{aligned}$$

(32)

$$\begin{aligned}&\int \left( \overline{m}^2-\overline{x}^2 \right) g (\overline{x}) {\mathrm {d}} {\overline{x}} \nonumber \\&\quad = \int \left( \overline{m}^2-\overline{x}^2 \right) \left[ g (\overline{x}_0) + \sum _{n=1}^{N} \frac{ g^{(n)} (\overline{x}_0) }{n!} \left( \overline{x}-\overline{x}_0 \right) ^n \right] {\mathrm {d}} {\overline{x}} \nonumber \\&\quad = g (\overline{x}_0) \left( \overline{m}^2 \, \overline{x} - \frac{\overline{x}^3}{3} \right) \nonumber \\&\qquad + \sum _{n=1}^{N} \frac{ g^{(n)} (\overline{x}_0) }{n!} \left[ \frac{\overline{m}^2 - \overline{x}_0^{\, 2}}{n+1} \left( \overline{x}-\overline{x}_0\right) ^{n+1} \right. \nonumber \\&\qquad \left. - \frac{2 \overline{x}_0}{n+2} \left( \overline{x} - \overline{x}_0 \right) ^{n+2} - \frac{1}{n+3} \left( \overline{x}-\overline{x}_0\right) ^{n+3} \right] \nonumber \\&\qquad + \text {const.} \, , \end{aligned}$$

(33)

where $f (\overline{x})$ and $g (\overline{x})$ are the arcsin functions (see Eqs. C1 and C6) and $f^{(n)} (\overline{x})$ and $g^{(n)} (\overline{x})$ are the corresponding n-th derivatives (see Eqs. C2 and C7). Functions 3 and 4 show the computation of the integrals in Eqs. (32) and (33) in a general interval [a, b]. In order to improve the accuracy of the algorithm, we choose $\overline{x}_0$ to be the middle point of the interval [a, b].

The integrals of Eq. (24) can be solved for each case by following the procedure described above (for details refer to Appendix B). Algorithm 4 illustrates how to compute the quadrature coefficients with this procedure. At the beginning of the algorithm, the coordinates of node j are considered only in their absolute value and sorted in ascending order to comply with the conditions imposed for symmetry: $0 \le \overline{x}_j \le \overline{y}_j \le \overline{z}_j$. The quadrature coefficients $\beta _{ij}$ computed for $\overline{m} = 3,4,6$ are reported in Appendix D.

4 Numerical results

To assess the accuracy of the computation of the partial volumes with respect to the order N of truncation of the Taylor series expansions, we compute the relative error on the total volume of the spherical neighborhood:

$$\begin{aligned} \epsilon _{ V } = \Bigg \Vert \frac{\sum \limits _{j \in \overline{\mathcal {H}}_i} \beta _{ij} +1}{\frac{4}{3} \pi \, \overline{m}^3} - 1 \Bigg \Vert \, . \end{aligned}$$

(34)

The sum of all the quadrature coefficients $\beta _{ij}$ and the volume $V_i = 1$ of node i is the numerical value of the sphere volume, whereas $(4/3) \pi \overline{m}^3$ is its analytical value. As shown in Fig. 10, the accuracy in the computation of the partial volumes is improved by increasing the value of N. Furthermore, the proposed algorithm reaches values of the errors very close to machine precision with $\overline{m} \ge 3$ and $N=20$.

Fig. 10

Relative errors on the computation of the total volume of the neighborhood obtained with Algorithm 4 with different order N of truncation of the Taylor series expansions. The values of $\overline{m}$ vary by $\Delta \overline{m} = 0.5$

We show hereinafter several numerical results that confirm the improvements in the peridynamic integration in 3D problems. In particular, we compare the numerical results of Algorithm 1, arguably the most commonly used, with those of the new algorithm (Algorithm 4). We use $N=4$ as the order of truncation for the Taylor series in Algorithm 4 since this value assures accurate results with low computational cost.

4.1 Geometrical quantities

To assess the performance of the proposed algorithm, we compute two geometrical quantities that reflect the accuracy in the computation of the partial volumes. The first one is the neighborhood volume, computed as:

$$\begin{aligned} V_{ \mathcal {H} } = 1+ \sum \limits _{j \in \overline{\mathcal {H}}_i} \beta _{ij} \, . \end{aligned}$$

(35)

The analytical value of the neighborhood volume is equal to the volume of a sphere: $V_{an} = (4/3) \pi \overline{m}^3$. The relative error on the neighborhood volume can be computed as in Eq. (34). The improvements obtained by the novel algorithm are evident in Fig. 11a, b.

The second geometrical quantity for the comparison of the algorithms is the weighted volume m (Eq. (18)). The analytical computation of the weighted volume is carried out using spherical coordinated ($\phi$ is the azimuthal angle and $\varphi$ is the polar angle):

$$\begin{aligned} \begin{aligned} m_{an}&= \int _{\mathcal {H}_{{\mathbf {x}}}} \exp \left( -\frac{\Vert {\varvec{\xi }} \Vert ^2}{\delta ^2} \right) \, \Vert {\varvec{\xi }} \Vert ^2 {\mathrm {d}} {V}_{{\mathbf {x}}'} = \int _{0}^{\delta } \int _{0}^{2 \pi } \int _{0}^{\pi } \exp \left( -\frac{r^2}{\delta ^2} \right) \, r^2 \cdot r^2 \sin \varphi {\mathrm {d}} {\varphi } {\mathrm {d}} {\phi } {\mathrm {d}} {r} \\&= \left( \frac{3}{2} \sqrt{\pi } \, \text{ erf } (1) - 5 \exp (-1) \right) \pi \delta ^5 \, , \end{aligned} \end{aligned}$$

(36)

where $r = \Vert {\varvec{\xi }} \Vert$ and $\text{ erf } (\cdot )$ is the Gaussian error function. The relative error on the weighted volume can be computed as:

$$\begin{aligned} \epsilon _{ m } = \Bigg \Vert \frac{m}{m_{ an }}-1 \Bigg \Vert \, . \end{aligned}$$

(37)

Figure 11c, d show the comparison between Algorithms 1 and 4, with a significant improvement of the accuracy in the latter one.

Fig. 11

Geometrical quantities (neighborhood volume and weighted volume) and their relative errors computed with Algorithm 1 and Algorithm 4. The plot is realized with values of $\overline{m}$ varying by $\Delta \overline{m} = 0.05$

4.2 Coefficients of the elasticity tensor

The mechanical properties of isotropic linearly elastic materials are described by the $4^{\text{ th }}$-order elasticity tensor ${\mathbf {C}}$. As in [13], we investigate the convergence behavior of the coefficients of the elasticity tensor. In state-based peridynamics, the elasticity tensor of a point in the bulk is given as [32]

$$\begin{aligned} C_{pqrs} ({\mathbf {x}}) = \int _{\mathcal {H}_{{\mathbf {x}}}} \int _{\mathcal {H}_{{\mathbf {x}}}} \underline{\mathbb {K}}_{pr} [{\mathbf {x}}] \langle {\varvec{\xi }}, {\varvec{\zeta }} \rangle \, \xi _q \, \zeta _s {\mathrm {d}} {V}_{{\mathbf {x}}''} {\mathrm {d}} {V}_{{\mathbf {x}}'} \, , \end{aligned}$$

(38)

where $\underline{\mathbb {K}}$ is the modulus state which operates on two bonds, ${\varvec{\xi }} = {\mathbf {x}}' - {\mathbf {x}}$ and ${\varvec{\zeta }} = {\mathbf {x}}'' - {\mathbf {x}}$. The modulus state in a linear peridynamic solid model [2, 32] is derived as

$$\begin{aligned} \underline{\mathbb {K}}_{pr} [{\mathbf {x}}] \langle {\varvec{\xi }}, {\varvec{\zeta }} \rangle= & {} \frac{\underline{\omega } \langle {\varvec{\xi }} \rangle }{m_{{\mathbf {x}}}} \left( \frac{3 \left( 3K - 5 \mu \right) }{m_{{\mathbf {x}}}} \, \underline{\omega } \langle {\varvec{\zeta }} \rangle \, \underline{x} \langle {\varvec{\xi }} \rangle \, \underline{x} \langle {\varvec{\zeta }} \rangle \right. \nonumber \\&\left. + 15 \mu \, {\varvec{\Delta }} ({\varvec{\zeta }} - {\varvec{\xi }}) \right) \frac{\xi _{p}}{\Vert {\varvec{\xi }} \Vert } \, \frac{\zeta _{r}}{\Vert {\varvec{\zeta }} \Vert } \, , \end{aligned}$$

(39)

where ${\varvec{\Delta }}$ is the Dirac delta function defined as

$$\begin{aligned} {\varvec{\Delta }} ({\varvec{\zeta }} - {\varvec{\xi }}) := {\left\{ \begin{array}{ll} 1 &{} \text {if } {\varvec{\zeta }}={\varvec{\xi }} \, , \\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(40)

A component of the tensor ${\mathbf {C}}$ is therefore computed as [32]

$$\begin{aligned} \begin{aligned} C_{pqrs}&= \int _{\mathcal {H}_{{\mathbf {x}}}} \int _{\mathcal {H}_{{\mathbf {x}}}} \frac{\underline{\omega } \langle {\varvec{\xi }} \rangle }{m_{{\mathbf {x}}}} \left( \frac{3 \left( 3K - 5 \mu \right) }{m_{{\mathbf {x}}}} \, \underline{\omega } \langle {\varvec{\zeta }} \rangle \, \underline{x} \langle {\varvec{\xi }} \rangle \, \underline{x} \langle {\varvec{\zeta }} \rangle \right. \\&\quad \left. + 15 \mu \, {\varvec{\Delta }} ({\varvec{\zeta }} - {\varvec{\xi }}) \right) \frac{\xi _p \xi _q}{\Vert {\varvec{\xi }} \Vert } \, \frac{\zeta _r \zeta _s}{\Vert {\varvec{\zeta }} \Vert } {\mathrm {d}} {V}_{{\mathbf {x}}''} {\mathrm {d}} {V}_{{\mathbf {x}}'} \\&= \int _{\mathcal {H}_{{\mathbf {x}}}} \underline{\omega } \langle {\varvec{\xi }} \rangle \xi _p \xi _q \left( \frac{3 \left( 3K - 5 \mu \right) }{ \left( m_{{\mathbf {x}}} \right) ^2} \int _{\mathcal {H}_{{\mathbf {x}}}} \underline{\omega } \langle {\varvec{\zeta }} \rangle \, \zeta _r \zeta _s {\mathrm {d}} {V}_{{\mathbf {x}}''} \right. \\&\quad \left. + \frac{15 \mu }{m_{{\mathbf {x}}}} \int _{\mathcal {H}_{{\mathbf {x}}}} {\varvec{\Delta }} ({\varvec{\zeta }} - {\varvec{\xi }}) \frac{\zeta _r \zeta _s}{\Vert {\varvec{\xi }} \Vert \Vert {\varvec{\zeta }} \Vert } {\mathrm {d}} {V}_{{\mathbf {x}}''} \right) {\mathrm {d}} {V}_{{\mathbf {x}}'} \\&= \frac{3 \left( 3K - 5 \mu \right) }{ \left( m_{{\mathbf {x}}} \right) ^2} \int _{\mathcal {H}_{{\mathbf {x}}}} \underline{\omega } \langle {\varvec{\xi }} \rangle \, \xi _p \xi _q {\mathrm {d}} {V}_{{\mathbf {x}}'} \int _{\mathcal {H}_{{\mathbf {x}}}} \underline{\omega } \langle {\varvec{\zeta }} \rangle \, \zeta _r \zeta _s {\mathrm {d}} {V}_{{\mathbf {x}}''} \\&\quad + \frac{15 \mu }{m_{{\mathbf {x}}}} \int _{\mathcal {H}_{{\mathbf {x}}}} \underline{\omega } \langle {\varvec{\xi }} \rangle \frac{\xi _p \xi _q \xi _r \xi _s}{\Vert {\varvec{\xi }} \Vert ^2} {\mathrm {d}} {V}_{{\mathbf {x}}'} \, . \end{aligned} \end{aligned}$$

(41)

For isotropic linearly elastic materials, there are only two coefficients of the tensor ${\mathbf {C}}$ which are independent from the others. The analytical value of the coefficients, for instance, $C_{1111}$ and $C_{1122}$ are

$$\begin{aligned} C_{1111}^{an} = K + \frac{4}{3} \mu \, , \qquad C_{1122}^{an} = K - \frac{2}{3} \mu \, . \end{aligned}$$

(42)

Any component of the tensor ${\mathbf {C}}$ in a node i can be computed numerically from Eq. (41) as

$$\begin{aligned} \begin{aligned} C_{pqrs}&= \frac{3 \left( 3K - 5 \mu \right) }{ \left( m_i \right) ^2} \left( \sum _{j \in \mathcal {H}_i} \underline{\omega }_{ij} \, \xi _p \, \xi _q \, \beta _{ij} V \right) \\&\quad \times \left( \sum _{k \in \mathcal {H}_i} \underline{\omega }_{ik} \, \zeta _r \, \zeta _s \, \beta _{ik} V \right) \\&\quad + \frac{15 \mu }{m_i} \sum _{j \in \mathcal {H}_i} \underline{\omega }_{ij} \frac{\xi _p \xi _q \xi _r \xi _s}{\Vert {\varvec{\xi }} \Vert ^2} \beta _{ij} V \, , \end{aligned} \end{aligned}$$

(43)

where ${\varvec{\xi }} = {\mathbf {x}}_j - {\mathbf {x}}_i$ and ${\varvec{\zeta }} = {\mathbf {x}}_k - {\mathbf {x}}_i$. The values of the Young’s modulus $E = 1 \,\text {GPa}$ and of the Poisson’s ratio $\nu = 0.2$ are chosen, which yield the following bulk and shear moduli: $K=555.56 \,\text {MPa}$ and $\mu =416.67 \,\text {MPa}$. Figure 12a, c show the results of these computation, respectively, for the components $C_{1111}$ and $C_{1122}$. The relative errors on these coefficients are computed as

$$\begin{aligned} \epsilon _{ 1111 } = \Bigg \Vert \frac{C_{1111}}{C_{1111}^{ an }}-1 \Bigg \Vert \, , \qquad \epsilon _{ 1122 } = \Bigg \Vert \frac{C_{1122}}{C_{1122}^{ an }}-1 \Bigg \Vert \, , \end{aligned}$$

(44)

and are shown in Fig. 12b, d. It is evident that the proposed algorithm provides, on average, smaller errors. Furthermore, the oscillatory behavior as $\overline{m}$ increases is much smoother than that of Algorithm 1.

Fig. 12

Coefficients of the $4^{\text{ th }}$-order elasticity tensor and their relative errors computed with Algorithms 1 and 4. The values of $\overline{m}$ vary by $\Delta \overline{m} = 0.05$

4.3 Manufactured problem

A “manufactured” problem, which consists in determining the force density distribution in a body under a prescribed displacement field, is solved analytically and numerically. Following what was shown in [14] for a 2D problem, a body is subjected to the displacements

$$\begin{aligned} {\left\{ \begin{array}{ll} u = c_{u 1} \, x^2 + c_{u 2} \, y^2 + c_{u 3} \, z^2 + c_{u 4} \, x y + c_{u 5} \, y z + c_{u 6} \, x z \, , \\ v = c_{v 1} \, x^2 + c_{v 2} \, y^2 + c_{v 3} \, z^2 + c_{v 4} \, x y + c_{v 5} \, y z + c_{v 6} \, x z \, , \\ w = c_{w 1} \, x^2 + c_{w 2} \, y^2 + c_{w 3} \, z^2 + c_{w 4} \, x y + c_{w 5} \, y z + c_{w 6} \, x z \, , \end{array}\right. } \end{aligned}$$

(45)

where there are 18 independent coefficients for the quadratic terms. The force density derived from this displacement field is given as [14]

$$\begin{aligned} {\left\{ \begin{array}{ll} b_1^{an} = - \frac{3K - 5 \mu }{3} \left( 2 c_{u 1} + c_{v 4} + c_{w 6} \right) - 2 \mu \left( 3 c_{u 1} + c_{u 2} + c_{u 3} + c_{v 4} + c_{w 6} \right) , \\ b_2^{an} = - \frac{3K - 5 \mu }{3} \left( c_{u 4} + 2 c_{v 2} + c_{w 5} \right) - 2 \mu \left( c_{u 4} + c_{v 1} + 3 c_{v 2} + c_{v 3} + c_{w 5} \right) , \\ b_3^{an} = - \frac{3K - 5 \mu }{3} \left( c_{u 6} + c_{v 5} + 2 c_{w 3} \right) - 2 \mu \left( c_{u 6} + c_{v 5} + c_{w 1} + c_{w 2} + 3 c_{w 3} \right) , \end{array}\right. } \end{aligned}$$

(46)

where $K=555.56 \,\text {MPa}$ and $\mu =416.67 \,\text {MPa}$. Note that the force density vector ${\mathbf {b}}^{an}$ is constant for all the points in the bulk of the material, i.e., in all points that have a distance from the boundary of the body greater than or equal to $2\delta$. Since $c_{u 5}$, $c_{v 6}$ and $c_{w 4}$ do not contribute to ${\mathbf {b}}^{an}$, these coefficients are considered to be equal to 0. The values of the other coefficients are chosen randomly as follows: $c_{u 1} = 0.6$, $c_{u 2} = 1.3$, $c_{u 3} = 0.8$, $c_{u 4} = 0.5$, $c_{u 6} = 1.8$, $c_{v 1} = 1.1$, $c_{v 2} = 1.6$, $c_{v 3} = 0.7$, $c_{v 4} = 1$, $c_{v 5} = 1.2$, $c_{w 1} = 0.3$, $c_{w 2} = 1.2$, $c_{w 3} = 0.1$, $c_{w 5} = 1.7$ and $c_{w 6} = 0.6$.

We consider only one node in the bulk of a body at which the force density vector ${\mathbf {b}}$ is computed with Eq. (20). The relative errors on the components of ${\mathbf {b}}$ are given as

$$\begin{aligned} \epsilon _{ b_p } = \Bigg \Vert \frac{b_p}{b_p^{ an }}-1 \Bigg \Vert \quad \text {with } p = 1,2,3 \, . \end{aligned}$$

(47)

Figure 13 shows the results of the numerical computation. Algorithm 4 allows to obtain, on average, smaller relative errors and a smoother convergence behavior also in this case.

Fig. 13

Components of the force density vector and their relative errors computed with Algorithms 1 and 4. The values of $\overline{m}$ vary by $\Delta \overline{m} = 0.1$

5 Conclusions

The peridynamic theory is a nonlocal reformulation of classical continuum mechanics based on integrals over the neighborhoods of nodes. Therefore, the numerical integration of peridynamic equations determines to a great extent the accuracy of the results. In particular, the quadrature weights, i.e., the partial areas in 2D (intersections between the circular neighborhood and the square cells) and the partial volumes in 3D (intersections between the spherical neighborhood and the cubic cells), should be computed accurately.

We developed an innovative algorithm able to compute quasi-analytically the partial volumes. We use the expression “quasi-analytical” because a truncated Taylor series expansion of some functions, whose integrals are not explicitly solvable, is performed to carry out the integration. However, the new algorithm computes accurately the quadrature weights with very little computational effort, i.e., with a relatively low order of truncation of the Taylor series. The computational time required by the proposed algorithm is negligible compared to the time required to compute the bond forces and the peridynamic equilibrium equation. In particular, if $\overline{m}$ is constant in the whole domain, the same quadrature weights can be computed only once and used for every neighborhood in the body. A similar approach is also used to simplify the algorithm for the analytical computation of the partial areas, which was already developed in the literature.

Several examples have been presented to show the capabilities of the newly proposed algorithm. The numerical values of the geometrical quantities (volume of the neighborhood and weighted volume), of the coefficients of the elasticity tensor and of the manufactured problem obtained with the new algorithm are compared with those obtained with the most commonly used algorithm for the computation of the partial volumes. As the $\overline{m}$-ratio increases, the proposed algorithm provides, on average, smaller errors and a smoother convergence behavior. For the sake of convenience, the quadrature coefficients for $\overline{m} = 3, 4, 6$ are reported in Appendix D.

Appendices

Appendix A: Analytical computation of partial areas

We propose a new algorithm for the computation of the quadrature coefficients in 2D (Algorithm 2) that solves the following integral:

$$\begin{aligned} \beta _{ij} = 2^s \int _{a_x}^{b_x} \int _{\overline{y}_1}^{\min \left( \overline{y}_2, \sqrt{\overline{m}^2-\overline{x}^2} \right) } {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \, , \end{aligned}$$

(A1)

where $\overline{x}_1=\overline{x}_j-0.5$, $\overline{x}_2=\overline{x}_j+0.5$, $\overline{y}_1=\overline{y}_j-0.5$ and $\overline{y}_2=\overline{y}_j+0.5$ are the coordinates of the sides of the square cell and s is the number of symmetries of the cell with respect to the neighborhood ($s=1$ if $\overline{x}_j=0$ and $s=0$ if $\overline{x}_j\ne 0$, see Fig. 8a). The upper and lower limits of the outer integral, respectively, $b_x$ and $a_x$, are scalar values that can be computed at the beginning of the algorithm. The value of the lower limit $a_x$ depends on whether the cell–neighborhood intersection is symmetric, as shown in Fig. 8a, or not. In the former case, the lower limit of the integration domain in $\overline{x}$ direction is set to $a_x=0$ and the value of the integral is multiplied by 2 (given that $s=1$). In the latter case, the lower limit is the smallest $\overline{x}$ coordinate of the cell, i.e., $a_x=\overline{x}_1$. These conditions can be written as

$$\begin{aligned} a_x = \max \left( 0,\overline{x}_1 \right) \, . \end{aligned}$$

(A2)

Since only cells with $\overline{y}_j \ge \overline{x}_j \ge 0$ are considered for symmetry reasons (see Fig. 14), there are 5 possible cases of square–circle intersections depending on which corners of the cell lie inside the neighborhood:

• case-1 if the corner $(\overline{x}_2,\overline{y}_2)$, the farthest from node i, lies inside the neighborhood, i.e., $\overline{x}_2^{\, 2} + \overline{y}_2^{\, 2} \le \overline{m}^2$, as shown in Fig. 15a;

• case-2 if only the corner $(\overline{x}_2,\overline{y}_2)$ lies outside the neighborhood, i.e., $a_x^{\, 2} + \overline{y}_2^{\, 2} \le \overline{m}^2 < \overline{x}_2^{\, 2} + \overline{y}_2^{\, 2}$, as shown in Fig. 15b;

• case-3 if the corners $(\overline{x}_2,\overline{y}_2)$ and $(a_x,\overline{y}_2)$ lie outside the neighborhood and the others lie inside, i.e., $\overline{x}_2^{\, 2} + \overline{y}_1^{\, 2} \le \overline{m}^2 < a_x^{\, 2} + \overline{y}_2^{\, 2}$, as shown in Fig. 15c;

• case-4 if only the corners $(a_x,\overline{y}_1)$ lies inside the neighborhood, i.e., $a_x^{\, 2} + \overline{y}_1^{\, 2} \le \overline{m}^2 < \overline{x}_2^{\, 2} + \overline{y}_1^{\, 2}$, as shown in Fig. 15d;

• case-5 if the corner $(a_x,\overline{y}_1)$, the closest to node i, lies outside the neighborhood, i.e., $a_x^{\, 2} + \overline{y}_1^{\, 2} > \overline{m}^2$, as shown in Fig. 15e.

The comparison of these cases with the cases of the approach in [13] is summarized in Table 1.

Table 1 Comparison of the cases in Fig. 4 of [13] with the cases in Fig. 15 derived from the new approach for the computation of the partial areas

Case-1 and case-5 are trivial since $\beta _{ij} = 1$ and $\beta _{ij} = 0$, respectively. Furthermore, the quadrature coefficient in case-3 and case-4 can be computed with the same formulae if the upper limit of the integral in $\overline{x}$ direction is defined as

$$\begin{aligned} b_x = \min \left( \overline{x}_2, \sqrt{\overline{m}^2-\overline{y}_1^{\, 2}} \right) \, . \end{aligned}$$

(A3)

The value of $b_x$ is indeed equal to $\overline{x}_2$ in case-3, as shown in Fig. 15c, and to the $\overline{x}$ coordinate of the intersection between the boundary of the neighborhood and the lower side of the cell, as shown in Fig. 15d.

Fig. 14

Cases of intersection for $\overline{m}=3.25$ in 2D depending on which corners of the cell lie inside the neighborhood. Note that the cell–neighborhood intersection of node (0, 3) is symmetric with respect to the $\overline{y}$-axis, so actually only the half of it is considered, namely the half in the first quadrant

Fig. 15

Possible cases of intersections between neighborhood and cell in 2D. The gray line is a portion of the boundary of the neighborhood

For later use, the following indefinite integral is analytically solved as

$$\begin{aligned} \int \sqrt{\overline{m}^2-\overline{x}^2} \, {\mathrm {d}} {\overline{x}}= & {} \frac{1}{2} \, \overline{m}^2 \, \arcsin \left( \frac{\overline{x}}{\overline{m}} \right) \nonumber \\&+ \frac{1}{2} \, \overline{x} \, \sqrt{\overline{m}^2-\overline{x}^2} + \text {const.} \, . \end{aligned}$$

(A4)

This solution will be used to compute the definite integrals in different intervals. Now, we show how to compute the quadrature coefficient if the considered cell belongs to case-2. Equation (A1) can be rewritten as

$$\begin{aligned} \beta _{ij} = 2^s \int _{a_x}^{b_x} \left( \min \left( \overline{y}_2, \sqrt{\overline{m}^2-\overline{x}^2} \right) - \overline{y}_1 \right) {\mathrm {d}} {\overline{x}} \, . \end{aligned}$$

(A5)

In case-2 (see Fig. 15b), there is an intersection between the boundary of the neighborhood and the upper side of the cell, which has an $\overline{x}$ coordinate equal to

$$\begin{aligned} \overline{x}_{ e }= \sqrt{\overline{m}^2-\overline{y}_2^{\, 2}} \, . \end{aligned}$$

(A6)

The integral in Eq. (A5) must be splitted because the integrand has different values in the intervals $[a_x,\overline{x}_{ e }]$ and $[\overline{x}_{ e },b_x]$. Then, the integral can be solved analytically by using Eq. (A4):

$$\begin{aligned} \begin{aligned}&\text {Case-2} \ \Rightarrow \ \beta _{ij} \\&\quad = 2^s \left[ \int _{a_x}^{\overline{x}_{ e }} \left( \overline{y}_2 - \overline{y}_1 \right) {\mathrm {d}} {\overline{x}} + \int _{\overline{x}_{ e }}^{b_x} \left( \sqrt{\overline{m}^2-\overline{x}^2} - \overline{y}_1 \right) {\mathrm {d}} {\overline{x}} \right] \\&\quad = 2^s \left[ \overline{y}_2 \left( \overline{x}_{ e } - a_x \right) +\frac{1}{2} \, \overline{m}^2 \, \arcsin \left( \frac{b_x}{\overline{m}} \right) + \frac{1}{2} \, b_x \, \sqrt{\overline{m}^2-b_x^{\, 2}} \right. \\&\qquad \left. - \frac{1}{2} \, \overline{m}^2 \, \arcsin \left( \frac{\overline{x}_{ e }}{\overline{m}} \right) - \frac{1}{2} \, \overline{x}_{ e } \, \sqrt{\overline{m}^2-\overline{x}_{ e }^{\, 2}} - \overline{y}_1 \left( b_x - a_x \right) \right] \, . \end{aligned} \end{aligned}$$

(A7)

Similarly, the quadrature coefficient for a cell belonging to case-3 or case-4 is analytically computed from Eq. (A5) as follows:

$$\begin{aligned} \begin{aligned}&\text {Case-3 or case-4} \ \Rightarrow \ \beta _{ij} \\&\quad = 2^s \int _{a_x}^{b_x} \left( \sqrt{\overline{m}^2-\overline{x}^2} - \overline{y}_1 \right) {\mathrm {d}} {\overline{x}} \\&\quad = 2^s \left[ \frac{1}{2} \, \overline{m}^2 \, \arcsin \left( \frac{b_x}{\overline{m}} \right) + \frac{1}{2} \, b_x \, \sqrt{\overline{m}^2-b_x^{\, 2}} \right. \\&\qquad \left. - \frac{1}{2} \, \overline{m}^2 \, \arcsin \left( \frac{a_x}{\overline{m}} \right) - \frac{1}{2} \, a_x \, \sqrt{\overline{m}^2-a_x^{\, 2}} - \overline{y}_1 \left( b_x - a_x \right) \right] \, . \end{aligned} \end{aligned}$$

(A8)

The computation of the partial area of a cell is summarized in Algorithm 2. Function 1 is used to compute the integral of Eq. (A4) in a general interval between a and b. The proposed algorithm yields exactly the same results of the algorithm for the computation of the partial areas presented in [13], but its implementation is simpler because it is based on a smaller number of cases.

Appendix B: Quasi-analytical computation of partial volumes

We can rewrite Eq. (24) that describes the integral to compute the quadrature coefficients as follows:

$$\begin{aligned} \beta _{ij} = 2^s \int _{a_x}^{b_x} \int _{a_y}^{\min \left( \overline{y}_2, \sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_1^{\, 2}} \right) } \left[ \min \left( \overline{z}_2, \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}^2} \right) - \overline{z}_1 \right] {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \, , \end{aligned}$$

(B1)

where $\overline{x}_1=\overline{x}_j-0.5$, $\overline{x}_2=\overline{x}_j+0.5$, $\overline{y}_1=\overline{y}_j-0.5$, $\overline{y}_2=\overline{y}_j+0.5$, $\overline{z}_1=\overline{z}_j-0.5$ and $\overline{z}_2=\overline{z}_j+0.5$ are the coordinates of the faces of the cubic cell and s is the number of symmetries of the cell with respect to the neighborhood (see Fig. 8b, c). $a_x$, $a_y$ and $b_x$ are scalar values computed as shown in Eqs. (25) and (26).

Since the integrand and the upper limit of the inner integral in Eq. (B1) are discontinuous functions, the integral domain should be split into subdomains in which only continuous functions are integrated. The integral is split differently for each of the 10 cases represented in Fig. 9. The cases are differentiated depending on the intersections between the boundary of the neighborhood and the edges of the cell parallel to the $\overline{x}$-axis and the faces parallel to the $\overline{x}$-$\overline{y}$ plane. These intersections are indeed used to split the integral of Eq. (B1), as shown in next subsections. To begin with, we consider a cell completely within the neighborhood (case-1 in Fig. 9a) and decrease gradually the $\overline{m}$-ratio to find other cases. We also need to check that, for the considered cells with $\overline{z}_j \ge \overline{y}_j \ge \overline{x}_j \ge 0$, other cases of intersections are not possible.

1.1 Case-1

In case-1, the cell is completely within the neighborhood, as shown in Fig. 9a. The condition for which this case is verified is that the farthest node with coordinates $(\overline{x}_2,\overline{y}_2,\overline{z}_2)$ is inside the neighborhood:

$$\begin{aligned} \overline{x}_2^{\, 2} + \overline{y}_2^{\, 2} + \overline{z}_2^{\, 2} \le \overline{m}^2 \, . \end{aligned}$$

(B2)

In this case, the solution of Eq. (B1) is trivial:

$$\begin{aligned} \beta _{ij} = 1 \, . \end{aligned}$$

(B3)

1.2 Case-2

In case-2, the boundary of the neighborhood intersects the edge of the cell between the vertices $(a_x,\overline{y}_2,\overline{z}_2)$ and $(\overline{x}_2,\overline{y}_2,\overline{z}_2)$, as shown in Fig. 9b. Therefore, the condition in this case is

$$\begin{aligned} a_x^{\, 2} + \overline{y}_2^{\, 2} + \overline{z}_2^{\, 2} \le \overline{m}^2 < \overline{x}_2^{\, 2} + \overline{y}_2^{\, 2} + \overline{z}_2^{\, 2} \, . \end{aligned}$$

(B4)

To be sure that there are no other possible intersections with edges parallel to the $\overline{x}$-axis and faces parallel to the $\overline{x}$-$\overline{y}$ plane, we need to check that the vertices $(\overline{x}_2,a_y,\overline{z}_2)$ and $(\overline{x}_2,\overline{y}_2,\overline{z}_1)$ lie within the neighborhood, so that the edge between $(a_x,a_y,\overline{z}_2)$ and $(\overline{x}_2,a_y,\overline{z}_2)$ and the face on the plane $\overline{z} = \overline{z}_1$ are, respectively, within the neighborhood. The condition for the vertex $(\overline{x}_2,a_y,\overline{z}_2)$ being within the neighborhood is given as

$$\begin{aligned} \overline{x}_2^{\, 2} + a_y^{\, 2} + \overline{z}_2^{\, 2} \le \overline{m}^2 \, . \end{aligned}$$

(B5)

We rewrite the condition in Eq. (B5) as

$$\begin{aligned} a_x^{\, 2} - a_x^{\, 2} + \overline{x}_2^{\, 2} + a_y^{\, 2} + \overline{y}_2^{\, 2} - \overline{y}_2^{\, 2} + \overline{z}_2^{\, 2} \le \overline{m}^2 \, . \end{aligned}$$

(B6)

By comparing this inequality with the condition on the left-hand side in Eq. (B4), we obtain:

$$\begin{aligned} \begin{aligned}&- a_x^{\, 2} + \overline{x}_2^{\, 2} + a_y^{\, 2} - \overline{y}_2^{\, 2} \le 0 \\&\quad \Rightarrow \quad \overline{y}_2^{\, 2} - a_y^{\, 2} \ge \overline{x}_2^{\, 2} - a_x^{\, 2} \, . \end{aligned} \end{aligned}$$

(B7)

If the cell has two symmetries as shown in Fig. 8c ($s=2$, $a_x=a_y=0$), Eq. (B7) becomes $\overline{y}_2^{\, 2} \ge \overline{x}_2^{\, 2}$ which is always verified. If the cell has one symmetry as shown in Fig. 8b ($s=1$, $a_x=0$, $\overline{x}_2=0.5$, $\overline{y}_j\ge 1$), Eq. (B7) becomes $2\overline{y}_j \ge 0.5^2$ which is always verified. If the cell has no symmetries ($s=0$), Eq. (B7) becomes $2\overline{y}_j \ge 2\overline{x}_j$ which is always verified. Similarly, one can show that also the vertex $(\overline{x}_2,\overline{y}_2,\overline{z}_1)$ lies within the neighborhood.

In this case (see Fig. 9b), the outer integral of Eq. (B1) should be split at the intersection of the boundary of the neighborhood with the edge between the vertices $(a_x,\overline{y}_2,\overline{z}_2)$ and $(\overline{x}_2,\overline{y}_2,\overline{z}_2)$, namely at

$$\begin{aligned} \overline{x}_{e_1} = \sqrt{\overline{m}^2-\overline{y}_2^{\, 2} - \overline{z}_2^{\, 2}} \, . \end{aligned}$$

(B8)

Furthermore, the inner integral should be split in correspondence of the arc of circle with equation

$$\begin{aligned} \overline{y}_{f_1} (\overline{x}) = \sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}} \, , \end{aligned}$$

(B9)

which is given by the intesection of the boundary of the neighborhood with the plane $\overline{z} = \overline{z}_2$ (where the face of the cell lies). Therefore, Eq. (B1) becomes:

$$\begin{aligned} \begin{aligned} \beta _{ij}&= 2^s \left[ \int _{a_x}^{\overline{x}_{e_1}} \int _{a_y}^{\overline{y}_2} \overline{z}_2 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}}\right. \\&\quad + \int _{\overline{x}_{e_1}}^{b_x} \int _{a_y}^{\overline{y}_2} \min \left( \overline{z}_2, \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}^2} \right) {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \\&\quad \left. - \int _{a_x}^{b_x} \int _{a_y}^{\overline{y}_2} \overline{z}_1 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \right] \\&= 2^s \left[ \int _{a_x}^{\overline{x}_{e_1}} \int _{a_y}^{\overline{y}_2} \overline{z}_2 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} + \int _{\overline{x}_{e_1}}^{b_x} \int _{a_y}^{ \sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}} } \overline{z}_2 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \right. \\&\quad + \int _{\overline{x}_{e_1}}^{b_x} \int _{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}}}^{\overline{y}_2} \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}^2} {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \\&\quad \left. - \int _{a_x}^{b_x} \int _{a_y}^{\overline{y}_2} \overline{z}_1 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \right] \, . \end{aligned} \end{aligned}$$

(B10)

Note that the upper limit of the inner integral is $\overline{y}_2$ because the face of the cell on the plane $\overline{z} = \overline{z}_1$ is completely within the neighborhood. Since the solution of the inner integral of the last term in Eq. (B10) is similar to the integral solved in Eq. (27), the quadrature coefficients in case-2 can be computed as

$$\begin{aligned} \begin{aligned} \beta _{ij}&= 2^s \left[ \overline{z}_2 \left( \overline{y}_2 - a_y \right) \left( \overline{x}_{e_1} - a_x \right) \right. \\&\quad + \overline{z}_2 \int _{\overline{x}_{e_1}}^{b_x} \left( \sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}} - a_y \right) {\mathrm {d}} {\overline{x}} \\&\quad \left. + \int _{\overline{x}_{e_1}}^{b_x} \frac{1}{2} \left( \left( \overline{m}^2 - \overline{x}^2 \right) \arcsin \left( \frac{\overline{y}_2}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \right. \right. \\&\quad + \overline{y}_2 \, \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}_2^{\, 2}} \\&\quad \left. - \left( \overline{m}^2 - \overline{x}^2 \right) \, \arcsin \left( \frac{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}}}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \right. \\&\quad \left. - \overline{z}_2 \sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}} \right) {\mathrm {d}} {\overline{x}}\\&\quad - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( b_x-a_x \right) \bigg ] \, . \end{aligned} \end{aligned}$$

(B11)

The integrals in Eq. (B11) are of the types solved in Eqs. (27), (32) and (33). To shorten the formulae, we define the following functions (similar to Functions 2, 3 and 4 used in Algorithm 4):

$$\begin{aligned} I_1 (a,b,k_1)&:= \int _a^b \sqrt{\overline{m}^2-\overline{x}^2-k_1^{\, 2}} \, {\mathrm {d}} {\overline{x}} \nonumber \\&= \frac{1}{2} \, \left( \overline{m}^2 - k_1^{\, 2} \right) \left[ \arcsin \left( \frac{b}{\sqrt{\overline{m}^2-k_1^{\, 2}}} \right) \right. \nonumber \\&\quad \left. - \arcsin \left( \frac{a}{\sqrt{\overline{m}^2-k_1^{\, 2}}} \right) \right] \nonumber \\&\quad + \frac{1}{2} \, b \, \sqrt{\overline{m}^2-b^2-k_1^{\, 2}} \nonumber \\&\quad - \frac{1}{2} \, a \, \sqrt{\overline{m}^2-a^2-k_1^{\, 2}} \, , \end{aligned}$$

(B12)

$$\begin{aligned} I_2 (a,b,k_2)&:= \int _a^b \left( \overline{m}^2-\overline{x}^2 \right) \arcsin \left( \frac{k_2}{ \sqrt{ \overline{m}^2-\overline{x}^2 } } \right) {\mathrm {d}} {\overline{x}}\nonumber \\&= \int _a^b \left( \overline{m}^2-\overline{x}^2 \right) \nonumber \\&\quad \times \left[ f (\overline{x}_0) + \sum _{n=1}^{N} \frac{ f^{(n)} (\overline{x}_0) }{n!} \left( \overline{x}-\overline{x}_0 \right) ^n \right] {\mathrm {d}} {\overline{x}} \nonumber \\&= f (\overline{x}_0) \left( \overline{m}^2 \left( b-a \right) - \frac{1}{3} \left( b^3-a^3 \right) \right) \nonumber \\&\quad + \sum _{n=1}^{N} \frac{ f^{(n)} (\overline{x}_0) }{n!} \nonumber \\&\quad \times \left[ \frac{\overline{m}^2 - \overline{x}_0^{\, 2}}{n+1} \left( \left( b-\overline{x}_0\right) ^{n+1} - \left( a-\overline{x}_0\right) ^{n+1} \right) \right. \nonumber \\&\quad \left. - \frac{2 \overline{x}_0}{n+2} \left( \left( b - \overline{x}_0 \right) ^{n+2} - \left( a - \overline{x}_0 \right) ^{n+2} \right) \right. \nonumber \\&\quad \left. - \frac{1}{n+3} \left( \left( b-\overline{x}_0\right) ^{n+3} - \left( a-\overline{x}_0\right) ^{n+3} \right) \right] \, , \end{aligned}$$

(B13)

$$\begin{aligned} I_3 (a,b,k_3)&:= \int _a^b \left( \overline{m}^2-\overline{x}^2 \right) \arcsin \left( \frac{ \sqrt{ \overline{m}^2-\overline{x}^2-k_3^{\, 2} } }{ \sqrt{ \overline{m}^2-\overline{x}^2 } } \right) {\mathrm {d}} {\overline{x}} \nonumber \\&= \int _a^b \left( \overline{m}^2-\overline{x}^2 \right) \nonumber \\&\quad \times \left[ g (\overline{x}_0) + \sum _{n=1}^{N} \frac{ g^{(n)} (\overline{x}_0) }{n!} \left( \overline{x}-\overline{x}_0 \right) ^n \right] {\mathrm {d}} {\overline{x}} \nonumber \\&= g (\overline{x}_0) \left( \overline{m}^2 \left( b-a \right) - \frac{1}{3} \left( b^3-a^3 \right) \right) \nonumber \\&\quad + \sum _{n=1}^{N} \frac{ g^{(n)} (\overline{x}_0) }{n!}\nonumber \\&\quad \times \left[ \frac{\overline{m}^2 - \overline{x}_0^{\, 2}}{n+1} \left( \left( b-\overline{x}_0\right) ^{n+1} - \left( a-\overline{x}_0\right) ^{n+1} \right) \right. \nonumber \\&\quad \left. - \frac{2 \overline{x}_0}{n+2} \left( \left( b - \overline{x}_0 \right) ^{n+2} - \left( a - \overline{x}_0 \right) ^{n+2} \right) \right. \nonumber \\&\quad \left. - \frac{1}{n+3} \left( \left( b-\overline{x}_0\right) ^{n+3} - \left( a-\overline{x}_0\right) ^{n+3} \right) \right] \, , \end{aligned}$$

(B14)

where $f (\overline{x})$ and $g (\overline{x})$ are functions defined in Appendix C and their corresponding n-th derivatives $f^{(n)} (\overline{x})$ and $g^{(n)} (\overline{x})$ are computed as in Eqs. (C2) and (C7). The parameter $k_1$ can be equal to $a_y$, $\overline{y}_2$, $\overline{z}_1$ or $\overline{z}_2$, $k_2$ to $a_y$ or $\overline{y}_2$, and $k_3$ to $\overline{z}_1$ or $\overline{z}_2$ depending on the cases.

Using the previous definitions, Eq. (B11) is solved as follows:

$$\begin{aligned} \begin{aligned} \beta _{ij}&= 2^s \left[ \overline{z}_2 \left( \overline{y}_2 - a_y \right) \left( \overline{x}_{e_1} - a_x \right) + \overline{z}_2 \, I_1 (\overline{x}_{e_1}, b_x, \overline{z}_2) \right. \\&\quad - \overline{z}_2 a_y \left( b_x - \overline{x}_{e_1} \right) + \frac{1}{2} I_2 (\overline{x}_{e_1}, b_x, \overline{y}_2) \\&\quad + \frac{1}{2} \overline{y}_2 \, I_1 (\overline{x}_{e_1}, b_x, \overline{y}_2) - \frac{1}{2} I_3 (\overline{x}_{e_1}, b_x, \overline{z}_2) \\&\quad \left. - \frac{1}{2} \overline{z}_2 \, I_1 (\overline{x}_{e_1}, b_x, \overline{z}_2) - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( b_x-a_x \right) \right] \\&= 2^s \left[ \frac{1}{2} \overline{z}_2 \, I_1 (\overline{x}_{e_1}, b_x, \overline{z}_2) + \frac{1}{2} \overline{y}_2 \, I_1 (\overline{x}_{e_1}, b_x, \overline{y}_2) \right. \\&\quad + \frac{1}{2} I_2 (\overline{x}_{e_1}, b_x, \overline{y}_2) - \frac{1}{2} I_3 (\overline{x}_{e_1}, b_x, \overline{z}_2) + \overline{z}_2 \overline{y}_2 \left( \overline{x}_{e_1} - a_x \right) \\&\quad \left. - \overline{z}_2 a_y \left( b_x - a_x \right) - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( b_x-a_x \right) \right] . \end{aligned} \end{aligned}$$

(B15)

1.3 Case-3

In case-3, the boundary of the neighborhood intersects the face of the cell on the plane $\overline{z} = \overline{z}_2$, but does not intersect any edge parallel to the $\overline{x}$-axis, as shown in Fig. 9c. Therefore, the condition in this case is

$$\begin{aligned} \overline{x}_2^{\, 2} + a_y^{\, 2} + \overline{z}_2^{\, 2} \le \overline{m}^2 < a_x^{\, 2} + \overline{y}_2^{\, 2} + \overline{z}_2^{\, 2} \, . \end{aligned}$$

(B16)

The condition on the right-hand side implies that there are no intersections of the boundary of the neighborhood with the edge of the cell between the vertices $(a_x,\overline{y}_2,\overline{z}_2)$ and $(\overline{x}_2,\overline{y}_2,\overline{z}_2)$. Similarly, the condition on the left-hand side implies that there are no intersections with the edge between the vertices $(a_x,a_y,\overline{z}_2)$ and $(\overline{x}_2,a_y,\overline{z}_2)$. With the same approach illustrated at the beginning of Sect. B.2, one can also show that the vertex $(\overline{x}_2,\overline{y}_2,\overline{z}_1)$ lies within the neighborhood for the considered cells ($\overline{z}_j \ge \overline{y}_j \ge \overline{x}_j \ge 0$), so that the face of the cell on the plane $\overline{z} = \overline{z}_1$ is completely inside the neighborhood.

The quadrature coefficient in case-3 is therefore computed as

$$\begin{aligned} \begin{aligned} \beta _{ij}&= 2^s \left[ \int _{a_x}^{b_x} \int _{a_y}^{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}}} \overline{z}_2 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \right. \\&\quad + \int _{a_x}^{b_x} \int _{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}}}^{\overline{y}_2} \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}^2} {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \\&\quad \left. - \int _{a_x}^{b_x} \int _{a_y}^{\overline{y}_2} \overline{z}_1 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \right] \\&= 2^s \left[ \overline{z}_2 \int _{a_x}^{b_x} \left( \sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}} - a_y \right) {\mathrm {d}} {\overline{x}} \right. \\&\quad \left. + \int _{a_x}^{b_x} \frac{1}{2} \left( \left( \overline{m}^2 - \overline{x}^2 \right) \arcsin \left( \frac{\overline{y}_2}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \right. \right. \\&\quad + \overline{y}_2 \, \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}_2^{\, 2}} \\&\quad - \left( \overline{m}^2 - \overline{x}^2 \right) \, \arcsin \left( \frac{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}}}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \\&\quad \left. - \overline{z}_2 \sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}} \right) {\mathrm {d}} {\overline{x}} \\&\quad - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( b_x-a_x \right) \bigg ] \, . \end{aligned} \end{aligned}$$

(B17)

Using Eqs. (B12), (B13) and (B14), Eq. (B17) is solved as follows:

$$\begin{aligned} \begin{aligned} \beta _{ij}&= 2^s \left[ \overline{z}_2 \, I_1 (a_x, b_x, \overline{z}_2) - \overline{z}_2 a_y \left( b_x - a_x \right) \right. \\&\quad + \frac{1}{2} I_2 (a_x, b_x, \overline{y}_2) + \frac{1}{2} \overline{y}_2 \, I_1 (a_x, b_x, \overline{y}_2) \\&\quad - \frac{1}{2} I_3 (a_x, b_x, \overline{z}_2) - \frac{1}{2} \overline{z}_2 \, I_1 (a_x, b_x, \overline{z}_2) \\&\quad \left. - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( b_x-a_x \right) \right] \\&= 2^s \left[ \frac{1}{2} \overline{z}_2 \, I_1 (a_x, b_x, \overline{z}_2) + \frac{1}{2} \overline{y}_2 \, I_1 (a_x, b_x, \overline{y}_2) \right. \\&\quad + \frac{1}{2} I_2 (a_x, b_x, \overline{y}_2) - \frac{1}{2} I_3 (a_x, b_x, \overline{z}_2) \\&\quad \left. - \overline{z}_2 a_y \left( b_x - a_x \right) - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( b_x-a_x \right) \right] \, . \end{aligned} \end{aligned}$$

(B18)

1.4 Case-4

In case-4, the boundary of the neighborhood intersects the edge of the cell between the vertices $(a_x,a_y,\overline{z}_2)$ and $(\overline{x}_2,a_y,\overline{z}_2)$ and the face on the plane $\overline{z} = \overline{z}_1$ lies completely within the neighborhood, as shown in Fig. 9d. Therefore, the conditions in this case are

$$\begin{aligned} a_x^{\, 2} + a_y^{\, 2} + \overline{z}_2^{\, 2} \le \overline{m}^2 < \overline{x}_2^{\, 2} + a_y^{\, 2} + \overline{z}_2^{\, 2} \text { and } \overline{x}_2^{\, 2} + \overline{y}_2^{\, 2} + \overline{z}_1^{\, 2} \le \overline{m}^2 \, . \end{aligned}$$

(B19)

The intersection of the boundary of the neighborhood with the edge between the vertices $(a_x,\overline{y}_2,\overline{z}_2)$ and $(\overline{x}_2,\overline{y}_2,\overline{z}_2)$ is given as

$$\begin{aligned} \overline{x}_{e_2} = \sqrt{\overline{m}^2-a_y^{\, 2} - \overline{z}_2^{\, 2}} \, . \end{aligned}$$

(B20)

Given the conditions in previous case, there are no intersections of the boundary of the neighborhood with the edge of the cell between the vertices $(a_x,\overline{y}_2,\overline{z}_2)$ and $(\overline{x}_2,\overline{y}_2,\overline{z}_2)$.

The quadrature coefficient in case-4 is therefore computed as

$$\begin{aligned} \begin{aligned} \beta _{ij}&= 2^s \left[ \int _{a_x}^{\overline{x}_{e_2}} \int _{a_y}^{\sqrt{\overline{m}^2 -\overline{x}^2 - \overline{z}_2^{\, 2}}} \overline{z}_2 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}}\right. \\&\quad + \int _{a_x}^{\overline{x}_{e_2}} \int _{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}}}^{\overline{y}_2} \sqrt{\overline{m}^2-\overline{x}^2 -\overline{y}^2} {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \\&\quad \left. + \int _{\overline{x}_{e_2}}^{b_x} \int _{a_y}^{\overline{y}_2} \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}^2} {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} - \int _{a_x}^{b_x} \int _{a_y}^{\overline{y}_2} \overline{z}_1 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \right] \\&= 2^s \left[ \overline{z}_2 \int _{a_x}^{\overline{x}_{e_2}} \left( \sqrt{\overline{m}^2 -\overline{x}^2 - \overline{z}_2^{\, 2}} - a_y \right) {\mathrm {d}} {\overline{x}} \right. \\&\quad \left. + \int _{a_x}^{\overline{x}_{e_2}} \frac{1}{2} \left( \left( \overline{m}^2 - \overline{x}^2 \right) \arcsin \left( \frac{\overline{y}_2}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \right. \right. \\&\quad + \overline{y}_2 \, \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}_2^{\, 2}} \\&\quad \left. \left. - \left( \overline{m}^2 - \overline{x}^2 \right) \, \arcsin \left( \frac{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}}}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \right. \right. \\&\quad \left. - \overline{z}_2 \sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}} \right) {\mathrm {d}} {\overline{x}} \\&\quad \left. + \int _{\overline{x}_{e_2}}^{b_x} \frac{1}{2} \left( \left( \overline{m}^2 - \overline{x}^2 \right) \arcsin \left( \frac{\overline{y}_2}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \right. \right. \\&\quad + \overline{y}_2 \, \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}_2^{\, 2}} \\&\quad \left. - \left( \overline{m}^2 - \overline{x}^2 \right) \, \arcsin \left( \frac{a_y}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \right. \\&\quad \left. - a_y \sqrt{\overline{m}^2-\overline{x}^2 - a_y^{\, 2}} \right) {\mathrm {d}} {\overline{x}} \\&\quad - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( b_x-a_x \right) \bigg ] \, . \end{aligned} \end{aligned}$$

(B21)

Using Eqs. (B12), (B13) and (B14), Eq. (B21) is solved as follows:

$$\begin{aligned} \begin{aligned} \beta _{ij}&= 2^s \left[ \overline{z}_2 \, I_1 (a_x, \overline{x}_{e_2}, \overline{z}_2) - \overline{z}_2 a_y \left( \overline{x}_{e_2} - a_x \right) \right. \\&\quad + \frac{1}{2} I_2 (a_x, \overline{x}_{e_2}, \overline{y}_2) + \frac{1}{2} \overline{y}_2 \, I_1 (a_x, \overline{x}_{e_2}, \overline{y}_2) \\&\quad - \frac{1}{2} I_3 (a_x, \overline{x}_{e_2}, \overline{z}_2) - \frac{1}{2} \overline{z}_2 \, I_1 (a_x, \overline{x}_{e_2}, \overline{z}_2) \\&\quad + \frac{1}{2} I_2 (\overline{x}_{e_2}, b_x, \overline{y}_2) + \frac{1}{2} \overline{y}_2 \, I_1 (\overline{x}_{e_2}, b_x, \overline{y}_2) \\&\quad - \frac{1}{2} I_2 (\overline{x}_{e_2}, b_x, a_y) - \frac{1}{2} a_y \, I_1 (\overline{x}_{e_2}, b_x, a_y) \\&\quad \left. - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( b_x-a_x \right) \right] \\&= 2^s \left[ \frac{1}{2} \overline{z}_2 \, I_1 (a_x, \overline{x}_{e_2}, \overline{z}_2) + \frac{1}{2} \overline{y}_2 \, I_1 (a_x, b_x, \overline{y}_2) \right. \\&\quad - \frac{1}{2} a_y \, I_1 (\overline{x}_{e_2}, b_x, a_y) + \frac{1}{2} I_2 (a_x, b_x, \overline{y}_2) \\&\quad - \frac{1}{2} I_2 (\overline{x}_{e_2}, b_x, a_y) - \frac{1}{2} I_3 (a_x, \overline{x}_{e_2}, \overline{z}_2) \\&\quad \left. - \overline{z}_2 a_y \left( \overline{x}_{e_2} - a_x \right) - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( b_x-a_x \right) \right] . \end{aligned} \end{aligned}$$

(B22)

1.5 Case-5

In case-5, the boundary of the neighborhood intersects both the edge of the cell between the vertices $(a_x,a_y,\overline{z}_2)$ and $(\overline{x}_2,a_y,\overline{z}_2)$ and the face on the plane $\overline{z} = \overline{z}_1$, as shown in Fig. 9e. Therefore, the conditions in this case are

$$\begin{aligned} a_x^{\, 2} + a_y^{\, 2} + \overline{z}_2^{\, 2} \le \overline{m}^2< \overline{x}_2^{\, 2} + a_y^{\, 2} + \overline{z}_2^{\, 2} \text { and } \overline{m}^2 < \overline{x}_2^{\, 2} + \overline{y}_2^{\, 2} + \overline{z}_1^{\, 2} \, . \end{aligned}$$

(B23)

With the same approach illustrated at the beginning of Sect. B.2, one can also show that the vertices $(a_x,\overline{y}_2,\overline{z}_1)$ and $(\overline{x}_2,a_y,\overline{z}_1)$ lie within the neighborhood for the considered cells ($\overline{z}_j \ge \overline{y}_j \ge \overline{x}_j \ge 0$), so that there is an intersection with the edge between $(a_x,\overline{y}_2,\overline{z}_1)$ and $(\overline{x}_2,\overline{y}_2,\overline{z}_1)$ and the edge between $(a_x,a_y,\overline{z}_1)$ and $(\overline{x}_2,a_y,\overline{z}_1)$ lies completely within the neighborhood.

The intersection of the boundary of the neighborhood with the edge between the vertices $(a_x,\overline{y}_2,\overline{z}_2)$ and $(\overline{x}_2,\overline{y}_2,\overline{z}_2)$ is given in Eq. (B20), whereas the intersection with the edge between $(a_x,\overline{y}_2,\overline{z}_1)$ and $(\overline{x}_2,\overline{y}_2,\overline{z}_1)$ is given as

$$\begin{aligned} \overline{x}_{e_3} = \sqrt{\overline{m}^2-\overline{y}_2^{\, 2} - \overline{z}_1^{\, 2}} \, . \end{aligned}$$

(B24)

Note that $\overline{x}_{e_2} \le \overline{x}_{e_3}$ since:

$$\begin{aligned} \begin{aligned}&\overline{m}^2 - a_y^{\, 2} - \overline{z}_2^{\, 2} \le \overline{m}^2 - \overline{y}_2^{\, 2} - \overline{z}_1^{\, 2} \\&\quad \Rightarrow \quad \overline{z}_2^{\, 2} - \overline{z}_1^{\, 2} \ge \overline{y}_2^{\, 2} - a_y^{\, 2} \, . \end{aligned} \end{aligned}$$

(B25)

If the cell has two symmetries ($s=2$, $a_y=0$), Eq. (B25) becomes $2\overline{z}_j \ge 0.5^{\, 2}$ which is always verified ($\overline{z}_j \ge 1$). If the cell has one or no symmetries, Eq. (B25) becomes $2\overline{z}_j \ge 2\overline{y}_j$ which is always verified.

In case-5, the boundary of the neighborhood intersects both faces on the planes $\overline{z} = \overline{z}_2$ and $\overline{z} = \overline{z}_1$. The equation of the former intersection is written in Eq. (B9), while the latter is given as

$$\begin{aligned} \overline{y}_{f_2} (\overline{x}) = \sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_1^{\, 2}} \, . \end{aligned}$$

(B26)

The quadrature coefficient in case-5 is computed as

$$\begin{aligned} \begin{aligned} \beta _{ij}&= 2^s \left[ \int _{a_x}^{\overline{x}_{e_2}} \int _{a_y}^{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}}} \overline{z}_2 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}}\right. \\&\quad + \int _{a_x}^{\overline{x}_{e_2}} \int _{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}}}^{\overline{y}_2} \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}^2} {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \\&\quad + \int _{\overline{x}_{e_2}}^{\overline{x}_{e_3}} \int _{a_y}^{\overline{y}_2} \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}^2} {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \\&\quad + \int _{\overline{x}_{e_3}}^{b_x} \int _{a_y}^{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_1^{\, 2}}} \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}^2} {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \\&\quad \left. - \int _{a_x}^{\overline{x}_{e_3}} \int _{a_y}^{\overline{y}_2} \overline{z}_1 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} - \int _{\overline{x}_{e_3}}^{b_x} \int _{a_y}^{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_1^{\, 2}}} \overline{z}_1 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \right] \\&= 2^s \left[ \overline{z}_2 \int _{a_x}^{\overline{x}_{e_2}} \left( \sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}} - a_y \right) {\mathrm {d}} {\overline{x}} \right. \\&\quad + \int _{a_x}^{\overline{x}_{e_2}} \frac{1}{2} \left( \left( \overline{m}^2 - \overline{x}^2 \right) \arcsin \left( \frac{\overline{y}_2}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \right. \\&\quad + \overline{y}_2 \, \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}_2^{\, 2}} \\&\quad - \left( \overline{m}^2 - \overline{x}^2 \right) \, \arcsin \left( \frac{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}}}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \\&\quad \left. - \overline{z}_2 \sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_2^{\, 2}} \right) {\mathrm {d}} {\overline{x}} \\&\quad + \int _{\overline{x}_{e_2}}^{\overline{x}_{e_3}} \frac{1}{2} \left( \left( \overline{m}^2 - \overline{x}^2 \right) \arcsin \left( \frac{\overline{y}_2}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \right. \\&\quad + \overline{y}_2 \, \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}_2^{\, 2}} \\&\quad - \left( \overline{m}^2 - \overline{x}^2 \right) \, \arcsin \left( \frac{a_y}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \\&\quad \left. - a_y \sqrt{\overline{m}^2-\overline{x}^2 - a_y^{\, 2}} \right) {\mathrm {d}} {\overline{x}} \\&\quad + \int _{\overline{x}_{e_3}}^{b_x} \frac{1}{2} \left( \left( \overline{m}^2 - \overline{x}^2 \right) \arcsin \left( \frac{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_1^{\, 2}}}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \right. \\&\quad + \overline{z}_1 \, \sqrt{\overline{m}^2-\overline{x}^2-\overline{z}_1^{\, 2}} \\&\quad - \left( \overline{m}^2 - \overline{x}^2 \right) \, \arcsin \left( \frac{a_y}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \\&\quad \left. - a_y \sqrt{\overline{m}^2-\overline{x}^2 - a_y^{\, 2}} \right) {\mathrm {d}} {\overline{x}} \\&\quad - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( \overline{x}_{e_3}-a_x \right) \\&\quad \left. - \overline{z}_1 \int _{\overline{x}_{e_3}}^{b_x} \left( \sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_1^{\, 2}} - a_y \right) {\mathrm {d}} {\overline{x}} \right] \, . \end{aligned} \end{aligned}$$

(B27)

Using Eqs. (B12), (B13) and (B14), Eq. (B27) is solved as follows:

$$\begin{aligned} \begin{aligned} \beta _{ij}&= 2^s \left[ \overline{z}_2 \, I_1 (a_x, \overline{x}_{e_2}, \overline{z}_2) - \overline{z}_2 a_y \left( \overline{x}_{e_2} - a_x \right) \right. \\&\quad + \frac{1}{2} I_2 (a_x, \overline{x}_{e_2}, \overline{y}_2) + \frac{1}{2} \overline{y}_2 \, I_1 (a_x, \overline{x}_{e_2}, \overline{y}_2) \\&\quad - \frac{1}{2} I_3 (a_x, \overline{x}_{e_2}, \overline{z}_2) - \frac{1}{2} \overline{z}_2 \, I_1 (a_x, \overline{x}_{e_2}, \overline{z}_2) \\&\quad + \frac{1}{2} I_2 (\overline{x}_{e_2}, \overline{x}_{e_3}, \overline{y}_2) + \frac{1}{2} \overline{y}_2 \, I_1 (\overline{x}_{e_2}, \overline{x}_{e_3}, \overline{y}_2) \\&\quad - \frac{1}{2} I_2 (\overline{x}_{e_2}, \overline{x}_{e_3}, a_y) - \frac{1}{2} a_y \, I_1 (\overline{x}_{e_2}, \overline{x}_{e_3}, a_y) \\&\quad + \frac{1}{2} I_3 (\overline{x}_{e_3}, b_x, \overline{z}_1) + \frac{1}{2} \overline{z}_1 \, I_1 (\overline{x}_ {e_3}, b_x, \overline{z}_1) \\&\quad - \frac{1}{2} I_2 (\overline{x}_{e_3}, b_x, a_y) - \frac{1}{2} a_y \, I_1 (\overline{x}_{e_3}, b_x, a_y) \\&\quad - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( \overline{x}_{e_3}-a_x \right) \\&\quad - \overline{z}_1 \, I_1 (\overline{x}_ {e_3}, b_x, \overline{z}_1) + \overline{z}_1 a_y \left( b_x-\overline{x}_{e_3} \right) \bigg ] \\&= 2^s \left[ \frac{1}{2} \overline{z}_2 \, I_1 (a_x, \overline{x}_{e_2}, \overline{z}_2) + \frac{1}{2} \overline{y}_2 \, I_1 (a_x, \overline{x}_{e_3}, \overline{y}_2)\right. \\&\quad - \frac{1}{2} \overline{z}_1 \, I_1 (\overline{x}_ {e_3}, b_x, \overline{z}_1) \\&\quad - \frac{1}{2} a_y \, I_1 (\overline{x}_{e_2}, b_x, a_y) + \frac{1}{2} I_2 (a_x, \overline{x}_{e_3}, \overline{y}_2) \\&\quad - \frac{1}{2} I_2 (\overline{x}_{e_2}, b_x, a_y) - \frac{1}{2} I_3 (a_x, \overline{x}_{e_2}, \overline{z}_2) \\&\quad + \frac{1}{2} I_3 (\overline{x}_{e_3}, b_x, \overline{z}_1) - \overline{z}_2 a_y \left( \overline{x}_{e_2} - a_x \right) \\&\quad - \overline{z}_1 \overline{y}_2 \left( \overline{x}_{e_3}-a_x \right) + \overline{z}_1 a_y \left( b_x-a_x \right) \bigg ] . \end{aligned} \end{aligned}$$

(B28)

1.6 Case-6

In case-6, the face of the cell on the plane $\overline{z} = \overline{z}_2$ is completely outside the neighborhood and the face on the plane $\overline{z} = \overline{z}_1$ is completely inside, as shown in Fig. 9f. Therefore, the condition in this case is

$$\begin{aligned} \overline{x}_2^{\, 2} + \overline{y}_2^{\, 2} + \overline{z}_1^{\, 2} \le \overline{m}^2 < a_x^{\, 2} + a_y^{\, 2} + \overline{z}_2^{\, 2} \, . \end{aligned}$$

(B29)

The quadrature coefficient in case-6 is computed as

$$\begin{aligned} \begin{aligned} \beta _{ij}&= 2^s \left[ \int _{a_x}^{b_x} \int _{a_y}^{\overline{y}_2} \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}^2} {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} - \int _{a_x}^{b_x} \int _{a_y}^{\overline{y}_2} \overline{z}_1 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \right] \\&= 2^s \left[ \int _{a_x}^{b_x} \frac{1}{2} \left( \left( \overline{m}^2 - \overline{x}^2 \right) \arcsin \left( \frac{\overline{y}_2}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \right. \right. \\&\quad + \overline{y}_2 \, \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}_2^{\, 2}} \\&\quad - \left( \overline{m}^2 - \overline{x}^2 \right) \, \arcsin \left( \frac{a_y}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \\&\quad \left. - a_y \sqrt{\overline{m}^2-\overline{x}^2 - a_y^{\, 2}} \right) {\mathrm {d}} {\overline{x}} \\&\quad - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( b_x-a_x \right) \bigg ] \, . \end{aligned} \end{aligned}$$

(B30)

Using Eqs. (B12), (B13) and (B14), Eq. (B30) is solved as follows:

$$\begin{aligned} \begin{aligned} \beta _{ij}&= 2^s \left[ \frac{1}{2} I_2 (a_x, b_x, \overline{y}_2) + \frac{1}{2} \overline{y}_2 \, I_1 (a_x, b_x, \overline{y}_2) \right. \\&\quad - \frac{1}{2} I_2 (a_x, b_x, a_y) - \frac{1}{2} a_y \, I_1 (a_x, b_x, a_y) \\&\quad \left. - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( b_x-a_x \right) \right] \\&= 2^s \left[ \frac{1}{2} \overline{y}_2 \, I_1 (a_x, b_x, \overline{y}_2) - \frac{1}{2} a_y \, I_1 (a_x, b_x, a_y)\right. \\&\quad + \frac{1}{2} I_2 (a_x, b_x, \overline{y}_2) \\&\quad \left. - \frac{1}{2} I_2 (a_x, b_x, a_y) - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( b_x-a_x \right) \right] . \end{aligned} \end{aligned}$$

(B31)

1.7 Case-7

In case-7, the boundary of the neighborhood intersects the edge of the cell between the vertices $(a_x,\overline{y}_2,\overline{z}_1)$ and $(\overline{x}_2,\overline{y}_2,\overline{z}_1)$, as shown in Fig. 9g. Therefore, the condition in this case is

$$\begin{aligned} a_x^{\, 2} + \overline{y}_2^{\, 2} + \overline{z}_1^{\, 2} \le \overline{m}^2 < \overline{x}_2^{\, 2} + \overline{y}_2^{\, 2} + \overline{z}_1^{\, 2} \, . \end{aligned}$$

(B32)

With the same approach illustrated at the beginning of Sect. B.2, one can also show that the vertex $(\overline{x}_2,a_y,\overline{z}_1)$ lies within the neighborhood for the considered cells ($\overline{z}_j \ge \overline{y}_j \ge \overline{x}_j \ge 0$), so that the edge between $(a_x,a_y,\overline{z}_1)$ and $(\overline{x}_2,a_y,\overline{z}_1)$ lies completely within the neighborhood. The intersection of the boundary of the neighborhood with the edge between the vertices $(a_x,\overline{y}_2,\overline{z}_1)$ and $(\overline{x}_2,\overline{y}_2,\overline{z}_1)$ is given by $\overline{x}_{e_3}$ in Eq. (B24).

Therefore, the quadrature coefficient in case-7 is computed as

$$\begin{aligned} \begin{aligned} \beta _{ij}&= 2^s \left[ \int _{a_x}^{\overline{x}_{e_3}} \int _{a_y}^{\overline{y}_2} \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}^2} {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \right. \\&\quad + \int _{\overline{x}_{e_3}}^{b_x} \int _{a_y}^{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_1^{\, 2}}} \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}^2} {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \\&\quad \left. - \int _{a_x}^{\overline{x}_{e_3}} \int _{a_y}^{\overline{y}_2} \overline{z}_1 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} - \int _{\overline{x}_{e_3}}^{b_x} \int _{a_y}^{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_1^{\, 2}}} \overline{z}_1 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \right] \\&= 2^s \left[ \int _{a_x}^{\overline{x}_{e_3}} \frac{1}{2} \left( \left( \overline{m}^2 - \overline{x}^2 \right) \arcsin \left( \frac{\overline{y}_2}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \right. \right. \\&\quad + \overline{y}_2 \, \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}_2^{\, 2}} \\&\quad - \left( \overline{m}^2 - \overline{x}^2 \right) \, \arcsin \left( \frac{a_y}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \\&\quad \left. - a_y \sqrt{\overline{m}^2-\overline{x}^2 - a_y^{\, 2}} \right) {\mathrm {d}} {\overline{x}} \\&\quad + \int _{\overline{x}_{e_3}}^{b_x} \frac{1}{2} \left( \left( \overline{m}^2 - \overline{x}^2 \right) \arcsin \left( \frac{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_1^{\, 2}}}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \right. \\&\quad + \overline{z}_1 \, \sqrt{\overline{m}^2-\overline{x}^2-\overline{z}_1^{\, 2}} \\&\quad - \left( \overline{m}^2 - \overline{x}^2 \right) \, \arcsin \left( \frac{a_y}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \\&\quad \left. - a_y \sqrt{\overline{m}^2-\overline{x}^2 - a_y^{\, 2}} \right) {\mathrm {d}} {\overline{x}} \\&\quad - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( \overline{x}_{e_3}-a_x \right) \\&\quad \left. - \overline{z}_1 \int _{\overline{x}_{e_3}}^{b_x} \left( \sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_1^{\, 2}} - a_y \right) {\mathrm {d}} {\overline{x}} \right] \, . \end{aligned} \end{aligned}$$

(B33)

Using Eqs. (B12), (B13) and (B14), Eq. (B33) is solved as follows:

$$\begin{aligned} \begin{aligned} \beta _{ij}&= 2^s \left[ \frac{1}{2} I_2 (a_x, \overline{x}_{e_3}, \overline{y}_2) + \frac{1}{2} \overline{y}_2 \, I_1 (a_x, \overline{x}_{e_3}, \overline{y}_2) \right. \\&\quad - \frac{1}{2} I_2 (a_x, \overline{x}_{e_3}, a_y) - \frac{1}{2} a_y \, I_1 (a_x, \overline{x}_{e_3}, a_y) \\&\quad + \frac{1}{2} I_3 (\overline{x}_{e_3}, b_x, \overline{z}_1) + \frac{1}{2} \overline{z}_1 \, I_1 (\overline{x}_ {e_3}, b_x, \overline{z}_1)\\&\quad - \frac{1}{2} I_2 (\overline{x}_{e_3}, b_x, a_y) - \frac{1}{2} a_y \, I_1 (\overline{x}_{e_3}, b_x, a_y) \\&\quad - \overline{z}_1 \left( \overline{y}_2-a_y \right) \left( \overline{x}_{e_3}-a_x \right) - \overline{z}_1 \, I_1 (\overline{x}_ {e_3}, b_x, \overline{z}_1) \\&\quad + \overline{z}_1 a_y \left( b_x-\overline{x}_{e_3} \right) \bigg ] \\&= 2^s \left[ \frac{1}{2} \overline{y}_2 \, I_1 (a_x, \overline{x}_{e_3}, \overline{y}_2) - \frac{1}{2} \overline{z}_1 \, I_1 (\overline{x}_ {e_3}, b_x, \overline{z}_1) \right. \\&\quad - \frac{1}{2} a_y \, I_1 (a_x, b_x, a_y) + \frac{1}{2} I_2 (a_x, \overline{x}_{e_3}, \overline{y}_2) \\&\quad - \frac{1}{2} I_2 (a_x, b_x, a_y) + \frac{1}{2} I_3 (\overline{x}_{e_3}, b_x, \overline{z}_1) \\&\quad \left. - \overline{z}_1 \overline{y}_2 \left( \overline{x}_{e_3}-a_x \right) + \overline{z}_1 a_y \left( b_x-a_x \right) \right] . \end{aligned} \end{aligned}$$

(B34)

1.8 Case-8 or case-9

In case-8 or case-9, the edge of the cell between the vertices $(a_x,a_y,\overline{z}_1)$ and $(\overline{x}_2,a_y,\overline{z}_1)$ may be intersected by the boundary of the neighborhood or may be completely within the neighborhood, but all the other edges parallel to the $\overline{x}$-axis are completely outside the neighborhood, as shown in Fig. 9h, i. Therefore, the condition in this case is

$$\begin{aligned} a_x^{\, 2} + a_y^{\, 2} + \overline{z}_1^{\, 2} \le \overline{m}^2 < a_x^{\, 2} + \overline{y}_2^{\, 2} + \overline{z}_1^{\, 2} \, . \end{aligned}$$

(B35)

The intersection of the boundary of the neighborhood with the edge between the vertices $(a_x,a_y,\overline{z}_1)$ and $(\overline{x}_2,a_y,\overline{z}_1)$ is given as

$$\begin{aligned} \overline{x}_{e_4} = \sqrt{\overline{m}^2-a_y^{\, 2} - \overline{z}_1^{\, 2}} \, . \end{aligned}$$

(B36)

Case-8 and case-9 can be treated as a single case because of the definition of the upper limit of the outer integral as $b_x = \min \left( \overline{x}_2, \overline{x}_{e_4} \right)$ (see Eq. (26)).

Therefore, the quadrature coefficient in case-8 and case-9 is computed as

$$\begin{aligned} \begin{aligned} \beta _{ij}&= 2^s \left[ \int _{a_x}^{b_x} \int _{a_y}^{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_1^{\, 2}}} \sqrt{\overline{m}^2-\overline{x}^2-\overline{y}^2} {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}}\right. \\&\quad \left. - \int _{a_x}^{b_x} \int _{a_y}^{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_1^{\, 2}}} \overline{z}_1 {\mathrm {d}} {\overline{y}} {\mathrm {d}} {\overline{x}} \right] \\&= 2^s \left[ \int _{a_x}^{b_x} \frac{1}{2} \left( \left( \overline{m}^2 - \overline{x}^2 \right) \arcsin \left( \frac{\sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_1^{\, 2}}}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \right. \right. \\&\quad + \overline{z}_1 \, \sqrt{\overline{m}^2-\overline{x}^2-\overline{z}_1^{\, 2}} \\&\quad - \left( \overline{m}^2 - \overline{x}^2 \right) \, \arcsin \left( \frac{a_y}{\sqrt{\overline{m}^2-\overline{x}^2}} \right) \\&\quad \left. - a_y \sqrt{\overline{m}^2-\overline{x}^2 - a_y^{\, 2}} \right) {\mathrm {d}} {\overline{x}} \\&\quad \left. - \overline{z}_1 \int _{a_x}^{b_x} \left( \sqrt{\overline{m}^2-\overline{x}^2 - \overline{z}_1^{\, 2}} - a_y \right) {\mathrm {d}} {\overline{x}} \right] \, . \end{aligned} \end{aligned}$$

(B37)

Using Eqs. (B12), (B13) and (B14), Eq. (B37) is solved as follows:

$$\begin{aligned} \begin{aligned} \beta _{ij}&= 2^s \left[ \frac{1}{2} I_3 (a_x, b_x, \overline{z}_1) + \frac{1}{2} \overline{z}_1 \, I_1 (a_x, b_x, \overline{z}_1) - \frac{1}{2} I_2 (a_x, b_x, a_y) \right. \\&\quad \left. - \frac{1}{2} a_y \, I_1 (a_x, b_x, a_y) - \overline{z}_1 \, I_1 (a_x, b_x, \overline{z}_1) + \overline{z}_1 a_y \left( b_x-a_x \right) \right] \\&= 2^s \left[ - \frac{1}{2} \overline{z}_1 \, I_1 (a_x, b_x, \overline{z}_1) - \frac{1}{2} a_y \, I_1 (a_x, b_x, a_y)\right. \\&\quad \left. - \frac{1}{2} I_2 (a_x, b_x, a_y) + \frac{1}{2} I_3 (a_x, b_x, \overline{z}_1) + \overline{z}_1 a_y \left( b_x-a_x \right) \right] . \end{aligned} \end{aligned}$$

(B38)

1.9 Case-10

In case-10, the cell is completely outside the neighborhood, as shown in Fig. 9j. The condition for which this case is verified is that the closest node with coordinates $(a_x,a_y,\overline{z}_1)$ lies outside the neighborhood:

$$\begin{aligned} \overline{m}^2 < a_x^{\, 2} + a_y^{\, 2} + \overline{z}_1^{\, 2} \, . \end{aligned}$$

(B39)

In this case, the solution of Eq. (B1) is trivial:

$$\begin{aligned} \beta _{ij} = 0 \, . \end{aligned}$$

(B40)

Appendix C: Derivatives for the Taylor series expansion

We need to perform the Taylor series expansion of the function:

$$\begin{aligned} f(\overline{x}) := \arcsin \left( \frac{k_2}{ \sqrt{ \overline{m}^2-\overline{x}^2 } } \right) \, . \end{aligned}$$

(C1)

Therefore, we have to compute the derivatives of $f(\overline{x})$, which will be denoted as $f^{(n)} (\overline{x})$ where $n > 1$ is the order of the derivative. After taking the first derivatives, one can recognize the following recursive pattern:

$$\begin{aligned} f^{(n)} (\overline{x}) = \frac{ \sum \limits _{p=1}^{\lfloor 3n/2 \rfloor } \left( \sum \limits _{q=1}^{p} c(n,p,q) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q-1} \right) \overline{x}^{ 3n-2p} }{ \left( \overline{m}^2 - \overline{x}^2 \right) ^n \left( \overline{m}^2 - \overline{x}^2 - k_2^{\, 2} \right) ^{n-1/2} } \, , \end{aligned}$$

(C2)

where c(n, p, q) are some coefficients depending on the order n of the corresponding derivative and on the indices p and q. In order to compute these coefficients c, we take the derivative of $f^{(n-1)} (\overline{x})$ and the final solution should be equal to $f^{(n)} (\overline{x})$:

$$\begin{aligned} \begin{aligned}&\frac{{\mathrm{d}}}{{\mathrm{d}}\overline{x}} \, f^{(n-1)} (\overline{x}) \\&\quad = \frac{{\mathrm{d}}}{{\mathrm{d}}\overline{x}} \left[ \frac{ \sum \nolimits _{p=1}^{\lfloor 3(n-1)/2 \rfloor } \left( \sum \nolimits _{q=1}^{p} c(n-1,p,q) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q-1} \right) \overline{x}^{3(n-1)-2p} }{ \left( \overline{m}^2 - \overline{x}^2 \right) ^{n-1} \left( \overline{m}^2 - \overline{x}^2 - k_2^{\, 2} \right) ^{n-3/2} } \right] \\&\quad = \left\{ \left[ \sum \limits _{p=1}^{\lfloor 3(n-1)/2 \rfloor } \left( \sum \limits _{q=1}^{p} c(n-1,p,q) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q-1} \right) \right. \right. \\&\qquad \times \left. \left. \left( 3n-2p-3 \right) \overline{x}^{3n-2p-4} \right] \cdot \left( \overline{m}^2 - \overline{x}^2 \right) ^{n-1} \left( \overline{m}^2 - \overline{x}^2 - k_2^{\, 2} \right) ^{n-3/2}\right. \\&\qquad \left. - \left[ \sum \limits _{p=1}^{\lfloor 3(n-1)/2 \rfloor } \left( \sum \limits _{q=1}^{p} c(n-1,p,q) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q-1} \right) \overline{x}^{3n-2p-3} \right] \right. \\&\qquad \left. \cdot \Bigg [ \left( n-1 \right) \left( \overline{m}^2 - \overline{x}^2 \right) ^{n-2} \left( -2\overline{x} \right) \left( \overline{m}^2 - \overline{x}^2 - k_2^{\, 2} \right) ^{n-3/2}\right. \\&\qquad \left. + \left( \overline{m}^2 - \overline{x}^2 \right) ^{n-1} \left( n-\frac{3}{2} \right) \left( \overline{m}^2 - \overline{x}^2 - k_2^{\, 2} \right) ^{n-5/2} \left( -2\overline{x} \right) \Bigg ] \right\} \\&\qquad \cdot \frac{1}{ \left( \overline{m}^2 - \overline{x}^2 \right) ^{2(n-1)} \left( \overline{m}^2 - \overline{x}^2 - k_2^{\, 2} \right) ^{2n-3} } \, . \end{aligned} \end{aligned}$$

(C3)

We multiply the numerator and denominator by $\left( \overline{m}^2 - \overline{x}^2 \right) ^{-n+2} \left( \overline{m}^2 - \overline{x}^2 - k_2^{\, 2} \right) ^{-n+5/2}$, so that the denominator is equal to the denominator of $f^{(n)} (\overline{x})$. Therefore, the numerator becomes:

$$\begin{aligned} \begin{aligned}&\left\{ \left[ \sum \limits _{p=1}^{\lfloor 3(n-1)/2 \rfloor } \left( \sum \limits _{q=1}^{p} c(n-1,p,q) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q-1} \right) \right. \right. \\&\qquad \left. \left. \times \left( 3n-2p-3 \right) \overline{x}^{3n-2p-4} \right] \cdot \left( \overline{m}^2 - \overline{x}^2 \right) \left( \overline{m}^2 - \overline{x}^2 - k_2^{\, 2} \right) \right. \\&\qquad - \left. \left[ \sum \limits _{p=1}^{\lfloor 3(n-1)/2 \rfloor } \left( \sum \limits _{q=1}^{p} c(n-1,p,q) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q-1} \right) \overline{x}^{3n-2p-3} \right] \right. \\&\qquad \left. \cdot \left[ -2 \overline{x} \left( n-1 \right) \left( \overline{m}^2 - \overline{x}^2 - k_2^{\, 2} \right) - 2\overline{x} \left( n-\frac{3}{2} \right) \left( \overline{m}^2 - \overline{x}^2 \right) \right] \right\} \\&\quad = \left\{ \left[ \sum \limits _{p=1}^{\lfloor 3(n-1)/2 \rfloor } \left( \sum \limits _{q=1}^{p} c(n-1,p,q) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q-1} \right) \right. \right. \\&\qquad \left. \left. \times \left( 3n-2p-3 \right) \overline{x}^{3n-2p-4} \right] \cdot \left( \overline{m}^4 - 2 \overline{m}^2 \overline{x}^2 - \overline{m}^2 k_2^{\, 2} + \overline{x}^4 + k_2^{\, 2} \overline{x}^2 \right) \right. \\&\left. \qquad - \left[ \sum \limits _{p=1}^{\lfloor 3(n-1)/2 \rfloor } \left( \sum \limits _{q=1}^{p} c(n-1,p,q) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q-1} \right) \overline{x}^{3n-2p-3} \right] \right. \\&\left. \qquad \cdot \left[ \left( -4n+5 \right) \overline{m}^2 \overline{x} + \left( 4n-5 \right) \overline{x}^3 + 2 \left( n-1 \right) k_2^{\, 2} \overline{x} \right] \right\} \\&\quad = \left\{ \sum \limits _{p=1}^{\lfloor 3(n-1)/2 \rfloor } \left( 3n-2p-3 \right) \right. \\&\qquad \left. \times \left( \sum \limits _{q=1}^{p} c(n-1,p,q) \, \overline{m}^{2(p-q+2)} \, k_2^{\, 2q-1} \right) \overline{x}^{3n-2p-4} \right. \\&\qquad \left. + \sum \limits _{p=1}^{\lfloor 3(n-1)/2 \rfloor } \left( -2n+4p+1 \right) \right. \\&\qquad \left. \times \left( \sum \limits _{q=1}^{p} c(n-1,p,q) \, \overline{m}^{2(p-q+1)} \, k_2^{\, 2q-1} \right) \overline{x}^{3n-2p-2} \right. \\&\qquad \left. + \sum \limits _{p=1}^{\lfloor 3(n-1)/2 \rfloor } \left( -3n+2p+3 \right) \right. \\&\qquad \left. \times \left( \sum \limits _{q=1}^{p} c(n-1,p,q) \, \overline{m}^{2(p-q+1)} \, k_2^{\, 2q+1} \right) \overline{x}^{3n-2p-4} \right. \\&\qquad \left. + \sum \limits _{p=1}^{\lfloor 3(n-1)/2 \rfloor } \left( -n-2p+2 \right) \right. \\&\qquad \left. \times \left( \sum \limits _{q=1}^{p} c(n-1,p,q) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q-1} \right) \overline{x}^{3n-2p}\right. \\&\qquad \left. + \sum \limits _{p=1}^{\lfloor 3(n-1)/2 \rfloor } \left( n-2p-1 \right) \right. \\&\qquad \left. \times \left( \sum \limits _{q=1}^{p} c(n-1,p,q) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q+1} \right) \overline{x}^{3n-2p-2} \right\} \, . \end{aligned} \end{aligned}$$

(C4)

We can now change the lower and upper limits of the summations to equalize the exponents of the numerator of $f^{(n)} (\overline{x})$ as follows:

$$\begin{aligned} \begin{aligned}&\left\{ \sum \limits _{p=3}^{\lfloor 3(n-1)/2 \rfloor +2} \left( 3n-2p+1 \right) \right. \\&\quad \left. \left( \sum \limits _{q=1}^{p-2} c(n-1,p-2,q) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q-1} \right) \overline{x}^{3n-2p} \right. \\&\quad \left. + \sum \limits _{p=2}^{\lfloor 3(n-1)/2 \rfloor +1} \left( -2n+4p-3 \right) \right. \\&\quad \left. \left( \sum \limits _{q=1}^{p-1} c(n-1,p-1,q) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q-1} \right) \overline{x}^{3n-2p} \right. \\&\quad \left. + \sum \limits _{p=3}^{\lfloor 3(n-1)/2 \rfloor +2} \left( -3n+2p-1 \right) \right. \\&\quad \left. \left( \sum \limits _{q=2}^{p-1} c(n-1,p-2,q-1) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q-1} \right) \overline{x}^{3n-2p}\right. \\&\quad \left. + \sum \limits _{p=1}^{\lfloor 3(n-1)/2 \rfloor } \left( -n-2p+2 \right) \right. \\&\quad \left. \left( \sum \limits _{q=1}^{p} c(n-1,p,q) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q-1} \right) \overline{x}^{3n-2p} \right. \\&\quad \left. + \sum \limits _{p=2}^{\lfloor 3(n-1)/2 \rfloor +1} \left( n-2p+1 \right) \right. \\&\quad \left. \left( \sum \limits _{q=2}^{p} c(n-1,p-1,q-1) \, \overline{m}^{2(p-q)} \, k_2^{\, 2q-1} \right) \overline{x}^{3n-2p} \right\} \, . \end{aligned} \end{aligned}$$

(C5)

Therefore, c(n, p, q) can be computed from Eq. (C5) (see Algorithm 3).

Also, we need the Taylor series expansion of a similar function:

$$\begin{aligned} g(\overline{x}) := \arcsin \left( \frac{ \sqrt{ \overline{m}^2-\overline{x}^2-k_3^{\, 2} } }{ \sqrt{ \overline{m}^2-\overline{x}^2 } } \right) \, . \end{aligned}$$

(C6)

By repeating the previous procedure for $g(\overline{x})$, we obtain the same coefficients with a negative sign:

$$\begin{aligned} g^{(n)} (\overline{x}) = \frac{ - \sum \limits _{p=1}^{\lfloor 3n/2 \rfloor } \left( \sum \limits _{q=1}^{p} c(n,p,q) \, \overline{m}^{2(p-q)} \, k_3^{\, 2q-1} \right) \overline{x}^{\, 3n-2p} }{ \left( \overline{m}^2 - \overline{x}^{\, 2} \right) ^n \left( \overline{m}^2 - \overline{x}^{\, 2} - k_3^{\, 2} \right) ^{n-1/2} } \, . \end{aligned}$$

(C7)

Appendix D: Quadrature coefficients for $\overline{m} = 3, 4, 6$

We report in Tables 2, 3 and 4 the values of the quadrature coefficients derived from Algorithm 4 for $\overline{m} = 3, 4, 6$, respectively. The Taylor series expansion is truncated at an order $N=20$ to maintain the errors of the computations close to machine precision (see Fig. 10). The bonds are identified by the coordinates $(\overline{x}_j, \overline{y}_j, \overline{z}_j)$ of node j in the system of reference specified in Sect. 3.2, as shown in Fig. 16. The quadrature coefficients which are not listed in the tables are equal to 0.

Table 2 Quadrature coefficients for $\overline{m} = 3$

Table 3 Quadrature coefficients for $\overline{m} = 4$

Table 4 Quadrature coefficients for $\overline{m} = 6$

Fig. 16

The quadrature coefficient $\beta _{ij}$ (for $\overline{m}=3$) of the cell identified, for instance, by the coordinates (1, 1, 2) of node j, is reported in the third row of Table 2