1 Introduction

The numerical analysis of large-deformation dynamic processes in fluid-saturated porous media is extremely relevant to a number of geotechnical problems, such as the study of earthquake-induced landslides [2] and vibratory pile installation [3, 4]. However, the numerical modelling of large deformations is known to be particularly challenging when attempted through conventional, mesh-based numerical methods such as the Finite Element Method (FEM), which often lead to aborted numerical simulations or misleading results due to excessive mesh distortion. To remedy mesh-distortion issues, specific remeshing techniques have been introduced, such as in the case of, e.g., Arbitrary Lagrangian Eulerian (ALE) [5] and Coupled Eulerian Lagrangian (CEL) modelling [6]. Alternatively, several mesh-free/meshless methods have also been proposed, such as the Smoothed Particle Hydrodynamics (SPH) method [7,8,9,10], the Material Point Method (MPM) [11, 12], the element-free Galerkin method [13], the Particle Finite Element Method (PFEM) [14,15,16,17,18], and other mesh-free methods [19,20,21,22]. A recent review on the subject of large deformation modelling can be found, for instance, in Soga et al. [2] and Chen et al. [23].

Over the past few years, MPM has been increasingly recognised as a suitable approach for large-deformation modelling, as it combines the advantages of both Lagrangian and Eulerian methods. MPM uses a background mesh for solving all governing equations in their discrete form, while relevant state variables are stored at Material Points (MPs) that can freely move through the background mesh. This work looks specifically at the MPM modelling of coupled hydro-mechanical problems in geo-engineering, which has recently been the subject of several valuable contributions [24,25,26,27,28,29,30,31,32,33,34,35,36,37]. Building on existing FEM literature [38], the MPM solution of dynamic two-phase problems has most often been tackled using one of two alternative mathematical formulations: (i) the u–p formulation, in which the total solid displacement (u) and the pore fluid pressure (p) are adopted as primary unknowns, or (ii) the v–w formulation, in which the velocities of the solid (v) and fluid (w) phases are considered instead. The main difference between these two options lies in whether or not the relative acceleration of the fluid with respect to the solid is taken into account – in fact, the relative acceleration of the pore fluid is neglected in the u–p formulation [38]. Although the u–p formulation is known to be inaccurate for fast dynamic phenomena, a number of coupled MPM implementations have been developed based on this approach [24,25,26, 29, 31]. Conversely, the accelerations of both the solid and fluid phases are exactly represented in formulations of the v–w type (in essence equivalent to the u–U form described by Zienkiewicz et al. [38], where u and U are the total displacements of the solid and fluid phases, respectively), which are therefore applicable to any dynamic regime. In the light of this consideration, several MPM implementations have been built on the v–w approach [1, 27, 28, 30, 32,33,34,35,36, 39, 40].

Another key aspect that affects the computational performance of MPM is the adopted time integration algorithm. It is well known that the implicit version of MPM [41,42,43,44,45,46,47,48] generally allows for larger time steps and can be more stable. However, previous implicit MPMs have so far mainly been developed for the analysis of single-phase problems. For two-phase applications, most coupled MPMs adopt explicit time integration, although a very few instances of semi-implicit and fully implicit schemes have recently begun to emerge in the literature [48, 49]. To obtain better computational efficiency with respect to explicit algorithms (especially for long-lasting consolidation problems) and enable accurate MPM modelling both of slow and fast dynamic problems, this paper for the first time proposes a fully implicit coupled MPM using a complete three-field (i.e., u–p–U) formulation.

As standard MPM formulations often use low-order shape functions over the background mesh for the relevant field variables (usually two), pore pressure instabilities may arise in the vicinity of the so-called undrained-incompressible limit. Similarly to that observed for two-phase FEM models, the violation of the well-known inf-sup condition can result in undesired pore pressure oscillations and, overall, inaccurate results [50, 51]. A typical countermeasure (often applied in FEM) is to use different orders of interpolation for the primary variables – e.g., in u–p-based two-phase models, the displacement field would require shape functions of higher order than for the pore pressure [52]. However, the computational convenience of equal/low-order interpolation in MPM has promoted the development of MPMs that can suppress pore pressure instabilities by means of fractional time stepping [28], polynomial pressure projection [48], and reduced integration [1, 27, 30, 40]. Zheng et al. [1] recently proposed an explicit coupled MPM in which numerical instabilities are substantially alleviated by combining selective reduced integration with a patch recovery of pore pressures based on Moving Least Square Approximation (MLSA).

The main motivation of this paper is to develop a new fully implicit, stabilised coupled MPM for dynamic hydromechanical problems under different regimes of material deformation (small versus large) and dynamic motion (slow versus fast). The proposed method for the first time builds on a three-field formulation of the underlying coupled problem, and adopts the Generalised Interpolation Material Point (GIMP) method proposed by Bardenhagen and Kober [53] to mitigate the spurious stress oscillations associated in the original MPM with MP cell-crossing. The three-field formulation adopts equal-order interpolation for the selected primary variables, i.e., solid displacement (u), pore pressure (p), and fluid displacement (U). The resulting u–p–U formulation enables accurate analysis of slow as well as fast dynamic phenomena [54], and has been successfully implemented/verified in FEM [55,56,57,58]. In the context of FEM, the u–p–U approach has also been shown to be a generally good remedy against undrained pore pressure instabilities, although it is not always effective in 2D/3D problems when all primary unknowns are interpolated with shape functions of the lowest order [55]. Since similar issues have also been experienced in MPM/GIMP calculations, the MLSA-based patch recovery proposed by Zheng et al. [1] is incorporated in the implicit MPM presented herein, so as to improve the recovery of pore pressures to the MPs and mitigate the effects of hydro-mechanical instabilities. The resulting u–p–U MPM enhanced with MLSA-based patch recovery is straightforward to implement in an implicit coupled MPM code, and also efficient owing to the use of a single set of MPs to represent both the solid and fluid phases – the alternative option of using two sets of MPs has been explored, e.g., by Soga et al. [2].

The remainder of this paper focuses on the formulation and verification of the proposed implicit MPM. Emphasis is on the verification of its accuracy under different regimes of material deformation (small versus large) and dynamic motion (slow versus fast). Special attention is also devoted to highlighting the computational convenience of implicit MPM modelling in comparison to the explicit MPM.

2 u–p–U formulation for dynamic hydromechanical problems

The dynamic response of water-saturated porous media, such as soils, is considered here. The mass density of the soil-water mixture is obtained from the individual phase densities as \(\rho =n\rho _s+\left( 1-n\right) \rho _w\), where the subscripts s and w denote the solid and water phases, respectively, and n is the volume porosity. Based on the well established effective stress principle, the behaviour of the solid skeleton is assumed to be governed by the effective stress \(\varvec{\sigma }'\), defined, in vector notation, as \(\varvec{\sigma }' = \varvec{\sigma } + {\varvec{m}}{p}\), where \(\varvec{\sigma }\) is the total stress, p is the pore water pressure, and \({\varvec{m}}\) is the vector representation of the Kronecker tensor. In what follows, bold symbols indicate matrices and vectors; positive values are used for tensile total/effective stress components and compressive pore pressures.

The equations governing the dynamic motion of a fully saturated porous medium are hereafter summarised following the work of Zienkiewicz and co-workers [54, 59]. The momentum balance for the whole two-phase mixture prescribes that

$$\begin{aligned} {\mathbf {S}}^{\mathrm {T}}\varvec{\sigma }-\rho \ddot{{\varvec{u}}}-\rho _w\ddot{{\varvec{u}}}_r+\rho {\varvec{b}}={\varvec{0}} \end{aligned}$$
(1)

where \({\mathbf {S}}\) is a differential divergence operator defined for 2D problems as [59]

$$\begin{aligned} {\mathbf {S}} = { \left[ \begin{array}{cc} \frac{\partial }{\partial {x}} &{} 0\\ 0 &{} \frac{\partial }{\partial {y}} \\ \frac{\partial }{\partial {y}} &{} \frac{\partial }{\partial {x}} \end{array} \right] } \end{aligned}$$
(2)

while \({{\varvec{u}}}\), \({{\varvec{u}}_r}\), and \({\varvec{b}}\) denote the absolute displacement of the soil skeleton, the displacement of the water phase relative to the solid phase, and an external body acceleration field, respectively. Following Zienkiewicz and Shiomi [54], the relative water displacement is defined as \({\varvec{u}}_r = n\left( {\varvec{U}}-{\varvec{u}}\right)\), where \({\varvec{U}}\) is the absolute displacement of the water phase.

To ensure the equilibrium of the mixture and its individual phases, the following momentum balance equation for the pore water must also be fulfilled [54, 59]:

$$\begin{aligned} \nabla {p}-{\varvec{R}}-\rho _w\ddot{{\varvec{u}}}-\rho _w\frac{\ddot{{\varvec{u}}}_r}{n}+\rho _w{\varvec{b}}={\varvec{0}} \end{aligned}$$
(3)

where \({\varvec{R}}\) is the drag force exchanged by the soil skeleton and the pore water due to their relative motion. \({\varvec{R}}\) is proportional to the relative discharge velocity \(\dot{{\varvec{u}}}_r = n\left( \dot{{\varvec{U}}}-\dot{{\varvec{u}}}\right)\) according to Darcy’s law:

$$\begin{aligned} {\varvec{R}} = \frac{n\rho _wg}{k}\left( \dot{{\varvec{U}}}-\dot{{\varvec{u}}}\right) \end{aligned}$$
(4)

in which the hydraulic conductivity k is assumed to be isotropic for simplicity, and g is the gravitational acceleration. It should be noted that convective terms are neglected in Equations (1) and (3) [59].

The flow of pore water must also obey the following mass conservation equation [54, 59]:

$$\begin{aligned} \nabla \cdot \dot{{\varvec{u}}}_r+\nabla \cdot \dot{{\varvec{u}}}+\frac{\dot{{p}}}{Q} = {\varvec{0}} \end{aligned}$$
(5)

The stiffness constant Q in Equation (5) is defined as \(1/{Q}={n}/{K_w}+\left( {1-n}\right) /{K_s}\), where \(K_w\) and \(K_s\) are the bulk moduli of the water phase and soil particles, respectively.

The use of \({\varvec{u}}\), p, and \({\varvec{U}}\) (in lieu of \({\varvec{u}}_r\)) as primary variables in Equations (1), (3) and (5) gives rise to a u–p–U dynamic coupled formulation. Therefore, each node in the background mesh is associated with, for 2D plane strain problems, five unknown degrees of freedom, i.e., two soil displacement components for the solid and the fluid phases and one pore pressure variable. More details regarding the fundamentals of the numerical formulation can be found in [54, 59] and are not included in this study for reasons of brevity.

Given the focus of this work on the first implementation/verification of a new implicit MPM, the case of a linear elastic solid phase is exclusively considered in what follows. Accordingly, the constitutive relationship between effective stress (\(\dot{\varvec{\sigma }}'\)) and strain (\(\dot{\varvec{\varepsilon }}\)) rates can be expressed as

$$\begin{aligned} \dot{\varvec{\sigma }}' = {\mathbf {D}}^e\dot{\varvec{\varepsilon }} \end{aligned}$$
(6)

where the elastic stiffness matrix of the solid skeleton (\({\mathbf {D}}^e\)) is used in combination with a linearised/infinitesimal definition of the strain rate [1, 47, 53, 60,61,62,63]. It is known that the MPM suffers from numerical oscillations when considering large deformation analysis [1, 64, 65], and these oscillations become more significant for the simulation of large-deformation processes in (nearly incompressible) fluid-infiltrated porous materials. In this work, the main focus lies in the numerical implementation of an implicit time integration algorithm and the corresponding validation of its stability and hydromechanical performance for both slow and fast dynamic coupled problems. Note that the stress and strain measure adopted in this study is not fully work-conjugate [66]. Fully general modelling of large deformations can be achieved by adopting well-established finite strain measures [67] as well as performing necessary corrections to ensure objective stress–strain work conjugate pairs [66] – such an extension would not be expected to heavily impact the hydromechanical performance of the proposed method and will be investigated in a future study.

With reference to a fully saturated porous medium, the boundary conditions for soil/water displacement and pore pressure are all of a Dirichlet type in the considered three-field formulation:

$$\begin{aligned} {\varvec{u}}({\varvec{x}},t)&= \tilde{{\varvec{u}}}(t) \quad {\text{on}} \quad {\varGamma} _u(t) \end{aligned}$$
(7a)
$$\begin{aligned} {\varvec{U}}({\varvec{x}},t)&= \tilde{{\varvec{U}}}(t) \quad \text {on} \quad {\varGamma} _U(t) \end{aligned}$$
(7b)
$$\begin{aligned} {\varvec{p}}({\varvec{x}},t)&= \tilde{\varvec{{p}}}(t) \quad \text {on} \quad {\varGamma} _p(t) \end{aligned}$$
(7c)

where \(\tilde{{\varvec{u}}}(t)\), \(\tilde{{\varvec{U}}}(t)\), and \(\tilde{\varvec{{p}}}(t)\) are the prescribed boundary values – possibly varying in time – of the soil and water displacements, and pore pressures, respectively. Conversely, a (total) surface traction is represented as a Neumann boundary condition:

$${\varvec{\sigma }}({\mathbf {x}},t)\cdot \mathbf {G_{\tau }}= \tilde{\varvec{\tau }}(t) \quad \text {on} \quad {\varGamma }_\tau (t) $$
(8a)

where \(\mathbf {G_{\tau }}\) is a matrix containing components of the unit vector normal to the boundary surface \(\varGamma\) [59], and \(\tilde{\varvec{\tau }}(t)\) is a prescribed surface traction vector.

The modelling of impermeable boundaries requires the enforcement of nil (components of) soil-water relative velocity (\(\dot{{\varvec{u}}}_r\)) along certain spatial directions. Such a condition is easily fulfilled in the verification examples presented in Section 4, where cases with impermeable boundaries that are also kinematically constrained are exclusively considered (i.e., \({{\varvec{u}}}_{x\,\text {and/or}\,y}= {\varvec{0}}\)): therefore, imposing \({{\varvec{u}}}_{x\,\text {and/or}\,y}={{\varvec{U}}}_{x\,\text {and/or}\,y}= {\varvec{0}}\, \forall t\) also automatically fulfills the impermeability requirement in terms of relative velocity.

3 Numerical implementation of implicit GIMP-patch method

This section provides relevant technical details regarding the numerical formulation and implementation of the implicit GIMP-patch method proposed in this study. In particular, spatial discretisation, time integration, and mitigation of numerical instabilities are discussed.

3.1 Spatial discretisation

The primary variables \({\varvec{u}}\), p , and \({\varvec{U}}\) are first approximated using their nodal values (\(\bar{{\varvec{u}}}\), \(\bar{{\varvec{p}}}\), and \(\bar{{\varvec{U}}}\)) in the background mesh:

$$\begin{aligned} {\varvec{u}} = {\mathbf {N}}_u \bar{{\varvec{u}}}, \qquad p = {\varvec{N}}_p \bar{{\varvec{p}}}, \qquad {\varvec{U}} = {\mathbf {N}}_U \bar{{\varvec{U}}} \end{aligned}$$
(9)

where \({\mathbf {N}}_u\), \({\varvec{N}}_p\), and \({\mathbf {N}}_U\) are matrices containing shape functions of the same low order (bilinear in 2D problems) for the interpolation of solid displacements, pore pressures, and fluid displacements, respectively. Substituting the above approximations (Equation (9)) into the weak forms of the governing equations ((1), (3) and (5)) leads to the following discrete system of ordinary differential equations:

$$\begin{aligned}&{\left[ \begin{array}{ccc} {\mathbf {M}}_u &{} {\mathbf {0}} &{} {\mathbf {0}} \\ {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}}\\ {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {M}}_U \end{array} \right] } {\left[ \begin{array}{c} \ddot{\bar{{\varvec{u}}}}\\ \ddot{\bar{{\varvec{p}}}}\\ \ddot{\bar{{\varvec{U}}}} \end{array} \right] } + {\left[ \begin{array}{ccc} {\mathbf {C}}_1 &{} {\mathbf {0}} &{} -{\mathbf {C}}_2 \\ {\mathbf {0}} &{} {\mathbf {0}} &{} {\mathbf {0}}\\ -{\mathbf {C}}^\mathrm {T}_2 &{} {\mathbf {0}} &{} {\mathbf {C}}_3 \end{array} \right] } {\left[ \begin{array}{c} \dot{\bar{{\varvec{u}}}}\\ \dot{\bar{{\varvec{p}}}}\\ \dot{\bar{{\varvec{U}}}} \end{array} \right] }\nonumber \\&\quad + {\left[ \begin{array}{ccc} {\mathbf {K}}_u &{} -{\mathbf {G}}_1 &{} {\mathbf {0}} \\ -{\mathbf {G}}^\mathrm {T}_1 &{} {\mathbf {P}} &{} -{\mathbf {G}}^\mathrm {T}_2\\ {\mathbf {0}} &{} -{\mathbf {G}}_2 &{} {\mathbf {0}} \end{array} \right] } {\left[ \begin{array}{c} {\bar{{\varvec{u}}}}\\ {\bar{{\varvec{p}}}}\\ {\bar{{\varvec{U}}}} \end{array} \right] }= {\left[ \begin{array}{c} \bar{{\varvec{f}}}_s\\ {{\varvec{0}}}\\ \bar{{\varvec{f}}}_w \end{array} \right] } \end{aligned}$$
(10)

where: \({\mathbf {M}}_u\) and \({\mathbf {M}}_U\) are consistent mass matrices for the soil and water phases; \({\mathbf {C}}_1\), \({\mathbf {C}}_2\), and \({\mathbf {C}}_3\) are damping matrices physically associated with grain-fluid drag; \({\mathbf {K}}_u\) is the stiffness matrix of the solid skeleton; \({\mathbf {P}}\) is a compressibility matrix determined by the bulk stiffness of the solid grains and pore water; and \({\mathbf {G}}_1\) and \({\mathbf {G}}_2\) are two matrices describing the hydromechanical coupling between the skeleton deformation and pore water flow. The expressions for the matrices emerging from the spatial discretisation process are as follows [54]:

$$\begin{aligned}&{\mathbf {M}}_u= \int \nolimits _{\varOmega }^{} {\mathbf {N}}_u^{{T}}\left( 1-n\right) \rho _s{\mathbf {N}}_u \mathrm {d}\varOmega \nonumber \\&\quad {\mathbf {M}}_U= \int \nolimits _{\varOmega }^{} {\mathbf {N}}_U^{{T}}n\rho _w{\mathbf {N}}_U \mathrm {d}\varOmega \nonumber \\&\quad {\mathbf {C}}_1= \int \nolimits _{\varOmega }^{} {\mathbf {N}}_u^{{T}}n^2{k}^{-1}{\mathbf {N}}_u \mathrm {d}\varOmega \nonumber \\&\quad {\mathbf {C}}_\mathrm {2}= \int \nolimits _{\varOmega }^{} {\mathbf {N}}_u^{{T}}n^\mathrm {2}{k}^{\mathrm {-1}}{\mathbf {N}}_U \mathrm {d}\varOmega \nonumber \\&\quad {\mathbf {C}}_3= \int \nolimits _{\varOmega }^{} {\mathbf {N}}_U^{{T}}n^2{k}^{-1}{\mathbf {N}}_U \mathrm {d}\varOmega \nonumber \\&\quad {\mathbf {K}}_u= \int \nolimits _{\varOmega }^{} {\mathbf {B}}^\mathrm {T}_{u}{\mathbf {D}}^e {\mathbf {B}}_u \mathrm {d}\varOmega \nonumber \\&\quad {\mathbf {G}}_\mathrm {1}= \int \nolimits _{\varOmega }^{} {\mathbf {B}}^\mathrm {T}_{u}{\varvec{m}}\left( \mathrm {1}-n\right) {\mathbf {N}}_p \mathrm {d}\varOmega \nonumber \\&\quad {\mathbf {G}}_2 = \int \nolimits _{\varOmega }^{} {\mathbf {B}}^\mathrm {T}_{U}{\varvec{m}}n{\mathbf {N}}_p \mathrm {d}\varOmega \nonumber \\&\quad {\mathbf {P}} = \int \nolimits _{\varOmega }^{} {\varvec{N}}_p^{{T}}\frac{\mathrm {1}}{Q}{\varvec{N}}_p \mathrm {d}\varOmega \end{aligned}$$
(11)

where \({\mathbf {B}}_{u}\) and \({\mathbf {B}}_{U}\) are compatibility matrices containing spatial derivatives of the shape functions. The nodal force vectors in Equation (10), \(\bar{{\varvec{f}}}_s\) and \(\bar{{\varvec{f}}}_w\), relate to external body forces and surface tractions:

$$\begin{aligned} \bar{{\varvec{f}}}_s&= \int \nolimits _{\varGamma _{\tau }}^{}{\mathbf {N}}_u^\mathrm {T}\tilde{\varvec{\tau }}(t)\mathrm {d}{\varGamma} _{\tau }+ \int \nolimits _{\varOmega }^{}{\mathbf {N}}_u^\mathrm {T}\left( \mathrm {1}-n\right) \rho _s{\varvec{b}}\mathrm {d}\varOmega \end{aligned}$$
(12a)
$$\begin{aligned} \bar{{\varvec{f}}}_w&= \int \nolimits _{\varOmega }^{}{\mathbf {N}}_U^\mathrm {T}n\rho _w{\varvec{b}}\mathrm {d}\varOmega \end{aligned}$$
(12b)

In regular MPM, \({\mathbf {N}}_u\), \({\mathbf {N}}_U\) and \({\varvec{N}}_p\) would feature the same (bi)linear shape functions as in standard FEM. It is well-known, however, that regular MPM may suffer from stress oscillations when MPs cross grid cell boundaries due to discontinuous shape function gradients. GIMP was proposed by Bardenhagen and Kober [53] to reduce such oscillations, with the shape functions being constructed by integrating linear FEM shape functions \({N}_i(x)\) over the MP support domain \(\varOmega _{mp}\). In one dimension, the GIMP shape functions \({S}_{i,mp}\) and their gradients \(\nabla {S}_{i,mp}\) are calculated as

$$\begin{aligned} {S}_{i,mp}= & {} \frac{1}{V_{mp}}\int \nolimits _{\varOmega _{mp}\cap \varOmega }^{}\chi _{mp}({\varvec{x}}){N}_i({\varvec{x}})\mathrm {d}x \end{aligned}$$
(13)
$$\begin{aligned} \nabla {S}_{i,mp}= & {} \frac{1}{V_{mp}}\int \nolimits _{\varOmega _{mp}\cap \varOmega }^{}\chi _{mp}({\varvec{x}})\nabla {N}_i({\varvec{x}})\mathrm {d}x \end{aligned}$$
(14)

over the problem domain \(\varOmega\), where \(V_{mp}\) is the MP volume and \(\chi _{mp}\) is the “particle characteristic function”:

$$\begin{aligned} \chi _{mp}({\varvec{x}})=\left\{ \begin{aligned} 1&,&\text {if }{{\varvec{x}} \in \varOmega _{mp}} \\ 0&,&\text {otherwise} \\ \end{aligned} \right. \end{aligned}$$
(15)

The support domain \(\varOmega _{mp}\) is assumed to be of size \(2l_p\) (\(l_p\) is half the length of the material point domain) in each dimension, and can be computed by dividing the grid cell size by the initial number of MPs within a grid cell along the considered direction. In 2D and 3D problems, the shape functions are obtained by multiplying the individual 1D functions for the different directions. In the framework of GIMP, the matrices in Equation (10) are redefined for a specific grid cell node as follows:

$$\begin{aligned} {\mathbf {M}}_{u,i}= & {} \sum _{mp=1}^{N_{mp}}{\mathbf {S}}_{u,i}^{{T}}({\varvec{x}}_{mp})m_{u,mp}{\mathbf {S}}_{u,i}({\varvec{x}}_{mp})\nonumber \\= & {} \sum _{mp=1}^{N_{mp}}{\mathbf {S}}_{u,i}^{{T}}({\varvec{x}}_{mp})(1-n)\rho _{s,mp}V_{mp}{\mathbf {S}}_{u,i}({\varvec{x}}_{mp}) \end{aligned}$$
(16a)
$$\begin{aligned} {\mathbf {M}}_{U,i}= & {} \sum _{mp=1}^{N_{mp}}{\mathbf {S}}_{U,i}^{{T}}({\varvec{x}}_{mp})m_{U,mp}{\mathbf {S}}_{U,i}({\varvec{x}}_{mp})\nonumber \\= & {} \sum _{mp=1}^{N_{mp}}{\mathbf {S}}_{U,i}^{{T}}({\varvec{x}}_{mp})n\rho _{w,mp}V_{mp}{\mathbf {S}}_{U,i}({\varvec{x}}_{mp}) \end{aligned}$$
(16b)
$$\begin{aligned} {\mathbf {C}}_{1, i}= & {} \sum _{mp=1}^{N_{mp}}{\mathbf {S}}_{u,i}^{{T}}({\varvec{x}}_{mp})n^2{k}^{-1}{\mathbf {S}}_{u,i}({\varvec{x}}_{mp})V_{mp} \end{aligned}$$
(16c)
$$\begin{aligned} {\mathbf {C}}_{2, i}= & {} \sum _{mp=1}^{N_{mp}}{\mathbf {S}}_{u,i}^{{T}}({\varvec{x}}_{mp})n^2{k}^{-1}{\mathbf {S}}_{U,i}({\varvec{x}}_{mp})V_{mp} \end{aligned}$$
(16d)
$$\begin{aligned} {\mathbf {C}}_{3, i}= & {} \sum _{mp=1}^{N_{mp}}{\mathbf {S}}_{U,i}^{{T}}({\varvec{x}}_{mp})n^2{k}^{-1}{\mathbf {S}}_{U,i}({\varvec{x}}_{mp})V_{mp} \end{aligned}$$
(16e)
$$\begin{aligned} {\mathbf {K}}_{u,i}= & {} \sum _{mp=1}^{N_{mp}}\nabla {\mathbf {S}}^\mathrm {T}_{u,i}({\varvec{x}}_{mp}){\mathbf {D}}^e\nabla {\mathbf {S}}_{u,i}({\varvec{x}}_{mp})V_{mp} \nonumber \\= & {} \sum _{mp=1}^{N_{mp}} {\mathbf {B}}^\mathrm {T}_{u,i}({\varvec{x}}_{mp}){\mathbf {D}}^e{\mathbf {B}}_{u,i}({\varvec{x}}_{mp})V_{mp} \end{aligned}$$
(16f)
$$\begin{aligned} {\mathbf {G}}_{\mathrm {1},i}= & {} \sum _{mp=1}^{N_{mp}}\nabla {\mathbf {S}}^\mathrm {T}_{u,i}({\varvec{x}}_{mp}){\varvec{m}}(1-n){S}_{p,i}({\varvec{x}}_{mp})V_{mp}\nonumber \\= & {} \sum _{mp=1}^{N_{mp}} {\mathbf {B}}^\mathrm {T}_{u,i}({\varvec{x}}_{mp}){\varvec{m}}(1-n){S}_{p,i}({\varvec{x}}_{mp})V_{mp} \end{aligned}$$
(16g)
$$\begin{aligned} {\mathbf {G}}_{\mathrm {2},i}= & {} \sum _{mp=1}^{N_{mp}}\nabla {\mathbf {S}}^\mathrm {T}_{U,i}({\varvec{x}}_{mp}){\varvec{m}}n{S}_{p,i}({\varvec{x}}_{mp})V_{mp}\nonumber \\= & {} \sum _{mp=1}^{N_{mp}} {\mathbf {B}}^\mathrm {T}_{U,i}({\varvec{x}}_{mp}){\varvec{m}}n{S}_{p,i}({\varvec{x}}_{mp})V_{mp} \end{aligned}$$
(16h)
$$\begin{aligned} {P}_{i}= & {} \sum _{mp=1}^{N_{mp}}{S}^\mathrm {T}_{p,i}({\varvec{x}}_{mp})\frac{\mathrm {1}}{Q}{S}_{p,i}({\varvec{x}}_{mp})V_{mp} \end{aligned}$$
(16i)

where the subscript i defines the \(i^{th}\) grid cell node, \({\varvec{x}}_{mp}\) are the coordinates of the MPs, and \(N_{mp}\) is the total number of MPs. Similarly, the external force vectors in Equation (12) are re-written as

$$\begin{aligned}&\bar{{\varvec{f}}}_{s,i} = \sum _{mp=1}^{N_{bmp}}{\mathbf {S}}^\mathrm {T}_{u,i}({\varvec{x}}_{mp})\tilde{\varvec{\tau }}(t)+ \sum _{mp=1}^{N_{bmp}}{\mathbf {S}}^\mathrm {T}_{u,i}({\varvec{x}}_{mp})m_{u,mp}{\varvec{b}} \end{aligned}$$
(17a)
$$\begin{aligned}&\bar{{\varvec{f}}}_{w,i} = \sum _{mp=1}^{N_{bmp}}{\mathbf {S}}^\mathrm {T}_{u,i}({\varvec{x}}_{mp})m_{U,mp}{\varvec{b}} \end{aligned}$$
(17b)

The full set of governing equations after spatial discretisation can be globally represented in the following compact form:

$$\begin{aligned} {\mathbf {M}}{\varvec{a}} + {\mathbf {C}}{\varvec{v}} + {\mathbf {K}}{\varvec{d}} = \bar{{\varvec{f}}} \end{aligned}$$
(18)

where: \({\mathbf {M}}\), \({\mathbf {C}}\), and \({\mathbf {K}}\) are the generalised mass, damping, and stiffness matrices, respectively; \(\bar{{\varvec{f}}}\) is a time-varying external load term; and \({\varvec{a}}=\left[ \ddot{\bar{{\varvec{u}}}}, \ddot{\bar{{\varvec{p}}}}, \ddot{\bar{{\varvec{U}}}}\right] ^\mathrm {T}\), \({\varvec{v}}=\left[ \dot{\bar{{\varvec{u}}}}, \dot{\bar{{\varvec{p}}}},\dot{\bar{{\varvec{U}}}}\right] ^\mathrm {T}\), and \({\varvec{d}} =\left[ \bar{{\varvec{u}}}, \bar{{\varvec{p}}}, \bar{{\varvec{U}}}\right] ^\mathrm {T}\) are the generalised nodal acceleration, velocity, and displacement vectors, respectively.

3.2 Time integration

The time integration of Equation (18) is performed using the well-established Newmark algorithm [68]. It is worth recalling that, in MPM computations, the problem domain is discretised into a set of MPs that carry relevant information (i.e., about mass, volume, velocity, acceleration, strain, stress), while the underlying governing equations are solved at the background grid cell nodes. Given the problem solution at the MPs for an arbitrary time step n, the corresponding variables are first mapped to the grid nodes in terms of nodal vectors of (generalised) acceleration \({\varvec{a}}_{n}\), velocity \({\varvec{v}}_{n}\), and displacement \({\varvec{d}}_{n}\), and then the global set of discrete governing equations are solved for the subsequent step \(n+1\). In compliance with Newmark’s time integration and the GIMP shape functions, the nodal values of the following variables are calculated at step n as

$$\begin{aligned} {m}_{\alpha ,i}^{n}={\sum _{mp=1}^{N_{mp}} S_{\alpha ,i}({\varvec{x}}_{mp,n}){m_{\alpha ,mp}}} \quad (\alpha =u,U) \end{aligned}$$
(19a)
$$\begin{aligned} {\varvec{v}}_{\alpha ,i}^{n}= \frac{\sum \limits _{mp=1}^{N_{mp}}S_{\alpha ,i}({\varvec{x}}_{mp,n}){m_{\alpha ,mp}}{{{\varvec{v}}}}_{\alpha ,mp}}{{m}_{\alpha ,i}^{n}} \quad (\alpha =u,U) \end{aligned}$$
(19b)
$$\begin{aligned} {\varvec{a}}_{\alpha ,i}^{n} = \frac{\sum \limits _{mp=1}^{N_{mp}} S_{\alpha ,i}({\varvec{x}}_{mp,n}){m_{\alpha ,mp}}{{{\varvec{a}}}}_{\alpha ,mp}}{{m}_{\alpha ,i}^{n}} \quad (\alpha =u,U) \end{aligned}$$
(19c)

where: the subscript \(\alpha\) indicates either the solid (\(\alpha =u\)) or water (\(\alpha =U\)) phase; the subscripts i and mp stand for the \(i^{th}\) grid node and the \(mp^{th}\) MP, respectively; the superscript and subscript n are associated with the \(n^{th}\) time step; \(m_{\alpha ,mp}\) represents the MP mass corresponding to either the solid (\(\alpha =u\), \(m_{u,mp}=(1-n)\rho _{s,mp}V_{mp}\)) or the water phase (\(\alpha =U\), \(m_{U,mp}=n\rho _{s,mp}V_{mp}\)); \({m}_{\alpha ,i}\), \({\varvec{v}}_{\alpha ,i}\), and \({\varvec{a}}_{\alpha ,i}\) are the generalised nodal mass, velocity, and acceleration, respectively, which can be used to determine the global vectors \({\varvec{v}}_{n}\) and \({\varvec{a}}_{n}\). Since the background mesh is reset to its original position at the end of each calculation step, the vector \({\varvec{d}}_{n}\) is always entirely populated by nil entries (i.e., \({\varvec{d}}_{n} = {\varvec{0}}\)).

The Newmark algorithm adopts two time integration parameters, \(\gamma\) and \(\beta\), in the corresponding recurrence relations for stepping from n to \(n+1\) [69]:

$$\begin{aligned} {\varvec{a}}_{n+1}= & {} {\varvec{a}}_{n} + \varDelta {\varvec{a}} \end{aligned}$$
(20a)
$$\begin{aligned} {\varvec{v}}_{n+1}= & {} {\varvec{v}}_{n} + \varDelta t \left[ \left( 1-\gamma \right) {\varvec{a}}_{n} + \gamma {\varvec{a}}_{n+1}\right] \end{aligned}$$
(20b)
$$\begin{aligned} {\varvec{d}}_{n+1}= & {} {\varvec{d}}_{n} + {\varvec{v}}_{n}\varDelta t + \frac{\varDelta t^2}{2}\left[ \left( 1-2\beta \right) {\varvec{a}}_{n} + 2 \beta {\varvec{a}}_{n+1}\right] \end{aligned}$$
(20c)

in which \(\varDelta t = t_{n+1}-t_{n}\) is the time step size. Substituting Equation (20c) into Equations (20a) and (20b), the recurrence relations for the acceleration \({\varvec{a}}_{n+1}\) and the velocity \({\varvec{v}}_{n+1}\) can be rewritten as

$$\begin{aligned}&{\varvec{a}}_{n+1} = \frac{f_1}{\varDelta t^2}\left( {\varvec{d}}_{n+1}-{\varvec{d}}_n\right) -\frac{f_1}{\varDelta t}{\varvec{v}}_n\nonumber \\&\quad -\left( \frac{f_1}{2}-1\right) {\varvec{a}}_n \end{aligned}$$
(21a)
$$\begin{aligned}&{\varvec{v}}_{n+1} = \frac{f_2}{\varDelta t}\left( {\varvec{d}}_{n+1}-{\varvec{d}}_n\right) -\left( f_2-1\right) {\varvec{v}}_n\nonumber \\&\quad -\left( \frac{f_2}{2}-1\right) {\varvec{a}}_n\varDelta t \end{aligned}$$
(21b)

where \(f_1 =1/\beta\) and \(f_2=\gamma /\beta\). In the case of linear elastodynamics, Newmark time integration is unconditionally stable, non-dissipative, and second-order accurate when \(\beta = 0.25\) and \(\gamma = 0.5\), which is the sole parameter pair considered in the remainder of this study. The final algebraic system of fully discretised equations, after substituting Equations (21a)-(21b) into Equation (18), is

$$\begin{aligned}&\overline{{\mathbf {K}}}\varDelta {\varvec{d}}_{n+1} = \bar{{\varvec{f}}}_{n+1} - {\varvec{f}}^{int}_{n} + {\mathbf {M}}_n\left[ \frac{f_1}{\varDelta t}{\varvec{v}}_n+\left( \frac{f_1}{2}-1\right) {\varvec{a}}_n\right] \nonumber \\&\quad +{\mathbf {C}}_n\left[ \left( f_2-1\right) {\varvec{v}}_n + \left( \frac{f_2}{2}-1\right) {\varvec{a}}_n\varDelta t\right] \end{aligned}$$
(22)

where \(\overline{{\mathbf {K}}}=\displaystyle \frac{f_1}{\varDelta t^2}{\mathbf {M}}_n+\frac{f_2}{\varDelta t}{\mathbf {C}}_n+{\mathbf {K}}_n\) is an algorithmic dynamic stiffness matrix, and \({\varvec{f}}^{int}_{n}=\left[ {\varvec{f}}^{int}_{u,n}, {\varvec{f}}^{int}_{p,n}, {\varvec{f}}^{int}_{U,n}\right] ^\mathrm {T}\) is the internal nodal force vector:

$$\begin{aligned}&{\varvec{f}}^{int}_{u,i} = \sum _{mp=1}^{N_{mp}} {\mathbf {B}}^\mathrm {T}_{u,i}\left( {\varvec{x}}_{mp,n}\right) \nonumber \\&\quad \left[ \varvec{\sigma }'_{mp,n}-\left( 1-n\right) {\varvec{m}}p_{mp,n}\right] V_{mp,n} \end{aligned}$$
(23a)
$$\begin{aligned}&{f}^{int}_{p,i} = \sum _{mp=1}^{N_{mp}}\left[ -\left( 1-n\right) {S}_{p,i}({\varvec{x}}_{mp,n})\varepsilon ^u_{vol,mp}\right. \nonumber \\&\quad \left. -{S}_{p,i}({\varvec{x}}_{mp,n})\frac{p_{mp,n}}{Q}-n{S}_{p,i}({\varvec{x}}_{mp,n})\varepsilon ^U_{v,mp}\right] V_{mp,n} \end{aligned}$$
(23b)
$$\begin{aligned}&{\varvec{f}}^{int}_{U,i} = -\sum _{mp=1}^{N_{mp}} {\mathbf {B}}^\mathrm {T}_{U,i}\left( {\varvec{x}}_{mp,n}\right) n{\varvec{m}}p_{mp,n}V_{mp,n} \end{aligned}$$
(23c)

and \(\varepsilon ^u_{vol,mp}\) and \(\varepsilon ^U_{vol,mp}\) are the volumetric strain of the soil and water phases at the \({mp}^{th}\) MP.

Even in the presence of linear constitutive equations, the solution of a large deformation problem is intrinsically non-linear and must be carried out iteratively [48]. For this purpose, each time step is solved in combination with a Modified Newton-Raphson iteration scheme [70]. Its algorithmic description is provided in Algorithm 1, where the superscript k denotes the \(k^{th}\) iteration within a given time step out of a maximum number equal to \(k_{max}\), \(\varvec{\psi }^{(k)}_{n+1}\) is the vector of nodal residuals at the \(k^{th}\) iteration (\(\Vert \varvec{\psi }^{(k)}_{n+1}\Vert\) is its \(L_2\) norm), and \(\xi\) is the prescribed error tolerance – here set equal to \({1.0 \times 10^{-6}}\). When convergence is reached according to the prescribed error tolerance, all relevant variables are updated at the MPs using computed nodal values:

$$\begin{aligned} {\varvec{a}}_{mp, n+1} = {\sum _{i=1}^{N_{node}} {\mathbf {S}}_{u,i}({\varvec{x}}_{mp,n}){{\varvec{a}}_{i,n+1}}} \end{aligned}$$
(24a)
$$\begin{aligned} {\varvec{v}}_{mp, n+1} = {\sum _{i=1}^{N_{node}} {\mathbf {S}}_{u,i}({\varvec{x}}_{mp,n}){{\varvec{v}}_{i,n+1}}} \end{aligned}$$
(24b)
$$\begin{aligned} \varvec{\sigma }'_{mp, n+1} = \varvec{\sigma }'_{mp, n} +{\mathbf {D}}^e{\sum _{i=1}^{N_{node}} {\mathbf {B}}_{u,i}({\varvec{x}}_{mp,n}){\bar{{\varvec{u}}}_{i,n+1}}} \end{aligned}$$
(24c)
$$\begin{aligned} p_{mp,n+1} = p_{mp,n} + \sum _{i =1}^{N_{node}} S_{p,i}({\varvec{x}}_{mp,n}){\bar{p}}_{i,n+1} \end{aligned}$$
(24d)
$$\begin{aligned} {\varvec{x}}_{mp, n+1} = {\varvec{x}}_{mp,n} +{\sum _{i =1}^{N_{node}} {\mathbf {S}}_{u,i}({\varvec{x}}_{mp,n}){\bar{{\varvec{u}}}_{i,n+1}}} \end{aligned}$$
(24e)

where \(N_{node}\) is the total number of nodes.

It should be pointed out that the algorithmic dynamic stiffness matrix \(\overline{{\mathbf {K}}}\) in the fully discretised equation (22) tends to be populated by small diagonal terms that are related to the compressibility of the soil–water mixture. Such small diagonal terms can render the governing equations difficult to solve, as the \(\overline{{\mathbf {K}}}\) matrix may lose its positive-definiteness. As the PARDISO solver includes a preconditioning approach that is based on maximum weighted matching and algebraic multilevel incomplete \(LDL^{\mathrm {T}}\) factorization, it enables an efficient and robust solution of the reference linear system. For solving discrete systems of this kind, the PARDISO package [71] from the Intel Math Kernel Library has been introduced into the in-house implicit coupled MPM code due to its convenience in numerical implementation.

figure a

3.3 Mitigating numerical instabilities in coupled MPM

Due to its similarity to FEM, MPM can suffer from numerical instabilities when low-order interpolation is equally adopted for the all the primary variables. This is the case for (nearly) incompressible hydromechanical problems in porous media, giving rise to undesired oscillations in the pore pressure field [51, 72, 73]. Although previous FEM experience has shown the beneficial effects of a three-field u–p–U formulation, pore pressure instabilities may still arise in 2D/3D problems when the same low-order interpolation is adopted for all field variables [55]. To alleviate pore pressure instabilities in coupled MPM computations, a patch recovery of pore pressure increments based on the Moving Least Square Approximation (MLSA) has been recently proposed by Zheng et al. [1] in combination with an explicit coupled MPM. The same patch recovery technique is also exploited within the implicit MPM presented herein. Hence, an intermediate mapping stage is introduced, in which nodal pore pressure increments are first mapped to central Gauss integration points (GPs), instead of directly to the MPs as implied by Equation (24d). Such a GP-mapping operation is performed as follows:

$$\begin{aligned} \varDelta p_{gp,n+1} = \sum _{i=1}^{N_{n}} S_{p,i}({\varvec{x}}_{gp,n}){\bar{p}}_{i,n+1} \end{aligned}$$
(26)

where \({\varvec{x}}_{gp}\) indicates the position of a generic central GP in the background mesh. Note that since this mapping is only performed to evaluate pore pressure increments, the computed results are found not to suffer from spurious hourglass modes [73].

Fig. 1
figure 1

Patch recovery of pore pressure increments from GPs to MPs using MLSA

Full size image

After obtaining incremental pore pressures at the central GPs through Equation (26), their final recovery to the MPs is performed. Following Zienkiewicz and Zhu [74], the pore pressure increments are evaluated at the MPs through a patch recovery stage based on a moving least squares approximation (MLSA). As shown in Figure 1, a patch of four quadrilateral cells can always be identified for any internal node i. Within such a patch, a rectangular area can be delimited around the node by using the central GPs in the four grid cells. It is thus possible to introduce, for the pore pressure increments (\(\varDelta {p}\)), the following polynomial approximation of order q in the considered rectangular domain \(\varOmega _i\) (bounded by the red dashed lines in Figure 1):

$$\begin{aligned} \varDelta {{p}({x}, {y})} = {\varvec{Q}}({x},{y}){\varvec{a}} \end{aligned}$$
(27)

where (x, y) is the location of the GPs in \(\varOmega _{i}\), and \({\varvec{Q}}\) and \({\varvec{a}}\) are vectors containing polynomial basis functions and interpolation degrees-of-freedom, respectively. In general, different shape functions may be chosen to approximate the incremental pore pressure field. Similarly to Zheng et al. [1], a linear version of \({\varvec{Q}}(x_i,y_i) = [1\ x_i\ y_i]\) is adopted in this study, which gives rise to the interpolation plane in Figure 1 after the determination of the coefficients in \({\varvec{a}} = [a_0\ a_1\ a_2]^\mathrm {T}\). Based on a posteriori error estimator, the relative error at the sampling GPs is calculated as

$$\begin{aligned} E({\varvec{a}}) = \sum _{i=1}^{N_{gp}}\left[ \varDelta {p_{gp,n+1}}(x_{i},y_{i})-{\varvec{Q}}(x_{i},y_{i}){\varvec{a}}\right] ^2 \end{aligned}$$
(28)

where \(N_{gp}\) is the total number of GPs in the approximation domain \(\varOmega _{i}\), and \((x_{i},y_{i})\) are the coordinates of the GPs. Minimising the error with respect to \({\varvec{a}}\) leads to the following linear system:

$$\begin{aligned} {\mathbf {A}}{\varvec{a}} = {\varvec{b}} \end{aligned}$$
(29)

where \({\mathbf {A}}=\displaystyle {\sum _{i=1}^{N_{gp}}{\varvec{Q}}^{{T}}(x_{i},y_{i}){\varvec{Q}}(x_{i},y_{i})}\) and \({\varvec{b}} = \displaystyle {\sum _{i=1}^{N_{gp}}{\varvec{Q}}^{{T}}(x_{i},y_{i}){\varDelta {p}}_{gp,n+1}(x_{i},y_{i})}\).

Finally, the pore pressure increments at the MPs located in the approximation domain \(\varOmega _i\) can be obtained as

$$\begin{aligned} \varDelta {{p}_{mp,n+1}} ={\varvec{Q}}(x_{mp},y_{mp}){\varvec{a}} \end{aligned}$$
(30)

and these can be used to compute the final pore pressure values for step \(n+1\). For MPs near the domain boundary, there are insufficient grid cells to form a complete patch. For these cases, the pore pressure increments are determined by extending internal patches up to the MP position. Similar strategies for determining stresses at the boundary nodes in FEM can be found in previous studies [70, 75, 76].

4 Numerical examples

This section presents the result of several examples to support the suitability of the proposed implicit GIMP-patch method. All numerical results have been obtained through sequential computations on a computer equipped with an Intel Xeon E5-1620, 16GB RAM and x64-based processor. As mentioned by Vermeer and Verruijt [77], numerical solutions of consolidation problems often exhibit oscillating pore pressures when the chosen time step violates the minimum-time-step criterion. The chosen time steps in all considered examples approximately meet this minimum-time-step criterion and inaccurate pore pressure distributions with significant oscillations are not observed in this study.

4.1 1D coupled problems with small deformations

4.1.1 Example 1: consolidation of a soil column

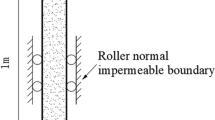
The static, small-strain 1D consolidation of a linear elastic soil column is first considered as a well-established verification example for coupled poromechanical problems [30, 57]. Figure 2a shows the geometry and associated boundary conditions for the one-dimensional consolidation model. The width (w) and initial height (\(H_0\)) of the problem domain are \({0.1}{\hbox {m}}\) and \({1.0}{\hbox {m}}\), respectively. The bottom boundary has both solid and water displacements totally fixed, whereas only vertical u-U displacements are allowed along the lateral boundaries. In this boundary configuration, the drainage of pore water is only allowed through the top free surface. A vertical uniform static load \(p_a\) of \({1.0}{\hbox {kPa}}\) is instantaneously applied at the top surface.

Table 1 Hydromechanical properties of the soil-water mixture in the considered verification examples
Full size table
Fig. 2
figure 2

One-dimensional consolidation model

Full size image

The MPM discretisation of the system is shown in Figure 2b. The model is discretised by means of 10 4-node quadrilateral grid cells (elements) of size \({0.1}{\hbox {m}} \times {0.1}{\hbox {m}}\), with each cell initially hosting four equally-spaced MPs. The hydromechanical properties assumed for the soil-water mixture are are listed in Table 1. Both the new implicit GIMP-patch method and the explicit GC-SRI-patch method proposed by Zheng et al. [1] have been tested against Terzaghi’s analytical solution [78] for comparative purposes. The GIMP-patch and GC-SRI-patch results have been obtained using time-step sizes \(\varDelta t\) of \({1.0 \times 10^{-3}}{\hbox {s}}\) and \({1.0 \times 10^{-5}}{\hbox {s}}\), respectively.

Figure 3 compares the numerical and analytical solutions for different values of the dimensionless time factor \(T_v\), defined as

$$\begin{aligned} T_v=\frac{c_vt}{H_v^2} \end{aligned}$$

where \(H_v\) is the drainage path length (here equal to the thickness of the soil layer), and \(c_v\) is the coefficient of consolidation:

$$\begin{aligned} \displaystyle {c_v=\frac{k}{\rho _wg(1/E_c+1/Q)}} \end{aligned}$$

with \(E_c = \frac{E(1-\nu )}{(1-2\nu )(1+\nu )}\) being the constrained 1D stiffness of the soil skeleton obtained as a combination of the Young’s modulus E and Poisson’s ratio \(\nu\). The analytical solution of the problem can be represented in terms of normalised pore pressure (\(P=p/p_a\)) and layer thickness (\(H = H_v/H_0\)) for the aforementioned boundary/initial conditions:

$$\begin{aligned} P(H,T_v) =\sum _{m=1}^{\infty }\frac{2}{M}\sin (MH)e^{-M^2T_v} \end{aligned}$$
(31)

where \(M = (m-\frac{1}{2})\pi\). The corresponding average degree of consolidation \(U_s\) assumes the following expression:

$$\begin{aligned} U_s =1-\sum _{m=1}^{\infty }\frac{2}{M^2}e^{-M^2T_v} \end{aligned}$$
(32)
Fig. 3
figure 3

1D small-deformation consolidation of an elastic soil column: comparison between analytical and MPM (implicit GIMP-patch and explicit GC-SRI-patch) solutions

Full size image

Figure 3 shows excellent agreement between the analytical and MPM solutions – both for the implicit GIMP-patch and explicit GC-SRI-patch methods. More quantitatively, Figure 4 displays how the relative pore pressure error (\(e_p\)) increases with the time step size both for the implicit and explicit MPMs. For a given value of the time factor \(T_v\), the reference error measure \(e_p\) is defined over the spatial domain as follows:

$$\begin{aligned} e_p \left( T_v\right) =\frac{\sqrt{\sum \limits _{mp=1}^{N_{mp}}\left[ P_{mp}^{*}\left( T_v\right) -P_{mp}\left( T_v\right) \right] ^2}}{N_{mp}} \end{aligned}$$
(33)

where \(P_{mp}^{*}\left( T_v\right)\) and \(P_{mp}\left( T_v\right)\) are the analytical and numerical pore pressure solutions at the MP locations (normalised with respect to the maximum excess pore pressure, which is equal to \(p_a\) at any depth – Figure 2). It is apparent that \(e_p\) grows with \(\varDelta t\) more slowly for the implicit GIMP-patch method – in a similar way for the two \(T_v\) values considered. It is also interesting to note that the implicit solution obtained with \(\varDelta t = {1.0 \times 10^{-3}}{\hbox {s}}\) is characterised by a level of accuracy that the explicit method achieves with a \(\varDelta t\) around 100 times smaller. This expected finding confirms the computational convenience of implicit modelling for transient problems of medium-large duration.

Fig. 4
figure 4

Dependence of the relative pore pressure error \(e_p\) on the time step size for the considered implicit and explicit MPMs (small deformation consolidation)

Full size image

The gradual reduction in relative error \(e_p\) upon grid refinement is shown for \(T_v=0.5\) in Figure 5 – for the proposed implicit GIMP-patch method in comparison to MPM and GIMP solutions (i.e., without patch recovery of pore pressures). Due to the small settlement experienced by the soil layer in the considered example, MPM and GIMP solutions are practically coincident, and exhibit first-order convergence with respect to the number of grid cells (i.e., the ratio between the soil layer thickness and grid cell size). The implicit GIMP-patch method returns generally smaller \(e_p\) values, with a convergence rate decreasing from 2 to 1 as the problem domain is more finely discretised.

Fig. 5
figure 5

Dependence of the relative pore pressure error \(e_p\) on the grid cell size at \(T_v= 0.5\) (small deformation consolidation)

Full size image

4.1.2 Example 2: dynamic consolidation of a soil column under harmonic loading

The dynamic steady-state response of an elastic soil column to a harmonic surface load is considered as a second verification case. Specifically, the same kind of system as in Figure 2 is analysed in combination with a time-varying surface load, \(p_a = \mathrm {cos}(\omega t)\), where \(\omega\) is the angular frequency. This problem was first studied by Zienkiewicz et al. [38], who provided an analytical solution that has served numerous numerical verification studies – even in the recent context of meshfree modelling [22, 79]. In this case, the soil column width (w) and height (\(H_0\)) are \({0.2}{\hbox {m}}\) and \({10.0}{\hbox {m}}\), respectively, and it has been discretised into 50 4-node quadrilateral grid cells (with cell size equal to \({0.2}{\hbox {m}} \times {0.2}{\hbox {m}}\)). The relevant hydromechanical properties are listed in Table 1.

As discussed by Zienkiewicz et al. [38], the dynamic steady-state response of the system spans three possible regimes of hydro-mechanical coupling (Figure 6), depending on the values of two relevant dimensionless factors, namely \(\varPi _1\) and \(\varPi _2\):

$$\begin{aligned} \varPi _1 = \frac{kV_c^2}{g\beta \omega H_0^2}, \quad \varPi _2 = \frac{\omega ^2H_0^2}{V_c^2} \end{aligned}$$

where \(V_c = \sqrt{\left( E_c+K_w/n\right) /\rho }\) is the compression wave velocity, \(E_c\) the constrained 1D modulus defined above, and \(\beta = \rho _w/\rho\). In Figure 6, Zone I is associated with slow hydromechanical phenomena, in which the role played by inertial effects is from limited to negligible. The opposite end of the spectrum is represented by \(\varPi _1\)-\(\varPi _2\) combinations in zone III, which is associated with fast dynamic consolidation and significant relative accelerations between the solid and the water phases. Moderately fast processes take place within the intermediate zone II, where the assumption of negligible relative solid-fluid acceleration is normally acceptable. In order to verify the implicit GIMP-patch method under different consolidation regimes, seven \(\varPi _1\)-\(\varPi _2\) pairs (\(P_1\)-\(P_7\)) have been considered – see Figure 6 and Table 2.

Fig. 6
figure 6

\(\varPi _1\)-\(\varPi _2\) pairs considered in the implicit GIMP-patch simulation of dynamic consolidation – cf. [38]

Full size image
Table 2 Parameter specification for the \(\varPi _1\)-\(\varPi _2\) pairs indicated in Figure 6
Full size table

Figure 7 compares analytical and GIMP-patch solutions in terms of steady-state profiles of normalised pore pressure \(P=p/p_a^{max}\) (with \(p_a^{max}\) being the maximum value of the time-varying surface loading and equal to \({1.0}{\hbox {kPa}}\)). It should be noted that the combination of such a loading condition and the considered material properties gives rise to minimal surface settlement of the soil column (with the maximum settlement never larger than \({10^{-5}}{\hbox {m}}\) for the considered seven \(\varPi _1\)-\(\varPi _2\) pairs). The numerical results for the seven simulation cases in Fig. 6 have been obtained using a time step size of \(\varDelta t = {1.0\times 10^{-4}}{\hbox {s}}\). No explicit GC-SRI-patch solutions have been computed in this case, due to the significant calculation time that the attainment of a harmonic steady state would require using a time step size of the order of \(\varDelta t = {1.0\times 10^{-5}}{\hbox {s}}\). The numerical–analytical comparisons in Figure 7 confirm the suitability of the proposed MPM over the whole range of dynamic consolidation speeds, including in the presence of significant solid-fluid relative accelerations (zone III).

Fig. 7
figure 7

Performance of the GIMP-patch method under different dynamic consolidation regimes

Full size image

4.1.3 Example 3: propagation of a shock pressure wave

The ability of the implicit GIMP-patch method to reproduce 1D wave propagation along an elastic soil column is assessed. The same kind of boundary conditions as described in Section 4.1.1 have been considered for a soil column of width and height equal to \(w= {2.5\times 10^{-3}}{\hbox {m}}\) and \(H_0= {2.5}{\hbox {m}}\), respectively. The domain is constrained along the lateral boundaries (\(u_x =0\) and \(U_x =0\)) and totally fixed at the bottom boundary (\(u_i =0\) and \(U_i =0\)) – as a result of such constraints, the drainage of pore water is only allowed through the top free surface. The relevant hydromechanical properties of the soil–water mixture are reported in Table 1 – note that the same values have been set for \(E_c\) and \(K_w/n\), so as to obtain an equal distribution of the external load over the solid and fluid phases. Wave motion along the soil column is triggered by imposing a uniform vertical load \(p_a\) of \({1.0}{\hbox {kPa}}\), which is instantaneously applied and then held constant at the top of the soil column. To accurately capture the propagation of shock waves, a fine spatial discretisation is necessary. For the case under consideration, the soil column has been discretised into 1000 4-node quadrilateral grid cells with a cell size of \({2.5 \times 10^{-3}}{\hbox {m}}\).

For the selected material properties and applied loading conditions, two shock waves are normally generated which propagate from the top to the bottom of the column. One wave (called the undrained wave) features the synchronous motion of soil and water at the same velocity, while the two phases move asynchronously in a second wave (the damped wave) that propagates with a lower speed [80, 81]. The propagation velocities of the undrained (\(V_u\)) and damped (\(V_d\)) waves can be respectively calculated as

$$\begin{aligned} V_u= & {} \sqrt{\frac{E_c+K_w/n}{\rho }} = {2236}{\hbox {m/s}} \end{aligned}$$
(34)
$$\begin{aligned} V_d= & {} \sqrt{\frac{K_w}{\rho _w}}\sqrt{\frac{nE_c}{(1-n)K_w+nE_c}} = {1118}{\hbox {m/s}} \end{aligned}$$
(35)

To mobilise different hydromechanical coupling regimes, low and high values of the hydraulic conductivity have been considered, i.e., \(k = {1.0\times 10^{-5}}{\hbox {m/s}}\) and \(k = {1.0\times 10^{-3}}{\hbox {m/s}}\). Comparative MPM solutions have been obtained using both the implicit and explicit MPMs developed by the authors. For the explicit method, the time step \(\varDelta t\) needs to be smaller than the critical time step \(\varDelta t_{cr} = {l}/{V_u}\) [82], which is \({1.12\times 10^{-6}}{\hbox {s}}\) for the reference material properties in Table 1. In order to achieve satisfactory accuracy in explicit calculations, a rather small time step size of \(\varDelta t = {6.0\times 10^{-7}}{\hbox {s}}\) has been chosen, while a larger time step of \(\varDelta t = {1.0\times 10^{-6}}{\hbox {s}}\) has been set for the proposed implicit method. In the latter case, such a choice is driven by accuracy rather than stability – a shock propagation problem will always require fine time stepping for rapid dynamics to be accurately captured.

Fig. 8
figure 8

Propagation of a shock pressure wave: comparison between analytical and MPM (implicit GIMP-patch and explicit GC-SRI-patch) solutions

Full size image

Figure 8 illustrates both the explicit and implicit solutions in terms of normalised excess pore pressure (\(P=p/p_a\)) at a point 0.4 m below the top surface. In the case of a higher hydraulic conductivity (Figure 8a), the presence of both the undrained and damped waves can be observed despite the inevitable Gibbs oscillations (caused by the fast load application). In particular, their arrival times at the reference depth equal \({1.79\times 10^{-4}}{\hbox {s}}\) and \({3.58\times 10^{-4}}{\hbox {s}}\), respectively, which is consistent with the theoretical propagation speeds – cf. Equations (34) and (35). As the hydraulic conductivity decreases, only the undrained wave remains visible, which is consistent with the results in Figure 8b [80]. Also in this second case, the first arrival of the undrained wave complies with the theoretical propagation speed – arrival in \({1.79\times 10^{-4}}{\hbox {s}}\); then, due to wave reflection at the fixed bottom boundary, the undrained wave passes again through the reference location at a time equal to \({2.06\times 10^{-3}}{\hbox {s}}\) and results in a doubling of the pore pressure magnitude. The good agreement between numerical and analytical solutions [80] further supports the overall applicability of the proposed implicit method. The high frequency oscillations that are visible in Figure 8 could be significantly alleviated by more gradual application of the external load, or by resorting to numerical algorithms more specifically conceived for shock wave propagation problems [83, 84].

4.2 Example 4: large-deformation 1D consolidation of a soil column

The case of a two-phase elastic soil column undergoing large-deformation consolidation [1, 61, 85] is tackled here using the proposed implicit GIMP-patch method. It should be pointed out that this numerical example has previously been solved using explicit coupled MPMs by Tran and Sołowski [61] and Zheng et al. [1]. Their solutions used the same time step size of \(\varDelta t = {1.0\times 10^{-6}}{\hbox {s}}\) and were verified against the consolidation solution provided by Xie and Leo [86] based on Gibson’s large deformation theory [85].

With reference to the same problem layout in Figure 2, an elastic soil column of width (w) and height (\(H_0\)) equal to \({0.1}{\hbox {m}}\) and \({1.0}{\hbox {m}}\), respectively, is considered. The problem domain is discretised into 10 4-node quadrilateral grid cells of size \({0.1}{\hbox {m}} \times {0.1}{\hbox {m}}\), while the relevant hydromechanical material properties of the mixture are given in Table 1. The boundary conditions are exactly the same as shown in Figure 2, and an instantaneous external loading of \(p_a = {200.0}{\hbox {kPa}}\) is applied as a surface compression. The time step size \(\varDelta t\) for the proposed implicit MPM is chosen as \({1.0\times 10^{-4}}{\hbox {s}}\), which is 100 times larger than that adopted for the previous explicit calculations [1, 61].

Fig. 9
figure 9

Comparison between implicit GIMP-patch, explicit GC-SRI-patch and analytical consolidation solutions – large deformation analysis

Full size image

Figure 9 shows the comparison between the implicit GIMP-patch, explicit GC-SRI-patch, and analytical solutions in terms of excess pore pressure and settlement of the top surface. It is clear that that the two MPM solutions compare well with each other and also match with the analytical large-deformation solution. However, slight oscillations in pore pressure can still be observed in both the implicit and explicit solutions near the upper domain surface. Such oscillations are arguably caused by the small nodal mass issue [87] and cell crossing that frequently occur during the settlement of the column top surface.

The behaviour of the implicit GIMP-patch method upon grid refinement is also examined in the presence of (1D) large deformations. As an example, Figure 10 displays the dependence of the relative pore pressure error \(e_p\) (computed using Equation (33)) on the grid cell size at \(U_s = 0.5\) (i.e., 50% of consolidation). Similarly to the small deformation consolidation case (Figure 5), the order of convergence varies from 2 to 1 upon progressive grid refinement. The reduction in the convergence order for this large deformation consolidation problem can be attributed to the fact that a larger group of material points will be crossing the cell edges, which can cause additional errors that weaken the benefit of the proposed MLSA-based patch recovery. Similar observations and conclusions also can be found in the previous work of Charlton et al. [45].

Fig. 10
figure 10

Dependence of the relative pore pressure error \(e_p\) on the grid cell size at \(U_s = 0.5\) (large deformation consolidation)

Full size image

4.3 Example 5: 2D slumping block

The 2D consolidation of an elastic slumping block is analysed as a final case – see also Zhao and Choo [48] and Zheng et al. [1]. The width and depth of the block are \({4.0}{\hbox {m}}\) and \({2.0}{\hbox {m}}\), respectively. Taking advantage of symmetry, only the right half of problem domain is considered, as is shown in Figure 11 together with the domain boundary conditions and applied gravitational acceleration ramp. For comparison purposes, the same material properties as adopted by Zheng et al. [1] for the same problem have been retained – see Table 1. The problem domain has been discretised using \(16\times 16\), 4-node quadrilateral grid cells of size \({0.125}{\hbox {m}} \times {0.125}{\hbox {m}}\). Implicit GIMP-patch simulations have been performed using a time step size equal to \(\varDelta t = {1.0\times 10^{-3}}{\hbox {s}}\).

Fig. 11
figure 11

Layout of the 2D slumping block problem and corresponding application ramp for the gravitational acceleration

Full size image

To further highlight the stabilisation benefits of the patch recovery, the above problem has been solved using two versions of the proposed implicit MPM, namely GIMP and GIMP-patch – i.e., with the former using no patch recovery of pore pressures. Figure 12 shows the excess pore pressure field at \(t = {0.18}{\hbox {s}}\) resulting from both methods. Notwithstanding the underlying three-field formulation, the implicit GIMP (with equal-order interpolation) still produces a checkerboard pore pressure pattern when no patch recovery is performed, which is consistent with the observations of Gajo et al. [55]. Such a pattern becomes increasingly pronounced as time elapses, and causes a sudden abortion of the GIMP simulation at approximately \(t = {0.21}{\hbox {s}}\). In contrast, the numerical solution obtained using the proposed MLSA-based patch recovery is completely oscillation-free throughout the whole duration of the analysis.

Fig. 12
figure 12

Excess pore pressure distributions at \(t = {0.18}{\hbox {s}}\) with implicit GIMP and GIMP-patch methods

Full size image

Figure 13 displays the excess pore pressure fields obtained at different times (\(t = {0.1}{}\), 0.3, \({0.5}{\hbox {s}}\)) using both the implicit GIMP-patch and explicit GC-SRI-patch methods (with a time step size of \(\varDelta t = {1.0\times 10^{-5}}{\hbox {s}}\)). For further comparison, the time evolution of the excess pore pressure at three selected points (P1, P2 and P3 in Figure 11) is also shown in Figure 14. As expected, a build-up in pore pressure occurs during the gravitational ramp, whereas the following pressure dissipation develops non-monotonically due to the so-called Mandel–Cryer effect [88, 89] – see Figs. 13 and 14. Both methods provide very comparable solutions for the same problem, with smooth/stable pore pressure fields obtained in both cases.Similar conclusions regarding the mutual verification of the two methods are suggested by Figure 15 in terms of the final displacement (vector norm of the solid displacement), deviatoric stress (defined by \(\sqrt{\frac{1}{2}[(\sigma _1-\sigma _2)^2+(\sigma _2-\sigma _3)^2 +(\sigma _3-\sigma _1)^2]}\), where \(\sigma _1\), \(\sigma _2\) and \(\sigma _3\) are principal stresses) and mean stress (defined by \(\frac{1}{3}\left( \sigma '_x+\sigma '_y+\sigma '_z\right)\), where \(\sigma '_x\), \(\sigma '_y\) and \(\sigma '_z\) are normal effective stresses) fields at \(t = {0.5}{\hbox {s}}\). The comparison with the results returned by Zheng et al. [1]’s explicit method supports the overall suitability of the proposed implicit GIMP-patch method, which can be used to solve transient hydromechanical problems with large time steps. In addition, the authors found a good match between the results obtained with the proposed method and those obtained with the smoothed particle finite element method by Yuan et al. [90], which further demonstrates the excellent performance of the implicit GIMP-patch method.

Fig. 13
figure 13

Excess pore pressure field at different times obtained for a 2D slumping block using the implicit GIMP-patch method (left) and explicit GC-SRI-patch method (right)

Full size image
Fig. 14
figure 14

Time evolution of the excess pore pressure at three different locations (points P1, P2, P3 in Figure 11) obtained for a 2D slumping block using the implicit GIMP-patch method and the explicit GC-SRI-patch method

Full size image
Fig. 15
figure 15

Solid displacement, deviatoric stress, and mean stress fields obtained at \(t = {0.5}{\hbox {s}}\) using the implicit GIMP-patch method (left) and the explicit GC-SRI-patch method (right)

Full size image

4.4 Calculation time

To compare in more detail the computational performance of the two considered MPMs, selected time steps (giving the same order of accuracy) and associated calculation times (CT) are reported in Table 3 for verification examples 1, 4, and 5. Note that the implicit and explicit time steps used for the 1D small-deformation consolidation benchmark (Example 1 in Section 4.1.1) have been selected based on a dedicated sensitivity study (see Figure 4) and re-adopted to solve the 2D slumping block problem (Example 5 in Section 4.3). A coarser background mesh was employed for the 1D large-deformation consolidation problem (Example 4, in Section 4.2), which enabled the use of larger time steps in both the explicit and implicit analyses.

Table 3 Computational performance of the considered implicit and explicit MPMs in relation to the verification examples 1, 4, and 5
Full size table

The benefit of the implicit method in terms of calculation time is readily apparent in Table 3 and follows directly from the enabled use of large time steps. However, it is worth noting that the relative difference in calculation time between the implicit and the explicit codes tends to gradually decrease as the problem domain is discretised with a larger number of MPs and grid cells (e.g., as in the 2D slumping block example). This is due to the implicit solver (in this case, the PARDISO solver), which solves the full system of equations. The PARDISO solver is based on a direct solver [91], which has numerical factorisation as the major step in the solution, which for 2D problems has an order of complexity \(O\left( n^{3/2}\right)\) (where n is the size of the vector of unknowns). In the explicit method, the increase in time is simply proportional to the number of unknowns. Therefore, as the size of the problem increases, the implicit method becomes less advantageous. This aspect should be borne in mind when tackling relatively large problems, which may require, e.g., parallel computing techniques for faster solution when using the implicit GIMP-patch method.

5 Conclusion

This paper has presented a fully implicit, stabilised MPM for dynamic coupled problems in porolelastic media – the extension to elastoplastic porous media has recently been tackled by Zheng et al. [92]. The proposed method is based on a three-field u–p–U formulation of the governing conservation laws and equal/low-order interpolation of the three primary variables, namely solid displacement, pore pressure, and water displacement. Combining enhanced GIMP interpolation functions with a Moving Least Square Approximation (MLSA)-based patch recovery scheme for pore pressures has been shown to produce accurate, stable and oscillation-free results. In particular, five 1D/2D poroelastic examples have been used to demonstrate the good performance of the implicit MPM in comparison with analytical solutions (where available) and MPM solutions obtained through the explicit GC-SRI-patch method previously proposed by the same authors. The proposed implicit GIMP-patch method is proven to provide robust numerical solutions for dynamic coupled problems over different inertial and deformation regimes.

The computational benefit of the implicit method is substantial and stems directly from the possibility to use larger time steps. However, it has also been pointed out that its relative advantage with respect to the explicit algorithm tends to reduce as problems of increasing size are tackled. In addition, it should be pointed out that the proposed GIMP-patch method solves the relative governing equations with respect to the current configuration, and the possible occurrence of large strains using suitable finite strain measures (objective stress-strain work-conjugate pairs) is not considered in the current formulation. Future work will be devoted to boosting the computational performance (e.g., via parallel computing using the Pardiso solver), as well as to including more realistic soil constitutive models and fully work-conjugate formulations [66] for the solution of a wider class of large-deformation geotechnical problems.