1 Introduction

Laser powder bed fusion (LPBF) is an additive manufacturing (AM) process consisting of either a laser or an electron beam selectively melting a bed of metal powder in a layer-by-layer fashion. LPBF technology has grown exponentially over the last several decades thanks to its ability to produce components with small geometrical features covering a large range of scales [1]. LPBF allows close-to-freeform production and has radically changed the approach to design, moving from the so-called design for manufacturing to functional design, where the functionality of the component is optimized with very few constraints coming from the manufacturing process [2]. While several metal alloys can be processed by means of LPBF technology, the most common are iron, titanium, nickel, and aluminum alloys [3]. In the present work, an LPBF process of stainless steel 316L is considered.

Despite the above-mentioned potentiality, widespread adoption of LPBF technology is hindered by the lack of standardization and repeatability associated with the complexity of the LPBF process. Nowadays, one of the main issues that the research community is trying to address is to understand the process–structure–property–performance relationship occurring in LPBF products [4]. Several studies have investigated the effects of LPBF process parameters at different scales [5,6,7,8], from micro-structure to part-deflection, but a deterministic, holistic model has not yet been developed.

Since the process is principally thermally driven, most of the process-induced flaws in the final structures are influenced by the thermal history of the part, i.e., by the spatio-temporal evolution of the temperature field within the structure [9, 10]. In fact, a specific region of the structure can lead to higher residual heat compared to others and thus to locally varying micro-structural properties which directly affect the final performance (e.g., yield stress, fatigue life, etc.) of the component [11, 12]. Therefore, a purely empirical process parameter optimization might be ineffective and lead to very high costs, in terms of machine time, powder consumption, and energy usage.

Numerical modeling and simulations can play an important role enabling prediction of the thermal history in LPBF components without undergoing long and expensive trial-and-error campaigns. Due to the extreme spatio-temporal ranges involved and the complexity of the physical process, LPBF simulations are challenging from both a modeling and a numerical perspective. For detailed reviews on LPBF process simulations, interested readers are referred to [13,14,15].

The finite element method (FEM) is often used to perform numerical analysis of LPBF problems. Some authors have tried to employ adaptive mesh refinement and coarsening [16,17,18,19]; however, the most widespread solution is to adopt reduced/surrogate models of the thermal problem, which in the following we refer to as part-scale models.

Many different part-scale thermal models have been developed and validated, but this area of research is far from complete. These models play a key role in both thermo-mechanical and microstructural predictions. In fact, even if residual stresses and microstructural properties are generated at the local scale and have a strong dependency on the cooling rates, they are also influenced by the geometry of the structure due to the complex process–structure–property–performance relationship in AM processes discussed above.

The so-called pragmatic approach, first presented by [20], activates blocks of agglomerated layers at a given temperature (e.g., the melting temperature in [20] and a material-dependent relaxation temperature in [21]). Results obtained using this method are in good agreement with experimental measurements of part deflection, but no validation is provided for the thermal model. Moreover, this method requires a conformal mesh. This may lead to very large systems when complex geometries are investigated, since the generated mesh may be over-refined in parts of the domain, where critical geometrical features (e.g., sharp corners, small holes, etc.) are present.

[22] develop a quasi-static thermo-mechanical model for the fast prediction of thermal distortion in LPBF processes using a thermal circuit network on a voxelized representation of the part domain. In such a model, Hoelzel and co-workers also neglect thermal inertia effects. Such a choice is justified as the mechanical problem is quasi-static at part-scale, and no validation is provided for the thermal model.

A part-scale thermal model employing the virtual domain approximation is presented by [23], allowing for a domain reduction, since heat losses through the powder and the base plate are modeled by means of an equivalent heat transfer coefficient. Such a model shows a relative error below \(15\%\) with respect to temperature measurements obtained by means of thermocouples on an oblique square prism of \(30\times 30\times 80\) \(\hbox {mm}^3\) printed using Ti-6Al-4V.

Another part-scale thermal model based on a highly efficient matrix-free GPU computation is introduced by [24] leading to a speed-up factor higher than \(\times 4\) with respect to classical CPU-based implementations. The base plate temperature of a \(20\times 20\times 20\) \(\hbox {mm}^3\) cubic specimen is measured by means of a K-type thermocouple embedded in the center of the build plate. To and co-workers assume adiabatic boundary conditions at the solid/powder interface and conduct a thorough sensitivity analysis with respect to the other calibrated parameters.

[25] propose a part-scale thermal model using graph-theoretic approach. The model is validated with respect to experimental thermal measurements for a 250 \(\hbox {cm}^3\) volume impeller. Good agreement among the results obtained using the graph-theoretic approach and experimental measurements is reported. However, the authors assume linear thermal parameters and their results strongly depend on the chosen number of nodes, as well as a gain factor which controls the rate of heat diffusion through the nodes. Both these parameters have been calibrated in a previous work [26] for the same material and AM machine as in [25] but, since they have no direct physical meaning, turn out to be rather complex to calibrate accurately.

In [27] an immersed boundary method, the Finite Cell Method, is employed to implement a part-scale thermo-mechanical model. The model is then validated with respect to experimental measurements on part deflection and residual strains carried out at the National Institute of Standards and Technology (NIST) for the AM 2018 Benchmark Series [28]. However, no temperature measurements were provided to validate the accuracy of the predicted temperature field.

Avoiding a conformal mesh discretization by means of an implicit representation of the part geometry, the numerical method adopted in the present work follows the line of thought presented in [27, 29]. However, in the present contribution, we introduce a local–global approach, which may better capture the multi-scale feature of LPBF processes, employing different thermal models at the small and large spatial scales.

In particular, a part-scale thermal model is developed and experimentally validated using a modified version of the two-level method first presented by [30] and analyzed in detail in [31]. Such a numerical approach is a local–global methodology which allows one to couple the results of a local, finer discretization with a coarser, global representation of the problem solutions. One of the main advantages of this approach is its ability to keep both the local and the global discretization on a structured Cartesian grid, making the mesh generation process computationally inexpensive and, at the same time, avoiding continuous re-meshing [32].

Compared to other immersed boundary approaches, the proposed two-level method allows for different treatment of the spatial scales on two separate meshes. In contrast, the Finite Cell Method (FCM) [33,34,35], the Cut-FEM [36], as well as the other popular immersed boundary approaches require, at least in their traditional formulation, refinement and coarsening schemes to address multi-scale problems. Considering multi-material problems, in [37], a similar approach based on the weak coupling of two non-boundary conformal meshes at the material interface has been presented and successfully employed for biomedical applications. Moreover, in the two-level method, the scale separation can be achieved not only in space, but also in time. In fact, the simple structure of both the local and the global mesh makes a full parallelization of the code possible. However, both these possibilities are left to future studies and not included in the present contribution.

[38] demonstrated that the dwell temperature, i.e., the temperature of the powder-bed upper surface at the instance of laser activation, plays a crucial role in the resulting melt-pool shape during the layer printing process, leading to different microstructure and porosity in the final part. Starting from this observation, we aim at the development of a part-scale thermal model which—exploiting the multi-scale nature of the two-level method—delivers an accurate prediction of the dwell temperature. One of the key features of the proposed model is that the powder-bed is included in the computational domain. As demonstrated by the presented results, this assumption allows us to easily calibrate the physical parameters of our model and, at the same time, achieve a remarkable agreement with respect to the measured experimental data.

The outline of this paper is as follows. In Sect. 2, the governing equations of the considered physical problem at the local and global scale are presented. Section 3 describes the numerical implementation details of the part-scale two-level approach. In Sect. 4, the proposed methodology is first validated with respect to experimental measurements taken from [38] for an AM cylindrical component, and then is applied to simulate the complete LPBF process of a topologically optimized beam structure. Finally, in Sect. 5 we draw the main conclusions and possible further extensions to the present contribution.

2 Governing equations

In the present section, a thermal model for LPBF process simulation based on the two-level method at part-scale is presented. More details on thermal models in welding and additive manufacturing can be found by the interested readers in [39,40,41].

2.1 Thermal problem

Considering a material obeying Fourier’s law of heat conduction, the LPBF thermal process can be modeled by means of the heat transfer diffusion equation:

$$\begin{aligned} \rho c \dfrac{\partial T}{\partial t}-\nabla \cdot \left( \kappa \nabla T \right) =Q, \end{aligned}$$
(1)

where T indicates the temperature field, \(\rho =\rho (T)\) the temperature-dependent density of the material, \(c=c(T)\) the temperature-dependent specific heat capacity, \(\kappa =\kappa (T)\) the temperature-dependent thermal conductivity, t the time, and Q an equivalent heat source. The latent heat term associated to the material phase-change is neglected in the presented work, due to its negligible influence when macroscopic, part-scale thermal effects are investigated (see, e.g., [42]). Boundary conditions will be discussed in detail in Sect. 2.4.

2.2 The two-level method

The two-level method is based on a re-formulation of the heat transfer equation (1) as two coupled problems referred in the following as the local and the global problem. Let us consider a global domain \(\Omega _+\) and a local domain \(\Omega _-\subset \Omega _+\), such that, following the notation introduced in [30], \(T^+\) and \(T^-\) are the local and the global solution, respectively. The thermal conductivity \(\kappa\) is defined as

$$\begin{aligned} \kappa := {\left\{ \begin{array}{ll} \kappa _+ &{} \text {in } \Omega _+\setminus \Omega _- \\ \kappa _- &{} \text {in } \Omega _- \end{array}\right. } \end{aligned}$$
(2)

with \(\rho _+\), \(\rho _-\), \(c_+\), and \(c_-\) defined analogously. We note some or all of these parameters may depend on time, space, or temperature. This dependence is understood if not explicitly denoted.

Let \(\gamma\) denote the interface between local and global problems, across which information is exchanged. For \(\eta \in H^{-1/2}\left( \gamma \right)\), \(\eta \xi _{\gamma } \in H^{-1}\left( \Omega _+\right) = H^1(\Omega _+)'\) is defined as the linear functional such that:

$$\begin{aligned} \int _{\Omega _+} \left( \eta \xi _{\gamma }\right) w = \int _{\gamma } \eta w \quad \quad \forall w \in H_{\Gamma _D}^1\left( \Omega _+\right) , \end{aligned}$$
(3)

consistent with the notation used in [43,44,45].

To achieve a more efficient numerical solution, which is necessary to deal with the LPBF thermal problem at part-scale, the original formulations of the global and local problem as presented by [30,31,32] are slightly changed, such as

$$\begin{aligned} c_+\rho _+\dfrac{\partial T^+}{\partial t} - \nabla \cdot \left( \kappa _+\nabla T^+ \right)&= Q +\left( \kappa _+ - \kappa _-\right) \frac{\partial T^-}{\partial {\varvec{n}} } \xi _{\gamma } \qquad \text {in } \Omega _+ \end{aligned}$$
(4)
$$\begin{aligned} c_-\rho _-\dfrac{\partial T^-}{\partial t} - \nabla \cdot \left( \kappa _-\nabla T^- \right)&= Q \qquad \text {in } \Omega _-, \end{aligned}$$
(5)

with boundary conditions defined as in a following section. The problems (4) and (5) are then solved in an iterative manner until convergence is satisfied.

When compared to the two-level method as implemented in [30, 32], this formulation greatly simplifies and reduces the cost of the assembly and evaluation process. More specifically, this novel formulation reduces the number of necessary integral evaluations, no longer needs the storage and evaluation of the derivatives of \(\kappa\), and avoids the necessity of evaluating volumetric integrals non-conformal to the mesh discretization, which may ultimately require the application of an adaptive integration scheme, such as the ones adopted in other immersed boundary approaches (e.g., the Finite Cell Method [33] or the Cut Finite Element Method [36]).

As a consequence, one incurs a minor loss of consistency in the following sense: Let \(T^* \in H^1(\Omega _+)\) denote the exact solution of (1), \(T^+ \in H^1 (\Omega _+)\) the exact solution of (4), and \(T^- \in H^1(\Omega _-)\) the exact solution of (5). Then the following consistency conditions are satisfied:

$$\begin{aligned} \int _{\Omega _+ \setminus \Omega _- } \left( T^* - T^+\right) v&= 0 \qquad \text {for all } v \text { in } H^1\left( \Omega _+\right) , \end{aligned}$$
(6)
$$\begin{aligned} \int _{\Omega _- } \left( T^* - T^-\right) q&= 0 \qquad \text {for all } q \text { in } H^1\left( \Omega _-\right) . \end{aligned}$$
(7)

However, the more stringent condition on \(T^+\):

$$\begin{aligned} \int _{\Omega _+ \cap \Omega _- } \left( T^* - T^+\right) v&= 0 \qquad \text {for all } v \text { in } H^1\left( \Omega _+\right) , \end{aligned}$$
(8)

which holds for the formulation shown in [30,31,32], no longer applies. In practice, we find this error is small, provided that the jump across \(\gamma\) is not overly large (following the theory for the related Fat-boundary method given in [44]). Indeed, for many problems, the scale separation between the global and local mesh is sufficiently large such that the discretization error dominates over this region, and any additional error incurred by the loss of consistency is negligible in comparison.

2.3 Two-level method derivation

We now provide a brief derivation for the modified two-level method (4)–(5). We consider the steady version of (1):

$$\begin{aligned} \begin{aligned} -\nabla \cdot \left( \kappa \nabla T \right)&=Q \quad \text { in } \Omega _+,\\ \kappa \frac{\partial T}{\partial {\varvec{n}}}&= 0 \quad \text { on } \partial \Omega _+. \end{aligned} \end{aligned}$$
(9)

The derivation for the unsteady problem follows from similar arguments, and we have chosen to consider the steady problem here in the interest of clarity. Assume that \(T^*\) is a strong solution of (9) in a domain \(\Omega _+\), with the local domain \(\Omega _- \subset \Omega _+\), and the interface between \(\Omega _+\setminus \Omega _-\) and \(\Omega _-\) denoted as \(\gamma\). Define \(\kappa\) as in (2) and let \(T^+\), and \(T^-\) be such that (6), (7) hold. Assume additionally that \(T^*\) is regular enough near \(\gamma\) such that:

$$\begin{aligned} \frac{\partial T^*}{\partial {\varvec{n}}^+ }\big |_{\gamma }&= - \frac{\partial T^*}{\partial {\varvec{n}}^- } \big |_{\gamma }, \end{aligned}$$
(10)

where \({\varvec{n}}^{+/-}\) denote the outward-pointing normals from either side of \(\gamma\).

Multiplying (9) by a test function \(v \in H^1(\Omega _+)\) gives:

$$\begin{aligned} \begin{aligned} -\int _{\Omega _+} \nabla \cdot \left( \kappa \nabla T^*\right) v&= \int _{\Omega _+}Q v \end{aligned} \end{aligned}$$
(11)

From (6), (7):

$$\begin{aligned} -\int _{\Omega _+} \nabla \cdot \left( \kappa \nabla T^*\right) v&= -\int _{\Omega _+\setminus \Omega _-} \nabla \cdot \left( \kappa _+ \nabla T^+\right) v -\int _{\Omega _-} \nabla \cdot \left( \kappa _- \nabla T^-\right) v. \end{aligned}$$
(12)

Integration by parts yields:

$$\begin{aligned} \begin{aligned} \int _{\Omega _+} \kappa \nabla T^* \cdot \nabla v&= \int _{\Omega _+\setminus \Omega _-} \kappa _+ \nabla T^+ \cdot \nabla v + \int _{\Omega _-} \kappa _- \nabla T^- \cdot \nabla v - \int _{\gamma } \kappa _+ \frac{\partial T^+}{\partial {\varvec{n}}}v + \int _{\gamma } \kappa _- \frac{\partial T^-}{\partial {\varvec{n}}}v , \end{aligned} \end{aligned}$$
(13)

where we have defined the normal vector \({\varvec{n}}\) on \(\gamma\) such that it is outward-pointing on \(\Omega _+\setminus \Omega _-\). Rearranging (13) gives:

$$\begin{aligned} \begin{aligned} \int _{\Omega _+\setminus \Omega _-} \kappa _+ \nabla T^+ \cdot \nabla v - \int _{\gamma } \kappa _+ \frac{\partial T^+}{\partial {\varvec{n}}}v + \int _{\gamma } \kappa _- \frac{\partial T^-}{\partial {\varvec{n}}}v&= \int _{\Omega _+} \kappa \nabla T^* \cdot \nabla v - \int _{\Omega _-} \kappa _- \nabla T^- \cdot \nabla v \\&= \int _{\Omega _+\setminus \Omega _- } \kappa \nabla T^* \cdot \nabla v. \end{aligned}\end{aligned}$$
(14)

By the assumption (10):

$$\begin{aligned} \int _{\Omega _+\setminus \Omega _-} \kappa _+ \nabla T^+ \cdot \nabla v + \int _{\gamma } \left( \kappa _- - \kappa _+\right) \frac{\partial T^-}{\partial {\varvec{n}}}v&= \int _{\Omega _+\setminus \Omega _- } \kappa \nabla T^* \cdot \nabla v. \end{aligned}$$
(15)

We then observe that:

$$\begin{aligned} \int _{\Omega _+} \kappa _+ \nabla T^+ \cdot \nabla v + \int _{\gamma } \left( \kappa _- - \kappa _+\right) \frac{\partial T^-}{\partial {\varvec{n}}}v&= \int _{\Omega _+\setminus \Omega _- } \kappa \nabla T^* \cdot \nabla v + \int _{\Omega _-} h v, \end{aligned}$$
(16)

for an arbitrary extension h in \(H^1(\Omega _-)\), sufficiently regular such that, for all v in \(H^1(\Omega _-)\):

$$\begin{aligned} \int _{\Omega _-} \kappa _- \nabla T^{+} \cdot \nabla v&= \int _{\Omega _-} h v. \end{aligned}$$
(17)

From (16), we may derive the modified two-level formulation (4)–(5).

Remark

Equation (16) and the subsequent modified two-level formulation (4)–(5) assume that \(T^*\) is sufficiently regular near \(\gamma\) such that (10) holds, at least approximately. From this, we may assume that \(\partial T^+ / \partial {\varvec{n}} = - \partial T^- / \partial {\varvec{n}}\) on \(\gamma\) to arrive at (4), (16). However, if (10) does not hold, then (4) no longer applies. In such a case, one may use the following formulation instead:

$$\begin{aligned} c_+\rho _+\dfrac{\partial T^+}{\partial t} - \nabla \cdot \left( \kappa _+\nabla T^+ \right)&= Q + {\kappa _+\frac{\partial T^+}{\partial {\varvec{n}} }\xi _{\gamma }} - \kappa _-\frac{\partial T^-}{\partial {\varvec{n}} } \xi _{\gamma } \qquad \text {in } \Omega _+ \end{aligned}$$
(18)
$$\begin{aligned} c_-\rho _-\dfrac{\partial T^-}{\partial t} - \nabla \cdot \left( \kappa _-\nabla T^- \right)&= Q \qquad \text {in } \Omega _-, \end{aligned}$$
(19)

with the term highlighted in red to show the difference between (4) and (18). In the simulations performed in the present work, we have sufficient regularity along \(\gamma\) such that we may apply (4), and this formulation will be assumed hereafter. In our computations (not shown), we found the two methods differed by less than .1%. For cases in which it is possible to employ (4)–(5), it is generally preferable over (18)–(19), as the convergence of the corresponding numerical scheme is typically faster. We add that a full theoretical investigation of (4)–(5), (18)–(19) is beyond the scope of the current work and will be explored in detail in an upcoming work.

2.4 Local and global problem boundary conditions

Fig. 1
figure 1

Thermal problem boundary conditions (BCs) in the local a global b domains

Full size image

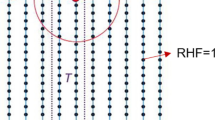
To capture the multi-scale nature of the LPBF process, the two-level method distinguishes between a local domain \(\Omega _-\) and a global domain \(\Omega _+\), which we model differently in the proposed thermal model. Figure 1 depicts the boundary conditions (BCs) on the local and global domain. The temperature continuity with the global solution is enforced by means of Dirichlet BCs on the lateral and lower surfaces, while on the lower surface of the global domain, Fig. 1b, the temperature is fixed to the build plate temperature \(T_{bp}\) and adiabatic BCs are applied on the lateral surfaces of the build plate. Finally, a zero-jump condition is imposed on the fluxes on the immersed local domain boundaries. As can be observed in Fig. 1, the local domain dissipates heat by convection and radiation through the upper surface (see Fig. 1a) by means of a heat loss flux term defined as follows:

$$\begin{aligned} \kappa \nabla T_-= h_\mathrm{{conv}}(T_- - T_{amb})+\sigma _\mathrm{{SB}}\varepsilon (T_-^4 - T_{amb}^4), \end{aligned}$$
(20)

where \(h_\mathrm{{conv}}\) is the heat transfer coefficient by convection due to the inert gas (Argon) flow present in the chamber, \(T_{amb}\) is the ambient temperature of the building chamber, \(\sigma _\mathrm{{SB}}=5.87\times 10^{-8}\) [\(\hbox {W/m}^2/\hbox {K}^4\)] is the Stefan–Boltzmann constant, and \(\varepsilon\) the emissivity of the powder bed. The global domain dissipates heat by conduction through the lateral surfaces of the powder bed and by convection through the upper surface. These two heat dissipation modes are modeled by means of two heat loss flux terms defined as:

$$\begin{aligned} \kappa \nabla T_+&= h_\mathrm{{conv}}(T_+ - T_{amb}), \end{aligned}$$
(21)
$$\begin{aligned} \kappa \nabla T_+&= h_\mathrm{{pow}}(T_+ - T_{amb}), \end{aligned}$$
(22)

where \(h_\mathrm{{pow}}\) is the heat transfer coefficient by conduction through the powder.

Most of these quantities are unknown and not readily measurable, and thus required a calibration procedure to be estimated. Radiation effects are neglected in the global domain, since they play a minor role in regions far from the heat affected region, which we consider lying entirely within the local domain. As described in Fig. 1b, global domain BCs are completed by adiabatic and Dirichlet BCs on the lateral and lower surfaces of the build plate, respectively. Finally, to avoid jumps among the local and the global domain temperature fields, a zero-jump temperature condition is imposed in the local problem on the lateral and bottom surfaces of \(\Omega _-\), while, in the global problem, a zero-jump temperature flux condition is enforced on the lateral and bottom surfaces of \(\Omega _-\) which are immersed in the global domain.

Due to the specific features of the two-level method as presented in [30], the powder-bed is directly included in our thermal model. In general, immersed boundary methods do not require one to model the powder bed at part-scale [27]. However, to impose temperature and flux continuity on the immersed local domain boundaries, the two-level method needs a physical solution on such boundaries, thus powder is included in our physical model. Modeling the powder surely increases the accuracy of the thermal model, but, on the other hand, it introduces potential numerical instabilities due to the discontinuous integration in the elements cut by the boundaries of the solidified domain.

3 Numerical implementation

In the present work, we employ the two-level method [30, 32], an immersed boundary finite element method employing a local–global approach, together with an agglomerated layer activation procedure to solve the thermal problem defined in Sect. 2 for an LPBF problem at part-scale.

3.1 Two-level algorithms

The application of the two-level method may be done in several ways. Here, we consider two particular implementations, which we will refer to as the sequential two-level method and as the parallel two-level method, with details in the following.

We consider an iteration k at a generic time step n. We note that all variables indexed with k refer to the current iteration, while those indexed with n are from the preceding time step. For simplicity, we assume a standard Backward Euler time-stepping scheme, though we stress that the algorithm may be employed with any time integration technique. The two approaches are described in the following:

Sequential two-level method:

Step k: Obtain local solution \(T_k^-\):

$$\begin{aligned} \begin{aligned} c_-|_{T_{k-1}^-} \rho _-|_{T_{k-1}^-} T_k^- - \Delta t \nabla \cdot \left( \kappa _-|_{T_{k-1}^-} \nabla T_k^- \right)&= \Delta t Q + c_-|_{T_{k-1}^-} \rho _-|_{T_{k-1}^-} T_{n-1}^- \qquad \text{ in } \Omega _-, \\ T_{k}^-&= T_{k-1}^+ \qquad \text { on } \gamma . \end{aligned} \end{aligned}$$
(23)

Step k+1: Obtain global solution \(T_k^+\):

$$\begin{aligned} \begin{aligned} c_+|_{T_{k-1}^+} \rho _+|_{T_{k-1}^+} T_k^+ - \Delta t \nabla \cdot \left( \kappa _+|_{T_{k-1}^+} \nabla T_k^+ \right)&= \Delta t Q + c_+|_{T_{k-1}^+} \rho _+|_{T_{k-1}^+} T_{n-1}^+ \\&+ \Delta t \left( \kappa _+|_{T_{k-1}^+} - \kappa _- |_{T_k^-}\right) \frac{\partial T_k^-}{\partial {\varvec{n}}} \xi _{\gamma } \qquad \text{ in } \Omega _+, \\ T_{k}^+&= T_{0} \qquad \text { on } \Gamma _D. \end{aligned} \end{aligned}$$
(24)

Step k+2: Relaxation: \(T_k^+ = \theta T_{k}^+ + (1-\theta )T_{k-1}^+\), \(0<\theta \le 1\).

Step k+3: Check convergence. If reached, terminate. Else, return to step k.

Parallel two-level method:

Step k: Obtain local solution \(T_k^-\):

$$\begin{aligned} \begin{aligned} c_-|_{T_{k-1}^-} \rho _-|_{T_{k-1}^-} T_k^- - \Delta t \nabla \cdot \left( \kappa _-|_{T_{k-1}^-} \nabla T_k^- \right)&= \Delta t Q + c_-|_{T_{k-1}^-} \rho _-|_{T_{k-1}^-} T_{n-1}^- \qquad \text{ in } \Omega _-, \\ T_{k}^-&= T_{k-1}^+ \qquad \text { on } \gamma . \end{aligned} \end{aligned}$$
(25)

Step k+1: Obtain global solution \(T_k^+\):

$$\begin{aligned} \begin{aligned} c_+|_{T_{k-1}^+} \rho _+|_{T_{k-1}^+} T_k^+ - \Delta t \nabla \cdot \left( \kappa _+|_{T_{k-1}^+} \nabla T_k^+ \right)&= \Delta t Q + c_+|_{T_{k-1}^+} \rho _+|_{T_{k-1}^+} T_{n-1}^+ \\&\quad+ \Delta t \left( \kappa _+|_{T_{k-1}^+} - \kappa _- |_{T_{k-1}^-}\right) \frac{\partial T_{k-1}^-}{\partial {\varvec{n}}} \xi _{\gamma } \qquad \text{ in } \Omega _+, \\ T_{k}^+&= T_{0} \qquad \text { on } \Gamma _D. \end{aligned} \end{aligned}$$
(26)

Step k+2: Relaxation: \(T_k^+ = \theta T_{k}^+ + (1-\theta )T_{k-1}^+\), \(0<\theta \le 1\).

Step k+3: Check convergence. If reached, terminate. Else, return to step k.

In Eqs. (24) and (26) \(\Gamma _D\) is the Dirichlet boundary which in our case corresponds to the lower surface of the base plate and \(T_0=T_{bp}\). In the following, the relaxation parameter \(\theta\) is set equal to 1, i.e., no relaxation is applied.

The sequential and parallel formulations are similar, with a key distinction: in step \(k+1\), the sequential method utilizes the output \(T_k^+\) of step k on the right hand side of Eq. (24), while the parallel method uses the value \(T_{k-1}^-\) computed at the previous iteration as force term in Eq. (26). While this means that the parallel method may require more iterations to converge, it also means that steps k and \(k+1\) are independent of each other, and hence may be computed in parallel. Depending on the computational resources available, the greater parallelism offered by this approach may provide faster computation when compared to the fewer necessary iterations when using the sequential approach. We note that these different algorithms can be seen as Gauss–Seidel (sequential) or Jacobi (parallel) versions of domain decomposition schemes [46,47,48]. In the following, we adopt the sequential implementation of the two-level method. In fact, due to the limited number of computational cores on our machine, we prefer to exploit the faster convergence rate of the former solution, but for different architectures, the latter might lead to a remarkable computational speed-up.

3.2 Agglomerated layers activation

Fig. 2
figure 2

Two level activation strategy: Two level activation strategy: a beginning of the analysis, b layer diffusion step, c heating step, d cooling step

Full size image

Figure 2 depicts the layer-by-layer activation scheme adopted in our implementation. To compute an entire LPBF process at part-scale, we employ an agglomerated layer activation strategy (see, e.g., [20, 27, 49]). As in Fig. 2(a), we start first solving a steady-state thermal problem on the build-plate to define our initial conditions before the first layer is activated. In the present implementation, at each layer activation step, a set of 20 physical layers is inserted into the problem, adding a new layer of global domain elements into the system. The local domain discretization is then shifted upward by the agglomerated layer thickness. Once this mesh update is performed, we compute a layer diffusion step (Fig. 2b), where the residual heat of the previous solution diffuses into the newly activated agglomerated layer. In our implementation, we initialize the new nodes of the newly activated layer at the ambient temperature, and allow one time step to let the heat diffuse into the new layer; however, we note that the solution in the area covered by the local domain, within the global domain, does not correspond to a physical temperature. Successively, a heating step occurs, Fig. 2c, where a heat source is applied uniformly at the Gauss points of the new layers lying within the geometry of the part. Such a set of Gauss point is evaluated by means of an inside–outside test performed directly on the original .stl file of the part as acquired from a CAD environment. Finally, the solidified domain is obtained during the cooling step, Fig. 2d. Such a thermal cycle is repeated until the final part is completed.

In the present work, we define the equivalent heat source Q as

$$\begin{aligned} Q=\dfrac{4 \eta P}{\pi l_d^2 t_a} \end{aligned}$$
(27)

with \(\eta\) the absorptivity of the material, P the nominal power of the laser beam, \(l_d\) the laser spot size, and \(t_a\) the thickness of the activated layer. This definition corresponds to a local, high-intensity heat source instantly activated over the entire portion of the printed geometry in the new agglomerated layer, as depicted in Fig. 2c. Therefore, in our implementation the heating activation step lasts few microseconds due to the high energy input resulting from the adopted physical model. In the following, we evaluate the heating activation time step increment \(\Delta t_A\) as follows:

$$\begin{aligned} \Delta t_A = \dfrac{2l_d}{v} \end{aligned}$$
(28)

with v the laser velocity. The time step in Eq. (28) is defined to provide an instantaneous application of the heat power. In fact, the heat power source in Eq. (27) is not scaled to the activation layer but instead is a concentrated heat source.

The last step of our thermal cycle is the cooling step, wherein the heat source is set equal to zero and the heat is dissipated by conduction through the solidified domain and the surrounding powder and by convection and radiation through the upper surface as described in Sect. 2.4. In the following numerical analysis, a backward Euler implicit time integration scheme is adopted to integrate over time, Eq. (1).

We employ the so-called birth–death element activation scheme ([50]). In fact, new elements in the global domain are generated as each agglomerated layer is activated. The birth–death element activation scheme is chosen, since in a structured, cartesian grid-like discretization—such as the one employed by the two-level method—the new element layer generation procedure is straightforward [27]. About half of the computational resources are thereby saved during the course of a complete analysis, since no space has to be previously allocated for inactive elements, as required, e.g., by the quiet element method [51].

3.3 Material properties

Table 1 Temperature-dependent material properties of solid SS 316L from [52]. Values at temperatures higher than the maximum temperature (\(1400\,^{\circ }\hbox {C}\)) have been extrapolated
Full size table

In the following, we consider components printed with stainless steel 316L (SS 316L). Such a metal alloy is one of the most widespread materials for metal AM products, thus its material properties are well-known and readily available, even for the high temperatures involved in LPBF processes. In Table 1, we report the temperature-dependent material properties for solid SS 316L as measured by [52]. Since we include powder in the computational domain, we need to define thermal properties for the powder domain region as well. The relationship between powder and solid density and heat capacity is then defined as follows:

$$\begin{aligned} \rho _\mathrm{{pow}}&=(1-\phi )\rho _\mathrm{{sol}}, \end{aligned}$$
(29)
$$\begin{aligned} c_\mathrm{{pow}}&= c_\mathrm{{sol}}, \end{aligned}$$
(30)

whereas assuming spherical particles, the relationship between powder and solid thermal conductivity is given by [53]:

$$\begin{aligned}&\dfrac{\kappa _\mathrm{{pow}}}{\kappa _\mathrm{{gas}}}= \left( 1 - \sqrt{1-\phi }\right) \left( 1+\dfrac{\dfrac{4}{3} \sigma _\mathrm{{SB}} T^3 d_\mathrm{{pow}}}{\kappa _\mathrm{{gas}}}\right) +\sqrt{1-\phi } \dfrac{2}{1-\dfrac{\kappa _\mathrm{{gas}}}{\kappa _\mathrm{{sol}}}} \left( \dfrac{2}{1-\dfrac{\kappa _\mathrm{{gas}}}{\kappa _\mathrm{{sol}}}} \ln \left( \dfrac{\kappa _\mathrm{{sol}}}{\kappa _\mathrm{{gas}}}\right) -1\right) \\ &\quad+\sqrt{1-\phi }\dfrac{\dfrac{4}{3} \sigma _\mathrm{{SB}} T^3 d_\mathrm{{pow}}}{\kappa _\mathrm{{gas}}}, \end{aligned}$$
(31)

where \(\kappa _\mathrm{{gas}}\) is the conductivity of the inert gas (Argon) present in the build chamber, and \(d_\mathrm{{pow}}\) is the average diameter of the powder particles. The adopted values of the above quantities are described in Sect. 4. Due to the immersed nature of the two-level method, in both local and global domain there are elements cut by the boundaries of the solidified domain.

The immersed boundary method can efficiently deal with discontinuous integration at void–material interfaces [33, 54], whereas numerical instabilities occur when we need to integrate across an interface between two different materials, such as the powder–solid interface in the thermal model described in Sect. 2. To overcome such a numerical issue, we introduce a smoothing factor S multiplying \(k_\mathrm{{pow}}\) and defined as follows:

$$\begin{aligned} S=(1+\sqrt{\nabla T^T \nabla T}h_\mathrm{{el}}\delta ), \end{aligned}$$
(32)

where \(h_\mathrm{{el}}\) is the nominal element length and \(\delta\) a scaling factor which we set equal to 0.2. As can be noticed, the smoothing factor S defined in Eq. 32 depends on the temperature gradient, and thus it almost vanishes when temperature gradients are close to zero as occurs in the layer diffusion and cooling steps. In contrast, it plays an important role in stabilizing the solution during the heating step, when high temperature gradients are involved. Such a kind of numerical instabilities are well known in the literature on immersed boundary methods, e.g., in [37] to alleviate such a numerical issue, it is introduced a penalty term penalizing the jump at the material interface within the same element.

3.4 Domain discretization

The core idea behind the two-level method is to separate the local and the global scales using two different domains, both of which are discretized separately using potentially very different element length. Moreover, the immersed nature of this numerical approach allows us to employ simple cartesian grids to discretize both the local and the global domain. These general concepts of the method can be also applied in the context of part-scale AM thermal process analyses. In particular, in the article at hand, we employ tetrahedral linear elements with a nominal element length \(h_\mathrm{{el}}\) of \(4\, \mathrm{{mm}}\) for the global domain and \(1\, \mathrm{{mm}}\) for the local domain.

3.5 Error metrics

To quantify the accuracy of our simulated results with respect to the experimental measurements, we employ two metrics, namely, the maximum relative percentage error on the dwell temperature \(\epsilon _\mathrm{{max}}\) and the sample Pearson correlation coefficient P defined as follows:

$$\begin{aligned}&\epsilon _\mathrm{{max}}\% = \mathrm{max}{\dfrac{T_{n,i}-T_{m,i}}{T_{m,i}}}\times 100\% \qquad i=1,..,N_\mathrm{{agg}}, \end{aligned}$$
(33)
$$\begin{aligned}&\text {P}(N,M)\% = \dfrac{\sum _{i=1}^{N_\mathrm{{agg}}}(T_{n,i}-{\bar{T}}_{n})(T_{m,i} -{\bar{T}}_{m})}{\sqrt{\sum _{i=1}^{N_\mathrm{{agg}}}(T_{n,i}-{\bar{T}}_{n})^2\sum _{i=1}^{N_\mathrm{{agg}}} (T_{m,i}-{\bar{T}}_{m})^2}}\times 100\%, \end{aligned}$$
(34)

where \(T_{m,i}\) and \(T_{n,i}\) are the average dwell temperature values of measured and simulated results, respectively, at the \(i^{th}\) agglomerated layer on the local domain upper surface, \(N_\mathrm{{agg}}\) is the number of agglomerated layers, M and N are \(N_\mathrm{{agg}}\times 1\) vectors containing the average measured and simulated dwell temperatures at each agglomerated layer, and \({\bar{T}}_{m}\) and \({\bar{T}}_{n}\) are defined as

$$\begin{aligned} {\bar{T}}_{m} = \frac{1}{N_\mathrm{{agg}}}\sum _{i=1}^{N_\mathrm{{agg}}} T_{m,i},\quad {\bar{T}}_{n} = \frac{1}{N_\mathrm{{agg}}}\sum _{i=1}^{N_\mathrm{{agg}}} T_{n,i}. \end{aligned}$$

Therefore, a correlation \(P=100\%\) indicates a perfect correlation between the numerical results and the experimental measurements.

4 Results and discussion

All the numerical analyses discussed in this section have been obtained using an in-house developed code written in FreeFEM++ [55] on a desktop computer provided with \(\hbox {Intel}^\circledR\)  \(\hbox {Xeon}^{\mathrm{TM}}\)  W-2123, CPU@3.9GHz, RAM 256Gb.

4.1 Model validation on a 3D printed cylinder

To calibrate and validate the accuracy of the proposed numerical method, we consider the LPBF printing process of a cylinder as reported by Williams et al. [38] and depicted in Fig. 3a. Williams and co-workers measure the average temperature on the upper powder layer before laser activation, which they refer to as dwell temperature. According to their experimental findings, the dwell temperature is controlled by the interlayer cooling time (ILCT) and plays a crucial role in defining the microstructure and thus the mechanical properties of AM parts.

We have replicated their experiment using the previously presented part-scale two-level method. The simulated dwell temperature evolution at the last layer of the LPBF process is shown in Fig. 3b using the model parameters reported in Table 2, which have been calibrated following a procedure similar to the one described in [56]. In Fig. 4, we report the simulated and the measured dwell temperatures during the entire 3D printing process. The dwell temperature results obtained by means of the two-level part-scale model shows good agreement with the experimental measurements reported in [38]. The maximum relative error \(\epsilon _\mathrm{{max}}\) is equal to \(13.95\%\) and occors at the second agglomerated layer, i.e., in a transitory step, while the relative error is kept always below \(2.5\%\) after the 15th activation step. The Pearson correlation coefficient as defined in Sect. 3.5 is equal to \(99.74\%\), indicating an almost perfect correlation among the measured and the predicted dwell temperature results, providing strong evidence for the reliability of the proposed part-scale thermal model.

Fig. 3
figure 3

3D virtual model and thermal simulation results of a cylinder

Full size image
Table 2 LPBF process and model parameters
Full size table
Fig. 4
figure 4

Simulated and measured surface temperature of the cylinder taken just before the laser passes over each layer considering an ILCT of 11s

Full size image

4.2 Thermal analysis of a topologically optimized structure

Fig. 5
figure 5

3D virtual model of topologically optimized beam structure taken from [57] (measures are in millimeters)

Full size image

To test the capability of the proposed numerical framework to deal with complex geometries, we compute the part-scale thermal analysis of a topologically optimized beam structure. The optimized structure depicted in Fig. 5 was obtained in [57] using a phase-field-based topology optimization procedure as presented in [58, 59]. In Fig. 6, we report the temperature field distribution on the topologically optimized part and on the local domain at three different steps of the process as well as the corresponding local domain mesh. Observing the results reported in Fig. 6, we can observe the two-level domain concept in action. We observe that the local domain is able to capture the small geometrical details of the optimized structure with a very high resolution. Meanwhile, the coupled global domain solution approximates the temperature field in the remaining regions of the part, substantially accounting for the thermal history at the scale of the entire component. The approach does not require any meshing of the considered geometry, since the domain is treated in an implicit fashion, making the analysis setup straightforward and suitable to deal with geometric flaws and complex geometries.

Fig. 6
figure 6

Temperature distribution at different layers. On the left it is reproduced the simulated temperature field on both the growing printed geometry and the local domain; on the right the top view showing the local domain temperature distribution and the corresponding domain discretization

Full size image

5 Conclusions

In the present contribution, we have applied the two-level framework, first introduced in [30, 32] for high-fidelity thermal models, to the analysis at the scale of an entire 3D printed component. The extension of the physical model in the implemented two-level framework allows us to simulate the complete printing process of parts with complex geometries, without requiring any conformal mesh generation step. In turn, we obtain a smooth workflow from the CAD model to the thermal analysis of AM components. The presented numerical results show the effectiveness of the proposed approach.

There are several potential perspectives for the present work. First, the structured discretization grids of both the local and the global domain call for a massive code parallelization. Such a code optimization step would lead to a remarkable speed-up in the overall computational time, fully exploiting the potentiality of the proposed numerical framework and opening the possibility to compute thermal analysis of an entire build plate. Second, we aim at extending the proposed part-scale thermal model to a multi-physics setting, considering a weakly coupled thermo-mechanical problem formulation.

As shown in our numerical examples, there is ample potential to use the machinery shown here to better unify the development and analysis of topologically optimized components, as the potential reduction in cost afforded by the two-level method can greatly accelerate forward solves during the optimization process. In fact, the optimization routine may require the numerical solution of many thousands of problems. In this aim, the extension of the machinery shown here to include data-driven and reduced order methods, including POD- and DMD-based methods, as well as concepts from scientific machine learning, may allow for even more efficient numerical solutions.