1 Introduction

1.1 Background and motivation

The requirements for future vehicle models regarding safety, costs, development times and environmental impact have increased steadily over the last years. This causes new challenges for the automotive development process. The continuation of the digitization and virtualization of the development process allows for an accelerated and very efficient development and is therefore of vital importance to overcome these growing challenges. An increasingly virtual and reliable product development necessitates simulation methods and models with reasonable predictive power. These methods and models must be validated and optimized in the best possible way making use of observations extracted from a few cost and time intensive real-world experiments. As the number of experiments needs to be reduced to increase efficiency, the amount and complexity of extracted information will increase in the future. This calls for novel validation methods, which make use of the available experimental observations in the best possible way during the validation process.

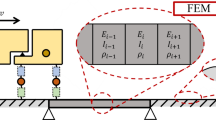
The guide on verification and validation in computational solid mechanics (V&V 10) authored by the American Society of Mechanical Engineers (ASME) Standards Committee provides an overview of a standardized verification and validation process (see Fig. 1a) [1]. This process describes all steps which are necessary to generate and document information about the reliability and confidence in results of numerical simulations [1]. The verification includes the code as well as the calculation verification and determines whether a mathematical model and its solution is represented by the computational model (domain of mathematics) [1]. The subsequent validation assesses the ability of the model to predict the reality of interest considering the intended use of the model (domain of physics) [1]. This includes two parts, the validation experiments and the accuracy assessment resulting in a quantitative metric describing the similarity between experiment and simulation [1].

Fig. 1
figure 1

Flow chart of the V&V 10 process (a) based on Schwer [1] and visualization of the automotive development loops (b) based on Schöneburg [2]

Full size image

Figure 1b shows an exemplary corresponding approach used in the automotive development process [2]. This process is based on the development loops which are controlled by a functional check on the simulation (left) and experiment (right) loop respectively [2]. During the early phase, new developments are analyzed and optimized using virtual prototypes and numerical simulations within the virtual development cycle [2]. After the achievement of a certain development stage, the development loop is extended to the experimental domain considering the respective subsystems [2]. The experimental activities increase steadily during the development process, while the usage of the virtual prototype is reduced [2]. The final release as well as the certification is currently primarily based on final real prototypes and experimental tests, while the virtual certification is part of ongoing debate [2]. Considering the future role of the virtual vehicle development, the predictive power of simulation methods and models is of vital importance and needs to be quantified and improved based on the results of the validation process.

In general, the intended digitization and virtualization of the automotive development process includes the reduction of cost and time-intensive experimental investigations. To obtain comprehensive insights based on a small amount of experiments, the complexity of the analyzed load cases will increase in the future [2]. In addition, the maximum possible amount of information needs to be extracted out of every single experiment. This can be achieved using elaborate and sometimes novel measurement technologies such as X-ray car crash or Gobo measurements [3, 4]. These measurement technologies provide extensive and, in many cases, complexly structured data sets. The structure of the measurement data is affected by the spatial and temporal distribution of measurement points as well as by the wide range of anisotropic measurement uncertainties.

One main challenge is to ensure the best possible utilization of the maximum amount of detected information from experimental observations during the validation process. This needs to result in data sets, which cannot only be used for the assessment of the similarity between experiment and simulation, but also for the efficient derivation of improvement measures in order to increase the predictive power of the used model or method if necessary.

1.2 Validation methods

This section provides a brief overview of a selection of validation methods commonly used in the field of vehicle crash. One approach is to focus on geometric distance metrics such as mean, maximum or spatially resolved distances between nodes of the finite element (FE) simulation and the respective position in the experiment for a certain point in time [5]. Depending on the load case, these quantitative metrics can be supplemented by a qualitative distinction between different deformation modes [5]. Another approach is based on the objective assessment of the similarity of temporally resolved measurement signals (e.g. force signals, trajectories, accelerations) using objective metrics such as the Cora (correlation & analysis) rating, which is based on a combination of a corridor rating and a cross-correlation rating [5,6,7,8,9]. Especially in the case of small-scale experimental setups, available full-field measurements can be used and compared with the strain fields predicted by the numerical simulation [10, 11]. Furthermore, the precise superimposition of simulated and experimental video data using photogrammetric three-dimensional evaluation methods can be used to qualitatively compare the respective behavior [12]. The comparison of multiple (stochastic) simulations with corresponding experiments using, for example, a principle component analysis (PCA) allows for deep insights in case of available high-resolution three-dimensional measurements [13, 14]. Depending on the reality of interest, the detailed post-crash comparison of damages can be useful which, depending on the materials, can be based on damage phenomena such as delamination or fracture patterns [15, 16].

The methods described above place different and in some instances very high demands on the completeness of the experimental observations. In general, the achievable informative value resulting out of these validation methods is directly dependent on the density of available experimental information and thus often significantly limited. In addition, the methods mainly concentrate on a qualitative or quantitative comparison of the simulated and experimental results without the provision of data sets allowing for the identification of possible causes of observed deviations. The separate and in many cases manual processing of experimental observations extracted by different measurement systems is time and cost intensive. In addition, this processing does not take full advantage of the complementary characteristic of information contained in the different measurements.

The approach of the ‘Grey-Box-Processing’ validation method presented in this study is based on the assumption that the best possible utilization of experimental information extracted by different measurement systems can be achieved by an automated and combined integration into the finite element simulation domain. The integration of simulated (virtual) and real data is already used for other purposes and domains, some examples are given in the next paragraph.

1.3 Integration of measurement data into the simulation domain

The combination of observations of a system of interest with the corresponding numerical model is known as data assimilation, which originally was used in the field of weather forecasting [17]. By constraining a model with observations and eliminating observation gaps, the data assimilation methodology in general allows for an increase in value of observation and model respectively [18]. The applied approaches can be divided in sequential (‘dynamic observer’) and variational (‘direct observer’) assimilation schemes [19]. Sequential assimilation schemes determine a correction of a forecast, known as the background state vector \(\varvec{ x}_i^b\) at time \(t_i\), based on observations \(\varvec{ y}_i\) in order to identify an improved state vector, the so-called analysis \(\varvec{ x}_i^a\) [19]. The analysis is then used to calculate the new background \(\varvec{ x}^b_{i+1}\) based on the model which can be summarized as

$$\begin{aligned}&\varvec{ x}_i^a =\varvec{ x}_i^b + \varvec{ K}_i \left( \varvec{ y}_i - \mathcal {H}_i\left( \varvec{ x}_i^b\right) \right) , \end{aligned}$$
(1)
$$\begin{aligned}&\varvec{ x}_{i+1}^b = \mathcal {M}_{i, i+1}\left( \varvec{ x}_i^a\right) , \end{aligned}$$
(2)

with the non-linear observation and model operator \(\mathcal {H}_i\), \(\mathcal {M}_{i, i+1}\) as well as the so-called ‘gain matrix’ \(\varvec{ K}_i\), which can be calculated using the weighted, non-linear least squares assimilation problem [19]. Variational assimilation schemes consider all states with available observations within an assimilation window at the same time and solve a constrained minimization problem iteratively using a gradient optimization method [19]. Both assimilation schemes described above cannot only be used in order to determine the analysis \(\varvec {x}^a_i\) but also to estimate unknown model parameters using

$$\begin{aligned} \varvec{ x}_{i+1} = \mathcal {M}_{i, i+1}\left( \varvec{ x}_i, \varvec{ e}_i\right) \end{aligned}$$
(3)

with the unknown parameters of the model \(\varvec{ e}_i\) [19]. Wikle and Berliner describe data assimilation using the Bayesian framework [20]. Assuming linear operators and Gaussian error distributions, they show the close linkage to the statistical interpolation method Kriging (or optimal interpolation). Gaussian Process prediction which—in the field of geostatistics—is also known as Kriging [21, 22], is one part of the method proposed in this study (see Sect. 2.1).

The combination of data assimilation methods with the finite element method is well-known, for example for the estimation of unknown model parameters [23,24,25] or the, in some instances, real-time estimation of the state of a system considering observations [26,27,28].

Further engineering domain application examples, where observations are ‘assimilated’ or rather transferred into the simulation domain can be found in the field of structural health monitoring. The current structural loading of large ships can be determined based on numerical simulations supplemented or rather updated by real-time sensor data [29]. Similar approaches are used in the field of aerospace engineering, where the smoothing element analysis or the inverse finite element analysis are used in order to determine the current deformation and the structural loading conditions based on in-situ measurements [30, 31]. Other examples are the finite element model update, constitutive equation gap, virtual fields, equilibrium gap or the reciprocity gap method used in the field of constitutive material parameter identification based on full-field measurements [32]. Further approaches make use of experimental observations to correct models (for example plasticity models) by combining phenomenological constitutive models with machine learning methods, which try to predict a high dimensional error response surface representing a data-driven correction of the model [33]. Similar to this, observed residuals between model predictions and additional information (higher fidelity simulation or experimental data)—for example in manufacturing process simulation—can be modeled using the Kriging method to create a high accuracy hybrid model [34]. The adaption of the initial shape of a structure in the numerical model based on measurements of the real initial part is another example of the integration of measured data into the simulation domain [35].

The exemplarily mentioned methods can be used to identify specific model parameters, estimate the current state of an observed system or compensate observed model errors. However, these methods do not aim to generate comprehensive data sets during the validation process intended to be used for the temporal and spatial identification and especially the physically based interpretation and quantification of deviations between one single experiment and one corresponding finite element simulation, even based on sparse observations. In contrast to the information provided by the methods described above, this would enable a physically based quantification of the predictive power and an in-depth assessment of deviations. The in-depth assessment must allow for the identification of possible causes for deviations, even in the case of complex components, load cases or ‘deviation scenarios’. This would enable a precise subsequent adjustment of the model conducted by the development engineer leading to an increase in predictive power. In contrast to identification problems, the deviation scenarios, or rather the causes for deviations, which need to be determined during validation process could be of arbitrary nature (possibly not parameterizable such as geometrical or general oversimplification, contact issues, etc.). To meet the requirements for this in-depth assessment, a new approach needs to be developed.

1.4 Goals of the study

The aim of this study is the development of a novel validation method which allows for the iterative integration of complexly structured experimental position measurements into the simulation domain. The approach is based on adaptive, artificial boundary conditions. These boundaries are embedded in the FE model to enforce that the simulation leads to deformations comparable to those from the experiment. The corresponding artificial forces can be interpreted as penalizations if the deformation of the simulation differs from the deformation of the experiment. Note that uncertainty of experimental results is included here. The objective of this iterative integration is the extraction of extensive data sets which describe deviations between the experimental and simulated result by means of spatially and temporally resolved, physically based characteristic values. Another goal of the study is the three-dimensional reconstruction of the experimental result based on the combination of incomplete experimental observations and the knowledge about physical properties and interrelations inherent in the FE model.

In this paper, the comprehensive method is presented in detail. In addition, simulation-based investigations are conducted using load cases of increasing complexity and assuming ‘ideal’ two- (e.g. X-ray) and three-dimensional measurements. The investigations focus on the general applicability of the method and the quality of generated data sets.

2 The ‘Grey-Box-Processing’ method

During application of the ‘Grey-Box-Processing’ validation method, deterministic finite element models (white-box) are iteratively combined with a data-driven completion (black-box) of incomplete experimental observations. The focus of the proposed validation method is on the best possible utilization of sparse and heterogeneous observations for identification and quantitative assessment of deviations between experiment and simulation as well as on the quantification of the predictive power of the finite element simulation based on physically interpretable characteristic values. For this reason, the ‘processing’ term is introduced in order to clearly differentiate from grey-box ‘modeling’ strategies (see for example [34, 36]).

The following subsections provide a theoretic outline of the overall method. First of all, an overview of the iterative procedure is given. In the second part of the section, different approaches are presented which are essential to transfer experimental information into the numerical simulation domain during the ‘Grey-Box-Processing’.

2.1 Iterative procedure

The most important input data of the procedure are (possibly complexly structured) experimental measurement data and an initial finite element model of the analyzed load case. The results of the corresponding finite element simulation using the initial model include, inter alia, the nodal displacements \({\varvec{ u}}{}^{n}_{i}\) of node n at time step i. The measurement data consists of position data \(({\varvec{ x}_\mathrm{Exp}})_{i}^{\eta _{i}}\) and related measurement uncertainties \((\varvec{\sigma }_\mathrm{Exp})^{\eta _{i}}_{i}\) at time step i. The superscript \(\eta _{i} \in H_{i}\) designates points of the real structure, which were detectable by at least one measurement system at the respective time step i and which could be assigned to the corresponding nodes \(n \in N\) of the finite element model, whereby \(H_i \subset N\). The complexity of the structure of the experimental data depends on the spatial and temporal measurement resolution as well as on the potentially wide range and anisotropy of measurement uncertainties. This is particularly seen in X-ray measurements.

In addition, a copy \(f^\mathrm{Fem}\) of the initial finite element model needs to be available, which is configured to receive and process experimental information. The overall method, which is described in the following, is based on the usage of this simulation model. The result generated by means of this simulation model will be referred to as the result of the ‘adapted simulation’ or the so-called ‘hybrid data set’.

The first step of the iterative procedure is the determination of an estimated position \(({\varvec{ x}_\mathrm{Est}}){}^{n}_{i+1}\) of nodes n at time step \(i+1\) (see Fig. 2a). The estimation could be based on different assumptions. One example is to assume that the results of the initial simulation can be used in order to get a rough approximation of the behavior of the real structure in the experiment during the next time step. Using the nodal displacements of the simulation results based on the initial finite element model (\(({\varvec{ u}_\mathrm{Est}}){}^{n}_{i}= {\varvec{ u}}{}^{n}_{i}\)) and the results of the adapted simulation \(({\varvec{ x}_\mathrm{Sim}}){}^{n}_{i}\), an estimated position \(({\varvec{ x}_\mathrm{Est}}){}^{n}_{i+1}\) for the next time step can be calculated according to

$$\begin{aligned} ({\varvec{ x}_\mathrm{Est}}){}^{n}_{i+1}= ({\varvec{ x}_\mathrm{Sim}}){}^{n}_{i}+ ({\varvec{ u}_\mathrm{Est}}){}^{n}_{i}. \end{aligned}$$
(4)

The assumption of a constant velocity of the respective nodes could be another approach. In this case, the calculation of an estimated position would be based on the velocity of the previous time step drawn from the results of the adapted simulation.

Fig. 2
figure 2

Simplified representation of the overall workflow. Determining an estimated nodal position of the next time step (a), calculation of deviations at nodes with measurement data \(\eta _{i+1}\) (b), completion of experimental observations by interpolating deviations using Gaussian Process prediction (c) as well as integration of complemented experimental data into the FE domain using adaptive boundary conditions representing a synthetic, dynamic solution corridor (d)

Full size image

Based on the estimated positions, deviations \({\varDelta \varvec{ x}}_{i+1}^{\eta _{i+1}}\) between the estimated and the measured positions at nodes with measurement data \(\eta _{i+1}\) are calculated (see Fig. 2b) using

$$\begin{aligned} {\varDelta \varvec{ x}}_{i+1}^{\eta _{i+1}} = ({\varvec{ x}_\mathrm{Est}})_{i+1}^{\eta _{i+1}} - ({\varvec{ x}_\mathrm{Exp}})_{i+1}^{\eta _{i+1}}. \end{aligned}$$
(5)

During the next step of the procedure, ‘synthetic measurement data’ is generated at nodes without experimental measurement data using Gaussian Process prediction (see Fig. 2c). This single step of the method is comparable with the approach presented by Yang et al., where observed residuals between model predictions and additional information (higher fidelity simulation or experimental data)—for example in manufacturing process simulation—are represented using the Kriging method to create a high accuracy hybrid model [34]. A Gaussian Process (GP) can be seen as the generalization of the Gaussian distribution allowing for the definition of distributions over functions [37]. The GP is defined by (parameterized) mean and covariance function characterizing the functions properties and allowing for the introduction of prior knowledge [37]. Bayesian inference is used in order to update the prior distribution using available observations [37]. The resulting posterior allows for the prediction of function value and corresponding variance for unseen data points [37]. In this application, the ‘observations’ are defined by the calculated deviations \({\varDelta \varvec{ x}}\) and the corresponding measurement uncertainties \(\varvec{\sigma }_\mathrm{Exp}\). The Gaussian process prediction also considers the estimated nodal positions \({\varvec{ x}_\mathrm{Est}}\) and takes into account an appropriate similarity measure using geodetic or Euclidean distances between the estimated positions of the nodes of the structure. For reasons of scope, the theoretical background, a detailed description of the application as well as the achievable results using this machine learning approach will be part of an additional publication. The focus of this study is on the general feasibility of the iterative procedure, which is why ‘ideal’ isotropic and anisotropic measurement data is used for numerical studies in Sect. 3. The described step results in a fully complemented data set containing position and uncertainty data of the experiment for all nodes n of the simulation model using

$$\begin{aligned} \begin{aligned} (({\varvec{ x}_\mathrm{Int}}){}^{n}_{i+1}, (\varvec{\sigma }_\mathrm{Int}){}^{n}_{i+1})&= f^\mathrm{Int}({\varDelta \varvec{ x}}_{i+1}^{\eta _{i+1}}, (\varvec{\sigma }_\mathrm{Exp})^{\eta _{i+1}}_{i+1}, ({\varvec{ x}_\mathrm{Est}}){}^{n}_{i+1}). \end{aligned} \end{aligned}$$
(6)

The complemented positions \({\varvec{ x}_\mathrm{Int}}\) as well as the associated uncertainties \(\varvec{\sigma }_\mathrm{Int}\) are result of the Gaussian Process prediction (\(f^\mathrm{Int}\)) [21]. The latter are affected by the measurement uncertainties as well as by the uncertainty caused by the interpolation.

The last step of the iterative procedure is the transfer of the complemented experimental results into the FE simulation domain by means of adaptive, artificial boundary conditions as well as the continuation of the finite element calculation for the next time step (\(t_i \rightarrow t_{i+1}\)). The artificial boundary conditions form a synthetic, dynamic solution corridor in the adapted simulation model. The synthetic solution corridor restricts the dynamic behavior of the modeled structure during the finite element calculation of the next time step according to the complemented experimental observations (see Fig. 2d). Two different methods were developed which allow to consider the adaptive, artificial boundary condition in the adapted simulation model. These approaches are presented in detail in Sect. 2.2.

By means of the integration of simulated and experimental data sets, so-called hybrid data sets are generated. These hybrid data sets contain, inter alia, information about the physical interaction between a finite element structure and the dynamic, synthetic solution corridor. These physically based sets of data allow for the identification and quantitative assessment of deviations between simulation and experiment and therefore an extensive deviation analysis. The analysis is here based on spatially and temporally resolved forces \(\varvec{ F}{}^{n}_{i}\) caused by the synthetic boundary conditions acting on the structure. Based on the detected forces, time-resolved energy data or similar time-resolved characteristic values \(\kappa _{i}\) can be calculated. Additionally, any other scalar characteristic value \(\xi \) can be used to describe the spatial and temporal type (punctiform/extensive, short-term/long-term) and level of interaction between the solution corridor and the structure in the finite element model. The hybrid data sets, which are a result of the adapted simulation model, additionally provide an updated information about the nodal positions in the next time step \(({\varvec{ x}_\mathrm{Sim}}){}^{n}_{i+1}\). The calculation of the updated positions takes into account the complexly structured experimental data as well as the knowledge about physical properties and interrelations inherent in the FE model.

For this reason, the developed approach enables the favorable ability to generate a three-dimensional reconstruction of the experimental behavior, even in case of very incomplete (e.g. two-dimensional) experimental measurement data. In this case, the effect of a detected in-plane deviation on the structural out-of-plane behavior can be determined based on the physical knowledge inherent in the FE model. The last step of the iterative procedure can be summarized as

$$\begin{aligned} (({\varvec{ x}_\mathrm{Sim}}){}^{n}_{i+1}, \varvec{ F}{}^{n}_{i+1}, \kappa _{i+1}, \xi ) = f^\mathrm{Fem}_{i}\left( ({\varvec{ x}_\mathrm{Int}}){}^{n}_{i+1}, (\varvec{\sigma }_\mathrm{Int}){}^{n}_{i+1}\right) . \end{aligned}$$
(7)

The updated positions are considered as the input of the process for the next iteration. This closed-loop process ensures a continuous similarity between the results of the adapted simulation and the experimental observation over the course of the time steps. The continuous similarity leads to limited deviations \({\varDelta \varvec{ x}}_{i+1}^{\eta _{i+1}}\) and therefore allows for a completion of incomplete experimental observations and the deviation analysis over the whole simulation time even in the case of bifurcations in the structural behavior or large accumulated deviations.

2.2 Integration of measurement data and generation of hybrid data sets

The iterative procedure described above requires an appropriate interface, which allows for the transfer of complemented experimental observations into the FE domain. In this study, the finite element analysis solver LS-DYNA (explicit time integration) is used [38]. The fundamental idea of the developed interface is the integration of the complemented experimental information by means of a synthetic, dynamic solution corridor in the FE simulation. The center of this synthetic solution corridor represents the complemented experimental observations, the width correlates with the associated uncertainties (e.g. defined by specific levels of confidence). This kind of integration allows for the identification and quantitative assessment of deviations taking into account the level of data confidence. In this study, two different approaches were developed and analyzed (see Fig. 3), which will be presented below.

Fig. 3
figure 3

Exemplary visualization of the presented methods. Generation of a synthetic solution corridor using a virtual reference geometry (a) and virtual enveloping surfaces (b). For purposes of visualization, the position of the FE structure shown in the example using the reference geometry (a) is not congruent with the center of the solution corridor or rather the experimental observation, whereas the FE structure in the example using enveloping surfaces is placed in the middle of the solution corridor

Full size image

2.2.1 Virtual reference geometry

The so-called ‘virtual reference geometry’ is basically a finite element representation of a virtual replica of the analyzed structure and is included in the adapted FE simulation model (see Fig. 3a). The virtual reference geometry consists of LS-DYNA Null Shell elements, which are not considered during the element processing [39]. Furthermore, a specific connection is implemented between respective nodes of the virtual reference geometry and the analyzed structure, which are coincident at the initial point in time \(t_0\). The connection is realized by means of nonlinear and anisotropic spring elements.

The displacements of the nodes of the virtual reference geometry between time step i and \(i+1\) are prescribed based on the complemented experimental observations. A displacement of the FE nodes of the analyzed structure, which does not coincide with the displacement of the virtual reference geometry (respectively the displacement of the experiment), leads to restoring forces \(\varvec{ F}{}^{n}_{i+1}\) towards the nodes of the reference geometry. These spatially and temporally resolved force signals are stored in the hybrid data set and can be used during the deviation analysis. The nonlinear and anisotropic acting forces are defined as a function of the distance l between the connected nodes by

$$\begin{aligned} F(l) = \alpha \cdot \left[ \left( \frac{1}{1-\frac{\vert l \vert }{l_\mathrm{max} }}\right) ^{\beta }-1\right] . \end{aligned}$$
(8)

The parameter \(l_{\max }\) describes an anisotropic, spatially as well as temporally resolved maximum length of the coupling elements and is correlated with the respective uncertainty of the complemented experimental data \((\varvec{\sigma }_\mathrm{Int}){}^{n}_{i}\) (e.g. the 95% confidence region of the posterior Gaussian process). Assuming the same amount of spatial deviations between nodes of the virtual reference geometry (representing the experiment) and the analyzed FE structure, the approach leads to larger restoring forces at nodes with low observation uncertainties compared to nodes with high observation uncertainties. The synthetic, dynamic solution corridor therefore results from the combination of the dynamic position of the nodes of the virtual reference geometry and the dynamic, nonlinear and anisotropic spring forces acting between the reference geometry and the analyzed FE structure. The exponential structure of the function ensures that the analyzed FE-structure is forced to remain inside the synthetic solution corridor while the forces tend to infinity at the borders of the synthetic solution corridor. Parameters \(\alpha \) and \(\beta \) can be used, if necessary, in order to manually adjust the load curves depending on the requirements resulting from the analyzed load case (see Fig. 4a).

Fig. 4
figure 4

Restoring forces acting between the reference geometry and the FE structure considering different parameters \(\alpha \) and \(\beta \) using Eq. (8) (a) as well as illustration of the effect of parameter \(\gamma \) according to Eq. (9) (b)

Full size image

In addition to Eq. (8), an alternative function is defined, which allows for the implementation of an inner zone of the synthetic solution corridor where no restoring forces occur (see Fig. 4b). This inner zone can be used in case of very large observation uncertainties. For this reason, the parameter \(\gamma \) (\(0 \le \gamma < 1\)) is used, which describes the ratio between the inner zone and the overall synthetic solution corridor. In this case, the calculation of the restoring forces follows

$$\begin{aligned} F(l)&= {\left\{ \begin{array}{ll} 0, &{} {l < \gamma \cdot l_\mathrm{max}},\\ \alpha \cdot \left[ \left( \frac{1}{1-\frac{\vert l \vert - \gamma \cdot l_\mathrm{max}}{l_\mathrm{max} \cdot (1-\gamma ) }}\right) ^{\beta }-1\right] , &{} {\gamma \cdot l_\mathrm{max} \le l \le l_\mathrm{max}.} \end{array}\right. } \end{aligned}$$
(9)

2.2.2 Virtual enveloping surfaces

The second approach makes use of so-called ‘virtual enveloping surfaces’ and standard finite element contact algorithms (see Fig. 3b). This approach was already presented and analyzed by the authors within a comprehensive feasibility study looking at small-scale simulation models and corresponding ‘virtual experimental data sets’ [40].

The virtual enveloping surfaces represent the acceptance borders of the dynamic, synthetic solution corridor and follow prescribed trajectories which are determined based on the complemented experimental observations. Similar to the approach described above, the width of the solution corridor (or rather the margin between the enveloping surfaces) is correlated to the uncertainty of the complemented experimental data. The dynamic surfaces are implemented using a prescribed motion for all nodes of the virtual object and LS-DYNA Null Shell elements. This approach leads to hybrid data sets containing the information about temporally and spatially resolved contact forces \(\varvec{ F}{}^{n}_{i}\) between the FE structure and the borders of the synthetic solution corridor. In contrast to the above-described approach using the virtual reference geometry, the interaction will not take place until the borders of the synthetic solution corridor are reached. This behavior can conceptually be deemed to be similar to the ‘reference geometry approach’ using Eq. (9) with \(\gamma \approx 1\).

3 Results and discussion

Within the following section, the results of a comprehensive parameter study are presented. The focus of this study is on the integration of experimental results into the FE simulation domain and the generation of so-called hybrid data sets (see Fig. 2d), which is the substantial part of the overall approach. The suitability of the proposed methods are analyzed based on their functional capability considering isotropic and severely anisotropic measurement uncertainties as well as based on the analyzability and informative value of the generated hybrid data sets. Therefore, the availability of complete (two- or three-dimensional) measurement data is assumed during the parameter study, which means that either ‘ideal’ measurement data is available or the completion described above (see Fig. 2a–c) already took place.

The implementation and integration of the completion of incomplete measurement data using the described steps (see Fig. 2a–c and Eqs. (4)–(6)) into the overall workflow is part of a current research project and will be presented in a future publication.

Different load cases of increasing complexity are used to analyze various aspects of the approaches and the impact of different parameters. For this purpose, synthetic experimental data sets are used. These data sets are generated using two FE simulation models. Deviations between the results are triggered by slight changes in the simulation setup. The result of the unchanged simulation model is referred to as the ‘virtual experiment’, while the result of the modified model is assumed to be the corresponding simulation.

3.1 Symmetrical bending load case

The first load case resembles a simple elastic plate under symmetric bending (see Fig. 5a). One end of the plate is fixed in space. Nodes of the opposite free edge are loaded with concentrated nodal forces \(F_z(t)\). The maximum summed load is reduced by 50% in the simulation compared to the virtual experiment (see Fig. 5b). The simulation setup results in a maximum nodal velocity of \(v_{\max } \approx 15.3\) km/h and a maximum deflection of \(u_{\max }\approx 130\) mm during the virtual experiment. For this load case, isotropic and homogeneous measurement uncertainties are assumed which lead to a homogeneous width of the solution corridor or rather an isotropic and homogeneous maximum length \(l_{\max }\) of the coupling elements. A measurement frequency of 10 kHz is used. The objectives using the first load case are the verification of the respective implementation, the understanding of impacts of different parameters as well as the comparison of the two methods described above.

Fig. 5
figure 5

Simulation setup and boundary conditions of the symmetrical bending load case (a) as well as boundary load curves used for ‘virtual experiment’ and corresponding simulation (b)

Full size image

For this reason, a full factorial analysis was conducted taking into account specific values for \(\alpha \), \(\beta \) and \(\gamma \) considering the method using the reference geometry. In addition, different widths of the solution corridor were tested (\(l_\mathrm{max}=1\) mm, \(l_\mathrm{max}=2\) mm). The following results focus on \(l_\mathrm{max}=1\) mm. Figure 6 shows the expected significant impact of the parameters on the utilization of the synthetic solution corridor which is generated by the reference geometry and the coupling elements.

Fig. 6
figure 6

Utilization of the synthetic solution corridor during symmetric bending considering the reference geometry. Impact of \(\alpha \) and \(\beta \) on the relative length \(l/l_{\max }\) of an exemplary coupling element between the FE structure and the reference geometry using \(\gamma =0\) (a) as well as \(\gamma =0.75\) (b)

Full size image

While higher values of \(\alpha \), \(\beta \) lead to a lower utilization of the solution corridor (see Fig. 6a) and recognizable oscillations in the sum of acting restoring forces \(F_z\) (see Fig. 7a), lower values allow for a more extensive utilization of the solution corridor and smoother restoring forces. The implementation of the inner zone without restoring forces leads to the intended effect. The late and abrupt occurrence of restoring forces leads to significant oscillations in the length of the coupling element (see Fig. 6b) and the respective restoring forces (see Fig. 7b). The hypothesis is, that this behavior is caused by the reduced action length and the high difference in velocity which is not the case using the continuous action in case of \(\gamma =0\). Despite of this behavior, the inner zone without restoring forces could be useful in case of very large uncertainties to prevent restoring forces within a specific level of confidence. In general, similar results were observed for larger values of \(l_\mathrm{max}\).

Fig. 7
figure 7

Sum of acting restoring forces between FE structure and reference geometry during symmetric bending using different \(\alpha \), \(\beta \) as well as \(\gamma =0\) (a) and \(\gamma =0.75\) (b)

Full size image

The utilization of the solution corridor is not only affected by the design of the restoring forces load functions (see Eqs. (8) and (9)) but also by the general level of acting forces depending on the considered load case. This means that the global and local utilization of the solution corridor needs to be monitored and the restoring forces load curves must be adjustable. This is possible using the parameters \(\alpha \) and \(\beta \). While both parameters affect the behavior in a similar manner, \(\beta =2\) is used henceforth and \(\alpha \) is used as a load case dependent parameter of the method. If the parameter \(\alpha \) is set too high with respect to the general level of forces, the local and global utilization of the solution corridor would be too low, while too small values lead to rapidly increasing restoring forces at the border of the solution corridor comparable with the effects using \(\gamma \ne 0\).

To allow for an energy-based quantification of deviations using the hybrid data set, the available energy data is discussed in the following. According to the documentation of the FE solver LS-DYNA, the simulation energy balance can be noted as

$$\begin{aligned} \begin{aligned} E_\mathrm{kin}^0 + E_\mathrm{int}^0 + W_\mathrm{ext}^\mathrm{total} = {}&E_\mathrm{kin} + E_\mathrm{int} + E_\mathrm{sl} + E_\mathrm{rw}\ {}+ E_\mathrm{damp} + E_\mathrm{hg}\\ \approx {}&E_\mathrm{kin} + E_\mathrm{int}\\ = {}&E_\mathrm{total} \end{aligned} \end{aligned}$$
(10)

with the kinetic energy \(E_\mathrm{kin}\), the internal energy \(E_\mathrm{int}\) (including reversible strain energy and work done by irreversible deformations), as well as sliding (\(E_\mathrm{sl}\)), rigid wall (\(E_\mathrm{rw}\)), damping (\(E_\mathrm{damp}\)) and hourglass energy (\(E_\mathrm{hg}\)) [41]. The latter four are considered to be negligible compared to the remaining energy values, the initial kinetic (\(E_\mathrm{kin}^0\)) and internal energy (\(E_\mathrm{int}^0\)) are zero in the analyzed case. Considering the above-described assumptions, the energy balance of the virtual experiment and the adapted simulation (hybrid data set) can be described according to:


Virtual experiment:

$$\begin{aligned} W_\mathrm{ext}^\mathrm{Exp}&= E_\mathrm{kin}^\mathrm{Exp} + E_\mathrm{int}^\mathrm{Exp} \end{aligned}$$
(11)

Hybrid data set:

$$\begin{aligned} W_\mathrm{ext}^\mathrm{Hybrid} + W_\mathrm{Ref Geo}&= E_\mathrm{kin}^\mathrm{Hybrid} + E_\mathrm{int}^\mathrm{Hybrid} \end{aligned}$$
(12)

Figure 8 shows a comparison of the left-hand sides of Eqs. (11) and (12) considering the symmetric bending load case. It can be seen, that the sum of the external work by the reference geometry and by the boundary condition of the hybrid data set (\(W_\mathrm{Ref Geo} + W_\mathrm{Ext}\)) is approximately identical to the external work of the virtual experiment (red dotted line) for most of the parameter combinations. The initial deviations caused by the different boundary conditions of the two simulations are therefore completely compensated by the influence of the reference geometry. This fact can be used to quantify deviations in a detailed manner which is described in detail looking at more realistic load cases at the end of this section.

Fig. 8
figure 8

Comparison of energy values of virtual experiment and hybrid data set using the reference geometry. Sum of external work by reference geometry \(W_\mathrm{Ref Geo}\) and boundary condition of adapted simulation \(W_\mathrm{Ext}\) as well as external work of virtual experiment (red) considering different \(\alpha \), \(\beta \) as well as \(\gamma =0\) (a) and \(\gamma =0.75\) (b)

Full size image

To allow for a comparison of the two different methods which use either a reference geometry or enveloping surfaces, the same data set was analyzed considering enveloping surfaces. Figure 9 shows the observed contact forces (a) as well as the above-described comparison of energy values (b). The observed contact forces, which are acting between the enveloping surfaces and the FE structure show significant oscillations comparable to the restoring forces using \(\gamma \ne 0\) (see Fig. 7b). This emphasizes the already mentioned similarity of those approaches.

Fig. 9
figure 9

Sum of acting contact forces in x, y, and z direction (a) as well as sum of work done by the enveloping surfaces \(W_\mathrm{Env surf}\) and by the boundary condition of the adapted simulation \(W_\mathrm{Ext}\) compared with external work of the virtual experiment (b)

Full size image

The information about the spatial distribution of acting forces (\(F_z\)), which is also part of the generated hybrid data set, is shown in Fig. 10. The method using the reference geometry leads to a very clear and accurate distribution of acting forces (see Fig. 10a), while the quality of the force signal considering the enveloping surfaces leads to a force distribution which is difficult to interpret (see Fig. 10b).

Fig. 10
figure 10

Spatial distribution of acting restoring forces (\(F_z\)) using the reference geometry (a) and of acting contact forces using the enveloping surfaces (b) (color figure online)

Full size image

Based on the results presented above as well as in a previous study [40], it can be seen, that the method using enveloping surfaces is less suitable looking at the generated hybrid data sets as well as at the limited possibilities regarding the creation of inhomogeneous and anisotropic solution corridors. Therefore, the method using the reference geometry is chosen for further investigations. In addition, based on the findings, usage of the parameter \(\gamma \) will be limited to special cases with extremely high measurement uncertainties (e.g. the X-ray direction).

3.2 Unsymmetrical bending load case

The second load case is based on the described symmetric bending load case. The elastic plate of the symmetrical bending load case (part 1) is supplemented by a second elastic plate (part 2), which is attached orthogonally on one longitudinal edge of the simple plate (see Fig. 11a). This L-shaped beam leads to unsymmetrical bending with a significant displacement in all directions (see Fig. 11b). Concentrated nodal forces \(F_z(t)\) are based on the load curve used during symmetric bending (see Fig. 5b), the load curve is scaled to a maximum value of \(F_z=250~N\). The used setup leads to a maximum nodal velocity of \(v_\mathrm{max}=52\) km/h and a maximum deflection of \(u_\mathrm{max}=190\) mm. The deviations between the virtual experiment and corresponding simulation are triggered in two different ways. For the first case, concentrated nodal forces are reduced by 50% in the simulation compared to the virtual experiment. The second case is based on a reduction of the shell thickness of part 2 by 50% in the simulation, while all other parameters are identical to those used in the model of the virtual experiment.

Fig. 11
figure 11

Simulation setup and boundary conditions (a) of the unsymmetrical bending load case as well as deformed structure showing the resulting displacements \(u_\mathrm{res}\) (\(t=50\) ms) (b) (color figure online)

Full size image

Measurements are only taken from part 1, a measurement frequency of 10 kHz is used. Measurement uncertainties are considered to be homogeneous but severely anisotropic. It is assumed, that the measurements contain almost no information in y-direction (\(l_{y}^{\max }\rightarrow \infty \)), while uncertainties in x and z-direction lead to a width of the solution corridor of \(l_{x}^{\max }=l_{z}^{\max }=1\) mm. This is a very simplified approximation of the case using X-ray measurements and a detector which is placed within the x–z-plane.

The objective of the evaluation using the unsymmetrical bending load case is the verification of the implementation of anisotropic measurement uncertainties using the reference geometry and the analyzability of generated hybrid data sets. The anisotropy is implemented using multiple coupling elements for each nodal pair which only act in respective directions. Restoring forces result out of the superposition of the direction-dependent restoring forces, which means that isotropic measurement uncertainties (e.g. in x–z-plane) are modeled as quasi-isotropic. Another objective is the verification of the ability to reconstruct the three-dimensional experimental result based on the combination of incomplete (e.g. two-dimensional) measurement data with the physical knowledge inherent in the FE model as already described in detail in the method section.

First of all, the example considering the deviation caused by a reduction of concentrated nodal forces by 50% is analyzed. Figure 12 shows the sum of acting restoring forces (a) as well as the corresponding spatial distribution of the restoring forces \(F_z(t=50\) ms) (b). The restoring forces curves show a smooth shape, the observed spatial distribution is revealing and in conjunction with the—in this test case—known cause of deviations. Based on the information contained in the hybrid data set, the responsible engineer can efficiently narrow down the cause of deviation and can adjust the initial model, which especially in case of more complex components and deviation scenarios (see Sect. 3.3) would not be possible based on a classical geometrical comparison between experiment and simulation, even in case of ‘ideal’ measurements. While no borders of the solution corridor in y-direction are given (\(l_{y}^{\max }\rightarrow \infty \)), restoring forces \(F_y\) can be found to be zero and a decoupled movement (y-direction) between the FE structure and the reference geometry can be seen (see close up in Fig. 12b). The experimental observations contain no information about the structural behavior in y-direction. Therefore, the reference geometry operates within the initial y-plane. After the future implementation of the iterative procedure, which is described in the method section, the reference geometry’s y-position would be updated during every iteration based on the resulting position given in the hybrid data set.

Fig. 12
figure 12

Acting restoring forces in x, y, and z direction (a) as well as spatial distribution of acting restoring forces \(F_z(t=50\) ms) (b) during unsymmetrical bending considering reduced boundary load curve in simulation compared with virtual experiment (color figure online)

Full size image

The successful implementation of the anisotropic measurement uncertainties can also be verified based on the utilization of the synthetic solution corridor (see Fig. 13a). It can be seen, that the length of the exemplary coupling element in x- and z direction is limited to values below 1 mm, while the length in y-direction is not limited. The load case-dependent parameter of the restoring force curves was adjusted to \(\alpha =0.01\) (\(\beta =2\)), which leads to a reasonable local and global utilization of the solution corridor.

Fig. 13
figure 13

Visualization of the utilization of synthetic solution corridor based on length of an exemplary coupling element (a) and depiction of the three-dimensional reconstruction effect based on two-dimensional (x–z plane) measurement data looking at Node 1271 (located at the middle of the structure’s free edge) considering reduced boundary load curve in simulation compared with virtual experiment (b)

Full size image

To evaluate the ability to reconstruct the three-dimensional behavior of the experiment based on two-dimensional measurements and physical knowledge inherent in the FE model, the y-displacement of exemplary node 1271 (see Fig. 11a) is shown in figure 13b for virtual experiment and hybrid data set. It can be seen, that a very accurate reconstruction of the experiment’s y-displacement is achieved by integrating incomplete measurement data into the FE simulation which is the generation of hybrid data sets. The considered case can be assumed to be an ‘ideal case’, while the cause of the deviation (reduced concentrated nodal forces \(F_z(t)\)) is completely located within the x–z-plane which allows for an almost exact reconstruction. This would not always be possible. However, the example shows a fundamental capability of the approach to merge incomplete experimental measurements with physical knowledge inherent in the simulation model in order to reconstruct the experiment. The quality of the reconstruction considering a—in this sense—‘non-ideal case’ is analyzed using the second deviation case (reduced part 2 shell thickness).

Figure 14a shows the external work of the virtual experiment and the hybrid data set. Subtraction of the energy balance of the hybrid data set (see Eq. (12)) and the virtual experiment (see Eq. (11)) leads to

$$\begin{aligned} W_\mathrm{Ref Geo}&= W_\mathrm{ext}^\mathrm{Exp}-W_\mathrm{ext}^\mathrm{Hybrid} + E_\mathrm{total}^\mathrm{Hybrid} -E_\mathrm{total}^\mathrm{Exp}. \end{aligned}$$
(13)

The work done by the reference geometry can be used to quantify the difference in total energy \(\varDelta E_\mathrm{total}\) and external work \(\varDelta W_\mathrm{ext}\) between experiment and simulation and therefore the general similarity of those. While the cause of the deviation is known in this test case, the quality of the energy based quantification can be verified. The verification makes use of the—in this case—known fact that the deviation is caused by the difference in external work (concentrated nodal forces), while the remaining parameters and therefore the total energies are identical. Using this information, it can be seen that the difference in external work can be determined very accurately evaluating the work done by the reference geometry (see Fig. 14b). This proves the capability of an energy-based quantification of the deviations between experiment and simulation.

Fig. 14
figure 14

Energy values during unsymmetrical bending considering reduced boundary load curve in simulation compared with virtual experiment. Visualization of external work during bending \(W_\mathrm{ext}\) in virtual experiment and hybrid data set (a) as well as comparison of the difference between those values \(\varDelta W_\mathrm{ext}\) and the work done by the reference geometry \(W_\mathrm{Ref~Geo}\) (b)

Full size image

To verify the generality of the above-described observations, a second case of deviation is considered. The deviation is triggered by a reduction of the part 2 shell thickness by 50%. The corresponding results are shown in Fig. 15 (\(\alpha =0.1\), \(\beta =2\)). It can be seen, that the three-dimensional reconstruction of the virtual experiment based on two-dimensional measurement data shows comparably good results despite the fact that the triggered deviation takes extensive effect on the behavior in y-direction as well (see Fig. 15a). Figure 15b shows the energy values of the second deviation case. To assess the validity of the deviation quantification based on the work of the reference geometry, the—in the normal use case—unknown fact is used, that the external work is identical in simulation and experiment. The work done by the reference geometry can then be used to quantify the deviation in total energy \(\varDelta E_\mathrm{total}\) which is found to be possible very precisely.

Fig. 15
figure 15

Three-dimensional reconstruction and energy values during unsymmetrical bending with reduced part 2 shell thickness in the simulation compared with virtual experiment. Visualization of the three-dimensional reconstruction effect based on two-dimensional (x–z plane) measurement data looking at Node 1271 located at the middle of the structure’s free edge (a). Figure (b) shows the comparison of the difference in total energy \(\varDelta E_\mathrm{total}\) of virtual experiment and hybrid data set with the work done by the reference geometry \(W_\mathrm{Ref~Geo}\)

Full size image

3.3 Pedestrian safety load case

To analyze the transferability of the observations presented above on more complex and realistic automotive load cases, two pedestrian safety load cases are considered in the following. Both setups make use of a very detailed FE model of a hood assembly (see Fig. 16a) which is extracted from the NHTSA Honda Accord FE model [42]. The hood is fixed in space at the attachment points. In the first load case, the pedestrian headform impact scenario is simplified to achieve a gradual increase in complexity. The scenario is abstracted by means of generic concentrated nodal forces acting on nodes within the highlighted area (see Fig. 16b). The already mentioned bell-shaped load curve (see Fig. 5b) is used. The curve is scaled to a maximum value that leads to a transmission of external work of \(W_\mathrm{ext}\approx 170\) J. This value is comparable to the work done by the LSTC pedestrian child headform impactor FE model [43] which is used in the final load case (see Fig. 16c). The used impact scenario follows a common combination of the respective parameters (\(m_{I}=3.5\) kg, \(v_{I}=35\) km/h, \(\theta =50^\circ \), see [44]).

Fig. 16
figure 16

Setup of the pedestrian safety load cases. Detailed (partially transparent) depiction of the used hood of the Honda Accord FE model (a) [42], simplified simulation setup using concentrated nodal forces acting in the highlighted area (b) and simulation setup using a pedestrian headform impactor model provided by LSTC [43] (color figure online)

Full size image

Measurements are only taken at the outermost part of the hood (see Fig. 16b, green part). Comparable to the above described L-shaped beam, the reference geometry is only defined for the measured part. Measurement uncertainties are assumed to be isotropic and homogeneous, a measurement frequency of 10 kHz is used. Numerous deviation scenarios were analyzed. The results presented in the following focus on the deviation which is triggered by a reduction of the shell thickness of the support structure (see Fig. 16a, yellow part) by 33% in the simulation compared to the virtual experiment.

Figure 17 shows the information about the spatial distribution of the utilization of the solution corridor (a) as well as of the restoring forces in z-direction \(F_z(t=11\) ms) (b). The load case dependent parameter was set to \(\alpha =0.1\) (\(\beta =2\)). The results are very revealing and in conjunction with the—in this case—known cause of deviation. The time-resolved information about the utilization of the solution corridor and the acting restoring forces clearly indicate the deviation in the supporting effect of the inner support structure (see Fig. 16a, yellow part).

Fig. 17
figure 17

Utilization of the solution corridor \(l/l_{\max }\) (a), acting restoring forces \(F_z\) (b) as well as deviations in the resulting nodal displacements \(\varDelta u_\mathrm{res}\) between experiment and simulation at \(t=11\) ms (c) during concentrated nodal forces load case considering reduced shell thickness of the support structure (see Fig. 16a, yellow) in the simulation compared to the virtual experiment (color figure online)

Full size image

This extensive information base contained in the hybrid data set not only allows for the identification and quantification of deviations between experiment and simulation but also for an efficient identification of the cause of deviation leading to a precise subsequent adjustment of the initial model by a development engineer. Beside the quantification of the predictive power of a finite element simulation based on physically interpretable characteristic values (e.g. energy based), this enabled identification and elimination of causes of deviations—especially based on sparse and heterogeneous observations—is the principal benefit of the proposed method. This would not be possible based on a classical, geometrically based comparison between experiment and simulation (see full-field deviation in the resulting displacement \(\varDelta u_\mathrm{res}\), Fig. 17c), even in case of ‘ideal’ measurements. This is even more significant considering two-dimensional (e.g. X-ray) measurements, larger accumulated deviations or kinematic bifurcations.

The verification of the energy-based quantification of the observed deviation follows the strategy described above using Eq. (13) and the—in this test case—known fact of the equality of the external work. Figure 18a shows the total energy \(E_\mathrm{total}\) of the virtual experiment and the hybrid data set. In addition, the external work \(W_\mathrm{ext}\) of the virtual experiment is shown in order to illustrate, that the assumptions made in Eq. (10) are not necessarily valid in the case of large multi-body simulation models. Despite this, a very accurate quantification of the difference in energy absorption capability of the hood assembly (\(\varDelta E_\mathrm{total}\)) is possible using the work done by the reference geometry \(W_\mathrm{Ref Geo}\) (see Fig. 18b). This proves the capability of an energy-based quantification of the deviations between experiment and simulation and therefore the applicability of the hybrid data set for the quantification of the predictive power of the finite element simulation even in case of complex geometries, load cases and deviation scenarios.

Fig. 18
figure 18

Energy values during concentrated nodal forces load case. Visualization of external work during concentrated nodal forces load case \(W_\mathrm{ext}\) and the total energy \(E_\mathrm{total}\) in virtual experiment and hybrid data set (a) as well as comparison of the difference between those total energy values \(\varDelta E_\mathrm{total}\) and the work done by the reference geometry \(W_\mathrm{Ref~Geo}\) (b).

Full size image

The results of the second load case using the pedestrian child headform impactor are shown in Figs. 19 and 20 (\(\alpha =0.1\), \(\beta =2\)). In accordance to the described observations, the spatial distribution of the utilization of the solution corridor and the restoring forces allow for a very good interpretation of deviations and show the relation between cause (reduced shell thickness of support structure—known in this test case) and effect in the early phase of the impact (\(t=2.5\) ms, see Fig. 19).

Fig. 19
figure 19

Utilization of the solution corridor \(l/l_{\max }\) (a) and acting restoring forces \(F_z\) (b) at \(t=2.5\) ms during pedestrian head-form impactor load case considering reduced shell thickness of the support structure (see Fig. 16a, yellow) in the simulation compared to the virtual experiment (color figure online)

Full size image

Figure 20b shows, that the energy-based quantification of the deviation between virtual experiment and simulation is very accurate even in case of a pedestrian headform test setup which is very close to the real load case.

Fig. 20
figure 20

Energy values during pedestrian head-form load case. Visualization of external work done by the pedestrian head-form impactor \(W_\mathrm{ext}\) and the total energy \(E_\mathrm{total}\) in virtual experiment and hybrid data set (a) as well as comparison of the difference between those total energy values \(\varDelta E_\mathrm{total}\) and the work done by the reference geometry \(W_\mathrm{Ref~Geo}\) (b)

Full size image

4 Conclusion

In this study, a novel validation method for use in vehicle safety applications is presented and evaluated using simulation-based investigations. The implementation of the developed approach provides an interface allowing for the comprehensive integration of experimental observations into the simulation domain. This integration is based on the iterative generation of a synthetic, dynamic solution corridor using adaptive boundary conditions. By means of this solution corridor, the freedom of movement of the analyzed structure is restricted according to the experimental observations and the associated uncertainties.

The developed method was analyzed using different load cases of increasing complexity and considering ideal isotropic and anisotropic measurement data. Based on a parameter study, the characteristics of different implementations as well as the advantages and disadvantages are analyzed in detail. The method using a virtual reference geometry and nonlinear elastic, anisotropic and possibly inhomogeneous coupling elements in order to generate a synthetic solution corridor is found to be most suitable. This method enables the processing of severely anisotropic and inhomogeneous measurement uncertainties. Generated hybrid data sets allow for a very precise identification and quantification of deviations based on the spatially and temporally resolved interaction between the analyzed structure and the synthetic solution corridor. In addition, the hybrid data sets clearly indicate possible causes of deviations even in case of very complex structures, load cases or deviation scenarios and thus significantly support the process of the adjustment of the initial simulation model by a development engineer in order to increase the predictive power of the finite element simulation.

The applicability of the method to reconstruct the three-dimensional experimental results based on the intelligent combination of incomplete (e.g. two-dimensional X-ray) measurement data with the physical knowledge inherent in the FE model was analyzed. Observed results based on different deviation scenarios demonstrate a great potential of the method regarding a three-dimensional reconstruction. All directional components of the nodal trajectories contained in the hybrid data set are almost identical to the corresponding trajectories of the ‘virtual experiment’. This includes the direction without experimental observations (e.g. the X-ray direction).

The results of this study indicate that the developed approach allows for a significant improvement in the utilization of experimental observations during the validation process compared to the state of the art. The informative value of the validation process is significantly less dependent on the mere density of available experimental observations but rather on an appropriate experimental setup leading to the observability of important key points and directions. A separate and manual processing of these key point measurements would lead to a strongly limited informative value of the validation. In contrast, the simultaneous processing and combination of these measurements with the information inherent in the FE model allows to take full advantage of the complementary characteristic of information extracted by various measurement systems. The integration allows not only for the identification and quantification of deviations, but also for a comprehensive interpretation and assessment of these deviations due to the physical interpretability of generated characteristic data (e.g. forces acting between the FE structure and the solution corridor). Another added value compared to the state-of-the-art validation methods is the ability of the method to fill in temporal and spatial observation gaps and reconstruct the three-dimensional behavior of the experiment based on sparse observation data and the physical knowledge inherent in the FE model.

The obtained results show that the application of the ‘Grey-Box-Processing’ validation method can be very useful for the identification and quantitative assessment of deviations between experiment and simulation in the domain of vehicle safety. Furthermore, the comprehensive comparison of experimental results with multiple (stochastic) simulations as well as the direct comparison of different simulations is made possible using this approach. The implementation and integration of the machine learning based completion of incomplete measurement data into the overall iterative workflow will allow to process non-ideal measurement data with spatial and temporal observation gaps. The last steps of the integration are part of a current research project. After this final integration, an additional simulation-based validation will take place using different ‘virtual experimental’ scenarios and ‘virtual measurement strategies’ resulting in more or less sparse observations. The results will be presented in a future publication.