Nonlocal dynamic Kirchhoff plate formulation based on nonlocal operator method

Abstract

In this study, we propose a nonlocal operator method (NOM) for the dynamic analysis of (thin) Kirchhoff plates. The nonlocal Hessian operator is derived based on a second-order Taylor series expansion. The NOM does not require any shape functions and associated derivatives as ’classical’ approaches such as FEM, drastically facilitating the implementation. Furthermore, NOM is higher order continuous, which is exploited for thin plate analysis that requires $C^1$ continuity. The nonlocal dynamic governing formulation and operator energy functional for Kirchhoff plates are derived from a variational principle. The Verlet-velocity algorithm is used for the time discretization. After confirming the accuracy of the nonlocal Hessian operator, several numerical examples are simulated by the nonlocal dynamic Kirchhoff plate formulation.

Introduction

As a common engineering structure, plate/shell is widely used in civil engineering, aerospace and other fields. The mechanical analysis of rectangular thin plates has always been one of the research focuses of scholars and engineers. The governing equation of the Kirchhoff plate bending problem is a fourth-order partial differential equation whose deflection is an independent variable. The numerical method for developing this problem has a wide scientific significance for solving plate/shell problems.

The analysis of Kirchhoff plate bending problems poses challenges to ’classical’ finite element formulations [1,2,3,4,5], which are only $C^0$ continuous. However, the Kirchhoff plate problem is a fourth-order partial differential equation which requires a $C^1$ formulation if weak form based methods such as FEM are employed. An efficient alternative are so-called meshless methods as many of them are higher order continuous. The approximation function of the meshless method [6,7,8,9,10,11] represented by the Element-free Galerkin method EFG [12,13,14,15] is highly smooth, that is, and the high-order continuity is satisfied, meantime the meshless method is easy to form high-order. The approximate function has significant advantages to the numerical solutions for higher-order partial-differential equations.

Rabczuk [16] devised a meshfree method for thin shell analysis for finite strains and arbitrary evolving cracks exploiting the higher order continuity of the EFG shape functions and avoiding any rotational degrees of freedom. Mohammed et al. [17, 18] presented a meshless method to analyze the mechanical response of elastic thin plates. However, since meshless shape functions are commonly rational functions, more integration points are needed to evaluate the weak form. For example, Brebbia [6] employed $6 \times 6$ quadrature points, which significantly reduces the computational efficiency. An interesting alternative to meshless methods is isogeometric analysis (IGA) [19, 20], which also fulfills the higher order continuity requirement needed for thin plate analysis. This method takes advantage of NURBS/B-Spline basis functions, which are commonly used in computer-aided-design (CAD) to describe the geometries. IGA has been successfully applied to the analysis of plates and shells for instance in [21,22,23,24,25]. As CAD geometries are surface representations, they are particularly suited for plates and shells. One difficulty occurs for multi-patch geometries, which are still difficult to deal with.

In this study, we take advantage of nonlocal theories as suggested for instance in nonlocal continuum field theories with various physical fields [26], peridynamics (PD) [27], nonlocal plasticity, (nonlocal) damage mechanics [28] and nonlocal vector calculus [29]. Nonlocal operator method (NOM) [30, 31] is a nonlocal numerical method for solving partial differential equations. The method is based on so-called differential operators. In contrast to finite elements, the NOM only needs neighboring points to develop nonlocal derivatives. Similar to the machine learning approach [32, 33], it can solve PDEs directly instead of the need of shape functions, which plays an equivalent role as the derivatives of the shape functions in the meshless methods or the FEM. And, therefore, the complexity of the nonlocal operator method is significantly reduced. The nonlocal strong form can be derived by a variational derivation on the functional defined by nonlocal operators. This paper presents a nonlocal operator method to predict the dynamic response of Kirchhoff plates exploiting the higher order continuity of the NOM.

The paper is organized as follows: We first briefly review the NOM and derive the nonlocal Hessian operator for Kirchhoff plates in Sect. 2. In Sect. 3, we derive the nonlocal dynamic Kirchhoff plate formulation by a variational formulation. Section 4 presents details about the numerical implementation before we demonstrate the performance of the formulation through several benchmark problems in Sect. 5. We conclude the manuscript in Sect. 6.

Outline of nonlocal operator method and derivation of nonlocal Hessian operator for Kirchhoff plate

Outline of nonlocal operator method

Fig. 1

Schematic diagram of NOM

We consider a Kirchhoff plate occupying a domain $\mathbf \Omega$ as illustrated in Fig. 1. Let us denote the spatial coordinates with ${\mathbf {x}}_i$, ${\mathbf \xi }_{ij}:={\mathbf {x}}_j-{\mathbf {x}}_i$ is relative position vector from ${\mathbf {x}}_i$ to ${\mathbf {x}}_j$; $w_i:=w({\mathbf {x}}_i,t)$ and $w_j:=w({\mathbf {x}}_j,t)$ are the displacement value for ${\mathbf {x}}_i$ and ${\mathbf {x}}_j$, respectively; the relative displacement area for the spatial vector ${\mathbf \xi }_{ij}$ is $w_{ij}:=w_j-w_i$.

The support and the dual-support are two fundamental principles in NOM. The domain, in which every spatial point ${\mathbf {x}}_j$ forms the spatial vector ${\mathbf \xi }_{ij}$ from ${\mathbf {x}}_i$ to ${\mathbf {x}}_j$ is called the support $\mathcal S_{i}$ of point ${\mathbf {x}}_i$, see Fig. 1b. We can write $\mathcal S_{{\mathbf {x}}}=\{{\mathbf {x}}_2,{\mathbf {x}}_3,{\mathbf {x}}_5,{\mathbf {x}}_6\}$. The dual-support of ${\mathbf {x}}_i$ is defined as a union of points which supports include ${\mathbf {x}}$, i.e.

$$\begin{aligned} \mathcal S_{i}'=\{{\mathbf {x}}_j|{\mathbf {x}}_i \in \mathcal S_{j}\} \end{aligned}$$

(1)

The dual-support of point ${\mathbf {x}}_j$ forms the dual-vector ${\mathbf \xi }'_{ij}(={\mathbf {x}}_i-{\mathbf {x}}_j)$ in $\mathcal S_{i}'$ and is denoted as $\mathcal S_{{\mathbf {x}}}'=\{{\mathbf {x}}_3,{\mathbf {x}}_6\}$; ${\mathbf \xi }'_{ij}$ is the $\mathcal S_{j}$ relative position space vector. NOM requires fundamental nonlocal operators that replace the local operators in calculus. Thus, the functional designed to construct a residual and tangent stiffness matrix is formulated in terms of the nonlocal differential operator. The higher order nonlocal operator $\tilde{\partial }_\alpha w_i$ for the scalar field w in support $\mathcal S_{i}$ can be expressed as [34]

$$\begin{aligned} \tilde{\partial }_\alpha w_i:= \int _{\mathcal S_i}\phi ({\mathbf \xi }_{ij}) w_{ij} {\mathbf {s}}_{ij} d V_j \cdot \Big (\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) {\mathbf {s}}_{ij} {\mathbf {s}}_{ij}^T d V_j\Big )^{-1}, \end{aligned}$$

(2)

where $\phi ({\mathbf \xi }_{ij})$ represents the weight function, ${\mathbf \xi }_{ij}$ represents relative position vector. ${\mathbf {s}}_{ij}$ represent the list of polynomials. For example, the polynomials and the higher order nonlocal operator in 2D with maximal second-order derivatives are ${\mathbf {s}}_{ij}=(x_{ij},y_{ij},x_{ij}^2/2,x_{ij} y_{ij},y_{ij}^2/2)^T$ and $\tilde{\partial }_\alpha w_i=(\frac{{\partial w_i}}{ \partial x},\frac{{\partial w_i}}{ \partial y},\frac{{\partial ^2w_i}}{ \partial x^2},\frac{{\partial ^2 w_i}}{ \partial xy },\frac{{\partial ^2 w_i}}{ \partial y^2})^T$.

Using nodal integration, the higher order nonlocal operator and it’s variation for a vector field w in discrete forms are

$$\begin{aligned} \tilde{\partial }_\alpha w_i&=\sum _{j\in \mathcal S_{i}}{ \phi }({\mathbf \xi }_{ij}) w_{ij} {\mathbf {s}}_{ij} \Delta V_{j} \cdot \Big (\sum _{j \in \mathcal S_{i}}{\phi }({\mathbf \xi }_{ij}) {\mathbf {s}}_{ij} {\mathbf {s}}_{ij}^T \Delta V_{j}\Big )^{-1} \end{aligned}$$

(3)

$$\begin{aligned} \tilde{\partial }_\alpha \delta w_i&=\sum _{j\in \mathcal S_{i}}{ \phi }({\mathbf \xi }_{ij}) (\delta w_{j}-\delta w_{i}) {\mathbf \xi }_{ij} \Delta V_{j} \cdot \Big (\sum _{j\in \mathcal S_{i}}{ \phi }({\mathbf \xi }_{ij}) {\mathbf {s}}_{ij} {\mathbf {s}}_{ij}^T \Delta V_{j}\Big )^{-1}. \end{aligned}$$

(4)

We use a penalty energy functional to obtain the linear field of the scalar field to eliminate zero-energy modes. The higher order operator energy functional for a scalar field w at a point ${\mathbf {x}}_i$ is defined as

$$\begin{aligned} \mathcal F_i^{hg}=&\frac{\alpha _w}{2 m_i} \int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij})\big ({\mathbf {s}}_{ij}^T\tilde{\partial }_\alpha w_i -w_{ij}\big )^2 d V_j, \end{aligned}$$

(5)

where $m_i(=\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) {\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}d V_j)$ is the normalization coefficient and $\alpha _w$ is the penalty coefficient. The nonuniform aspect of the deformation is defined as ${\mathbf {s}}_{ij}^T\tilde{\partial }_\alpha w_i -w_{ij}$, and the stability of the NOM is greatly enhanced while ${\mathbf {s}}_{ij}^T\tilde{\partial }_\alpha w_i -w_{ij}$ is enforced explicitly.

Derivation of nonlocal Hessian operator for Kirchhoff plate

In this part, we derive the second-order nonlocal Hessian operator and its variation. The second derivative and its variation in 1D is given as

$$\begin{aligned} \frac{d^2 w_i}{d x^2}&=2\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) w_{ij}\left({\mathbf \xi }_{ij}^2-\frac{K_{3i}}{K_{2i}}{\mathbf \xi }_{ij}\right) d V_j \cdot K_{4i}^{-1} \end{aligned}$$

(6)

$$\begin{aligned} \tilde{\nabla }^T\tilde{\nabla }\delta w_i&=2\int _{\mathcal S_i}\phi \left({\mathbf \xi }_{ij}\right) \delta w_{ij}({\mathbf \xi }_{ij}^2- \frac{K_{3i}}{K_{2i}} {\mathbf \xi }_{ij}) d V_j \cdot K_{4i}^{-1}. \end{aligned}$$

(7)

To devise the nonlocal Hessian operator in 2D, let us define first the vector ${\mathbf \xi }_{ij}=(x_{ij},y_{ij})^T$. It can be shown that the second-order shape tensor for point ${\mathbf {x}}_i$ is computed by [30]

$$\begin{aligned} {\mathbf {K}}_{2i}=\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) {\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij} d V_j=\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij})\begin{bmatrix} x_{ij}^2 &{} x_{ij} y_{ij}\\ x_{ij} y_{ij} &{} y_{ij}^2\\ \end{bmatrix}d V_j \end{aligned}$$

(8)

and the third-order shape tensor for point ${\mathbf {x}}_i$ by

$$\begin{aligned} {\mathbf {K}}_{3i}&=\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) {\mathbf \xi }_{ij}^3 d V_j\nonumber \\&=\Big (\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) x_{ij}\begin{bmatrix} x_{ij}^2 &{} x_{ij} y_{ij}\\ x_{ij} y_{ij} &{} y_{ij}^2\\ \end{bmatrix}d V_j,\nonumber \\&\quad \int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) y_{ij}\begin{bmatrix} x_{ij}^2 &{} x_{ij} y_{ij}\\ x_{ij} y_{ij} &{} y_{ij}^2\\ \end{bmatrix} d V_j\Big )\nonumber \\&=\Big (\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) \begin{bmatrix} x_{ij}^3 &{} x_{ij}^2 y_{ij}\\ x_{ij}^2 y_{ij} &{} x_{ij} y_{ij}^2\\ \end{bmatrix}d V_j,\nonumber \\&\quad \int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) \begin{bmatrix} x_{ij}^2 y_{ij} &{} x_{ij} y_{ij}^2\\ x_{ij} y_{ij}^2 &{} y_{ij}^3\\ \end{bmatrix} d V_j\Big )=({\mathbf {K}}_{3i}^x,{\mathbf {K}}_{3i}^y) \end{aligned}$$

(9)

with ${\mathbf \xi }_{ij}^n:=\underbrace{{\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}\otimes \cdots \otimes {\mathbf \xi }_{ij}}_{\text {n terms}}$.

which finally leads to

$$\begin{aligned} {\mathbf {K}}_{3i} {\mathbf {K}}_{2i}^{-1} {\mathbf \xi }_{ij}=({\mathbf {K}}_{3i}^x {\mathbf {K}}_{2i}^{-1} {\mathbf \xi }_{ij},{\mathbf {K}}_{3i}^y {\mathbf {K}}_{2i}^{-1} {\mathbf \xi }_{ij}). \end{aligned}$$

(10)

The fourth-order shape tensor for point ${\mathbf {x}}_i$ is computed by

$$\begin{aligned} {\mathbf {K}}_{4i}& =\int _{\mathcal S_i} \phi (\varvec{\xi }_{ij})\varvec{\xi }_{ij}^4 d V_j \\& =\int _{\mathcal S_i} \phi (\varvec{\xi }_{ij})\left[\begin{array}{ll} x_{ij}^2 \left[\begin{array}{ll} x_{ij}^2 & {} x_{ij} y_{ij}\\ x_{ij} y_{ij} & {} y_{ij}^2\\ \end{array}\right]& {} x_{ij} y_{ij}\left[\begin{array}{ll} x_{ij}^2 & {} x_{ij} y_{ij}\\ x_{ij} y_{ij} & {} y_{ij}^2\\ \end{array}\right]\\ y_{ij}x_{ij}\left[\begin{array}{ll} x_{ij}^2 & {} x_{ij} y_{ij}\\ x_{ij} y_{ij} & {} y_{ij}^2\\ \end{array}\right]& {} y_{ij}^2\left[\begin{array}{ll} x_{ij}^2 & {} x_{ij} y_{ij}\\ x_{ij} y_{ij} & {} y_{ij}^2\\ \end{array}\right] \end{array}\right]d V_j \\& =\int _{\mathcal S_i} \phi (\varvec{\xi }_{ij})\left[\begin{array}{ll} \left[\begin{array}{ll} x_{ij}^4 & {} x_{ij}^3 y_{ij}\\ x_{ij}^3 y_{ij} & {} x_{ij}^2 y_{ij}^2\\ \end{array}\right]& {} \left[\begin{array}{ll} x_{ij}^3 y_{ij} & {} x_{ij}^2 y_{ij}^2\\ x_{ij}^2 y_{ij}^2 & {} x_{ij}y_{ij}^3\\ \end{array}\right]\\ \left[\begin{array}{ll} x_{ij}^3 y_{ij} & {} x_{ij}^2 y_{ij}^2\\ x_{ij}^2 y_{ij}^2 & {} x_{ij}y_{ij}^3\\ \end{array}\right]& {} \left[\begin{array}{ll} x_{ij}^2y_{ij}^2 & {} x_{ij} y_{ij}^3\\ x_{ij} y_{ij}^3 & {} y_{ij}^4\\ \end{array}\right] \end{array}\right]d V_j=\left[\begin{array}{ll}{\mathbf {K}}_{4i}^{xx}& {}{\mathbf {K}}_{4i}^{xy}\\ {\mathbf {K}}_{4i}^{yx}& {}{\mathbf {K}}_{4i}^{yy}.\end{array}\right] \end{aligned}$$

(11)

The second-order Taylor series extension for a scalar field w is given as

$$\begin{aligned} w_{j}=w_{i}+\nabla w_{i}\cdot {\mathbf \xi }_{ij}+\frac{1}{2!}\nabla ^T\nabla w_{i}:{\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}+O(\mid {\mathbf \xi }_{ij}\mid ^3) \end{aligned}$$

(12)

so that we obtain

$$\begin{aligned} w_{ij}=\nabla w_i\cdot {\mathbf \xi }_{ij}+\frac{1}{2}\nabla ^T\nabla w_i:{\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}+O(\mid {\mathbf \xi }_{ij}\mid ^3) \end{aligned}$$

(13)

which finally results in the following Hessian nonlocal operator

$$\begin{aligned} \frac{1}{2}\nabla ^T\nabla w_i:{\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}= w_{ij}-\nabla w_i\cdot {\mathbf \xi }_{ij} \end{aligned}$$

(14)

and

$$\begin{aligned}&\frac{1}{2}\nabla ^T\nabla w_i:\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}){\mathbf \xi }_{ij}^4 d V_j&=\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) (w_{ij}{\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}\nonumber \\&\quad -\nabla w_i\cdot {\mathbf \xi }_{ij}^3)d V_j. \end{aligned}$$

(15)

The weighted tensor $\frac{1}{2}\nabla ^T\nabla w:{\mathbf {K}}_{4i}$ can be simplified to

$$\begin{aligned} \frac{1}{2}\nabla ^T\nabla w_i:{\mathbf {K}}_{4i}&=\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) (w_{ij}{\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}-\nabla w_i\cdot {\mathbf \xi }_{ij}^3) d V_j\nonumber \\&=\int _{\mathcal S_i}\phi ({\mathbf \xi }_{ij}) w_{ij}{\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}d V_j\nonumber \\&\quad -\nabla w_i\cdot \int _{\mathcal S_i}\phi ({\mathbf \xi }_{ij}) {\mathbf \xi }_{ij}^3 d V_j \nonumber \\&=\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) w_{ij}{\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}d V_j\nonumber \\&\quad -\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) w_{ij} {\mathbf \xi }_{ij} d V_j \cdot \Big (\int _{\mathcal S_{i}}{ \phi }({\mathbf \xi }_{ij}) {\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij} \text {d}V_{j}\Big )^{-1}{\mathbf {K}}_{3i}\nonumber \\&=\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) w_{ij}{\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}d V_j\nonumber \\&\quad -\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) w_{ij} {\mathbf \xi }_{ij} d V_j \cdot {\mathbf {K}}_{2i}^{-1}{\mathbf {K}}_{3i}\nonumber \\&=\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) w_{ij}({\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}- {\mathbf {K}}_{3i} {\mathbf {K}}_{2i}^{-1} {\mathbf \xi }_{ij}) d V_j. \end{aligned}$$

(16)

Note that the rank of ${\mathbf {K}}_{4i}$ is 3 and the 2D nonlocal Hessian operator has only three independent variables where $\frac{\partial ^2 \delta w_i}{\partial x\partial y}=\frac{\partial ^2 \delta w_i}{\partial y\partial x}$, let ${\mathbf {K}}_{4i}^{-1}$ as the pseudo-inverse of ${\mathbf {K}}_{4i}$ in this study.

For the scalar field w, the 2D nonlocal Hessian operator for point ${\mathbf {x}}_i$ can be written in matrix form as

$$\begin{aligned} \tilde{\nabla }^T\tilde{\nabla }w_i=\begin{bmatrix}\frac{\partial ^2 w_i}{\partial x^2}&{}\frac{\partial ^2 w_i}{\partial x\partial y}\\ \frac{\partial ^2 w_i}{\partial y\partial x}&{} \frac{\partial ^2 w_i}{\partial y^2}. \end{bmatrix} \end{aligned}$$

(17)

We let ${\mathbf {K}}_{3i}^x {\mathbf {K}}_{2i}^{-1}, {\mathbf {K}}_{3i}^y {\mathbf {K}}_{2i}^{-1}$ and the pseudo-inverse of ${\mathbf {K}}_{4i}$ be explicitly written as

$$\begin{aligned} {\mathbf {K}}_{3i}^x {\mathbf {K}}_{2i}^{-1}= \begin{bmatrix} a_{11} &{} a_{12} \\ a_{12} &{} a_{22} \\ \end{bmatrix}; {\mathbf {K}}_{3i}^y {\mathbf {K}}_{2i}^{-1}= \begin{bmatrix} b_{11} &{} b_{12} \\ b_{12} &{} b_{22} \\ \end{bmatrix} \end{aligned}$$

(18)

$$\begin{aligned} {\mathbf {K}}_{4i}^{-1}= \begin{bmatrix} \begin{bmatrix} c_{1} &{} c_{2} \\ c_{2} &{} c_{3} \\ \end{bmatrix} &{} \begin{bmatrix} c_{2} &{} c_{3} \\ c_{3} &{} c_{4} \\ \end{bmatrix} \\ \begin{bmatrix} c_{2} &{} c_{3} \\ c_{3} &{} c_{4} \\ \end{bmatrix} &{} \begin{bmatrix} c_{3} &{} c_{4} \\ c_{4} &{} c_{5} \\ \end{bmatrix} \\ \end{bmatrix} \end{aligned}$$

(19)

To facilitate the calculation ${\mathbf {K}}_{4i}^{-1}$ , we convert ${\mathbf {K}}_{4i}$ to a $3\times 3$ matrix yielding

$$\begin{aligned} \begin{bmatrix} c_{1} &{} c_{2} &{} c_{3} \\ c_{2} &{} c_{3} &{} c_{4} \\ c_{3} &{} c_{4} &{} c_{5} \\ \end{bmatrix} ^{-1}=\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) \begin{bmatrix} x_{ij}^{4} &{} x_{ij}^{3} y_{ij} &{} x_{ij}^{2} y_{ij}^{2} \\ x_{ij}^{3} y_{ij} &{} x_{ij}^{2} y_{ij}^{2} &{} x_{ij} y_{ij}^{3} \\ x_{ij}^{2} y_{ij}^{2} &{} x_{ij} y_{ij}^{3} &{} y_{ij}^{4} \end{bmatrix}d V_j \end{aligned}$$

(20)

Since ${\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}-{\mathbf {K}}_{3i} {\mathbf {K}}_{2i}^{-1} {\mathbf \xi }_{ij}$ is a matrix ${\mathbf {Q}}_{2 \times 2}$ with the terms ${Q}_{12}={Q}_{21}$. Remove the repeated terms in matrix ${\mathbf {Q}}$, and the remain terms ${Q}_{11},{Q}_{12},{Q}_{22}$ in matrix ${\mathbf {Q}}$ can be reconstituted a vector ${\mathbf {L}}_{3 \times 1}=({Q}_{11},{Q}_{12},{Q}_{22})^T$. Then Eq.16 can be rewritten as

$$\begin{aligned}&\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) \begin{bmatrix} x_{ij}^{4} &{} x_{ij}^{3} y_{ij} &{} x_{ij}^{2} y_{ij}^{2} \\ x_{ij}^{3} y_{ij} &{} x_{ij}^{2} y_{ij}^{2} &{} x_{ij} y_{ij}^{3} \\ x_{ij}^{2} y_{ij}^{2} &{} x_{ij} y_{ij}^{3} &{} y_{ij}^{4} \end{bmatrix}d V_j \left[ \begin{array}{c} \frac{\partial ^{2} w_i}{\partial x^{2}} \\ \frac{\partial ^{2} w_i}{\partial x \partial y} \\ \frac{\partial ^{2} w_i}{\partial y^{2}} \end{array}\right] \nonumber \\&\quad =\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) w_{ij} {\mathbf {L}}_{i}d V_j \end{aligned}$$

(21)

Finally, $\left( {\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}-{\mathbf {K}}_{3i} {\mathbf {K}}_{2i}^{-1} {\mathbf \xi }_{ij} \right) : {\mathbf {K}}_{4i}^{-1}$ can be obtained by reconstituting terms in Eq.21 and can be expressed as

$$\begin{aligned} \left( {\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}-{\mathbf {K}}_{3i} {\mathbf {K}}_{2i}^{-1} {\mathbf \xi }_{ij}\right) : {\mathbf {K}}_{4i}^{-1}=\begin{bmatrix} e_{i11} &{} e_{i12} \\ e_{i21} &{} e_{i22} \end{bmatrix} \end{aligned}$$

(22)

where

$$\begin{aligned} e_{i11}&=c_{1} (x_{ij}^2-a_{11} x_{ij}-a_{12} y_{ij})+c_{2} (x_{ij} y_{ij}-a_{12} x_{ij}-a_{22} y_{ij})\\&\quad +c_{3} (y_{ij}^2-b_{12} x_{ij}-b_{22} y_{ij}) \\ e_{i12}&=e_{i21}=c_{2} (x_{ij}^2-a_{11} x_{ij}-a_{12} y_{ij})+c_{3} (-a_{12} x_{ij}-a_{22} y_{ij}\\&\quad +x_{ij} y_{ij})+c_{4} (y_{ij}^2-b_{12} x_{ij}-b_{22} y_{ij}) \\ e_{i22}&= c_{3} (x_{ij}^2-a_{11} x_{ij}-a_{12} y_{ij})+c_{4} (-a_{12} x_{ij}-a_{22} y_{ij}\\&\quad +x_{ij} y_{ij})+c_{5} (y_{ij}^2-b_{12} x_{ij}-b_{22} y_{ij}). \end{aligned}$$

The explicit form of the nonlocal Hessian operator in 2D can finally be expressed by

$$\begin{aligned} \tilde{\nabla }^T\tilde{\nabla }w_i=2\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) w_{ij} \begin{bmatrix} e_{i11} &{} e_{i12} \\ e_{i21} &{} e_{i22} \\ \end{bmatrix} d V_j. \end{aligned}$$

(23)

Note that $e_{i11},e_{i12},e_{i22}$ are calculated for each neighbor in the support domain. As a result, the variation of nonlocal Hessian operator can be obtained in explicit form as

$$\begin{aligned} \tilde{\nabla }^T\tilde{\nabla }\delta w_i&=2\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) (\delta w_j-\delta w_i)\begin{bmatrix} e_{i11} &{} e_{i12} \\ e_{i21} &{} e_{i22} \\ \end{bmatrix} d V_j. \end{aligned}$$

(24)

Derivation of nonlocal dynamic Kirchhoff plate formulation

Classical elastic plate theory

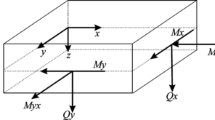
Kirchhoff plate theory assumes that the normal stress in the thickness direction can be ignored and the normal of the midplane of the plate remains normal after deformation. Hence, all stresses and strains can be expressed by the deflection w of the midplane of the plate. Considering the plate element shown in Fig. 2, the in-plane displacements u and v can, therefore, be expressed in terms of the first derivatives of w, i.e.

$$\begin{aligned}&u(x,y,z)&=-z {\frac{\partial w}{\partial x}}; \,\, v(x,y,z)\nonumber \\&\quad =-z {\frac{\partial w}{\partial y}};\,\, w (x,y,z)\simeq w (x,y,0)\cong w(x,y). \end{aligned}$$

(25)

Fig. 2

Deformed configuration of a Kirchhoff plate in bending

The strain resultant ${\varvec{\kappa }}$ can be obtained by

$$\begin{aligned} {\varvec{\kappa }}=\begin{bmatrix} \kappa _x, \kappa _y, \kappa _{xy}\end{bmatrix}^T=\begin{bmatrix} -\frac{\partial ^2 w}{\partial x^2}, -\frac{\partial ^2 w}{\partial y^2}, -\frac{2 \partial ^2 w}{\partial x\partial y} \end{bmatrix}^T, \end{aligned}$$

(26)

where $\kappa _x$ and $\kappa _y$ indicates the curvature of the midplane of the plate in the x- and y- direction while $\kappa _{xy}$ refers to the torsion, respectively.

The stress resultants of the Kirchhoff plate are given by

$$\begin{aligned} {\mathbf {M}}=\begin{bmatrix}M_x, M_y, M_{xy}\end{bmatrix}^T, \end{aligned}$$

(27)

where $M_x$ and $M_y$ are the bending moment per unit length around the y- and negative x-axes, respectively, while $M_{xy}(=M_{yx})$ is the torque per unit length.

With a linear stress distribution in the z-direction and assuming a thickness of t, the stresses can be computed by

$$\begin{aligned} \sigma _x=\frac{12 M_x }{t^3} z; \sigma _y=\frac{12 M_y }{t^3} z; \tau _{xy}&=\tau _{yx}={\frac{12 M_{xy}}{t^3} z}. \end{aligned}$$

(28)

The Cauchy stress tensor can also be expressed in terms of the linear strain tensor assuming Hooke’s law:

$$\begin{aligned} \sigma&=\frac{E}{1-\nu ^2} \big (\nu \,\text{ tr } \varepsilon \, {\mathbf {I}}_{2\times 2}+(1-\nu ) \varepsilon \big ) \end{aligned}$$

(29)

with

$$\begin{aligned} \varepsilon&=\begin{bmatrix}\varepsilon _{11} &{} \varepsilon _{12}\\ \varepsilon _{21}&{} \varepsilon _{22}.\end{bmatrix} \end{aligned}$$

Finally, the constitutive model can be formulated in terms of the stress and strain resultants by

$$\begin{aligned} {\mathbf {M}}={\mathbf {D}}_{plate}{\varvec{\kappa }}, \end{aligned}$$

(30)

where ${\mathbf {D}}_{plate}$ is the constitutive matrix defined as

$$\begin{aligned} {\mathbf {D}}_{plate}=\frac{E t^3}{12(1-\nu ^2)}\left[ \begin{array}{ccc} 1 &{} \nu &{} 0 \\ \nu &{} 1 &{} 0 \\ 0 &{} 0 &{} \frac{1-\nu }{2} \\ \end{array} \right] =\ D_0\left[ \begin{array}{ccc} 1 &{} \nu &{} 0 \\ \nu &{} 1 &{} 0 \\ 0 &{} 0 &{} \frac{1-\nu }{2} \\ , \end{array} \right] \end{aligned}$$

(31)

where $D_0=\frac{E t^3}{12(1-\nu ^2)}$ is the Kirchhoff plate’s bending stiffness, such that Eq.(30) can be rewritten as

$$\begin{aligned} \overline{{\mathbf {M}}}=\begin{bmatrix}M_x&{} M_{xy}\\ M_{yx}&{} M_y\end{bmatrix}=D_0 \big (\nu \,\text{ tr }\overline{{\varvec{\kappa }}}\, {\varvec{I}}_{2\times 2}+ (1-\nu )\overline{{\varvec{\kappa }}}\big ) \end{aligned}$$

(32)

$$\begin{aligned} \overline{{\varvec{\kappa }}}=\nabla ^T\nabla w=\begin{bmatrix}\frac{\partial ^2 w}{\partial x^2}&{}\frac{\partial ^2 w}{\partial x\partial y}\\ \frac{\partial ^2 w}{\partial y\partial x}&{} \frac{\partial ^2 w}{\partial y^2}. \end{bmatrix} \end{aligned}$$

(33)

Nonlocal dynamic Kirchhoff plate formulation

The total Lagrange energy functional for the Kirchhoff plate can be expressed as

$$\begin{aligned} L({\dot{w}},w)&=\int _{\Omega }\frac{1}{2}\rho t {\dot{w}}^2\text {d}\Omega \nonumber \\&\quad -\int _\Omega \left( \frac{1}{2}\overline{{\mathbf {M}}} :\overline{{\varvec{\kappa }}} -q_z w\right)\text {d}\Omega - \int _{\partial \Omega }\overline{M_n} \frac{\partial w}{\partial n} d S\nonumber \\&=\int _{\Omega }\frac{1}{2}\rho t {\dot{w}}^2\text {d}\Omega -\int _\Omega \left( \frac{1}{2}\overline{{\mathbf {M}}}: \nabla ^T\nabla w -q_z w\right)\text {d}\Omega \nonumber \\&\quad - \int _{\partial \Omega }\overline{M_n} \frac{\partial w}{\partial n} d S \end{aligned}$$

(34)

with ${\dot{w}}=\frac{\partial w}{\partial t}$; $\rho$ is the density of the plate and $q_z$ a distributed load in the z-direction. Replacing the local Hessian $\nabla ^T\nabla w$ with the nonlocal Hessian $\tilde{\nabla }^T\tilde{\nabla }w$ in Eq.34, we obtain

$$\begin{aligned} L({\dot{w}},w)&=\int _{\Omega }\frac{1}{2}\rho t {\dot{w}}^2\text {d}\Omega -\int _\Omega \left( \frac{1}{2}\overline{{\mathbf {M}}}:\tilde{\nabla }^T\tilde{\nabla }w -q_z w\right)\text {d}\Omega \nonumber \\&\quad - \int _{\partial \Omega }\overline{M_n} \frac{\partial w}{\partial n} d S \end{aligned}$$

(35)

The integral of the Lagrangian L between two time steps $t_1$ and $t_2$ is $\digamma =\int _{t_1}^{t_2} L({\dot{w}},w) d t$. According to the principle of least action, we can write

$$\begin{aligned} \digamma =&\int _{t_1}^{t_2}\int _{\Omega }\frac{1}{2}\rho t {\dot{w}}^2 \text {d}\Omega \text {d}t-\int _{t_1}^{t_2}\int _\Omega \left( \frac{1}{2}\overline{{\mathbf {M}}}: \tilde{\nabla }^T\tilde{\nabla }w -q_z w\right)d \Omega \text {d}t \nonumber \\&\quad -\int _{t_1}^{t_2} \int _{\partial \Omega }\overline{M_n} \frac{\partial w}{\partial n} d S \text {d}t. \end{aligned}$$

(36)

Omitting the external work term $\int _{t_1}^{t_2} \int _{\partial \Omega }\overline{M_n} \frac{\partial w}{\partial n} d S \text {d}t$, the first variation of $\delta \digamma$ leads to

$$\begin{aligned} \delta \digamma =&\int _{t_1}^{t_2}\int _\Omega (\rho t {\dot{w}}\cdot \delta {\dot{w}}- \overline{{\mathbf {M}}}: \tilde{\nabla }^T\tilde{\nabla }\delta w + q_z \delta w )\text {d}\Omega \text {d}t\\ =&\int _{t_1}^{t_2}\int _\Omega (-\rho _i t \ddot{w_i}\cdot \delta w_i-\overline{{\mathbf {M}}_i}:\tilde{\nabla }^T\tilde{\nabla }\delta w_i +q_z \delta w_i) \text {d}\Omega \text {d}t\\ =&\int _{t_1}^{t_2}\int _\Omega \big (-\rho _i t \ddot{w_i}\cdot \delta {w_i}-\overline{{\mathbf {M}}_i}:[2\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) (\delta w_{ij}({\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}\\&\quad - {\mathbf {K}}_{3i }{\mathbf {K}}_{2i}^{-1} {\mathbf \xi }_{ij}) dV_j : {\mathbf {K}}_{4i}^{-1}]+q_z \delta w_i \big )\text {d}\Omega \text {d}t\\ =&\int _{t_1}^{t_2}\int _\Omega \big ( -\rho _i t \ddot{w_i}\cdot \delta {w_i}- 2\int _{\mathcal S_i} \overline{{\mathbf {M}}_i} \\&\quad \phi ({\mathbf \xi }_{ij}) (\delta w_j-\delta w_i)({\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}- {\mathbf {K}}_{3i } {\mathbf {K}}_{2i}^{-1} {\mathbf \xi }_{ij}) dV_j : {\mathbf {K}}_{4i }^{-1} +q_z \delta w_i \big )\text {d}\Omega \text {d}t\\ =&\int _{t_1}^{t_2}\int _\Omega \Big (-\rho _i t \ddot{w_i}\cdot \delta {w_i}- 2\{\int _{\mathcal S_i'} [\overline{{\mathbf {M}}_j} \phi ({\mathbf \xi }_{ji}) \delta w_i\\&\quad ({\mathbf \xi }_{ji}\otimes {\mathbf \xi }_{ji}- {\mathbf {K}}_{3i } {\mathbf {K}}_{2i }^{-1} {\mathbf \xi }_{ji}) :{\mathbf {K}}_{4i }^{-1}]dV_j -\\&\int _{\mathcal S_i} [ \overline{{\mathbf {M}}_i} \phi ({\mathbf \xi }_{ij}) \delta w_i({\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}- {\mathbf {K}}_{3j} {\mathbf {K}}_{2j}^{-1} {\mathbf \xi }_{ij}) : {\mathbf {K}}_{4j}^{-1} ]dV_j \}+ q_z \delta w_i\Big ) \text {d}\Omega \text {d}t, \end{aligned}$$

where the boundary condition $\delta w(t_1)=0,\,\delta w(t_2)=0$ is considered in the above derivation. According to Hamilton’s principle, for any $\delta w_i$, the first variation of the functional $\digamma$ should be zero, which leads to

$$\begin{aligned}&2\int _{\mathcal S_i} \overline{{\mathbf {M}}_i} \phi ({\mathbf \xi }_{ij}) ({\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}- {\mathbf {K}}_{3i} {\mathbf {K}}_{2i}^{-1} {\mathbf \xi }_{ij}) : {\mathbf {K}}_{4i}^{-1} dV_j\nonumber \\&\quad -2\int _{\mathcal S_i'} \overline{{\mathbf {M}}_j} \phi ({\mathbf \xi }_{ji}) ({\mathbf \xi }_{ji}\otimes {\mathbf \xi }_{ji}- {\mathbf {K}}_{3j} {\mathbf {K}}_{2j}^{-1} {\mathbf \xi }_{ji}) : {\mathbf {K}}_{4j}^{-1} dV_j\nonumber \\&+q_z =\rho _i t \ddot{ w} _i \,\,\, \forall {\mathbf {x}}_i\in \Omega . \end{aligned}$$

(37)

The nonlocal form is correlated to the local form by

According to Eq.23, we devise the explicit form of $\tilde{\nabla }^T\tilde{\nabla }:\overline{{\mathbf {M}}_i}$

$$\begin{aligned}&\tilde{\nabla }^T\tilde{\nabla }: \overline{{\mathbf {M}}_i}=2\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}) \overline{{\mathbf {M}}_i} \cdot \begin{bmatrix} e_{i11} &{} e_{i12} \\ e_{i21} &{} e_{i22} \\ \end{bmatrix} d V_j\nonumber \\&\quad -2\int _{\mathcal S_i'} \phi ({\mathbf \xi }_{ji}) \overline{{\mathbf {M}}_j} \cdot \begin{bmatrix} e_{j11} &{} e_{j12} \\ e_{j21} &{} e_{j22} \\ \end{bmatrix} d V_j. \end{aligned}$$

(39)

As Eq. 37 suffers from zero-energy modes, we introduce the so-called nonlocal operator energy functional, which is described in the next section.

Operator energy functional

For the Kirchhoff plate, the maximal order of partial derivatives in Eq.37 is two, hence we select the second order of nonlocal operators in Eq.5. The operator energy functional for second order nonlocal operators of a scalar field w for point ${\mathbf {x}}_i$ can be expressed as

$$\begin{aligned} \mathcal F_i^{hg}=&\frac{\alpha _w}{2 m_i} \int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij})\big ({\mathbf {s}}_{ij}^T\tilde{\partial }_\alpha w_i -w_{ij}\big )^2 d V_j, \end{aligned}$$

(40)

where ${\mathbf {s}}_{ij}=(x_{ij},y_{ij},x_{ij}^2/2,x_{ij} y_{ij},y_{ij}^2/2)^T$, $\tilde{\partial }_\alpha w_i=(\frac{{\partial w_i}}{ \partial x},\frac{{\partial w_i}}{ \partial y},\frac{\partial ^2 w_i}{ \partial x^2},\frac{\partial ^2 w_i}{ \partial xy },\frac{\partial ^2 w_i}{ \partial y^2})^T$.

The first variation of $\mathcal F_i^{hg}$ is

$$\begin{aligned} \delta \mathcal F_i^{hg}=&\frac{\alpha _w}{ m_i} \int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij})\big ({\mathbf {s}}_{ij}^T\tilde{\partial }_\alpha w_i -w_{ij}\big )^T\big (\tilde{\partial }_\alpha \delta w_i {\mathbf {s}}_{ij}^T-\delta w_{ij}\big ) d V_j\nonumber \\ =&\frac{\alpha _w}{ m_i} \int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij})\big ({\mathbf {s}}_{ij}^T\tilde{\partial }_\alpha w_i -w_{ij}\big )^T \tilde{\partial }_\alpha \delta w_i {\mathbf {s}}_{ij}^Td V_j \nonumber \\&\quad -\frac{\alpha _w}{ m_i} \int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij})\big ({\mathbf {s}}_{ij}^T\tilde{\partial }_\alpha w_i -w_{ij}\big )^T \delta w_{ij}d V_j\nonumber \\ =&\frac{\alpha _w}{ m_i} \int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij})\big ({\mathbf {s}}_{ij}^T\tilde{\partial }_\alpha w_i -w_{ij}\big ){\mathbf {s}}_{ij}^T d V_j \cdot \tilde{\partial }_\alpha \delta w_i\nonumber \\&\quad -\frac{\alpha _w}{ m_i} \int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij})\big ({\mathbf {s}}_{ij}^T\tilde{\partial }_\alpha w_i -w_{ij}\big )^T \delta w_{ij}d V_j\nonumber \\ =&\frac{\alpha _w}{ m_i}\bigg (\tilde{\partial }_\alpha w_i \int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij}){\mathbf {s}}_{ij}{\mathbf {s}}_{ij}^Td V_j-\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij})w_{ij}{\mathbf {s}}_{ij}^Td V_j\bigg )\cdot \tilde{\partial }_\alpha \delta w_i-\nonumber \\&\frac{\alpha _w}{ m_i} \int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij})\big ({\mathbf {s}}_{ij}^T\tilde{\partial }_\alpha w_i -w_{ij}\big )^T \delta w_{ij}d V_j\nonumber \\ =&\frac{\alpha _w}{ m_i}\bigg (\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij})w_{ij}{\mathbf {s}}_{ij}^Td V_j-\int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij})w_{ij}{\mathbf {s}}_{ij}^Td V_j\bigg )\cdot \tilde{\partial }_\alpha \delta w_i-\nonumber \\&\frac{\alpha _w}{ m_i} \int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij})\big ({\mathbf {s}}_{ij}^T\tilde{\partial }_\alpha w_i -w_{ij}\big )^T \delta w_{ij}d V_j\nonumber \\ =&\frac{\alpha _w}{ m_i} \int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij})\big (w_{ij}-{\mathbf {s}}_{ij}^T\tilde{\partial }_\alpha w_i \big ) ^T (\delta w_{j} -\delta w_{i} )d V_j. \end{aligned}$$

(41)

Taking the variation of $\int _{\Omega } \mathcal F_i^{hg}d V_i$ yields

$$\begin{aligned}&\int _{\Omega } \mathcal F_i^{hg}d V_i=\int _{\Omega }\frac{\alpha _w}{ m_i} \int _{\mathcal S_i} \phi ({\mathbf \xi }_{ij})\big (w_{ij}-{\mathbf {s}}_{ij}^T\tilde{\partial }_\alpha w_i \big ) ^T\nonumber \\&\quad (\delta w_{j} -\delta w_{i} )d V_jd V_i\nonumber \\&=\int _{\Omega } \left( \int _{\mathcal S_i'} \frac{\alpha _w}{m_j}\phi ({\mathbf \xi }_{ji} )(w_{ji} -\tilde{\partial }_\alpha w_j{\mathbf {s}}_{ji}^T )d V_j \right. \nonumber \\&\quad \left. -\int _{\mathcal S_i} \frac{\alpha _w}{m_i} \phi ( {\mathbf \xi }_{ij})(w_{ij} -\tilde{\partial }_\alpha w_i{\mathbf {s}}_{ij}^T )d V_j\right) \delta w_id V_i. \end{aligned}$$

(42)

For the scalar field w, the internal force due to the operator energy functional is given by

$$\begin{aligned} \int _{\mathcal S_i'} {\varvec{f}}_{ji} d V_j-\int _{\mathcal S_i} {\varvec{f}}_{ij} d V_j, \end{aligned}$$

(43)

where ${\varvec{f}}_{ij} =\frac{\alpha _w}{m_i} \phi ({\mathbf \xi }_{ij} )(w_{ij} -\tilde{\partial }_\alpha w_i\,{\mathbf {s}}_{ij}^T )$ indicates the zero-energy internal force. Finally, the correspondence between local and nonlocal formulation and the operator functional enhanced governing equation of Kirchhoff plate can be expressed as

$$\begin{aligned}&\int _{\mathcal S_i}\Big (2 \phi ({\mathbf \xi }_{ij})\overline{{\mathbf {M}}_i} \cdot \begin{bmatrix} e_{i11} &{} e_{i12} \\ e_{i21} &{} e_{i22} \\ \end{bmatrix} +\frac{\alpha _w}{m_i} \phi ({\mathbf \xi }_{ij})(w_{ij} -\tilde{\partial }_\alpha w_i\,{\mathbf {s}}_{ij}^T )\Big )dV_j-\nonumber \\&\int _{\mathcal S_i'} \Big (2 \phi ({\mathbf \xi }_{ji}) \overline{{\mathbf {M}}_j} \cdot \begin{bmatrix} e_{j11} &{} e_{j12} \\ e_{j21} &{} e_{j22} \\ \end{bmatrix} +\frac{\alpha _w}{m_j}\phi ({\mathbf \xi }_{ji} )(w_{ji} -\tilde{\partial }_\alpha w_j{\mathbf {s}}_{ji}^T )\Big )\nonumber \\&\quad dV_j +q_z =\rho _i t \ddot{ w} _i \,\,\, \forall {\mathbf {x}}_i \in \Omega . \end{aligned}$$

(45)

Kirchhoff plate boundary conditions

Let us consider the boundary conditions shown in Fig. 3, which can be classified into:

Fig. 3

The Kirchhoff plate bending problem’s boundary conditions

1. Clamped boundary conditions, where the deflection and the slope of the mid-plane is zero. The positioning shift ${\overline{w}}$ and the section rotation ${\overline{\theta }}$ are both zero. The boundary conditions are in the direction parallel to the y-axis (as $x=0$ clamped boundary):

$$\begin{aligned} w|_{x=0}=0 ; \,\,\frac{\partial w}{\partial x}|_{x=0}=0. \end{aligned}$$

(46)

Parallel to the $x-$axis (as $y=0$ clamped boundary), the Kirchhoff plate boundary conditions is

$$\begin{aligned} w|_{y=0}=0 ; \,\, \frac{\partial w}{\partial y}|_{y=0}=0. \end{aligned}$$

(47)

2. Simply supported Kirchhoff plate boundary conditions where the plate is free to rotate about a line but prevented from deflecting. The positioning shift ${\overline{w}}$ and moment $\overline{M_n}$ value is zero: parallel to the $y-$axis (as $x=a$ simply supported boundary), the boundary conditions is

$$\begin{aligned}&w|_{x=a}=0 ; \,\,{M_x}|_{x=a}=-D_0 (\frac{\partial ^2 w}{\partial x^2}+\nu \frac{\partial ^2 w}{\partial y^2})_{x=a}=0 \end{aligned}$$

(48)

and Eq.46 can be written as

$$\begin{aligned}&w|_{x=a}=0 ; \,\,{M_x}|_{x=a}=-D_0\frac{\partial ^2 w}{\partial x^2}|_{x=a}=0 \end{aligned}$$

(49)

Similarly, parallel to the $x-$ axis (as $y=b$ simply supported boundary), the boundary conditions is

$$\begin{aligned}&w|_{y=b}&=0 ; \,\,{M_y}|_{y=b}=-D_0 (\nu \frac{\partial ^2 w}{\partial x^2}+ \frac{\partial ^2 w}{\partial y^2})_{y=b}\nonumber \\& =-D_0\frac{\partial ^2 w}{\partial y^2}|_{y=b}=0. \end{aligned}$$

(50)

Numerical implementation

The domain $\Omega$ is decomposed into N points occupying a volume $\Delta V_i$:

$$\begin{aligned} \Omega =\sum _{i=1}^N\Delta V_i. \end{aligned}$$

(51)

For each point, the support is denoted by

$$\begin{aligned} \mathcal S_i=\{i,j_1,j_2,...,j_{n_i}\}, \end{aligned}$$

(52)

where $j_1,...,j_k,...,j_{n_{i}}$ are the global indices of the neighbors of point ${\mathbf {x}}_i$ and $n_i$ represents the number of neighbors in support domain $\mathcal S_i$. The out-of-plane transversal force between points are computed by

$$\begin{aligned} {\varvec{T}}_{ij}&=\big (2\overline{{\mathbf {M}}_i} \phi ({\mathbf \xi }_{ij}) ({\mathbf \xi }_{ij}\otimes {\mathbf \xi }_{ij}- {\mathbf {K}}_{3i} {\mathbf {K}}_{2i}^{-1} {\mathbf \xi }_{ij}) : {\mathbf {K}}_{4i}^{-1}+{\varvec{f}}_{ij}\big ) \nonumber \\&\quad \Delta V_i\Delta V_j\nonumber \\&=\Big (2 \phi ({\mathbf \xi }_{ij})\overline{{\mathbf {M}}_i} \cdot \begin{bmatrix} e_{i11} &{} e_{i12} \\ e_{i21} &{} e_{i22} \\ \end{bmatrix} +\frac{\alpha _w}{m_i} \phi ({\mathbf \xi }_{ij})(w_{ij} -\tilde{\partial }_\alpha w_i\,{\mathbf {s}}_{ij}^T )\Big )\nonumber \\&\quad \Delta V_i\Delta V_j\nonumber \\ {\varvec{T}}_{ji}&= \big (2 \overline{{\mathbf {M}}_j} \phi ({\mathbf \xi }_{ji}) ({\mathbf \xi }_{ji}\otimes {\mathbf \xi }_{ji}- {\mathbf {K}}_{3j} {\mathbf {K}}_{2j}^{-1} {\mathbf \xi }_{ji}) : {\mathbf {K}}_{4j}^{-1}+{\varvec{f}}_{ji}\big )\Delta V_i\Delta V_j\nonumber \\&=\Big (2 \phi ({\mathbf \xi }_{ji}) \overline{{\mathbf {M}}_j} \cdot \begin{bmatrix} e_{j11} &{} e_{j12} \\ e_{j21} &{} e_{j22} \\ \end{bmatrix} +\frac{\alpha _w}{m_j}\phi ({\mathbf \xi }_{ji} )(w_{ji} -\tilde{\partial }_ \alpha w_j{\mathbf {s}}_{ji}^T )\Big )\nonumber \\&\quad \Delta V_i\Delta V_j. \end{aligned}$$

(53)

Finally, we get the internal force $\varvec{\mathcal {P}}_{ij}$ between points as

$$\begin{aligned} \varvec{\mathcal {P}}_{ij}=\sum _ {j \in \mathcal S_i}{\varvec{T}}_{ij}-\sum _ {j \in \mathcal S_i'}{\varvec{T}}_{ji}. \end{aligned}$$

(54)

So that in discrete form, Newton’s equation of motion is expressed as

$$\begin{aligned} {\varvec{F}}_i-{\varvec{P}}_i={\mathbb {M}}_i \ddot{{w_i}}(t), \end{aligned}$$

(55)

where t is the time, ${ w}_i(t)=\big ({ { w}_1}(t),\ldots ,{ { w}_{N}}(t)\big )$ is the ensemble of the position vector of N points, ${\varvec{F}}_i$ is the external force vector and ${\varvec{P}}_i$ denotes the internal force vector; ${\mathbb {M}}_i$ refers to the mass of the point. In this paper, the velocity and displacement is updated via the Verlet-Velocity scheme [35]:

$$\begin{aligned}&{ w_i}(t+{\Delta t})&={ w_i}(t)+{\dot{{ w_i}}}(t)\Delta t +\frac{1}{2{\mathbb {M}}_i}[{\varvec{F}}_i(t)-{\varvec{P}}_i(t)]{\Delta t}^2\nonumber \\&\dot{{ w_i}}(t+{\Delta t})&=\dot{{ w_i}}(t)+\frac{1}{2{\mathbb {M}}_i}\Big ([{\varvec{F}}_i(t)-{\varvec{P}}_i(t)]+[{\varvec{F}}_i(t+\Delta t)\nonumber \\&\quad -{\varvec{P}}_i(t+\Delta t]\Big ){\Delta t}. \end{aligned}$$

(56)

For reasons of stability, we applied a damping term to each point

$$\begin{aligned} {\varvec{F}}_i^s=-c\dot{{ w_i}} \end{aligned}$$

(57)

${\varvec{F}}_i^s$ representing the damping force for each point, $\dot{{w_i}}$ represents the velocity (vector) of the point, and c is a damping coefficient.

The main implementation process of higher order explicit NOM for the dynamic analysis of Kirchhoff plate can be summarized as follows:

1. Discretization of the solution domain and initialization
(i) Create geometry and discretize the solution domain.
(ii) Initialize the internal force of ${\varvec{P}}_{i}= 0$ and assign values to the corresponding parameters: Young’s modulus E, Poisson’s ratio $\nu$, Density $\rho$ , Number of neighbors for each point etc.
2. Calculate shape tensor
(i) For each point, calculate second, third and forth order shape tensor ${\mathbf {K}}_{2i}, {\mathbf {K}}_{3i}, {\mathbf {K}}_{4i}$ by solving problem Eqs.8–11.
(ii) Calculate the inverse (pseudo-inverse) of the shape tensor ${\mathbf {K}}_{2i}^{-1}$, ${\mathbf {K}}_{3i}^y{\mathbf {K}}_{2i}^{-1}$, ${\mathbf {K}}_{3i}^y{\mathbf {K}}_{2i}^{-1}$,${\mathbf {K}}_{4i}^{-1}$.
3.Calculate the nonlocal Hessian operator
For each point, calculate the nonlocal Hessian operator $\tilde{\nabla }^T\tilde{\nabla }w_i$ by solving Eqs.17-23.
4.Calculate the Kirchhoff plate constitutive model
(i) Calculate Kirchhoff plate’s bending stiffness and strain resultant $D_0, \overline{{\varvec{\kappa }}}$ by solving Eqs.31 and 33.
(ii) Calculate Kirchhoff plate constitutive model by solving Eq.32.
5.Calculate the Kirchhoff plate internal force between points
For each neighbor point $j\in \mathcal S_i$, calculate ${\varvec{T}}_{ij}, {\varvec{T}}_{ji}, {\varvec{P}}_{ij}$ by solving Eqs.51 - 52 and add ${\varvec{P}}_{ij}$ to ${\varvec{P}}_{i}$ and add $-{\varvec{P}}_{ij}$ to ${\varvec{P}}_{j}$.
6. Applying the boundary conditions to solution
(i) Apply the external force ${\varvec{F}}_i$, damping force $\varvec{F}_i^s$ and displacement boundary conditions to the specified points, according to Newton’s second law ${\varvec{F}_i}-{\varvec{P}_i}+ {\varvec{F}_{i}^{s}} ={\mathbb {M}}_i \ddot{{w_i}}(t)$, calculate each point’s acceleration $\ddot{{w_i}}$.
(ii) Update each point’s velocity and displacement through the Verlet-Velocity scheme.

Numerical examples

The proposed nonlocal dynamic Kirchhoff plate formulation is implemented in Wolfram Mathematica. After verifying the accuracy of the nonlocal Hessian operator, several benchmark problems are studied and compared to results obtained by ABAQUS using the S4R plate/shell element [36].

Verification of nonlocal Hessian operator

Let us consider a simply supported square Kirchhoff plate with a width of $a_0=10$m and thickness t=0.01m. The plate is subjected to a uniform pressure of $q_z=100N/m^{2}$. Young’s modulus and Poisson’s ratio are E=30GPa and $\nu$=0.3, respectively. The number of neighbors of each point is set to $n=24$. To test the accuracy of the nonlocal Hessian operator, we assume $\Upsilon =1,3$ (see Eq.58). The analytical solution of this problem is given in [37], i.e.

$$\begin{aligned}&w=\frac{4 q_0 {a_0}^4}{\pi ^5 D_0}\sum _{\Upsilon =1,3,...}^{\infty } \frac{1}{\Upsilon ^5}\nonumber \\&\quad \Big (1-\frac{\alpha _\Upsilon \tanh \alpha _\Upsilon +2}{2 \cosh \alpha _\Upsilon }\cosh \frac{2 \alpha _\Upsilon y}{a_0}+\frac{\alpha _\Upsilon }{2\cosh \alpha _\Upsilon }\frac{2y}{a_0}\sinh \frac{2\alpha _\Upsilon y}{a_0}\Big )\nonumber \\&\quad \sin \frac{\Upsilon \pi x}{a_0} \end{aligned}$$

(58)

with $\alpha _\Upsilon =\frac{\Upsilon \pi }{2}$.

We employ the quintic spline function as weight function

$$\begin{aligned} \phi ({\mathbf \xi })=\alpha _d \Big ((1-\xi /h)_+^5-6(\frac{2}{3}-\xi /h)_+^5+15(\frac{1}{3}-\xi /h)_+^5\Big ) \end{aligned}$$

(59)

with $\xi =\Vert {\mathbf \xi }\Vert$, h is the maximum length of support, $\alpha _d$= $(3^5/40,\,$ ${3^7 7/478 \pi },\,{3^7/40\pi })$ with different dimensional space d and $x_+=\text{ max }(0,x)$.

To accurately represent the relative error of the operator, we consider points at $y=0$. Figs. 5, 6 show the deflection curve of the numerical simulation ( $\frac{\partial ^2 w}{\partial x^2},\frac{\partial ^2 w}{\partial x\partial y}, \frac{\partial ^2 w}{\partial y^2}$ ) compared to the analytical solution. We also check the error in the L2-norm given by

$$\begin{aligned} \Vert w\Vert _{L2}=\sqrt{\frac{\sum _j (w_j-w_j^{exact})\cdot (w_j-w_j^{exact}) \Delta V_j}{\sum _j w^{exact}_j\cdot w_j^{exact} \Delta V_j}} \end{aligned}$$

(60)

which is shown in Fig. 4.

Fig. 4

The L2-norm’s convergence for $\frac{\partial ^2 w}{\partial x^2}$

Fig. 5

Deflection curve of analytical solutions and relative error(y=0). a Contour of the deflection $\frac{\partial ^2 w}{\partial x^2}$ for $\Upsilon$=1; b Contour of the deflection $\frac{\partial ^2 w}{\partial x\partial y}$ for $\Upsilon$=1; c Contour of the deflection $\frac{\partial ^2 w}{\partial y^2}$ for $\Upsilon$=1

Fig. 6

Deflection curve of analytical solutions and relative error(y=0). a Contour of the deflection $\frac{\partial ^2 w}{\partial x^2}$ for $\Upsilon$=3; b Contour of the deflection $\frac{\partial ^2 w}{\partial x\partial y}$ for $\Upsilon$=3; c Contour of the deflection $\frac{\partial ^2 w}{\partial y^2}$ for $\Upsilon$=3

Nonlocal dynamic Kirchhoff plate formulation with simply supported boundary condition

We now focus on a simply supported square Kirchhoff plate with a width of $a_0=1$m and thickness t=0.01m. Young’s modulus and Poisson’s ratio are E=200GPa and $\nu$=0.3, respectively. A uniform pressure of $q_z=100N/m^{2}$ is applied to the plate. The number of neighbors in the domain of influence of each point is set to $n=24$. The distance between points is selected as $\Delta x$=0.01 m leading to 10201 points. For the ABAQUS model—as a comparison—we discretized the plate into $100 \times 100$ elements using the same input parameters.

Simply supported boundary conditions are assumed:

$$\begin{aligned} w(x,0)=w(x,1)=w(0,y)=w(1,y)=0 \quad x,y\in [0,1]. \end{aligned}$$

(61)

Contour plots of the deflection can be found in Figs. 7 and 8, respectively.

Fig. 7

Comparison of the deflection contour under uniform pressure load a ABAQUS, b nonlocal operator method

Fig. 8

Comparison of the deflection for nodes in $y = 0.5$ under uniform pressure load

Nonlocal dynamic Kirchhoff plate formulation with clamped boundary condition

Next, a plate using clamped boundary conditions is studied. The geometry and the parameters of the previous section are adopted. The clamped boundary conditions are given by

$$\begin{aligned}&w(x,0)=w(x,1)=w(0,y)=w(1,y)=0 \nonumber \\&\frac{\partial w(0,y)}{\partial x}= \frac{\partial w(1,y)}{\partial x}= \frac{\partial w(x,0)}{\partial y}= \frac{\partial w(x,1)}{\partial y}=0 \quad x,y\in [0,1]. \end{aligned}$$

(62)

Contour plots of the deflection are illustrated in Figs. 9 and 10, respectively.

Fig. 9

Comparison of the deflection contour under uniform pressure load a ABAQUS, bnonlocal operator method

Fig. 10

Comparison of the deflection for nodes in $y = 0.5$ under uniform pressure load

Transient test of nonlocal dynamic Kirchhoff plate formulation with simply supported boundary condition

The last example is a simply supported plate where the damping is omitted. A uniform pressure of $q_z=100N/m^{2}$ is applied to the plate and the neighbors assigned to each point is set to $n=30$. All other parameters are adopted from the previous example. Figure 11 shows the deflection field at different times.

Fig. 11

The evolution the deflection contour using ABAQUS and nonlocal operator method at different time

Conclusions

In this paper, a nonlocal dynamic Kirchhoff plate formulation based on a nonlocal operator method is proposed. Therefore, we derived the explicit form of the nonlocal Hessian operator taking advantage of a second order Taylor series expansion. The nonlocal operator energy functional is also derived and the relationship between local and nonlocal formulations is interpreted. In the numerical simulation section, we first verify the accuracy of the nonlocal Hessian operator for the Kirchhoff plate and compare it to analytical solutions. Subsequently, the nonlocal dynamic Kirchhoff plate formulation with different type boundary conditions (clamped and simply supported) is studied and compared to simulations obtained by ABAQUS. In the future, we intend to extend the formulation for nonlinear dynamic fracture exploiting the advantages and flexibility of NOM in this direction.