Skip to main content
SpringerLink
Log in

An optimization method based on the Legendre wavelets for 3D rotating, squeezing and stretching magnetohydrodymanic flow in a channel with porous wall

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

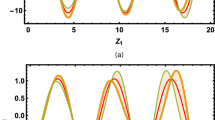
In this paper, the 3D flow in a rotating channel with the lower permeable stretching wall is investigated. The unsteady squeezing flow in the presence of transverse magnetic flux is mathematically modeled by utilizing Navier-Stokes equations. A new optimal wavelet method based on coupling the Legendre wavelets and the hat functions with some auxiliary convergence-control parameters is proposed to solve the obtained fourth-order system of nonlinear differential equations. In the proposed method, the residual function and its error of norm two are employed for converting the main problem into an optimization one to optimally choose the auxiliary convergence-control parameters. The main idea behind this approach is to reduce solving such problems to those of solving optimization ones which greatly simplifies the problem and also leads to obtaining a good approximate solution for the problem under consideration.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Munawar S, Mehmood A, Ali A (2012) Three-dimensional squeezing flow in a rotating channel of lower stretching porous wall. Comput Math Appl 64:1575–1586

    Article  MathSciNet  Google Scholar 

  2. Ali A, Mehmood A (2008) Homotopy analysis of unsteady boundary layer flow adjacent to permeable stretching surface in a porous medium. Commun Nonlinear Sci Numer Simul 13:340–349

    Article  MathSciNet  Google Scholar 

  3. Mehmood A, Ali A (2006) Analytic solution of generalized three-dimensional flow and heat transfer over a stretching plane wall. Int Commun Heat Mass Transf 33:1243–1252

    Article  Google Scholar 

  4. Ariel PD (2001) Axisymmetric flow of a second grade fluid past a stretching sheet. Int J Eng Sci 39:529–553

    Article  Google Scholar 

  5. Zaturska MB, Banks WHH (2003) New solutions for flow in a channel with porous walls and/or non-rigid walls. Fluid Dyn Res 33:57–71

    Article  MathSciNet  Google Scholar 

  6. Shadloo-Jahromi A, Kharati-Koopaee M, Bavi O (2020) Friction factor calculation in nanochannels comprising different wall hydrophobicities and superhydrophobic structures: Molecular dynamic simulations. Int Commun Heat Mass Transf 117:104763

    Article  Google Scholar 

  7. Elbashbeshy EMA, Bazid MAA (2004) Heat transfer over an unsteady stretching surface. Heat Mass Transf 41(1):1–4

    Article  Google Scholar 

  8. Fang T, Zhang J (2008) Flow between two stretchable disks-an exact solution of the Navier-Stokes equations. Int Commun Heat Mass Transf 35:892–895

    Article  Google Scholar 

  9. Robert A, Gorder V, Sweet E, Vajravelu K (2010) Analytical solutions of a coupled nonlinear system arising in a flow between stretching disks. Appl Math Comput 216:1513–1523

    MathSciNet  MATH  Google Scholar 

  10. Tamayol A, Hooman K, Bahrami M (2010) Thermal analysis of flow in a porous medium over a permeable stretching wall. Transp Porous Media 85(3):661–676

    Article  MathSciNet  Google Scholar 

  11. Munawar S, Mehmood A, Ali A (2011) Effects of slip on flow between two stretchable disks using optimal homotopy analysis method. Can J Appl Sci 1(2):50–68

    Article  Google Scholar 

  12. Borkakoti AK, Bharali A (1983) Hydromagnetic flow and heat transfer between two horizontal plates, the lower plate being a stretching sheet. Q Appl Math 41:461–467

    Article  Google Scholar 

  13. Hayat T, Saleem N, Elamboud YA, Asghar S (2011) Effect of induced magnetic field on peristaltic flow of a second order fluid in a symmetric channel. Int J Numer Methods Fluids 67:537–558

    Article  Google Scholar 

  14. Vajravelu K, Kumar BVR (2004) Analytical and numerical solutions of a coupled non-linear system arising in a three-dimensional rotating flow. Int J Non Linear Mech 39:13–24

    Article  Google Scholar 

  15. Mehmood A, Ali A (2007) Analytic homotopy solution of generalized three-dimensional channel flow due to uniform stretching plate. Acta Mech Sin 23:503–510

    Article  MathSciNet  Google Scholar 

  16. Mehmood A, Ali A (2011) Across mass transfer phenomenon in a channel of lower stretching wall. Chem Eng Commun 198:678–691

    Article  Google Scholar 

  17. Ullah A, Shah Z, Kumam P, Ayaz M, Islam S, Jameel M (2019) Viscoelastic MHD nanofluid thin film flow over an unsteady vertical stretching sheet with entropy generation. Processes 7(5):262

    Article  Google Scholar 

  18. Shadloo-Jahromi A, Kharati-Koopaee M, Bavi O (2021) Molecular dynamics simulation of fluid flow through nanochannels consisting of different superhydrophobic patterns. Int Commun Heat Mass Transf 124:105278

    Article  Google Scholar 

  19. Crane LJ (1970) Flow past a stretching plate. Z Angew Math Phys 21:645

    Article  Google Scholar 

  20. Sobamowo MG, Kamiyo OM, Yinusa AA, Akinshilo TA (2020) Magneto-squeezing flow and heat transfer analyses of third grade fluid between two disks embedded in a porous medium using Chebyshev spectral collocation method. Eng Appl Sci Lett 4:305–322

    Google Scholar 

  21. Yinusa AA, Sobamowo MG, Usman MA, Abubakar EH (2021) Exploration of three dimensional squeezed flow and heat transfer through a rotating channel with coupled dufour and soret influences. Therm Sci Eng Prog 21:100788

    Article  Google Scholar 

  22. Hamza EA, Macdonald DA (1981) A fluid film squeezed between two parallel plane surfaces. J Fluid Mech 109:147–160

    Article  Google Scholar 

  23. Hamza EA (1991) The magnetohydrodynamic effects on a fluid film squeezed between two rotating surfaces. J Phys D Appl Phys 24:547–554

    Article  Google Scholar 

  24. Rashidi MM, Shahmohamadi H, Dinarvand S (2008) Unsteanalytic approximate solutions for unsteady two-dimensional and axisymmetric squeezing flows between parallel plates. Math Probl Eng 2008:12 (Article ID 935095)

    Article  Google Scholar 

  25. Kurosaka M (1973) The oscillatory boundary layer growth over the top and bottom plates of a rotating channel. J Fluids Eng 95:68–71

    Article  Google Scholar 

  26. Pop I, Soundelgekar VM (1975) On unsteady boundary layers in rotating flow. J Inst Math Appl 15:343–349

    Article  Google Scholar 

  27. Takhar HS, Chamkha AJ, Nath G (2002) Mhd flow over a moving plate in a rotating fluid with magnetic field, hall currents, and free stream velocity. Int J Eng Sci 40(13):1511–1527

    Article  Google Scholar 

  28. Heydari MH, Avazzadeh Z, Atangana A (2021) Orthonormal shifted discrete Legendre polynomials for solving a coupled system of nonlinear variable-order time fractional reaction-advection-diffusion equations. Appl Numer Math 161:425–436

    Article  MathSciNet  Google Scholar 

  29. Heydari MH, Avazzadeh Z (2021) Jacobi-Gauss-Lobatto collocation approach for non-singular variable-order time fractional generalized Kuramoto-Sivashinsky equation. Eng Comput. https://doi.org/10.1007/s00366-021-01283-0

    Article  Google Scholar 

  30. Elkot NA, Zaky MA, Doha EH, Ameen IG (2021) On the rate of convergence of the Legendre spectral collocation method for multi-dimensional nonlinear Volterra-Fredholm integral equations. Commun Theor Phys 73:025002

    Article  MathSciNet  Google Scholar 

  31. Ezz-Eldien SS, Wang Y, Abdelkawy MA, Zaky MA, Machado JT, Aldraiweesh AA (2020) Chebyshev spectral methods for multi-order fractional neutral pantograph equations. Nonlinear Dyn 100:3785–3797

    Article  Google Scholar 

  32. Kim H, Kim KH, Jang B (2020) Shifted Jacobi spectral-Galerkin method for solving fractional order initial value problems. J Comput Appl Math 380:112988

    Article  MathSciNet  Google Scholar 

  33. Heydari MH, Hooshmandasl MR, Ghaini FM, Fereidouni F (2013) Two-dimensional Legendre wavelets for solving fractional Poisson equation with Dirichlet boundary conditions. Eng Anal Bound Elem 37:1331–1338

    Article  MathSciNet  Google Scholar 

  34. Heydari MH, Hooshmandasl MR, Ghaini FM, Cattani C (2015) Wavelets method for the time fractional diffusion-wave equation. Phys Lett A 379:71–76

    Article  MathSciNet  Google Scholar 

  35. Heydari MH, Hosseininia M, Avazzadeh Z (2020) An efficient wavelet-based approximation method for the coupled nonlinear fractal—fractional 2D Schrödinger equations. Eng Comput. https://doi.org/10.1007/s00366-020-00934-y

    Article  Google Scholar 

  36. Hosseininia M, Heydari MH, Ghaini FM, Avazzadeh Z (2019) A wavelet method to solve nonlinear variable-order time fractional 2D Klein-Gordon equation. Comput Math Appl 78:3713–3730

    Article  MathSciNet  Google Scholar 

  37. Heydari MH (2019) Chebyshev cardinal wavelets for nonlinear variable-order fractional quadratic integral equations. Appl Numer Math 144:190–203

    Article  MathSciNet  Google Scholar 

  38. Dehestania H, Ordokhani Y, Razzaghi M (2020) Fractional-order Bessel wavelet functions for solving variable order fractional optimal control problems with estimation error. Int J Syst Sci 51(6):1032–1052

    Article  MathSciNet  Google Scholar 

  39. Heydari MH, Hooshmandasl MR, Ghaini FM, Cattani C (2014) A computational method for solving stochastic Itô-Volterra integral equations based on stochastic operational matrix for generalized hat basis functions. J Comput Phys 270:402–415

    Article  MathSciNet  Google Scholar 

  40. Tripathi MP, Baranwal VK, Pandey RK, Singh OP (2013) A new numerical algorithm to solve fractional differential equations based on operational matrix of generalized hat functions. Commun Nonlinear Sci Numer Simul 18:1327–1340

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Shiraz University of Technology, Shiraz, Iran

    M. H. Heydari

  2. Department of Mechanical and Aerospace Engineering, Shiraz University of Technology, Shiraz, Iran

    O. Bavi

Authors
  1. M. H. Heydari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. O. Bavi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. H. Heydari.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Heydari, M.H., Bavi, O. An optimization method based on the Legendre wavelets for 3D rotating, squeezing and stretching magnetohydrodymanic flow in a channel with porous wall. Engineering with Computers 38 (Suppl 3), 2583–2592 (2022). https://doi.org/10.1007/s00366-021-01421-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-021-01421-8

Keywords

Mathematics Subject Classification

Search

Navigation