Abstract
Hexahedral (hex) meshes can be generated for CAD models of complex thin-walled components by isolating thin-sheet and long-slender regions, quad meshing one of the bounding faces, and sweeping the quad mesh through the volume to create hex elements. Continuing the work in Sun et al. (Proc Eng 163:225–237, 2016), where an improved approach to thin-sheet identification was presented, an enhanced automatic method for long-slender region identification is proposed in this paper. The objective is to improve the efficiency and decomposition quality compared to existing long-slender region identification processes. Geometric measures such as the edge length and the face width are employed to generate sizing measures, which are in turn used to identify candidate long-slender regions. Careful consideration is given to the generation and positioning of the cutting faces required to isolate the long-slender regions by assessing a priori quad mesh quality on the wall faces. It is shown that a significant reduction in the number of degrees of freedom (DOF) can be achieved by applying anisotropic hex elements on the identified regions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
There is a strong demand in industry for the automatic and efficient meshing of CAD models of complex components. Currently, fully automatic algorithms are available in 3D for the generation of tetrahedral (tet) meshes. However, a major shortcoming of tet meshing is the computational cost of the resulting analysis. In thin-sheet regions especially, where element size is constrained by the thickness of the region, the DOF can be excessive. For large scale nonlinear analysis such as bird-strike or fan blade-off analysis of a whole aero engine, the number of DOF can reach tens or hundreds of millions and reducing this number is an obvious ambition. In these cases, tet meshing is often eschewed in favour of hex meshing due to the superior performance of well-structured hex meshes in both accuracy and efficiency.
Fully automatic methods for hex meshing solid models with good quality elements have been under investigation for many years [2,3,4,5,6,7,8]. Although significant research has been carried out, the complexity of the models that can be automatically processed is very restricted. Recently published methods such as PolyCube [9] and the 3D cross field [10,11,12,13] have shown great potential to automatically generate full hex meshes for complex geometries, but a general robust solution has yet to be realised. Common practice is for most geometry to be manually decomposed into a collection of sub-volumes, to which automatic meshing strategies can be applied. The time and human effort taken for this tedious decomposition process often outweighs the advantages offered by hex meshes in terms of accuracy and computational speed. It is therefore a worthwhile ambition to develop approaches to automatically identify and isolate regions where certain known meshing techniques can be applied. This allows partial automatic hex meshing of complex geometries, and allows any manual preparation efforts to be focused on the characteristics of the remaining regions.
The most useful and widely applied semi-automatic meshing technique is sweep meshing [5, 14,15,16], where a collection of quad mesh elements is swept from source faces to target faces. Much research has been developed to automatically decompose the model into sweepable sub-volumes [17,18,19,20]. However, in general these methods only work on simple geometries. For many complex components in the aviation or automobile industry, a substantial fraction of the total volume is formed from thin-sheet regions. One reasonable strategy which has been adopted is decomposing the model to isolate the thin-sheet regions [1, 21]. Once identified, hex meshes can be generated by quad meshing one of the bounding faces and sweeping the mesh through the thickness.
In this paper the approach is taken one step further by decomposing the model into three kinds of regions: thin-sheet, long-slender and the residual regions, as shown in Fig. 1. Thin-sheet and long-slender regions can be easily meshed using sweeping algorithms. The residual regions can be manually decomposed into meshable blocks to generate a full hex mesh, or meshed with tet elements to create a hex-dominant mesh.
The remainder of this paper is organised as follows: Sect. 2 introduces related work about automatic model decomposition for hex meshing; Sect. 3 details the process of the proposed long-slender region identification and partitioning strategy; Sect. 4 demonstrates the decomposition results on industrial models and comparison with results in [22]; Sect. 5 gives a discussion of the approach. Finally the conclusions are drawn in Sect. 6.
2 Related work
Much research has been carried out on model decomposition for hex meshing. Lu et al. [18] proposed an approach using a pen-based user interface to assist the mesh generation process. This approach takes a freehand stroke as an input and uses gestures to create the cutting faces to partition the model. It is a great challenge to understand the input stroke and the approach requires significant experience from the user to get a satisfactory result. Lu et al. [17] described an approach for feature recognition where, after the identification of features, cutting faces are created based on a set of identified edge loops. While these edge loops offer good guidance to the decomposition process they may generate unsuitable cutting faces. Wu et al. [19] presented a method for identifying a general swept volume in a CAD model. The method begins with extracting all potential sweep directions and identifying relevant face sets bounding the sweeps. Several criteria are set up and assigned a weight to evaluate the cutting faces. However, the source face of the swept volume in the work is currently limited to planar faces, and the moving path is assumed to be a straight line perpendicular to the source face. Boussuge et al. [20] developed a method for identifying extrusion primitives in a CAD model. A construction graph is generated during a recursive process to decompose a model into extrusion primitives. One limitation of this method is that the extrusion operation is only related to planar faces. Therefore, faces belonging to curved features will not be recognised effectively. Several assumptions are made to simplify the process and more effort needs to be spent on the range of shapes that can be robustly identified.
Robinson et al. [21] proposed a thin-sheet region identification process based on the medial object (MO) or medial axis transform of the CAD geometry. The medial faces of the geometry are first generated to decide the local thickness of a region. This is followed by the creation of 2D medial axis on each medial face which is used to approximate the lateral dimension for the region. Regions with an aspect ratio (lateral dimension/local thickness) exceeding the specified value are identified as thin-sheets, with these regions of the model being isolated and replaced with shell elements. The thin-sheet identification based on the MO is restricted by the lack of a robust and efficient implementation of 3D MO. A more robust and efficient approach to thin-sheet identification has been proposed based on interrogation and manipulation of face pairs [1], which are the opposite bounding faces of the potential thin-sheet regions.
Makem et al. [22] proposed an approach to identify long-slender regions in a model, once the thin-sheets of material had been removed using method in [21]. A sizing ellipsoid is generated on each edge, centred at its midpoint. The edge length and edge curvature are measured to determine the length of the ellipsoid axis in the edge direction. The width of the two adjacent faces and the local thickness are measured to represent the dimensions of the other two ellipsoid axes. Long-slender ellipsoids with one principal axis much larger than the other two are identified. A “closed loop” search is initiated, which uses the long-slender ellipsoids to look for closed loop of faces bounding a long-slender region. Cutting planes are generated using the edge tangent and surface normal at an offset away from the long-slender-complex region interface.
To define a sizing ellipsoid, a centre point and three orthogonal vectors which define the principal axes are required. However, the metric vectors defining the edge length, face width and the thickness in [22] are not always orthogonal. As a consequence, a lot of effort was spent on transforming the metric vectors to get three equivalent orthogonal vectors which can correctly indicate the local shape property. In addition, an offset is made away from the long-slender and complex region interface for every cutting face, an example of which is shown in Fig. 2a. This has two drawbacks. Firstly, it complicates the decomposition process, especially if the target is a hex mesh and the offset is not required. Secondly, if the long-slender region is adjacent to a thin-sheet region, making an offset of the long-slender region also requires effort when creating a conformal mesh between the two regions at the interface. The desired decomposition for this model is without an offset, as shown in Fig. 2b. In this paper a novel, simplified and robust approach for long-slender region identification is presented. The circumstances in which an offset is required have also been clarified.
3 Long-slender region identification
3.1 Overview
Let D 1, D 2 and D 3 represent the characteristic dimensions of a region in a CAD model in three directions. The long-slender region is defined as a region where the characteristic dimension in one direction is much larger than that in the other two, i.e., \({D_1} \gg {D_2} \approx {D_3}.\) A long-slender region consists of two cap faces (source and target for sweep meshing) and a collection of wall faces, Fig. 3. A cap face is an end face of a long-slender region which has similar lateral dimensions in every direction, while wall faces have large aspect ratios.
The process of identifying a long-slender region in a general solid is summarized here with reference to the model in Fig. 4 (which is a subset of the model in Fig. 1 and is described in detail in the following sections). The input to the process is a model with the thin-sheets already removed, Fig. 4a. While the thin-sheet removal could be achieved in a number of ways, the work described in [1] was used here. For each edge in the model, the edge length and face width of the faces it bounds are measured. Edges which bound two faces with large aspect ratio (length/width) are selected, as shown in Fig. 4b. Faces bounded by more than one identified edge are identified by topology interrogation, as shown in Fig. 4c. Among these faces, those that bound a possible long-slender region (forming a closed loop of faces) are identified based on topological and geometrical checks described below. For the example model in Fig. 4, there will be two groups of faces, Fig. 4d. Cutting faces are calculated based on the selected points at the end of each group of faces, Fig. 4e, and are used to decompose the model. Regions with an aspect ratio [see Eq. (1)] greater than the pre-defined value are then identified as long-slender regions, shaded dark in Fig. 4f.
The approach for long-slender region identification described herein is implemented using the C# language and .NET framework APIs in Siemens NX 10 [23] on a 3.4 GHz Intel Core (TM) i7-2600 CPU machine with 16 GB RAM. Geometrical measures (e.g., edge length) and operations (e.g., calculating intersections, fitting curves, splitting body) are achieved using the NX geometry engine via APIs.
3.2 Identify candidate edges and faces
A candidate edge is defined as an edge which bounds a possible long-slender region, as identified by the fact both of the faces it bounds have a large aspect ratio. The aspect ratio R E of an edge relative to a face is defined as the edge length L over the face width W,
The edge length can be calculated using
where \(\gamma =\gamma (t)\) is the underlying curve of the edge in R 3, \(t \in [0,1].\) For a face, many different measures could be used to represent face width. In this work, it is defined as follows. Let F be a face and P be the midpoint of a bounding edge \({\gamma _1}\), Fig. 5. T is the unit tangent vector of curve \(\gamma\) at point P, given by
Let П be a plane at point P with T being the normal, given by
The face width W is approximated by the arc length of the intersection curve between П and F, as \(\widehat {{PQ}}\) in Fig. 5.
Once all of the edges in the model have been assessed, a candidate face is identified as a face bounded by at least two candidate edges. Example candidate edges and candidate faces are shown in Fig. 4b and c, respectively. After the candidate edges and faces are identified, three dictionaries are constructed to store the topology relationships between them.
-
Dictionary 1: stores the two bounded candidate faces of each candidate edge, i.e., {edge: face 1, face 2};
-
Dictionary 2: stores the bounding candidate edges of each candidate face, i.e., {face: edge 1, edge 2, edge 3, ...};
-
Dictionary 3: stores the adjacent candidate faces of each candidate face, i.e., {face: face 1, face 2, face 3,...}. Two adjacent candidate faces share at least one candidate edge.
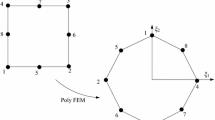
Figure 6 gives an example of the relationships stored in the three dictionaries where E 1, E 2, E 3 are candidate edges (in bold) and F 1, F 2, F 3, and F 4 are candidate faces. In Fig. 6b, the bounded candidate faces of E 1 are F 1 and F 2; the bounding candidate edges of F 2 are E 1, E 2, and E 3; the adjacent candidate faces of F 2 are F 1, F 3, and F 4.
3.3 Identify T-Loops and G-Loops
A T-Loop is a set of candidate faces. Each candidate face in the set has at least two adjacent candidate faces. To identify a T-Loop, firstly one candidate face is selected. If it has more than one adjacent candidate face in Dictionary 3 then it is inserted into a set. Its adjacent candidate faces are then selected, and they are added into the same set if they have more than one candidate face in Dictionary 3. A face will not be added repeatedly if it is already in the set. The process continues until there are no new candidate faces identified. Figure 7a shows an example of a T-Loop which is comprised of nine candidate faces (F 1–F 9). The order in which the candidate faces are identified is illustrated in Fig. 7b.
Faces in a T-Loop may bound zero, one, or multiple long-slender regions. Topological information alone does not offer enough information to determine if the faces bound a long-slender region. For example, in Fig. 8, for some aspect ratios, a T-Loop can be identified which does not form valid bounding faces for a long-slender region (e.g., F 1, F 2, F 3 and F 4), because while they are adjacent they do not span a loop of faces around a volume.
A G-Loop is a subset of a T-Loop which bounds one possible long-slender region. A G-Loop is identified based on a geometrical check. After obtaining a T-Loop, the candidate edges in a T-Loop are ordered based on the arc length. A slice is made at the midpoint of the shortest candidate edge using a plane which is oriented normal to the tangent vector at the midpoint, Fig. 9a. (The plane will be referred to as the “slicing plane” in the following section). For efficiency the slice is only made with faces in the current T-Loop. This slice will result in points being created on each edge, and curves being created on each face. For the slicing section, as shown in Fig. 9b, if a closed loop of curves is created by the split, then the candidate faces that these curves lie on comprise a G-Loop, as shown by the shaded faces in Fig. 9c. The faces and edges in a G-Loop are identified and stored using the following rules.
-
Let \(P_{0}^{\prime }\) be the midpoint of the shortest candidate edge;
-
Start with \(P_{0}^{\prime }\) and walk along the closed curves on the slicing section. The ith end point and curve on the path will be stored as \(P_{i}^{\prime }\) and \(C_{i}^{\prime }\) respectively, as shown in Fig. 9b;
-
The candidate edge that \(P_{i}^{\prime }\) lies on is stored as E i and the candidate face that \(C_{i}^{\prime }\) lies on is stored as F i , as shown in Fig. 9d.
This process will identify one G-Loop, but there may be other G-Loops within the same T-Loop set. The slicing test is made again for the shortest edge among those that do not belong to any current G-Loop, and that have not yet been tested. For example, after the identification of the first G-Loop shown in Fig. 9, there are two residual candidate edges as shown in Fig. 10a. A slice is made at the midpoint of the shortest one to split all faces in the T-Loop. In this instance, another closed curve loop is identified, meaning another G-Loop exists, as the highlighted faces shown in Fig. 10b. The process continues until every candidate edge in a T-Loop has either been rejected or classified as belonging to a G-Loop.
3.4 Group the end points of the edges of a G-Loop
The G-Loop contains all the wall faces for a long-slender region, but it needs two cap faces to completely define the region. Here, the end points of the candidate edges in a G-Loop are classified into two groups, each of which corresponds to a specific cap face. As such, two end points of the same edge should be classified into different groups. The classification is performed based on the positions of the end points relative to the slicing plane generated during the G-Loop identification process. The relative position of a point to a plane can be calculated using the dot product of the normal of the plane and a vector which starts from the plane and ends with the point. Since the slicing plane always passes through the midpoint of the shortest candidate edge \(P_{0}^{\prime }\), a vector is created as \(P_{0}^{\prime }P_{i}^{j}\) as shown in Fig. 11a, where \(P_{i}^{j}\) is the end point of an edge E i , {j = 0, 1}. For all edges, the end points for which the dot product has the same sign (+ or −) will lie on the same side of the plane and be classified into the same group.
It is possible in some cases that the two end points of an edge lie on the same side of the slicing plane, as shown in Fig. 11b. If this happens, the intersection point between the edge and the slicing plane is used to define the relative position of the end point. To achieve this, two new points are created at the midpoints between the intersection point and the two end points, e.g., P A and P B in Fig. 11b. Vectors pointing to the midpoints will be used to calculate the dot product, e.g., \(P_{0}^{\prime }{P_{\text{A}}}\) and \(P_{0}^{\prime }{P_{\text{B}}}\). The result will be used to indicate the sign of the corresponding end point which is closest to the midpoint.
3.5 Identify and assess edges at the end of the wall faces
In [22], the cap face of a long-slender region is either an existing face, or formed by a cutting face offset from the long-slender and complex region interface. One objective in this work is to use existing edges at the end of the wall faces as possible bounding entities for cutting faces, instead of making an offset for all possible edges. Here, a cap face can be one of three different types, which will be explained with reference to the model in Fig. 12.
-
Type-1: is an existing face in the model;
-
Type-2: results from an offset cutting face;
-
Type-3: results from a cutting face bounded by one or more existing edges at the end of the wall faces.
The motivation of identifying long-slender regions is to enable a swept hex mesh to be applied to the regions. This means that once a long-slender region has been identified and a hex mesh is created by sweeping a quad mesh along its length, each wall face will have a good quality structured quad meshes on it. Therefore, for each candidate face, the edges joining the end points are assessed to determine whether a good quality quad mesh can be applied.
3.5.1 The net number of positive and negative singularities on a surface
A structured quad mesh has no mesh singularities. These are interior nodes where more or less than 4 elements meet. Negative singularities occur if < 4 elements meet at a node and positive singularities occur if > 4 elements meet at the node, Fig. 13. The net number of quad mesh singularities on a surface can be calculated using the following equation [24]
where θ i is the corner angle, Fig. 13; n i the optimum number of elements at a vertex; k g the geodesic curvature of the edges; K the Gaussian curvature of the face; n + and n − the number of positive singularities and negative singularities, respectively. The term\(~{n_+} - {n_ - }\) is used to indicate the net number of mesh singularities by setting either \({n_+}\) or \({n_ - }\) to be zero. The optimum number of elements n i can be calculated using
Combined with the Gauss–Bonnet theorem [25],
where χ(R) is the Euler characteristic of the region R and α i is the exterior junction angle, which is the change of the tangent vector of adjacent curves when walking around the boundary curves in a CCW direction, as shown in Fig. 13, then it can be shown that
With the fact that,
Eq. (8) can be simplified to
3.5.2 Edge assessment and classification
To be suitable for sweep meshing, the wall face of a long-slender region should be four-sided and contain no inner loops. In Eq. (10), let \(\chi =1\) and N = 4. To have a net number of zero singularities,
To have a good quality, it is required that the number of elements at each corner should be greater than zero. Therefore,
The existence of a positive and negative mesh singularity pair may not be apparent purely by observing the corners of the domain, as shown in Fig. 14a. To solve this, sample points are created along the edge joining the two end points, e.g., S 1, S 2, S 3, \(S_{1}^{\prime }\), \(S_{2}^{\prime }\) and \(S_{3}^{\prime }\) as shown in Fig. 14b. Creating lines between the sample points allows sub-regions to be formed, e.g., \({P_1}{S_1}S_{1}^{\prime }P_{1}^{\prime }\). Equation (12) should hold for each sub-region. Let \(n_{{\text{s}}}^{1}\) be the number of elements at a sample point in its first sub-region and n s the total number of elements at a sample point created along the edge, then
a The net number of mesh singularities is zero, but there are two pairs of positive and negative singularities; b sample points created on the identified edges and the domain is subdivided into sub-regions. The interval between sample points should be such that the curve does not turn too much between points, e.g., \(\mathop \smallint \nolimits^{} {k_{\text{g}}}{\text{d}}s \leqslant \frac{\pi }{4}\), see Eq. (5)
For this example, \(n_{{\text{s}}}^{1}\) at the sample point S 1 is zero, which means that to achieve a good quality quad mesh singularities must be introduced in that sub-region.
Equations (12) and (13) are used to assess an edge at the end of the wall face, which is traversed in the process introduced in the following Sect. 3.5.3. If multiple edges lie between the end points they are treated as one edge. The assessment process is explained with reference to the example wall face end conditions shown in Fig. 15, where in each case points P 1 P 2, the solid lines, and the dashed lines represent the end points, the candidate edges, and edges to be assessed, respectively. Let n 1 and n 2 be the optimum number of elements at the corner of the end points P 1 and P 2. P 1 represents the first point of an edge that is traversed. The traversed edge will be classified as one of the three types:
-
Type-1 edge: it can be used for constructing the cap face. This decision is made if both Eqs. (12) and (13) are satisfied, e.g., Fig. 15a.
-
Type-2 edge: it cannot be used for constructing the cap face and an offset is required. This happens if n 1 = 0, e.g., Fig. 15b, or n 1 = 1, but Eqs. (12) and (13) are not satisfied at the other end point or sample points, e.g., Fig. 15c–f.
-
Type-3 edge: it cannot be used for constructing the cap face and no offset is required. This is the case when n 1 > 1, e.g., Fig. 15g, h. The bounding edges of the cap face on this wall face will be determined later.
3.5.3 End point traversal
For each end point group, the end point with minimum arc length to the slicing plane is selected (it is referred to as the closest end point in the following section). This end point defines the furthest possible position of the cap face relative to the slicing plane. Starting from this point, the edges bounding it are traversed, assessed and classified. The process will stop if it comes to an edge classified as a type-2 or type-3 edge. In Fig. 16, the traversal starts from point P 0. In one direction, it identifies edge e 3, e 4 as type-1 edges and e 2 as a type-2 edge. In the other direction, it identifies e 0 as a type-3 edge. Edges that are not traversed will be given a null type, as e 1 in Fig. 16.
For an end point that is not in the above traversal loop, e.g., point P 1 in Fig. 17, if the arc length to the slicing plane is close to that of the closest end point, i.e., within a defined tolerance T, the same traversal process can be performed. It is possible that the same edge is assigned two different type classifications if traverse starts from the two different vertices of the same edge. For example, in Fig. 15d, a traversal will start from both P 1 and P 2 if their arc lengths to the slicing plane is within the tolerance. It will be assigned as a type-2 edge in one traversal while a type-3 edge in the other traversal. In this case, the edge will take the type-2 as the final result.
3.6 Define the cap face
Based on the analysis in the last section, different types of cap faces are created following the logic in the diagram in Fig. 18.
The type-1 cap face can be easily identified, e.g., the highlighted face at the left end of the model in Fig. 12a. The type-2 and type-3 cap faces will both result from cutting faces. The cutting face herein is defined based on a set of bounding edges. In the following section, the process of creating the cutting face is detailed.
3.6.1 Cutting face for the type-2 cap face
To create the cutting face for the type-2 cap face, sample points are created along each type-3 edge, as shown in Fig. 19a where the dashed line represents a type-3 edge, S i the sample points, P 1, P 2 the end points of the candidate edges E 1, E 2. Let P 0 represent the closest end point and E 0 represent the edge it lies on. For each sample point and end point on the type-3 edge, its closest point on edge E 0 are calculated, e.g., S 2 → P S−2, S 3 → P S−3, and P 1, P 2, S 1, S 4 → P 0. The furthest one from P 0 is identified and offset away from P 0 at a distance of one element length L, as the point P offset shown in Fig. 19a. A plane is created normal to the tangent vector at the offset point and the intersection curves with the candidate faces in the G-Loop are calculated. These curves are used as the boundary of the cutting face, as shown in Fig. 19b.
3.6.2 Cutting face for the type-3 cap face
As stated earlier, the type-3 cutting face is bounded by existing edges at the end of the wall face. The cutting face herein is defined based on a set of bounding edges, one on each face in the G-Loop. The bounding edge can either be an existing edge or a newly created curve. If all bounding edges are existing, the cutting face is created just by filling the boundaries, e.g., the cutting face at the right end of the long-slender region in Fig. 20.
Otherwise, there is a need to determine other bounding points/edges of the cutting face using the information from the type-1 edges. The idea is to create a plane using the end points of the type-1 edges, and then to calculate the intersection points between the plane and the candidate edges in a G-Loop, on which the bounding point of the cutting face is not defined. After all bounding points are obtained, the bounding edge can be created by fitting a curve between two bounding points on a face. If there are at least three non-collinear end points, the plane is created using a least squares fit to these end points. Suppose the coefficient of x is not zero, a 3D plane is described as
To calculate the coefficient a, b, c in matrix form
A least squares fit is performed by pre-multiplying a transpose matrix to both sides
After the matrix multiplication
Suppose the plane passes through the centroid of all points and x, y and z are defined as the coordinates relative to the centroid, then \(\mathop \sum \nolimits^{} {y_i}=\mathop \sum \nolimits^{} {z_i}=\mathop \sum \nolimits^{} {x_i}=0\). The equation can be simplified as
The coefficients a, b and c can then be calculated. The above result is based on the assumption that the coefficient of x is not zero, which is not always true. But at least one of the coefficients must be non-zero if the points span a plane. The other two calculations are also carried out with the assumption that the coefficients of y and z are not zero. The one which has the maximum determinant of the left matrix in Eq. (18) is selected to determine the coefficients. For the model in Fig. 21, there are seven faces in the G-Loop, so it needs seven bounding edges to create the cutting face. Three of them are from existing edges, as shown in bold lines in the different orientations of the model given in Fig. 21a, b. A plane is fitted using the end points of the existing edges, Fig. 21c. The intersection points between this plane and the other three candidate edges in the G-Loop are calculated as shown in Fig. 21d. Four fitted curves are created as shown in dashed lines in Fig. 21e. The cutting face is generated by filling the region bounded by the fitted curves and existing edges, Fig. 21f.
For a fitted curve on the wall face, the same assessment as in Sect. 3.5 is carried out to make sure that a good quality structured quad mesh can be generated if the wall face is divided by the fitted curve. If a good quality quad mesh cannot be generated, an offset will be made. Note, the generated plane does not need to pass through the end points of the existing edges of the candidate faces. Therefore, the intersection curves between the plane and the faces in the G-Loop do not guarantee to form a closed shape with the existing edges. Rather the above process is used to obtain the closed boundary of the cutting face.
If the number of end points of the identified type-1 edges is less than three, or more than three but collinear, a plane will be created at the closest end point and normal to its tangent vector, as shown in Fig. 22. The following process of obtaining the bounding points and bounding curves is the same as described above.
3.7 Volume decomposition and long-slender region identification
After the cutting face has been used to partition the model, the resulting long-slender region will be identified. Different approaches are used to identify the long-slender regions based on the number of cutting faces required.
-
No cutting faces required: no decomposition is required as the entire region is a long-slender region. The two cap faces will be the source and target faces in a swept mesh.
-
One cutting face required: this means that one cap face for the long-slender region exists in the original model. After decomposition, the region bounded by the cap face is identified as a long-slender region. The existing cap face and the cap face resulting from the cutting face on the other end will be the source and target faces. For example, the left long-slender region in Fig. 4f has one cap face which exists and only one cutting face is generated.
-
Two cutting faces required: this means that no cap faces exist in the original model (the right long-slender region in Fig. 4f). The region that contains the midpoint of the shortest edge in a G-Loop will be identified as the long-slender region. The two cap faces resulting from the cutting faces will be the source and target faces.
For the identified long-slender region, edges that come from candidate edges in the original model are identified. The average arc length L V of these edges is calculated and used to represent the dimension of the long-slender region along the axis direction. The slicing section during the process of identifying a G-Loop is used to decide the dimensions in the other directions. The smallest circle that contains all the end points of the curves in a closed loop is calculated, and its diameter 2r is used as the dimension of the long-slender region in the other dimensions, as shown in Fig. 23. A volume aspect ratio R V is defined as R V = L V/2r. A region with a volume aspect ratio larger than the pre-defined value will be identified as a long-slender region.
4 Results
The long-slender region identification is implemented after the thin-sheet regions have been identified and removed as described in [1]. The long-slender region identification results for models shown in [1] are given in Fig. 24, where the thin-sheet, long-slender and residual regions are coloured in dark grey, black and light grey, respectively. The time spent on the process, the number of the thin-sheet regions and long-slender regions are summarized in Table 1. For all examples, R E = 3 and R V = 1. Note the periodic faces (i.e., with only 2 continuous bounding edges) for the model in Fig. 24a are divided into two prior to the identification.
To compare the efficiency, the approach proposed in this paper is implemented on the same model as used in [22]. In [22], it is stated that it takes 10 min to identify the long-slender regions, while it takes approximately 1 min using the approach described in this paper. The result is shown in Fig. 25.
In [22] an offset is made at every cutting plane, which in many cases is not necessary to support the creation of good quality hex meshes. In this work an offset is made only when it is needed to ensure a good mesh quality. Figure 26a, b compares the results where the offset is included in (a) and not included in (b).
4.1 DOF reduction
A representative industrial model, the CRESCENDO compressor inter-casing [26], is used to demonstrate the DOF reduction using the anisotropic hex elements on the identified thin-sheet and long-slender regions. For clarity, 1/6 of the model is used. The original model and the decomposed model are shown in Fig. 27a, b, respectively. There are 46 thin-sheet regions, 28 long-slender regions, and 4 residual regions. The identified thin-sheets and long-slender regions occupy about 97.9% of the total part volume. Four analysis models are created for comparison.
a The original model; b the decomposed model, thin-sheets in dark grey, long-slender regions in black, residual regions in light grey; c tet elements meshed model; d thin-sheet regions meshed with isotropic hex element; e thin-sheet regions meshed with anisotropic hex element; f anisotropic hex elements applied to both the thin-sheet and long-slender regions
-
Tet mesh: the model is meshed with 10-node tet elements of a size of 4 mm, Fig. 27c;
-
Isotropic hex for thin-sheets: the thin-sheets are meshed with isotropic 8-node hex elements of 4 mm and the remainder is tet meshed, Fig. 27d;
-
Anisotropic hex for thin-sheets: the thin-sheets are meshed with anisotropic 8-node hex element with an aspect ratio (lateral dimensions to thickness) varying up to 5 and the reminder is tet meshed, Fig. 27e;
-
Anisotropic hex for thin-sheets and long-slender regions: both the thin-sheet and long-slender regions are meshed with anisotropic 8-node hex element with an aspect ratio varying up to 5 and with tet elements in the residual regions, Fig. 27f.
Note for the three mixed element analysis models, pyramid elements are generated to transition between hex elements and tet elements. The meshes were created in NX.
The DOF of the four analysis models is summarized in Table 2. By applying anisotropic hex elements to the thin-sheet regions, a DOF reduction of 82.3% can be achieved relative to the tet mesh. By further applying anisotropic hex elements to the long-slender regions, further reduction of 11.8% can be achieved. The DOF of this analysis model is 5.9% of the analysis model with an isotropic tet mesh.
A modal analysis was conducted for these analysis models. The analysis time for the different analysis models is given in Table 3. With the long-slender regions meshed with anisotropic hex elements, the analysis time reduces to 1.4 min, which is 3.2% of the analysis time compared to the isotropic tet meshed model.
Figure 28 compares the discrepancy in the modal frequencies of the mixed element meshed analysis models relative to the tet meshed model. The analysis model where thin-sheet regions are meshed with similar size isotropic hex elements shows similar accuracy. For the two models using the anisotropic hex elements, the maximum discrepancy is under 2%.
5 Discussion
A new approach for automatic identification of long-slender regions in general solids is described in this paper. There are four key parameters mentioned in previous sections, namely the edge aspect ratio R E, the volume aspect ratio R V, the offset distance L when creating the type-2 cap face, and the distance tolerance T when assessing edges. The aspect ratios R E and R V are used to down-select the candidate regions. Increasing the aspect ratio will result in fewer regions being identified as long-slender. As the purpose of this method is to support hex meshing, the aspect ratio R E and R V of a long-slender region does not need to be very high. For the included examples R E was 3 and R V was 1. The offset distance L is selected to be the maximum target element size and the distance tolerance T is selected as the minimum target element size. This guarantees that there will be no sliver volumes resulting in the residual regions.
When identifying a G-Loop, which is the loop of bounding faces of a long-slender region, a slice is made at the midpoint of the shortest candidate edge. It is required that, on the slicing section, the intersection curves with the faces in the G-Loop form a closed loop and each end point of the intersection curve lies on a candidate edge. The present implementation does not consider the existence of any inner loops on the wall face. For example, there is no long-slender region identified for the model in Fig. 29 due to the existence of a feature on one candidate face, which results in an inner loop on that face. In future, features on the candidate faces in a G-Loop need to be isolated first. Another potential problem is when the edge dihedral angle changes significantly along the length of the long-slender region, e.g., from 90° to 180°, so that the optimum mesh topology is different on the source and target faces.
The described approach demonstrates a great improvement in term of efficiency compared to Makem’s [22] approach. Part of the efficiency is due to the fact that different sizing metrics are used here. For each edge, only the edge length and the face widths are calculated without the need to calculate the thickness. No effort is spent on constructing three orthogonal vectors from the metric vectors to represent the principal axes of an ellipsoid. The characteristic length of a region is compared to the minimum circle containing the cross section to determine whether it is a long-slender region. In addition, when deciding the cutting face in [22], a chain of circles called “bracelet” is initiated at the midpoint of the shortest candidate edge. It is reformed at intervals along the edge in opposite direction away from the midpoint. The process terminates if the bracelet is broken and the position of the cutting face is determined. This process is time consuming. By moving the bracelet along the edge, it can only guarantee the continuity of the edges rather than the faces. For the approach described herein, the cutting faces are generated directly at the end points of the edges. After decomposition, the wall faces can be checked to avoid the existence of internal face loops, such as bosses, if necessary.
The creation of the cutting face has been considered carefully in this paper to determine whether an offset is required where the long-slender region meets the rest of the model. The decision of whether to make an offset of the cutting face is determined by the edge corner angle and the number of singularities on the wall faces of the long-slender region. An offset is made only when it is required to guarantee the resulting wall faces of the sweepable long-slender region will not contain any singularities.
It has been demonstrated that the DOF and analysis time can be significantly reduced by applying anisotropic hex elements in the thin-sheet and long-slender regions while similar accuracy can be achieved. The anisotropic geometrical characteristic of the identified long-slender regions can also facilitate the control of mesh element size and gradation so that the hex elements change from a highly stretched shape away from the interfaces to a size at the interface more compatible with the adjacent tet elements, as shown in Fig. 30. This ensures that transition elements at the interface have a proper aspect ratio and are, therefore, good quality. In future, an approach for automatically generating and sizing the hex-tet mixed mesh applied to complex thin-walled components will be developed for the decomposition provided by this work. A non-manifold model will be created to capture the interfaces between adjacent sub-volumes, which will be used to guarantee a conformal mesh.
6 Conclusions
This paper describes an improved approach for the automatic identification of the long-slender regions. It has been shown that:
-
New sizing metrics are used to identify the long-slender region, which has greatly simplified the process compared to existing techniques;
-
Procedures have been developed to assess if an offset is required at the ends of the long-slender region which terminate with complex geometry. The cutting faces are generated directly at the end of the long-slender region if no offset is required;
-
Significant DOF saving can be achieved by applying anisotropic hex elements to the identified long-slender region.
References
Sun L, Tierney CM, Armstrong CG, Robinson TT (2016) Automatic decomposition of complex thin walled CAD models for hexahedral dominant meshing. Proc Eng 163:225–237
Blacker T (1996) The cooper tool. In: 5th international meshing roundtable, pp 1–17
Knupp PM (1999) Applications of mesh smoothing: copy, morph, and sweep on unstructured quadrilateral meshes. Int J Numer Methods Eng 45(1):37–45
Staten ML, Canann SA, Owen SJ (1999) BMSweep: locating interior nodes during sweeping. Eng Comput 15(3):212–218
White DR, Saigal S, Owen SJ (2004) CCSweep: automatic decomposition of multi-sweep volumes. Eng Comput 20(3):222–236
Cook WA, Oakes WR (1982) Mapping methods for generating three-dimensional meshes. Comput Mech Eng 8:67–72
White DR, Mingwu L, Benzley SE, Sjaardema GD (1995) Automated hexahedral mesh generation by virtual decomposition. In 4th international meshing roundtable, pp 165–176
Price Ma, Armstrong CG, Sabin Ma (1995) Hexahedral mesh generation by medial surface subdivision: part I. Solids with convex edges. Int J Numer Methods Eng 38(19):3335–3359
Gregson J, Sheffer A, Zhang E (2011) All-hex mesh generation via volumetric polycube deformation. In: Computer graphics forum, vol 30(5). Wiley, pp 1407–1416
Kowalski N, Ledoux F, Frey P (2016) Smoothness driven frame field generation for hexahedral meshing. Comput Des 72:65–77
Li Y, Liu Y, Xu W, Wang W, Guo B (2012) All-hex meshing using singularity-restricted field. ACM Trans Graph 31(6):1
Nieser M, Reitebuch U, Polthier K (2011) Cubecover—parameterization of 3d volumes. Comput Graph Forum 30(5):1397–1406
Huang J, Tong Y, Wei H, Bao H (2011) Boundary aligned smooth 3D cross-frame field. ACM Trans Graph 30(6):143
Knupp PM (1998) Next-generation sweep tool: a method for generating all-hex meshes on two-and-one-half dimensional geometries. In: Proceedings of the 7th international meshing roundtable. pp 505–513
Scott MA, Benzley SE, Owen SJ (2006) Improved many-to-one sweeping. Int J Numer Methods Eng 65(3):332–348
Ruiz-Gironés E, Roca X, Sarrate J (2009) A new procedure to compute imprints in multi-sweeping algorithms. In: Proceedings of the 18th international meshing roundtable. pp 281–299
Lu Y, Gadh R, Tautges TJ (2001) Feature based hex meshing methodology: feature recognition and volume decomposition. Comput Des 33(3):221–232
Lu JHC, Song I, Quadros WR, Shimada K (2010) Pen-based user interface for geometric decomposition for hexahedral mesh generation. In: Proceedings of the 19th international meshing roundtable. pp 263–278
Wu H, Gao S (2014) Automatic swept volume decomposition based on sweep directions extraction for hexahedral meshing. Proc Eng 82:136–148
Boussuge F, Léon JC, Hahmann S, Fine L (2015) Idealized models for FEA derived from generative modeling processes based on extrusion primitives. Eng Comput 31(3):513–527
Robinson TT, Armstrong CG, Fairey R (2011) Automated mixed dimensional modelling from 2D and 3D CAD models. Finite Elem Anal Des 47(2):151–165
Makem JE, Armstrong CG, Robinson TT (2012) Automatic decomposition and efficient semi-structured meshing of complex solids. Eng Comput 30(3):345–361
Siemens plm software, “NX.” [Online]. http://www.plm.automation.siemens.com/en_us/products/nx/index.shtml. Accessed 4 June 2016
Armstrong CG, Fogg HJ, Tierney CM, Robinson TT (2015) Common themes in multi-block structured quad/hex mesh generation. Proc Eng 124:70–82
Do Carmo MP (1976) Differential geometry of curves and surfaces. Prentice-Hall International Inc., New Jersey
CRESCENDO, Collaborative and robust engineering using simulation capability enabling next design optimisation. [Online]. http://www.crescendo-fp7.eu/. Accessed 4 June 2016
Acknowledgements
The authors wish to acknowledge the financial support provided by Innovate UK: the work reported herein was funded via GHandI (TSB 101372), a UK Centre for Aerodynamics project. Figures 24e, f, 25 and 27 are created using Rolls-Royce models provided through the European Community’s Seventh Framework Programme (FP7/2007–2013) under Grant Agreement No. 234344 (http://www.crescendo-fp7.eu).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sun, L., Tierney, C.M., Armstrong, C.G. et al. An enhanced approach to automatic decomposition of thin-walled components for hexahedral-dominant meshing. Engineering with Computers 34, 431–447 (2018). https://doi.org/10.1007/s00366-017-0550-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00366-017-0550-x