1 Introduction and Main Results

Let \({\textsf {E}}\) be a compact subset of \({\mathbb {C}}\) with at least \(n+1\) points. The nth Chebyshev polynomial of \({\textsf {E}}\), denoted \(T_n^{\textsf {E}}\), is the unique monic polynomial of degree n which minimises the supremum norm on \({\textsf {E}}\). In other words, \(T_n^{\textsf {E}}\) is the polynomial

$$\begin{aligned} T_{n}^{\textsf {E}}(z) = z^{n}+\sum _{k=0}^{n-1}a_kz^k \end{aligned}$$
(1.1)

which satisfies

$$\begin{aligned} \Vert T_n^{\textsf {E}}\Vert _{\textsf {E}}{:=}\max _{z\in {\textsf {E}}} |T_n^{{\textsf {E}}}(z)|= \min _{b_0, b_1, \ldots , b_{n-1} \in {\mathbb {C}}} \max _{z\in {\textsf {E}}} \left| z^{n}+\sum _{k=0}^{n-1} b_k z^k\right| . \end{aligned}$$
(1.2)

Facts regarding existence and uniqueness of \(T_n^{\textsf {E}}\) can be found in, e.g., [33, 47]. See also [17, 20] for a recent account on the basic theory of Chebyshev polynomials. These polynomials were initially studied by Chebyshev [15, 16] in the case where \({\textsf {E}}=[-1,1]\). In this situation, he showed that the polynomials are explicitly given by the formula

$$\begin{aligned} T_n(x){:}{=}T_n^{[-1,1]}(x) = 2^{1-n}\cos \bigl (n\arccos (x)\bigr ),\quad |x|\le 1. \end{aligned}$$
(1.3)

This representation further hints at a property of the Chebyshev polynomials that holds for arbitrary compact subsets of the real line. A monic degree n polynomial, \(P_n\), is the Chebyshev polynomial of \({\textsf {E}}\subset {\mathbb {R}}\) if and only if there exist points \(x_0<x_1<\cdots <x_n\) in \({\textsf {E}}\) such that

$$\begin{aligned} P_n(x_k)=(-1)^{n-k}\Vert P_n\Vert _{\textsf {E}},\quad k=0, 1, \ldots , n. \end{aligned}$$
(1.4)

This characterising property of the Chebyshev polynomials is called alternation and one can use it to prove several facts concerning their asymptotic behaviour (see, e.g., [17, 18]).

It should be noted that alternation fails to hold for Chebyshev polynomials of non-real compact subsets of \({\mathbb {C}}\). Instead, the asymptotics of such polynomials is typically studied using potential theoretic methods. This is an approach dating back to Faber [23], Fekete [24], and Szegő [52]. Faber investigated Chebyshev polynomials by constructing trial polynomials, the so-called Faber polynomials, from the associated conformal map which maps the exterior of \({\textsf {E}}\) to the exterior of the closed unit disk, \(\overline{{\mathbb {D}}}\). Of course, the existence of this conformal map assumes that the complement of \({\textsf {E}}\) is simply connected on the Riemann sphere \(\overline{{\mathbb {C}}}:={\mathbb {C}}\cup \{\infty \}\). Throughout the paper, we shall make use of the following important notions

  • \(\text {Cap}({\textsf {E}})\), the logarithmic capacity of \({\textsf {E}}\)

  • \(G_{\textsf {E}}(\,\cdot \,){:}{=}G_{{\textsf {E}}}(\,\cdot , \infty )\), the Green’s function for \(\overline{{\mathbb {C}}}\setminus {\textsf {E}}\) with pole at \(\infty \)

  • \(\mu _{\textsf {E}}\), the equilibrium measure of \({\textsf {E}}\)

Recall also the relation

$$\begin{aligned} \int \log \vert x-z\vert \,d\mu _{\textsf {E}}(x)=G_{\textsf {E}}(z)+\log \text {Cap}({\textsf {E}}). \end{aligned}$$
(1.5)

For a more in depth account of potential theory, we refer the reader to, e.g., [8, 26, 28, 32, 38].

1.1 Widom Factors for \(T_n^{\textsf {E}}\)

One way of quantatively describing the norm of the Chebyshev polynomials using logarithmic capacity is via the Faber–Fekete–Szegő theorem which states that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert T_n^{{\textsf {E}}}\Vert _{\textsf {E}}^{1/n} = \text {Cap}({\textsf {E}}) \end{aligned}$$
(1.6)

for any compact set \({\textsf {E}}\subset {\mathbb {C}}\) (see, e.g., [38, Chapter 5.5]). This implies that \(\text {Cap}({\textsf {E}})^n\) is the leading order behaviour of \(\Vert T_n^{{\textsf {E}}}\Vert _{{\textsf {E}}}\), and (1.6) limits the way that the so-called Widom factors defined by

$$\begin{aligned} {\mathcal {W}}_{n,\infty }({\textsf {E}}) {:}{=} \frac{\Vert T_n^{\textsf {E}}\Vert _{\textsf {E}}}{\text {Cap}({\textsf {E}})^n} \end{aligned}$$
(1.7)

can grow as n increases. For a wide variety of sets, this quantity is known to be bounded in n and its asymptotic behaviour is of particular interest. See, e.g., [6, 7, 20] for more details.

Another classical result in the theory of Chebyshev polynomials is

Theorem

(Szegő, Schiefermayr) Let \({\textsf {E}}\subset {\mathbb {C}}\) be a compact set. Then

$$\begin{aligned} \Vert T_n^{\textsf {E}}\Vert _{\textsf {E}}\ge \text {Cap}({\textsf {E}})^n \end{aligned}$$
(1.8)

and if \({\textsf {E}}\subset {\mathbb {R}}\), we even have

$$\begin{aligned} \Vert T_n^{\textsf {E}}\Vert _{\textsf {E}}\ge 2\text {Cap}({\textsf {E}})^n. \end{aligned}$$
(1.9)

While (1.8) goes back to Szegő [52], the inequality in (1.9) is more recent and due to Schiefermayr [41]. We shall present a proof of these statements below. Partly because our method will be used in later parts of the paper and is much shorter than the one presented in [41], and partly for completeness. Our proof rests on the following formula for capacity of polynomial preimages.

Lemma

[38, Theorem 5.2.5] Let \({\textsf {E}}\) be a compact subset of \({\mathbb {C}}\) and suppose \(P(z) = \sum _{k=0}^{m}a_kz^k\) is a polynomial with \(a_m\ne 0\). If

$$\begin{aligned} {\textsf {E}}_P {:}{=} \bigl \{z:P(z)\in {\textsf {E}}\bigr \} = P^{-1}({\textsf {E}}), \end{aligned}$$
(1.10)

then

$$\begin{aligned} G_{{\textsf {E}}_P}(z) = \frac{1}{m}G_{\textsf {E}}\bigl (P(z)\bigr )\quad \text {and}\quad \text {Cap}({\textsf {E}}_P) = \left( \frac{\text {Cap}({\textsf {E}})}{|a_m|}\right) ^{1/m}. \end{aligned}$$
(1.11)

Proof of theorem

Let \({\textsf {E}}\subset {\mathbb {C}}\) be an arbitrary compact set. Clearly,

$$\begin{aligned} {\textsf {E}}\subset (T_n^{\textsf {E}})^{-1}\Big (\bigl \{z:|z|\le \Vert T_n^{{\textsf {E}}}\Vert _{{\textsf {E}}}\bigr \}\Big ). \end{aligned}$$

Applying (1.11) together with the facts that \(\text {Cap}\) is monotone with respect to set inclusion and a disk of radius \(r>0\) has capacity equal to r, we obtain that

$$\begin{aligned} \text {Cap}({\textsf {E}})\le \text {Cap}\Big (\bigl \{z:|z|\le \Vert T_n^{{\textsf {E}}}\Vert _{{\textsf {E}}}\bigr \}\Big )^{1/n} = \Vert T_n^{{\textsf {E}}}\Vert ^{1/n}. \end{aligned}$$
(1.12)

This proves (1.8).

If \({\textsf {E}}\subset {\mathbb {R}}\), then \(T_n^{{\textsf {E}}}\) is easily shown to have only real coefficients. Hence

$$\begin{aligned} {\textsf {E}}\subset (T_n^{\textsf {E}})^{-1}\Big (\bigl \{z:z\in \bigl [-\Vert T_n^{\textsf {E}}\Vert _{\textsf {E}},\Vert T_n^{{\textsf {E}}}\Vert _{\textsf {E}}\bigr ]\bigr \}\Big ). \end{aligned}$$

As the capacity of an interval [a, b] equals \({(b-a)}/{4}\), yet another application of (1.11) implies that

$$\begin{aligned} \text {Cap}({\textsf {E}})\le \text {Cap}\Big (\bigl \{z:z\in \bigl [-\Vert T_n^{\textsf {E}}\Vert _{\textsf {E}},\Vert T_n^{{\textsf {E}}}\Vert _{\textsf {E}}\bigr ]\bigr \}\Big )^{1/n} = \left( \frac{\Vert T_n^{\textsf {E}}\Vert _{\textsf {E}}}{2}\right) ^{1/n}, \end{aligned}$$
(1.13)

proving (1.9). \(\square \)

Remark

Note that the above theorem can be restated in terms of the Widom factors as

$$\begin{aligned} {\mathcal {W}}_{n,\infty }({\textsf {E}})\ge 1 \; \text { for } \; {\textsf {E}}\subset {\mathbb {C}}\end{aligned}$$
(1.14)

and

$$\begin{aligned} {\mathcal {W}}_{n,\infty }({\textsf {E}})\ge 2 \; \text { when } \; {\textsf {E}}\subset {\mathbb {R}}. \end{aligned}$$
(1.15)

The sets for which the Szegő lower bound (1.8) is saturated for some value of n were determined in [19]. With \(O\partial (\,\cdot \,)\) denoting the outer boundary and \(\partial {\mathbb {D}}\) the unit circle, the authors proved that

$$\begin{aligned} {\mathcal {W}}_{n,\infty }({\textsf {E}}) = 1 \quad \text {if and only if } \quad O\partial ({\textsf {E}}) =P^{-1}(\partial \mathbb {D}) \end{aligned}$$
(1.16)

for some polynomial P of degree n. Regarding Schiefermayr’s lower bound, it was proven in [56] (see also [19]) that for \({\textsf {E}}\subset {\mathbb {R}}\),

$$\begin{aligned} {\mathcal {W}}_{n,\infty }({\textsf {E}}) = 2\quad \text {if and only if }\quad {\textsf {E}}= P^{-1}\bigl ([-2,2]\bigr ) \end{aligned}$$
(1.17)

for some degree n polynomial P.

Now the question remains in which cases we have an asymptotic saturation of these lower bounds. More precisely, when does it happen that

$$\begin{aligned}\lim _{n\rightarrow \infty }{\mathcal {W}}_{n,\infty }({\textsf {E}}) = 1 \text { or }2?\end{aligned}$$

It is known that if \({\textsf {E}}\) is the closure of a Jordan domain with boundary curve of class \(C^{2+\epsilon }\) (i.e., its coordinates are \(C^{2+\epsilon }\) functionsFootnote 1 of arc length), then

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathcal {W}}_{n,\infty }({\textsf {E}})=1. \end{aligned}$$
(1.18)

This was first shown in the case where \({\textsf {E}}\) has analytic boundary by Faber [23] and then extended to the case where the boundary curve is of class \(C^{2+\epsilon }\) by Widom [59]. However, there may well be many other connected sets \({\textsf {E}}\subset {\mathbb {C}}\) for which (1.18) holds.

For \({\textsf {E}}\subset {\mathbb {R}}\), Totik [57] completely characterised the sets which asymptotically saturate the Schiefermayr lower bound (1.9). He proved that

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathcal {W}}_{n,\infty }({\textsf {E}})= 2 \end{aligned}$$
(1.19)

if and only if \({\textsf {E}}\) is an interval, in which case \({\mathcal {W}}_{n,\infty }({\textsf {E}}) = 2\) for every n.

One may ask — and this is a main point of the present article — if there are more subsets \({\textsf {E}}\subset {\mathbb {C}}\) for which (1.19) holds true. Widom [59] conjectured that any sufficiently nice set which contains an arc component should satisfy (1.19). However, this was shown to be false even in the case of Jordan arcs. In particular, Thiran and Detaille [55] observed that if \({\textsf {E}}_\alpha = \{z: |z|=1,\, |\arg z|\le \alpha \}\) with \(\alpha \in (0,\pi )\), then

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathcal {W}}_{n,\infty }({\textsf {E}}_\alpha )= 2\cos ^2\left( \alpha /4\right) <2. \end{aligned}$$
(1.20)

See also [22, 44, 45].

The aim of this article is to study sets \({\textsf {E}}\subset {\mathbb {C}}\) which satisfy (1.19) and investigate what properties may lie behind. First of all, by combining results of Stahl [51] and Alpan [4], we are able to prove the following result which essentially is a reformulation of [4, Theorem 1.3].

Theorem 1.1

Let \({\textsf {E}}\subset {\mathbb {C}}\) be a Jordan arc of class \(C^{2+\epsilon }\). Then

$$\begin{aligned} \limsup _{n\rightarrow \infty }{\mathcal {W}}_{n,\infty }({\textsf {E}})\le 2 \end{aligned}$$
(1.21)

and equality holds if and only if \({\textsf {E}}\) is a straight line segment.

In [4], Alpan showed that (1.21) is always satisfied and gave a condition for when equality holds true in terms of the boundary behaviour of the Green’s function. He also drew the conclusion that the inequality is strict if the arc fails to be analytic. Our contribution consists of showing that the only smooth arc for which equality holds is an interval. We show this using the S-property which was introduced and studied in detail by Stahl (see, e.g., [34, 48, 49, 51] and Definition 2.1 below). To be more precise, our proof hinges on the connection between the S-property and what are known as Chebotarev sets.

In this paper we shall exhibit several examples of sets \({\textsf {E}}\) satisfying (1.19) and one of the properties that these sets have in common, apart from being polynomial preimages of an interval, is the fact that they all satisfy the S-property. This suggests that the S-property could be of importance for a set \({\textsf {E}}\) to satisfy (1.19).

Fig. 1
figure 1

\({\textsf {E}}_2\), \({\textsf {E}}_5\) and \({\textsf {E}}_{11}\)

Full size image

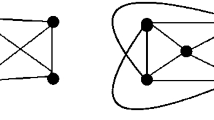
Our studies were initiated by the following family of examples, as illustrated in Fig. 1.

Theorem 1.2

For \(m\in {\mathbb {N}}\), let

$$\begin{aligned} {\textsf {E}}_m {:}{=} \bigl \{z: z^m\in [-2,2]\bigr \}. \end{aligned}$$
(1.22)

Then

$$\begin{aligned} {\mathcal {W}}_{mn,\infty }({\textsf {E}}_m)=2, \quad n\ge 1 \end{aligned}$$
(1.23)

and (1.19) holds true, that is,

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathcal {W}}_{n,\infty }({\textsf {E}}_m)= 2. \end{aligned}$$
(1.24)

In addition, \(n\mapsto {\mathcal {W}}_{2nm+l,\infty }({\textsf {E}}_m)\) is monotonically decreasing for \(1<{l}/{m}<2\). Moreover,

$$\begin{aligned} {\mathcal {W}}_{l,\infty }({\textsf {E}}_m) = 2^{l/m}, \quad 0<l<2m \end{aligned}$$
(1.25)

and, in particular,

$$\begin{aligned} {\mathcal {W}}_{2m-1,\infty }({\textsf {E}}_m) = 2^{2-1/m}\rightarrow 4 \; \text{ as } \; m\rightarrow \infty . \end{aligned}$$
(1.26)

Remark

Since \(\text {Cap}([-2,2]) = 1\), (1.11) implies that \(\text {Cap}({\textsf {E}}_m) = 1\) for all \(m\in {\mathbb {N}}\). Hence \({\mathcal {W}}_{n,\infty }({\textsf {E}}_m) = \Vert T_n^{{\textsf {E}}_m}\Vert _{{\textsf {E}}_m}\) for all \(n\ge 1\).

Based on numerical evidence, we conjecture that \(n\mapsto {\mathcal {W}}_{2nm+l,\infty }({\textsf {E}}_m)\) is monotonically increasing for \(0<{l}/{m}<1\). However, we have not yet been able to prove this. The latter part of the theorem shows that the limit in (1.24) by no means is uniform in m. It also exemplifies that no matter how large we take \(n\in {\mathbb {N}}\), there always exist a compact connected set \({\textsf {E}}\subset {\mathbb {C}}\) and \(l\ge n\) so that \({\mathcal {W}}_{l,\infty }({\textsf {E}})>4-\epsilon \).

Extremal polynomials of the sets \({\textsf {E}}_m\) were previously studied by Peherstorfer and Steinbauer [35]. They established a connection, for \(q\in [1, \infty )\), between \(L^q\) minimal polynomials on \({\textsf {E}}_m\) and specific weighted \(L^q\) minimal polynomials on [0, 1], using the canonical change of variables \(x=z^m\). In this paper, we will employ a similar change of variables, focusing on the case where \(q=\infty \). This approach allows us to establish a relationship between the Chebyshev polynomials of \({\textsf {E}}_m\) and weighted minimal polynomials on \([-1, 1]\).

Theorem 1.2 handles preimages of a line segment under monomials in the complex plane. The following result gives a complete picture for such preimages of arbitrary quadratic polynomials.

Theorem 1.3

Let \(P(z) = z^2+az+b\) for \(a, b \in {\mathbb {C}}\) and form \({\textsf {E}}_P {:}{=} \{z:P(z)\in [-2,2]\}\). Then

$$\begin{aligned} {\mathcal {W}}_{2n,\infty }({\textsf {E}}_P)=2, \quad n\ge 1 \end{aligned}$$
(1.27)

and

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathcal {W}}_{2n+1,\infty }({\textsf {E}}_P)= \sqrt{2\left| c+\sqrt{c^2-4}\right| }, \end{aligned}$$
(1.28)

where \(c = b-a^2/4\) and \(z+\sqrt{z^2-4}\) maps the exterior of \([-2,2]\) to the exterior of the closed disk of radius 2 centered at 0. In particular, for \(c\in [-2,2]\) we have

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathcal {W}}_{2n+1,\infty }({\textsf {E}}_P)= 2. \end{aligned}$$
(1.29)

Remark

By [42, Theorem 4] (see also [29, Proposition 3.3]), the preimage \(P^{-1}([-2,2])\) is connected if and only if it contains all zeros of \(P'\). In our setting, this implies that \({\textsf {E}}_P\) is connected precisely when \(c\in [-2,2]\) and hence

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathcal {W}}_{n,\infty }({\textsf {E}}_P) = 2 \end{aligned}$$
(1.30)

exactly in case \({\textsf {E}}_P\) is connected.

The result in (1.28) also illustrates that we can only hope for a universal upper bound on \({\mathcal {W}}_{n, \infty }({\textsf {E}})\) within the class of compact connected sets.

1.2 Orthogonal Polynomials with Respect to \(\mu _{\textsf {E}}\)

The Chebyshev polynomials are the monic polynomials minimising the \(L^\infty \) norm on a given compact set \({\textsf {E}}\subset {\mathbb {C}}\). The same investigation on minimal polynomials can be undertaken for any \(L^p\) norm. We shall in particular consider the sequence of monic orthogonal polynomials with respect to equilibrium measure \(\mu _{\textsf {E}}\). These are the polynomials

$$\begin{aligned} P_{n}^{\mu _{\textsf {E}}}(z)=z^{n}+\sum _{k=0}^{n-1}c_kz^k \end{aligned}$$
(1.31)

which satisfy

$$\begin{aligned} \int P_n^{\mu _{\textsf {E}}}(z)\overline{\displaystyle {P_m^{\mu _{\textsf {E}}}(z)}}\,d\mu _{{\textsf {E}}}(z) = C_n\cdot \delta _{n,m}, \end{aligned}$$
(1.32)

where \(C_n>0\) and \(\delta _{n,m}\) is the Kronecker delta. It is well-known and easy to prove that all \(P_{n}^{\mu _{\textsf {E}}}\) are minimal with respect to the \(L^2(\mu _{{\textsf {E}}})\)-norm in the sense that

$$\begin{aligned} \Vert P_{n}^{\mu _{\textsf {E}}}\Vert _{L^2(\mu _{\textsf {E}})}^2 {:}{=}\int |P_{n}^{\mu _{\textsf {E}}}(z)|^2 \,d\mu _{{\textsf {E}}}(z) = \min _{b_0, b_1, \ldots , b_{n-1}\in {\mathbb {C}}} \int \left| z^n+\sum _{k=0}^{n-1}b_kz^k\right| ^2d\mu _{{\textsf {E}}}(z).\nonumber \\ \end{aligned}$$
(1.33)

In line with (1.7), we define the Widom factors corresponding to the \(L^2\) minimisers on \({\textsf {E}}\) by

$$\begin{aligned} {\mathcal {W}}_{n,2}({\textsf {E}})&{:}{=} \frac{\Vert \displaystyle {P_n^{\mu _{\textsf {E}}}}\Vert _{L^2(\mu _{\textsf {E}})}}{\text {Cap}({\textsf {E}})^n}. \end{aligned}$$
(1.34)

The name is appropriate since Widom [59] gave a complete description of the asymptotics of \({\mathcal {W}}_{n,2}({\textsf {E}})\) in the case where \({\textsf {E}}\) is a finite union of Jordan curves and arcs of class \(C^{2+\epsilon }\). Recent results of Alpan and Zinchenko [5] suggest a relation between the asymptotics of \({\mathcal {W}}_{n,2}({\textsf {E}})\) and \({\mathcal {W}}_{n,\infty }({\textsf {E}})\). In fact, the method we will use to prove Theorem 1.2 relies on results of Bernstein [9, 10] where certain weighted Chebyshev polynomials are related to a class of orthogonal polynomials. This is what initially motivated our study of \({\mathcal {W}}_{n,2}({\textsf {E}}_m)\) and we have the following result.

Theorem 1.4

With \({\textsf {E}}_m\) as defined in (1.22), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathcal {W}}_{n,2}({\textsf {E}}_m)^2 = 2. \end{aligned}$$
(1.35)

Moreover, \(n\mapsto {\mathcal {W}}_{2nm+l,2}({\textsf {E}}_m)^2\) is monotonically increasing for \(0<{l}/{m}<1\) and monotonically decreasing for \(1<{l}/{m}<2\).

Exactly the same monotonicity along subsequences was observed numerically for \({\mathcal {W}}_{n,\infty }({\textsf {E}}_m)\). However, we can only prove the part concerning monotonic decrease in this setting. By relating Theorems 1.2 and 1.4, we get the following result which complements the results of [5].

Corollary 1.5

The Widom factors for \({\textsf {E}}_m\) satisfy that

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathcal {W}}_{n,2}({\textsf {E}}_m)^2 = \lim _{n\rightarrow \infty }{\mathcal {W}}_{n,\infty }({\textsf {E}}_m). \end{aligned}$$
(1.36)

Based on the results of [5], it was conjectured in [21] that if \({\textsf {E}}\) is a smooth Jordan arc, then

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathcal {W}}_{n,2}({\textsf {E}})^2 = \lim _{n\rightarrow \infty }{\mathcal {W}}_{n,\infty }({\textsf {E}}). \end{aligned}$$
(1.37)

It is known that (1.37) holds for straight line segments and circular arcs as in (1.20), see [21] and [5]. In our case we are not dealing with a single Jordan arc but rather a union of Jordan arcs. Nevertheless, our approach may still shed new light on the above conjecture.

1.3 Outline

This article is organised as follows. In Sect. 2 we discuss the S-property and the Chebotarev problem, and use these concepts to present a proof of Theorem 1.1. In Sect. 3 we consider Chebyshev polynomials on quadratic preimages of \([-2,2]\) and illustrate how Bernstein’s method for determining the asymptotic behaviour of weighted Chebyshev polynomials on an interval (summarised in the appendix) can be applied to solve problems in the complex plane. We specifically establish Theorem 1.2 for \(m=2\) and extend this result to Theorem 1.3, which completely describes the asymptotic behavior of the Widom factors for quadratic preimages of \([-2,2]\). The findings for \({\textsf {E}}_2\) are extended to the setting of all \({\textsf {E}}_m\) sets in Sect. 4, demonstrating the alternation properties of Chebyshev polynomials in this context and providing a complete proof of Theorem 1.2. Interestingly, the monotonicity result follows from transforming the problem to the unit circle and introducing appropriate trial polynomials, as outlined in Lemma 4.2.

In Sect. 5 we consider polynomials orthogonal with respect to equilibrium measure of \({\textsf {E}}_m\) and prove Theorem 1.4, that the associated Widom factors converge to 2. We also show that the numerically observed, and only partially proven, monotonic behavior of the corresponding Chebyshev norms holds for the orthogonal polynomials in this setting. Additional insight into this monotonicity is presented in Sect. 6, drawing upon conformal mappings and geometric considerations.

Ultimately, we address potential future research directions in Sect. 7. With Conjecture 7.1, we propose a potential connection between Shabat polynomial preimages and the convergence of Widom factors to 2. This conjecture finds support in numerical simulations. We hold the view that a fundamental prerequisite for sets to exhibit such Widom factors lies in the geometric S-property.

2 The S-Property and Chebotarev Sets

We now direct our focus towards compact sets \({\textsf {E}}\subset {\mathbb {C}}\) exhibiting a certain symmetry property which turns out to be of importance regarding the convergence behaviour \(\lim _{n\rightarrow \infty }{\mathcal {W}}_{n, \infty }({\textsf {E}})=2\). In fact, this is exactly what we will use to prove Theorem 1.1.

The symmetry property in question is called the S-property and was introduced by Stahl in the 1980s to study certain extremal domains in the complex plane. The “S” in the name is therefore ambiguous; it can be read as symmetry but also as Stahl. We will present a simplified version of the S-property, adapted to our needs, following [50, Definition 2]. For a more comprehensive exploration of its connection to extremal domains of meromorphic functions, we direct the reader to [48, 49, 51].

Definition 2.1

Let \({\textsf {E}}\subset {\mathbb {C}}\) be a compact set with \(\text {Cap}({\textsf {E}})>0\) and suppose \({\mathbb {C}}\setminus {\textsf {E}}\) is connected. Assume further that there exists a subset \({\textsf {E}}_0\subset {\textsf {E}}\) with \(\text {Cap}({\textsf {E}}_0) = 0\) such that

$$\begin{aligned} {\textsf {E}}\setminus {\textsf {E}}_0 = \bigcup _{i\in I}\gamma _i \end{aligned}$$
(2.1)

where the \(\gamma _i\)’s are disjoint open analytic Jordan arcs and \(I\subset {\mathbb {N}}\). Then \({\textsf {E}}\) is said to satify the S-property if

$$\begin{aligned} \frac{\partial G_{\textsf {E}}}{\partial n_+}(z) = \frac{\partial G_{\textsf {E}}}{\partial n_-}(z) \end{aligned}$$
(2.2)

holds for all \(z\in {\textsf {E}}\setminus {\textsf {E}}_0\), where \(n_+\) and \(n_-\) denote the unit normals from each side of the arcs.

Remark

The assumption of the arcs \(\gamma _i\) being analytic is redundant, as mild smoothness conditions coupled with the fulfillment of (2.2) imply the analyticity of these arcs. This observation is mentioned in [50] without providing a formal proof. The initial question to address in the context of reducing the smoothness of individual arcs pertains to the existence of the normal derivatives in (2.2). The proof of [58, Proposition 2.2] invokes the Kellogg–Warschawski theorem [37, Theorem 3.6] to establish that if the coordinates of the arcs are differentiable and their derivatives are Hölder continuous, then the normal derivatives of \(G_{\textsf {E}}\) exist along each \(\gamma _i\). Consequently, it is reasonable to discuss the fulfillment of (2.2) for arcs belonging to the class \(C^{2+\epsilon }\). In [4, Theorem 1.4], it is established that with this smoothness assumption, the arcs \(\gamma _i\) indeed become analytic when (2.2) is satisfied.

The concept of Chebotarev sets is closely related to the S-property. These sets are characterized by having minimal capacity while being constrained to include a specific collection of points. To elaborate, the Chebotarev problem, originally posed as a question to Pólya [36], revolves around the quest for the following set:

Definition 2.2

Given a finite number of points \(\alpha _1,\ldots ,\alpha _m\in {\mathbb {C}}\), the compact connected set \({\textsf {E}}\) that contains these points and has minimal logarithmic capacity among all such sets is called the Chebotarev set of \(\alpha _1,\ldots ,\alpha _m\). It is denoted by \({\textsf {E}}(\alpha _1,\dotsc ,\alpha _m)\).

That such sets exist and are unique was proven by Grötzsch [27]. He also characterised the Chebotarev sets in terms of the behaviour of certain quadratic differentials. Stahl [51, Theorem 11] proved that any solution to a Chebotarev problem must satisfy the S-property. In fact, he gave both necessary and sufficient conditions for a set to be a Chebotarev set in terms of the S-property and additional geometric conditions.

For further properties of Chebotarev sets, see, e.g., [31, Chapter 1]. The case of \(m=3\) is studied in detail in this monograph.

Interestingly, there is also a relation between Chebotarev sets and polynomial preimages of intervals. Schiefermayr [43] proved that if P is a polynomial and \(P^{-1}([-1,1])\) is connected, then this preimage is the solution to a Chebotarev problem. More specifically, if \(\alpha _1,\ldots ,\alpha _m\) is an enumeration of the distinct simple zeros of \(P^2-1\) then

$$\begin{aligned} P^{-1}([-1,1]) = {\textsf {E}}(\alpha _1,\dotsc ,\alpha _m). \end{aligned}$$
(2.3)

In particular, any such polynomial preimage satisfies the S-property.

By combining Stahl’s results on minimal capacity with recent results of Alpan, we can easily prove that equality is possible in (1.21) only for straight line segments. In this case, as we know, \({\mathcal {W}}_{n,\infty }({\textsf {E}})=2\) for every n.

Proof of Theorem 1.1

Let \({\textsf {E}}\) be a Jordan arc of class \(C^{2+\epsilon }\), connecting two complex points a and b. The fact that

$$\begin{aligned} \limsup _{n\rightarrow \infty }{\mathcal {W}}_{n,\infty }({\textsf {E}})\le 2 \end{aligned}$$
(2.4)

is precisely the content of [4, Theorem 1.3]. For equality to hold, it must be so that (2.2) holds at all interior points of the arc. As explained in the remark following Definition 2.1, this implies that \({\textsf {E}}\) is an analytic Jordan arc possessing the S-property. By [51, Theorem 11], \({\textsf {E}}\) is therefore the solution to the Chebotarev problem corresponding to the points a and b. Hence \({\textsf {E}}(a,b) = [a,b]\), where [a, b] denotes the straight line segment in \({\mathbb {C}}\) between a and b (see, e.g., [31]). This completes the proof.\(\square \)

In the remainder of this article, we will examine polynomial preimages of \([-2, 2]\). All the sets under consideration, provided they are connected, share the common feature of satisfying the S-property, making them minimal sets for a Chebotarev problem.

3 Quadratic Preimages

The general framework is sets of the form

$$\begin{aligned} {\textsf {E}}_m {:}{=} \bigl \{z: z^m\in [-2,2]\bigr \}. \end{aligned}$$
(3.1)

These are star-shaped connected sets which are invariant under rotations by \(\pi /m\) radians, see Fig. 1. Furthermore, [43, Theorem 2] implies that \({\textsf {E}}_m\) is the Chebotarev set corresponding to the collection of points

$$\begin{aligned} \bigl \{2^{1/m}e^{i \pi k/m}: k=1,\dotsc ,2m \bigr \}. \end{aligned}$$
(3.2)

To begin with, we consider the case where \(m=2\) even though our results are true for any \(m\in {\mathbb {N}}\). The motivation for this is that we more transparently can provide an intuition for the problem when \(m=2\). We end the section by also considering the setting of a general quadratic preimage.

Consider the set

$$\begin{aligned} {\textsf {E}}_2 = \bigl \{z:z^2\in [-2,2]\bigr \} = \bigl [-\sqrt{2},\sqrt{2}\,\bigr ]\cup i\bigl [-\sqrt{2},\sqrt{2}\,\bigr ], \end{aligned}$$
(3.3)

which has the shape of a “plus sign”. Equation (1.11) implies that the Green’s function for \(\overline{{\mathbb {C}}}\setminus {\textsf {E}}_2\) with pole at \(\infty \) is given by

$$\begin{aligned} G_{{\textsf {E}}_2}(z) = \frac{G_{[-2,2]}(z^2)}{2} = \log |z|+o(1),\quad z\rightarrow \infty . \end{aligned}$$
(3.4)

From this, and in line with (1.11), we also see that \(\text {Cap}({\textsf {E}}_2) = 1\) and hence

$$\begin{aligned} {\mathcal {W}}_{n,\infty }({\textsf {E}}_2) = \Vert T_n^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}. \end{aligned}$$
(3.5)

Recall now that a lemma from [30] states that if \({\textsf {E}}\) is an infinite compact set and P a polynomial of degree m with leading coefficient \(a_m\), then

$$\begin{aligned} T_{nm}^{P^{-1}({\textsf {E}})} = (T_n^{{\textsf {E}}}\circ P)/{a_m^{n}}. \end{aligned}$$
(3.6)

For a recent proof, see [19]. In our setting this immediately implies that

$$\begin{aligned} T_{2n}^{{\textsf {E}}_2}(z) = T_{n}^{[-2,2]}(z^2), \end{aligned}$$
(3.7)

as was also proven in [35]. Therefore, all the Chebyshev polynomials of even degree for \({\textsf {E}}_2\) can be determined explicitly. This further implies that we can calculate “half” of the norms, that is,

$$\begin{aligned} {\mathcal {W}}_{2n,\infty }({\textsf {E}}_2) = \Vert T_{2n}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2} = \Vert T_{n}^{[-2,2]}\Vert _{[-2,2]} = 2. \end{aligned}$$
(3.8)

What is left to determine are the Chebyshev polynomials of odd degree for \({\textsf {E}}_2\). The set \({\textsf {E}}_2\) is symmetric since it is invariant under rotations by \(\pi /2\) radians. More precisely,

$$\begin{aligned} i{\textsf {E}}_2 = \{iz: z\in {\textsf {E}}_2\} = {\textsf {E}}_2. \end{aligned}$$
(3.9)

Since we further have that \((-i)^nT_n^{{\textsf {E}}_2}(iz)\) is a monic polynomial of degree n and

$$\begin{aligned} \max _{z\in {\textsf {E}}_2}\left| (-i)^nT_{n}^{{\textsf {E}}_2}(iz)\right| = \max _{z\in {\textsf {E}}_2}\left| T_{n}^{{\textsf {E}}_2}(z)\right| , \end{aligned}$$
(3.10)

it follows by uniqueness of the Chebyshev polynomials that

$$\begin{aligned} (-i)^nT_{n}^{{\textsf {E}}_2}(iz) = T_{n}^{{\textsf {E}}_2}(z). \end{aligned}$$
(3.11)

From this relation we get certain conditions on the coefficients of \(T_{2n+1}^{{\textsf {E}}_2}\). Several of them will vanish and considering degrees of the form \(4n+l\) with \(l\in \{1, 3\}\), we have

$$\begin{aligned} \begin{aligned} T_{4n+l}^{{\textsf {E}}_2}(z)&= z^{4n+l}+\sum _{k=0}^{n-1}a_k z^{4k+l}, \quad a_k\in \mathbb {R}. \end{aligned} \end{aligned}$$
(3.12)

In particular, \(T_{4n+l}^{{\textsf {E}}_2}\) has a zero at the origin of order at least l. However, as we shall see below, this is the precise order of the zero.

Before stating our main characterisation of \(T_{4n+l}^{{\textsf {E}}_2}\), we recall that an alternating set for a function \(f:I\rightarrow \mathbb {C}\) is an ordered sequence of points \(\{x_k\}\subset I\) such that

$$\begin{aligned} f(x_k)= \sigma (-1)^{k}\Vert f\Vert _I,\quad |\sigma |=1. \end{aligned}$$
(3.13)

Lemma 3.1

For \(l\in \{1,3\}\), the Chebyshev polynomial \(T_{4n+l}^{{\textsf {E}}_2}\) is characterised by alternation in the following way:

  • \(T_{4n+l}^{{\textsf {E}}_2}\) has alternating sets consisting of \(n+1\) points on each of the sets \(i^{k}[ 0,\sqrt{2} ]\), \(k=0,1,2, 3.\)

  • \(T_{4n+l}^{{\textsf {E}}_2}\) can be represented as in (3.12).

Proof

We have already motivated why (3.12) should hold for \(T_{4n+l}^{{\textsf {E}}_2}\). This also implies that \(T_{4n+l}^{{\textsf {E}}_2}\) is purely real on the real axis and purely imaginary on the imaginary axis. Now, basic theory for Chebyshev polynomials implies that \(T_{4n+l}^{{\textsf {E}}_2}\) has at least \(4n+l+1\) extremal points (see, e.g., [33, Lemma 2.5.3]).

By (3.11), the number of extremal points on each of the rays

$$\begin{aligned} i^{k}[0,\sqrt{2}], \quad k=0, 1, 2, 3, \end{aligned}$$

coincide. For this reason, each ray must contain at least \(n+1\) extremal points. Again, because of (3.11), it is sufficient to focus on alternation along one of these rays. Therefore, we confine our analysis to the interval \([0,\sqrt{2}]\), where \(T_{4n+l}^{{\textsf {E}}_2}\) is real-valued.

If there were two adjacent extremal points on \([0,\sqrt{2}]\) with the same sign, then this would imply that the derivative \((T_{4n+l}^{{\textsf {E}}_2})'\) should have at least \(4\left( n+1\right) \ge 4n+l+1\) zeros. But this is a contradiction since the degree of the derivative is \(4n+l-1\).

To prove the other direction, we apply the intermediate value theorem in the following way. Suppose Q is a polynomial which can be represented as in (3.12). Then Q will be real-valued on the real line and imaginary-valued on the imaginary axis. Assume further that Q possesses alternating sets as in the statement of the lemma. If \(Q\ne T_{4n+l}^{{\textsf {E}}_2}\), then

$$\begin{aligned} \Vert Q\Vert _{{\textsf {E}}_2} > \Vert T_{4n+l}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2} \end{aligned}$$

and it follows from the intermediate value theorem that \(Q-T_{4n+l}^{{\textsf {E}}_2}\) must have a zero between any two consecutive points in the alternating sets for Q. But this amounts to at least \(4n+l\) zeros in addition to the zero of multiplicity l at 0. Hence the number of zeros would be greater than the degree of \(Q-T_{4n+l}^{{\textsf {E}}_2}\) which is impossible. Therefore, we conclude that \(Q = T_{4n+l}^{{\textsf {E}}_2}\). \(\square \)

One implication of this lemma is the fact that all the zeros of \(T_{2n+1}^{{\textsf {E}}_2}\) are simple, except the one at \(z=0\) for \(T_{4n+3}^{{\textsf {E}}_2}\). A further implication is that we can determine the first few Chebyshev polynomials for \({\textsf {E}}_2\) explicitly:

$$\begin{aligned} T_{1}^{{\textsf {E}}_2}(z)&= z, \end{aligned}$$
(3.14)
$$\begin{aligned} T_{3}^{{\textsf {E}}_2}(z)&=z^3, \end{aligned}$$
(3.15)
$$\begin{aligned} T_{5}^{{\textsf {E}}_2}(z)&= z^5-\frac{5\left( 3-\frac{15^{2/3}}{\root 3 \of {9+4\sqrt{6}}}+\root 3 \of {15(9+4\sqrt{6})}\right) ^4}{5184}z. \end{aligned}$$
(3.16)

Since already the expression for \(T_5^{{\textsf {E}}_2}\) gets rather complicated, there seems to be no simple closed form for \(T_{2n+1}^{{\textsf {E}}_2}\) when n is large.

Lemma 3.1 also implies that the image of \({\textsf {E}}_2\) under \(T_{2n+1}^{{\textsf {E}}_2}\) is again a plus-shaped set, namely

$$\begin{aligned} T_{4n+l}^{{\textsf {E}}_2}({\textsf {E}}_2) = \bigcup _{k=0}^{3}i^k\bigl [0,\Vert T_{4n+l}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}\bigr ] = \frac{\Vert T_{4n+l}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}}{\sqrt{2}}{\textsf {E}}_2. \end{aligned}$$
(3.17)

To further understand the behaviour of \(\Vert T_{4n+l}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}\), we introduce the preimage

$$\begin{aligned} {\textsf {E}}_2^{n, l} {:}{=} (T_{4n+l}^{{\textsf {E}}_2})^{-1}\bigl (T_{4n+l}^{{\textsf {E}}_2}({\textsf {E}}_2)\bigr ) = (T_{4n+l}^{{\textsf {E}}_2})^{-1}\left( \bigcup _{k=0}^{3}i^k\bigl [0,\Vert T_{4n+l}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}\bigr ]\right) \end{aligned}$$
(3.18)

which clearly contains \({\textsf {E}}_2\) as a subset. Due to the alternating property described in Lemma 3.1, we deduce that \({\textsf {E}}_{2}^{n,l}\) is connected and a finite union of Jordan arcs. These in turn intersect at the zeros of \(T_{4n+l}^{{\textsf {E}}_2}\). Moreover, \({\textsf {E}}_{2}^{n,l}\) is nothing but the Chebotarev set corresponding to the points

$$\begin{aligned} (T_{4n+l}^{{\textsf {E}}_2})^{-1}\Bigl (\bigl \{i^k\Vert T_{4n+l}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}:k=0,1,2,3\bigr \}\Bigr ). \end{aligned}$$
(3.19)

Applying (1.11) and using the fact that \(\text {Cap}(\alpha {\textsf {E}}) = |\alpha |\text {Cap}({\textsf {E}})\) for any \(\alpha \in {\mathbb {C}}\), we see that

$$\begin{aligned} \text {Cap}({\textsf {E}}_{2}^{n,l}) = \text {Cap}\left( \frac{\Vert T_{4n+l}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}}{\sqrt{2}}{\textsf {E}}_2\right) ^{1/{4n+l}} = \left( \frac{\Vert T_{4n+l}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}}{\sqrt{2}}\right) ^{1/{4n+l}}. \end{aligned}$$
(3.20)
Fig. 2
figure 2

The norm of \(T_n^{{\textsf {E}}_2}\) plotted as a function of the degree n. The three natural subsequences are highlighted in different colors (Color figure online)

Full size image

Rearranging this equality leads to the identity

$$\begin{aligned} \Vert T_{4n+l}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2} = \sqrt{2}\text {Cap}({\textsf {E}}_{2}^{n,l})^{4n+l}. \end{aligned}$$
(3.21)

Since \({\textsf {E}}_{2}^{n,l}\supset {\textsf {E}}_2\), we have \(\text {Cap}({\textsf {E}}_2^{n,l})\ge \text {Cap}({\textsf {E}}_2) = 1\) and conclude that

$$\begin{aligned} \Vert T_{4n+l}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}\ge \sqrt{2}. \end{aligned}$$
(3.22)

Note that the reasoning outlined above follows the same method of proof that we employed to prove the lower bounds of Szegő and Schiefermayr in the introduction. However, the conclusion is not equally strong. The lower bound in (3.22) is saturated for \(T_{1}^{{\textsf {E}}_2}\), but otherwise not. Using \(zT_{2n}^{{\textsf {E}}_2}(z)\) as a trial polynomial, we find that

$$\begin{aligned} \Vert T_{2n+1}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}\le \Vert zT_{2n}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}\le \sqrt{2}\Vert T_{2n}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2} = 2^{3/2}. \end{aligned}$$
(3.23)

This upper bound is only saturated by \(T_{3}^{{\textsf {E}}_2}\). To close the gap between \(\sqrt{2}\) and \(2^{3/2}\) in the limit as \(n\rightarrow \infty \), additional insight is needed. We shall settle this issue in the next subsection.

At this point, we would like to highlight an intriguing observation that, to date, remains partially open. Recall that the Remez algorithm [39, 40] uses the theory of alternation to numerically compute Chebyshev polynomials of real compact sets. This algorithm was generalised to the complex setting by Tang [54] and further refined by Modersitzki and Fischer [25]. Using an implementation of this generalised algorithm, we can compute the norms of the Chebyshev polynomials for degree up to at least 60. What materialised for \({\textsf {E}}_2\) is illustrated in Fig. 2. As we already know, \(\Vert T_{n}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}=2\) for all even n. For odd n, there are two natural subsequences counting modulo 4. It seems that \(n\mapsto \Vert T_{4n+1}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}\) is monotonically increasing, while \(n\mapsto \Vert T_{4n+3}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}\) appears to be monotonically decreasing. Unfortunately, we can only provide a proof for the latter.

Similar patterns, which align with Theorem 1.4 and are partially covered by Theorem 1.2, emerge for the general \({\textsf {E}}_m\) sets and for subsequences modulo 2m, as illustrated in Fig. 5.

3.1 A Related Weighted Problem and the Proof of Theorem 1.2 for \(m=2\)

Rather than employing (3.21) and attempting to directly estimate the capacity of \({\textsf {E}}_2^{n, l}\), we shall shift the minimax problem to a weighted problem on \({\mathbb {R}}\) which can, in turn, be solved using a method of Bernstein [9, 10].

Based on (3.12), the Chebyshev polynomials of odd degree for \({\textsf {E}}_2\) can be represented as

$$\begin{aligned} T_{4n+l}^{{\textsf {E}}_2}(z) = z^{4n+l}+\sum _{k=0}^{n-1}a_kz^{4k+l} = z^{l}\left( z^{4n}+\sum _{k=0}^{n-1}a_kz^{4k}\right) = z^lQ_{n,l}(z^4), \end{aligned}$$
(3.24)

where \(Q_{n,l}\) is a real monic polynomial of degree n. Note that \(Q_{n,l}\) has the property that it minimises

$$\begin{aligned} \max _{z\in {\textsf {E}}_2}| z^l | \bigl \vert Q_{n,l}(z^4) \bigr \vert \end{aligned}$$
(3.25)

among all monic polynomials of degree n. Since \(|z^{1/4}|\) is single-valued, we can change the variables via the transformation \(x = z^4/2-1\) and obtain that \(Q_{n,l}\) minimises

$$\begin{aligned} \max _{x\in [-1,1]}2^{l/4}(x+1)^{{l}/{4}}\left| Q_{n,l}\bigl (2(x+1)\bigr )\right| . \end{aligned}$$
(3.26)

Put differently, and noting that \(2^{-n} Q_{n,l} (2(x+1) )\) is monic, we see that

$$\begin{aligned} \Vert T_{4n+l}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2} = 2^{n+{l}/{4}} \min _{b_0, b_1, \ldots , b_{n-1}\in {\mathbb {R}}} \max _{x\in [-1,1]}(x+1)^{{l}/{4}}\left| x^n+\sum _{k=0}^{n-1} b_k x^k \right| . \end{aligned}$$
(3.27)

In the case of \(l=0\), we are back at the classical problem solved by Chebyshev and the polynomials \(T_n\) of (1.3). For \(l=2\), the solution is given by the so-called Chebyshev polynomials of the third kind, denoted \(V_n\). This is easily seen by noting that

$$\begin{aligned} (x+1)^{1/2} V_n(x)=\sqrt{2} \cos \bigl ( (n+1/2)\arccos (x)\bigr ) \end{aligned}$$
(3.28)

oscillates on \([-1, 1]\) between precisely \(n+1\) extrema of equal magnitude. However, we are interested in the cases \(l=1, 3\) where no such simple formulas seem to be available.

The key is to recall that \(T_n\) and \(V_n\) are also orthogonal polynomials. Both are special cases of the Jacobi polynomials \(P_n^{(\alpha , \beta )}\) which have been studied in detail and are orthogonal with respect to \((1-x)^\alpha (1+x)^\beta \) on \([-1, 1]\). If we have a non-negative weight function w defined on \([-1, 1]\), we will use the notation \({T_n^{w}}\) to represent the minimiser of

$$\begin{aligned} \max _{x\in [-1,1]}w(x)|P_n(x)|, \end{aligned}$$
(3.29)

where \(P_n\) ranges over all monic polynomials of degree n. This minimizer is uniquely defined for sufficiently large n under the conditions that w does not vanish at infinitely many points and wP is bounded for some polynomial P.

A naive comparison of the \(L^\infty \) and \(L^2\) norms suggests that \({T_n^w}\) could be related to the monic orthogonal polynomials with respect to \(w(x)^2/\sqrt{1-x^2}\) on \([-1,1]\). In our setting, the weight is given by

$$\begin{aligned} w_l(x)=(x+1)^{l/4} \end{aligned}$$
(3.30)

and we thus search for a relation between \({T_n^{w_l}}\) and \(P_n^{(-1/2, \,\beta _l)}\) for \(\beta _l=(l-1)/2\). In special cases (such as \(l=0, 2\)) we have an exact match and the polynomials coincide. But even for general l, there are striking similarities between the polynomials. In [9], Bernstein proved that \(w_l P_n^{(-1/2, \, \beta _l)}\) is asymptotically alternating on \([-1,1]\) as \(n\rightarrow \infty \) and because of that, \(P_n^{(-1/2, \, \beta _l)}\) are excellent trial polynomials when studying the limit of \(\Vert w_l T_n^{w_l}\Vert _{[-1,1]}\).

We shall formulate Bernstein’s full result below. As the proof is only available in French or Russian, we decided to include a detailed review of this method in the appendix. While our presentation primarily adheres to Bernstein’s original proof, we are able to streamline some arguments by integrating findings from Achieser and Chebyshev alongside Bernstein’s work.

Theorem 3.2

(Bernstein [10]) Suppose \(\alpha _k\in \mathbb {R}\) and \(b_k\in [-1,1]\) for \(k=0, 1, \ldots , m\). Consider a weight function \(w:[-1,1]\rightarrow [0,\infty )\) of the form

$$\begin{aligned} w(x) = w_0(x)\prod _{k=0}^{m}|x-b_k|^{\alpha _k}, \end{aligned}$$
(3.31)

where \(w_0\) is Riemann integrable and satisfies \(1/M \le w_0(x) \le M\) for some constant \(M\ge 1\). Then

$$\begin{aligned} \Vert w T_n^w \Vert _{[-1, 1]}= 2^{1-n}\exp \left\{ \frac{1}{\pi }\int _{-1}^{1} \frac{\log w(x)}{\sqrt{1-x^2}}dx\right\} \bigl (1+o(1)\bigr ) \end{aligned}$$
(3.32)

as \(n\rightarrow \infty \).

With Bernstein’s theorem at hand, we can now prove Theorem 1.2. We isolate the following lemma since it will be used multiple times in the rest of the article.

Lemma 3.3

For any \(z\in {\mathbb {C}}\), we have

$$\begin{aligned} \frac{1}{\pi }\int _{-1}^{1}\frac{\log |x-z|}{\sqrt{1-x^2}}dx = \log \frac{\left| z+\sqrt{z^2-1}\right| }{2}, \end{aligned}$$
(3.33)

where \(z+\sqrt{z^2-1}\) maps \({\mathbb {C}}\setminus [-1,1]\) conformally onto \({\mathbb {C}}\setminus \overline{{\mathbb {D}}}\). In particular, for \(z\in [-1,1]\) the integral is constantly equal to \(-\log 2\).

Proof

Recall that the Green’s function for \(\overline{{\mathbb {C}}}\setminus [-1,1]\) with pole at \(\infty \) is given by

$$\begin{aligned} G_{[-1,1]}(z) = \log \left| z+\sqrt{z^2-1}\right| . \end{aligned}$$
(3.34)

Since the integral on the left-hand side of (3.33) is nothing but the potential for the equilibrium measure of \([-1, 1]\), we conclude that

$$\begin{aligned} \frac{1}{\pi }\int _{-1}^{1}\frac{\log |x-z|}{\sqrt{1-x^2}}dx =G_{[-1,1]}(z)+\log \text {Cap}\bigl ([-1,1]\bigr )=\log \frac{\left| z+\sqrt{z^2-1}\right| }{2} \nonumber \\ \end{aligned}$$
(3.35)

for \(z\notin [-1,1]\). If instead \(z \in [-1,1]\), we find by continuity of \(G_{[-1,1]}\) on \({\mathbb {C}}\) and monotone convergence that

$$\begin{aligned} \frac{1}{\pi }\int _{-1}^{1}\frac{\log |x-z|}{\sqrt{1-x^2}}dx&= \lim _{\epsilon \downarrow 0}\frac{1}{\pi }\int _{-1}^{1}\frac{\log |x-(z+i\epsilon )|}{\sqrt{1-x^2}}dx\\&= \lim _{\epsilon \downarrow 0}\log \frac{\left| (z+i\epsilon )+\sqrt{(z+i\epsilon )^2-1}\right| }{2}\\&=\log \frac{\left| z+\sqrt{z^2-1}\right| }{2} = -\log 2. \end{aligned}$$

This completes the proof. \(\square \)

We are now in position to prove the limiting result for \({\textsf {E}}_2\). As we shall see in Sect. 4, the method of proof actually handles all cases in Theorem 1.2.

Proof of Theorem 1.2 for \(m=2\)

It follows directly from (3.7) that (1.23) holds in this case. To see that (1.24) is valid, we let \(w_l(x) = (x+1)^{{l}/{4}}\) with \(l=1,3\). Theorem 3.2 implies that

$$\begin{aligned} \Vert w_l T_n^{w_l}\Vert _{[-1,1]} = 2^{1-n}\exp \left\{ \frac{l}{4\pi }\int _{-1}^{1}\frac{\log (x+1)}{\sqrt{1-x^2}}dx\right\} \bigl (1+o(1)\bigr ) \end{aligned}$$
(3.36)

as \(n\rightarrow \infty \). Applying Lemma 3.3 gives us that the the exponential on the right-hand side reduces to

$$\begin{aligned} \exp \left\{ \frac{l}{4}\cdot \log \frac{1}{2}\right\} = 2^{-{l}/{4}}. \end{aligned}$$
(3.37)

By (3.27), we therefore find that

$$\begin{aligned} \Vert T_{4n+l}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2} = 2^{n+{l}/{4}}\Vert w_l T_n^{w_l}\Vert _{[-1,1]} = 2\bigl (1+o(1)\bigr ) \end{aligned}$$
(3.38)

as \(n\rightarrow \infty \). Recalling that (3.5) holds, since \(\text {Cap}({\textsf {E}}_2) = 1\), this proves that \({\mathcal {W}}_{n,\infty }({\textsf {E}}_2)\rightarrow 2\) as \(n\rightarrow \infty \). \(\square \)

We will furnish a proof of (1.25) and the assertion regarding monotonicity in Sect. 4.

3.2 General Quadratic Preimages

We proceed by considering general quadratic preimages of \([-2, 2]\) and show that our method can be applied to this case as well. Of course, such preimages need not be connected and we should not expect the Widom factors to always converge to 2.

As in Theorem 1.3, we shall consider sets of the form

$$\begin{aligned} {\textsf {E}}_P=\bigl \{z: P(z)\in [-2,2]\bigr \}, \end{aligned}$$
(3.39)

where \(P(z)=z^2+az+b\) and \(a,b\in \mathbb {C}\). Now, let us present a proof of this result.

Proof of Theorem 1.3

By (1.11), we have \(\text {Cap}({\textsf {E}}_P) = 1\) and thus

$$\begin{aligned} {\mathcal {W}}_{n,\infty }({\textsf {E}}_P) = \Vert T_{n}^{{\textsf {E}}_P}\Vert _{{\textsf {E}}_P}. \end{aligned}$$
(3.40)

The first part of the theorem (i.e., (1.27) for even degree) is easily handled by (3.6). In order to prove (1.28), we note that

$$\begin{aligned} z^2+az+b = \left( z+\frac{a}{2}\right) ^2+c, \quad c=b-a^2/4. \end{aligned}$$
(3.41)

Therefore, it suffices to consider the case of

$$\begin{aligned} {\textsf {E}}_{P_c} = \bigl \{z: z^2+c\in [-2,2]\bigr \}. \end{aligned}$$
(3.42)

As \(z\in {\textsf {E}}_{P_c}\) if and only if \(-z\in {\textsf {E}}_{P_c}\), we deduce that

$$\begin{aligned} T_{2n+1}^{{\textsf {E}}_{P_c}}(z)=z^{2n+1}+\sum _{k=0}^{n-1}a_kz^{2k+1}, \quad a_k\in {\mathbb {C}}. \end{aligned}$$
(3.43)

Hence, since \(|\sqrt{z}|=\vert z\vert ^{1/2}\) is single-valued, we can apply the change of variables \(x = (z^2+c)/2\) leading to

$$\begin{aligned} \Vert T_{2n+1}^{{\textsf {E}}_{P_c}}\Vert _{{\textsf {E}}_{P_c}} = 2^{n+{1}/{2}}\min _{b_0, b_1, \ldots , b_{n-1}\in \mathbb {R}} \max _{x\in [-1,1]}\sqrt{\vert x-c/2 \vert } \left| x^n +\sum _{k=0}^{n-1}b_kx^k\right| . \end{aligned}$$
(3.44)
Fig. 3
figure 3

The set \({\textsf {E}}_{P_{c}}\) together with the norms of \(T_n^{{\textsf {E}}_{P_{c}}}\) for \(c = -3/2\)

Full size image
Fig. 4
figure 4

The set \({\textsf {E}}_{P_{c}}\) together with the norms of of \(T_n^{{\textsf {E}}_{P_{c}}}\) for \(c = i/2\)

Full size image

Since the weight function \(\sqrt{\vert x- c/2\vert }\) is of the form (3.31) — in fact, we only need \(w_0\) for \(c\notin [-2, 2]\) — Theorem 3.2 implies that

$$\begin{aligned} \Vert T_{2n+1}^{{\textsf {E}}_{P_c}}\Vert _{{\textsf {E}}_{P_c}}= 2^{3/2}\exp \left\{ \frac{1}{2\pi }\int _{-1}^{1}\frac{\log |x-c/2|}{\sqrt{1-x^2}}dx\right\} \bigl (1+o(1)\bigr ) \end{aligned}$$
(3.45)

as \(n\rightarrow \infty \). Using Lemma 3.3 to rewrite the exponential term, we conclude that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert T_{2n+1}^{{\textsf {E}}_{P_c}}\Vert _{{\textsf {E}}_{P_c}} = 2^{3/2}\cdot \sqrt{\frac{\bigl \vert {c}/{2}+\sqrt{\left( {c}/{2}\right) ^2-1}\bigr \vert }{2}} = \sqrt{2\left| c+\sqrt{c^2-4}\right| }\qquad \quad \end{aligned}$$
(3.46)

and the proof is complete. \(\square \)

Remark

As the attentive reader may have noticed, we employ a different change of variables in the proof of Theorem 1.3 compared to what is used for \({\textsf {E}}_2\). This is because we no longer have the same degree of symmetry at our disposal. In principle, one could have applied the change of variables \(x=z^2/2\) for \({\textsf {E}}_2\) as well. However, it seems more appropriate to leverage all the available structure, especially considering the distinct behavior of \(\Vert T_{4n+l}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}\) for \(l=1, 3\).

As pointed out in the introduction, \({\textsf {E}}_P\) is only connected when \(c\in [-2, 2]\). For otherwise the critical value of \(z^2+c\) lies outside \([-2, 2]\). The corresponding sets have the shape of a “stretched plus” and we appear to loose the monotonicity of

$$\begin{aligned} n \mapsto \Vert T_{4n+l}^{{\textsf {E}}_P} \Vert _{{\textsf {E}}_P}, \quad l=1, 3 \end{aligned}$$
(3.47)

whenever \(c\ne 0\), see Fig. 3. For \(c\in {\mathbb {R}}\setminus [-2, 2]\), the set \({\textsf {E}}_P\) is either purely real or purely imaginary and consists of two disjoint intervals of the same length. This case is well-understood and the fact that \(n\mapsto {\mathcal {W}}_{n, \infty }({\textsf {E}}_P)\) is asymptotically periodic goes back to Achieser [1, 2]. Remarkably, this pattern persists for all non-real values of c where \({\textsf {E}}_P\) comprises two disjoint analytic Jordan arcs of opposite sign. See Fig. 4 for such an example including the corresponding norms.

4 General m-Stars

The aim of this section is to generalise the content of Sect. 3 to the general setting of \(m\ge 2\) and in particular prove Theorem 1.2. As the strategy is very similar, we shall not provide all details in the proof. Let us first state the alternation result that still holds in this setting.

Lemma 4.1

For \(n,l\in \mathbb {N}\) and \(0\le l<2m\), the polynomial \(T_{2nm+l}^{{\textsf {E}}_m}\) is characterised by the following two properties:

  • for \(x\in [0,2^{1/m}]\) and \(k=0, 1, \ldots , 2m-1\), the polynomial \(T_{2nm+l}^{{\textsf {E}}_m}(e^{i\pi k/m} x)\) has an alternating set consisting of \(n+1\) points,

  • \(T_{2nm+l}^{{\textsf {E}}_m}\) is of the form

    $$\begin{aligned} T_{2nm+l}^{{\textsf {E}}_m}(z) = z^{2nm+l}+\sum _{k=0}^{n-1}a_{2km+l}z^{2km+l}, \quad a_{2km+l}\in {\mathbb {R}}. \end{aligned}$$
    (4.1)

Proof

We first show that \(T_{2nm+l}^{{\textsf {E}}_m}\) can be represented as in (4.1). Since \(z\in {\textsf {E}}_m\) if and only if \(e^{i\pi /m}z\in {\textsf {E}}_m\), we find that

$$\begin{aligned} \max _{z\in {\textsf {E}}_m}\left| T_{2nm+l}^{{\textsf {E}}_m}(e^{i\pi /m}z)\right| = \max _{z\in {\textsf {E}}_m}\left| T_{2nm+l}^{{\textsf {E}}_m}(z)\right| . \end{aligned}$$
(4.2)

By comparing leading coefficients and referring to the uniqueness of Chebyshev polynomials, we conclude that

$$\begin{aligned} T_{2nm+l}^{{\textsf {E}}_m}(e^{i\pi /m}z) = e^{2\pi i n}e^{i\pi l/m}T_{2nm+l}^{{\textsf {E}}_m}(z). \end{aligned}$$
(4.3)

Hence, by writing

$$\begin{aligned} T_{2nm+l}^{{\textsf {E}}_m}(z) = z^{2nm+l}+\sum _{k=0}^{2nm+l-1}a_kz^{k}, \end{aligned}$$
(4.4)

we see that

$$\begin{aligned} e^{i\pi (k-l)/m}a_k=a_k. \end{aligned}$$
(4.5)

For \(a_k\) to be non-zero, it is thus necessary that \(e^{i\pi (k-l)/m}=1\). In other words, \(k=2mj+l\) for some integer j. We also note that \({\textsf {E}}_m\) is conjugate symmetric in the sense that \(z\in {\textsf {E}}_m\) if and only if \(\overline{z}\in {\textsf {E}}_m\). This implies that \(a_k\in \mathbb {R}\) for all k.

To prove the alternating property, one argues in the same way as in Lemma 3.1 and we leave the details to the reader. \(\square \)

There is a certain overlap between the Chebyshev polynomials corresponding to different \({\textsf {E}}_m\) sets. Indeed, for \(m, k\in {\mathbb {N}}\) we have

$$\begin{aligned} {\textsf {E}}_{mk} = \bigl \{z:z^{mk}\in [-2,2]\bigr \} = \bigl \{z: z^k\in {\textsf {E}}_m\bigr \} \end{aligned}$$
(4.6)

and we thus gather from (3.6) that

$$\begin{aligned} T_{kn}^{{\textsf {E}}_{mk}}(z) = T_{n}^{{\textsf {E}}_m}(z^k), \quad n\ge 1. \end{aligned}$$
(4.7)

This can also be proven directly using Lemma 4.1 which we now briefly illustrate. Due to (4.1), we have

$$\begin{aligned} T_{k(2nm+l)}^{{\textsf {E}}_{mk}}(z) = (z^k)^lQ(z^k), \quad 0\le l<2m, \end{aligned}$$
(4.8)

where Q is a monic polynomial of degree 2nm. Since \(z^k\) maps \({\textsf {E}}_{mk}\) onto \({\textsf {E}}_m\), we conclude that Q is the minimal monic polynomial for

$$\begin{aligned} \min _{b_0,b_1,\dotsc ,b_{2nm-1}\in {\mathbb {R}}}\max _{z\in {\textsf {E}}_m}\left| z^l\left( z^{2nm}+\sum _{j=0}^{2nm-1}b_{j}z^{j}\right) \right| . \end{aligned}$$
(4.9)

But this expression is minimised by \(T_{2nm+l}^{{\textsf {E}}_m}\) and hence

$$\begin{aligned} T_{k(2nm+l)}^{{\textsf {E}}_{mk}}(z) = T_{2nm+l}^{{\textsf {E}}_m}(z^k), \quad n\ge 1. \end{aligned}$$
(4.10)

As a consequence of (4.10), we see that \(\Vert T_{k(2nm+l)}^{{\textsf {E}}_{mk}}\Vert _{{\textsf {E}}_{mk}}=\Vert T_{2nm+l}^{{\textsf {E}}_m}\Vert _{{\textsf {E}}_m}\) for all \(n\ge 1\). Monotonicity of one of these subsequences therefore implies monotonicity of the other.

As for notation, let \(T_n^{(\alpha ,\beta )}\) denote \(T_n^w\) where

$$\begin{aligned} w(x):=w^{(\alpha , \beta )}(x)= (1-x)^\alpha (1+x)^\beta ,\quad x\in [-1,1]. \end{aligned}$$
(4.11)

Note that \(w^{(\alpha , \beta )}(-x)=w^{(\beta , \alpha )}(x)\), and consequently

$$\begin{aligned} T_n^{(\alpha , \beta )}(-x)=(-1)^nT_n^{(\beta , \alpha )}(x). \end{aligned}$$
(4.12)

Regarding monotonicity, we have the following result:

Lemma 4.2

Let \(T_n^{(\alpha , \beta )}\) be defined as above and suppose that \(\alpha =0\) or 1/2. Then the sequence

$$\begin{aligned} n\mapsto 2^n \Vert w^{(\alpha ,\beta )} T_n^{(\alpha , \beta )} \Vert _{[-1, 1]} \end{aligned}$$
(4.13)

is constant for \(\beta =1/2\) and monotonically decreasing for \(\beta >1/2\).

Proof

The idea is to utilize the recently obtained results from [11] and relate the minimax problem at hand to a corresponding problem on the unit circle. By combining [11, Theorem 1] and [11, Theorem 6], we find that

$$\begin{aligned} 2^{n+\alpha } \Vert w^{(\alpha , 0)} T_n^{(\alpha , 0)} \Vert _{[-1, 1]}= 2\min _{a_0, a_1, \ldots , a_{2n-1}\in {\mathbb {C}}} \max _{|z|=1} |z-1|^{2\alpha -1} \left| z^{2n}+\sum _{k=0}^{2n-1} a_k z^k \right| \nonumber \\ \end{aligned}$$
(4.14)

for any \(\alpha \ge 1/2\). Since \(T_n^{\partial {\mathbb {D}}}(z)=z^n\), this sequence is trivially constant when \(\alpha =1/2\). By multiplying by \(z^2\), we infer that

$$\begin{aligned}&\max _{|z|=1} |z-1|^{2\alpha -1} \left| z^{2n}+\sum _{k=0}^{2n-1} a_k z^k \right| = \max _{|z|=1} |z-1|^{2\alpha -1} \left| z^2 \left( z^{2n}+\sum _{k=0}^{2n-1} a_k z^k \right) \right| \\&\quad \ge \min _{a_0, a_1, \ldots , a_{2n+1}\in {\mathbb {C}}} \max _{|z|=1} |z-1|^{2\alpha -1} \left| z^{2(n+1)}+\sum _{k=0}^{2n+1} a_k z^k \right| \end{aligned}$$

and hence it follows that the right-hand side of (4.14) is decreasing in n for \(\alpha >1/2\).

We can also deduce from [11, Theorems 1 and 6] that

$$\begin{aligned} 2^{n+\alpha +1/2} \Vert w^{(\alpha , 1/2)} T_n^{(\alpha , 1/2)} \Vert _{[-1, 1]}= 2\min _{a_0, a_1, \ldots , a_{2n}\in {\mathbb {C}}} \max _{|z|=1} |z-1|^{2\alpha -1} \left| z^{2n+1}+\sum _{k=0}^{2n} a_k z^k \right| ,\nonumber \\ \end{aligned}$$
(4.15)

again for \(\alpha \ge 1/2\). A similar procedure applies in this case. The statement in the lemma follows by interchanging \(\alpha \) and \(\beta \), keeping (4.12) in mind. \(\square \)

We are now in position to prove Theorem 1.2 in full generality. Recall that \(\text {Cap}({\textsf {E}}_m) = 1\) as a consequence of (1.11).

Proof of Theorem 1.2

The proof of (1.23) follows from (4.7) if we interchange m and k and then set \(k=1\). In order to prove (1.24), it suffices to show that \({\mathcal {W}}_{2nm+l, \infty }({\textsf {E}}_m)\rightarrow 2\) as \(n\rightarrow \infty \) for each \(l\in \{1, \dotsc , m-1, m+1, \dotsc , 2\,m-1\}\). We thus fix \(l<2\,m\) (with \(l\ne m\)) and apply the change of variables \(x = z^{2m}/2-1\) in (4.1) to obtain that

$$\begin{aligned} \Vert T_{2nm+l}^{{\textsf {E}}_m}\Vert _{{\textsf {E}}_m} = 2^{n+{l}/{2m}} \min _{b_0, b_1, \ldots , b_{n-1}\in {\mathbb {R}}} \max _{x\in [-1,1]} |x+1|^{{l}/{2m}}\left| x^n+\sum _{k=0}^{n-1}b_kx^k\right| ,\nonumber \\ \end{aligned}$$
(4.16)

recalling that \(|z^{1/2m}|\) is single-valued. Theorem 3.2 gives us that the minimum on the right-hand side behaves like

$$\begin{aligned} 2^{1-n}\exp \left\{ \frac{l}{2\pi m}\int _{-1}^{1}\frac{\log |x+1|}{\sqrt{1-x^2}} dx\right\} \bigl (1+o(1)\bigr ) \end{aligned}$$
(4.17)

as \(n\rightarrow \infty \), and Lemma 3.3 implies that

$$\begin{aligned} \exp \left\{ \frac{l}{2\pi m}\int _{-1}^{1}\frac{\log |x+1|}{\sqrt{1-x^2}}dx\right\} = 2^{-{l}/{2m}}. \end{aligned}$$
(4.18)

Combining these formulas yields

$$\begin{aligned} \Vert T_{2nm+l}^{{\textsf {E}}_m}\Vert _{{\textsf {E}}_m} = 2\bigl (1+o(1)\bigr ) \end{aligned}$$
(4.19)

as \(n\rightarrow \infty \). Since \(\text {Cap}({\textsf {E}}_m) = 1\), it readily follows that \({\mathcal {W}}_{2nm+l, \infty }({\textsf {E}}_m) \rightarrow 2\) as \(n\rightarrow \infty \) and this proves (1.24).

The statement on monotonicity follows directly from Lemma 4.2. By (4.16), we have

$$\begin{aligned} \Vert T_{2nm+l}^{{\textsf {E}}_m}\Vert _{{\textsf {E}}_m} = 2^{n+{l}/{2m}} \Vert w^{(0, \, l/2m)} T_n^{(0, \, l/2m)} \Vert _{[-1, 1]} \end{aligned}$$
(4.20)

and thus \(n\mapsto {\mathcal {W}}_{2nm+l, \infty }({\textsf {E}}_m)\) is monotonically decreasing for \(l/2m>1/2\), that is, \(m<l<2m\).

Fig. 5
figure 5

The norms of \(\Vert T_{6n+l}^{{\textsf {E}}_3}\Vert _{{\textsf {E}}_3}\) for \(0\le n\le 4\) and \(0\le l \le 5\) (Color figure online)

Full size image

To prove (1.25), we simply note that the representation in (4.1) implies that \(T_{l}^{{\textsf {E}}_m}(z) = z^l\) for all \(l<2\,m\) so that

$$\begin{aligned} {\mathcal {W}}_{l, \infty }({\textsf {E}}_m) = \Vert T_l^{{\textsf {E}}_m}\Vert _{{\textsf {E}}_m} = 2^{l/m}, \quad 0<l<2m. \end{aligned}$$
(4.21)

In particular, we have \({\mathcal {W}}_{2\,m-1, \infty }({\textsf {E}}_m) = \Vert T_{2\,m-1}^{{\textsf {E}}_m}\Vert _{{\textsf {E}}_m} = 2^{(2\,m-1)/m} = 2^{2-1/m}\) and the proof is complete. \(\square \)

As follows from (4.20) and (4.14), we have

$$\begin{aligned} {\mathcal {W}}_{2nm+l,\infty }({\textsf {E}}_m) = 2\min _{a_0, a_1, \ldots , a_{2n-1}\in {\mathbb {C}}} \max _{|z| = 1} |z-1|^{l/m-1} \left| z^{2n}+\sum _{k=0}^{2n-1} a_k z^k \right| . \end{aligned}$$
(4.22)

Utilizing the lower bound of [11, Eq. (40)], we thus conclude that

$$\begin{aligned} {\mathcal {W}}_{2nm+l,\infty }({\textsf {E}}_m)\ge 2+\frac{\pi ^2}{8nm^2}. \end{aligned}$$
(4.23)

Remark

Throughout this exposition, we opted to consider polynomial preimages of \([-2, 2]\), the canonical interval of capacity one. Consequently, \({\textsf {E}}_m\) consistently possesses an even number of edges and symmetry in both the real and imaginary axes. Had we chosen the interval [0, 4] as our starting point, our sets would have encompassed all symmetric star graphs, including those with an odd number of edges. It is worth noting that the method of proof extends seamlessly to this scenario, and the equivalent of Theorem 1.2 holds for such sets as well. To be specific, if we let

$$\begin{aligned} {\textsf {S}}_m=\bigl \{ z: z^m\in [0, 4] \bigr \}, \end{aligned}$$
(4.24)

then \({\mathcal {W}}_{mn, \infty }({\textsf {S}}_m)=2\) for all \(n\ge 1\) and \(\lim _{n\rightarrow \infty }{\mathcal {W}}_{n, \infty }({\textsf {S}}_m)=2\).

As a consequence of (1.26), we see that it is possible to construct Widom factors arbitrarily close to 4. Furthermore, we note that the value in (1.25) is \(<2\) for \(0<l/m<1\) and \(>2\) for \(l/m>1\). Similar to the case of \(m=2\), this result aligns with the numerics presented in Fig. 5. Once more, the plot indicates monotonicity along the natural subsequences (mod 2m), as was partially proven in Theorem 1.2.

In the next section we shall prove that if \(\displaystyle {P_{n}^{\mu _{{\textsf {E}}_m}}}\) denotes the monic orthogonal polynomial with respect to equilibrium measure \(\mu _{{\textsf {E}}_m}\), then

$$\begin{aligned} n\mapsto \Vert P_{2nm+l}^{\mu _{{\textsf {E}}_m}}\Vert ^2_{L^2(\mu _{{\textsf {E}}_m})} \end{aligned}$$
(4.25)

is monotonic for any fixed \(l<2m\). In fact, this sequence increases when \(l/m <1\) and decreases for \(l/m>1\). This matches the numerically suggested and partially proven behavior for the sup-norms of the Chebyshev polynomials.

5 Related Orthogonal Polynomials

We now turn our attention to the orthogonal polynomials with respect to the equilibrium measure of \({\textsf {E}}_m\). Recall that if \(\mu \) is a probability measure supported on the outer boundary of \({\textsf {E}}_m\), then \(\mu =\mu _{{\textsf {E}}_m}\) precisely when (1.5) holds. With this result at hand, we can explicitly determine \(\mu _{{\textsf {E}}_m}\) (see also [35]).

Lemma 5.1

Let \({\textsf {E}}_m\) be defined as in (1.22). The equilibrium measure of \({\textsf {E}}_m\) is absolutely continuous with respect to arc length measure and given by

$$\begin{aligned} d\mu _{{\textsf {E}}_m}(z) = \frac{|z^{m-1}|}{\pi \sqrt{4-z^{2m}}} |dz|, \quad z\in {\textsf {E}}_m. \end{aligned}$$
(5.1)

Proof

A straightforward computation shows that the measure defined in (5.1) is a probability measure on \({\textsf {E}}_m\). We proceed to show that it satisfies (1.5). Note that if \(\zeta , z\in \mathbb {C}\) then

$$\begin{aligned} \log | \zeta -z^m | = \sum \log | \zeta ^{1/m}-z |, \end{aligned}$$
(5.2)

where the sum is taken over all the mth roots of \(\zeta \). Using this, we can compute the potential for the measure in question and arrive at

$$\begin{aligned} \frac{1}{\pi }\int _{{\textsf {E}}_m}\log | x-z | \frac{\vert x^{m-1}\vert }{\sqrt{4-x^{2m}}} \vert dx\vert&=\frac{1}{\pi }\sum _{k=1}^{2m}\int _{0}^{2^{1/m}} \log |e^{i\pi k/m}x-z |\frac{x^{m-1} }{\sqrt{4-x^{2m}}}dx \nonumber \\&= \frac{1}{m\pi }\sum _{k=1}^{m}\int _{-2}^{2} \frac{\log | e^{i\pi k/m}t^{1/m}-z |}{\sqrt{4-t^2}}dt \nonumber \\&= \frac{1}{m\pi }\int _{-2}^{2}\frac{\log |t- z^m|}{\sqrt{4-t^2}}dt = \frac{1}{m}G_{[-2,2]}(z^m). \end{aligned}$$
(5.3)

The last equality follows from the fact that \(dt/(\pi \sqrt{4-t^2})\) is the equilibrium measure of \([-2,2]\) which is a set of logarithmic capacity one.

By (1.11), we have

$$\begin{aligned} \frac{1}{m}G_{[-2,2]}(z^m)=G_{{\textsf {E}}_m}(z) \end{aligned}$$
(5.4)

and consequently (5.1) holds true since also \(\text {Cap}( {\textsf {E}}_m )=1\). \(\square \)

As in Sect. 1.2, we shall use the notation \(\displaystyle {P_n^{\mu _{{\textsf {E}}_m}}}\) for the monic orthogonal polynomials with respect to \(\mu _{{\textsf {E}}_m}\). Recall that these polynomials minimise the integrals

$$\begin{aligned} \int _{{\textsf {E}}_m}\left| P_{n}\right| ^2d\mu _{{\textsf {E}}_m} \end{aligned}$$
(5.5)

among all monic polynomials of degree n. Just as in Lemma 4.1, one can use the symmetries of \({\textsf {E}}_m\) to show that for \(n, l \in {\mathbb {N}}\) and \(0\le l<2m\), we have

$$\begin{aligned} P_{2nm+l}^{\mu _{{\textsf {E}}_m}}(z) = z^{2nm+l}+\sum _{k=0}^{n-1}a_{2km+l}z^{2km+l}, \quad a_{2km+l}\in \mathbb {R}. \end{aligned}$$
(5.6)

We are now ready to prove Theorem 1.4.

Proof of Theorem 1.4

Fix \(m\ge 2\), let \(n\in {\mathbb {N}}\) and suppose \(0\le l<2m\). By Lemma 5.1 and with \(P_{2nm+l}^{\mu _{{\textsf {E}}_m}}\) as in (5.6), we have

$$\begin{aligned} \Vert P_{2nm+l}^{\mu _{{\textsf {E}}_m}}\Vert _{L^2(\mu _{{\textsf {E}}_m})}^2&= \frac{1}{\pi }\int _{{\textsf {E}}_m}\left| z^{2nm+l}+\sum _{k=0}^{n-1}a_{2km+l}z^{2km+l}\right| ^2 \frac{\vert z^{m-1}\vert }{\sqrt{4-z^{2m}}}\vert dz \vert \nonumber \\&=\frac{2m}{\pi }\int _{[0, {2^{1/m}}]} \left| z^{2nm}+\sum _{k=0}^{n-1}a_{2km+l}z^{2km}\right| ^2 \frac{\vert z^{m+2l-1}\vert }{\sqrt{4-z^{2m}}} \vert dz\vert \nonumber \\&=\frac{1}{\pi }\int _{0}^{4}\left( x^n+\sum _{k=0}^{n-1}a_{2km+l}x^k\right) ^2 \frac{x^{l/m-1/2}}{\sqrt{4-x}} dx. \end{aligned}$$
(5.7)

Realising that the above integral is minimised precisely for the Jacobi polynomials (suitably rescaled to [0, 4]), we can compute it explicitly. Following Szegő [53, Chapter IV], we adopt the notation

$$\begin{aligned} P_n^{(\alpha , \beta )}(x)= {n+\alpha \atopwithdelims ()n} _2F_1\left( -n, n+\alpha +\beta +1; \alpha +1; \frac{1-x}{2} \right) \end{aligned}$$
(5.8)

and note that the leading coefficient of \(P_n^{(\alpha , \beta )}\) is given by

$$\begin{aligned} 2^{-n}{2n+\alpha +\beta \atopwithdelims ()n}= \frac{\Gamma (2n+\alpha +\beta +1)}{2^n \Gamma (n+1)\Gamma (n+\alpha +\beta +1)}. \end{aligned}$$
(5.9)

The integral in (5.7) can thus be written as

$$\begin{aligned} & \frac{2^{4n+l/m} \Gamma (n+1)^2 \Gamma (n+l/m)^2}{\pi \Gamma (2n+l/m)^2}\nonumber \\ & \quad \int _{-1}^{1}\left( P_n^{(-1/2, l/m-1/2)}(x)\right) ^2(1-x)^{-{1}/{2}}(1+x)^{l/m-1/2}dt \nonumber \\ & \quad = \frac{2^{4n+2l/m} \Gamma (n+{1}/{2}) \Gamma (n+1) \Gamma (n+{l}/{m}) \Gamma (n+{l}/{m}+1/2)}{\pi (2n+{l}/{m}) \Gamma (2n+l/m)^2} \quad \end{aligned}$$
(5.10)

since

$$\begin{aligned} & \int _{-1}^1 \left( P_n^{(\alpha , \beta )}(x) \right) ^2 (1-x)^\alpha (1+x)^\beta dx \nonumber \\ & \quad = \frac{2^{\alpha +\beta +1} \Gamma (n+\alpha +1) \Gamma (n+\beta +1)}{(2n+\alpha +\beta +1) \Gamma (n+1) \Gamma (n+\alpha +\beta +1)}. \end{aligned}$$
(5.11)

Applying Legendre’s duplication formula, the expression in (5.10) reduces to

$$\begin{aligned} \frac{2 \Gamma (2n+1) \Gamma (2n+2l/m)}{(2n+l/m) \Gamma (2n+l/m)^2} \end{aligned}$$
(5.12)

and recalling that \(\Gamma (x+a)/\Gamma (x+b)\sim x^{a-b}\) as \(x\rightarrow \infty \), we deduce that

$$\begin{aligned} \Vert P_{2nm+l}^{\mu _{{\textsf {E}}_m}}\Vert _{L^2(\mu _{{\textsf {E}}_m})}^2 \rightarrow 2 \; \text{ as } \; n\rightarrow \infty . \end{aligned}$$
(5.13)

In order to prove the claimed monotonicity along subsequences, we introduce the quantity

$$\begin{aligned} \gamma _n(s) {:}{=} \frac{2 \Gamma (2n+1) \Gamma (2n+2s)}{(2n+s) \Gamma (2n+s)^2}, \quad s\ge 0. \end{aligned}$$
(5.14)

Note that \(\Vert P_{2nm+l}^{\mu _{{\textsf {E}}_m}}\Vert _{L^2(\mu _{{\textsf {E}}_m})}^2 = \gamma _{n}({l}/{m})\) and

$$\begin{aligned} \frac{\gamma _{n+1}(s)}{\gamma _{n}(s)}&= \frac{\Gamma (2n+3) \Gamma (2n+2s+2) (2n+s) \Gamma (2n+s)^2}{\Gamma (2n+1) \Gamma (2n+2s) (2n+s+2) \Gamma (2n+s+2)^2} \nonumber \\&=\frac{(2n+1) (2n+2) (2n+2s) (2n+2s+1)}{(2n+s) (2n+s+1)^2 (2n+s+2)}. \end{aligned}$$
(5.15)

Since

$$\begin{aligned} \frac{(x+1)(x+2s)}{(x+s)(x+s+1)}=\frac{x^2+2xs+x+2s}{x^2+2xs+x+s^2+s} \end{aligned}$$
(5.16)

and

$$\begin{aligned} \frac{2s}{s^2+s}=\frac{2}{s+1} > rless 1 \; \text{ for } \; s\lessgtr 1, \end{aligned}$$
(5.17)

it follows that \(\gamma _{n+1}(s)/\gamma _n(s) > rless 1\) for \(s\lessgtr 1\). In this way, we have obtained the desired monotonicity statement. \(\square \)

The sets \({\textsf {E}}_m\) appear to be the first examples beyond the framework of single Jordan arcs for which (1.37) is fulfilled. We wonder how far one can push the conditions on \({\textsf {E}}\) in the conjecture of [21].

6 A Further Investigation Regarding \({\mathcal {W}}_{2n+1, \infty }({\textsf {E}}_2)\)

The plot in Fig. 2 indicates that \(\Vert T_{2n+1}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}\lessgtr 2\) depending on whether n is even or odd. As proven in Sect. 3, \(T_{4n+l}^{{\textsf {E}}_2}\) has a zero of order l at \(z=0\) (for \(l=1, 3\)). However, there is no apparent explanation for why a zero with greater multiplicity would necessarily result in a higher sup-norm. In this section we shall study the preimages defined in (3.18) in more detail and try to shed more light on the pattern revealed by Fig. 2.

As explained in Sect. 3, \({\textsf {E}}_{2}^{n,l}\) consists of the base set \({\textsf {E}}_2\) together with certain “decorations”. At all the points where \(T_{4n+l}^{{\textsf {E}}_2}\) has a zero, a new “crossing” will appear and each of the four preimages

$$\begin{aligned} (T_{4n+l}^{{\textsf {E}}_2})^{-1}\Bigl ( i^k \bigl [0, \Vert T_{4n+l}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}\bigr ]\Bigr ), \quad k=0, 1, 2, 3 \end{aligned}$$
(6.1)

consists of \(4n+l\) arcs. While \(2n+1\) of these arcs lie on \({\textsf {E}}_2\), the remaining \(2n+l-1\) are orthogonal to \({\textsf {E}}_2\) (except for the \(l-1\) arcs emanating at the origin). It can be shown that every arc in \({\textsf {E}}_2^{n, l}\) has harmonic measure equal to \({1}/{4(4n+l)}\), for instance, by examining a conformal map from \({\mathbb {C}}\setminus {\textsf {E}}_2^{n,l}\) onto \({\mathbb {C}}\setminus \overline{{\mathbb {D}}}\). The typical shape of an \({\textsf {E}}_2^{n, l}\) set is illustrated in Figs. 6, 7 below.

Fig. 6
figure 6

On the left: \({\textsf {E}}_2^{2,1}\) and on the right: \(\Phi ({\textsf {E}}_{2}^{2,1})\)

Full size image
Fig. 7
figure 7

On the left: \({\textsf {E}}_2^{2,3}\) and on the right: \(\Phi ({\textsf {E}}_{2}^{2,3})\)

Full size image

With (3.21) in mind, we see that understanding the behaviour of \(\Vert T_{4n+l}^{{\textsf {E}}_2} \Vert _{{\textsf {E}}_2}\) equates to effectively estimating the capacity of \({\textsf {E}}_2^{n, l}\). Since the zeros of \(T_{4n+l}^{{\textsf {E}}_2}\) are hard to determine explicitly—we only know by [12] that they distribute according to equilibrium measure of \({\textsf {E}}_2\) as \(n\rightarrow \infty \)—it seems difficult to estimate this capacity directly. We get a better picture by considering the conformal map

$$\begin{aligned} \Phi (z) = \sqrt{{z^2}/{2}+\sqrt{\left( {z^2}/{2}\right) ^2-1}\,} \end{aligned}$$
(6.2)

which maps \({\mathbb {C}}\setminus {\textsf {E}}_2\) onto \({\mathbb {C}}\setminus \overline{{\mathbb {D}}}\). When applying \(\Phi \), the complement of \({\textsf {E}}_2^{n, l}\) is mapped onto the complement of the closed unit disk accompanied by certain “protrusions”, see Figs.  6, 7. By construction, all these \(4(2n+l-1)\) protrusions have the same equilibrium measure relative to \(\Phi ({\textsf {E}}_2^{n, l})\). Hence their combined mass relative to equilibrium measure amounts to

$$\begin{aligned} \frac{2n+l-1}{4n+l}. \end{aligned}$$
(6.3)

As we shall argue below, the fact that this quantity is \(<1/2\) for \(l=1\) but \(>1/2\) for \(l=3\) seems to explain why \(\Vert T_{2n+1}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2}\lessgtr 2\) for n even and odd, respectively.

Consider the sets

$$\begin{aligned} S(n,l){:}{=}\partial \mathbb {D}\, \cup \bigcup _{k=1}^{4(2n+l-1)} \exp \Bigl \{\frac{\pi ik/2}{2n+l-1}\Bigr \} \,[1,R_{n, l}], \end{aligned}$$
(6.4)

where \(R_{n, l}>1\) is a suitable constant depending on n and l. These sets have a straightforward structure, allowing us to compute their capacity, and they also bear a resemblance to the configuration of \(\Phi ({\textsf {E}}_2^{n, l})\). Although it may seem that way at first glance, the protrusions in \(\Phi ({\textsf {E}}_2^{n,l})\) are not perfectly straight line segments, and their distribution on \(\partial {\mathbb {D}}\) is not entirely uniform. One can show that by selecting \(R_{n,l}\) in such a way that

$$\begin{aligned} \mu _{S(n, l)}(\partial {\mathbb {D}}) = \frac{2n+1}{4n+l}, \end{aligned}$$
(6.5)

the inequality \(\text {Cap}( S(n, l) )^{4n+l} \lessgtr \sqrt{2}\) holds, depending on whether \(l=1\) or 3. For example, by performing a straightforward calculation, we find that

$$\begin{aligned} \text {Cap}\bigl (S(n,1)\bigr ) = {\Bigl (\cos \Bigl (\frac{\pi n}{4n+1}\Bigr )\Bigr )}^{-1/4n} \end{aligned}$$
(6.6)

and from this expression, one can infer that \(\text {Cap}(S(n,1) )^{4n+1} \rightarrow \sqrt{2}\) in a monotonically increasing manner. Taking (3.21) into account, we now possess additional evidence indicating that \(\Vert T_{4n+1}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2} \rightarrow 2\) from below. This nicely complements the established fact that \(\Vert T_{4n+3}^{{\textsf {E}}_2}\Vert _{{\textsf {E}}_2} \rightarrow 2\) from above.

7 Outlook and Perspective

A key finding of this paper has been to show that, beyond intervals, there exist compact subsets of \({\mathbb {C}}\) for which the Widom factors converge to 2. Specifically, the sets \({\textsf {E}}_m\) as defined in Theorem 1.2 and illustrated in Fig. 1 exhibit this property when \(m\ge 2\), and the same holds for any other symmetric star graph with an odd number of edges. It is reasonable to inquire whether or not there are more sets \({\textsf {E}}\subset {\mathbb {C}}\) for which \({\mathcal {W}}_{n,\infty }({\textsf {E}})\rightarrow 2\). As explained below, we believe the answer is indeed affirmative.

Recall that if P is a complex polynomial and \(P'(z)=0\), then z is called a critical point and \(w=P(z)\) a critical value for P. Polynomials with at most two critical values, say \(c_1\) and \(c_2\), are known as Shabat polynomials (or generalised Chebyshev polynomials), see [13, 46]. Since this class of polynomials is invariant under non-degenerate linear transformations, we may assume that \(c_1\), \(c_2\) are real with \(c_1\le c_2\). It is a known fact (see, e.g., [13] or [29]) that for Shabat polynomials, the preimage \(P^{-1}([c_1,c_2])\) is a planar tree with as many edges as the degree of P. In fact, one can establish a bijection between the set of bicolored planer trees and the set of equivalence classes of Shabat polynomials. Moreover, with respect to the point at \(\infty \), every edge of \(P^{-1}([c_1,c_2])\) has equal harmonic measure and any subset of an edge has equal harmonic measure from both sides. Trees with these properties are also called “balanced trees” and they satisfy the S-property of Definition 2.1. A remarkable result of Bishop [14] shows that balanced trees are dense in all planar continua (i.e., compact connected subsets of \({\mathbb {C}}\)) with respect to the Hausdorff metric.

For \(n\ge 2\), the polynomial \(P_n(z)=z^n\) has one critical point (namely, \(z=0\)) and one critical value \(w=0\). So the preimage \(P_n^{-1}([0,4])\) is a balanced tree and when \(n=2m\), this tree coincides with \({\textsf {E}}_m\) as defined in (1.22). Another example of a Shabat polynomial (with critical values \(w=0, 1\)) is

$$\begin{aligned} P(z)=\frac{8}{729} (z+1) \Bigl (z^2-\frac{3}{2}z+\frac{9}{2}\Bigr )^3 \end{aligned}$$
(7.1)

By use of the algorithm mentioned in Sect. 3, one can compute the norms of \(T_n^{{\textsf {E}}_P}\) for degree up to 40 with a precision of \(10^{-2}\). The outcome and the corresponding tree is illustrated in Fig. 8.

Fig. 8
figure 8

The set \({\textsf {E}}_P = P^{-1}([0,1])\) and its associated Widom factors

Full size image

Similar plots for other Shabat polynomials lead to the same pattern and we thus have the courage to hypothesize that the first part of Theorem 1.2 applies to all balanced trees.

Conjecture 7.1

Let P be a Shabat polynomial with critical values in \(\{c_1,c_2\}\) and consider the preimage \({\textsf {E}}_P{:}{=}P^{-1}([c_1,c_2])\). Then

$$\begin{aligned} \lim _{n\rightarrow \infty } {\mathcal {W}}_{n, \infty } ({\textsf {E}}_P)=2. \end{aligned}$$
(7.2)

Since any balanced tree satisfies the S-property, one may speculate if this conjecture can be extended to a larger class of sets. In fact, if the property of every edge having equal harmonic measure turns out to not play a role, it would be natural to formulate the conjecture for so-called generalised Shabat polynomials. This class was introduced in [29] and allows for more than two critical values as long as they all belong to \([c_1,c_2]\). The preimage \(P^{-1}([c_1,c_2])\) is connected (in fact, a tree) if and only if \([c_1,c_2]\) contains all the critical values of P. The ideal scenario would be that the conjecture holds true for all connected sets characterised by the S-property.

Regrettably, our current method of proof does not exhibit a clear path for generalisation within the context of Shabat polynomials and the S-property. Novel strategies and ideas are required to advance our understanding in this domain.