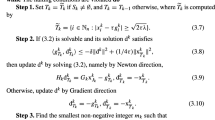Optimal Recovery from Inaccurate Data in Hilbert Spaces: Regularize, But What of the Parameter?

Abstract

In Optimal Recovery, the task of learning a function from observational data is tackled deterministically by adopting a worst-case perspective tied to an explicit model assumption made on the functions to be learned. Working in the framework of Hilbert spaces, this article considers a model assumption based on approximability. It also incorporates observational inaccuracies modeled via additive errors bounded in $\ell _2$. Earlier works have demonstrated that regularization provides algorithms that are optimal in this situation, but did not fully identify the desired hyperparameter. This article fills the gap in both a local scenario and a global scenario. In the local scenario, which amounts to the determination of Chebyshev centers, the semidefinite recipe of Beck and Eldar (legitimately valid in the complex setting only) is complemented by a more direct approach, with the proviso that the observational functionals have orthonormal representers. In the said approach, the desired parameter is the solution to an equation that can be resolved via standard methods. In the global scenario, where linear algorithms rule, the parameter elusive in the works of Micchelli et al. is found as the byproduct of a semidefinite program. Additionally and quite surprisingly, in case of observational functionals with orthonormal representers, it is established that any regularization parameter is optimal.

Appendix

This additional section collects justifications for a few facts that were mentioned but not explained in the main text. These facts are: the uniqueness of a Chebyshev center for the model- and data-consistent set (see p. 1.3), the efficient computation of the solution to (7) when $\Lambda \Lambda ^* = \mathrm {Id}_{\mathbb {R}^m}$ (see p. 2.2), the form of Newton method when solving Eq. (29) (see p. 8), and the reason why the constraint in (41) always implies the constraint in (40) (see pp. 4.1 and 4.2).

1.1 Uniqueness of the Chebyshev Center

Let $\widehat{f_1},\widehat{f_2}$ be two Chebyshev centers, i.e., minimizers of $\max \{ \Vert f-g\Vert : \Vert P_{\mathcal {V}^\perp } g \Vert \le \varepsilon , \Vert \Lambda g - y\Vert \le \eta \}$ and let $\mu$ be the value of the minimum. Consider $\overline{g} \in H$ such that $\Vert (\widehat{f_1}+\widehat{f_2})/2 - \overline{g}\Vert = \max \{ \Vert (\widehat{f_1}+\widehat{f_2})/2 - g\Vert : \Vert P_{\mathcal {V}^\perp } g \Vert \le \varepsilon , \Vert \Lambda g - y\Vert \le \eta \}$. Then

$$\begin{aligned} \mu&\le \Vert (\widehat{f_1}+\widehat{f_2})/2 - \overline{g}\Vert \le \frac{1}{2} \Vert \widehat{f_1} - \overline{g}\Vert + \frac{1}{2} \Vert \widehat{f_2} - \overline{g}\Vert \\&\le \frac{1}{2} \max \{ \Vert \widehat{f_1}-g\Vert : \Vert P_{\mathcal {V}^\perp } g \Vert \le \varepsilon , \Vert \Lambda g - y\Vert \le \eta \}\\&\quad + \frac{1}{2} \max \{ \Vert \widehat{f_2}-g\Vert : \Vert P_{\mathcal {V}^\perp } g \Vert \le \varepsilon , \Vert \Lambda g - y\Vert \le \eta \}\\&= \frac{1}{2} \mu + \frac{1}{2} \mu = \mu . \end{aligned}$$

Thus, equality must hold all the way through. This implies that $\widehat{f_1} - \overline{g} = \widehat{f_2} - \overline{g}$, i.e., that $\widehat{f_1} = \widehat{f_2}$, as expected.

1.2 Computation of the Regularized Solution

Let $(v_1,\ldots ,v_n)$ be a basis for $\mathcal {V}$ and let $u_1,\ldots ,u_m$ denote the Riesz representers of the observation functionals $\lambda _1,\ldots ,\lambda _m$, which form an orthonormal basis for $\mathrm{{im}}(\Lambda ^*)$ under the assumption that $\Lambda \Lambda ^* = \mathrm {Id}_{\mathbb {R}^m}$. With $C \in \mathbb {R}^{m \times n}$ representing the cross-Gramian with entries $\langle u_i,v_j \rangle = \lambda _i(v_j)$, the solution to the regularization program (7) is given, even when H is infinite dimensional, by

$$\begin{aligned} f_\tau = \tau \sum _{i=1}^m a_i u_i + \sum _{j=1}^n b_j v_j, \end{aligned}$$

where the coefficient vectors $a \in \mathbb {R}^m$ and $b \in \mathbb {R}^n$ are computed according to

$$\begin{aligned} b = \big ( C^\top C \big )^{-1} C^\top y \qquad \text{ and } \qquad a = y-Cb. \end{aligned}$$

This is fairly easy to see for $\tau =0$ and it has been established in Foucart, Liao, Shahrampour, and Wang [10, Theorem 2] for $\tau =1$, so the general result follows from Proposition 3. Alternatively, it can be obtained by replicating the steps from the proof of the case $\tau = 1$ with minor changes.

1.3 Newton Method

Equation (29) takes the form $F(\tau ) = 0$, where

$$\begin{aligned} F(\tau ) = \lambda _{\min }((1-\tau ) R + \tau S) - \frac{(1-\tau )^2 \varepsilon ^2 - \tau ^2 \eta ^2}{(1-\tau ) \varepsilon ^2 - \tau \eta ^2 + (1-\tau )\tau (1-2\tau ) \delta ^2}. \end{aligned}$$

Newton method produces a sequence $(\tau _k)_{k \ge 0}$ converging to a solution using the recursion

$$\begin{aligned} \tau _{k+1} = \tau _k - \frac{F(\tau _k)}{F'(\tau _k)}, \qquad k \ge 0. \end{aligned}$$

(50)

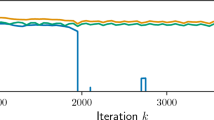
In order to apply this method, we need the ability to compute the derivative of F with respect to $\tau$. Setting $\lambda _{\min } = \lambda _{\min }((1-\tau )R+\tau S)$, this essentially reduces to the computation of $d \lambda _{\min }/d\tau$, which is performed via the argument below. Note that the argument is not rigorous, as we take for granted the differentiability of the eigenvalue $\lambda _{\min }$ and of a normalized eigenvector h associated with it. However, nothing prevents us from applying the scheme (50) using the expression for $d \lambda _{\min }/d\tau$ given in (51) below and agree that a solution has been found if the output $\tau _K$ satisfies $F(\tau _K) < \iota$ for some prescribed tolerance $\iota >0$. Now, the argument starts from the identities

$$\begin{aligned} ((1-\tau )R+\tau S) h = \lambda _{\min } h \qquad \text{ and } \qquad \langle h,h \rangle =1, \end{aligned}$$

which we differentiate to obtain

$$\begin{aligned} (S-R)h + ((1-\tau )R+\tau S) \frac{\mathrm{{d}}h}{\mathrm{{d}}\tau } = \frac{\mathrm{{d}} \lambda _{\min }}{\mathrm{{d}} \tau } h + \lambda _{\min } \frac{\mathrm{{d}}h}{\mathrm{{d}} \tau } \qquad \text{ and } \qquad 2 \Big \langle h, \frac{\mathrm{{d}}h}{\mathrm{{d}}\tau } \Big \rangle = 0. \end{aligned}$$

By taking the inner product with h in the first identity and using the second identity, we derive

$$\begin{aligned} \langle (S-R)h , h \rangle = \frac{\mathrm{{d}} \lambda _{\min }}{\mathrm{{d}}\tau }, \qquad \text{ i.e., } \qquad \frac{\mathrm{{d}} \lambda _{\min }}{\mathrm{{d}}\tau } = \Vert S h\Vert ^2 - \Vert Rh\Vert ^2. \end{aligned}$$

According to Lemma 9, this expression can be transformed, after some work, into

$$\begin{aligned} \frac{\mathrm{{d}} \lambda _{\min }}{\mathrm{{d}}\tau } = \frac{1-2\tau }{\tau (1-\tau )} \, \frac{\lambda _{\min }(1-\lambda _{\min })}{1-2\lambda _{\min }}. \end{aligned}$$

(51)

1.4 Relation Between Semidefinite Constraints

Suppose that the constraint in (41) holds for a regularization map $\Delta _\tau$. In view of the expressions

$$\begin{aligned}&\Delta _\tau = \big ( (1-\tau ) P_{\mathcal {V}^\perp } + \tau \Lambda ^* \Lambda \big )^{-1} (\tau \Lambda ^*) \quad \text{ and } \\&\mathrm {Id}- \Delta _\tau \Lambda = \big ( (1-\tau ) P_{\mathcal {V}^\perp } + \tau \Lambda ^* \Lambda \big )^{-1} ((1-\tau ) P_{\mathcal {V}^\perp }), \end{aligned}$$

this constraint also reads

$$\begin{aligned} \begin{bmatrix} c P_{\mathcal {V}^\perp } &{} | &{} 0\\ \hline 0 &{} | &{} d \, \mathrm {Id}_{\mathbb {R}^m} \end{bmatrix} \succeq \begin{bmatrix} (1-\tau ) P_{\mathcal {V}^\perp }\\ \hline \tau \Lambda \end{bmatrix} \big ( (1-\tau ) P_{\mathcal {V}^\perp } + \tau \Lambda ^* \Lambda \big )^{-2} \begin{bmatrix} (1-\tau ) P_{\mathcal {V}^\perp } \; | \; \tau \Lambda ^* \end{bmatrix}. \end{aligned}$$

Multiplying on the left by $\begin{bmatrix} P_{\mathcal {V}^\perp } \; | \; \Lambda ^* \end{bmatrix}$ and on the right by $\begin{bmatrix} P_{\mathcal {V}^\perp } \\ \hline \Lambda \end{bmatrix}$ yields

$$\begin{aligned}&c P_{\mathcal {V}^\perp } + d \Lambda ^* \Lambda \\&\quad \succeq ( (1-\tau ) P_{\mathcal {V}^\perp } + \tau \Lambda ^* \Lambda ) \big ( (1-\tau ) P_{\mathcal {V}^\perp }+ \tau \Lambda ^* \Lambda \big )^{-2} ( (1-\tau ) P_{\mathcal {V}^\perp } + \tau \Lambda ^* \Lambda ) = \mathrm {Id}. \end{aligned}$$

This is the constraint in (40).