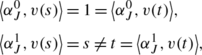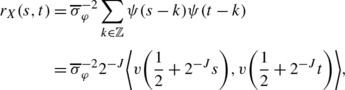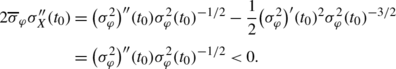A Smirnov–Bickel–Rosenblatt Theorem for Compactly-Supported Wavelets

Abstract

In nonparametric statistical problems, we wish to find an estimator of an unknown function f. We can split its error into bias and variance terms; Smirnov, Bickel and Rosenblatt have shown that, for a histogram or kernel estimate, the supremum norm of the variance term is asymptotically distributed as a Gumbel random variable. In the following, we prove a version of this result for estimators using compactly-supported wavelets, a popular tool in nonparametric statistics. Our result relies on an assumption on the nature of the wavelet, which must be verified by provably-good numerical approximations. We verify our assumption for Daubechies wavelets and symlets, with N=6,…,20 vanishing moments; larger values of N, and other wavelet bases, are easily checked, and we conjecture that our assumption holds also in those cases.

Appendix: Proofs

We will need the following result, which is a version of Theorem 1 in Hüsler [11]. The result concerns the maxima of centered Gaussian processes whose variance functions are periodic; such processes are called cyclostationary. In Hüsler’s original result, the maxima of a sequence of processes was shown to converge to a Gumbel random variable. In our result, we will specialize to a single process and show that this convergence occurs uniformly.

Let (X(t):t≥0) be a centered Gaussian process with continuous sample paths, continuous variance function σ ²(t) with maximum 1, and correlation function r(s,t). We will assume the following conditions:

• (i) σ(t)=1 only at points t ₁,t ₂,…, with t _k+1−t _k >h ₀ for all k, and some h ₀>0.

• (ii) The number m _T of points t _k in [0,T] satisfies T≤Km _T for some K>0.

• (iii) In a neighborhood of each t _k ,

  $$\sigma(t) = 1 - \bigl(a + \gamma_k(t)\bigr)\vert t-t_k \vert ^{\alpha} $$

  for some a>0, α∈(0,2], and functions γ _k (t) such that for any ε>0, there exists δ ₀>0 with

  $$\max\bigl\{\bigl \vert \gamma_k(t) \bigr \vert :t \in J_k^{\delta_0}\bigr\} < \varepsilon, $$

  where $J_{k}^{\delta_{0}} :=\{t : \vert t-t_{k} \vert < \delta \}$.

• (iv) For any ε>0, there exists δ ₀>0 such that

  $$r(s, t) = 1 - \bigl(b + \gamma(s, t)\bigr)\vert s - t \vert ^{\alpha}, $$

  where b>0, γ(s,t) is continuous at all points (t _k ,t _k ), and

  $$\sup\bigl\{\bigl \vert \gamma(s, t) \bigr \vert : s, t \in J^{\delta_0} \bigr\} < \varepsilon, $$

  for $J^{\delta} := \bigcup_{k \le m_{T}} J_{k}^{\delta}$.

• (v) There exist α ₁,C>0 such that, for any s,t≤T,

  $$\mathbb{E}\bigl[\bigl(X(s)-X(t)\bigr)^2\bigr] \le C\vert s-t \vert ^{\alpha_1}. $$

• (vi) The function

  $$\delta(v) :=\sup\bigl\{\bigl \vert r(s, t) \bigr \vert : v \le \vert s-t \vert ,\ s, t \le T\bigr\} $$

  satisfies δ(v)<1 for v>0, and δ(v)log(v)→0 as v→∞.

Lemma A.1

Under the above conditions, let T=T(n)→∞ as n→∞, and define

$$M(T) :=\max_{t \in[0, T]} \bigl \vert X(t) \bigr \vert , $$

and $\mu(u) := H^{a/b}_{\alpha}\phi(u)/u$, where ϕ is the Gaussian density function and the constant $H^{a/b}_{\alpha}$ is given by Hüsler [11]. Further define

$$u(\tau) := \mu^{-1}(\tau/m_T). $$

Then for any τ ₀>0, we have

$$\sup_{\tau\in(0, \tau_0]} \biggl \vert \frac{\mathbb{P}(M(T) > u(\tau ))}{1 - e^{-\tau}} - 1 \biggr \vert \to0 $$

as n→∞.

Proof

Our argument proceeds as in the proof of Theorem 1 in Hüsler [11]. We note that our conditions are Hüsler’s conditions (A1)–(A3), (B1)–(B4) and (1), for a fixed process X _n (t)=X(t), with α=β.

For τ≤τ ₀, u(τ)≥u(τ ₀)→∞, and by definition,

$$m_T \mu\bigl(u(\tau)\bigr) = \tau. $$

The approximation errors in parts (i) and (ii) of Hüsler’s proof are thus O(g(S)τ) and O(ρ _c τ), respectively. In part (iii), we note that

$$u(\tau)^2 = 2 \log(T/\tau) - \log\log(T/\tau) + O(1), $$

so Hüsler’s term (4) is of order

and term (5) is of order

In Hüsler’s final display, we may thus write

$$\mathbb{P}\bigl(M_n(T) \le u(\tau)\bigr) = \exp\bigl\{-\bigl(1+o(1) \bigr)\tau\bigr\} + o(\tau). $$

As the process X(t) does not depend on n, the error in each of these approximations depends only on u=u(τ), and the above limits hold as u→∞. (This can be seen from the precise form of the errors, as given in [13, §3.1], and in Hüsler’s proof.) Since u is decreasing in τ, the limits are therefore uniform in τ small.

Consider the function

$$f(x, y; \tau) :=\log \biggl(\frac{1 - \exp(-(1 + x)\tau )}{\tau} + y \biggr), $$

defined on 0≤τ≤τ ₀, $\vert x \vert \le\frac{1}{2}$, $\vert y \vert \le\frac{1}{2} (1 - \exp(-\frac{1}{2}\tau_{0}))/\tau_{0}$. The derivatives

$$\frac{\delta f}{\delta x} = \frac{\exp(-(1 + x)\tau)}{\exp f}, \qquad \frac{\delta f}{\delta y} = \frac{1}{\exp f} $$

are finite and continuous in x, y and τ, so by the mean value inequality, for n large,

As the above limits are uniform in τ≤τ ₀, the result follows. □

We now apply this result to a cyclostationary process, composed of scaling functions φ, which we can use to model the variance of estimators $\hat {f}(j_{n})$.

Lemma A.2

Define the cyclostationary Gaussian process

$$X(t) :=\overline {\sigma }_{\varphi }^{-1} \sum_{k \in\mathbb{Z}} \varphi(t - k) Z_k, \quad Z_k \overset {\mathrm {i.i.d.}}{\sim }N(0, 1). $$

For any γ ₀∈(0,1), j _n →∞,

$$\sup_{\gamma\in(0, \gamma_0]} \biggl \vert \gamma^{-1} \mathbb{P} \biggl( \sup_{t \in[0, 2^{j_n}]} \bigl \vert X(t) \bigr \vert > \frac{x(\gamma )}{a(j_n)} + b(j_n) \biggr) - 1 \biggr \vert \to0 $$

as n→∞.

Proof

For fixed γ, the result is a consequence of Theorem 2 in Giné and Nickl [9]; the statement uniform over (0,γ ₀] follows, replacing Theorem 1 of Hüsler [11] in Giné and Nickl’s proof with Lemma A.1. The conditions of Giné and Nickl’s theorem are satisfied by Assumptions 2.1 and 2.2, as follows:

• (i) X has almost-sure derivative

  $$X'(t) :=\overline {\sigma }_{\varphi }^{-1} \sum _{k \in\mathbb{Z}} \varphi'(t-k) Z_k, $$

  so is continuous. X′ is also the mean square derivative:

  $$\begin{aligned}[c] &h^{-1}\mathbb{E}\bigl[\bigl(X(t+h)-X(t)-hX'(t) \bigr)^2\bigr] \\ &\quad {}= h^{-1} \sum_{k \in\mathbb{Z}} \bigl(\varphi(t-h-k) - \varphi(t-k) -h\varphi'(t-k) \bigr)^2, \end{aligned} $$

  which tends to 0 as h→0, since the sum has finitely many nonzero terms.

• (ii) For i=0,1, define functions f _i (x):=x ⁱ on [0,1], having wavelet expansions

  $$f_i = \sum_{k=0}^{2^J-1} \alpha_{J, k}^i \varphi_{J,k} + \sum _{j=J}^{\infty}\sum_{k=0}^{2^j-1} \beta_{j,k}^i \psi_{j,k} $$

  in our wavelet basis on the interval, for some J≥j ₀, 2^J≥6K. As ψ is twice continuously differentiable and φ and ψ have compact support, by Corollary 5.5.4 in Daubechies [7], ψ has at least two vanishing moments. Thus

  $$\beta_{j,k}^i = \bigl\langle x^i, \psi_{j,k} \bigr\rangle= 0, $$

  and

  $$f_i(t) = \sum_{k=0}^{2^J-1} \alpha_{J,k}^i \varphi_{J,k}(t). $$

  For t∈[0,1], let v(t) denote the vector $(\varphi_{J,k}(t)) \in\mathbb{R}^{2^{J}}$, so $f_{i}(t) = \langle \alpha^{i}_{J}, v(t) \rangle$. Given s≠t, we have

  

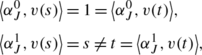
  so the vectors v(s), v(t) are linearly independent.

  For s,t∈ℝ, define

  $$r_X(s, t) :=\mathbb {C}\mathrm {ov}\bigl[X(s), X(t)\bigr], \qquad \sigma^2_X(t) := \mathbb {V}\mathrm {ar}\bigl[X(t)\bigr] = r_X(t, t). $$

  Then, if s,t∈[−K,K],

  

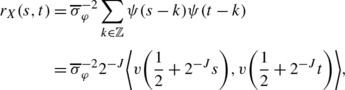
  so by Cauchy-Schwarz,

  $$r_X(s, t)^2 < \sigma_X^2(s) \sigma_X^2(t). $$

  If s,t∈[k−K,k+K] for some k∈ℤ, the same applies by cyclostationarity. If not, then as φ is supported on [1−K,K], we have r _X (s,t)=0. However, for any t∈[0,1], $\langle\alpha^{1}_{J}, v(\frac{1}{2} + 2^{-J}t) \rangle= 1$, so

  $$\sigma_X^2(t) = \overline {\sigma }_{\varphi }^{-2} 2^{-J} \bigl \Vert v(t)\bigr \Vert ^2 > 0, $$

  and by cyclostationarity the same holds for all t∈ℝ. We thus again obtain

  $$r_X(s, t)^2 < \sigma_X^2(s) \sigma_X^2(t). $$

• (iii) We have

  $$\sigma_X^2(t) = \overline {\sigma }_{\varphi }^{-2} \sigma_{\varphi}^2(t), $$

  so by Assumption 2.2, $\sup_{t \in[0,1]} \sigma_{X}^{2}(t) = 1$, and this maximum is attained at a unique t ₀∈[0,1). If t ₀∈(0,1), this satisfies the conditions of the theorem directly; if not we may proceed as in Proposition 9 of Giné and Nickl [9]. $\sigma_{\varphi}^{2}$ is twice differentiable,

  $$2\overline {\sigma }_{\varphi }\sigma_X'(t_0) = \bigl( \sigma_{\varphi}^2\bigr)'(t_0) \sigma_{\varphi}^2(t_0)^{-1/2} = 0, $$

  and

  

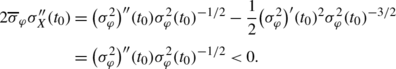
  Finally, let v′(t) denote the vector $(\varphi'_{J,k}(t)) \in \mathbb{R}^{\mathbb{Z}}$. Then for t∈[0,1],

  $$\bigl\langle\alpha^1_J, v'(t) \bigr \rangle= f_1'(t) = 1, $$

  so

  

  (4.1)

• (iv) Since φ has support [1−K,K],

  $$\sup_{s,t:\vert s-t \vert \ge2K-1} \bigl \vert r_X(s, t) \bigr \vert = 0. $$

 □

We may now bound the variance of $\hat {f}(j_{n})$. We will show that the variance process is distributed as the process X from the above lemma, so can be controlled similarly.

Proof of Theorem 2.3

Let $I_{n} :=[0, 2^{j_{n}}]$. The process

$$X_n(t) :=\frac{\hat {f}(j_n) - \bar {f}(j_n)}{c(j_n)}\bigl(2^{-j_n}t\bigr), \quad t \in I_n, $$

is distributed as

$$\overline {\sigma }_{\varphi }^{-1}2^{-j_n/2} \Biggl( \sum_{k\in K_{j_0}} Z_{j_0,k} \varphi_{j_0,k}\bigl(2^{-j_n}t\bigr) + \sum _{j = j_0}^{j_n-1} \sum _{k \in K_j} Z_{j,k} \psi_{j,k} \bigl(2^{-j_n}t\bigr) \Biggr) $$

for $Z_{j,k} \overset {\mathrm {i.i.d.}}{\sim }N(0, 1)$, so by an orthogonal change of basis, as

$$\overline {\sigma }_{\varphi }^{-1} 2^{-j_n/2} \sum_{k\in K_{j_n}} Z_k \varphi_{j_n,k}\bigl(2^{-j_n}t\bigr), \quad Z_k \overset {\mathrm {i.i.d.}}{\sim }N(0, 1). $$

For a regular wavelet basis, X _n is distributed on I _n as the process X from Lemma A.2, so we are done.

For a basis on the interval, set $J_{n} :=[2K, 2^{j_{n}} - 2K]$, and K _n :=I _n ∖J _n . On J _n , X _n is distributed as the process X from Lemma A.2, and we have

so for u _n (j _n ):=x(γ _n )/a(j _n )+b(j _n ),

For X _n to be large on K _n , one of the 4K variables

$$Z_k,\quad k \in\bigl\{0, \dots, 2K-1, 2^{j_n}-2K, \dots, 2^{j_n}-1\bigr\}, $$

must be large. Thus, by a simple union bound, for a constant C>0 depending on φ, the above probability is at most

$$8K\varPhi\bigl(-Cu_n(j_n)\bigr) \lesssim e^{-C^2u_n(j_n)^2/2}/u_n(j_n) = o(\gamma_n). $$

The result then follows by Lemma A.2, applied to the process X on J _n . □