On the limit distribution of the power function induced by a design prior

Abstract

The hybrid frequentist-Bayesian approach to sample size determination is based on the expectation of the power function of a test with respect to a design prior for the unknown parameter value. In clinical trials this quantity is often called probability of success (PoS). Determination of the limiting value of PoS as the number of observations tends to infinity, that is crucial for well defined sample size criteria, has been considered in previous articles. Here, we focus on the asymptotic behavior of the whole distribution of the power function induced by the design prior. Under mild conditions, we provide asymptotic results for the three most common classes of hypotheses on a scalar parameter. The impact of the design parameters choice on the distribution of the power function and on its limit is discussed.

1 Introduction

The power of a statistical test is a function of the unknown parameter of a model, used for pre-experimental evaluation of success probability of a trial. In the standard frequentist approach to sample size determination, the power function is evaluated at a fixed value of the parameter, typically a relevant effect or effects difference (design-value). Then, the sample size is selected as the smallest number of observations such that the power at the design-value exceeds a given threshold. Hence, the resulting sample sizes depend on the design-value. The hybrid frequentist-Bayesian approach avoids such local optimality by assigning a probability distribution (design prior) to multiple design-values. The design prior induces a probability distribution on the power function, that is typically summarized by its expected value for sample size selection. This quantity is known as Bayesian predictive power (Spiegelhalter and Freedman 1986), assurance (O’Hagan and Stevens 2001), probability of success (Rufibach et al. 2016). Even though the literature presents a certain degree of variability, in the following we will use the latter terminology and the acronym PoS, as discussed in Kunzmann et al. (2021). For other references on PoS and related quantities see Rufibach et al. (2016), Chuang-Stein (2006), Liu (2010), Muirhead and Soaita (2013), Wang et al. (2013). For references on the general topic of Bayesian sample size determination, hybrid methods included, see also Joseph et al. (1997), Wang and Gelfand (2002), Spiegelhalter et al. (2004), Sahu and Smith (2006), Brutti et al. (2014), Ciarleglio et al. (2015). Similarly to the standard frequentist approach, using PoS, the sample size is selected so that the value of PoS is sufficiently large. For a convenient choice of the threshold, one has to take into account the maximum achievable value of PoS as the number of observations tends to infinity, that is not necessarily equal to one. This asymptotic result has been established in Brutti et al. (2008) in a very special case and later generalized in Eaton et al. (2013). Both these articles restrict their attention to the convergence of the sequence of the expected values defining PoS, with no consideration on other aspects of the distribution of the power. More recently, Rufibach et al. (2016) argued that the expectation may be inappropriate to summarize the distribution of the power and they suggest a deeper study of the impact of the design prior on the whole density function. However they do not consider asymptotics. The goal of the present paper is to connect and widen the scope of these two contributions, by considering the whole distribution of the power function induced by the design prior and by studying the convergence of the sequence of random power functions.

The structure of the paper is as follows. In Sect. 2 we present the main theoretical results, namely the convergence of the sequence of random power functions in the most commonly used testing setups in clinical trials. In Sect. 3 we specialize these results to the normal model; an application is illustrated in Sect. 3.1. Section 4 extends previous results to two relevant asymptotic tests, the Wald test and the Sign test; Sect. 4.3 discusses problems arising with models for dependent data. Finally, Sect. 5 contains some concluding remarks.

2 Methodology

Let $X_1,...X_n$ be a random sample from $f_n(\cdot \vert \theta )$, $\theta \in \Omega \subseteq {\mathbb {R}}^1$, where $f_n(\cdot \vert \theta )$ is the joint probability mass or density function. Let us consider the hypotheses

$$\begin{aligned} H_0: \theta \in \Omega _0 \qquad vs \qquad H_1: \theta \in \Omega _1 \end{aligned}$$

(1)

where $\Omega _0 \cup \Omega _1 = \Omega$, with $\Omega _0 \cap \Omega _1 = \emptyset$. Let $\beta _n(\theta )$ be the power function of a test, that is the probability of rejecting $H_0$ computed with respect to $f_n(\cdot \vert \theta )$. In the standard frequentist approach, a design value $\theta _d$ is fixed and the sample size is selected so that $\beta _n(\theta _d)$ is sufficiently large. In order to avoid the specific choice of $\theta _d$, one can introduce a probability distribution on alternative guessed values for $\theta$. This design distribution is an instrumental tool for defining a scenario under which we want to select the sample size that, in general, avoids local optimality [see for instance Brown et al. (1987) and, more rencently, Kunzmann et al. (2021)]. The design prior has not to be confused with the usual (analysis) prior based on pre-experimental information that is employed for fully Bayesian posterior analysis. Note that, consistently with its role of describing a scenario, the design prior must be informative and, in particular, it should be sufficiently concentrated on values close to $\theta _d$. In the present paper we do not consider analysis priors since, following a hybrid frequentist-Bayesian approach, $\beta _n(\theta )$ is the power function of a frequentist test. For further details and discussion on design and analysis priors see Brutti et al. (2014) and references therein.

Let ${\mathbb {P}}_\Theta (\cdot )$ be a design probability measure on $\Omega$ and $(\beta _n(\Theta ); n \in {\mathbb {N}})$ the corresponding sequence of random variables with values in [0, 1]. Let ${\mathbb {P}}_\Theta (\Omega _i) = \pi _i$, $i = 0,1$. Without loss of generality, in the following we assume $\pi _1 > 0$. Let

$$\begin{aligned} Y_n = \beta _n(\Theta ), \; e_n = {\mathbb {E}}_\Theta [Y_n], \; G_n(y) = {\mathbb {P}}_\Theta (Y_n \le y), \; p_n(y) = 1 - G_n(y), \; y \in [0,1]. \end{aligned}$$

We are interested in providing general results for the convergence of the sequence $Y_n$ to a limit random variable $Y_\infty$ and in determining the expressions of

$$\begin{aligned} e_{\infty } = {\mathbb {E}}_\Theta [Y_\infty ], \quad G_\infty (y) = {\mathbb {P}}_\Theta (Y_\infty \le y), \quad p_\infty (y) = 1 - G_\infty (y), \quad y \in [0,1]. \end{aligned}$$

The quantities $\beta _n(\theta _d)$, $e_n$ and $p_n(y)$ can be used to define the following sample size determination criteria:

$$\begin{aligned} n^\star _{\beta }= & {} \min \{n \in {\mathbb {N}}: \beta _n(\theta _d) > \lambda _\beta \} \end{aligned}$$

(2)

$$\begin{aligned} n^\star _{e}= & {} \min \{n \in {\mathbb {N}}: e_n > \lambda _e \} \end{aligned}$$

(3)

$$\begin{aligned} n^\star _{p}= & {} \min \{n \in {\mathbb {N}}: p_n(y) > \lambda _p \}, \end{aligned}$$

(4)

where $\lambda _i \in (0,1)$, for $i = \beta ,e,p$. Note that the knowledge of the limiting values $e_\infty = \lim _{n\rightarrow \infty } e_n$ and $p_\infty (y) = \lim _{n\rightarrow \infty } p_n(y)$ is necessary to fix $\lambda _e$ and $\lambda _p$ so that the corresponding criteria can be fulfilled. This aspect will be further illustrated in the examples of Sect. 3.1.

In this paper we consider the following classes of problems:

• (A) null and alternative one-sided hypotheses, i.e. $\Omega _0 = (-\infty ,\theta _0], \Omega _1 = (\theta _0,+\infty )$ (or reverse);

• (B) point-null hypothesis versus a one-sided alternative, i.e. $\Omega _0 = \{\theta _0\}, \Omega _1 = (\theta _0,+\infty )$ (or $\Omega _1= (-\infty ,\theta _0)$);

• (C) point-null hypothesis versus a two-sided alternative, i.e. $\Omega _0 = \{\theta _0\}, \Omega _1 = {\mathbb {R}} \setminus \{\theta _0\}$.

For these classes of problems we consider either size-$\alpha$ consistent or consistent tests defined as follows.

Definition 1

(size-$\alpha$ consistency) For any given $\alpha \in (0,1)$, a test is size-$\alpha$ consistent if, for all $\theta \in \Omega$, the sequence $(\beta _n(\theta ); n \in {\mathbb {N}})$ converges to the limiting power function $\beta _\infty (\theta )$, that is

for tests (A)

$$\begin{aligned} \beta _{\infty }(\theta ) = \lim _{n \rightarrow \infty } \beta _n(\theta ) = \left\{ \begin{array}{cl} 0 &{} \quad \theta < \theta _0 \\ \alpha &{} \quad \theta = \theta _0 \\ 1 &{} \quad \theta > \theta _0 \end{array} \right. , \end{aligned}$$

(5)

for tests (B) and (C)

$$\begin{aligned} \beta _{\infty }(\theta ) = \lim _{n \rightarrow \infty } \beta _n(\theta ) = \left\{ \begin{array}{cl} \alpha &{} \quad \theta = \theta _0 \\ 1 &{} \quad \theta \in \Omega _1 \end{array} \right. . \end{aligned}$$

(6)

Fig. 1 represents $\beta _n(\theta )$, for several values of n, and $\beta _{\infty }(\theta )$ as functions of $\theta$ in the three cases A, B, C.

Fig. 1

Values of $\beta _n(\theta )$ for increasing sample sizes (dashed lines) and $\beta _{\infty }(\theta )$ (solid line) with respect to $\theta$ in the three cases A, B, C

Definition 2

(consistency) A test is consistent if, for all $\theta \in \Omega$, the sequence $(\beta _n(\theta ); n \in {\mathbb {N}})$ converges to the limiting power function

$$\begin{aligned} \beta _{\infty }(\theta ) = \lim _{n \rightarrow \infty } \beta _n(\theta ) = \left\{ \begin{array}{cl} 0 &{} \quad \theta \in \Omega _0 \\ 1 &{} \quad \theta \in \Omega _1 \end{array} \right. . \end{aligned}$$

(7)

The limit power function $\beta _\infty (\theta )$ in (7) corresponds to the perfect test with all error probabilities equal to 0. In cases B and C, if $\alpha = \alpha _n \rightarrow 0$ as $n \rightarrow \infty$, then the test is consistent according to (7) [see van der Vaart (1998)].

The following results study the convergence of the sequence of power functions $\beta _n(\Theta )$ for the classes of problems A, B and C.

Result A (one-sided hypotheses) Consider $H_0: \theta \le \theta _0 \text { vs } H_1: \theta > \theta _0$ and let ${\mathbb {P}}_\Theta (\cdot )$ be a design prior probability measure for $\Theta$, such that ${\mathbb {P}}_\Theta (\Theta =\theta _0)= 0$. Consider the sequence of power functions $\beta _n(\Theta )$ for a test that satisfies either (5) or (7). As $n \rightarrow \infty$, if $\pi _i >0$, $i = 0,1$, then

$$\begin{aligned} Y_n=\beta _n(\Theta ) \; {\mathop {\longrightarrow }\limits ^{as}} \; Y_\infty \sim \text {Ber}(\pi _1) \end{aligned}$$

(8)

and

$$\begin{aligned} e_\infty = \pi _1 \qquad p_\infty (y) = \left\{ \begin{array}{cl} 1 &{} \quad y = 0\\ \pi _1 &{} \quad 0< y < 1\\ 0 &{} \quad y = 1 \end{array} \right. . \end{aligned}$$

(9)

If $\pi _1 = 1$, then $Y_n {\mathop {\longrightarrow }\limits ^{as}} 1$.

Proof of Result A

Recalling the definition of almost sure convergence, proof follows from Conditions (5) and (7) and from the assumption on ${\mathbb {P}}_\Theta$. $\square$

Result B (point-null vs one-sided alternative) Consider the hypotheses $H_0: \theta = \theta _0 \, \text { vs } \, H_1: \theta > \theta _0$ and let ${\mathbb {P}}_\Theta (\cdot )$ be a design probability measure on $\Omega$. Consider the sequence of power functions $\beta _n(\Theta )$. If $\pi _i > 0$, $i= 0,1$, then $\diamond$ under Condition (6), as $n \rightarrow \infty$,

$$\begin{aligned} Y_n=\beta _n(\Theta ) \; {\mathop {\longrightarrow }\limits ^{s}} \; Y_\infty , \quad \text { where} \quad Y_\infty = \left\{ \begin{array}{ll} \alpha &{} \quad \pi _0 \\ 1 &{} \quad \pi _1 \end{array} \right. \end{aligned}$$

(10)

and

$$\begin{aligned} e_\infty = \alpha \, \pi _0 + \pi _1 \qquad p_\infty (y) = \left\{ \begin{array}{cl} 1 &{} \quad 0 \le y<\alpha \\ \pi _1 &{} \quad \alpha \le y < 1\\ 0 &{} \quad y = 1 \end{array} \right. ; \end{aligned}$$

(11)

$\diamond$ under Condition (7), as $n \rightarrow \infty$,

$$\begin{aligned} Y_n=\beta _n(\Theta ) \; {\mathop {\longrightarrow }\limits ^{s}} \; Y_\infty \sim \text {Ber}(\pi _1) \end{aligned}$$

(12)

and $e_\infty$ and $p_\infty (y)$ are given in (9).

If $\pi _1 = 1$, then $Y_n {\mathop {\longrightarrow }\limits ^{s}} 1$.

Proof of Result B

It follows from the definition of sure convergence, from Conditions (6) and (7) and from the assumptions on ${\mathbb {P}}_\Theta$. $\square$

Result C (point-null vs two-sided alternative) Consider the hypotheses $H_0: \theta = \theta _0$ vs $H_1: \theta \ne \theta _0$ and let ${\mathbb {P}}_\Theta (\cdot )$ be a design probability measure on $\Omega$. Consider the sequence of power functions $\beta _n(\Theta )$. If $\pi _i > 0$, $i= 0,1$, then under Condition (6), the result in (10) holds; under Condition (7), the result in (12) holds. If $\pi _1 = 1$, then $Y_n {\mathop {\longrightarrow }\limits ^{s}} 1$.

Proof of Result C

See proof of Result B. $\square$

Remarks

• (i) In Result A, if (5) holds, the convergence of $\beta _n(\Theta )$ to $Y_\infty$ is almost sure since ${\mathbb {P}}_\Theta (\Theta = \theta _0)= 0$. Under the same conditions, $\beta _n(\Theta )$ converges surely (or pointwise) to $\beta _\infty (\Theta )$, where $\beta _\infty (\cdot )$ is defined in (5).

• (ii) In Result A, if (7) holds, the convergence in (8) is pointwise.

• (iii) Condition (5) is standard in one-sided testing as it is typically satisfied by size-$\alpha$ uniformly most powerful (UMP) tests. See, for instance, Sect. 3, cases A and B.

• (iv) Similarly, Condition (6) is standard in two-sided testing with point null hypothesis as it is typically satisfied by size-$\alpha$ UMP unbiased tests. See, for instance, Sect. 3, case C.

• (v) In case A, if $\Theta$ is a continuous r.v., we assume it has density function $f_\Theta (\cdot )$ on ${\mathbb {R}}$. In cases B and C, if $\Theta$ is a mixed r.v. such that $\pi _0 > 0$ and it is continuous on $\Omega _1$, we assume that its density on $\Omega _1$ is given by ${\tilde{f}}_\Theta (\theta ) = f_\Theta (\theta ) I_{\Omega _1}(\theta ) / \pi _1$, where $f_\Theta (\theta )$ is a density function on ${\mathbb {R}}$ [see “lump-and-smear priors” of Spiegelhalter et al. (2004)].

• (vi) In case A, $\pi _0$ and $\pi _1$ are induced by the density $f_\Theta (\cdot )$, i.e. $\pi _i = \int _{\Omega _i} f(\theta ) d\theta$, $i=0,1$. In cases B and C the design probability masses $\pi _0$ and $\pi _1$ are specified regardless of the choice of the density ${\tilde{f}}_\Theta (\cdot )$.

Nuisance parameter case

Assume now that $X_1,...,X_n$ is a random sample from $f_n(\cdot \vert \eta )$, where $\eta = (\theta , \xi )$ with $\theta$ a scalar parameter of interest and $\xi$ a nuisance parameter. Let $\beta _n(\theta ;{\hat{\xi }}_n)$ be the power function for testing hypotheses (1), where ${\hat{\xi }}_n$ is a consistent estimator of $\xi$. Assume that for large n, $\beta _n(\theta ;{\hat{\xi }}_n) \simeq \beta _n(\theta ;\xi )$ and that (5) and (6) hold for $\beta _n(\theta ;\xi )$. Then, results A, B and C also apply to $\beta _n(\Theta ;{\hat{\xi }}_n)$.

3 Normal model

In this section we specialize results of Sect. 2 by assuming that $X_1, \ldots , X_n$ is a random sample from $\text {N}(\theta , \sigma ^2)$, $\sigma ^2$ known. We consider UMP $\alpha$-size tests (for cases A and B) and UMP unbiased $\alpha$-size tests (for case C) on $\theta$ based on ${{\bar{X}}_n}\vert \theta \sim \text {N}(\theta , \sigma ^2/n)$. In addition, if a conjugate design prior is used, we provide, whenever available, explicit expressions of $e_n$ and $p_n(y)$ for finite n. In the last paragraph of this section we provide an example using a non-conjugate design prior.

Case A (one-sided hypotheses) Let us consider $H_0: \theta \le \theta _0 \text { vs } H_1: \theta > \theta _0$ as in Result A. The size-$\alpha$ UMP test rejects the null hypothesis if ${{\bar{X}}_n}>\theta _0+z_{1-\alpha }\sigma /\sqrt{n}$, $\alpha \in (0,1)$. The power function of the test is $\beta _n(\theta )=1-\Phi [\sqrt{n}(\theta _0-\theta )/\sigma +z_{1-\alpha }], \, \theta \in {\mathbb {R}},$ and it satisfies Condition (5) so that Result A holds. In particular, if we assume that $\Theta \sim \text {N}(\theta _d, \sigma ^2/n_d)$, $\theta _d \in {\mathbb {R}}$ and $n_d \in {\mathbb {R}}^+$, then $e_\infty =\pi _1=1-\Phi \left( \frac{\sqrt{n_d}(\theta _0-\theta _d)}{\sigma } \right)$. In this case, the explicit expressions of $e_n$ and $p_n(y)$ are available. First, consider $e_n$. Using the law of total probability [see, for instance, Rufibach et al. (2016)] we have that

$$\begin{aligned} e_n= & {} {\mathbb {E}}_\Theta \left[ {\mathbb {P}}_{{{\bar{X}}_n}\vert \Theta } \left( {{\bar{X}}_n}\ge \theta _0 + \frac{\sigma }{\sqrt{n}} z_{1-\alpha } \right) \right] \\= & {} \int _\Omega \left[ {\mathbb {P}}_{{{\bar{X}}_n}\vert \theta } \left( {{\bar{X}}_n}\ge \theta _0 + \frac{\sigma }{\sqrt{n}} z_{1-\alpha } \right) \right] f_\Theta (\theta ) d \theta \\= & {} {\mathbb {P}}_{{{\bar{X}}_n}} \left( {{\bar{X}}_n}\ge \theta _0 + \frac{\sigma }{\sqrt{n}} z_{1-\alpha } \right) \\= & {} 1-\Phi \left( \frac{\theta _0-\theta _d+\frac{\sigma }{\sqrt{n}} z_{1-\alpha }}{\sigma _d} \right) , \end{aligned}$$

where $f_\Theta (\cdot )$ is the density function of $\Theta$ on ${\mathbb {R}}$, and ${\mathbb {P}}_{{{\bar{X}}_n}}(\cdot )$ is the probability measure associated to the marginal distribution of ${{\bar{X}}_n}\sim \text {N} \left( \theta _d, \sigma ^2_d \right)$, with $\sigma ^2_d=\sigma ^2(1/n_d+1/n)$. Let us now consider $p_n(y)$. Since for any $y \in (0,1)$, $\beta _n(\theta )> y \Leftrightarrow \theta > \theta _0+ \delta _n(y),$ where $\delta _n(y) = \frac{\sigma }{\sqrt{n}}(z_{1-\alpha }-z_{1-y})$, it follows that

$$\begin{aligned} p_n(y)= \left\{ \begin{array}{ll} 1 &{} \quad y = 0 \\ 1-\Phi \left( \frac{\sqrt{n_d}}{\sigma } \left[ \theta _0-\theta _d + \delta _n(y) \right] \right) &{} \quad 0< y < 1 \\ 0 &{} \quad y = 1 \end{array} \right. . \end{aligned}$$

It is easy to double-check that, as $n \rightarrow \infty$, $e_n \rightarrow e_\infty$ and $p_n(y) \rightarrow p_\infty (y)$ given by (9) with $\pi _1 = 1-\Phi \left( \frac{\sqrt{n_d}(\theta _0-\theta _d)}{\sigma } \right)$.

Case B (point-null vs a one-sided alternative) Consider $H_0: \theta =\theta _0$ vs $H_1: \theta >\theta _0$ as in Result B. The size-$\alpha$ UMP test rejects the null hypothesis if ${{\bar{X}}_n}>\theta _0+z_{1-\alpha }\sigma /\sqrt{n}$, as in case A. The power function is now $\beta _n(\theta )=1-\Phi [\sqrt{n}(\theta _0-\theta )/\sigma +z_{1-\alpha }], \, \theta \in [\theta _0,+\infty )$, and it satisfies Condition (6) so that Result B holds. Let us now suppose that $\pi _0$ and $\pi _1$ are the prior probability masses assigned to the hypotheses and that, on $\Omega _1$, the design prior for $\Theta$ is a truncated normal density with parameters $(\theta _d, \sigma ^2/n_d)$ and support $(\theta _0,+\infty )$ (see remark (v)). In this case, the explicit expression of $e_n$ is not available, but numerical values of $e_n$ can be easily obtained noting that, for the law of total probabilities,

$$\begin{aligned} e_n = \alpha \, \pi _0 + {\mathbb {E}}_\Theta (\beta _n(\Theta ) \vert \Theta > \theta _0) \, \pi _1, \end{aligned}$$

where ${\mathbb {E}}_\Theta (\beta _n(\Theta ) \vert \Theta > \theta _0)$ can be numerically evaluated via Monte Carlo. Conversely, the expression of $p_n(y) = 1 - G_n(y)$ can be obtained explicitely by noting that $G_n(y) = {\mathbb {P}}_\Theta [A_n(y)]$, where

$$\begin{aligned} A_n(y)= \{ \theta \in \Omega : \beta _n(\theta ) \le y \} = \left\{ \begin{array}{ll} \emptyset &{} \quad 0 \le y< \alpha \\ \{\theta _0\} &{} \quad y=\alpha \\ \left[ \theta _0, \theta _0+\delta _n(y)\right] &{} \quad \alpha<y<1 \\ \Omega &{} \quad y=1 \end{array} \right. , \end{aligned}$$

with $\delta _n(y) = \frac{\sigma }{\sqrt{n}}(z_{1-\alpha }-z_{1-y})$ as in case A. Therefore

$$\begin{aligned} p_n(y)= \left\{ \begin{array}{ll} 1 &{} \quad 0 \le y< \alpha \\ 1-\pi _0 &{} \quad y=\alpha \\ 1-{\mathbb {F}}_\Theta [\theta _0+\delta _n(y)] &{} \quad \alpha<y<1 \\ 0 &{} \quad y=1 \end{array} \right. , \end{aligned}$$

where ${\mathbb {F}}_\Theta (\cdot )$ is the cdf of a truncated normal density with parameters $(\theta _d, \sigma ^2/n_d)$ and support $(\theta _0,+\infty )$. As $n \rightarrow \infty$, $\delta _n(y) \rightarrow 0$ for all $y \in (\alpha ,1)$ and ${\mathbb {F}}_\Theta [\theta _0+\delta _n(y)] \rightarrow \pi _0$; therefore $p_n(y)\rightarrow p_\infty (y)$ given by (11).

Case C (Point-null vs a two-sided alternative) Consider $H_0: \theta =\theta _0$ vs $H_1: \theta \ne \theta _0$, i.e. $\Omega _0 = \{\theta _0\}$ and $\Omega _1 = {\mathbb {R}} {\setminus } \{\theta _0\}$. The size-$\alpha$ unbiased UMP test rejects $H_0$ if $\frac{\sqrt{n} \vert {{\bar{X}}_n}-\theta _0\vert }{\sigma } > z_{1-\frac{\alpha }{2}}.$ Then the power function is

$$\begin{aligned} \beta _n(\theta ) = 1- \left[ \Phi \left( \frac{\sqrt{n}}{\sigma }(\theta _0-\theta )+z_{1-\frac{\alpha }{2}} \right) - \Phi \left( \frac{\sqrt{n}}{\sigma }(\theta _0-\theta )-z_{1-\frac{\alpha }{2}} \right) \right] , \; \theta \in {\mathbb {R}}, \end{aligned}$$

that satisfies Condition (6) so that Result C holds. As in case B, suppose that $\pi _0$ and $\pi _1$ are the prior probability masses assigned to $H_0$ and $H_1$; whereas, as in case A, $\Theta \sim \text {N}(\theta _d,\sigma ^2/n_d)$. In order to obtain the expression of $e_n$ note that

$$\begin{aligned} e_n = \alpha \, \pi _0 + {\mathbb {E}}_\Theta (\beta _n(\Theta ) \vert \, \Theta \ne \theta _0) \, \pi _1. \end{aligned}$$

Similarly to case A, using the law of total probabilities, we have that

$$\begin{aligned} {\mathbb {E}}_\Theta [\beta _n(\Theta ) \vert \, \Theta \ne \theta _0]= & {} {\mathbb {E}}_\Theta \left[ {\mathbb {P}}_{{{\bar{X}}_n}\vert \Theta } \left( \frac{\sqrt{n} \vert {{\bar{X}}_n}-\theta _0 \vert }{\sigma }> z_{1-\frac{\alpha }{2}} \right) \vert \, \Theta \ne \theta _0 \right] \\= & {} {\mathbb {P}}_{{{\bar{X}}_n}} \left( \frac{\sqrt{n} \vert {{\bar{X}}_n}-\theta _0 \vert }{\sigma } > z_{1-\frac{\alpha }{2}} \right) \\= & {} 1- \left[ \Phi \left( \frac{\theta _0-\theta _d+\frac{\sigma }{\sqrt{n}} z_{1-\frac{\alpha }{2}}}{\sigma _d} \right) - \Phi \left( \frac{\theta _0-\theta _d-\frac{\sigma }{\sqrt{n}} z_{1-\frac{\alpha }{2}}}{\sigma _d} \right) \right] , \end{aligned}$$

where ${\mathbb {P}}_{{{\bar{X}}_n}}(\cdot )$ is the probability measure associated to the marginal distribution of ${{\bar{X}}_n}\sim \text {N} \left( \theta _d, \sigma ^2_d \right)$, with $\sigma ^2_d=\sigma ^2(1/n_d+1/n)$ as in case A.

We can now obtain the expression of $p_n(y)$. Noting that $\forall n > 0$ $\beta _n(\theta )$ is:

• (i) continuous in ${\mathbb {R}}$, with values in $[\alpha ,1]$;

• (ii) monotone in $(-\infty ,\theta _0)$ and in $(\theta _0, \infty )$;

• (iii) symmetric w.r.t. its minimum point $\theta = \theta _0$;

then, for the intermediate value theorem, $\forall y \in (\alpha ,1)$ and $\forall n > 0$, there exists $a_n(y) > 0$ such that $\beta _n(\theta ) \le y \, \Leftrightarrow \, \theta \in [\theta _0-a_n(y), \theta _0+ a_n(y)].$ Hence,

$$\begin{aligned} A_n(y) = \{\theta \in \Omega : \beta _n(\theta \le y)\} = \left\{ \begin{array}{ll} \emptyset &{} \quad 0 \le y< \alpha \\ \{\theta _0\} &{} \quad y=\alpha \\ \left[ \theta _0 - a_n(y), \theta _0+a_n(y)\right] &{} \quad \alpha<y<1 \\ \Omega &{} \quad y=1 \end{array} \right. . \end{aligned}$$

Therefore

$$\begin{aligned} p_n(y)= 1 - {\mathbb {P}}_\Theta [A_n(y)] = \left\{ \begin{array}{ll} 1 &{} \quad 0 \le y< \alpha \\ 1-\pi _0 &{} \quad y=\alpha \\ 1-{\mathbb {F}}_\Theta [\theta _0+a_n(y)] + {\mathbb {F}}_\Theta [\theta _0-a_n(y)] &{} \quad \alpha<y<1 \\ 0 &{} \quad y=1 \end{array} \right. , \end{aligned}$$

where now ${\mathbb {F}}_\Theta (\cdot )$ is the cdf of a normal density of parameters $(\theta _d, \sigma ^2/n_d)$. Finally, note that, from Definition 1, $a_n(y) \rightarrow 0$ as $n \rightarrow \infty$ for $y \in (\alpha ,1)$. Then, as expected, $e_n \rightarrow e_\infty$ and $p_n(y) \rightarrow p_\infty (y)$ given by (11) since ${\mathbb {E}}_\Theta [\beta _n(\Theta ) \vert \, \Theta \ne \theta _0] \rightarrow 1$ and $a_n(y) \rightarrow 0$, $y \in (\alpha ,1)$.

Non-conjugate design priors

Although the use of a conjugate design prior has the advantage of yielding closed-form expressions for $e_n$ and $p_n(y)$ (in all cases but B) and of easing interpretation, this choice is not compulsory. If one is willing to use a non-conjugate prior, the following Monte Carlo steps can be implemented:

• 1. draw M values ${\tilde{\theta }}^{(1)}, \ldots , {\tilde{\theta }}^{(M)}$ from the design prior $f_{\Theta }$;

• 2. for each ${\tilde{\theta }}^{(j)}$ compute ${\tilde{y}}^{j}=\beta _n({\tilde{\theta }}^{(j)})$, $j = 1, \ldots , M$, where $\beta _n(\cdot )$ is the power function;

• 3. obtain the empirical distribution of $Y_n=\beta _n(\Theta )$ from draws ${\tilde{y}}^{(j)}$, $j = 1, \ldots , M$;

• 4. compute the Monte Carlo approximation of $e_n$ as the average of the values ${\tilde{y}}^{(j)}$;

• 5. compute the Monte Carlo approximation of $p_n(y)$ as the fraction of ${\tilde{y}}^{(j)} > y$.

As a specific example related to case A, we consider in Sect. 3.1 a truncated normal with support $[\theta _0,+\infty )$. We illustrate the consequences of truncation by numerical examples for finite n and for $n \rightarrow \infty$. Note that, in this case, $\pi _1 = {\mathbb {P}}(\Omega _1) = 1$, so that $Y_n {\mathop {\longrightarrow }\limits ^{as}} 1$ according to Result A.

Unknown variance case

Results obtained under the known variance assumption can be easily extended to the unknown variance case, adopting the formulation for the nuisance parameter introduced at the end of Sect. 2, with $\xi = \sigma ^2$ and ${\hat{\xi }}_n = S^2_n$ (sample variance). For the sake of brevity, let us focus on case A; case B and case C can be obtained similarly. According to the usual likelihood ratio test of size $\alpha$, $H_0$ is rejected if $\frac{\sqrt{n}(\bar{X}_n - \theta _0)}{S_n} > t_{n-1;1-\alpha }$, where $t_{n-1;\epsilon }$ is the $\epsilon -$quantile of the Student t distribution with $n-1$ degrees of freedom. It is easy to check that $\beta _n(\theta ;S_n) = 1 - F_{n-1}\left[ (\theta _0-\theta ) \frac{\sqrt{n}}{S_n} + t_{n-1;1-\alpha } \right]$, where $F_{n-1}(\cdot )$ is the cdf of the Student t distribution with $n-1$ degrees of freedom. Hence, for sufficiently large n, $\beta _n(\theta ;S_n) \simeq 1 - \Phi \left[ (\theta _0-\theta ) \frac{\sqrt{n}}{\sigma } + z_{1-\alpha } \right]$, which, regardless of $\sigma$, converges to $\beta _\infty (\theta )$ given in (5).

3.1 Application to clinical trials

Results of Sect. 3 can be used for two-samples problems. Let $Y_n$ the difference of sample means of experimental and placebo groups respectively, where the total sample size n is assumed equally allocated in the two groups. Under standard normality assumptions, $Y_n \sim \text {N}(\theta , 4\sigma ^2 /n)$, where $\sigma ^2$ is the common variance in the two groups and $\theta$ is the difference in treatment effects, with $\theta > \theta _0 = 0$ indicating superiority of the experimental treatment. For illustration we now consider an example on a clinical trial for the Restless Legs Syndrome, first presented in Muirhead and Soaita (2013) and discussed in Eaton et al. (2013). We refer to the context of Result A and consider a one-sided test of size $\alpha = 0.025$. The Authors assume a known variance $\sigma ^2 = 64$ and a clinically meaningful difference $\theta _d = 4$. In this case $\beta _n(\theta _d)$ reaches the threshold $\lambda _\beta = 0.80$ for $n^\star _{\beta } = 128$. Moreover, they consider a design prior distribution for $\theta$ with prior mean $\theta _d = 4$ and prior sample size $n_d = 4$.

Fig. 2

Values of $\beta _n(\theta _d)$ (solid line), $e_n$ (dashed line) and $e_n^{tr}$ (dotted line) as functions of n, with $\theta _d = 4$ and $n_d = 4,20,40,400$

Fig. 3

Values of $p_n(y)$ (first row) and $p_n^{tr}(y)$ (second row) as functions of n at $y = 0.5, 0.7, 0.9$ (first column) and as function of y for several sample sizes $n = 20,40,400$ (second column)

Figure  2 (top left panel) shows the behavior of $\beta _n(\theta _d)$ (solid line) and of $e_n$ (dashed line), obtained with the design prior mentioned before, as functions of n. The horizontal line denotes $e_{\infty } = \pi _1 = 0.691$. The dotted curve represents the values of PoS computed with respect to a normal design prior left truncated at $\theta _0=0$, with $\theta _d = 4$, $n_d = 4$, that we denote by $e_n^{tr}$. Note that, from (9), $e_{\infty }^{tr} = \pi _1 = 1$, regardless of the value of $n_d$. In the remaining panels of Fig. 2 we consider increasing values of $n_d$.

The main comments are the following.

• 1. In each panel the three curves are not uniformly ordered. Specifically, if we focus on power and PoS, there exists a value of the sample size ${\bar{n}}$ such that $\beta _n(\theta _d) > e_n$ definitively for $n > {\bar{n}}$. This behavior has been previously noticed for instance by Dallow and Fina (2011) and Rufibach et al. (2016). A similar remark applies to $\beta _n(\theta _d)$ and $e_n^{tr}$; whereas $e_n$ is uniformly smaller than $e_n^{tr}$.

• 2. As $n_d$ increases, the three curves tend to coincide and $e_{\infty }$ becomes closer and closer to 1. Moreover, the value of n such that $\beta _n(\theta _d)=e_n^{tr}$ gets smaller and smaller.

• 3. For a given threshold $\lambda _\beta = 0.80$, $n^\star _{\beta } = 128$, as designed. Conversely, using a normal design prior with a relatively small value of $n_d$ (top left panel), $n^\star _{e}$ does not exist, since $e_\infty < \lambda _\beta$. As a practical solution, if we tune the threshold for $e_n$ to be $\lambda _e = 0.8 \times e_\infty = 0.553$, we obtain $n^\star _{e} = 116$, which is even smaller than $n^\star _{\beta }$. Note that, in this case, if the truncated normal is used, $n^\star _{e} = 120$.

• 4. Recall that the design prior’s spirit requires $f_{\Theta }(\theta )$ to be substantially concentrated on $\theta _d$, i.e. “proper and very informative” [see Wang and Gelfand (2002), p. 197]. Hence, the choice $n_d = 4$ of the original example is not consistent with this idea and for this reason we have considered several larger values of $n_d$.

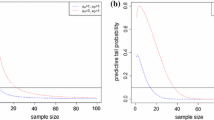
Figure 3 (first row) shows the plots of $p_n(y)$ using a normal design prior with $\theta _d = 4$ and $n_d = 20$. Specifically, in the left panel $p_n(y)$ is plotted against n for several values of y; the grey horizontal line represents the limiting value $p_\infty (y) = \pi _1 = 0.868$, $y \in (0,1)$. The smaller the value of y, the larger the value of $p_n(y)$ for a fixed n. For example, given a threshold $\lambda _p = 0.6$, we obtain $n^\star _p$ equal to 103, 166 and 282 respectively for $y = 0.5,0.7, 0.9$. The right panel shows how the functions $p_n(y)$ progressively approach $p_\infty (y)$ as the sample size increases, as a consequence of the convergence in law of $\beta _n(\Theta )$ to $Y_\infty = \text {Ber}(\pi _1)$, that follows from (8). In Fig. 3 (second row) a truncated normal design prior on $\Omega _1$ is considered and the values of $p_n^{tr}(y)$ are plotted against n and against y. In this case similar comments hold, noting that $p_\infty (y) = \pi _1 = 1$ and $Y_\infty = 1$ with probability 1. For example, given a threshold $\lambda _p = 0.6$, we obtain values for the optimal sample sizes smaller than those of the previous case; more specifically, we have $n^\star _p$ equal to 68, 109 and 186 respectively for $y = 0.5, 0.7, 0.9$.

In Tables 1 and 2 we consider some additional design scenarios and report the values of $\beta _n(\theta _d)$, $e_n$, $e_n^{tr}$, $p_n(y)$, $p_n^{tr}(y)$ as n increases. Note that, consistently with the curves shown in the previous figures, the values of $e_n$, $e_n^{tr}$, $p_n(y)$ and $p_n^{tr}(y)$ increase monotonically with $n_d$ only for sufficiently large values of $\theta _d$ and of n. As highlighted in Sect. 3, when the truncated normal design prior is considered $e_\infty ^{tr} = p_\infty ^{tr}(y) = 1$, whereas $e_\infty$ and $p_\infty (y)$ are strictly less than 1 for any finite value of $n_d$ and $y \in (0,1]$.

Table 1 Values of $\beta _n(\theta _d)$, $e_n$ and $e_n^{tr}$ for several choices of $\theta _d$ and $n_d$ as n increases

Table 2 Values of $p_n(y)$ and $p_n^{tr}(y)$, with $y = 0.7$, for several choices of $\theta _d$ and $n_d$ as n increases

4 Other examples

In this section we extend the results of Sect. 2 to two relevant asymptotic tests: Wald test (parametric) and Sign test (nonparametric). For simplicity we consider uniparametric models. Extension to the presence of a nuisance parameter can be easily handled as suggested at the end of Sect. 2. In Sect. 4.3 we discuss some problems of the proposed methodologies with models for dependent data.

4.1 Wald test

Let us consider a regular model and let ${\hat{\theta }}_n$ be the MLE of $\theta$ that is asymptotically normal, i.e. ${\hat{\theta }}_n {\mathop {\sim }\limits ^{\centerdot }} \text {N}\left( \theta , v_n^2(\theta )\right)$, with $v_n^2(\theta ) = I_n(\theta )^{-1}$, where $I_n(\theta )$ is the Fisher information. We assume that $v^2_n(\theta ) \rightarrow 0$ as $n \rightarrow \infty$ for all $\theta$. The Wald test for hypotheses (1) is based on the test statistic $W_0 = ({\hat{\theta }}_n -\theta _0)/v_n(\theta _0).$ In this setup, Results A, B and C still provide explicit expressions for $p_\infty$ and $e_\infty$. However, expressions of $e_n$ and $p_n(y)$ are not available in closed form, due to the presence of $v_n(\theta )$ in $\beta _n(\theta )$; nevertheless, their values can be numerically approximated via standard Monte Carlo by simulation from the design prior of $\Theta$.

Case A (One-sided hypotheses) The $\alpha$-level Wald test rejects $H_0: \theta \le \theta _0$ against $H_1: \theta > \theta _0$ if $W_0 > z_{1-\alpha }$. The approximate power function is then

$$\begin{aligned} \beta _n(\theta ) = {\mathbb {P}}\left[ {\hat{\theta }}_n > v_n(\theta _0) z_{1-\alpha } + \theta _0 \right] = 1-\Phi \left[ \frac{\theta _0 - \theta }{v_n(\theta )} + \frac{v_n(\theta _0)}{v_n(\theta )} z_{1-\alpha } \right] , \, \theta \in {\mathbb {R}}, \end{aligned}$$

that satisfies (5) and Result A follows.

Case B (Point-null hypothesis vs a one-sided alternative) The $\alpha$-level Wald test for the hypothesis $H_0: \theta = \theta _0$ against $H_1: \theta > \theta _0$ has the same rejection rule as in Case A and the same power function $\beta _n(\theta )$, restricted to the values of $\theta \in [\theta _0,\infty )$. It is easy to check that Condition (6) holds and Result B follows.

Case C (Point-null hypothesis vs a two-sided alternative) The $\alpha$-level Wald test rejects $H_0: \theta = \theta _0$ against $H_1: \theta \ne \theta _0$ if $\vert W_0 \vert > z_{1-\alpha /2}$. The approximate power function is then $\beta _n(\theta ) = 1-\left[ \Phi \left( \frac{\theta _0 - \theta }{v_n(\theta )} + \frac{v_n(\theta _0)}{v_n(\theta )} z_{1-\alpha /2} \right) - \Phi \left( \frac{\theta _0 - \theta }{v_n(\theta )} - \frac{v_n(\theta _0)}{v_n(\theta )} z_{1-\alpha /2} \right) \right] , \, \theta \in {\mathbb {R}}.$ Hence Condition (6) is satisfied and Result C follows.

4.2 Sign test

Following van der Vaart (1998) (Example 14.1, p.193), let us assume that $X_1,\ldots , X_n$ is a random sample from a distribution with cdf $F(x-\theta )$, where $\theta$ is the unique median. For the sake of brevity, let us examine case B; cases A and C can be dealt with similarly. Hence, consider $H_0: \theta = \theta _0$ against $H_1: \theta > \theta _0$ and, with no loss of generality, assume $\theta _0=0$. Let $T_n = n^{-1} \sum _{i=1}^n {\mathbb {I}} \{X_i > 0\}$ be the sign statistic whose expectation and variance are respectively equal to $\mu (\theta ) = 1-F(-\theta )$ and $v^2_n(\theta ) = \left[ 1-F(-\theta )\right] F(-\theta )/n$. By the normal approximation to the binomial distribution $[v_n(\theta )]^{-1} [T_n - \mu (\theta )]$ is asymptotically standard normal. Under the null hypothesis $\mu (0)=1/2$, $v^2_n(0)=1/4$, $\sqrt{n}(T_n - 1/2) \approx \text {N}(0,1/4)$ and the test rejects $H_0$ if $\sqrt{n}(T_n - 1/2) > \frac{1}{2} z_{1-\alpha }$. The power function is $\beta _n(\theta ) \simeq 1 - \Phi \left( \frac{\frac{1}{2} z_{1-\alpha } - \sqrt{n} [F(0)-F(-\theta )]}{v_n(\theta )}\right) .$ Noting that $F(0)-F(-\theta ) > 0$ for $\theta >0$, (6) holds with $\Omega _1 = (0,+\infty )$; then (10) and (11) of Result B follow.

4.3 Issues related to dependent data

Results of the present article have been essentially thought for i.i.d. data. Under these assumptions, the hypotheses of Results A-C are typically satisfied, as we have shown in the previous examples. Conversely, when the independence assumption is dropped, the regular convergence behavior of the power function (i.e. size-$\alpha$ consistency and consistency of Definitions 1 and 2) cannot be given for granted and establishing the limiting values of the power function is much trickier than it is for the independence case. An example is given by the test for first-order autocorrelation in a standard linear regression model. Specifically, consider the model ${\textbf{y}}={{\textbf{X}}}{{\textbf{b}}} + {\textbf{u}}$ where ${\textbf{y}}$ is a $n \times 1$ vector, ${\textbf{X}}$ a known $n \times k$ matrix of rank k, ${\textbf{b}}$ an unknown vector of parameters and ${\textbf{u}}^T=(u_1, \ldots , u_n)$ a vector of random unobserved components such that $u_i = \rho u_{i-1} + \epsilon _i$, where $\vert \rho \vert <1$ and $\epsilon _i$ are i.i.d. $\text {N}(0,\sigma ^2)$, with known $\sigma ^2>0$. To test the hypothesis of no autocorrelation, $H_0: \rho =0$, one can use the classical Durbin-Watson statistics, based on the differences ${\hat{u}}_i - {\hat{u}}_{i-1}$, where ${\hat{u}}_i$ is the i-th residual when the regression equation is estimated by least squares. It is well known that (see, for instance, Bartels (1992), Wan et al. (2007), Ansley and Newbold (1979), Tillman (1975)) the power function of the Durbin-Watson test against the alternative of first-order autocorrelation ($H_1: \rho >0$, for instance) is not necessarily monotonic as $\rho$ departs from the null hypothesis, that, in some cases, the power tends to 0 as $\rho$ tends to $\pm 1$ and that, in other case, its limiting values never reach unity. Research is then required to extend our results to dependent data, but this goes beyond the goal of the present article.

5 Conclusions

In this article we consider the distribution of the frequentist power function $\beta _n(\theta )$ of a test induced by a design prior on the parameter of interest. We study the asymptotic behavior of the sequence $\beta _n(\Theta )$ as the sample size tends to infinity. As a by-product, under fairly general assumptions, we derive the limiting value of PoS, already determined by Brutti et al. (2008) and Eaton et al. (2013), who, however, did not consider the whole limit distribution of $\beta _n(\Theta )$. Results of Sect. 2 are obtained for three fundamental classes of testing problems on a scalar parameter, with or without a nuisance parameter. These are the most widely used setups in clinical trial applications, where PoS is becoming more and more popular for sample size determination. General results for i.i.d. samples are then specialized to the normal model in Sect. 3. Asymptotic parametric and nonparametric examples are discussed in Sect. 4. As expected, the choice of the design prior is crucial for determining $e_\infty$ the limiting value of $e_n$, that can be interpreted as a measure of the goodness of the design. In a well designed experiment $e_\infty$ must be as close to one as possible; $e_\infty = 1$ if and only if the design prior assigns probability one to $\Omega _1$. In the normal example we illustrate the impact of location, scale and support of the design prior on the whole limit distribution and, consequently, on $e_\infty$ and $p_\infty (y)$. In practice, the conventional choice of a conjugate design prior implies $e_\infty < 1$. To let $e_\infty$ as close to one as possible, $\vert \theta _0-\theta _d \vert$ and/or $n_d$ have to be sufficiently large. Alternatively, one can give up conjugacy and use, for instance, a truncated normal on $\Omega _1$. Whatever the choice of the design prior is, the value $e_\infty$ must be taken into account in order to implement the sample size determination criterion (4), namely in order to fix an appropriate achievable value for the threshold $\lambda _e$ so as to ensure the existence of optimal sample size [see Brutti et al. (2008)].

An additional contribution of this paper is to study the entire distribution of $\beta _n(\Theta )$ (not only its expected value $e_n$) and to consider $p_n(y)$ that takes into account the variability of the design prior. The resulting sample size criterion is then more flexible, but less automatic then the criterion based on PoS, since it requires the specification of a value of y. As for $e_\infty$ we have also discussed the impact of the design prior on the value $p_\infty (y)$.

Finally note that the hybrid frequentist-Bayesian approach followed in this paper can be easily generalized to a fully Bayesian framework by replacing the classical test and power function with their Bayesian counterparts (see Spiegelhalter et al. (2004) and Brutti et al. (2014)).

Appendix

We provide here the R functions used to implement the examples of Sect. 3.1, related to one-sided tests on the location parameter of a normal model (case A).