Several new classes of space-filling designs

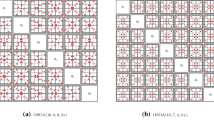
Abstract

Mappable nearly orthogonal arrays were recently proposed as a new class of space-filling designs for computer experiments. Inspired by mappable nearly orthogonal arrays, we propose several new classes of space-filling designs. The corresponding construction methods are provided. The resulting designs are more space-filling than mappable nearly orthogonal arrays while accommodating a large number of factors. In addition to the space-filling properties, the column orthogonality is also desirable for designs of computer experiments. Among the new constructed designs, one class is column-orthogonal, and the other two classes, providing many new column-orthogonal designs, are nearly column-orthogonal in the sense that each column is column-orthogonal to a large proportion of the other columns. The constructed designs are good choices for computer experiments due to their attractive space-filling properties and column orthogonality. The proposed construction methods are flexible in the choices of an orthogonal array and/or a strong orthogonal array and their usefulness is appealing. Many newly constructed space-filling designs are tabulated. The expansive replacement method and the generalized doubling play key roles in the constructions.

Appendix: Proofs of theorems

Proof of Theorem 1

From Construction 1, we have that A is an OA($\lambda s^2,s^{m_1})$ and B is an LH$(s, m_2)$ based on an SOA$(s,m_2,p^2,2+)$. Due to the expansive replacement method, any two columns from the same group for D must be two columns of a repeated B up to a row permutation, implying that D satisfies Definition 1(c) according to the definition of the SOA$(s,m_2,p^2,2+)$. Let $(d_1, d_2)$ be any two columns from different groups for D. According to the expansive replacement method, $(d_1, d_2)$ must be two columns of an OA($\lambda s^2,s^{m_1})$ up to a level permutation. Since any level permutation of an OA does not change its strength, $(d_1, d_2)$ is an OA with s levels. Therefore, D satisfies Definitions 1(a) and 1(b). This completes the proof. $\square$

Proof of Theorem 2

We only need to prove that the resulting design, say D, from Theorem 2 is column-orthogonal as its stratifications follow from Theorem 1. As B is column-orthogonal, then any two columns from the same group for D is column-orthogonal due to the expansive replacement method. According to the proof of Theorem 1, any two columns from different groups for D is an OA with s levels, and then is also column-orthogonal. This completes the proof. $\square$

In order to prove Theorem 3, we first give Lemmas 1, 2 and 3. From Step 1 of Construction 2, we have the following result.

Lemma 1

(Sun and Tang 2017a) Any four columns, derived by taking two columns from one group $C_{i_1}$ and two columns from another group $C_{i_2}$ with $i_1 \ne i_2$, must form an OA$(\lambda s^2, 4, p,4)$.

According to the specific structures of E and F in Step 2 of Construction 2, we have the following result.

Lemma 2

Any three columns, derived by taking two columns from E and one column from F, must form an OA$(\lambda p s^2, 3, p,3)$.

Lemma 2 allows many three-column arrays whose columns come from E and F to have strength three, and then allows the constructed D in (6) to have the stratification property of Definition 2(c).

Note that any linear level permutation of C in Step 2 of Construction 2 does not change its strength such that $u + C$ in F has the same strength as C for $u=1, \dots , p-1$. From Lemma 1, a direct result is given below.

Lemma 3

Any four columns, derived by taking two columns from one group $E_{i_1}$ and two columns from another group $F_{i_2}$ with $i_1 \ne i_2$, must form an OA$(\lambda p s^2,4, p,4)$.

Lemma 3 allows many four-column arrays whose columns come from E and F to have strength four, and then allows design D in (6) to have the stratification property of Definition 2(b).

Proof of Theorem 3

From (5), we have $D^*= HR$, where $H=(H_1, \dots , H_q)$ and $R=\textrm{diag}\{U,\dots ,U\}$ with U repeating q times. By Lemma 2, we see that (E, F) is an orthogonal array of strength 2, implying that H is column-orthogonal. By noting that U is also column-orthogonal, we have ${D^*}^T {D^*}=(HR)^T HR = R^T (H^T H) R = c_1 R^T R=c_2I_{2q}$, where $c_1$ and $c_2$ are two constants, and $I_{2q}$ is the identity matrix of order 2q. This shows that $D^*$ in (5) is column-orthogonal, so is D in (6).

Before showing the stratifications of D, we first consider two mappings $h_1(x)$ and $h_2(x)$. Note that any column d of D has the following form:

$$\begin{aligned} d=b p^2 + b' p \pm b'', \end{aligned}$$

(8)

where $(b, b',b'')$ up to a column permutation is $(e_{ik}, f_{ik'}, e_{jl})$, where $k'=k+1$ if $k\le m_2-1$ and $k'=1$ if $k = m_2$. Consider the mapping

$$\begin{aligned} h_1(x) = \left\lfloor \{ x+ (p^3-1)/2 \} / p \right\rfloor - (p^2-1)/2 \ \text{ with } \ x \in \Omega (p^3), \end{aligned}$$

which collapses the $p^3$ levels in $\Omega (p^3)$ into the $p^2$ levels in $\Omega (p^2)$. We need to show that $h_1(d)=bp+b'$, which means that the column d becomes the column $bp+b'$ after the mapping $h_1(x)$ is applied to each entry of d. By letting $r=b+(p-1)/2$, $r'= b' + (p-1)/2$ and $r''=\pm b'' + (p-1)/2$, we have

$$\begin{aligned} \begin{aligned} h_1(d)&= \left\lfloor \{ b p^2 + b' p \pm b'' + (p^3-1)/2\} / p \right\rfloor - (p^2-1)/2 \\&= \left\lfloor ( r p^2 + r'p + r'') / p \right\rfloor - (p^2-1)/2. \end{aligned} \end{aligned}$$

Since all entries of $(b, b', \pm b'')$ are in $\Omega (p)$, all entries of $(r, r', r'')$ must take values from $\{0, 1, \dots , p-1\}$. We then have $h_1(d)= r p + r' - (p^2-1)/2= bp+b'$. We next consider the mapping

$$\begin{aligned} h_2(x) = \left\lfloor \{ x+ (p^3-1)/2 \} / p^2 \right\rfloor - (p-1)/2 \ \text{ with } \ x \in \Omega (p^3), \end{aligned}$$

which collapses the $p^3$ levels in $\Omega (p^3)$ into the p levels in $\Omega (p)$. By the above similar discussion, we have $h_2(d)= b$.

We now prove the stratifications of D in Definition 2(b). Consider two columns $d_1$ and $d_2$ of D as in (8), and write them as

$$\begin{aligned} d_1=b_1 p^2 + b_1' p \pm b_1'' \quad \textrm{and} \quad d_2=b_2 p^2 + b_2' p \pm b_2''. \end{aligned}$$

Let us show that the array $(d_1, d_2)$ can be collapsed into an OA$(\lambda p s^2, 2, p^2, 2)$, that is to say, $(h_1(d_1),$ $h_1(d_2))=(b_1 p+b_1', b_2p+b_2')$ is an OA$(\lambda p s^2,2,p^2,2)$. In fact, this is true by noting the following two facts: (i) from Lemma 3, $(b_1, b_2, b_2, b_2')$ is an OA$(\lambda p s^2, 4, p, 4)$; (ii) $p^3x_1+p^2x_2+px_3+x_4$ establishes a one-to-one correspondence between the $p^4$ pairs $(x_1, x_2, x_3, x_4)$ with $x_1, x_2,x_3,x_4 \in \Omega (p)$ and the $p^4$ levels in $\Omega (p^4)$. This shows that D satisfies Definition 2(b).

Next, we prove the stratifications of D in Definition 2(c). Let us show that the array $(d_1, d_2)$ can be collapsed into an OA$(\lambda p s^2,2,{p^2 \times p}, 2)$ and an OA$(\lambda p s^2,2,{p \times p^2}, 2)$, that is to say, $(h_1(d_1), h_2(d_2))=(b_1 p + b_1', b_2)$ and $(h_2(d_1), h_1(d_2))$ $=(b_1, b_2p + b_2')$ are an OA$(\lambda p s^2,2,{p^2 \times p}, 2)$ and an OA$(\lambda p s^2,2,{p \times p^2},$ 2), respectively. In fact, this is true by noting the following two facts: (i) from Lemma 2, $(b_1, b_1', b_2)$ and $(b_1, b_2,b_2')$ are two OA$(\lambda p s^2, 3, p, 3)$’s; (ii) $px_1+x_2$ establishes a one-to-one correspondence between the $p^2$ pairs $(x_1, x_2)$ with $x_1, x_2 \in \Omega (p)$ and the $p^2$ levels in $\Omega (p^2)$. This shows that D satisfies Definition 2(c). This completes the proof. $\square$

Proof of Theorem 4

From the structures of $C^{(1)}$ and $C^{(2)}$, we have that the array $(c_{kj}^{(1)}, c_{ij}^{(1)}, c_{ij}^{(2)})$ is a repeated full factorial and is hence an OA$(\lambda s^3,3,s,3)$ for any $k \ne i$. From the expansive replacement method, $c_{kl}^{(1)}$ can be obtained by permuting levels in $c_{kj}^{(1)}$ for $l\ne j$. Because of this, the array $(c_{kl}^{(1)}, c_{ij}^{(1)}, c_{ij}^{(2)})$ with $l \ne j$ is also an OA$(\lambda s^3,3,s,3)$. Then we have that the array $(c_{kl}^{(1)}, c_{ij}^{(1)}, c_{ij}^{(2)})$ has strength 3 for any $k \ne i$. According to Theorem 4 of Zhou and Tang (2019), Definitions 3(a) and 3(b) can be verified for design D in (7). Since B is an LH$(s, m_2)$ based on an OA$(s, p^{m_2})$, any two columns from the same group for D can be collapsed into an OA$(\lambda s^3, p^2)$, implying that D satisfies Definition 3(c). This completes the proof. $\square$

Proof of Theorem 5

We only need to prove that the resulting design, say D, from Theorem 5 is column-orthogonal as its stratifications follow from Theorem 4. From Lemma 6.27 of Hedayat et al. (1999) and the definition of X, we see that $(GD_{\textrm{I}}(X)$, $GD_{\textrm{II}}(X))$ in Step 1 of Construction 3 is an OA($\lambda s^3,s^{2m_1})$. As B is column-orthogonal, then $(C^{(1)}, C^{(2)})$ is column-orthogonal according to the proof of Theorem 2, and the inner product of any two columns from the centered $(C^{(1)}, C^{(2)})$ equals zero. From (7), let $(d_i, d_j)$ be any two columns from the centered D, then we have $d_i=sc_i^{(1)} + c_i^{(2)}$ and $d_j=sc_j^{(1)} + c_j^{(2)}$, where $c_i^{(1)}, c_i^{(2)}, c_j^{(1)}$ and $c_j^{(2)}$ are from the centered $(C^{(1)}, C^{(2)})$, implying that $d_i^Td_j=0$ due to the column orthogonality of $(C^{(1)}, C^{(2)})$. This completes the proof. $\square$