Abstract
Subsampling is an efficient method to deal with massive data. In this paper, we investigate the optimal subsampling for linear quantile regression when the covariates are functions. The asymptotic distribution of the subsampling estimator is first derived. Then, we obtain the optimal subsampling probabilities based on the A-optimality criterion. Furthermore, the modified subsampling probabilities without estimating the densities of the response variables given the covariates are also proposed, which are easier to implement in practise. Numerical experiments on synthetic and real data show that the proposed methods always outperform the one with uniform sampling and can approximate the results based on full data well with less computational efforts.






Similar content being viewed by others
Notes
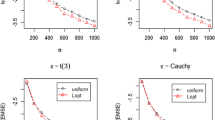
In Figures 1, 2, and 3, the three columns correspond to the three distributions of the basis coefficients (mvNormal, mvT3, mvT2), respectively, and the three rows correspond to the three distributions of random errors (Normal, T1, Hetero), respectively. For example, the figure in the first column and the first row is for the mvNormal-Normal datasets.
References
Ai M, Wang F, Yu J, Zhang H (2021) Optimal subsampling for large-scale quantile regression. J Complex 62:10512
Ai M, Yu J, Zhang H, Wang H (2021) Optimal subsampling algorithms for big data regression. Stat Sinica 31(2):749–772
Atkinson A, Donev AN, Tobias RD (2007) Optimum experimental designs, with SAS. Oxford University Press, New York
Cardot H, Ferraty F, Sarda P (2003) Spline estimators for the functional linear model. Stat Sin 13:571–591
Cardot H, Crambes C, Sarda P (2005) Quantile regression when the covariates are functions. J Nonparameter Stat 17(7):841–856
Cardot H, Crambes C, Sarda P (2004) Conditional quantiles with functional covariates: an application to ozone pollution forecasting. In: Compstat 2004 Proceedings, pp 769–776
Chen K, Müller H (2012) Conditional quantile analysis when covariates are functions, with application to growth data. J R Stat Soc B 74(2):67–89
Chen K, Breitner S, Wolf K et al (2021) Ambient carbon monoxide and daily mortality: a global time-series study in 337 cities. Lancet Planet Health 5(4):e191–e199
Claeskens G, Krivobokova T, Opsomer JD (2009) Asymptotic properties of penalized spline estimators. Biometrika 96(3):529–544
de Boor C (2001) A practical guide to splines. Springer, Berlin
Dobriban E, Liu S (2019) Asymptotics for sketching in least squares regression. In: Advances in Neural Information Processing Systems 32, pp 3675–3685
Drineas P, Magdon-Ismail M, Mahoney MW, Woodruff DP (2012) Fast approximation of matrix coherence and statistical leverage. J Mach Learn Res 13(1):3441–3472
Drineas P, Mahoney MW, Muthukrishnan S (2006) Sampling algorithms for \(l_2\) regression and applications. In: Proceedings of the Seventeenth Annual ACM-SIAM Symposium on Discrete Algorithm, pp 1127–1136
Fan Y, Liu Y, Zhu L (2021) Optimal subsampling for linear quantile regression models. Can J Stat 49(4):1039–1057
He S, Yan X (2022) Functional principal subspace sampling for large scale functional data analysis. Electron J Stat 16(1):2621–2682
Hjort NL, Pollard D (2011) Asymptotics for minimisers of convex processes. arXiv preprint arXiv:1107.3806
Homrighausen D, McDonald DJ (2019) Compressed and penalized linear regression. J Comput Graph Stat 29:309–322
Kato K (2012) Estimation in functional linear quantile regression. Ann Stat 40(6):3108–3136
Kinoshita H, Türkan H, Vucinic S et al (2020) Carbon monoxide poisoning. Toxicol Rep 7:169–173
Koenker R (2005) Quantile regression. Cambridge University Press, Cambridge
Koenker R, Bassett G (1978) Regression quantiles. Econometrica 46(1):33–50
Liu C, Yin P, Chen R et al (2018) Ambient carbon monoxide and cardio-vascular mortality: a nationwide time-series analysis in 272 cities in China. Lancet Planet Health 2(1):e12–e18
Liu H, You J, Cao J (2021) Functional L-optimality subsampling for massive data. arXiv preprint arXiv:2104.03446
Ma P, Mahoney MW, Yu B (2015) A statistical perspective on algorithmic leveraging. J Mach Learn Res 16(27):861–911
Mahoney MW (2011) Randomized algorithms for matrices and data. Found Trends Mach Learn 3:123–224
Ma P, Zhang X, Xing X, Ma J, Mahoney MW (2020) Asymptotic analysis of sampling estimators for randomized numerical linear algebra algorithms. In: Proceedings of the Twenty Third International Conference on Artificial Intelligence and Statistics, pp 1026–1035
Moazami S, Noori R, Amiri BJ et al (2016) Reliable prediction of carbon monoxide using developed support vector machine. Atmos Pollut Res 7(3):412–418
Raskutti G, Mahoney MW (2016) A statistical perspective on randomized sketching for ordinary least-squares. J Mach Learn Res 17(213):1–31
Reiss P, Huang L (2012) Smoothness selection for penalized quantile regression splines. Int J Biostat. https://doi.org/10.1515/1557-4679.1381
Ruppert D (2002) Selecting the number of knots for penalized splines. J Comput Graph Stat 11(4):735–757
Sang P, Cao J (2020) Functional single-index quantile regression models. Stat Comput 30(4):771–781
Shams R, Jahani A, Moeinaddini M, Khorasani N (2020) Air carbon monoxide forecasting using an artificial neural network in comparison with multiple regression. Model Earth Syst Environ 6:1467–1475
Shao Y, Wang L (2021) Optimal subsampling for composite quantile regression model in massive data. Stat Pap 63:1139–1161
Shao L, Song S, Zhou Y (2022) Optimal subsampling for large-sample quantile regression with massive data. Can J Stat. https://doi.org/10.1002/cjs.11697
Stone CJ (1985) Additive regression and other nonparametric models. Ann Stat 13(2):689–705
Wang H (2019) More efficient estimation for logistic regression with optimal subsamples. J Mach Learn Res 20(132):1–59
Wang H, Ma Y (2021) Optimal subsampling for quantile regression in big data. Biometrika 108(1):99–112
Wang H, Zhu R, Ma P (2018) Optimal subsampling for large sample logistic regression. J Am Stat Assoc 113(522):829–844
Wang S, Gittens A, Mahoney MW (2018) Sketched ridge regression: optimization perspective, statistical perspective, and model averaging. J Mach Learn Res 18(218):1–50
Yao Y, Wang H (2019) Optimal subsampling for softmax regression. Stat Pap 60(2):585–599
Yoshida T (2013) Asymptotics for penalized spline estimators in quantile regression. Commun Stat Theory M. https://doi.org/10.1080/03610926.2013.765477
Yu J, Wang H, Ai M, Zhang H (2020) Optimal distributed subsampling for maximum quasi-likelihood estimators with massive data. J Am Stat Assoc 117(537):265–276
Yuan M (2006) GACV for quantile smoothing splines. Comput Stat Data Ann 50(3):813–829
Yuan X, Li Y, Dong X, Liu T (2022) Optimal subsampling for composite quantile regression in big data. Stat Pap 63:1649–1676
Zhou S, Shen X, Wolfe D (1998) Local asymptotics for regression splines and confidence regions. Ann Stat 26(25):1760–1782
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 11671060) and the Natural Science Foundation Project of CQ CSTC (No. cstc2019jcyj-msxmX0267). The authors would like to thank the editor and the anonymous reviewers for their detailed comments and helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: proofs for theoretical results
Appendix A: proofs for theoretical results
To prove our theorems, we begin with the following several lemmas. Note that the subsampling model involves two kinds of random errors: sampling error and model error, so we need to consider these two types of randomness in the calculation.
Lemma 1
Under Assumptions 1 and 5, for any vector \( \varvec{\mu } \in \mathbb {R}^{K+p+1} \), there are some positive constants \( C_3\), \(C_4 \), \( C_5 \) and \( C_6 \) such that
where \( \sigma _{min}(\cdot ) \) and \(\sigma _{max}(\cdot ) \) denote the smallest and largest eigenvalues of a matrix, respectively. In addition, we have \(\Vert \varvec{G}\Vert _{\infty }=O(K^{-1})\) and \(\Vert \varvec{D}_q\Vert _{\infty }=O(K^{2q-1})\).
Proof
These results can be derived directly from Lemma S2 and S3 in the supplementary file of Liu et al. (2021). \(\square \)
Lemma 2
Under Assumptions 1, and 3–5, there are two positive constants \( C_7 \) and \( C_8 \) such that
and \(\Vert \varvec{H}_{\tau }\Vert _{\infty }=O(K^{-1})\).
Proof
From Assumption 3, we have that there are two positive constants \( c_{\epsilon } \) and \( C_{\epsilon } \) such that \( c_{\epsilon }\le f_{\epsilon \mid \varvec{X}(t)}(0,x(t))\le C_{\epsilon } \). On the other hand, by Lemma 1, we have \(\Vert \varvec{G}_{\tau }\Vert _{\infty }=O(K^{-1})\). Thus, the lemma can be directly proved by combining Lemma 1 with Assumptions 3 and 4. \(\square \)
Lemma 3
Let \( \psi _\tau (u)=\tau -I(u<0) \) and \( u_i=y_i-\varvec{B}^T_i\varvec{\theta }_0 \). Under the same assumptions as Theorem 3, for any non-zero \( \varvec{\delta } \in \mathbb {R}^{K+p+1}\), we have
where \( \left\{ \tau (1-\tau )(\varvec{V}_{\pi }+\eta \varvec{G})\right\} ^{-1/2}\varvec{W}\rightarrow {N(\varvec{0},\varvec{I})} \) in distribution.
Proof
Set
To prove the asymptotic normality of \( U_r \), it suffices to verify that \( U_r \) satisfies the Lindeberg-Feller conditions. Firstly, the conditional expectation and conditional variance are given by
From the fact that \( \textrm{P}(y_i<\int ^1_0 x_i(t)\beta (t)\textrm{d}t\mid x_i(t))=\tau \), we have
where \( b_i=\int _{0}^{1}x_i(t)b_a(t)\textrm{d}t \), and the third equality is from the definition of \( \varvec{\theta }_0 \) and the fourth equality is obtained by the Taylor expansion of the cumulative distribution function of the error \( \epsilon _i \) at point \(\epsilon _i=0 \). As a result, the unconditional expectation of \( U_r \) can be calculated as
More specifically, since \( x_i(t) \) are square integrable functions, by the Cauchy-Schwarz inequality in integral form, there exist constant c such that
Similarly, we have
Thus, by the property of B-spline function, \( \int _0^1\varvec{B}(t)\textrm{d}t = O(K^{-1}) \), and \( b_a(t)=O(K^{-d})\), we can find that \( \Vert \varvec{B}_i \Vert _{\infty }= O(K^{-1})\) and \( b_i=O(K^{-d})\) are satisfied. Putting them together, we obtain (A2).
On the other hand, according to law of total variance, the unconditional variance is given by
We first deal with the first term in (A3) as follows
Similarly, the second term in (A3) equals
Thus, substituting (A4) and (A5) into (A3), we have
Denote \(\xi _i = -\sqrt{\frac{K}{r}}\frac{R_i}{n\pi _i}\varvec{B}^T_i\varvec{\delta }\psi _\tau (u_i)\). We now check the Lindeberg-Feller conditions. For every \( \epsilon >0 \),
where
and the last equality holds by combining Assumption 6 and the fact that \( \mid \psi _\tau (u_i)\mid \le 1 \). Thus, by Lindeberg-Feller central limit theorem, it can be concluded that as \( n \rightarrow \infty \), \( r \rightarrow \infty \),
in distribution, which implies that the equation (A1) holds because \( \textrm{E}\left[ U_r\right] =O(\sqrt{rK}K^{-(d+1)})=o_P(1) \). This completes the proof. \(\square \)
Lemma 4
Let \( v_i=\sqrt{K/r}\varvec{B}^T_i\mathrm {\delta } \). Under the same assumptions as Theorem 3,
Proof
Let
Since
we can obtain the total expectation of \( M_r \) as follows
Now, we show the total variance of \( M_r \) satisfying \( \textrm{Var}[M_r]=o_P(1) \). Note that the variance of \( M_r \) can be evaluated as
where the second inequality is from the fact that
Thus, from (A8), (A9) and Assumption 6, and noting \( \textrm{E}\left[ M_r\right] =O(1) \), we have \( \textrm{Var}\left[ M_r\right] =o_P(\sqrt{K/r^3})=o_P(1) \). As a result, Lemma 4 holds by Chebyshev’s inequality. \(\square \)
In the following, we present the proofs of Theorems 1, 2, 3, 4, and 5 in turn.
Proof of Theorem 1 and 2
Theorem 1 can be proved similar to Theorem 1 of Yoshida (2013), and Theorem 2 can be obtained directly from Theorem 1 by considering Assumptions 4 and 5. Here we omit the details. \(\square \) \(\square \)
Proof of Theorem 3
Let
where \( u_i=y_i-\varvec{B}^T_i\varvec{\theta }_0 \) and \( v_i=\sqrt{r/K}\varvec{B}^T_i\varvec{\delta } \). It is easy to see that this function is convex and minimized at \(\sqrt{r/K}(\varvec{\tilde{\theta }}-\varvec{\theta }_0) \).
On the other hand, using Knight’s identity,
where \( \psi _\tau (u)=\tau -I(u<0) \), we have
where
From Lemma 3, \( Z_{1r}(\varvec{\delta }) \) in (A11) satisfies
where \(\left\{ \tau (1-\tau )(\varvec{V}_{\pi }+\eta \varvec{G})\right\} ^{-1/2}\varvec{W}\rightarrow {N(\varvec{0},\varvec{I})}\) in distribution. Furthermore, Lemma 4 and \( Z_{3r}(\varvec{\delta }) \) in (A11) yield
Therefore, from (A11), (A12) and (A13), we can obtain
Since \( Z_{r}(\varvec{\delta })/n\) is convex with respect to \( \varvec{\delta } \) and has unique minimizer, from the corollary in page 2 of Hjort and Pollard (2011), its minimizer, \( \sqrt{r/K}(\varvec{\tilde{\theta }}-\varvec{\theta }_0)\), satisfies that
Because the random vector is only \( \varvec{W}\) in asymptotic form of \( \varvec{\tilde{\theta }} \) and \( \tilde{\beta }(t)-\beta _0(t)=\varvec{B}^{T}(t)(\varvec{\tilde{\theta }}-\varvec{\theta }_0) \), the expectation of \( \tilde{\beta }(t)-\beta _0(t) \) can be written as
where \( b_{\lambda }(t)=-\frac{\lambda }{n}\varvec{B}^{T}(t)\varvec{H}_{\tau }^{-1}\varvec{D}_q\varvec{\theta }_0 \). Together with \( \tilde{\beta }(t)-\beta (t)= \tilde{\beta }(t)-\beta _0(t)+ \beta _0(t)-\beta (t) \), we have the asymptotic bias of \( \tilde{\beta }(t)\) as
Thus, we have
Combining the fact that
by the definition of \( \varvec{W} \) and Slutsky’s Theorem, we can obtain for \( t\in [0,1] \), as \(r, n\rightarrow \infty \),
Further, from the discussions before Theorem 2, we know that \( b_{\lambda }(t) \) and \( b_a(t) =o_P(1)\) are negligible. Thus, we have
So Theorem 3 is proved. \(\square \)
Proof of Theorem 4
Note that
where the last inequality is from the Cauchy-Schwarz inequality and the equality in it holds if and only if \( \pi _i \propto \Vert \varvec{H}^{-1}_{\tau }\varvec{B}_i\Vert _2 \). So the proof is completed by considering \(\sum _{i=1}^{n}\pi _i=1 \). \(\square \)
Proof of Theorem 5
Note that
where the last inequality is from the Cauchy-Schwarz inequality and the equality in it holds if and only if \( \pi _i \propto \Vert \varvec{B}_i\Vert _2 \). So the proof is completed by considering \(\sum _{i=1}^{n}\pi _i=1 \). \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Yan, Q., Li, H. & Niu, C. Optimal subsampling for functional quantile regression. Stat Papers 64, 1943–1968 (2023). https://doi.org/10.1007/s00362-022-01367-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00362-022-01367-z