1 Introduction

The over-reliance on a p-value of 0.05 and the prevalence of testing against zero rather than a practically meaningful or important effect size are two long-standing concerns of the statistical community (Wasserstein et al. 2019; Amrhein et al. 2019; Blake et al. 2019). Many prominent statisticians have encouraged researchers to reflect carefully on the form of their tests, and on factors to consider when setting parameters (e.g., Hodges and Lehmann 1954; Cohen 1988). Yet standard tests still dominate the scientific literature. There is thus a place for tools that encourage researchers to think more broadly about their statistical design.

The most common tool used in study design is the sample size calculator, available in numerous web implementations (e.g., Kohn & Senyak 2021) as well as in software repositories and commercial statistical software packages. Sample size calculators usually provide for a variety of study designs, such as continuous or binary outcomes and one group or two. However, typically the default—and sometimes, the only—test options are the t-test with a null value of 0; the default settings for alpha and power levels are the usual suspects; and results may only be provided as numbers. Sample size calculators encourage researchers to think about power and sample sizes, but rarely about other facets of their study design.

Power calculations in statistical packages such as SAS (SAS Institute Inc. 2013) and some specialist calculators such as G*power (Faul et al. 2007) allow tests against values other than zero and can display power vs. sample size graphs at different candidate alpha levels or effect sizes. We propose a visualization tool that extends such calculators to simultaneously consider multiple tests concerning minimum meaningful effect sizes, at multiple test levels.

Visualization has become an important component of statistical software packages, helping researchers understand their data through boxplots, clustering and so forth. One such tool is the funnel plot, developed by Light and Pillemer (1984) to identify publication bias in meta-analyses (Kossmeier et al. 2020a). Funnel plots map trial summary statistics onto a chart in which usually the horizontal axis is the effect size while the vertical axis is a measure of precision, usually the standard error (SE). The inverse relationship of SE to sample sizes suggests that the chart underlying a funnel plot could be used to inform sample size calculations.

Funnel plots have been enhanced with shading to identify regions of the chart that correspond to ranges of p-values for a standard test statistic (“contour-enhanced funnel plots”—Peters et al. 2008). Distinguishing regions in this manner aids visual interpretation of the statistical significance of the findings (Sterne et al. 2017). Another recent enhancement is to use color bands to highlight the power of the studies, creating “sunset funnel plots” (Kossmeier et al. 2020b). An enhancement to funnel plots that to our knowledge has not previously been considered is to visually distinguish findings concerning practically meaningful effects from those that are statistically significant but not meaningful.

In the following, we first present this enhancement to funnel plots. We then show how such generalized funnel plots can be adapted to a completely different purpose: viz, to act as sample size calculators that simultaneously display results for equivalence tests and inferiority and non-superiority tests in both directions, all at multiple test levels. (These tests are described in the next section.) As with a conventional Neyman-Pearson analysis, estimates of anticipated effect sizes and variances are required before selecting a sample size. A Neyman-Pearson analysis also requires that an alpha level for either a directional or two-sided test be selected prior to the study, and our tool is designed to assist rather than replace this step.

We describe an implementation of the tool. We argue that the tool’s use in study design could encourage researchers to think not only about the effect sizes that are practically meaningful and the costs of both Type I and Type II errors in their context, but also to think about whether a finding of non-inferiority, say, might be sufficient for their research purpose, or even whether a research question should be flipped.

2 Generalized funnel plots

2.1 Generalizing standard funnel plots

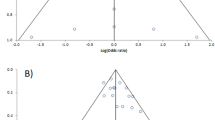
A conventional funnel plot of effect sizes versus the standard error depicts a triangular region, centred on the pooled mean, in which 95% of study findings should fall if there is no bias and no heterogeneity in the underlying true effects. We can identify two additional regions outside that triangle, corresponding to findings that are significantly greater than or significantly less than the pooled mean, given a one-sided test alpha of 0.025. Figure 1a uses shading to distinguish these three regions. The central triangle corresponds to findings that are not significantly different to the pooled mean, i.e., that would be inconclusive under a standard Null Hypothesis Significance Test (NHST) against the pooled mean. The plotted points are for illustrative purposes and are from van Aert and Niemeyer’s (2021) re-examination of a 2014 meta-analysis of studies into cognitive behaviour therapy for problem gamblers.

Fig. 1
figure 1

a A conventional funnel plot centred on the pooled mean divides the chart into three, corresponding to rejection regions of one-sided tests that the effect size is greater than or is less than the pooled mean, plus a region where both tests are inconclusive. b A funnel plot centred on zero. c Generalized funnel plot, showing regions of significance for tests against the minimum meaningful effect boundaries, here shown at ± 0.2. Each chart shows the same data from a meta-analysis in which the effect size is Hedges’ g and the meta-analysis outcome is depicted as a cross

Full size image

Figure 1b shows the same data in a funnel plot centred on zero. Findings in the region labelled inconclusive are not significantly different to zero at a two-sided test alpha level of 0.05. To interpret Fig. 1c, consider the superposition of two funnel plots respectively centred on the upper and the lower bound of meaningful effect sizes (shown here with magnitude 0.2, i.e., small on Cohen’s scale). Suppose each of the funnel plots is drawn with the same one-sided alpha level of 0.025. The region labelled “inconclusive” in Fig. 1c is the overlap of the “inconclusive” regions of the two plots, where the tests that the effect is significantly different to the upper bound and that it is significantly different to the lower bound are both rejected. The region labelled “equivalent” is the overlap of the “superior” region of the plot centred on the lower bound and the “inferior region” of the plot centred on the upper bound, and hence is where the effect is conclusively in the range of effect sizes that are not meaningful. The region labelled “superior” in Fig. 1c is where the superior regions overlap, and similarly for “inferior”. “Non-inferior” and “non-superior” are regions where one, but not both, plots are inconclusive.

This terminology is that used in comparative drug trials (e.g., Piaggio et al. 2006) because the regions in the chart correspond to the rejection regions of the tests used to establish whether one study arm is relatively superior (inferior, etc.) to the other arm.

Figure 1b shows that all but two of the findings in the meta-analysis are significantly different to zero at a two-sided alpha of 0.05. However, Fig. 1c shows that, assuming the smallest meaningful effect size is 0.2, only one study is consistent with a finding of superiority, that is, that the intervention brings an effect of meaningful size. On the other hand, all but one study is consistent with the finding that the outcomes with the intervention are non-inferior to those in the other study arm. The meta-analysis outcome indicates superiority at the higher signficance level.

2.2 Generalizing contour-enhanced funnel plots

Contour-enhanced funnel plots can similarly be generalized to highlight meaningful effect sizes. Contour-enhanced plots typically are centred on zero and consider two significance levels, giving three ranges: say, the p-values from two-sided NHSTs that are greater than 0.10, less than 0.01, or in-between. Figure 2a illustrates such an enhanced funnel plot. The darkest region corresponds to findings that are not significant at the least stringent test level. Usually, regions where findings are significantly greater than zero at a given test level are not distinguished from regions where findings are significantly less than zero at that level. By making this distinction, we have identified five regions in total. Figure 2b shows such a contour-enhanced plot adapted to highlight meaningful effects, again assuming the smallest meaningful magnitudes are symmetric about zero. There are now nine regions, as described in the figure legend.

Fig. 2
figure 2

a Contour-enhanced funnel plot uses shading to identify regions of different statistical significance. b Generalized enhanced funnel plot that uses tests against symmetric minimum meaningful effect boundaries, here at ± 0.2. Plotted data points are as in Fig. 1

Full size image

3 Adapting the funnel plots to be a study design tool

Consider the hypothesis that an effect size is greater than 0.2 and a second hypothesis that the effect size is greater than 0.3. The second hypothesis is said to be stronger than the first because it limits the effect size to a smaller range: whenever the second hypothesis is true, then so is the first. We will therefore say that a statistical test is stronger than another if it tests a stronger hypothesis, and both tests use the same alpha level. We will also say a test is stronger than another if both test the same hypothesis, but the first uses a more stringent alpha level, say, 0.05 rather than 0.10.

Suppose now that a researcher in the design stage of a study computes an anticipated sample size and SE, and plots these as a point on the charts in Fig. 1 or 2. The shade of the region in which the point falls will indicate the strongest of the tests under consideration that would be significant for such a finding. However, that test may not have the required power. A weaker test must then be employed to increase power.

The calculations behind the funnel plots are readily modified to ensure that the region in which a point corresponding to an anticipated effect size and SE falls is the strongest of the candidate tests with the required power. For technical details, see Online Resource 1: “Error rates and sample sizes for one-sided and equivalence tests”.Footnote 1 Figure 3a is the result of applying this modification to Fig. 2b with 80% power, and then translating the units on the vertical axis from SE to total sample size. SE and sample size have an inverse relationship that depends on the study design: this illustration assumes a two group design with equi-sized groups and an anticipated pooled variance of one. While the nominated units on the vertical axis in Fig. 3 have changed, the scaling has not, so a sample size difference of 16, say, represents an increasingly small distance as you go up the charts. The vertical lines in Fig. 3 are at two potential effect sizes; tracking either line upward confirms that as sample size increases, a stronger test is expected to have the desired power.

Fig. 3
figure 3

A generalized funnel plot modified to become a sample size calculator for multiple tests simultaneously. a Shows rejection regions for tests at one-sided alpha levels 0.025 and 0.005 while b also allows the unusually large value of 0.25. The heavy vertical lines are at candidate effect sizes, and assist with visually estimating the sample size needed for a test to have required power at that effect size

Full size image

The region labelled “inconclusive” is enlarged in Fig. 3a compared with that in Fig. 2b. This change is where tests on values that would be significant do not have adequate a priori power. The other regions in the chart are similarly affected, moving upward on the vertical scale to smaller SEs/larger sample sizes. Some regions where equivalence was found (that is, both tests for non-inferiority and non-superiority were significant) are now reduced to findings of either non-inferiority or non-superiority; see Online Resource 1 for clarification on this aspect.

An R-implementation of our tool was used to create the figures in this manuscript and is available online as a Shiny app at meraglim.shinyapps.io/genSSize. The R-code and documentation are available at github.com/JA090/generalized. The tool optionally creates colored versions of the charts. It currently caters for t-tests based on one and two group study designs, and for Pearson’s correlation using Fisher’s transformation. The t-tests are at a default 38 degrees of freedom that users are asked to refine after initial computations lead them to select an approximate sample size. Users must also enter desired power and at least one test alpha level. They may also nominate multiple anticipated effect sizes or correlations, to help gauge the sensitivity of the sample size estimate. These entries are presented as vertical lines through each of the values. Of interest are where these lines cross into regions representing another test. On clicking a crossing point, the required sample size is returned. To help position the cursor accurately, the ranges of displayed effect sizes and sample sizes can be modified.

An option overlays the rejection region boundaries for a NHST with zero null over the rejection regions for the various tests against minimum meaninful effect magnitudes. This faciltates comparison with conventional sample size calculations.

To emphasize its link with funnel plots, our tool also allows users to create generalized funnel plots such as those in Figs. 1 and 2. If this option is selected, the user is asked to supply lists of effect sizes and SEs of the studies. These are plotted as points along with the meta-analysis outcome, which can be selected from a fixed-effects or a maximum likelihood random-effects model provided through the metafor CRAN package (Viechtbauer 2010).

4 Discussion

We suggest visualization tools have a role in moving researchers away from dichotomous decision-making based on statistical significance, as called for by Amrhein et al. (2019) and many others. A valid question is whether it is worth asking researchers to consider tests of multiple hypotheses at multiple alpha levels, as our tool does, given the additional complexity. One answer is that researchers who only look for positive effects may miss reporting findings that add to the body of knowledge and may be useful to stakeholders in the research. For example, suppose a researcher hopes to establish superiority and anticipates a moderate effect size, say three times the smallest meaningful effect magnitude. Figure 1c shows that, even ignoring power, the anticipated standard error needs to be close to the smallest meaningful effect magnitude to plausibly seek a significant result at a two-sided alpha level of 0.05. In some cases, establishing non-inferiority may be enough for the research purpose and will be a more realistic goal if sample sizes are constrained. Setting a goal of non-inferiority may still allow a finding of superiority (US Food and Drug Administration 2016)—or vice versa, provided the required margins are selected prior to the study (Committee for Proprietary Medicinal Products 2001).

To determine the appropriate direction of a test, Neyman (1977, p. 104) argues that the hypothesis of interest should be set so that the errors deemed “more important to avoid” are Type I. This is because stronger control is exercised over these than over Type II errors. For instance, in a professional sport setting, a coach may believe it to be more costly to miss an opportunity to improve team motivation than it is to waste 10 min of each training session on a motivational routine that brings no additional benefits. If a team’s sports psychologist runs a small trial to help decide if the motivational routine should be continued, the hypothesis of interest should be flipped from superiority (does the routine bring a meaningfully large benefit?) to non-superiority. The test that must be rejected is then that the routine is beneficial, and a Type I error is incurred when a beneficial effect is rejected. In this situation, the routine will be continued unless the trial provides evidence that motivation is not improved.

Another valid question is whether a tool such as ours will provide researchers enough justification to move beyond the safety of p < 0.05 or whatever is their disciplinary norm. By displaying rejection regions for tests at two or more alpha levels, our tool at least allows researchers to compare their expected findings under different tests and different test levels. For example, suppose that a researcher planning a two-group trial has justified that the smallest meaningful effect magnitude is a Hedges’ g of 0.2, and that power needs to be 80%. Suppose they can also justify an anticipated effect size of about 0.8 but cannot feasibly gather more than 60 subjects. Figure 3a shows that the researcher cannot plausibly expect significant findings at a one-sided alpha level of 0.025. However, at this level, non-inferiority could be established. In addition, Fig. 3b shows that superiority might be established at a test level of 0.25. This extremely weak finding, in conjunction with the finding of non-inferiority, may still be useful to a stakeholder in applied research.

The balance of errors must also be considered when sample sizes are limited (Mudge et al. 2010). Relatively high Type II error rates are often accepted without question even though these errors may be important to a stakeholder. Researchers may be able to justify planning weaker test alpha levels to gain power. An intervention designed to make a person swim faster, jump higher, or score more points in some competition is less consequential than an intervention that has wide-reaching implications for human health at a population-level. The latter requires a much stronger level of evidence around its benefit and harms. Findings for which the evidence is statistically weak still inform a decision maker of which of the possible decisions is most compatible with the data, and they serve the broader purpose of adding to a body of knowledge through their contribution to meta-analyses.

Our tool allows researchers to compare expected outcomes for the tests involving minimum meaningful effect sizes with that from a standard NHST against zero effect. Using this option, our researcher limited to 60 subjects would be delighted to see they could expect significance at a two-sided alpha level of 0.05 and 80% power. This comparison highlights the fact that recognising that effects should be practically meaningful makes it harder to achieve significance when sample sizes are constrained. A pragmatic approach is to plan a conventional test with zero null at a conventional p-value together with tests against the minimum meaningful effect boundaries at a weaker alpha level. These tests can be conducted simultaneously without adjusting for multiple effects (Berger 1982; Goeman et al. 2010).

Our tool does not replace the need for a priori justification of test alpha levels for researchers working within an Neyman-Pearson framework, but it helps brings levels other than p < 0.05 into possible contention. It focusses attention on meaningful effect sizes and on tests other than testing the hypothesis of no effect. While work remains to develop the tool’s interface and extend its content to other families of tests, we believe it is a practical step toward encouraging scientists to think more broadly about the statistical tests they apply.