Abstract
In the present paper, two pivotal statistics are suggested to construct prediction intervals of future observations from the exponential and Pareto distributions in the context of ordered ranked set sample. Our study encompasses two cases. The first case, when the sample size is assumed to be fixed and the second case when the sample size is assumed to be a positive integer-valued random variable. In addition to deriving explicit forms for the distribution functions of the two pivotal statistics, we consider some special cases for the random size of the sample. Moreover, a simulation study is carried out to assess the efficiency of the suggested methods. Finally, an example representing lifetime data is analyzed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The idea of ranked set sampling (RSS) introduced by McIntyre (1952) was being as a procedure to improve the precision in estimation of average yield from large plots of arable crops without a large increase in the number of fields from which detailed expensive and tedious measurements needed to be collected. The RSS is a way used to work out the problems associated with getting a non-representative sample from a population. It uses simple random samples (SRS) to obtain a more structural and representative sample from the population and consequently to develop efficient inferential procedures.
Takahasi and Wakimoto (1968) provided the mathematical structure for the RSS. Balakrishnan (2007) introduced the concept of order statistics from independent and non-identically distributed (INID) random variables (RVs) to introduce the ordered ranked set sampling (ORSS). Moreover, Balakrishnan and Li (2008) proved that the best linear unbiased estimators based on the ORSS are more efficient than the best linear unbiased estimators based on the RSS for the two-parameter exponential, normal, and logistic distributions. Some Bayesian prediction problems based on the RSS and ORSS were studied by Mohie El-Din et al. (2015, 2017). They got the two-sample Bayesian prediction intervals for the observables from the Pareto distribution based on complete and censored data. Lately, there has been considerable development in the statistical literature based on RSS. Various of these works have used the parametric performance of RSS; see, e.g., Adatia (2000), Alodat and Al-Sagheer (2007), Chen et al. (2021), Qian et al. (2021), Sadek et al. (2015), Shaibu and Muttlak (2004), and Stokes (1995). On the other hand, some other works have used the nonparametric performance of RSS; see, e.g., Bhoj (2016), Bohn (1996), Gemayel et al. (2015), and Salehi et al. (2015).
An important obstacle that frequently faces the experimenter in life testing experiments is the prediction of unknown future observations based on current obtainable sample (informative sample). For instance, the experimenters or the manufacturers would like to put bounds for the life of their products so that their guarantee limits could be reasonably set, and customers would like to know the bounds for the life of the product to purchase those manufactured products. Many authors have considered the prediction of future events, especially future order statistics and generalized order statistics, in the life-testing experiments. Among these authors are Aly et al. (2019), Barakat et al. (2014a, 2020, 2021a), Fan et al. (2019), Hsieh (1996), Kaminsky and Nelson (1998), Lawless (2003), Shah et al. (2020), Valiollahi et al. (2017), and Wu et al. (2020).
When it is impossible to predict the size of the sample previously, because some observations continually get lost for several reasons, it is essential to consider that the size of the sample is an integer RV. This phenomenon is frequently found in many biological, agricultural and some quality control problems. Raqab (2001) found prediction intervals for the future generalized order statistics based on the exponential distribution. Barakat et al. (2011, 2018) attained prediction intervals for future exponential lifetimes based on random generalized order statistics. Recently, Barakat et al. (2021b) suggested a new method for constructing an efficient point predictor for the future order statistics when the sample size is a RV. The suggested point predictor is based on some characterization properties of the distributions of order statistics.
Censoring shows an important role in reliability and lifetime experiments when the experimenter cannot observe the lifetimes of all test units. The usual censoring schemes are type-I and type-II censoring which do not allow survival units to be removed from the test at points excluding the terminal point of the experiment. This will be important when a compromise between reduced time of experimentation and the observations of extreme lifetimes are observed. On the basis of a Type-II censored sample, Barakat et al. (2014b) developed two pivotal statistics to construct prediction intervals of future observations from any arbitrary continuous cumulative distribution function (CDF). The prediction intervals for future order statistics based on type II censoring have been studied by many authors, among them are Lawless (1977), Mohie El-Din et al. (2015, 2017), Patel (1989), Raqab and Barakat (2018), and Raqab and Nagaraja (1995).
Remark 1
Usually, the need of the prediction arises naturally in lifetime tests with type II censored sample as in the usual order statistics and record values. In RSS case we have two scenarios. Consider a random sample of size \(n^2\) of i.i.d RVs, where each of these RVs measures the lifetime of a repairable parallel system. According to the RSS technique, these RVs are divided into n sets (n SRSs) each of them contains n RVs. In the first scenario we apply the Type-II censored sample technique on the sets themselves. For example, we put all these sets independently in a lifetime test and wait to get the first failure “\(x^{*}_{1:n}\)”, then remove the set in which the first failure was appeared. Wait for the second failure to occur among the remaining sets and once we get it “\(x^{*}_{2:n},~x^{*}_{1:n}<x^{*}_{2:n}\)”, remove the set in which the second failure was appeared. Continue up to r failure and end the test at this stage to get the observed ORSS \(x^{*}_{1:n}\le x^{*}_{2:n}\le \ldots \le x^{*}_{r:n}.\) In the second scenario, we apply the usual RSS technique to determine the n failed systems (we assumed in RSS technique that these failed systems have the random failure-times \(X_{1(1:n)}, X_{2(2:n)}, \ldots ,\) and \( X_{n(n:n)}\)). After repairing all these failed items put them again in the lifetime test with censored sample (at r) by these way we get r observed ORSS \(x^{*}_{1:n}\le x^{*}_{2:n}\le \ldots \le x^{*}_{r:n},\) i.e., we first the get the unordered diagonal RVs \(x_{1(1:n)}, x_{2(2:n)}, \ldots ,\) and \( x_{n(n:n)},\) and then based on the Type-II censored sample we may get the first r observed ORSS \(x^{*}_{1:n}\le x^{*}_{2:n}\le \ldots \le x^{*}_{r:n}.\) The second scenario was adopted in Kotb (2016) and Mohie El-Din et al. (2017).
The novelty of this article is to apply a general method for predicting future observations from the exponential and Pareto distributions based on the ORSS when the sample size is assumed to be fixed or when the sample size is assumed to be a positive integer-valued RV. The rest of this article is organized as follows: In Sect. 2, the basic setup and description of the lifetime model based on the RSS are presented. In Sect. 3 the distributions of the two suggested pivotal quantities are derived. In Sect. 4, in order to examine the efficiency of the suggested methods, a simulation study is applied on the exponential and Pareto lifetime distributions for fixed sample size and for some cases of random sample size, such as binomial and discrete uniform random sample sizes. In Sect. 5, a real data set is analyzed by using the suggested methods. Finally, Sect. 6 is dedicated to some concluding remarks.
2 The model description
Assume that a SRS of size n is drawn from the population and is ranked with respect to the variable of interest. Subsequently, the unit with the first order is quantified and the remaining are not determined. Next, the second SRS of a size n is drawn, and the units of the sample are ranked by verdict (judgment), and only the unit with second order is quantified. This procedure is continued until the nth SRS of size n is drawn after that ranked it as well as the unit with order n is quantified. This achieves an observed RSS denoted by \(\mathbf{x} =\left( x_{1(1:n)}, x_{2(2:n)}, \ldots , x_{n(n:n)}\right) ,\) \(x_{i(i:n)}\equiv x_{i:n}\) \((i=1,2,\ldots ,n).\)

Generally, from Scheme 1, the procedure of ORSS can be described as follows: The n observed units within RSS are ordered and denoted by \(\mathbf{x} ^{*}= \left( x^{*}_{1:n}, x^{*}_{2:n}, \ldots , x^{*}_{n:n}\right) ,\) where \(x^{*}_{1:n}\le x^{*}_{2:n}\le \cdots \le x^{*}_{n:n}.\) We first note that \(x_{i(i:n)}\) \((i=1,2,\ldots ,n)\) are INID RVs . The probability density function (PDF), CDF, and survival function of \(x_{i(i:n)},\) denoted by \(f_{i:n}(x),\) \(F_{i:n}(x),\) and \(\overline{F}_{i:n}(x),\) respectively, are actually the PDF, CDF, and survival function of the ith order statistic from a SRS of size n, and are given by
and
respectively [cf. Mohie El-Din et al. (2017), see also Arnold et al. (1992) and David and Nagaraja (2003)], where \(I(0\le x<\infty )\) is the usual indicator function,
Assume that \(x^{*}_{i:n}\) (\(i=1,2,\ldots ,n)\) is the ORSS obtained by arranging \(x_{i(i:n)}\) \((i=1,2,\ldots ,n)\) in increasing order of magnitude. Then, using the results for order statistics from INID RVs [(see Balakrishnan (2007), Balakrishnan and Li (2008), and Barakat and Abdel Kader (2004)], the joint probability density function (JPDF) of \(x^{*}_{r:n}\) and \(x^{*}_{s:n}\) \((1\le r<s\le n)\) is given by
where \(\mathrm {Per}\mathbf {A}=\mathbf {\sum _{P}}\prod _{j=1}^{n}\left( q_{i,j}\right) \) is the permanent of the matrix \(\mathbf {A}=(q_{i,j})\) of size \(n\times n\),
Thus, we readily write the JPDF of \(x^{*}_{r:n}\) and \(x^{*}_{s:n}\) \((1\le r<s\le n)\) as
where \(\mathbf {\sum _{P}}\) is the sum over all n! permutations \((i_{1}, i_{2},\cdots , i_{n})\) of \((1, 2, \cdots , n).\) By substituting the PDF, CDF, and the survival function defined in (1), (2), and (3), respectively, into (6), the JPDF of \(x^{*}_{r:n}\) and \(x^{*}_{s:n}\) \((1\le r<s\le n)\) can be written as
It is further assumed that the lifetimes of the \(n^2\) units in the original n SRSs are independent RVs which follow either the exponential distribution, Exp(\(\theta \)), with the scale parameter \(\theta >0\) (remember that a RV \(X\sim \text{ Exp }(\theta )\) if its PDF is \(f(x)=\theta \exp (-\theta x)I(0\le x<\infty )\)) or Pareto distribution, Pareto(\(\beta \),\(\alpha \)), with the scale parameter \(\beta >0,\) and shape parameter \(\alpha >0\) (remember that a RV \(X\sim \text{ Pareto }(\beta ,\alpha )\) if its PDF is \(f(x)=\frac{\alpha }{\beta }\left( \frac{\beta }{x}\right) ^{\alpha +1}=\alpha \beta ^\alpha \exp (-(\alpha +1)\ln x)I(\beta \le x<\infty )\)). Upon making use of the identities
and
where \(i_{1}<i_{2}<\cdots <i_{n}\) are positive integers, the JPDF (7) based on Exp(\(\theta \)) and Pareto(\(\beta \),\(\alpha \)) can be simplified as
respectively, where \(\underline{l}=(l_{1},l_{2}, \ldots ,l_{r-1})\), \(\underline{j}=(j_{1},j_{2},\ldots ,j_{r-1}),\) \(\underline{\mathrm {v}}=(\mathrm {v}_{r+1},\mathrm {v}_{r+2}, \ldots ,\mathrm {v}_{s-1})\), \(\underline{h}=(h_{r+1},h_{r+2},\ldots ,h_{s-1}),\) \(\underline{\upsilon }=(\upsilon _{s+1},\upsilon _{s+2},\ldots ,\upsilon _{n}),\)
3 The suggested pivotal statistics and their CDFs
In this section, we will utilize the pivotal method to construct prediction intervals for the unknown value of future ORSS \(x^{*}_{s:n}\) \((s=r+1,r+2,\ldots ,n)\) based on the observed values \(x^{*}_{i:n}\) \((i=1,2,\ldots ,r).\) The pivotal method uses a pivotal quantity which is an explicit function of the observed values \(x^{*}_{1:n}\le x^{*}_{2:n}\le \cdots \le x^{*}_{r:n}\) and the unknown future ORSS \(x^{*}_{s:n}\) \((s=r+1, r+2,\ldots ,n).\) Moreover, the pivotal function is invertible and has a well defined CDF, for more details, see Barakat et al. (2014b). The pivotal quantities are essential tools for constructing the prediction intervals for the future ORSS. Namely, if Q is a pivotal quantity for the future ORSS \(X^{\star }_{s:n}\) \((s=r+1,\cdots ,n),\) then for any \(0<\delta <1,\) there will exist \(q_1\) and \(q_2\) depending on \(\delta \) and two functions \(\ell _1(x^{*}_{1:n},x^{*}_{2:n},\cdots ,x^{*}_{r:n})\) and \(\ell _2(x^{*}_{1:n},x^{*}_{2:n},\cdots ,x^{*}_{r:n})\) (not depending on \(x^\star _{s:n}\)) such that
Consequently, in this case the interval \([\ell _1,\ell _2]\) is a \(\delta 100\%\) predictive confidence interval (PCI) for \(x^\star _{s:n}.\) We suggest the following two pivotal quantities based on Exp(\(\theta \)) and Pareto(\(\beta \),\(\alpha \)), respectively, by
and
Remark 2
It is worth noting that the suggested pivotal quantities in (10) and (11) have salient features that they are scale-free and shape-free pivotal quantities, respectively. This fact enables us to use the pivotal quantities defined in (10) and (11) for any Exp\((\theta )\) with an unknown scale parameter, \(\theta ,\) and any Pareto\((\beta ,\alpha )\) with an unknown shape parameter \(\alpha .\)
3.1 The CDF of the pivotal statistic based on the exponential distribution
In this subsection, we derive the PDF and CDF of the pivotal statistic \(\Psi ^{ORSS}_{r,s:N}\) based on the Exp(\(\theta \)), when the sample size is assumed to be a positive integer-valued RV which is independent on all the lifetimes of the \(n^2\) units in the original n SRSs.
Theorem 3.1.1
Let \(x^{*}_{1:N}\le x^{*}_{2:N}\le \cdots \le x^{*}_{r:N}\) be the first observed ORSS based on Exp(\(\theta \)), where N is a positive integer-valued RV which is independent on all the lifetimes of the \(n^2\) units in the original n SRSs. Then, the CDF \(\mathrm {F_{\Psi ^{ORSS}_{r,s:N}}}\) of the pivotal quantity \(\Psi ^{ORSS}_{r,s:N}\) is given by
where \(\mathrm {P}_s(n)=\mathrm {P}(N=n|N\ \ge s)\) is the left truncated distribution of N at s. Moreover, a \((1-\gamma )100\%\) PCI for \(x^{*}_{s:N}\) \(( s=r+1,r+2,\ldots ,N)\) is \(\left[ x^{*}_{r:N},(1+\psi )x^{*}_{r:N} \right] ,\) where \(\mathrm {F_{\Psi ^{ORSS}_{r,s:N}}}(\psi )=1-\gamma .\)
Proof
First we note that, the JPDF of \(x^{*}_{r:N}\) and \(x^{*}_{s:N}\) \((1\le r<s\le N)\) takes the form
(see Raghunandanan and Patil (1972)), where the JPDF \(f_{r,s:n}^\star (x,y)\) is defined in (8). We now derive the JPDF of \(\chi _{r,s:N}=x^{*}_{s:N}-x^{*}_{r:N}\) and \(\tau =x^{*}_{r:N}\) by using the standard transformation method
Therefore, again by using the standard transformation method, the JPDF of \(\Psi ^{ORSS}_{r,s:N}=\frac{\chi _{r,s:N}}{\tau }\) and \(\tau \) is given by
Consequently, the PDF of \( \Psi ^{ORSS}_{r,s:N}\) is given by
After routine calculations, the CDF of \( \Psi ^{ORSS}_{r,s:N}\) can be obtained. \(\square \)
Corollary 3.1
Under the provisions of Theorem 3.1.1, if N is non-random integer, i.e., \(P(N = n) = 1)~ (n\ge s),\) then the CDF of \( \Psi ^{ORSS}_{r,s:N}\) takes the form
Corollary 3.2
Under the provisions of Theorem 3.1.1, if N has a binomial distribution with parameters \(\varsigma \) and p (i.e., \(N\sim \mathrm {Binomial}(\varsigma ,p)\)), the CDF of \( \Psi ^{ORSS}_{r,s:N}\) takes the form
where \(\mathrm {P}(N\ge s)=1-\sum ^{s-1}_{\eta =0}\left( \begin{array}{c} \varsigma \\ \eta \end{array}\right) p^{\eta }(1-p)^{\varsigma -\eta }.\)
Corollary 3.3
Under the provisions of Theorem 3.1.1, if N has a discrete uniform distribution with parameters \(\varsigma \) and \(\kappa \) (i.e., \(N\sim \mathrm {Uniform}(\kappa ,\varsigma )\)), the CDF of \( \Psi ^{ORSS}_{r,s:N}\) takes the form
where \(\mathrm {P}(N\ge s)=\left\{ \begin{array}{ll} 1, \qquad \qquad \quad \mathrm {if} \quad s\le \kappa , \\ \\ 1-\frac{s-\kappa }{\varsigma -\kappa +1},\quad \mathrm {if} \quad s>\kappa . \end{array}\right. \)
3.2 The CDF of the pivotal statistic based on the Pareto distribution
In this subsection, we derive the PDF and CDF of the pivotal statistic \(\varPhi ^{ORSS}_{r,s:N}\) based on the Pareto\((\beta ,\alpha )\) when the sample size is assumed to be a positive integer-valued RV. For simplicity, we take \(\beta =1.\)
Theorem 3.2.1
Assume that \(x^{*}_{1:N}\le x^{*}_{2:N}\le \cdots \le x^{*}_{r:N}\) are the first observed ORSS based on Pareto(\(1,\alpha \)), where N is a positive integer-valued RV, which is independent on all the lifetimes of the \(n^2\) units in the original n SRSs. Then, the CDF \(\mathrm {G_{\varPhi ^{ORSS}_{r,s:N}}}\) of statistic \(\varPhi ^{ORSS}_{r,s:N}\) is given by
Moreover, a \((1-\gamma )100\%\) PCI for \(x^{*}_{s:N}\) \(( s=r+1,r+2,\ldots ,N)\) is \(\left[ x^{*}_{r:N},{x^{*}}_{r:N}^{(1+\phi )} \right] ,\) where \(\mathrm {G_{\varPhi ^{ORSS}_{r,s:N}}}(\phi )=1-\gamma .\)
Proof
By using (9) and (13) (with replacing \(f_{r,s:N}^\star \) and \(f_{r,s:n}^\star \) by \(g_{r,s:N}^\star \) and \(g_{r,s:n}^\star ,\) respectively, in (13)), we get
We can obtain the JPDF of \(\varpi _{r,s:N}=\ln x^{*}_{s:N}-\ln x^{*}_{r:N} \) and \(\varrho =\ln x^{*}_{r:N} \) by using the standard transformation method
Thus, again by using the standard transformation method, the JPDF of \(\varPhi ^{ORSS}_{r,s:N}=\frac{\varpi _{r,s:N}}{\varrho }\) and \(\varrho \) is given by
If \(\beta =1,\) the PDF of \(\varPhi ^{ORSS}_{r,s:N}\) is given by
After routine calculations, the CDF of \(\varPhi ^{ORSS}_{r,s:N}\) can be obtained. \(\square \)
Corollary 3.4
Under the provisions of Theorem 3.2.1, if N is non-random integer, i.e., \(P(N = n) = 1)\) \((n\ge s),\) then the CDF of \( \varPhi ^{ORSS}_{r,s:N}\) takes the form
Corollary 3.5
Under the provisions of Theorem 3.2.1, if \(N\sim \mathrm {Binomial}(\varsigma ,p),\) the CDF of \( \varPhi ^{ORSS}_{r,s:N}\) takes the form
where \(\mathrm {P}(N\ge s)=1-\sum ^{s-1}_{\eta =0}\left( \begin{array}{c} \varsigma \\ \eta \end{array}\right) p^{\eta }(1-p)^{\varsigma -\eta }\).
Corollary 3.6
Under the provisions of Theorem 3.2.1, if \(N\sim \mathrm {Uniform}(\kappa ,\varsigma ),\) the CDF of \( \varPhi ^{ORSS}_{r,s:N}\) takes the form
where \(\mathrm {P}(N\ge s)=\left\{ \begin{array}{ll} 1, \qquad \qquad \quad \mathrm {if} \quad s\le \kappa , \\ \\ 1-\frac{s-\kappa }{\varsigma -\kappa +1},\quad \mathrm {if} \quad s>\kappa . \end{array}\right. \)
4 Simulation study
In the present section, we perform a Monte Carlo simulation study to examine the performance of the suggested PCIs for future ORSS based on the two important lifetime distributions Exp\((\theta )\) and Pareto\((1,\alpha ).\) Our study is carried out for a non-random sample size and the random sample size N, where N is binomially or uniformly distributed. Our goal here is to show the practical importance of the methods presented in the previous sections and making comparisons between the pivotal quantities \(\Psi ^{ORSS}_{r,s:N}\) and \(\varPhi ^{ORSS}_{r,s:N}.\) Though the complicated form of \( \mathrm {F_{\Psi ^{ORSS}_{r,s:N}}}(\psi ) \) and \( \mathrm {G_{\varPhi ^{ORSS}_{r,s:N}}}(\phi ) \) (see Theorems 3.1.1, 3.2.1 and their corollaries), simulation studies are conducted and the equations \( \mathrm {F_{\Psi ^{ORSS}_{r,s:N}}}(\psi ) = 1-\gamma \) and \( \mathrm {G_{\varPhi ^{ORSS}_{r,s:N}}}(\phi ) =1-\gamma \) are solved numerically using Mathematica 12 to obtain the probability coverage (PC) and average interval width (AIW) for \(x^{*}_{s:N}\) \((s=r+1,r+2,\ldots ,N)\) based on the pivotal quantities \(\Psi ^{ORSS}_{r,s:N}\) and \(\varPhi ^{ORSS}_{r,s:N}.\) Moreover, for each of the distributions Exp(1) and Pareto(1, 1) (note that, in view of Remark 2, the choice \(\theta =\alpha =1\) does not lose our study its generality), we generate ORSS, each of them has random size N, when the random sample size is assumed to be distributed as: \(\mathrm {Binomial}(7,p)\) \((p= 0.4,0.7,0.9)\) and \(\mathrm {Uniform}(2,7)\). The PCs and AIWs of the obtained PCIs are displayed in Tables 1, 2 and 3 for different choices of N.
We compare the performance of the two different pivotal quantities and assess the PCIs in terms of the AIWs and PCs. Generally, the PCIs in all cases of this study are good and acceptable in the sense of the PC and AIW. For example, in the all cases of our simulation study, the PCIs for prediction of the future events in the case of RSS are comparable, based on the PC and AIW, to those of Barakat et al. [7,8] for prediction of the future events in the case of SRS. On the other hand, we found that the increasing r comparing with N (or n) (i.e., decreasing the number of the unobserved (future) observations) yields a shorter AIW. Moreover, the results pertain to the pivotal quantity \(\Psi ^{ORSS}_{r,s:N}\) are generally better than the results that pertain to the pivotal quantity \(\Phi ^{ORSS}_{r,s:N}\) (even when \(P(N=n)=1\)). Finally, when \(N\sim \mathrm {Binomial}(\varsigma ,p),\) the increasing of p generally yields a shorter AIW.

5 Data analysis (Wooden toy prices)
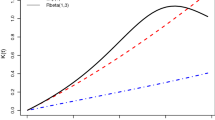
Here, we present the analysis of real data, which are fitted by the exponential and Pareto distributions, to illustrate and assess the methods described in Sect. 3. All the computations are conducted using Mathematica 12 software. These real data were presented in [Hand et al. (1994), p. 48]. The following, Table 4, are the prices (in \(\pounds \)) of the 31 different children’s wooden toys on sale in a Suffolk craft shop in April 1991. The quoted source uses them in exercises on graphical presentation of data. For checking whether the exponential and Pareto distributions are appropriate for describing these data, we first note that the Pareto distribution (with \(\beta =1\)) may only describe this data set if we slightly modified it by discarding the three observations 0.5000, 0.6500 and 0.9000, which have values less than 1, and approximate the value 0.9900 to 1. Therefore, for the exponential distribution we treat with the data given in Table 4, while for the Pareto distribution we treat with the same data after the preceding modification. We check whether the exponential and Pareto distributions are appropriate for describing these data sets by using three different goodness-of-fit tests, Cramér-von Mises, Pearson \(\chi ^{2},\) and Kolmogorov-Smirnov. Via these tests, we found that Exp(\(\widehat{\theta }=0.2358\)) and Pareto (\(\widehat{\beta }=1,\) \(\widehat{\alpha }=0.8694\)) are the best fitted distributions for these data sets, see Table 5. We also use the empirical distribution function to check whether the exponential and Pareto distributions are appropriate for describing these data sets. Figures 1 and 2 show, respectively, the empirical distribution function versus the fitted exponential and Pareto survival functions for the given data. Visually, the shown empirical functions for the fitted survival functions are very near, indicating very good fit.
Sticking to Scheme 1, a SRS of size 5 is selected randomly without replacement from each of the two data sets of sample size 31 (for the exponential distribution) and 28 (for the Pareto distribution), respectively. The first smallest observation is measured from each of the first two selected sets. Next, the second SRS of size 5 is selected randomly without replacement from the remaining data from each of the two data sets, and the second smallest observation is measured from each of the second selected sets. This procedure is continued until the fifth SRS of size 5 is selected randomly without replacement from the remaining data from each of the two data sets, and the largest observation is measured from each of the last selected sets. Therefore, we get the two RSSs (1.12,0.65,1.39,8.69,2.60) and (1.12,6.24,1.74,2.60,5.81) for Exp(0.2358) and Pareto(1,0.8694), respectively.
By using the procedure of ORSS in Schemes 2, we predict the last \((N-3)\) observations (which will be assumed to be unobserved), based on the first three observations when the sample size is supposed to be fixed or random, i.e. \(x^{*}_{4:5}\) and \(x^{*}_{5:5}\) when the sample size is fixed and \(x^{*}_{s:N}\) \((s=4,...,N)\) when the sample size N is a RV. The quantile values (for \(\gamma =0.05,~ 0.10\)), PCIs (for \(x^{*}_{s:N},\) \(s = 4,...,N\)), and their interval widths (IWs) are constructed based on the exponential and Pareto distributions and displayed in Tables 6 and 7.
In the most cases, the real values of \(x^{*}_{s:n}\) and \(x^{*}_{s:N}\) \((s=4,5)\) lay in the PCIs for the two distributions, see Table 6. Moreover, the results pertain to the exponential distribution are generally better than the results that pertain to the Pareto distribution based on the IW (this may be due to the exponential distribution has a better fitting than the Pareto distribution based on the p-value, as Table 5 shows). Finally, the binomially distribution assumption of the sample size generally gives a better result than the uniform distribution assumption.

6 Conclusion
By exploiting Theorems 3.1.1, 3.2.1, and their corollaries, a scale-free and shape-free pivotal quantities for the exponential and Pareto distributions were used, respectively, to construct prediction intervals for future observations based on the ORSS. The explicit forms of the PDFs and CDFs of the pivotal quantities were derived.
A simulation study was performed to scrutinize the efficiency of the proposed methods for different choices of the random sample size. This simulation study (Tables 1, 2 and 3) revealed that if we fixed the value of s, the average width of the predictive confidence interval of \( x^{*}_{s:N}\) decreases, with increasing r. On the other hand, if we fixed the value of r, the average width of the predictive confidence interval of \(x^{*}_{s:N}\) increases, with increasing s. Consistently, the average width of the predictive confidence interval of \(x^{*}_{s:N}\) decreases with increasing the value of the sample size.
In all cases, the average width of the predictive confidence interval of \( x^{*}_{s:N}\) based on the pivotal quantity \(\Psi ^{ORSS}_{r,s:N}\) is less than the corresponding average width of \(x^{*}_{s:N}\) based on the pivotal quantity \(\varPhi ^{ORSS}_{r,s:N}.\) In most cases, the average width of the predictive confidence interval of \(x^{*}_{s:n}\) for fixed sample size is less than the corresponding average width of \(x^{*}_{s:N}\) when the sample size is random. Constantly, the probability coverage is about to \( 1-\gamma .\) Finally, an example for real lifetime data is analyzed to demonstrate the applicability of the obtained results.
References
Adatia A (2000) Estimation of parameters of the half-logistic distribution using generalized ranked set sampling. Comput Stat Data Anal 33:1–13
Alodat MT, Al-Sagheer OA (2007) Estimation the location and scale parameters using ranked set sampling. J Appl Stat Sci 15:245–252
Aly AE, Barakat HM, El-Adll ME (2019) Prediction intervals of the record-values process. Revstat (Stat J) 17:401–427
Arnold BC, Balakrishnan N, Nagaraja HN (1992) A first course in order statistics. Wiley, New York
Balakrishnan N (2007) Permanents, order statistics, outliers, and robustness. Rev Mat Complut 20(1):7–107
Balakrishnan N, Li T (2008) Ordered ranked set samples and applications to inference. J Stat Plan Inference 138(11):3512–3524
Barakat HM, Abdel Kader YH (2004) Computing the moments of order statistics from nonidentical random variables. Stat Methods Appl 13:15–26
Barakat HM, El-Adll ME, Aly AE (2011) Exact prediction intervals for future exponential lifetime based on random generalized order statistics. Comput Math Appl 61(5):1366–1378
Barakat HM, Nigm EM, Aldallal RA (2014a) Exact prediction intervals for future current records and record range from any continuous distribution. SORT 38(2):251–270
Barakat HM, El-Adll ME, Aly AE (2014b) Prediction intervals of future observations for a sample of random size for any continuous distribution. Math Comput Simul 97:1–13
Barakat HM, Nigm EM, El-Adll ME, Yusuf M (2018) Prediction of future generalized order statistics based on exponential distribution with random sample size. Stat Pap 59(2):605–631
Barakat HM, Khaled OM, Ghonem HA (2020) Predicting future lifetime for mixture exponential distribution. Simul Comput Commun Stat https://doi.org/10.1080/03610918.2020.1715434
Barakat HM, Khaled OM, Ghonem HA (2021a) New method for prediction of future order statistics. QTQM 18:101–116
Barakat HM, Khaled OM, Ghonem HA (2021b) Predicting future order statistics with random sample size. AIMS Math 6(5):5133–5147
Bhoj DS (2016) New nonparametric ranked set sampling. Int J Comp Theoret Stat 3(1):23–27
Bohn LL (1996) A review of nonparametric ranked-set sampling methodology. Commun Stat Theory Methods 25(11):2675–2685
Chen W, Yang R, Yao D, Long C (2021) Pareto parameters estimation using moving extremes ranked set sampling. Stat Pap 62(3):1195–1211
David HA, Nagaraja HN (2003) Order statistics, 3rd edn. Wiley, New York
Fan W, Jiang Y, Huang S, Liu W (2019) Research and prediction of opioid crisis based on BP neural network and Markov chain. AIMS Math 4(5):1357–1368
Gemayel N, Stasny EA, Wolfe DA (2015) Bayesian nonparametric models for ranked set sampling. Lifetime Data Anal 21(2):315–329
Hand DJ, Daly F, McConway KJ, Lunn AD, Ostrowski E (1994) A handbook of small data sets. Chapman & Hall, London
Hsieh HK (1996) Prediction interval for Weibull observation, based on early-failure data. IEEE Trans Reliab 45(4):666–670
Kaminsky KS, Nelson PI (1998) Prediction of order statistics. In: Balakrishnan N, Rao CR (eds) Handbook of statistics. North-Holland, Amsterdam, vol. 17, pp. 431–450
Kotb MS (2016) Bayesian prediction bounds for the exponential type distribution based on ordered ranked set sampling. Econ Qual Control 31(1):45–54
Lawless JF (1977) Prediction intervals for the two parameter exponential distribution. Technometrics 19(4):469–472
Lawless JF (2003) Statistical models and methods for lifetime data. Wiley, New York
McIntyre GA (1952) A method for unbiased selective sampling, using ranked sets. Aust J Agric Res 3(4):385–390
Mohie El-Din MM, Kotb MS, Newer HA (2015) Bayesian estimation and prediction for Pareto distribution based on ranked set sampling. J Stat Appl Probab 4(2):2–11
Mohie El-Din M, Kotb M, Abd-Elfattah EF, Newer HA (2017) Bayesian inference and prediction of the Pareto distribution based on ordered ranked set sampling. Commun Stat Theory Methods 46(13):6264–6279
Patel JK (1989) Prediction intervals—a review. Commun Stat Theory Methods 18(7):2393–2465
Qian W, Chen W, He X (2021) Parameter estimation for the Pareto distribution based on ranked set sampling. Stat Pap 62(1):395–417
Raghunandanan K, Patil SA (1972) On order statistics for random sample size. Stat Neerlandica 26(4):121–126
Raqab MZ (2001) Optimal prediction-intervals for the exponential distribution, based on generalized order statistics. IEEE Trans Reliab 50(1):112–115
Raqab MZ, Barakat HM (2018) Prediction intervals for future observations based on samples of random sizes. J Math Stat 14(1):16–28
Raqab MZ, Nagaraja HN (1995) On some predictors of future order statistics. Metron 53(12):185–204
Sadek A, Sultan KS, Balakrishnan N (2015) Bayesian estimation based on ranked set sampling using asymmetric loss function. Bull Malays Math Sci Soc 38(2):707–718
Salehi M, Ahmadi J, Balakrishnan N (2015) Prediction of order statistics and record values based on ordered ranked set sampling. Commun Stat Simul Comput 85(1):77–88
Shah IA, Barakat HM, Khan AH (2020) Characterizations through generalized and dual generalized order statistics, with an application to statistical prediction problem. Stat Probab Lett 163:108–782
Shaibu AB, Muttlak HA (2004) Estimating the parameters of normal, exponential and gamma distributions using median and extreme ranked set samples. Statistica 64(1):75–98
Stokes L (1995) Parametric ranked set sampling. Ann Inst Stat Math 47(3):465–482
Takahasi K, Wakimoto K (1968) On unbiased estimates of the population mean based on the sample stratified by means of ordering. Ann Inst Stat Math 20(1):1–31
Valiollahi R, Asgharzadeh A, Kundu D (2017) Prediction of future failures for generalized exponential distribution under Type-I or Type-II hybrid censoring. Braz J Probab Stat 31(1):41–61
Wu P, Liang B, Xia Y, Tong X (2020) Predicting disease risks by matching quantiles estimation for censored data. Math Biosie Eng (AIMS) 17(5):4544–4562
Acknowledgements
The authors thank the Editor in Chief Prof. Werner G. Müller and reviewers for their valuable comments and suggestions to improve the paper.
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Barakat, H.M., Newer, H.A. Exact prediction intervals for future exponential and Pareto lifetimes based on ordered ranked set sampling of non-random and random size. Stat Papers 63, 1801–1827 (2022). https://doi.org/10.1007/s00362-022-01295-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00362-022-01295-y
Keywords
- Ordered ranked set sampling
- Random sample size
- Predicative interval
- Probability coverage
- Monte Carlo simulation