Extremal measures maximizing functionals based on simplicial volumes

Abstract

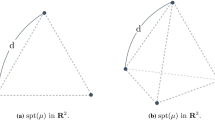
We consider functionals measuring the dispersion of a d-dimensional distribution which are based on the volumes of simplices of dimension $k\le d$ formed by $k+1$ independent copies and raised to some power $\delta$. We study properties of extremal measures that maximize these functionals. In particular, for positive $\delta$ we characterize their support and for negative $\delta$ we establish connection with potential theory and motivate the application to space-filling design for computer experiments. Several illustrative examples are presented.

Appendix

Lemma 2

Consider matrix A given by (2). The Laplacian of $\det ^{\alpha }(A)$ considered as a function of $x_1$ is

$$\begin{aligned} \sum _{i=1}^d \frac{\partial ^2 {\det }^{\alpha }(A)}{\partial \{x_1\}_i^2} = 2\alpha (2\alpha +d-k-1) \, {\det }^{\alpha }(A) \, ({\mathbf 1}_k^\top A^{-1} {\mathbf 1}_k) , \end{aligned}$$

(11)

where ${\mathbf 1}_k=(1,\ldots ,1)^\top \in \mathbb {R}^k$.

Proof

We have

$$\begin{aligned} \frac{\partial {\det }(A)}{\partial \{x_1\}_i}= & {} \det (A)\, \text{ trace }\left( A^{-1}\frac{\partial A}{\partial \{x_1\}_i}\right) \\ \frac{\partial ^2 {\det }(A)}{\partial \{x_1\}_i^2}= & {} - \det (A)\, \text{ trace }\left( A^{-1}\frac{\partial A}{\partial \{x_1\}_i}A^{-1}\frac{\partial A}{\partial \{x_1\}_i}\right) \\&+ \det (A)\, \text{ trace }^2\left( A^{-1}\frac{\partial A}{\partial \{x_1\}_i}\right) + \det (A)\, \text{ trace }\left( A^{-1}\frac{\partial ^2 A}{\partial \{x_1\}_i^2}\right) , \end{aligned}$$

where ${\partial A{/}{\partial } \{x_1\}_i = -[{{\mathbf 1}_k \Delta _i^\top +\Delta _i{\mathbf 1}_k^\top }]}$ and ${\partial ^2 A{/}{\partial } \{x_1\}_i^2 =2 {\mathbf 1}_k{\mathbf 1}_k^\top }$, with $\Delta _i=(\{x_2-x_1\}_i,\ldots ,\{x_{k+1}-x_1\}_i)^\top \in \mathbb {R}^k$. This gives

$$\begin{aligned} \frac{\partial ^2 {\det }(A)}{\partial \{x_1\}_i^2} = 2\,\det (A)\,\left\{ {\mathbf 1}_k^\top A^{-1}{\mathbf 1}_k(1-\Delta _i^\top A^{-1}\Delta _i)+({\mathbf 1}_k^\top A^{-1}\Delta _i)^2 \right\} . \end{aligned}$$

Noting that $\sum _{i=1}^d \Delta _i \Delta _i^\top =A$, we have $\sum _{i=1}^d \Delta _i^\top A^{-1}\Delta _i=\text{ trace }(I_k)=k$ and obtain

$$\begin{aligned} \sum _{i=1}^d \left( \frac{\partial {\det }(A)}{\partial \{x_1\}_i}\right) ^2= & {} {\det }^2(A)\, \sum _{i=1}^d \text{ trace }^2\left( A^{-1}\frac{\partial A}{\partial \{x_1\}_i}\right) \\= & {} {\det }^2(A)\, \sum _{i=1}^d \text{ trace }^2\left( A^{-1}[{\mathbf 1}_k \Delta _i^\top +\Delta _i{\mathbf 1}_k^\top ] \right) \\= & {} 4\, {\det }^2(A)\, {\mathbf 1}_k^\top A^{-1}{\mathbf 1}_k \end{aligned}$$

and

$$\begin{aligned} \sum _{i=1}^d \frac{\partial ^2 {\det }(A)}{\partial \{x_1\}_i^2}= & {} 2\,{\det }(A)\,{\mathbf 1}_k^\top A^{-1}{\mathbf 1}_k \, (d+1-k) . \end{aligned}$$

Now,

$$\begin{aligned} \frac{\partial {\det }^\alpha (A)}{\partial \{x_1\}_i}= & {} \alpha \, {\det }^{\alpha -1}(A) \, \frac{\partial {\det }(A)}{\partial \{x_1\}_i} \\ \frac{\partial ^2 {\det }^\alpha (A)}{\partial \{x_1\}_i^2}= & {} \alpha (\alpha -1)\, {\det }^{\alpha -2}(A)\, \left( \frac{\partial {\det }(A)}{\partial \{x_1\}_i}\right) ^2 + \alpha \det (A)^{\alpha -1} \, \frac{\partial ^2 {\det }(A)}{\partial \{x_1\}_i^2}, \end{aligned}$$

which finally gives (11). $\square$

A subgradient-type algorithm to maximize ${\widehat{\mathscr {D}}}_{k,-\infty }(\cdot )$.

Consider a design $X_n=(x_1,\ldots ,x_n)$, with each $x_i\in {\mathscr {X}}$, a convex subset of $\mathbb {R}^d$, as a vector in $\mathbb {R}^{n\times d}$. The function ${\widehat{\mathscr {D}}}_{k,-\infty }(\cdot )$ defined in (10) is not concave (due to the presence of $\min$), but is Lipschitz and thus differentiable almost everywhere. At points $X_n$ where it fails to be differentiable, we consider any particular gradient from the subdifferential,

$$\begin{aligned} \nabla {\widehat{\mathscr {D}}}_{k,-\infty }(X_n) = \nabla v_{j_1,\ldots ,j_{k+1}}(X_n) \end{aligned}$$

where $x_{j_1},\ldots ,x_{j_{k+1}}$ are such that ${\mathscr {V}}_k(x_{j_1},\ldots ,x_{j_{k+1}})={\widehat{\mathscr {D}}}_{k,-\infty }(X_n)$ and where $\nabla v_{j_1,\ldots ,j_{k+1}}(X_n)$ denotes the usual gradient of the function ${\mathscr {V}}_k(x_{j_1},\ldots ,x_{j_{k+1}})$. Our subgradient-type algorithm then corresponds to the following sequence of iterations, where the current design $X_n^{(t)}$ is updated into

$$\begin{aligned} X_n^{(t+1)} = P_{\mathscr {X}}\left[ X_n^{(t)} + \gamma _t \nabla {\widehat{\mathscr {D}}}_{k,-\infty }(X_n^{(t)})\right] , \end{aligned}$$

where $P_{\mathscr {X}}[\cdot ]$ denotes the orthogonal projection on ${\mathscr {X}}$ and $\gamma _t>0$, $\gamma _t \searrow 0$, $\sum _t \gamma _t=\infty$, $\sum _t \gamma _t^2 < \infty$.

Direct calculation gives

$$\begin{aligned} \frac{\partial v_{j_1,\ldots ,j_{k+1}}(X_n)}{\partial \{x_j\}_\ell } = \left\{ \begin{array}{l} 0 \quad \text{ if } j \not \in \{j_1,\ldots ,j_{k+1}\} \\ \frac{1}{2k!}\, \det ^{1/2}(A_{j_1,\ldots ,j_{k+1}})\, \text{ trace }\left[ A_{j_1,\ldots ,j_{k+1}}^{-1} \frac{\partial A_{j_1,\ldots ,j_{k+1}}}{\partial \{x_j\}_\ell } \right] \text{ otherwise }, \end{array}\right. \end{aligned}$$

where

$$\begin{aligned} A_{j_1,\ldots ,j_{k+1}} = \left( \left[ \begin{array}{ll} (x_{j_2}-x_{j_1})^\top \\ (x_{j_3}-x_{j_1})^\top \\ \vdots \\ (x_{j_{k+1}}-x_{j_1})^\top \\ \end{array} \right] \begin{array}{ll} \left[ (x_{j_2}-x_{j_1}) \ (x_{j_3}-x_{j_1}) \ \cdots (x_{j_{k+1}}-x_{j_1}) \right] \\ \\ \\ \\ \end{array} \right) , \end{aligned}$$

so that

$$\begin{aligned} \text{ trace }\left[ A_{j_1,\ldots ,j_{k+1}}^{-1} \frac{\partial A_{j_1,\ldots ,j_{k+1}}}{\partial \{x_j\}_\ell } \right] = 2 \left\{ A_{j_1,\ldots ,j_{k+1}}^{-1} \left[ \begin{array}{ll} \{(x_{j_2}-x_{j_1})\}_\ell \\ \{(x_{j_3}-x_{j_1})\}_\ell \\ \vdots \\ \{(x_{j_{k+1}}-x_{j_1})\}_\ell \\ \end{array} \right] \right\} _{j-1} \end{aligned}$$

for $j\in \{j_1,\ldots ,j_{k+1}\}$, $j\ne j_1$, and

$$\begin{aligned} \text{ trace }\left[ A_{j_1,\ldots ,j_{k+1}}^{-1} \frac{\partial A_{j_1,\ldots ,j_{k+1}}}{\partial \{x_{j_1}\}_\ell } \right] = - 2 \sum _{i=1}^{k} \left\{ A_{j_1,\ldots ,j_{k+1}}^{-1} \left[ \begin{array}{ll} \{(x_{j_2}-x_{j_1})\}_\ell \\ \{(x_{j_3}-x_{j_1})\}_\ell \\ \vdots \\ \{(x_{j_{k+1}}-x_{j_1})\}_\ell \\ \end{array} \right] \right\} _{i} . \end{aligned}$$