Bias-corrected quantile regression estimation of censored regression models

Abstract

In this paper, an extension of the indirect inference methodology to semiparametric estimation is explored in the context of censored regression. Motivated by weak small-sample performance of the censored regression quantile estimator proposed by Powell (J Econom 32:143–155, 1986a), two- and three-step estimation methods were introduced for estimation of the censored regression model under conditional quantile restriction. While those stepwise estimators have been proven to be consistent and asymptotically normal, their finite sample performance greatly depends on the specification of an initial estimator that selects the subsample to be used in subsequent steps. In this paper, an alternative semiparametric estimator is introduced that does not involve a selection procedure in the first step. The proposed estimator is based on the indirect inference principle and is shown to be consistent and asymptotically normal under appropriate regularity conditions. Its performance is demonstrated and compared to existing methods by means of Monte Carlo simulations.

1 Introduction

The censored regression model has been studied and extensively used in a wide range of applied economics literature. To estimate the parameters of censored regression models, the maximum likelihood estimator (MLE) is usually used under the assumption that the error terms have distribution functions with a known parametric form (e.g., that the error terms are normally distributed). Contrary to the least squares estimator in linear regression model, the MLE is not robust to departures from the parametric assumptions about the error term distribution. If the employed assumptions do not hold, the MLE is in general inconsistent (cf. Arabmazar and Schmidt 1982; Brännäs and Laitila 1989). The same applies also to Heckman’s two-step estimator (see Jonsson 2012).

To relax the strong assumptions of MLE, several semiparametric estimators have been introduced in the econometric literature. Relying on very weak identification assumptions, Powell (1984, 1986a) proposed the censored least absolute deviation (CLAD) and censored regression quantile (CRQ) estimators by imposing the restriction that the conditional quantile of the error term is zero. These consistent and asymptotically normal estimators were applied in many contexts (e.g., Fahr 2004; Melenberg and van Soest 1996), and furthermore, have been extended in many directions, which include random censoring (Honore et al. 2002; Portnoy 2003) as well as panel-data models (Honore 1992; Campbell and Honore 1993). In practice, the CRQ estimator is very appealing due to its robustness to misspecification of the error-term distribution and of the form of heteroskedasticity.

On the other hand, CRQ is difficult to compute exactly since its objective function is non-differentiable, non-convex, and more importantly, exhibits multiple local minima. The results using algorithms searching local minima (see Fitzenberger 1997b, for an overview) depend on the choice of the starting points, while the algorithms searching the global minimum (e.g., Fitzenberger and Winker 2007) can become relatively demanding in terms of computation time, especially if many regressors are involved. In Monte Carlo experiments, Fitzenberger (1997a) demonstrated a more severe drawback of the CRQ estimator in small samples than the mean-biasedness and inefficiency documented already by Paarsch (1984) and Moon (1989): the CRQ estimator exhibits a heavy-tailed asymmetric distribution in small samples. These observations made also by Fitzenberger and Winker (2007), for instance, are supported by larger differences between expected and median values of CRQ in some simple settings, and as argued by Khan and Powell (2001), can be attributed to the fact that the CRQ parameter estimates play two roles: while they are estimates of the regression parameters, they also determine which observations have positive conditional quantiles and can thus enter the minimization of the CRQ objective function. (Note that these unfavorable finite-sample properties are shared to some extent also by some alternatives to CLAD such as the symmetrically censored least squares of Powell (1986b). Other alternative estimator such as those by Horowitz (1986) and Honore and Powell (1994) do not exhibit such heavy-tailed finite-sample distributions, but require the error terms and the explanatory variables being independent, which is a rather strong assumption.)

Since Khan and Powell (2001) highlighted the inherent property of CLAD and CRQ that causes their poor small-sample performance—the joint identification of observations entering the objective function and of the quantile regression line, several stepwise estimation procedures have been proposed, for example, by Khan and Powell (2001) and Chernozhukov and Hong (2002). These methods select first a subset of observations to identify the quantile regression line and then apply the quantile regression (QR) on the selected observations. The first step can be achieved, for example, by a nonparametric selection procedure as in Buchinsky and Hahn (1998) and Khan and Powell (2001). Although asymptotically nearly equivalent to an ‘oracle’ QR estimator, the selection procedure in the first step works at a cost in finite samples. Alternatively, Chernozhukov and Hong (2002) developed a three-step estimation method that involves a parametric first step to circumvent the “curse-of-dimensionality” problem posed by nonparametric selection procedures. Its performance in small samples does not however improve upon the two-step estimators in simple regression models.

The finite-sample performance of the stepwise estimators does not seem substantially better than CLAD in studies of Khan and Powell (2001), Chernozhukov and Hong (2002), and most recently Tang et al. (2011). This might be due to relatively low precision of the initial nonparametric fit, for instance, but also due to a comparison with CLAD estimates based on favorable local minima rather than the global minimum. To improve upon the stepwise estimators, we introduce an alternative semiparametric estimator for the censored regression model under conditional quantile restriction. Contrary to the existing methods, we apply the linear regression QR estimator to all data (rather than to a preselected subsample) and then correct its bias caused by censoring. For the bias correction, indirect inference (II), which was suggested by Gouriéroux et al. (1993), is used. The indirect inference methodology is a simulation-based technique that is essentially used for estimation of the parameters of correctly specified but intractable models, but it can be employed as a bias correction method too (e.g., Gouriéroux et al. 2000, 2010).

Implementing the standard II approach requires knowledge of the error-term distribution at least up to a parametric form. To exploit only the conditional quantile restriction, we propose a new II methodology based on simulating the values of the error terms from a semiparametrically estimated distribution. The proposed II estimator is based on the standard linear QR (which allows for linear, quadratic, and polynomial functions of regressors) for two reasons. First, linear QR has desirable properties such as convexity of the objective function and a reasonably small variance in small samples. Second and more importantly, the properties of linear QR are known even under model misspecification (see Angrist et al. 2006) and can be used to construct a nonparametrically estimated error distribution for the II simulations and subsequent bias correction. Hence, the proposed bias-corrected QR procedure can be shown to be consistent and asymptotically normal. Its benefits in small samples are demonstrated by means of Monte Carlo simulations.

The remainder of the paper is organized as follows. Section 2 presents a review of relevant estimation methods of censored regression model and a brief overview of the indirect inference methodology. In Sect. 3, the proposed bias-corrected QR estimator is described in details. The asymptotic properties of the indirect estimator are discussed in Sect. 4 and the results of Monte Carlo experiments are presented in Sect. 5. Proofs are given in the appendices.

2 Estimation of censored regression model and indirect inference

The censored regression model and some relevant estimators are introduced in Sect. 2.1 and the indirect inference concept is described in Sect. 2.2.

2.1 Censored regression model

Let us define the censored regression model. First, data are supposed to be a random sample of size $n\in N$ originating from a latent linear regression model

$$\begin{aligned} y_{i}^{*}=x_{i}^{T}\beta ^{0}+\varepsilon _{i}, \end{aligned}$$

(1)

where $y_{i}^{*}\in R$ is the latent dependent variable, $x_{i}\in R^{k}$ is the vector of explanatory variables, $\beta ^{0}$ represents the k-dimensional parameter vector, and $\varepsilon _{i}$ is the unobserved error term with its conditional $\tau$-quantile, $\tau \in (0,1)$, being zero: $q_{\tau }(\varepsilon _{i}|x_{i})=0$. The observed responses $y_{i}$ equal to $y_{i}^{*}$ censored from below at some cut-off point $cp_{i}$:

$$\begin{aligned} y_{i}=\max \left\{ cp_{i},x_{i}^{T}\beta ^{0}+\varepsilon _{i}\right\} . \end{aligned}$$

(2)

We consider here only the case of fixed censoring with a known cut-off point $cp_{i}\equiv cp$, and without loss of generality, $cp=0$. An extension to random censoring is possible by the procedure of Honore et al. (2002).

The CRQ estimator is an extension of the classical linear QR to the censored regression model under a conditional quantile restriction. Since the conditional quantile function of $y_{i}$ in (2) is simply $\max \{0,x_{i}^{T}\beta ^{0}\}$, Powell (1986a) proposed the CRQ estimator $\widehat{\beta }_{n}^{ CRQ}$:

$$\begin{aligned} \widehat{\beta }_{n}^{ CRQ}=\underset{\beta \in B }{\arg \min }\sum \limits _{i=1}^{n}\rho _{\tau }\left( y_{i}-\max \big \{0,x_{i}^{T}\beta \big \}\right) , \end{aligned}$$

(3)

where B is a compact parameter space, $\rho _{\tau }(z)=\{\tau -I\left( z\le 0\right) \}z$ with $\tau \in (0,1)$, and $I(\cdot )$ denotes the indicator function. Note that CRQ can be interpreted as applying the linear QR estimator to the observations $x_{i}$ with $x_{i}^{T}\beta ^{0}>0$: only observations with $x_{i}^{T}\beta ^{0}>0$ carry information to identify and estimate the conditional quantiles of $y_{i}^{*}$ given $x_{i},x_{i}^{T}\beta ^{0}>0$, whereas observations with $x_{i}^{T}\beta ^{0}\le 0$ carry information that the conditional quantile of $y_{i}^{*}$ is negative and the conditional quantile of $y_{i}$ equals zero given $x_{i},x_{i}^{T}\beta ^{0}\le 0$, but they do not identify the conditional quantile of $y_{i}^{*}$ at $x_{i}$ and their contributions to the objective function (3) are independent of $\beta$ in a neighborhood of $\beta ^{0}$. This leads then to a heavy-tailed small-sample distribution of CRQ.

To eliminate this property, Khan and Powell (2001) proposed a two-step estimation method. In the first step, the observations with $x_{i}^{T}\beta ^{0}>0$ are determined by an initial semiparametric or nonparametric estimation, and in the second step, the standard QR estimation is conducted on the selected observations. Nevertheless, the finite sample results of Khan and Powell (2001) do not seem to generate a substantial advantage with respect to the CRQ estimator in terms of mean or median squared errors, possibly due to an imprecise selection of observations in the first step; alternatively, using a local rather than a global optimization algorithm for CRQ could have played a role.

Later, Chernozhukov and Hong (2002) proposed a semiparametric three-step estimator of the censored regression model under conditional quantile restriction. The initial subset of observations with $x_{i}^{T}\beta ^{0}>0$ is selected by a parametric binary-choice model (e.g., logit) and QR is used in the subsequent steps to obtain not only consistent estimates, but also a more precise selection of the observations with $x_{i}^{T}\beta ^{0}>0$. Their finite-sample results are however not substantially better than those of the two-step procedures: while having a smaller mean bias in small samples, the three-step estimates often exhibit a larger mean squared errors (cf. Tang et al. 2011, Sect. 5).

2.2 Parametric indirect inference

Our strategy for estimating the censored regression model will differ from the existing ones in that QR will be applied to all observations and its bias due to censoring will be corrected by means of the indirect inference (II). In this section, we therefore describe a general principle of (parametric) II introduced by Gouriéroux et al. (1993) and discuss how II can be applied as a bias correction method following Gouriéroux et al. (2000).

Consider a general model, for example, (1)–(2):

$$\begin{aligned} y_{i}=h(x_{i},\varepsilon _{i};\beta ), \end{aligned}$$

(4)

where $y_{i}$ represents the response variable, $x_{i}\in R^{k}$ is the vector of explanatory variables with a distribution function $G^{0}(\cdot )$, $\beta ^{0}\in B\subset R^{k}$ is the parameter vector, and $\varepsilon _{i}$ is the unobserved error term with a known conditional distribution function $F^{0}(\cdot |x_{i})$ (a generalization to a nonparametrically estimated distribution function will follow in Sect. 3).

To implement II, an instrumental criterion, which is a function of the observations $\{y_{i},x_{i}\}_{i=1}^{n}$ and of an auxiliary parameter vector $\theta \in \Theta \subset R^{q}$, $q\ge k$, has to be defined (e.g., linear QR applied to censored data). This criterion is minimized to estimate the auxiliary parameter vector:

$$\begin{aligned} \widehat{\theta }_{n}=\underset{\theta \in \Theta }{\arg \min \,}Q_{n}\big (\{y_{i}\}_{i=1}^{n},\theta \big ) \end{aligned}$$

(please note that the dependence on the explanatory variables $\{x_{i}\}_{i=1}^{n}$ is kept implicit as we do not consider simulating values of $x_{i}$, but work conditionally on observed $\{x_{i}\}_{i=1}^{n}$; see Gouriéroux et al. 1993, for details).

The data-generating process is then fully determined by $F^{0}$ and $\beta ^{0}$ and the instrumental criterion $Q_{n}$ is assumed to converge asymptotically to a non-stochastic limit that has a unique minimum $\theta ^{0}$:

$$\begin{aligned} \theta ^{0}=\underset{\theta \in \Theta }{\arg \min \,}Q_{\infty }\Big (F^{0},\beta ^{0},\theta \Big ). \end{aligned}$$

Evaluating it at any $F(\cdot |x_{i})$ and $\beta$ leads to the definition of the binding function $b(F,\beta )$:

$$\begin{aligned} b(F,\beta )=\underset{\theta \in \Theta }{\arg \min \,}Q_{\infty }(F,\beta ,\theta ), \end{aligned}$$

(5)

which implies that $\theta ^{0}=b(F^{0},\beta ^{0})$.

Under some regularity assumptions (see Assumptions A1–A4 in Gouriéroux et al. 1993), $\widehat{\theta }_{n}$ is a consistent estimator of $\theta ^{0}.$ Provided that $b(F^{0},\beta )$ is known and one-to-one, a consistent estimate $\widetilde{\beta }_{n}$ of $\beta ^{0}$ would be defined as $\widetilde{\beta }_{n}=b^{-1}(F^{0},\widehat{\theta }_{n})$ ($F^{0}$ is traditionally assumed to be fully known; auxiliary parameters of the error distribution have to be a part of the parameter vector $\theta$). Since the binding function is often difficult to compute, Gouriéroux et al. (1993) defined a simulation-based procedure to estimate the parameter $\beta ^{0}.$

Let $\{\widetilde{\varepsilon }^{1},\ldots ,\widetilde{\varepsilon }^{S}\}$ be S sets of error terms, where $\widetilde{\varepsilon }^{s}=\{\widetilde{\varepsilon }_{i}^{s}\}_{i=1}^{n},s=1,\ldots ,S$, are simulated from $F^{0}(\cdot |x_{i})$, $\widetilde{\varepsilon }_{i}^{s}|x_{i}\sim F^{0}(\cdot |x_{i})$, assuming this distribution is fully known. Then for any given $\beta$, one can generate S sets of simulated paths $\{\widetilde{y}^{1}(\beta ),\ldots ,\widetilde{y}^{S}(\beta )\}$ using model (4), where $\widetilde{y}^{s}(\beta )=\{\widetilde{y}_{i}^{s}(\beta )\}_{i=1}^{n}$ and $\widetilde{y}_{i}^{s}(\beta )=h(x_{i},\widetilde{\varepsilon }_{i}^{s};\beta )$ conditional on $x_{i}$ for $s=1,\ldots ,S$. From these simulated samples, S auxiliary estimates can be computed:

$$\begin{aligned} \widetilde{\theta }_{n}^{s}(\beta )=\underset{\theta \in \Theta }{\arg \min \,}Q_{n}\big (\{\widetilde{y}_{i}^{s}(\beta )\}_{i=1}^{n},\theta \big ). \end{aligned}$$

(6)

Under appropriate conditions, $\widetilde{\theta }_{n}^{s}(\beta )$ tends asymptotically to $b(F^{0},\beta )$, which allows to define the indirect inference estimator in the following way:

$$\begin{aligned} \widehat{\beta }_{n}^{II}=\underset{\beta \in B }{\arg \min \,}\left[ \widehat{\theta }_{n}-\frac{1}{S}\sum \limits _{s=1}^{S}\widetilde{\theta }_{n}^{s}\left( \beta \right) \right] ^{T}\Omega \left[ \widehat{\theta }_{n}-\frac{1}{S}\sum \limits _{s=1}^{S}\widetilde{\theta }_{n}^{s}\left( \beta \right) \right] , \end{aligned}$$

(7)

where $\Omega$ is a positive definite weighting matrix. This estimator can be shown to be consistent and asymptotically normal (see Proposition 1 and 3 in Gouriéroux et al. 1993). As in GMM estimation, the choice of $\Omega$ does not affect the asymptotic distribution of the estimator if $\mathrm {dim}(\beta )=\mathrm {dim}(\theta )$ and its choice will thus be asymptotically irrelevant.

To argue that II can be used as a bias correction technique, note that $\beta$ can represent the parameter value in the original model (4) (e.g., censored regression (1)–(2)) and $\theta$ the parameter value of the auxiliary biased criterion (e.g., linear QR applied to censored data). The binding function $b(F^{0},\beta )$ then maps the parameter values $\beta$ to biased estimates $\theta$ and its inverse $\widehat{\beta }_{n}^{II}=b^{-1}(F^{0},\widehat{\theta }_{n})$ maps the biased estimates back to the parameters in the original model; see Gouriéroux et al. (2000) for details.

3 Semiparametric indirect inference for censored regression

In this subsection, we introduce the semiparametric indirect estimation procedure to estimate the parameter vector of the censored regression model under conditional quantile restriction. As the linear quantile regression is used as an instrumental criterion and the distribution of $\varepsilon _{i}$ is unknown, a crucial ingredient of the procedure is the behavior of QR under misspecification (this is true even if quadratic or polynomial regression functions are used due to the kink of the true quantile function). Angrist et al. (2006) characterize the QR vector under misspecification as a minimizer of a weighted mean-squared approximation to the true conditional quantile function, assuming the almost-sure existence of the conditional density of the dependent variable, or equivalently, of the error term. As this result does not directly apply to the censored regression model, we modify their result to accommodate the fact that the error distribution is not continuous. In particular, we characterize the QR estimates under misspecification in terms of the distribution function of the error term rather than its density as Angrist et al. (2006) did.

Let us first introduce necessary notation. The conditional quantile function of the dependent variable $y_{i}$ is $\max \{0,x_{i}^{T}\beta ^{0}\}.$ For any quantile index $\tau \in (0,1),$ the QR vector is defined by:

$$\begin{aligned} \theta ^{0}=\underset{\theta \in \Theta }{\arg \min \,}E\left[ \rho _{\tau }(y_{i}-x_{i}^{T}\theta )\right] , \end{aligned}$$

(8)

where $\rho _{\tau }(z)=\{\tau -I\left( z\le 0\right) \}z$. Further, let $\Delta (x_{i},\beta ^{0},\theta )$ denote the QR specification error, $\Delta (x_{i},\beta ^{0},\theta )=x_{i}^{T}\theta -\max \{0,x_{i}^{T}\beta ^{0}\}$, and the observed residual $u_{i}$ be defined as $u_{i}=y_{i}-\max \{0,x_{i}^{T}\beta ^{0}\}$. Finally, let $F_{u}(u|x_{i})$ and $F_{y}(y|x_{i})$ be the conditional distribution functions of $u_{i}$ and $y_{i}$, respectively, and let $f_{u}(u|x_{i})$ and $f_{y}(y|x_{i})$ denote the corresponding conditional densities whenever they exist. For continuously distributed latent error $\varepsilon _{i}$ in model (1), $f_{u}(u|x_{i})$ and $f_{y}(y|x_{i})$ exist and will be used only for $u_{i}>-\max \{0,x_{i}^{T}\beta ^{0}\}$ and $y_{i}>0$, respectively.

Theorem 1

Suppose that $E(y_{i})$ and $E\Vert x_{i}\Vert ^{2}$ are finite, $\theta ^{0}$ uniquely solves (8), and $P\{\Delta (x_{i},\beta ^{0},\theta ^{0})=0\}=0.$ Then, $\bar{\theta }=\theta ^{0}$ uniquely solves the equation

$$\begin{aligned} \bar{\theta }=\underset{\theta \in \Theta }{\arg \min \,}E\left[ w(x_{i},\beta ^{0},\bar{\theta })\cdot \Delta ^{2}(x_{i},\beta ^{0},\theta )\right] , \end{aligned}$$

(9)

where

$$\begin{aligned} w(x_{i},\beta ^{0},\bar{\theta })={\left\{ \begin{array}{ll} \frac{F_{u}\{\Delta (x_{i},\beta ^{0},\bar{\theta })|x_{i}\}-\tau }{2\Delta (x_{i},\beta ^{0},\bar{\theta })} &{} \quad \mathrm{if }\quad \Delta (x_{i},\beta ^{0},\bar{\theta })\ne 0\\ w_{0}(x_{i}) &{} \quad \mathrm{if }\quad \Delta (x_{i},\beta ^{0},\bar{\theta })=0 \end{array}\right. }\text { } \end{aligned}$$

for any bounded function $w_{0}(x_{i}){:}R^{k}\rightarrow R_{0}^{+}.$

Proof

See Appendix 1. $\square$

Theorem 1 states that the linear QR vector depends on the weighting function $w(x_{i},\beta ^{0},\theta ^{0})$, which in turn is a function of the distribution function $F_{u}(\cdot |x_{i})$. Thus, for any other distribution function $\widetilde{F}_{\widetilde{u}}(\cdot )$ such that $\widetilde{F}_{\widetilde{u}}\{\Delta (x_{i},\beta ^{0},\theta ^{0})|x_{i}\}=F_{u}\{\Delta (x_{i},\beta ^{0},\theta ^{0})|x_{i}\},$ the weighting function remains unchanged and the linear QR yields the same vector $\theta ^{0}.$

Next, we consider Theorem 1 in the censored regression model with errors $\varepsilon _{i}\sim F_{\varepsilon }(\cdot |x{}_{i})$. To facilitate semiparametric estimation that does not require complete estimation of $F_{\varepsilon }(\cdot |x{}_{i})$, we will construct another distribution $\widetilde{F}_{\widetilde{\varepsilon }}(\cdot |x_{i})$ that is always from the same parametric family of distributions and that results in the same QR fits as $F_{\varepsilon }(\cdot |x{}_{i})$ by Theorem 1.

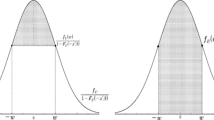
First, note that $u_{i}=\max \{\varepsilon _{i},-x_{i}^{T}\beta ^{0}\}$ for $x_{i}^{T}\beta ^{0}>0$ and $u_{i}=y_{i}$ for $x_{i}^{T}\beta ^{0}\le 0.$ Considering now different errors $\widetilde{\varepsilon }_{i}\sim \widetilde{F}_{\widetilde{\varepsilon }}(\cdot |x_{i})$, one can set $\widetilde{u}_{i}=\max \{\widetilde{\varepsilon }_{i},-x_{i}^{T}\beta ^{0}\}$ for $x_{i}^{T}\beta ^{0}>0$ and $\widetilde{u}_{i}=\widetilde{y}_{i}=\max \{0,x_{i}^{T}\beta ^{0}+\widetilde{\varepsilon }_{i}\}$ for $x_{i}^{T}\beta ^{0}<0.$ As the censoring points of $u_{i}$ and $\widetilde{u}_{i}$ are identical (conditionally on $x_{i}$), we essentially have to match the two latent continuous distributions of $\varepsilon _{i}$ and $\widetilde{\varepsilon }_{i}$. We will show that the distribution $\widetilde{\varepsilon }_{i}$ can be a normal one: $\widetilde{\varepsilon }_{i}\sim N(\mu _{\tau }\sigma (x_{i};\beta ^{0}),\sigma (x;\beta ^{0}))$, where $\mu _{\tau }$ is the $(1-\tau )$th conditional quantile of the standard normal distribution N(0, 1) and $\sigma ^{2}(x_{i};\beta ^{0})$ denotes the conditional variance. Specifically, we find $\sigma (x_{i};\beta ^{0})$ such that $\widetilde{F}_{\widetilde{u}}\{\Delta (x_{i},\beta ^{0},\theta ^{0})|x_{i}\}=F_{u}\{\Delta (x_{i},\beta ^{0},\theta ^{0})|x_{i}\}$ for any finite value of $x_{i}$. First note that $F_{u}\{\Delta (x_{i},\beta ^{0},\theta ^{0})|x_{i}\}=F_{y}(x_{i}^{T}\theta ^{0}|x_{i})$ (and analogously for $\widetilde{u}_{i}$ and $\widetilde{y}_{i}$): $\sigma (x_{i};\beta ^{0})$ has to be therefore chosen so that

$$\begin{aligned} F_{y}(x_{i}^{T}\theta ^{0}|x_{i})=\widetilde{F}_{\widetilde{y}}(x_{i}^{T}\theta ^{0}|x_{i}). \end{aligned}$$

(10)

The definition of $\sigma (x_{i};\beta ^{0})$ is irrelevant if $x_{i}^{T}\theta ^{0}<0$ as then $F_{y}(x_{i}^{T}\theta ^{0}|x_{i})=\widetilde{F}_{\widetilde{y}}(x_{i}^{T}\theta ^{0}|x_{i})=0$. Ignoring the case of $F_{y}(x_{i}^{T}\theta ^{0}|x_{i})=\tau$, which will be dealt with later, (10) for $x_{i}^{T}\theta ^{0}\ge 0$ means

$$\begin{aligned} F_{y}(x_{i}^{T}\theta ^{0}|x_{i})=\Phi \left( \frac{x_{i}^{T}\theta ^{0}-[x_{i}^{T}\beta ^{0}+\mu _{\tau }\sigma (x_{i};\beta ^{0})]}{\sigma (x_{i};\beta ^{0})}\right) =\Phi _{\tau }\left( \frac{x_{i}^{T}\theta ^{0}-x_{i}^{T}\beta ^{0}}{\sigma (x_{i};\beta ^{0})}\right) \end{aligned}$$

(11)

and

$$\begin{aligned} \sigma (x_{i};\beta ^{0})=\frac{x_{i}^{T}\theta ^{0}-x_{i}^{T}\beta ^{0}}{\Phi _{\tau }^{-1}(F_{y}(x_{i}^{T}\theta ^{0}|x_{i}))}, \end{aligned}$$

(12)

where $\Phi$ and $\Phi _{\tau }$ are the distribution functions of N(0, 1) and $N(\mu _{\tau },1)$, respectively (note that (12) leads to $\sigma (x_{i},\beta ^{0})=0$ for $x_{i}^{T}\theta ^{0}<0$). Therefore, having $\widetilde{\varepsilon }_{i}\sim N(\mu _{\tau }\cdot \sigma (x_{i};\beta ^{0}),\sigma (x_{i};\beta ^{0}))$ with $\sigma (x_{i},\beta ^{0})$ defined in (12) yields the same linear QR vector as the real data generated under $\varepsilon _{i}\sim F_{\varepsilon }(\cdot |x_{i})$ and the biases of the linear QR estimates in the censored regression model (1)–(2) both with the original data distribution $\varepsilon _{i}\sim F_{\varepsilon }(\cdot |x_{i})$ and with the data generated from $\widetilde{\varepsilon }_{i}\sim N(\mu _{\tau }\cdot \sigma (x_{i};\beta ^{0}),\sigma (x_{i};\beta ^{0}))$ will be equal.

For the case of $F_{y}(x_{i}^{T}\theta ^{0}|x_{i})=\tau$, i.e., $x_{i}^{T}(\theta ^{0}-\beta ^{0})\rightarrow 0$ for $x_{i}^{T}\beta ^{0}>0$, we consider the limit of (12) and define $\sigma (x_{i};\beta ^{0})$ as

$$\begin{aligned} \sigma (x_{i};\beta ^{0})= & {} \frac{\phi _{\tau }\{\Phi _{\tau }^{-1}[F_{y}(x_{i}^{T}\beta ^{0}|x_{i})]\}}{f_{y}(x_{i}^{T} \beta ^{0}|x_{i})}\nonumber \\= & {} \frac{\phi _{\tau }\{\Phi _{\tau }^{-1}[F_{y}(x_{i}^{T}\theta ^{0}|x_{i})]\}}{f_{y}(x_{i}^{T}\theta ^{0}|x_{i})}\,\,\,\hbox { if }F_{y}(x_{i}^{T}\theta ^{0}|x_{i})=\tau . \end{aligned}$$

(13)

If the bias correction of linear QR is to be performed by II, we can simulate the set of error terms $\{\widetilde{\varepsilon }^{1},\ldots ,\widetilde{\varepsilon }^{S}\}$ from $N(\mu _{\tau }\cdot \sigma (x_{i};\beta ),\sigma (x_{i};\beta ))$ instead of the original data distribution and calibrate over $\beta \in B$ (provided that $\sigma (x_{i},\beta )$ is known). However, $\beta$ is not identified in this case because Eq. (11) holds for any value $\beta$ substituted for $\beta ^{0}$ if definition (12) is used at that $\beta$. To achieve identification, $\beta ^{0}$ in (12) has to be replaced by an initial estimate or the denominator in (12) also has to be a function of $\beta$ instead of being equal to its true value at $\beta ^{0}$. We consider the latter strategy to achieve good performance even in very small samples. It is well known that the identification of the parameter vector in (1)–(2) under conditional quantile restriction relies on the observations with positive values of the index $x_{i}^{T}\beta ^{0}>0$ (Powell 1984, 1986a) since $F_{y}(x_{i}^{T}\beta ^{0}|x_{i})=\tau$ only if $x_{i}^{T}\beta ^{0}>0.$ We also exploit this fact and we define $\widetilde{\sigma }(x_{i};\beta )$ for $x_{i}^{T}\theta ^{0}\ge 0$ as

$$\begin{aligned} \widetilde{\sigma }(x_{i};\beta )={\left\{ \begin{array}{ll} \frac{x_{i}^{T}\theta ^{0}-x_{i}^{T}\beta }{\Phi _{\tau }^{-1}(F_{y_{i}}(x_{i}^{T}\theta ^{0}|x_{i}))} &{}\quad \text { if }\quad x_{i}^{T}\beta \le 0,\\ \frac{x_{i}^{T}\theta ^{0}-x_{i}^{T}\beta }{\Phi _{\tau }^{-1}(\min \{\max \{F_{y}(x_{i}^{T}\theta ^{0}|x_{i})-F_{y}(x_{i}^{T}\beta |x_{i})+\tau ,0\},1\})} &{}\quad \text { if }\quad x_{i}^{T}\beta >0; \end{array}\right. }\text { } \end{aligned}$$

(14)

($\widetilde{\sigma }(x_{i};\beta )=0$ for $x_{i}^{T}\theta ^{0}<0$).¹ Since $\widetilde{\sigma }(x_{i};\beta )=\sigma (x_{i};\beta )$ only if $\beta =\beta ^{0},$ (11) using $\widetilde{\sigma }(x_{i};\beta )$ will hold only at $\beta \equiv \beta ^{0}$ and the parameter vector $\beta$ can be identified (see Lemma 1 for details). Further, as (14) becomes indeterminate if $F_{y}(x_{i}^{T}\theta ^{0}|x_{i})=\tau$ or $F_{y}(x_{i}^{T}\theta ^{0}|x_{i})=F_{y}(x_{i}^{T}\beta |x_{i})$, we replace the definition of $\widetilde{\sigma }(x_{i};\beta )$ in such cases by (13) so that $\widetilde{\sigma }(x_{i};\beta )$ is continuous in $\beta$:

$$\begin{aligned} \widetilde{\sigma }(x_{i};\beta )= & {} \frac{\phi _{\tau }\left\{ \Phi _{\tau }^{-1}\left[ F_{y}\Big (x_{i}^{T}\theta ^{0}|x_{i}\Big )\right] \right\} }{f_{y}\Big (x_{i}^{T}\theta ^{0}|x_{i}\Big )}\,\,\,\hbox { if }F_{y}\Big (x_{i}^{T}\theta ^{0}|x_{i}\Big )=\tau \nonumber \\&\hbox { or }F_{y}\Big (x_{i}^{T}\theta ^{0}|x_{i}\Big )=F_{y}\Big (x_{i}^{T}\beta |x_{i}\Big ), \end{aligned}$$

(15)

where $\phi _{\tau }\left( \cdot \right)$ is the density function of $\Phi _{\tau }(\cdot )$ (note that the limit is the same for both cases of (14)).

With the definition (14) and (15) of $\widetilde{\sigma }(x_{i};\beta )$, which assumes knowledge of the true conditional distribution $F_{y}(x_{i}^{T}\theta ^{0}|x_{i})$ at $x_{i}^{T}\theta ^{0}$, we can define the infeasible indirect inference (III) estimator $\widehat{\beta }_{n}^{III}$ by

$$\begin{aligned} \widehat{\beta }_{n}^{III}=\underset{\beta \in B }{\arg \min \,}\left[ \widehat{\theta }_{n}-\frac{1}{S}\sum \limits _{s=1}^{S}\widetilde{\theta }_{n}^{s}(\beta )\right] ^{T}\Omega \left[ \widehat{\theta }_{n}-\frac{1}{S}\sum \limits _{s=1}^{S}\widetilde{\theta }_{n}^{s}(\beta )\right] , \end{aligned}$$

(16)

where $\widetilde{\theta }_{n}^{s}(\beta )=\underset{\theta \in \Theta }{\arg \min \,}\sum \nolimits _{i=1}^{n}\rho _{\tau }(\widetilde{y}_{i}^{s}(\beta )-x_{i}^{T}\theta )$ using simulated data $\widetilde{y}_{i}^{s}(\beta )=\max \{0,x_{i}^{T}\beta +\widetilde{\varepsilon }_{i}^{s}\}$, $\widetilde{\varepsilon }_{i}^{s}\sim N(\mu _{\tau }\cdot \widetilde{\sigma }(x_{i};\beta ^{0}),\widetilde{\sigma }(x_{i};\beta ^{0}))$ for $s=1,\ldots ,S$, and $\Omega$ is a positive definite weighting matrix. For the sake of brevity, these distributions $N(\mu _{\tau }\cdot \widetilde{\sigma }(x_{i};\beta ),\widetilde{\sigma }(x_{i};\beta ))$ will be referred to as $\widetilde{F}_{\widetilde{\varepsilon }(\beta )}$ within the binding function and its density will be denoted as $\widetilde{f}_{\widetilde{\varepsilon }(\beta )}$. The corresponding quantities for the response variable are $\widetilde{F}_{\widetilde{y}(\beta )}$ and $\widetilde{f}_{\widetilde{y}(\beta )}$.

To define a feasible indirect inference estimator, the simulated error distribution defined by $\widetilde{\sigma }(x_{i};\beta )$ has to be estimated by $N(\mu _{\tau }\cdot \widehat{\sigma }_{n}(x_{i};\beta ^{0}),\widehat{\sigma }_{n}(x_{i};\beta ^{0}))$ using an estimate $\widehat{\sigma }_{n}(x_{i};\beta )$. Denoting $\widehat{\theta }_{n}$ the linear QR estimate for the original data and $\widehat{F}_{y,n}(\cdot |x_{i})$ an estimate of $F_{y}(\cdot |x_{i}),$ we define $\widehat{\sigma }_{n}(x_{i};\beta )$ as

$$\begin{aligned} \widehat{\sigma }_{n}(x_{i};\beta )={\left\{ \begin{array}{ll} \frac{x_{i}^{T}\widehat{\theta }_{n}-x_{i}^{T}\beta }{\Phi _{\tau }^{-1}(\widehat{F}_{y,n}(x_{i}^{T}\widehat{\theta }_{n}|x_{i}))} &{} \quad \text { if }\quad x_{i}^{T}\beta \le 0,\\ \frac{x_{i}^{T}\widehat{\theta }_{n}-x_{i}^{T}\beta }{\Phi _{\tau }^{-1}(\min \{\max \{\widehat{F}_{y,n}(x_{i}^{T}\widehat{\theta }_{n}|x_{i})-\widehat{F}_{y,n}(x_{i}^{T}\beta |x_{i})+\tau ),0\},1\})} &{} \quad \text { if }\quad x_{i}^{T}\beta >0. \end{array}\right. }\text { } \end{aligned}$$

(17)

Since the denominators in (17) might take value 0, we again extend the definition (17) of $\widehat{\sigma }_{n}(x_{i};\beta )$ in such a way that the variance function $\widehat{\sigma }_{n}(x_{i};\beta )$ is continuous in $x_{i}$. For a given $\beta$ and any sequence $\{c_{n}\}_{n=1}^{\infty }$ such that $c_{n}=O(n^{-k_{0}})$, $k_{0}>0$, suppose that $|\widehat{F}_{y,n}(x_{i}^{T}\widehat{\theta }_{n}|x)-\widehat{F}_{y,n}(x_{i}^{T}\beta |x)|<c_{n}$ for $x_{i}^{T}\beta >0$ or $|\widehat{F}_{y,n}(x_{i}^{T}\widehat{\theta }_{n}|x_{i})-\tau |<c_{n}$ for $x_{i}^{T}\beta \le 0$; we refer to this event as the “zero-denominator” $ZD{}_{i,n}(\widehat{\theta }_{n},\beta )$. If $ZD{}_{i,n}(\widehat{\theta }_{n},\beta )$ occurs, then we use instead of (17) the linearly interpolated values

$$\begin{aligned} \widehat{\sigma }_{n}(x_{i};\beta )=\frac{x_{i}^{T}\widehat{\theta }_{n}-x_{m}^{T}\widehat{\theta }_{n}}{x_{M}^{T}\widehat{\theta }_{n}-x_{m}^{T}\widehat{\theta }_{n}}\widehat{\sigma }_{n}(x_{M};\beta )+\frac{x_{M}^{T}\widehat{\theta }_{n}-x_{i}^{T}\widehat{\theta }_{n}}{x_{M}^{T}\widehat{\theta }_{n}-x_{m}^{T}\widehat{\theta }_{n}}\widehat{\sigma }_{n}(x_{m};\beta ), \end{aligned}$$

(18)

where $m=\hbox {arg}\max _{j\le n}\{x_{j}^{T}\widehat{\theta }_{n}:x_{j}^{T}\widehat{\theta }_{n}<x_{i}^{T}\widehat{\theta }_{n}\hbox { and }I(ZD_{j,n}(\widehat{\theta }_{n},\beta ))=0\}$ and $M=\hbox {arg}\min _{j\le n}\{x_{j}^{T}\widehat{\theta }_{n}:x_{j}^{T}\widehat{\theta }_{n}>x_{i}^{T}\widehat{\theta }_{n}\hbox { and }I(ZD_{j,n}(\widehat{\theta }_{n},\beta ))=0\}$; if $m=\emptyset$ or $M=\emptyset$ (e.g., if $\widehat{\theta }_{n}=\beta$), $\widehat{\sigma }_{n}(x_{m};\beta )=1$ or $\widehat{\sigma }_{n}(x_{M};\beta )=1$, respectively. Alternatively, one can also use a straightforward analog of (15) and define

$$\begin{aligned} \widehat{\sigma }_{n}(x_{i};\beta )=\frac{\phi _{\tau }\left\{ \Phi _{\tau }^{-1}\left[ \widehat{F}_{y,n}\Big (x_{i}^{T}\widehat{\theta }_{n}|x_{i}\Big )\right] \right\} }{\hat{f}_{y,n}\Big (x_{i}^{T}\widehat{\theta }_{n}|x_{i}\Big )}, \end{aligned}$$

(19)

where $\hat{f}_{y,n}(\cdot |x_{i})$ is an estimate of the conditional density function $f_{y}(\cdot |x_{i}).$ As this requires an additional nonparametric estimator, we rely on definition (18). The corresponding theoretical results in Sect. 4 are however valid also for (19) if the uniform convergence of $\hat{f}_{y,n}(\cdot |x_{i})$ to $f_{y}(\cdot |x_{i})$ is imposed.

Having an estimate $\widehat{\sigma }_{n}(x_{i};\beta )$ defined by (17)–(18) (or (17) and (19)), the feasible indirect inference (FII) estimator $\widehat{\beta }_{n}^{FII}$ can be defined as

$$\begin{aligned} \widehat{\beta }_{n}^{FII}=\underset{\beta \in B }{\arg \min \,}\left[ \widehat{\theta }_{n}-\frac{1}{S}\sum \limits _{s=1}^{S}\widehat{\theta }_{n}^{s}(\beta )\right] ^{T}\Omega \left[ \widehat{\theta }_{n}-\frac{1}{S}\sum \limits _{s=1}^{S}\widehat{\theta }_{n}^{s}(\beta )\right] , \end{aligned}$$

(20)

where $\widehat{\theta }_{n}^{s}(\beta )=\underset{\theta \in \Theta }{\arg \min \,}\sum \nolimits _{i=1}^{n}\rho _{\tau }(\widehat{y}_{i}^{s}(\beta )-x_{i}^{T}\theta )$ using $\widehat{y}_{i}^{s}(\beta )=\max \{0,x_{i}^{T}\beta +\widehat{\varepsilon }_{i}^{s}\}$ and $\widehat{\varepsilon }_{i}^{s}\sim N(\mu _{\tau }\cdot \widehat{\sigma }_{n}(x_{i};\beta ),\widehat{\sigma }_{n}(x_{i};\beta )).$

Finally, let us remark that the proposed estimator $\widehat{\beta }_{n}^{FII}$ does not perform a selection procedure as it is done in Khan and Powell (2001) and Chernozhukov and Hong (2002), that is, the proposed estimation method is applied to all observations in the sample. Furthermore, our estimation procedure corrects the downward bias of linear QR caused by the censoring of the dependent variable and can be thus considered as a bias-correction method. The bias-correction procedure is based, similar to two-step estimators, on nonparametric estimates. Even though the bias-correction does not seem to be overly sensitive to the (lack of) precision of these nonparametric estimates, it could benefit from using some dimension reduction technique (e.g., Xia et al. 2002) to estimate $\sigma (x_{i},\beta )$ on a lower dimensional space in models with a large numbers of explanatory variables, especially discrete ones. Finally, the linear QR includes implicitly also quadratic and polynomial models since $x_{i}$ can contain both the values of covariates as well as their powers. In the simulations (see Sect. 5), we used for simplicity only the auxiliary model linear in variables as the quadratic auxiliary model, which can better approximate the true quantile function, did not perform substantially better than the linear one.

4 Large sample properties

In this section, the asymptotic properties of the indirect-inference estimators for the censored regression model, $\widehat{\beta }_{n}^{III}$ and $\widehat{\beta }_{n}^{FII}$, are derived. As our main result, we prove that $\widehat{\beta }_{n}^{III}$ and $\widehat{\beta }_{n}^{FII}$ are asymptotically equivalent and asymptotically normally distributed. Let us first introduce conditions required for establishing the consistency and asymptotic normality of the III estimator.

• A.1 The parameter spaces $\Theta$ and B are compact subsets of $R^{k}$ and the true parameter values are $\theta ^{0}\in \Theta ^{\circ }$ and $\beta ^{0}\in B^{\circ }$.

• A.2 The parameter vector $\theta ^{0}$ uniquely minimizes $E[\rho _{\tau }(y_{i}-x_{i}^{T}\theta )]$.

• A.3 The random vectors $\{(x_{i},y_{i})\}_{i=1}^{n}$ are independent and identically distributed with finite second moments. The support of $x_{i}\in X$ is assumed to be compact. Moreover, the index $x_{i}^{T}\theta ^{0}$ is continuously distributed, that is, there is at least one continuously distributed explanatory variable with $\theta _{j}^{0}\not =0$.

• A.4 The $\tau$th conditional quantile of $\varepsilon _{i}$ is zero. The error term $\varepsilon _{i}$ has the conditional distribution $F_{\varepsilon }(t|x_{i})$ with the conditional density function $f_{\varepsilon }(t|x_{i})$, which is uniformly bounded both in t and $x_{i}$, positive on its support, and uniformly continuous with respect to t and $x_{i}$.

• A.5 The following matrices are assumed to be finite and positive definite:

  • $J_{crq}=E\left[ I(x_{i}^{T}\beta ^{0}>0)f_{y}(x_{i}^{T}\beta ^{0}|x_{i})x_{i}x_{i}^{T}\right]$,

  • $J=E[I(x_{i}^{T}\theta ^{0}>0)f_{y}(x_{i}^{T}\theta ^{0}|x_{i})x_{i}x_{i}^{T}]$,

  • $\widetilde{J}=E\left[ I(x_{i}^{T}\theta ^{0}>0)\widetilde{f}_{\widetilde{y}(\beta ^{0})}(x_{i}^{T}\theta ^{0}|x_{i})x_{i}x_{i}^{T}\right]$,

  • $\Sigma =E[\{\tau -I(y_{i}<x_{i}^{T}\theta ^{0})\}^{2}x_{i}x_{i}^{T}]$,

  • $\widetilde{\Sigma }=E[\{\tau -I(\widetilde{y}_{i}^{s}(\beta ^{0})<x_{i}^{T}\theta ^{0})\}^{2}x_{i}x_{i}^{T}]$, and

  • $K=E[\{F_{y}(x_{i}^{T}\theta ^{0}|x_{i})-\tau \}^{2}x_{i}x_{i}^{T}]$.

• A.6 Denoting $\widetilde{F}^{0}=\widetilde{F}_{\widetilde{y}(\beta ^{0})}$, the link function $b(\widetilde{F}^{0},\beta )$ is a one-to-one mapping. Moreover, $b(F,\beta )$ is assumed to be continuous in $\beta$ and F (with respect to the supremum norm) at $\beta ^{0}$ and $\widetilde{F}^{0}$. Finally, $b(\widetilde{F}_{\widetilde{y}(\beta )},\beta )$ is continuously differentiable in $\beta \in U(\beta ^{0},\delta _{b}),\delta _{b}>0$, and $D=\partial b(\widetilde{F}_{\widetilde{y}(\beta ^{0})},\beta ^{0})/\partial \beta ^{T}$ has a full column rank.

• A.7 $P(\Delta (x_{i},\theta ^{0},\beta ^{0})=0)=0$ and $P(x_{i}^{T}\theta ^{0}=v)=0$ for any $v\in R$.

Let us provide a few remarks regarding the necessity of these assumptions. Assumptions A.1, A.2, and A.3 are essential for establishing the consistency and asymptotic normality of the QR estimates $\widehat{\theta }_{n}$ as argued in Angrist et al. (2006) as well as the consistency and asymptotic normality of $\widehat{\beta }_{n}^{III}.$ As shown in Angrist et al. (2006), compactness of the support of X, which is typically achieved by trimming in semiparametric estimation and is also required by Khan and Powell (2001), can be relaxed to the existence of finite $(2+\delta )$th moment of $x_{i}.$ In our proofs of the asymptotic properties of $\widehat{\beta }_{n}^{III}$, relaxing the compactness of X would additionally require ${\max }_{i\le n}\Vert x_{i}\Vert =o_{p}(n^{\alpha })$ for some $0<\alpha <1/2$ (this is an assumption closely related to the existence of finite $(2+\delta )$th moments; see Čížek 2006, Proposition 2.1). Moreover, we assume the existence of one continuous explanatory variable.

Next, Assumption A.4 is the standard assumption in quantile regression models (e.g., Powell 1986a), although the density function $f_{\varepsilon }(t|x_{i})$ is usually assumed to be positive only in a neighborhood of 0. Given the misspecification of the linear QR, it is convenient to assume non-zero density everywhere as $f_{\varepsilon }(t|x_{i})$ is evaluated for any $t=x_{i}^{T}\theta ^{0}$. Concerning Assumption A.5, it contains usual full-rank conditions used in censored and quantile regression models and is necessary for the identification of parameter vectors, see for example Khan and Powell (2001). In the case of J, $\widetilde{J}$, and $J_{crq}$, it rules out collinearity among the explanatory variables restricted to regions with $x_{i}^{T}\theta ^{0}>0$ and $x_{i}^{T}\beta ^{0}>0$, respectively (e.g., collinearity could arise if $x_{i}$ with a bounded support contains a dummy variable $d_{i}$ with so small coefficient that $x_{i}^{T}\beta ^{0}<0$ whenever $d_{i}=1$). Further, the first part of Assumption A.7 is imposed to simplify the proof of the consistency and asymptotic normality of the proposed estimator: it rules out the data without any censoring. The results remain valid even if there is no censoring, although some proofs would slightly differ. The second part of Assumption A.7 just formalizes the continuous-regressor Assumption A.3.

Finally, Assumption A.6 is the standard assumption necessary for defining the indirect inference estimator: the population QR estimates $\widetilde{\theta }(\beta )$ and $\widetilde{\theta }^{\prime }(\beta ^{\prime })$ for data simulated from the censored regression model with parameters $\beta$ and $\beta ^{\prime }$ should differ if $\beta \not =\beta ^{\prime }$. Note though that we require the link function to be one-to-one only at the distribution $\widetilde{F}^{0}=\widetilde{F}_{\widetilde{y}(\beta ^{0})}$ corresponding to the true parameter values $\beta ^{0}$. This should however not be very restrictive in practice. On the one hand, the uniqueness of the population QR estimates $\theta ^{0}$ and $\widetilde{\theta }(\beta )$ for some $\beta$ requires, apart from the full-rank conditions in A.5, that the distribution of the responses and linear regression function is continuous with strictly positive conditional densities at $x_{i}^{T}\theta ^{0}$ for $x_{i}^{T}\theta ^{0}>0$ (cf. Assumption A.5). For the simulated data $(x_{i}^{T}\theta ^{0},\widetilde{y}_{i}^{s}(\beta ))$, the continuity follows from the presence of at least one continuously distributed explanatory variable (Assumption A.3 and A.7) and from the latent errors $\varepsilon _{i}$ being Gaussian with uniformly bounded variances (see Appendix 2), which follows primarily from the compactness of the parameter and variable spaces (Assumptions A.1 and A.3). For the real data, which follow an unknown distribution, we however have to impose the uniqueness of $\theta ^{0}$ (Assumption A.2). On the other hand, the one-to-one link function also means that any change in $\beta$ results in a change of $\widetilde{\theta }(\beta )$. This holds trivially in the model without any censoring as the data generating process defined by $\beta$ then leads to the population QR estimates $\theta =b(\widetilde{F}^{0},\beta )=\beta$. If the censoring is present, $b(\widetilde{F}^{0},\beta )\not =\beta$, but the link function is still usually one-to-one: any change in $\beta$, for example an increase of the intercept, is reflected by the corresponding change in the censored population data, for example by shifting non-censored population data up. This is a direct consequence of the error distribution defining $\widetilde{F}^{0}$ being independent of $\beta$ and its conditional Gaussian density of $\varepsilon _{i}$ given $x_{i}$ being everywhere positive—the population data therefore always contain some non-censored responses at any $x_{i}$.

Although it is difficult to provide a more specific general condition which ensures that the link function is a bijection, one can detect the violation of this condition at least locally. Due to the local identification condition under model misspecification, which is represented here by the full rank of matrix D (cf. Theorem 3.1 of White 1982), singularity or near singularity of the estimated derivative of the link function will indicate that Assumption A.6 is violated. If one suspects that Assumption A.6 is violated, a possible approach is to enhance the auxiliary model in such a way that it better approximates the true model (the closer the auxiliary model is to the true model, the less likely Assumption A.6 is violated). In particular for the censored regression model, we can use, for example, quadratic functions of regressors and fit an auxiliary quadratic QR model rather than the linear one.

These assumptions are sufficient to derive the asymptotic distribution of the infeasible estimator. For the sake of simplicity of some proofs, we will additionally assume that the conditional error distribution $F_{\varepsilon }(\cdot |x_{i})$ has an infinite support (see Appendix 1 for details), but the stated results are valid in the general case as well.

Theorem 2

Let quantile $\tau \in (0,1)$, $\Omega$ be a non-singular $k\times k$ matrix, and $S\in N$ be a fixed number of simulated samples. Under Assumptions A.1–A.7, $\widehat{\beta }_{n}^{III}$ is a consistent estimator of $\beta ^{0}$ and it is asymptotically normal:

$$\begin{aligned} \sqrt{n}(\widehat{\beta }_{n}^{III}-\beta ^{0})\rightarrow N\left( 0,D^{-1}V(S)(D^{T})^{-1}\right) \end{aligned}$$

(21)

as $n\rightarrow +\infty$, where $V(S)=J^{-1}\Sigma J^{-1}+\frac{1}{S}\widetilde{J}^{-1}\widetilde{\Sigma }\widetilde{J}^{-1}+(1-\frac{1}{S})\widetilde{J}^{-1}K\widetilde{J}^{-1}-2J^{-1}K\widetilde{J}^{-1}$.

Proof

See Appendix 3. $\square$

The asymptotic variance matrix of $\widehat{\beta }_{n}^{III}$ derived in Theorem 2 consists of several parts. First, the matrices $\Sigma$ and $\widetilde{\Sigma }$ are the variances of the QR first-order conditions in the real and simulated data, respectively. Next, J and $\widetilde{J}$ are the corresponding Jacobian matrices defined in Assumption A.5. Finally, matrix K characterizes the unconditional covariance between the real and simulated data.

The next theorem shows that the feasible estimator $\widehat{\beta }_{n}^{FII}$ is asymptotically equivalent to the infeasible one $\widehat{\beta }_{n}^{III}$ provided that one extra assumption holds: the conditional distribution function and its nonparametric estimates, which are used in (17) to define $\widehat{\sigma }_{n}(x_{i};\beta )$, have to be smooth functions of the data. Additionally, the nonparametric estimate $\widehat{F}_{y,n}(z_{i}|x_{i})$ has to be consistent and to converge at a faster rate than the sequence $c_{n}=O(n^{-k_{0}})$, $k_{0}>0$, used in the definition of $\widehat{\sigma }_{n}(x_{i};\beta )$. This is however not a constraint as $k_{0}$ is arbitrary.

• A.8 For any compact sets $C_{x}\subset R^{k}$ and $C_{t}\subset R^{+}$, $\sup _{x\in C_{x}}\sup _{t\in C_{t}}|\widehat{F}_{y,n}(t|x_{i})-F_{y}(t|x_{i})|=O_{p}(n^{-k_{1}})$ for some $k_{1}>k_{0}>0$ and $\sup _{x\in C_{x}}\sup _{t\in C_{t}}|E\{\widehat{F}_{y,n}(t|x_{i})-F_{y}(t|x_{i})\}|=o_{p}(n^{-1/2})$. Moreover, $\widehat{F}_{y,n}(t|x_{i})$ is monotonic in t and $\widehat{F}_{y,n}(t|x_{i})=0$ for $t<0$ and any $x_{i}\in X$.

• A.9 The conditional distribution functions $F_{y}(z|x_{i}=x)$ are piecewise Lipschitz functions in x for any $z\in R$.

Assumption A.8 is satisfied for many bias-corrected estimators of conditional distribution functions. Assumption A.9 on the conditional distribution function then states explicitly a minimum requirement that facilitates a consistent estimation and hence validity of Assumption A.8, although stronger assumptions on the smoothness of $F_{y}(z|x_{i})$ are usually used (cf. Li and Racine 2008).

Theorem 3

Let the assumptions of Theorem 2 be satisfied. If Assumptions A.8–A.9 also hold, $\sqrt{n}(\widehat{\beta }_{n}^{FII}-\widehat{\beta }_{n}^{III})\rightarrow 0$ in probability as $n\rightarrow +\infty$.

Proof

See Appendix 3. $\square$

Theorem 3 shows that the feasible and infeasible II estimates, $\widehat{\beta }_{n}^{FII}$ and $\widehat{\beta }_{n}^{III}$, are asymptotically equivalent, and consequently, the asymptotic variance-covariance matrix of $\widehat{\beta }_{n}^{FII}$ is given by (21). All elements of matrix V(S) can be readily estimated in practice (after replacing $\theta ^{0}$ by $\widehat{\theta }_{n}$) as we explain now. First, let us note that, as a by-product of constructing estimate $\widehat{\sigma }_{n}(x_{i},\widehat{\beta }_{n}^{FII})$ of $\widetilde{\sigma }(x_{i},\beta ^{0})$ in the FII estimation procedure, we obtain along with the FII estimate $\widehat{\beta }_{n}^{FII}$ also estimates $\widehat{\theta }_{n}$, $\widehat{F}_{y,n}(x_{i}^{T}\widehat{\theta }_{n}|x_{i})$, and $\widehat{f}_{y,n}(x_{i}^{T}\widehat{\theta }_{n}|x_{i})$ of $\theta ^{0}$, $F_{y}(x_{i}^{T}\theta ^{0}|x_{i})$, and $f_{y}(x_{i}^{T}\theta ^{0}|x_{i})$, respectively, for all $i=1,\ldots ,n$; see formulas (18) and (19). Moreover, all these estimates are consistent by Lemmas 5, 2, and 3. Another by-product of the estimation procedure are S simulated samples $(x_{i},\widetilde{y}_{i}^{s}(\widehat{\beta }_{n}^{FII}))_{i=1}^{n}$ used to compute S auxiliary estimates $\hat{\theta }_{n}^{s}(\widehat{\beta }_{n}^{FII})$ in (20). Since random vectors $(x_{i},y_{i})$ are independent and identically distributed, $i=1,\ldots ,n$, most elements of the asymptotic variance matrix $D^{-1}[J^{-1}\Sigma J^{-1}+S^{-1}\widetilde{J}^{-1}\widetilde{\Sigma }\widetilde{J}^{-1}+(1-S^{-1})\widetilde{J}^{-1}\widetilde{K}\widetilde{J}^{-1}-2J^{-1}\widetilde{K}\widetilde{J}^{-1}](D^{T})^{-1}$ can be consistently estimated due to the law of large numbers by (cf. Assumption A.5)

• $\widehat{J}_{n}=n^{-1}\sum _{i=1}^{n}I(x_{i}^{T}\widehat{\theta }_{n}>0)\widehat{f}_{y,n}(x_{i}^{T}\widehat{\theta }_{n}|x_{i})x_{i}x_{i}^{T}$;

• $\widehat{\widetilde{J}}_{n}=n^{-1}\sum _{i=1}^{n}I(x_{i}^{T}\widehat{\theta }_{n}>0)\widetilde{f}_{\widetilde{y}(\beta ^{0})}(x_{i}^{T}\widehat{\theta }_{n}|x_{i})x_{i}x_{i}^{T}$, where $\widetilde{f}_{\widetilde{y}(\beta ^{0})}(\cdot |x_{i})$ denotes the density of $N(\mu _{\tau },\widehat{\sigma }_{n}(x_{i},\widehat{\beta }_{n}^{FII}))$;

• $\widehat{\Sigma }_{n}=n^{-1}\sum _{i=1}^{n}\{\tau -I(y_{i}<x_{i}^{T}\widehat{\theta }_{n})\}^{2}x_{i}x_{i}^{T}$;

• $\widehat{\widetilde{\Sigma }}_{n}=n^{-1}S^{-1}\sum _{i=1}^{n}\sum _{s=1}^{S}\{\tau -I(\widetilde{y}_{i}^{s}(\widehat{\beta }_{n}^{FII})<x_{i}^{T}\widehat{\theta }_{n})\}^{2}x_{i}x_{i}^{T}$, and

• $\widehat{K}_{n}=n^{-1}\sum _{i=1}^{n}\{\widehat{F}_{y,n}(x_{i}^{T}\widehat{\theta }_{n}|x_{i})-\tau \}^{2}x_{i}x_{i}^{T}$.

The only exception is the matrix $D=\partial b(\widetilde{F}_{\widetilde{y}(\beta ^{0})},\beta ^{0})/\partial \beta ^{T}$, which represents the derivative of the link function. As this derivative is defined in terms of the simulated model with $\widehat{y}_{i}^{s}(\beta )$ being drawn from $N(x_{i}^{T}\beta ,\widehat{\sigma }_{n}(x_{i},\beta ))$ given $x_{i}$ and censored at 0, we can draw an arbitrarily large sample representing the whole population and evaluate the link function and its derivative numerically as suggested by Gouriéroux et al. (1993). In particular, let $1\gg \delta >0$, an integer $N\gg n$, and $\tilde{x}_{k}$ and $\tilde{\varepsilon }_{k}$ be randomly drawn from the empirical distribution of $\{x_{i}\}_{i=1}^{n}$ and N(0, 1) for $k=1,\ldots ,N$. Denoting $\hat{\theta }_{N}(\beta )$ the auxiliary QR estimate obtained for data $(\tilde{x}_{k},\max \{0,\tilde{x}_{k}^{T}\beta +\tilde{\varepsilon }_{k}\widehat{\sigma }_{n}(\tilde{x}_{k},\beta )\})_{k=1}^{N}$, the derivative of the link function can be estimated by matrix $\hat{D}_{n}=(\hat{d}_{ij,n})_{i,j=1}^{k,k}$ with the ijth element equal to

$$\begin{aligned} \hat{d}_{ij,n}=\frac{\hat{\theta }_{i,N}(\beta +\delta e_{j})-\hat{\theta }_{i,N}(\beta )}{\delta }, \end{aligned}$$

where $\hat{\theta }_{i,N}$($\beta )$ denotes the ith element of $\hat{\theta }_{N}(\beta )$ and $e_{j}=(0,\ldots ,0,1,0,\ldots ,0)^{T}$ is the vector with the jth element equal to 1 and all other elements equal to 0. Note though that, given the discussion in Sect. 5.2, it can be advisable to use a better approximation of the estimator’s variance in small samples than the asymptotic distribution; for example, the bootstrap.

5 Monte Carlo simulations

Although we characterized the asymptotic properties of the proposed bias-corrected QR estimator, it is primarily aimed to improve the finite-sample performance of existing estimators. To analyze the benefits of the bias-correction performed by means of the indirect inference, this method is now compared with many existing estimators by means of Monte Carlo simulations. The simulation setting is described in Sect. 5.1 and the results are discussed in Sect. 5.2.

5.1 Simulation design

The data-generating process is similar to the one considered by Khan and Powell (2001):

$$\begin{aligned} y_{i}=\max \{\alpha +x_{1i}+\cdots +x_{ki}+\varepsilon _{i},0\} \end{aligned}$$

with the slope parameters equal to 1 and $\alpha$ chosen in each sample so that the censoring level is always the same; unless stated otherwise, the censoring level equals 50 %. The k regressors $x_{1i},\ldots ,x_{ki}$ are uniformly distributed on $\left\langle -\sqrt{3},\sqrt{3}\right\rangle$, but the results are qualitatively rather similar across other data distributions (e.g., $x_{i}$ being normally distributed). Further, we focus on the median regression case $\tau =0.5$. The error term $\varepsilon _{i}$ can thus follow various error distributions with the median equal to zero, such as the normal $N(0,\sigma _{x})$, Student $t_{d}$, and double exponential $DExp(\lambda )$ ones.

For this data-generating process, we consider the following estimators: (i) the standard Tobit MLE constructed for normal homoscedastic errors; (ii) the CLAD estimator; (iii) the two-step LAD of Khan and Powell (2001) based on their three initial estimators—the maximum score estimator (2S-MSC), the Nadaraya-Watson estimator of the propensity score (2S-NW), and the conditional quantile estimator (2S-LQR); (iv) the ‘infeasible’ LAD (IFLAD) defined as the QR estimator applied only to data points with $\alpha +\beta x_{i}\ge 0$; (v) the three-step estimator of Chernozhukov and Hong (2002) based on the initial logit estimator (3S-LOG); (vi) the proposed QR estimator with bias corrected by indirect inference (FII); and (vii) the corresponding infeasible indirect inference (III) estimator, which does not estimate the conditional error distribution, but ‘knows’ the true one.

The QR estimates were in all cases computed by the Barrodale and Roberts (BR) algorithm as implemented in the R package “quantreg.” The same package was also used for computing CLAD by an adapted BR algorithm; given that it only finds local minima, we searched the global minimum by exhaustive search of all elemental subsets if $k=1$, and due to infeasibility of this in higher dimensional models, started the adapted BR algorithm from the naive QR regression estimate if $k\ge 1$. For the indirect-inference based methods, we use the Nelder-Mead simplex method with multiple starting points as an optimization algorithm;² the number of simulated samples is $S=50$ by default. Further, many of the considered methods depend on some initial nonparametric estimators of the conditional mean, conditional quantile, and conditional distribution and density functions. The nonparametric estimators considered here are those by Racine and Li (2004) for the conditional mean and distribution function estimation, by Li and Racine (2008) for the conditional quantile estimation, and by Hall et al. (2004) for the conditional density estimation; we use their implementation in the R package “npreg,” which also includes the bandwidth choice by the least-squares cross-validation. The estimation and the bandwidth choice were based in all cases on the Gaussian kernel (the results are however insensitive to the kernel choice).

Finally, the bias-corrected QR estimator using the estimated values of the conditional distribution function can sometimes exhibit multiple minima in very small samples (in such cases, there are usually two minima found irrespective of the number of starting points). This concerns only the feasible estimator, but not the infeasible one: given the consistency of the nonparametric estimators, of the proposed II method, and the identification result in Lemma 1, multiple minima thus disappear as the sample size increases (as we practically observed in the simulation study). In the presence of multiple local minima, we simply use the average of the found local minima as the estimate. Unreported simulations indicate that multiple minima in small samples do not occur at all if the quadratic auxiliary model is used.

The results for all methods are obtained using 1000 simulations for $k\in \{1,3,5\}$ variables and sample sizes $n=50,100,$ and 200 and are summarized using the bias and root mean squared error (RMSE) of the slope estimates (the absolute bias is reported if $k>1$).

Table 1 The bias and root mean squared error of the indirect inference estimators based on S simulated samples in a model with the standard normal errors

5.2 Simulation results

Let us first discuss the number S of simulated samples and its influence on the estimates for standard normal errors, $k=1$, and $n=100$. As Table 1 documents, the II estimators are consistent for any fixed and finite S: the III estimator performs equally well for any $S=5,\ldots ,250$ and one could expect similar performance of FII in large samples once the bias of nonparametric estimation becomes small. At $n=100$ however, FII based on an increasing number S of simulated samples shows a diminishing negative finite-sample bias and an increasing RMSE (RMSE does not increase further for $S>250$). While the trade-off is not too large and we choose $S=50$ here, S should be set larger if one is concerned about the bias and can be set smaller if RMSE is important. A similar trade-off—a larger negative bias connected to a lower variance of estimates—will be also observed later in the case of some existing estimators.

Table 2 The bias and root mean squared error of all estimators in a model with the standard normal errors at different sample sizes $n=100$, 200, and 400

The first comparison of estimators is obtained for $\varepsilon _{i}\sim N(0,1)$, $k=1$, and $n=50,100$, and 200; see Table 2. The MLE estimator serves as a parametric benchmark, and given normality, performs best in all cases. First, CLAD exhibit large biases and RMSEs in small samples, especially with $n=50$ observations; this is due to the heavy right-tail of the CLAD distribution. Next, the existing two-step estimators exhibit relatively large RMSEs, which are however smaller than those of CLAD (except for 2S-MSC), and negative biases, which vary with the choice of the initial estimator. The fact that 2S-LQR performs better than the infeasible IFLAD in terms of RMSE is related to the difference in definitions: IFLAD uses data points with $\alpha +\beta x_{i}\ge 0$, whereas the two-step estimators rely on data points with $\alpha +\beta x_{i}\ge c$ (e.g., c is set to 0.05 here as done in Khan and Powell 2001). Increasing c reduces the bias, but increases the variance of estimates (especially for 2S-LQR) and vice versa. In comparison, the three-step estimator 3S-LOG has usually larger RMSEs than 2S-NW or 2S-LQR, but rather small finite-sample bias compared to all other semiparametric methods.

Looking at the two infeasible estimators, III exhibits always smaller RMSE than IFLAD, although the difference decreases with an increasing sample size. It is also interesting to note that IFLAD exhibits systematically a larger negative bias, whereas III leads to a smaller, but positive bias (or almost zero bias for $n=200$). This is reflected by the performance of the proposed FII estimator, which exhibits smaller biases and RMSEs than any of the existing semiparametric methods. One can also notice that, even though FII exhibits generally a smaller bias than the methods of Khan and Powell (2001), the bias of FII is negative in contrast to the bias of III. Finally, let us mention the variance of the II estimates implied by the asymptotic distribution in Theorem 2. While the simulated and asymptotic RMSE are approaching each other in the case of III, the asymptotic standard deviations differ substantially in the case of the feasible estimator FII. Given that the small-sample variance of FII is additionally related to the number S of simulated samples in the opposite way than in Theorem 2, see Table 1, it is not advisable to use the asymptotic distribution in small samples.

Table 3 The bias and root mean squared error of all estimators in a model with the standard normal, student, and double exponential errors; $n=100$

Table 4 The absolute bias and root mean squared error of all estimators in a model with the standard normal errors and $k=1$, 3, and 5 explanatory variables; $n=100$

The next set of results is obtained for five different error distributions, see Table 3 for $k=1$ and $n=100$. The first three distributions are homoscedastic—N(0, 1), $t_{5}$, and DExp(1), whereas the remaining two distribution are heteroscedastic—$N(0,ce^{0.75x})$ in the case of “positive” heteroscedasticity and $N(0,ce^{-0.75x})$ in the case of “negative” heteroscedasticity (c is always chosen so that the unconditional variance equals 1). The “Gaussian” MLE estimator serves again as a parametric benchmark, and in the case of homoscedasticity, performs very well across the tested (symmetric and unimodal) distributions. The performance of the semiparametric estimators under homoscedasticity does not substantially differ from the case with normal errors. Besides 2S-MSC, the semiparametric estimators possess smaller RMSEs than CLAD. The two-step estimators however exhibit relatively large negative biases compared to the three step estimator and the II estimator. The FII estimator is thus preferable in all cases.

The comparison substantially changes once the heteroscedastic errors are considered. The MLE estimates are now severely biased. In the “positive” heteroscedasticity scenario, CLAD exhibits large bias and RMSE. The existing two- and three-step estimators thus provide better estimates than CLAD in terms of RMSEs, and moreover, their biases increase (becoming less negative or even positive). The best performance can be attributed to 2S-LQR followed by FII. In the case of the “negative” heteroscedasticity, the differences among semiparametric estimators are much smaller and CLAD becomes the best performing estimator due to the fact that the observations with conditional median above zero have now very low variance (cf. Khan and Powell 2001). Note that the proposed FII is again the second best, now after CLAD.

Furthermore, let us consider a model with standard normal errors and multiple regressors, $k=1,3,5$; in Table 4, the sample size $n=100$ is used irrespective of the dimension k. Let us first state that the results obtained for $k=1$ in previous experiments for CLAD and 2S-MSC are not fully comparable to the results for $k=3$ and $k=5$ as the earlier ones ($k=1$) search for global minima while the latter ones ($k>1$) correspond to the local minima obtained by starting from the linear QR estimates. This of course reduces variability of the corresponding estimates, and in this experimental design, makes CLAD and 2S-MSC competitive. Nevertheless, one can observe that the semiparametric methods based on some initial k-dimensional nonparametric smoothing tend to increase their RMSE with k faster than methods based purely on one-dimensional (non)parametric estimation. The large part of this effect is related to the increases in the total absolute bias—see the biases of 2S-NW and 2S-LQR, which are similar for each individual parameter irrespective of k, but the total bias of k estimated parameter thus grows with k. The II bias-correction procedure is not affected by this and FII thus performs substantially better than 2S-NW and 2S-LQR for larger k. On the other hand, the performance of FII is matched by the three-step method of Chernozhukov and Hong (2002) at $k=5$ and also by the “local-minimum” CLAD.

Table 5 The bias and root mean squared error of all estimators in a model with the standard normal errors and 25 %, 37.5, and 50 % censored observations; $n=100$

Finally, let us shortly mention how the estimators are affected by the amount of censored observations in the data. Using standard normal errors, $k=1$, and $n=100$, we studied performance under the assumption that 50 % observations are censored. If the fraction of censored observations decreases towards zero, the asymptotic theory predicts that all considered semiparametric estimates will converge to the simple linear QR estimates. This is confirmed by the simulation results in Table 5: we see that, at lower levels of censoring and in particular for 25 % censored observations, the RMSEs of all semiparametric estimators are very close to each other (with the exception of 2S-MSC).

Altogether, all semiparametric alternatives to CLAD perform better than CLAD, although the differences are likely to be small for very large data sets. The proposed FII estimator performs equally well in large samples and is in many cases preferable to existing semiparametric methods in small and moderate samples.

6 Conclusion

We proposed a new estimation method for the censored regression models that—contrary to existing methods—relies on the linear QR estimates for the whole sample and that applies a bias-correction technique to obtain consistent estimates. For the bias correction, the indirect inference technique is applied and extended so that it allows sampling from a nonparametrically estimated distribution function. The consistency and asymptotic distribution of the proposed estimator were found and shown to be first-order independent of the initial nonparametric estimates of the auxiliary error distribution. Finally, one of the important benefits of this estimation approach is its small-sample performance as was demonstrated by means of Monte Carlo simulations.

Appendices

Appendix 1: Proof of Theorem 1

Proof of Theorem 1

The proof is almost identical to the proof of Theorem 2 in Angrist et al. (2006). We need to prove that the solution of

$$\begin{aligned} \theta ^{0}=\underset{\theta \in \Theta }{\arg \min \,}E\left[ \rho _{\tau }(y_{i}-x_{i}^{T}\theta )\right] \end{aligned}$$

(22)

is equal to the solution of

$$\begin{aligned} \bar{\theta }=\underset{\theta \in \Theta }{\arg \min \,}E\left[ w(x_{i},\beta ^{0},\bar{\theta })\cdot \Delta ^{2}(x_{i},\beta ^{0},\theta )\right] . \end{aligned}$$

(23)

Since the objective function in (23) is convex, any fixed point $\theta =\bar{\theta }$ is a solution of the corresponding first-order condition:

$$\begin{aligned} \mathcal {F}(\theta )=2\cdot E\left[ w(x_{i},\beta ^{0},\theta )\cdot \Delta (x_{i},\beta ^{0},\theta )\cdot x_{i}\right] =0. \end{aligned}$$

(24)

On the other hand, the first order condition for (22) is given by (cf. the proof of Theorem 2 in Angrist et al. 2006)

$$\begin{aligned} \mathcal {D}(\theta )=E\left[ \left\{ I\left( u_{i}\le \Delta (x_{i},\beta ^{0},\theta )\right) -\tau \right\} \cdot x_{i}\right] =0. \end{aligned}$$

(25)

By the law of iterated expectations, $D(\theta )$ can be written as

$$\begin{aligned} \mathcal {D}(\theta )=E\left[ \left\{ F_{u_{i}}\left( \Delta \big (x_{i},\beta ^{0},\theta \big )|x_{i}\right) -\tau \right\} \cdot x_{i}\right] =0. \end{aligned}$$

(26)

Further, it follows from the definition of $w(x_{i},\beta ^{0},\theta )$ that $F_{u_{i}}(\Delta (x_{i},\beta ^{0},\theta )|x_{i})-\tau =2\cdot w(x_{i},\beta ^{0},\theta )\cdot \Delta (x_{i},\beta ^{0},\theta )$ for any value of $\Delta \left( x_{i},\beta ^{0},\theta \right) \not =0$. As $P(\Delta (x_{i},\beta ^{0},\theta )=0|x_{i})=0$ and both $F_{u_{i}}(\Delta (x_{i},\beta ^{0},\theta )|x_{i})$ and $x_{i}$ are uniformly bounded by Assumption A.3, it holds that $E[\{F_{u_{i}}(\Delta (x_{i},\beta ^{0},\theta )|x_{i})-\tau \}\cdot x_{i}\cdot I\{\Delta (x_{i},\beta ^{0},\theta )=0\}]=0$, and consequently,

$$\begin{aligned} \mathcal {D}(\theta )= & {} E\left[ \left\{ F_{u_{i}}\left( \Delta \big (x_{i},\beta ^{0},\theta \big )|x_{i}\right) -\tau \right\} \cdot x_{i}\right] \\= & {} E\left[ \left\{ F_{u_{i}}\left( \Delta \big (x_{i},\beta ^{0},\theta \big )|x_{i}\right) -\tau \right\} \cdot x_{i}\cdot I\left\{ \Delta (x_{i},\beta ^{0},\theta )\not =0\right\} \right] \\= & {} 2\cdot E\left[ w(x_{i},\beta ^{0},\theta )\cdot \Delta \big (x_{i},\beta ^{0},\theta \big )\cdot x_{i}\right] =\mathcal {F}(\theta ). \end{aligned}$$

Because $\theta ^{0}$ is the unique solution of (22), it also uniquely solves (23) since the objective function in (23) is convex in $\theta .$ Therefore, $\theta =\theta ^{0}=\bar{\theta }$ solves both (22) and (23). $\square$

Appendix 2: Auxiliary lemmas

For the rest of the proofs, we introduce necessary notation. The norms $\Vert \cdot \Vert$ and $\Vert \cdot \Vert _{\infty }$ will refer to the Euclidean norm on $R^{d}$ and to the supremum norm in functional spaces, respectively. The $\delta$-neighborhood of a vector $t\in R^{d}$ is denoted $U(t,\delta )=\{t^{\prime }\in R^{d}:\Vert t^{\prime }-t\Vert <\delta \}$. The probability distribution and density functions of $N(-\mu _{\tau },1)$ are denoted $\Phi _{\tau }$ and $\phi _{\tau }$, respectively. Additionally, recall that $\rho _{\tau }(z)=\{\tau -I\left( z\le 0\right) \}z$ and its derivative is denoted $\varphi _{\tau }(z)=\tau -I(z\le 0)$.

Next, for $w_{i}=x_{i}$ or $w_{i}=(y_{i},x_{i}),$ let $E_{n}[f(w_{i})]$ denote $n^{-1}\sum \nolimits _{i=1}^{n}f(w_{i})$ and let $G_{n}[f(w_{i})]$ denote $n^{-1/2}\sum \nolimits _{i=1}^{n}\{f(w_{i})-E[f(w_{i})]\}.$ If we need to indicate a particular data distribution P of $w_{i}$, $G_{n,P}[f(w_{i})]=n^{-1/2}\sum \nolimits _{i=1}^{n}\{f(w_{i})-E_{P}[f(w_{i})]\}$ is used, assuming that $w_{i}\sim P$. For easier reading, we also use a simplified notation for the simulated distributions $\widetilde{F}(\beta )=\widetilde{F}_{\widetilde{y}(\beta )}$ and $\widehat{F}(\beta )=\widehat{F}_{\widehat{y}(\beta )}$.

For the sake of simplicity of some proofs, we will additionally assume that the conditional error distribution $F_{\varepsilon }(\cdot |x_{i})$ has (uniformly) an infinite support in order to guarantee that $\sup _{x\in X}F_{\varepsilon }(K|x)<1$ for any $K<\infty$, and by Assumption A.3, that $\sup _{x\in X}\sup _{\theta \in \Theta }F_{y}(x^{T}\theta |x)<K_{F}<1$. Consequently, the conditional variance $\widetilde{\sigma }(x_{i};\beta ^{0})$ defined in (14)–(15) is everywhere positive at the true $\beta ^{0}$, and given the compactness of B, $\Theta$, X, and A.7, $\widetilde{\sigma }(x_{i};\beta ^{0})>C_{\sigma }>0$ for all $x_{i}\in X$. If the limit expression (15) and Assumption A.4 are taken into account, one can observe that the variance function is also bounded from above: $\widetilde{\sigma }(x_{i};\beta )<K_{\sigma }$ for any $\beta \in B$ and all $x_{i}\in X$.

First, the following identification result is derived.

Lemma 1

Under Assumptions A.1–A.5 and A.7, $b(\widetilde{F}(\beta ^{0}),\beta ^{0})\ne b(\widetilde{F}(\beta ^{1}),\beta ^{1})$ for any $\beta ^{1}\in B$ such that $\beta ^{1}\ne \beta ^{0}$.

Proof

First, note that under the listed assumptions, $b(\widetilde{F}^{0},\beta )$ is one-to-one, where $\widetilde{F}^{0}=\widetilde{F}(\beta ^{0})$. Suppose that $b(\widetilde{F}^{0},\beta ^{0})=b(\widetilde{F}(\beta ^{0}),\beta ^{0})=b(\widetilde{F}(\beta ^{1}),\beta ^{1})$. Since $b(\widetilde{F}^{0},\beta )$ is one-to-one, the vector $\beta ^{0}$, which satisfies $b(\widetilde{F}^{0},\beta ^{0})=b(F_{y},\beta ^{0})=\theta ^{0}$ by Theorem 1, uniquely solves the QR moment condition

$$\begin{aligned} E[F_{y}(b(\widetilde{F}^{0},\beta ^{0})|x_{i})-\tau )\cdot x_{i}]=0 \end{aligned}$$

(27)

[see Eq. (26)]. As $F_{y}(t|x_{i})=0$ for any $t<0$ and $P(x_{i}^{T}\theta ^{0}=0)=0$ by Assumption A.7, (27) can be written as

$$\begin{aligned}&E[I(x_{i}^{T}b(F_{y},\beta ^{0})>0)\cdot \{F_{y}(x_{i}^{T}b(F_{y},\beta ^{0})|x_{i})-\tau \}\cdot x_{i}]\nonumber \\&\quad =E[I(x_{i}^{T}b(F_{y},\beta ^{0})<0)\cdot \tau \cdot x_{i}]=k_{0}. \end{aligned}$$

(28)

Next, the QR moment condition for the simulated data $\{\widetilde{y}_{i}^{s}(\beta ^{1}),x_{i}\}_{i=1}^{n}$ is [see Eqs. (25)–(26)]

$$\begin{aligned} E[(\widetilde{F}_{\widetilde{y}(\beta ^{1})}(x_{i}^{T}b\{\widetilde{F}(\beta ^{1}),\beta ^{1}\}|x_{i})-\tau )\cdot x_{i}]=0. \end{aligned}$$

(29)

Because the censored distribution $\widetilde{F}_{\widetilde{y}(\beta ^{1})}(t|x_{i})=0$ for all $t<0$, we can again rewrite it as

$$\begin{aligned}&E[I(x_{i}^{T}b\{\widetilde{F}(\beta ^{1}),\beta ^{1}\}>0)\cdot (\widetilde{F}_{\widetilde{y}(\beta ^{1})}(x_{i}^{T}\theta ^{0}|x_{i})-\tau )\cdot x_{i}]\nonumber \\&\quad =E[I(x_{i}^{T}b\{\widetilde{F}(\beta ^{1}),\beta ^{1}\}<0)\tau \cdot x_{i}]. \end{aligned}$$

Recalling that $\theta ^{0}=b(F_{y},\beta ^{0})=b(\widetilde{F}^{0},\beta ^{0})=b(\widetilde{F}(\beta ^{0}),\beta ^{0})=b(\widetilde{F}(\beta ^{1}),\beta ^{1})$ and that $\widetilde{F}_{\widetilde{y}(\beta )}(t|x_{i})=\Phi _{\tau }\{(t-x_{i}^{T}\beta )\widetilde{\sigma }^{-1}(x_{i},\beta )|x_{i}\}$ for $t>0$, (29) becomes

$$\begin{aligned}&E[I(x_{i}^{T}b(\widetilde{F}^{0},\beta ^{0})>0)\cdot (\Phi _{\tau }\{[x_{i}^{T}b(\widetilde{F}(\beta ^{1}),\\&\quad \beta ^{1})-x_{i}^{T}\beta ^{1}]\cdot \widetilde{\sigma }^{-1}(x_{i},\beta ^{1})|x_{i}\}-\tau )\cdot x_{i}]=k_{0}. \end{aligned}$$

By substituting (14),³ where $\theta ^{0}$ is replaced by $b(\widetilde{F}^{0},\beta ^{0})$, we get

$$\begin{aligned}&E\Biggr [I\left( x_{i}^{T}b\left( \widetilde{F}^{0},\beta ^{0}\right) >0\right) I\left( x_{i}^{T}\beta ^{1}\le 0\right) \\&\quad \times \left\{ \Phi _{\tau }\left( \frac{x_{i}^{T}b\Big \{\widetilde{F}\Big (\beta ^{1}\Big ),\beta ^{1}\Big \}-x_{i}^{T}\beta ^{1}}{x_{i}^{T}b\Big (\widetilde{F}^{0},\beta ^{0}\Big )-x_{i}^{T}\beta ^{1}}\cdot \Phi _{\tau }^{-1}\left\{ F_{y}\Big (x_{i}^{T}b\Big (\widetilde{F}^{0},\beta ^{0}\Big )|x_{i}\Big )\right\} \right) -\tau \right\} x_{i}\\&\quad +\,\,I\Big (x_{i}^{T}b\Big (\widetilde{F}^{0},\beta ^{0}\Big )>0\Big )I\Big (x_{i}^{T}\beta ^{1}>0\Big )\\&\quad \times \left\{ \Phi _{\tau }\left( \frac{x_{i}^{T}b\Big \{\widetilde{F}\Big (\beta ^{1}\Big ),\beta ^{1}\Big \} -x_{i}^{T}\beta ^{1}}{x_{i}^{T}b\Big (\widetilde{F}^{0},\beta ^{0}\Big )-x_{i}^{T}\beta ^{1}}\right. \right. \cdot \,\Phi _{\tau }^{-1}\left\{ F_{y}\Big (x_{i}^{T}b\Big (\widetilde{F}^{0},\beta ^{0} \Big )|x_{i}\Big )\right. \\&\left. \left. \left. \left. -\, F_{y}\Big (x_{i}^{T}\beta ^{1}|x_{i}\Big )+\tau \right\} \right) -\tau \right\} x_{i}\right] =k_{0}. \end{aligned}$$

Recalling again $b(\widetilde{F}^{0},\beta ^{0})=b(\widetilde{F}(\beta ^{0}),\beta ^{0})=b(\widetilde{F}(\beta ^{1}),\beta ^{1})$, we obtain

$$\begin{aligned}&E[I(x_{i}^{T}b(\widetilde{F}^{0},\beta ^{0})>0)\cdot I(x_{i}^{T}\beta ^{1}\le 0)\cdot \{F_{y}(x_{i}^{T}b(\widetilde{F}^{0},\beta ^{0})|x_{i})-\tau \}\cdot x_{i}\nonumber \\&\quad +\,I(x_{i}^{T}b(\widetilde{F}^{0},\beta ^{0})>0)\cdot I(x_{i}^{T}\beta ^{1}>0)\cdot \,\{F_{y}(x_{i}^{T}b(\widetilde{F}^{0},\beta ^{0})|x_{i})\nonumber \\&\quad -\,F_{y}(x_{i}^{T}\beta ^{1}|x_{i})\}\cdot x_{i}]=k_{0}. \end{aligned}$$

(30)

Using identity (28), (30) can be simplified to

$$\begin{aligned} E[I(x_{i}^{T}b(\widetilde{F}^{0},\beta ^{0})>0)\cdot I(x_{i}^{T}\beta ^{1}>0)\cdot (F_{y}(x_{i}^{T}\beta ^{1}|x_{i})-\tau )\cdot x_{i}]=0. \end{aligned}$$

(31)

By Powell (1986a), under Assumptions A.1–A.5 we know that $E[I(x_{i}^{T}\beta ^{0}>0)\cdot (F_{y}(x_{i}^{T}\beta ^{0}|x_{i})-\tau )\cdot x_{i}]=0$ which implies

$$\begin{aligned} E[I(x_{i}^{T}b(\widetilde{F}^{0},\beta ^{0})>0)\cdot I(x_{i}^{T}\beta ^{0}>0)\cdot (F_{y}(x_{i}^{T}\beta ^{0}|x_{i})-\tau )\cdot x_{i}]=0 \end{aligned}$$

since $\left\{ x_{i}\in R^{k}|I(x_{i}^{T}\beta ^{0}>0)I(x_{i}^{T}b(\widetilde{F}^{0},\beta ^{0})>0)\right\} {\subset }\left\{ x_{i}\in R^{k}|I(x_{i}^{T}\beta ^{0}>0)\right\} .$ Thus, we should have $\beta ^{0}=\beta ^{1}$ because $J_{crq}$ is positive definite by Assumption A.5.$\square$

The further auxiliary results presented in this section are proved in the discussion paper of Čížek and Sadikoglu (2014).

Theorem 4

Let $J=E[I(x_{i}^{\top }\theta >0)f_{y}(x_{i}^{T}\theta |x_{i})x_{i}x_{i}^{T}]$. Under Assumptions A.1–A.5 and A.7, it holds that

• 1. $Q_{n}(\theta )=E_{n}[\rho _{\tau }(y_{i}-x_{i}^{T}\theta )-\rho _{\tau }(y_{i}-x_{i}^{T}\theta ^{0})]\rightarrow Q_{\infty }(\theta )=E[\rho _{\tau }(y_{i}-x_{i}^{T}\theta )-\rho _{\tau }(y_{i}-x_{i}^{T}\theta ^{0})]$ as $n\rightarrow \infty$ for any $\theta \in \Theta$;

• 2. $\widehat{\theta }_{n}$ is a consistent estimator of $\theta ^{0}$, $\widehat{\theta }_{n}\mathop {\rightarrow }\limits ^{P}\theta ^{0}$ as $n\rightarrow \infty$;

• 3. for any sequence $\theta _{n}\mathop {\rightarrow }\limits ^{P}\theta ^{0}$, $n^{1/2}(\theta _{n}-\theta ^{0})=-J^{-1}G_{n}\{\varphi _{\tau }(y_{i}-x_{i}^{T}\theta ^{0})x_{i}\}+o_{p}(1)$ converges to a Gaussian process with covariance function $\Sigma =E[(\tau -I(y_{i}<x_{i}^{T}\theta ^{0}))(\tau -I(y_{i}<x_{i}^{T}\theta ^{0}))x_{i}x_{i}]$.

Additionally, suppose that, for sample size $n\in N$, data are independently and identically distributed according to probability distributions $P_{n}$, which satisfy Assumptions A.1–A.5 and A.7 uniformly in n. Denoting

$$\begin{aligned} r(y,x,\theta )={\left\{ \begin{array}{ll} [\rho _{\tau }(y-x^{T}\theta )-\rho _{\tau }(y-x^{T}\theta ^{0})\\ \quad -\,(\theta -\theta ^{0})^{T}(\tau -I\{y\le x^{T}\theta ^{0}\})\cdot x]/\Vert \theta -\theta ^{0}\Vert &{} \quad \mathrm{if }\quad \theta \ne \theta ^{0},\\ 0 &{} \quad \mathrm{if }\quad \theta =\theta ^{0}, \end{array}\right. } \end{aligned}$$

let us assume that

$$\begin{aligned}&\sup _{\theta ^{\prime },\theta ^{\prime \prime }\in U(\theta ^{0},\delta )}|E_{P_{n}}\{r(y_{i},x_{i},\theta ^{\prime })-r(y_{i},x_{i},\theta ^{\prime \prime })\}^{2}\nonumber \\&\quad -\,E_{P_{0}}\{r(y_{i},x_{i},\theta ^{\prime })-r(y_{i},x_{i},\theta ^{\prime \prime })\}^{2}|\rightarrow 0 \end{aligned}$$

(32)

as $n\rightarrow \infty$ for some $\delta >0$ and some distribution $P_{0}$, which satisfies assumptions A.1–A.5 and A.7. Then for any sequence $\theta _{n}\mathop {\rightarrow }\limits ^{P}\theta ^{0}$, $n^{1/2}(\theta _{n}-\theta ^{0})=-J^{-1}G_{n,P_{n}}\{\varphi _{\tau }(y_{i}-x_{i}^{T}\theta ^{0})x_{i}\}+o_{p}(1)$ as $n\rightarrow \infty$.

Proof

See Čížek and Sadikoglu (2014, Theorem 5). $\square$

Lemma 2

Under Assumptions A.1–A.5, A.7, and A.8, it holds for $n\rightarrow \infty$ that

$$\begin{aligned} \sup _{x\in X}\left| \widehat{F}_{y,n}(x_{i}^{T}\widehat{\theta }_{n}|x)-F_{y}(x_{i}^{T}\theta ^{0}|x)\right| =O_{p}\big (n^{-\min \{k_{1},1/2\}}\big ). \end{aligned}$$

Proof

See Čížek and Sadikoglu (2014, Lemma 7). $\square$

Lemma 3

Under Assumptions A.1–A.5, A.7, and A.8, it holds for any $\beta \in B$, sufficiently small $\delta >0$, $l\in \{1,2\}$, and $n\rightarrow \infty$ that

$$\begin{aligned}&\displaystyle |\widehat{\sigma }_{n}(x_{i};\beta )-\widetilde{\sigma }(x_{i};\beta )|=o_{p}(1),\end{aligned}$$

(33)

$$\begin{aligned}&\displaystyle \sup _{\beta \in U(\beta ^{0},\delta )}|\widehat{\sigma }_{n}(x_{i};\beta )-\widetilde{\sigma }(x_{i};\beta )|=o_{p}(1),\end{aligned}$$

(34)

$$\begin{aligned}&\displaystyle E|\widehat{\sigma }_{n}(x_{i};\beta )-\widetilde{\sigma }(x_{i};\beta )|^{l}=o(1),\end{aligned}$$

(35)

$$\begin{aligned}&\displaystyle E(\sup _{\beta \in U(\beta ^{0},\delta )}|\widehat{\sigma }_{n}(x_{i};\beta )-\widetilde{\sigma }(x_{i};\beta )|)^{l}=o_{p}(1). \end{aligned}$$

(36)

Proof

See Čížek and Sadikoglu (2014, Lemma 8). $\square$

Corollary 1

Under Assumptions A.1–A.5, A.7, and A.8, it holds for some $\delta >0$ and $n\rightarrow \infty$:

$$\begin{aligned} \sup _{\beta \in U(\beta ^{0},\delta )}\Vert \widehat{F}(\beta )-\widetilde{F}(\beta )\Vert _{\infty }= & {} \sup _{\beta \in U(\beta ^{0},\delta )}\sup _{t\in R}\left| \Phi _{\tau }\left[ \frac{t-x_{i}^{T}\beta }{\widehat{\sigma }_{n}(x_{i};\beta )}\right] -\Phi _{\tau }\left[ \frac{t-x_{i}^{T}\beta }{\widetilde{\sigma }(x_{i};\beta )}\right] \right| \nonumber \\= & {} o_{p}(1), \end{aligned}$$

$$\begin{aligned} \sup _{\beta \in U(\beta ^{0},\delta )}\sup _{t\in R}\left| \frac{1}{\widehat{\sigma }_{n}(x_{i};\beta )}\phi _{\tau }\left[ \frac{t-x_{i}^{T}\beta }{\widehat{\sigma }_{n}(x_{i};\beta )}\right] -\frac{1}{\widetilde{\sigma }(x_{i};\beta )}\phi _{\tau }\left[ \frac{t-x_{i}^{T}\beta }{\widetilde{\sigma }(x_{i};\beta )}\right] \right| =o_{p}(1). \end{aligned}$$

Further, function $\widetilde{F}(\beta )$ is continuous in $\beta$ on $U(\beta ^{0},\delta )$:

$$\begin{aligned} \lim _{\beta ^{\prime }\rightarrow \beta }\Vert \widetilde{F}(\beta ^{\prime })-\widetilde{F}(\beta )\Vert _{\infty }=\lim _{\beta ^{\prime }\rightarrow \beta }\sup _{t}\left| \Phi _{\tau }\left[ \frac{t-x_{i}^{T}\beta ^{\prime }}{\widetilde{\sigma }(x_{i};\beta ^{\prime })}\right] -\Phi _{\tau }\left[ \frac{t-x_{i}^{T}\beta }{\widetilde{\sigma }(x_{i};\beta )}\right] \right| =o_{p}(1). \end{aligned}$$

Proof

See Čížek and Sadikoglu (2014, Corollary 9).$\square$

Lemma 4

Under Assumptions A.1–A.5, A.7, and A.8, it holds for any $\beta \in B$, $1\le s\le S$, and $n\rightarrow \infty$ that

$$\begin{aligned} E\{\widehat{y}_{i}^{s}\left( \beta \right) -\widetilde{y}_{i}^{s}(\beta )\}^{2}=o(1), \end{aligned}$$

(37)

and for any $\beta \in B$, $\theta \in \Theta$, and $n\rightarrow \infty$, that

$$\begin{aligned} E\left| I(\widehat{y}_{i}^{s}(\beta )\le x_{i}^{T}\theta )-I(\widetilde{y}_{i}^{s}(\beta )\le x_{i}^{T}\theta )\right| ^{2}=o(1). \end{aligned}$$

(38)

Furthermore, statements (37) and (38) along with

$$\begin{aligned}&E\left| I(\widehat{y}_{i}^{s}(\beta ^{\prime })\le x_{i}^{T}\theta ^{\prime })I(\widehat{y}_{i}^{s}(\beta )\le x_{i}^{T}\theta )-I(\widetilde{y}_{i}^{s}(\beta ^{\prime })\le x_{i}^{T}\theta ^{\prime })I(\widetilde{y}_{i}^{s}(\beta )\le x_{i}^{T}\theta )\right| ^{2}\nonumber \\&\quad =o(1),\end{aligned}$$

(39)

$$\begin{aligned}&E\left| \rho _{\tau }(\widehat{y}_{i}^{s}(\beta ^{\prime })\le x_{i}^{T}\theta ^{\prime })I(\widehat{y}_{i}^{s}(\beta )\le x_{i}^{T}\theta )-\rho _{\tau }(\widetilde{y}_{i}^{s}(\beta ^{\prime })\le x_{i}^{T}\theta ^{\prime })I(\widetilde{y}_{i}^{s}(\beta )\le x_{i}^{T}\theta )\right| ^{2}\nonumber \\&\quad =o(1), \end{aligned}$$

(40)

and

$$\begin{aligned}&E\left| \rho _{\tau }(\widehat{y}_{i}^{s}(\beta ^{\prime })\le x_{i}^{T}\theta ^{\prime })\rho _{\tau }(\widehat{y}_{i}^{s}(\beta )\le x_{i}^{T}\theta )-\rho _{\tau }(\widetilde{y}_{i}^{s}(\beta ^{\prime })\le x_{i}^{T}\theta ^{\prime })\rho _{\tau }(\widetilde{y}_{i}^{s}(\beta )\le x_{i}^{T}\theta )\right| ^{2}\nonumber \\&\quad =o(1) \end{aligned}$$

(41)

hold also uniformly with respect to $\beta ,\beta ^{\prime }\in U(\beta ^{0},\delta )$ and $\theta ,\theta ^{\prime }\in U(\theta ^{0},\delta )$ for a sufficiently small $\delta >0$.

Proof

See Čížek and Sadikoglu (2014, Lemma 10). $\square$

Lemma 5

Under Assumptions A.1–A.5 and A.6–A.8, it holds for any $\beta \in B$, $1\le s\le S$, and $n\rightarrow \infty$ that

$$\begin{aligned} |\widehat{\theta }_{n}^{s}(\beta )-b(\widetilde{F}(\beta ),\beta )|=o_{p}(1), \end{aligned}$$

and in particular, $|\widehat{\theta }_{n}^{s}(\beta ^{0})-\theta ^{0}|=o_{p}(1).$

Proof

See Čížek and Sadikoglu (2014, Lemma 11). $\square$

Appendix 3: Proofs of the main asymptotic properties

The proofs in this section rely on the notation introduced at the beginning of Appendix 2.

Proof of Theorem 2

First, we show that $\beta ^{0}$ is identified. By definition (5), the instrumental criterion yields $\theta ^{0}$ at the true value of the parameter $\beta ^{0}$, $b(F_{y},\beta ^{0})=\theta ^{0}$. Theorem 1 and the construction of $\widetilde{F}$ in (10) then imply $b(\widetilde{F}(\beta ^{0}),\beta ^{0})=b(F_{y},\beta ^{0})=\theta ^{0}$. On the other hand, Lemma 1 indicates that, for any $\beta ^{1}\ne \beta ^{0}$, $\beta ^{1}\in B$, the QR yields different estimates: $b(\widetilde{F}(\beta ^{1}),\beta ^{1})\not =b(\widetilde{F}(\beta ^{0}),\beta ^{0})=\theta ^{0}$.

To prove consistency, note that $\widehat{\theta }_{n}\rightarrow \theta ^{0}=b(F_{y},\beta ^{0})$ by Theorem 4. Similarly for any $s=1,\ldots ,S$, $\widetilde{\theta }_{n}^{s}(\beta ^{0})\rightarrow b(\widetilde{F}(\beta ^{0}),\beta ^{0})=b(F_{y},\beta ^{0})=\theta ^{0}$ and $\widetilde{\theta }_{n}^{s}(\beta )\rightarrow b(\widetilde{F}(\beta ),\beta )\not =\theta ^{0}$ for $\beta \not =\beta ^{0}$ since, for a given $\beta \in B$, the data $(\widetilde{y}_{i}^{s}(\beta ),x_{i})_{i=1}^{n}$ also satisfy the assumptions of Theorem 4. The same holds also for $\sum _{s=1}^{S}\widetilde{\theta }_{n}^{s}(\beta ^{0})/S$ as the limits of $\widetilde{\theta }_{n}^{s}(\beta )$ are independent of s and S is finite. The III criterion (16) is thus a strictly convex function in $\widehat{\theta }_{n}$ and $\sum _{s=1}^{S}\widetilde{\theta }_{n}^{s}(\beta ^{0})/S$, which converges for any $\beta$ to

$$\begin{aligned} \underset{\beta \in B }{\arg \min \,}\left[ b(F_{y},\beta ^{0})-b(\widetilde{F}(\beta ),\beta )\right] ^{T}\Omega \left[ b(F_{y},\beta ^{0})-b(\widetilde{F}(\beta ),\beta )\right] . \end{aligned}$$

(42)

Hence by Assumption A.6, any minimizer $\widehat{\beta }_{n}^{III}$ of (16) satisfies $\sum _{s=1}^{S}\widetilde{\theta }_{n}^{s}(\widehat{\beta }_{n}^{III})/S\rightarrow \theta ^{0}$ in probability as $n\rightarrow \infty$ (Newey and McFadden 1994, Theorem 2.7). As the link function b is one-to-one continuous mapping (Assumption A.6) and the parameter space B is compact (Assumption A.1), $\widehat{\beta }_{n}^{III}$ has to converge in probability to $\beta ^{0}$, which is the unique minimum of (42) (cf. the proof of Theorem 1 in Gouriéroux et al. 1993).

The proof for asymptotic normality of $\widehat{\beta }_{n}^{III}$ is similar to the proof of Proposition 3 in Gouriéroux et al. (1993), which is however given for a twice continuously differentiable instrumental criterion. By taking the first-order condition of the optimization problem (16) with respect to $\beta$, the first-order condition is obtained almost surely:

$$\begin{aligned} \left[ \frac{1}{S}\sum \limits _{s=1}^{S}\frac{\partial \widetilde{\theta }_{n}^{s}(\widehat{\beta }_{n}^{III})^{T}}{\partial \beta }\right] \Omega \left[ \widehat{\theta }_{n}-\frac{1}{S}\sum \limits _{s=1}^{S}\widetilde{\theta }_{n}^{s}(\widehat{\beta }_{n}^{III})\right] =0. \end{aligned}$$

Applying the Taylor expansion around $\beta ^{0}$ to $\widehat{\theta }_{n}-\frac{1}{S}\sum \nolimits _{s=1}^{S}\widetilde{\theta }_{n}^{s}(\widehat{\beta }_{n}^{III})$, we obtain analogously to Gouriéroux et al. (1993, Eq. (51)) for some linear combination $\xi _{n}$ of $\beta ^{0}$ and $\widehat{\beta }_{n}^{III}$ and for $n\rightarrow \infty$ that

$$\begin{aligned}&\left[ \frac{1}{S}\sum \limits _{s=1}^{S}\frac{\partial \widetilde{\theta }_{n}^{s}(\widehat{\beta }_{n}^{III})^{T}}{\partial \beta }\right] \Omega \left[ \left\{ \widehat{\theta }_{n}-\frac{1}{S}\sum \limits _{s=1}^{S}\widetilde{\theta }_{n}^{s}(\beta ^{0})\right\} -\frac{1}{S}\sum \limits _{s=1}^{S}\frac{\partial \widetilde{\theta }_{n}^{s}(\xi _{n})^{T}}{\partial \beta }\left\{ \widehat{\beta }_{n}^{III}-\beta ^{0}\right\} \right] \nonumber \\&\quad =0, \end{aligned}$$

(43)

and due to the full-rank Assumption A.6, that

$$\begin{aligned} n^{1/2}(\widehat{\beta }_{n}^{III}-\beta ^{0})= & {} \left( \frac{\partial b^{T}}{\partial \beta }(\widetilde{F}(\beta ^{0}),\beta ^{0})\Omega \frac{\partial b}{\partial \beta ^{T}}(\widetilde{F}(\beta ^{0}),\beta ^{0})\right) ^{-1}\end{aligned}$$

(44)

$$\begin{aligned}&\times \frac{\partial b^{T}}{\partial \beta }(\widetilde{F}(\beta ^{0}),\beta ^{0})\Omega n^{1/2}\left[ \widehat{\theta }_{n}-\frac{1}{S}\sum \limits _{s=1}^{S}\widetilde{\theta }_{n}^{s}(\beta ^{0})\right] +o_{p}(1),\nonumber \\ \end{aligned}$$

(45)

where we used $\partial \widetilde{\theta }_{n}^{s}(\beta )/\partial \beta ^{T}\rightarrow \partial b(\widetilde{F}(\beta ),\beta )/\partial \beta ^{T}$ and $\partial b(\widetilde{F}(\widehat{\beta }_{n}^{III}),\widehat{\beta }_{n}^{III})/\partial \beta ^{T}\rightarrow \partial b(\widetilde{F}(\beta ^{0}),\beta ^{0})/\partial \beta ^{T}=D$ as $n\rightarrow \infty$ in probability (the required continuity of the derivative of the link function and the full rank of its derivative follow from Assumption A.6, whereas the continuity of $\widetilde{F}$ in $\beta$ follows from its Corollary 1).

Next, by Theorem 4, we have

$$\begin{aligned} n^{1/2}(\widehat{\theta }_{n}-\theta ^{0})=-J^{-1}G_{n}[\varphi _{\tau }(y_{i}-x_{i}^{T}\theta ^{0})x_{i}]+o_{p}(1). \end{aligned}$$

(46)

Since $\{\widetilde{y}_{i}^{s}(\beta ^{0}),x_{i}\}_{i=1}^{n}$ and $\widetilde{\varepsilon }_{i}^{s}\sim N(\mu _{\tau }\cdot \widetilde{\sigma }(x_{i};\beta ),\widetilde{\sigma }(x_{i};\beta ))$ satisfy Assumptions A.1–A.5 and A.7, Theorem 4 also implies

$$\begin{aligned} n^{1/2}(\widetilde{\theta }_{n}^{s}(\beta ^{0})-\theta ^{0})=-\widetilde{J}^{-1}G_{n}[\varphi _{\tau }(\widetilde{y}_{i}^{s}(\beta ^{0})-x_{i}^{T}\theta ^{0})x_{i}]+o_{p}(1) \end{aligned}$$

(47)

for any simulated path $s=1,\ldots ,S$ and $n\rightarrow \infty$. Thus, combining (46) and (47) yields

$$\begin{aligned} \begin{aligned} n^{1/2}\left[ \widehat{\theta }_{n}-\frac{1}{S}\sum \limits _{s=1}^{S}\widetilde{\theta }_{n}^{s}\big (\beta ^{0}\big )\right]&= -J^{-1}G_{n}\left[ \varphi _{\tau }\big (y_{i}-x_{i}^{T}\theta ^{0}\big )x_{i}\right] \\&\quad +\widetilde{J}^{-1}\frac{1}{S}\sum \limits _{s=1}^{S}G_{n}\left[ \varphi _{\tau }\big (\widetilde{y}_{i}^{s}\big (\beta ^{0}\big )-x_{i}^{T}\theta ^{0}\big )x_{i}\right] +o_{p}(1) \\&= \left[ -J^{-1},\frac{\widetilde{J}^{-1}}{S},\ldots ,\frac{\widetilde{J}^{-1}}{S}\right] \\&\quad \times \frac{1}{\sqrt{n}}\sum _{i=1}^{n}\left[ \begin{array}{c} \varphi _{\tau }(y_{i}-x_{i}^{T}\theta ^{0})\\ \varphi _{\tau }(\widetilde{y}_{i}^{1}(\beta ^{0})-x_{i}^{T}\theta ^{0})\\ \vdots \\ \varphi _{\tau }(\widetilde{y}_{i}^{S}(\beta ^{0})-x_{i}^{T}\theta ^{0}) \end{array}\right] \otimes x_{i}+o_{p}(1). \end{aligned} \end{aligned}$$

(48)

The random variables $\varphi _{\tau }(y_{i}-x_{i}^{T}\theta ^{0})x_{i}$ and $\varphi _{\tau }(\widetilde{y}_{i}^{s}(\beta ^{0})-x_{i}^{T}\theta ^{0})x_{i}$ have zero means (by the definition of $\theta ^{0}$) and finite variances and covariances (due to Assumption A.3), which are computed below. By the central limit theorem, the random vector in (48) thus converges in distribution to a normally distributed random vector. Using the notation $\Sigma$ and $\widetilde{\Sigma }$ from Assumption A.5 and denoting $\widetilde{K}_{0s}=cov\{\varphi _{\tau }(y_{i}-x_{i}^{T}\theta ^{0})x_{i},\varphi _{\tau }(\widetilde{y}_{i}^{s}(\beta ^{0})-x_{i}^{T}\theta ^{0})x_{i}\}$ and $\widetilde{K}_{rs}=cov\{\varphi _{\tau }(\widetilde{y}_{i}^{r}(\beta ^{0})-x_{i}^{T}\theta ^{0})x_{i},\varphi _{\tau }(\widetilde{y}_{i}^{s}(\beta ^{0})-x_{i}^{T}\theta ^{0})x_{i}\}$, which are independent of $r,s=1,\ldots ,S$, it follows that $n^{1/2}[\widehat{\theta }_{n}-S^{-1}\sum \nolimits _{s=1}^{S}\widetilde{\theta }_{n}^{s}(\beta ^{0})]$ is asymptotically normal with the variance-covariance matrix

$$\begin{aligned} \left[ -J^{-1},\frac{\widetilde{J}^{-1}}{S},\ldots ,\frac{\widetilde{J}^{-1}}{S}\right] \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \Sigma &{} \widetilde{K}_{0s} &{} \widetilde{K}_{0s} &{} \cdots &{} \widetilde{K}_{0s}\\ \widetilde{K}_{0s} &{} \widetilde{\Sigma } &{} \widetilde{K}_{rs} &{} \cdots &{} \widetilde{K}_{rs}\\ \widetilde{K}_{0s} &{} \widetilde{K}_{rs} &{} \widetilde{\Sigma } &{} \cdots &{} \vdots \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \widetilde{K}_{rs}\\ \widetilde{K}_{0s} &{} \widetilde{K}_{rs} &{} \cdots &{} \widetilde{K}_{rs} &{} \widetilde{\Sigma } \end{array}\right] \left[ \begin{array}{c} -J^{-1}\\ \widetilde{J}^{-1}/S\\ \vdots \\ \widetilde{J}^{-1}/S \end{array}\right] . \end{aligned}$$

This matrix can be rewritten as

$$\begin{aligned}&var\left( n^{1/2}\left\{ \widehat{\theta }_{n}-\frac{1}{S}\sum \limits _{s=1}^{S}\widetilde{\theta }_{n}^{s}\big (\beta ^{0}\big )\right\} \right) \nonumber \\&\quad =J^{-1}\Sigma J^{-1}+\frac{1}{S}\widetilde{J}^{-1}\widetilde{\Sigma }\widetilde{J}^{-1}+\left( 1-\frac{1}{S}\right) \widetilde{J}^{-1}\widetilde{K}_{rs}\widetilde{J}^{-1}-2J^{-1}\widetilde{K}_{0s}\widetilde{J}^{-1}, \end{aligned}$$

(49)

where

$$\begin{aligned} \widetilde{K}_{rs}= & {} E[\varphi _{\tau }(\widetilde{y}_{i}^{r}(\beta ^{0})-x_{i}^{T}\theta ^{0})x_{i}\cdot \varphi _{\tau }(\widetilde{y}_{i}^{s}(\beta ^{0})-x_{i}^{T}\theta ^{0})x_{i}]\\= & {} E_{x}[E[\varphi _{\tau }(\widetilde{y}_{i}^{r}(\beta ^{0})-x_{i}^{T}\theta ^{0})|x_{i}]\cdot E[\varphi _{\tau }(\widetilde{y}_{i}^{s}(\beta ^{0})-x_{i}^{T}\theta ^{0})|x_{i}]x_{i}x_{i}^{T})\\= & {} E[\widetilde{F}_{\widetilde{y}(\beta ^{0})}(x_{i}^{T}\theta ^{0}|x_{i})-\tau )(\widetilde{F}_{\widetilde{y}(\beta ^{0})}(x_{i}^{T}\theta ^{0}|x_{i})-\tau )x_{i}x_{i}^{T}] \end{aligned}$$

due to the independence of simulated errors $\{\widetilde{\varepsilon }_{i}^{r}\}_{i=1}^{n}$ and $\{\widetilde{\varepsilon }_{i}^{s}\}_{i=1}^{n}$, and consequently, of the simulated paths $\{\widetilde{y}_{i}^{r}(\beta ^{0})\}_{i=1}^{n}$ and $\{\widetilde{y}_{i}^{s}(\beta ^{0})\}_{i=1}^{n}$ (conditionally on $x_{i}$). Similarly, we can obtain $\widetilde{K}_{0s}=cov\{[F_{y}(x_{i}^{T}\theta ^{0}|x_{i})-\tau )x_{i}][(\widetilde{F}_{\widetilde{y}(\beta ^{0})}(x_{i}^{T}\theta ^{0}|x_{i})-\tau )x_{i}]\}$. By definition (10) of $\widetilde{F}_{\widetilde{y}(\beta ^{0})}$, $\widetilde{F}_{\widetilde{y}(\beta ^{0})}(x_{i}^{T}\theta ^{0}|x_{i})=F_{y}(x_{i}^{T}\theta ^{0}|x_{i})$ and thus $\widetilde{K}_{0s}=\widetilde{K}_{rs}=K$. Combining (44) and (49) then yields the asymptotic distribution of $n^{1/2}(\widehat{\beta }_{n}^{III}-\beta ^{0})$, which is normal with variance

$$\begin{aligned}&(D^{T}\Omega D)^{-1}D^{T}\Omega \nonumber \\&\quad \times \left\{ J^{-1}\Sigma J^{-1}+\frac{1}{S}\widetilde{J}^{-1} \widetilde{\Sigma }\widetilde{J}^{-1}+\left( 1-\frac{1}{S}\right) \widetilde{J}^{-1}K\widetilde{J}^{-1}-2J^{-1}K\widetilde{J}^{-1}\right\} \Omega D(D^{T}\Omega D)^{-1} \end{aligned}$$

(recall that $D=\partial b(\widetilde{F}(\beta ^{0}),\beta ^{0})/\partial \beta ^{T}$). Since D and $\Omega$ are full rank square matrices by Assumption A.6, the final expression follows from $(D^{T}\Omega D)^{-1}=D^{-1}\Omega ^{-1}(D^{T})^{-1}$. $\square$

Proof of Theorem 3

To establish the asymptotic equivalence result, we first need to prove that the feasible estimator $\hat{\beta }_{n}^{FII}$ is consistent. The argument is the same as in the case of the infeasible estimator in Theorem 2 (the first two paragraphs of the proof) provided that we establish $\widehat{\theta }_{n}^{s}(\beta ^{0})\rightarrow b(\widetilde{F}(\beta ^{0}),\beta ^{0})=b(F_{y},\beta ^{0})=\theta ^{0}$ and $\widehat{\theta }_{n}^{s}(\beta )\rightarrow b(\widetilde{F}(\beta ),\beta )\not =\theta ^{0}$ for $\beta \not =\beta ^{0}$. This however follows from Lemma 5, stating that $\widehat{\theta }_{n}^{s}(\beta )-b(\widetilde{F}(\beta ),\beta )=o_{p}(1)$ as $n\rightarrow \infty$ for any $\beta \in B$ and $s=1,\ldots ,S$. Theorem 2.7 of Newey and McFadden (1994) and the continuity of the one-to-one link function thus again implies that $\widehat{\beta }_{n}^{FII}\rightarrow \beta ^{0}$ in probability as $n\rightarrow \infty$.

Next, taking the first-order derivative of the optimization problem (20) with respect to $\beta$, the first-order condition is obtained:

$$\begin{aligned} \left[ \frac{1}{S}\sum \limits _{s=1}^{S}\frac{\partial \widehat{\theta }_{n}^{s}(\widehat{\beta }_{n}^{FII})^{T}}{\partial \beta }\right] \Omega \left[ \widehat{\theta }_{n}-\frac{1}{S}\sum \limits _{s=1}^{S}\widehat{\theta }_{n}^{s}(\widehat{\beta }_{n}^{FII})\right] =0. \end{aligned}$$

(50)

Applying the Taylor expansion around $\beta ^{0}$ to $\widehat{\theta }_{n}-\sum \nolimits _{s=1}^{S}\widetilde{\theta }_{n}^{s}(\widehat{\beta }_{n}^{FII})/S$, we obtain for some linear combination $\xi _{n}$ of $\beta ^{0}$ and $\widehat{\beta }_{n}^{FII}$ that

$$\begin{aligned}&\left[ \frac{1}{S}\sum \limits _{s=1}^{S}\frac{\partial \widehat{\theta }_{n}^{s}(\widehat{\beta }_{n}^{FII})^{T}}{\partial \beta }\right] \Omega \left[ \left\{ \widehat{\theta }_{n}-\frac{1}{S}\sum \limits _{s=1}^{S}\widehat{\theta }_{n}^{s}(\beta ^{0})\right\} -\frac{1}{S}\sum \limits _{s=1}^{S}\frac{\partial \widehat{\theta }_{n}^{s}(\xi _{n})^{T}}{\partial \beta }\left\{ \widehat{\beta }_{n}^{FII}-\beta ^{0}\right\} \right] \nonumber \\&\quad =0. \end{aligned}$$

(51)

We know from Lemma 5 that $\widehat{\theta }_{n}^{s}(\beta )\rightarrow b(\widetilde{F}(\beta ),\beta )$. As the consistency of $\widehat{\beta }_{n}^{FII}$ and Corollary 1 imply that $\widetilde{F}(\beta )$ is continuous in $\beta \in U(\beta ^{0},\delta )$ and that $\Vert \widehat{F}(\widehat{\beta }_{n}^{FII})-\widetilde{F}(\beta ^{0})\Vert =o_{p}(1)$ as $n\rightarrow \infty$, the continuity of the link function (Assumption A.6) implies that $\widehat{\theta }_{n}^{s}(\widehat{\beta }_{n}^{FII})\rightarrow b(\widetilde{F}(\beta ^{0}),\beta ^{0})=\theta ^{0}$; similarly, $\partial \widehat{\theta }_{n}^{s}(\widehat{\beta }_{n}^{III})/\partial \beta ^{T}\rightarrow \partial b(\widetilde{F}(\beta ^{0}),\beta ^{0})/\partial \beta ^{T}$, and $\partial \widehat{\theta }_{n}^{s}(\xi _{n})/\partial \beta ^{T}\rightarrow \partial b(\widetilde{F}(\beta ^{0}),\beta ^{0})/\partial \beta ^{T}$ in probability for $n\rightarrow \infty$.

Consequently, we have due to the full-rank Assumption A.6 that

$$\begin{aligned}&n^{1/2}(\widehat{\beta }_{n}^{FII}-\beta ^{0})\nonumber \\&\quad = \left( \frac{\partial b^{T}}{\partial \beta }(\widetilde{F}(\beta ^{0}),\beta ^{0})\Omega \frac{\partial b}{\partial \beta ^{T}}(\widetilde{F}(\beta ^{0}),\beta ^{0})\right) ^{-1}\frac{\partial b^{T}}{\partial \beta }(\widetilde{F}(\beta ^{0}),\beta ^{0})\Omega \nonumber \\&\qquad \times \, n^{1/2}\left[ \widehat{\theta }_{n}-\frac{1}{S}\sum \limits _{s=1}^{S}\widehat{\theta }_{n}^{s}(\beta ^{0})\right] +o_{p}(1). \end{aligned}$$

(52)

Recall that D denotes $\partial b(\widetilde{F}(\beta ^{0}),\beta ^{0})/\partial \beta ^{T}$. Subtracting (44) from (52) yields

$$\begin{aligned} n^{1/2}(\widehat{\beta }_{n}^{III}-\widehat{\beta }_{n}^{FII})= & {} (D^{T}\Omega D)^{-1}D^{T}\Omega \cdot n^{1/2}\left[ \frac{1}{S}\sum \limits _{s=1}^{S}\widetilde{\theta }_{n}^{s}(\beta ^{0})-\frac{1}{S}\sum \limits _{s=1}^{S}\widehat{\theta }_{n}^{s}(\beta ^{0})\right] \nonumber \\&+\,o_{p}\left( 1\right) . \end{aligned}$$

(53)

To prove the theorem, we have to show that the difference $\sum \nolimits _{s=1}^{S}\widetilde{\theta }_{n}^{s}(\beta ^{0})/S-\sum \nolimits _{s=1}^{S}\widehat{\theta }_{n}^{s}(\beta ^{0})/S$ is asymptotically negligible in probability. The estimates $\widetilde{\theta }_{n}^{s}(\beta ^{0})$ and $\widehat{\theta }_{n}^{s}(\beta ^{0})$ are obtained for data $y_{i}=\max \{x_{i}^{T}\beta ^{0}+\varepsilon _{i}^{s},0\}$, where $\varepsilon _{i}^{s}\sim N(\mu _{\tau }\sigma (x_{i}),\sigma (x_{i}))$ and $\sigma (x_{i})$ represent the conditional variance functions $\widetilde{\sigma }(x_{i};\beta ^{0})$ and $\widehat{\sigma }_{n}(x_{i};\beta ^{0})$, respectively. Thus, $\widetilde{\varepsilon }_{i}^{s}(\beta ^{0})|x_{i}$ follows a normal distribution with mean $\mu _{\tau }\widetilde{\sigma }(x_{i};\beta ^{0})$ and variance $\widetilde{\sigma }(x_{i};\beta ^{0})$ and $(x_{i},\widetilde{\varepsilon }_{i}^{s}(\beta ^{0}))$ follows their joint distribution $P_{0}$. On the other hand, $\widehat{\varepsilon }_{i}^{s}(\beta ^{0})|x_{i}$ is characterized a different conditional distribution, which is a normal distribution with mean $\mu _{\tau }\widehat{\sigma }_{n}(x_{i};\beta ^{0})$ and variance $\widehat{\sigma }_{n}(x_{i};\beta ^{0})$; the joint distribution of $(x_{i},\widehat{\varepsilon }_{i}^{s}(\beta ^{0}))$ is denoted $P_{n}$ (it has the same marginal distribution of $x_{i}$ as $P_{0}$).

We have already established that both $\widetilde{\theta }_{n}^{s}(\beta ^{0})$ and $\widehat{\theta }_{n}^{s}(\beta ^{0})$ are consistent estimators of $\theta ^{0}$. As the variance functions at $\beta ^{0}$ are bounded (see the introduction of Appendix 2), censored data simulated from $P_{0}$ and $P_{n}$ satisfy assumptions of Theorem 4 if condition (32) is verified. As all terms of $\{r(y_{i},x_{i},\theta ^{\prime })-r(y_{i},x_{i},\theta ^{\prime \prime })\}^{2}$ in condition (32) with their expectations varying with $P_{n}$ have the form $C_{2}(\theta ^{\prime },\theta ^{\prime \prime },\theta ^{0})\rho _{\tau }(y-x^{T}\theta ^{\prime })\rho _{\tau }(y-x^{T}\theta ^{\prime \prime })$, $C_{1}(\theta ^{\prime },\theta ^{\prime \prime },\theta ^{0})\rho _{\tau }(y-x^{T}\theta )I(y\le x^{T}\theta ^{0})$, or $C_{0}(\theta ^{\prime },\theta ^{\prime \prime },\theta ^{0})I(y\le x^{T}\theta ^{0})I(y\le x^{T}\theta ^{0})$ for some deterministic functions $C_{0}$, $C_{1}$, $C_{2}$ and some $\theta ^{\prime },\theta ^{\prime \prime }\in U(\theta ^{0},\delta )$, Lemma 4 implies the validity of condition (32). Consequently, we can write using the asymptotic linearity result of Theorem 4 for any $s=1,\ldots ,S$

$$\begin{aligned}&n^{1/2}\left[ \widetilde{\theta }_{n}^{s}(\beta ^{0})-\widehat{\theta }_{n}^{s}(\beta ^{0})\right] \\&\quad =-\widetilde{J}^{-1}G_{n,P_{0}}\left[ \varphi _{\tau }(\max \{0,x_{i}^{T}\beta ^{0}+\varepsilon _{i}^{s}\}-x_{i}^{T}\theta ^{0})x_{i}\right] \\&\quad \quad +\,\widetilde{J}^{-1}G_{n,P_{n}}\left[ \varphi _{\tau }(\max \{0,x_{i}^{T}\beta ^{0}+\varepsilon _{i}^{s}\}-x_{i}^{T}\theta ^{0})x_{i}\right] +o_{p}(1) \end{aligned}$$

as $n\rightarrow \infty$. Let us denote $g(x_{i},\varepsilon _{i}^{s};\beta ,\theta )=\varphi _{\tau }(\max \{0,\varepsilon _{i}^{s}+x_{i}^{T}\beta \}-x_{i}^{T}\theta )x_{i}$. Then

$$\begin{aligned}&n^{1/2}\left[ \widetilde{\theta }_{n}^{s}(\beta ^{0})-\widehat{\theta }_{n}^{s}(\beta ^{0})\right] \\&\quad = \widetilde{J}^{-1}\left\{ G_{n,P_{n}}\left[ g(x_{i},\varepsilon _{i}^{s};\beta ^{0},\theta ^{0})\right] -G_{n,P_{0}}\left[ g(x_{i},\varepsilon _{i}^{s};\beta ^{0},\theta ^{0})\right] \right\} +o_{p}(1). \end{aligned}$$

To verify the claim $n^{1/2}\left[ \widetilde{\theta }_{n}^{s}(\beta ^{0})-\widehat{\theta }_{n}^{s}(\beta ^{0})\right] =o_{p}(1)$, we have to prove that $G_{n,P_{n}}[g(x_{i},\varepsilon _{i}^{s};\beta ^{0},\theta ^{0})]-G_{n,P_{0}} [g(x_{i},\varepsilon _{i}^{s};\beta ^{0},\theta ^{0})]=(G_{n,P_{n}}-G_{n,P_{0}})[g(x_{i},\varepsilon _{i}^{s};\beta ^{0},\theta ^{0})]\overset{P}{\rightarrow }0$ as $n\rightarrow \infty$. We only have to show that $(G_{n,P_{n}}-G_{n,P_{0}})[g(x_{i},\varepsilon _{i}^{s};\beta ^{0},\theta ^{0})]\rightarrow 0$ in distribution since this is equivalent to the convergence to 0 in probability (cf., the proof of Van der Vaart 2000, Lemma 19.24); see also Čížek and Sadikoglu (2014) for details. This result follows from Van der Vaart and Wellner (1996), Theorem 2.8.9 once we verify their assumptions:

• 1. The class of functions $\mathcal {G}=\{g(x,\varepsilon ;\beta ,\theta ):\beta \in U(\beta ^{0},\delta ),\theta \in U(\theta ^{0},\delta )\},\delta >0,$ should satisfy the uniform entropy condition. Since $g(x,\varepsilon ;\beta ,\theta )=[\tau -I(\max \{0,x^{T}\beta +\varepsilon \}-x^{T}\theta \le 0)]x_{i}$, the class $\mathcal{G}$ forms a VC class by Van der Vaart and Wellner (1996, Lemma 2.6.18) and it thus satisfies the uniform entropy condition by Van der Vaart and Wellner (1996, Theorem 2.6.7).

• 2. Next, $P_{n}\bar{g}$ has to be bounded for an envelope function $\bar{g}$ of $\mathcal{G}$ and has to satisfy the Lindenberg condition $\limsup _{n\rightarrow \infty }P_{n}\bar{g}^{2}\{\bar{g}\ge \epsilon \sqrt{n}\}=0$ for every $\epsilon >0$. As the functions in $\mathcal{G}$ are bounded by a constant (see Assumption A.3), this requirement is also satisfied.

• 3. Finally, it has to hold that $\sup _{g,g^{\prime }\in \mathcal{G}}|E_{P_{n}}(g-g^{\prime })^{2}-E_{P_{0}}(g-g^{\prime })^{2}|\rightarrow 0$ as $n\rightarrow \infty$, where $E_{P}(g-g^{\prime })^{2}=E_{P}[I(\max \{0,x_{i}^{T}\beta +\varepsilon _{i}\}-x_{i}^{T}\theta \le 0)-I(\max \{0,x_{i}^{T}\beta ^{\prime }+\varepsilon _{i}\}-x_{i}^{T}\theta ^{\prime }\le 0)]^{2}x_{i}x_{i}^{T}$, $(x_{i},\varepsilon _{i})\sim P$, and $(\beta ,\theta )$ and $(\beta ^{\prime },\theta ^{\prime })$ correspond to functions g and $g^{\prime }$, respectively. This however directly follows from Lemma 4 as $x_{i}$ has a compact support by Assumption A.3.

Consequently, $n^{1/2}\left[ \widetilde{\theta }_{n}^{s}(\beta ^{0})-\widehat{\theta }_{n}^{s}(\beta ^{0})\right] =o_{p}(1)$ for any $s=1,\ldots ,S$ and it follows from Eq. (53) that $n^{1/2}(\widehat{\beta }_{n}^{III}-\widehat{\beta }_{n}^{FII})=(D^{^{\prime }}\Omega D)^{-1}D^{^{\prime }}\Omega o_{p}(1)=o_{p}(1).$ $\square$