Semiparametric Bayesian inference on generalized linear measurement error models

Abstract

The classical assumption in generalized linear measurement error models (GLMEMs) is that measurement errors (MEs) for covariates are distributed as a fully parametric distribution such as the multivariate normal distribution. This paper uses a centered Dirichlet process mixture model to relax the fully parametric distributional assumption of MEs, and develops a semiparametric Bayesian approach to simultaneously obtain Bayesian estimations of parameters and covariates subject to MEs by combining the stick-breaking prior and the Gibbs sampler together with the Metropolis–Hastings algorithm. Two Bayesian case-deletion diagnostics are proposed to identify influential observations in GLMEMs via the Kullback–Leibler divergence and Cook’s distance. Computationally feasible formulae for evaluating Bayesian case-deletion diagnostics are presented. Several simulation studies and a real example are used to illustrate our proposed methodologies.

1 Introduction

Generalized linear models (GLMs) are widely used to fit responses that do not satisfy the usual requirements of least-squares methods in biostatistics, epidemiology, and many other areas. However, the real data fitted via a GLM often involve covariates subject to measurement errors (Carroll et al. 2006; Singh et al. 2014). GLMs with covariates having measurement errors (MEs), which are often referred to as generalized linear measurement error models (GLMEMs), have received a lot of attention in past years. For example, Stefanski and Carroll (1985) developed a bias-adjusted estimator, a functional maximum likelihood estimator and an estimator exploiting the consequences of sufficiency for a logistic regression when covariates were subject to MEs; Stefanski and Carroll (1987) studied parameter estimation in GLM with canonical form when the explanatory vector was measured with an independent normal error; Buzas and Stefanski (1996) investigated instrumental variable estimation in GLMEMs with canonical link functions; Aitkin and Rocci (2002) presented an EM algorithm for maximum likelihood estimation in GLMs with continuous MEs in the explanatory variables; Battauz (2011) developed a Laplace-based estimator for GLMEMs; Battauz and Bellio (2011) proposed a structural analysis for GLMs when some explanatory variables were measured with error and the ME variance was a function of the true variables.

All the above mentioned studies assume that the covariate MEs in GLMEMs are distributed as a fully parametric distribution such as the multivariate normal distribution. However, in some applications, the covariate MEs in GLMEMs may not follow a fully parametric distribution but follow a non-normal distribution such as the skew-normal (Cancho et al. 2010) and skew-t (Lachos et al. 2010) and bimodal and heavy-tailed distributions (Lachos et al. 2011). Moreover, the violation of the parametric assumption on the covariate MEs may lead to unreasonable or even misleading conclusions. Therefore, it is of practical interest to consider a flexible distributional assumption on the covariate MEs in GLMEMs. The nonparametric method is one of the most widely adopted approaches to specify a flexible probability distribution for random variables or MEs in the Bayesian framework.

The Dirichlet process (DP) prior (Ferguson 1973) is the most popular nonparametric approach to specify a probability distribution for random variables or MEs in the Bayesian framework due to the availability of some efficient computational techniques. The nonparametric method has been successfully used to make statistical inference on various random effects models. For example, see Kleinman and Ibrahim (1998), Dunson (2006), Guha (2008), Lee et al. (2008), Chow et al. (2011), Tang and Duan (2012) and Tang et al. (2014). However, to the best of our knowledge, little work is done on Bayesian analysis of GLMEMs with the covariate MEs following a nonparametric distribution. Hence, this paper develops a semiparametric Bayesian approach to simultaneously obtain Bayesian estimations of parameters and covariates subject to MEs, and proposes two Bayesian case deletion diagnostics to detect the potential influential observations under the centered DP mixture model specification of the covariate MEs in GLMEMs. In this paper, a hybrid algorithm is presented to generate observations required for a Bayesian inference from the posterior distributions of parameters and covariates subject to MEs by combining the stick-breaking prior and the Gibbs sampler (Geman and Geman 1984) together with the Metropolis–Hastings algorithm.

Bayesian case deletion approaches to detect influential observations (or sets of observations) have been proposed for some statistical models such as linear regression models (Carlin and Polson 1991), GLMs (Jackson et al. 2012) and generalized linear mixed models (Fong et al. 2010) based on the Kullback–Leibler divergence (K–L divergence) and the conditional predictive ordinate. But, extending these existing Bayesian case deletion diagnostics to our considered GLMEMs is computationally challenging because of the complexity of the considered models and the unknown distribution of the covariate MEs. To this end, the well-known Markov chain Monte Carlo (MCMC) algorithm is employed to develop two computationally feasible Bayesian case deletion diagnostics to assess the effect of cases (or sets of observations) on posterior distributions or estimations of parameters based on the K–L divergence and Cook’s distance in this paper.

The rest of this paper is organized as follows. Section 2 introduces GLMEMs by using the centered DP mixture model to specify the distribution of covaraite MEs. Section 3 develops a Bayesian MCMC algorithm to make Bayesian inference on GLMEMs by using the Gibbs sampler together with the Metropolis–Hastings algorithm. Two Bayesian case deletion diagnostic measures are presented to detect influential observations based on the K–L divergence and Cook’s distance in Sect. 3. Several simulation studies and a real example are used to illustrate our proposed methodologies in Sect. 4. Some concluding remarks are given in Sect. 5. Technical details are presented in the Appendix.

2 Generalized linear measurement error models

For $i=1,\ldots ,n$, let $y_i$ denote the observed outcome variable, $\varvec{{x}}_i$ be a $r\times 1$ vector of the unobserved covariate variables, and $\varvec{{v}}_i$ be a $p\times 1$ vector of the observed covariate variables for the ith individual. Generally, the unobserved components of covariates may vary across different individuals. For simplicity, we assume that the unobserved components of covariates have the same components for $\varvec{{z}}_1,\ldots ,\varvec{{z}}_n$, where $\varvec{{z}}_i=(\varvec{{x}}_i^{\!\top \!},\varvec{{v}}_i^{\!\top \!})^{\!\top \!}$ for $i=1,\ldots ,n$. Given $\varvec{{z}}_i$, we assume that $y_i$’s are conditionally independent of each other, and the conditional distribution of $y_i$ is a one-parameter exponential family with a canonical parameter $\theta _i$ and a mean that is a function of $\varvec{{z}}_i$. That is, for $i=1,\ldots ,n$, the conditional probability density function of $y_i$ given $\varvec{{z}}_i$ is given by

$$\begin{aligned} p(y_{i}|\varvec{{z}}_i,\phi )=\mathrm{exp}\left\{ \frac{y_{i}\theta _{i}-b(\theta _{i})}{\phi }+c(y_{i},\phi )\right\} \end{aligned}$$

(2.1)

with $\mu _{i}=\mathrm{E}(y_{i}|\varvec{{z}}_i)=\dot{b}(\theta _{i})$ and $V_i= \mathrm{var}(y_{i}|\varvec{{z}}_i)=\phi \ddot{b}(\theta _{i})$, where $\phi$ is a scale parameter, $b(\cdot )$ and $c(\cdot ,\cdot )$ are specific differentiable functions, $\dot{b}(\theta _i)=\partial b(\theta _i)/\partial \theta _i$ and $\ddot{b}(\theta _i)=\partial ^{2}b(\theta _i)/\partial \theta _i^2$. The conditional mean $\mu _{i}$ is assumed to satisfy

$$\begin{aligned} \eta _{i}= h(\mu _{i})= \varvec{{x}}_i^{\!\top \!}\varvec{{\beta }}_{x}+\varvec{{v}}_i^{\!\top \!} \varvec{{\beta }}_{v}=\varvec{{z}}_i^{\!\top \!}\varvec{{\beta }}, \end{aligned}$$

(2.2)

where $h(\cdot )$ is a monotonic differentiable link function, $\varvec{{\beta }}=(\varvec{{\beta }}_x^{\!\top \!},\varvec{{\beta }}_v^{\!\top \!})^{\!\top \!}$ is a $(r+p)\times 1$ vector of unknown regression coefficients. Generally, there are two approaches to specify the ME structure. One is the structural ME model, and the other is the functional ME model. In a structural ME model, the special assumption is made on the distributional structure of the unobserved covariates, whilst nothing is assumed on the unobserved covariates in a functional ME model. Following Carroll et al. (2006), if the true covariate $\varvec{{x}}_i$ is measured m times for individual i, giving outcomes $\varvec{{w}}_{ij}$ for $j=1,\ldots ,m$, the structural ME model can be expressed as

$$\begin{aligned} \varvec{{w}}_{ij}=\varvec{{x}}_{i}+\varvec{{u}}_{ij}, \end{aligned}$$

(2.3)

where the MEs $\varvec{{u}}_{ij}$’s are assumed to follow an unknown distribution, and are independent of $\varvec{{x}}_{i}$.

Following Lee et al. (2008), we use the DP mixture model to specify the distribution of $\varvec{{u}}_{ij}$. That is, $\varvec{{u}}_{ij}\mathop {\sim }\limits ^\mathrm{i.i.d.}\sum _{g=1}^{\infty }\pi _g N_r(\varvec{{\alpha }}_g, \varvec{{\Omega }}_g)$ with $(\varvec{{\alpha }}_g, \varvec{{\Omega }}_g)\sim \mathscr {P}$ and $\mathscr {P}\sim \mathrm{DP}(\tau P_0)$, where $\pi _g$ is a random probability weight between 0 and 1 such that $0\le \pi _g\le 1$ and $\sum _{g=1}^{\infty }\pi _g=1$, $N_r(\varvec{{\alpha }}_g,\varvec{{\Omega }}_g)$ denotes the multivariate normal distribution with mean $\varvec{{\alpha }}_g$ and covariance matrix $\varvec{{\Omega }}_g$, $\mathscr {P}$ is a random probability with an unknown form, $P_0$ is a base distribution that serves as a starting-point for constructing the nonparametric distribution, and $\tau$ is a weight assigning a priori to the base distribution and represents the certainty of $P_0$ as the distribution of $\mathscr {P}$. The widely used distribution for $P_0$ is the multivariate normal distribution. The DP prior with the stick-breaking representation may yield non-zero mean of MEs (Yang et al. 2010), which is inconsistent with the classic assumption that mean of $\varvec{{u}}_{ij}$ is zero (Carroll et al. 2006).

Inspired by Yang et al. (2010), we consider the following truncated and centered DP (TCDP) mixture model for $\varvec{{u}}_{ij}$:

$$\begin{aligned} \varvec{{u}}_{ij}\mathop {\sim }\limits ^\mathrm{i.i.d.}\sum \limits _{g=1}^{G}\pi _g N_r(\varvec{{\alpha }}_g, \varvec{{\Omega }}_g)~~\mathrm{with}~~\varvec{{\alpha }}_g=\varvec{{\alpha }}_g^* -\sum \limits _{l=1}^{G}\pi _l\varvec{{\alpha }}_{l}^*~~\mathrm{and}~~(\varvec{{\alpha }}_g^*, \varvec{{\Omega }}_g)\mathop {\sim }\limits ^\mathrm{i.i.d.}P_{0},\qquad \end{aligned}$$

(2.4)

where G is the number of the truncated mixture components, $\pi _g$ is taken to be the following stick-breaking procedure:

$$\begin{aligned} \pi _1=\nu _1~~\mathrm{and}~~\pi _g=\nu _g\prod \limits _{l=1}^{g-1}(1-\nu _l)~~\mathrm{for}~g=2,\ldots ,G \end{aligned}$$

(2.5)

with $\nu _g\mathop {\sim }\limits ^\mathrm{i.i.d.} \mathrm{Beta}(1,\tau )$ for $g=1,\ldots ,G-1$, and $\nu _G=1$ so that $\sum _{g=1}^G\pi _g=1$.

Based on the above specified TCDP mixture model, it is quite difficult to sample observations from posterior distribution of $\varvec{{u}}_{ij}$ via the MCMC algorithm because of the complicated posterior distribution involved. To this end, we generate $\varvec{{u}}_{ij}$ from $N_r(\varvec{{\alpha }}_{L_{ij}},\varvec{{\Omega }}_{L_{ij}})$ in terms of a latent variable $L_{ij}\in \{1,\ldots ,G\}$, where $\varvec{{\alpha }}_{L_{ij}}=\varvec{{\alpha }}_{L_{ij}}^*-\sum _{g=1}^{G}\pi _g\varvec{{\alpha }}_g^*$ in which $\varvec{{\alpha }}_{L_{ij}}^*$ is sampled from the following reformulated model. Let $\varvec{{\pi }}=\{\pi _1,\ldots ,\pi _G\}$, $\varvec{{\alpha }}^*=\{\varvec{{\alpha }}_{1}^*,\ldots ,\varvec{{\alpha }}_{G}^*\}$ and $\varvec{{\Omega }}=\{\varvec{{\Omega }}_1,\ldots ,\varvec{{\Omega }}_G\}$ in which $\varvec{{\Omega }}_g=\mathrm{diag}(\omega _{g1},\ldots ,\omega _{gr})$ for $g=1,\ldots ,G$. It follows from Lee et al. (2008) that Equation (2.4) can be rewritten as

$$\begin{aligned} L_{ij}|\varvec{{\pi }}\mathop {\sim }\limits ^\mathrm{i.i.d.}\sum \limits _{g=1}^G\pi _g\delta _g(\cdot )~~\mathrm{and}~~(\varvec{{\pi }},\varvec{{\alpha }}^*,\varvec{{\Omega }})\sim f_{1}(\varvec{{\pi }})f_{2}(\varvec{{\alpha }}^*)f_{3}(\varvec{{\Omega }}), \end{aligned}$$

(2.6)

where $\delta _g(\cdot )$ is a discrete probability measure concentrated at g, $f_1(\varvec{{\pi }})$ is specified by the stick-breaking prior as given in Eq. (2.5), the prior distribution of $\varvec{{\alpha }}_g^*$ involved in $f_{2}(\varvec{{\alpha }}^*)=\prod _{g=1}^{G}p(\varvec{{\alpha }}_g^*)$ is given by

$$\begin{aligned} \varvec{{\alpha }}_g^*|\varvec{{\xi }},\varvec{{\Psi }}\mathop {\sim }\limits ^\mathrm{i.i.d.} N_r(\varvec{{\xi }},\varvec{{\Psi }}),~~\varvec{{\xi }}|\varvec{{\xi }}^0,\varvec{{\Psi }}^0{\sim }N_r(\varvec{{\xi }}^0,\varvec{{\Psi }}^0),~~\psi _{j}^{-1}|c_{1},c_{2}{\sim }\Gamma (c_{1},c_{2})\quad \mathrm{for}~j=1,\ldots ,r,\nonumber \\ \end{aligned}$$

(2.7)

where $\varvec{{\Psi }}=\mathrm{diag}(\psi _1,\ldots ,\psi _r)$, $\varvec{{\xi }}^0,\varvec{{\Psi }}^0,c_{1}$ and $c_{2}$ are hyperparameters whose values are assumed to be known, $\Gamma (c_1,c_2)$ denotes the Gamma distribution with parameters $c_1$ and $c_2$, and the prior distribution for $\omega _{gj}$ involved in $f_{3}(\varvec{{\Omega }})= \prod _{g=1}^{G}\prod _{j=1}^rp(\omega _{gj})$ is given by

$$\begin{aligned} \omega _{gj}^{-1}|\varphi _{j}^a, \varphi _{j}^b\sim \Gamma (\varphi _{j}^a, \varphi _{j}^b)~~\mathrm{and}~~\varphi _{j}^b|\varphi _{j}^c, \varphi _{j}^d\sim \Gamma (\varphi _{j}^c, \varphi _{j}^d), \end{aligned}$$

(2.8)

where $\varphi _{j}^a,\varphi _{j}^c$ and $\varphi _{j}^d$ are the pre-specified hyperparameters.

To complete specification of the covariate ME model, we require defining a true covariate model. Following Aitkin and Rocci (2002) and Gustafson (2004), the true covariate model for ${x}_{ki}$ ($k=1,\ldots ,r$) can be defined as

$$\begin{aligned} x_{ki}=\gamma _{k0}+\varvec{{\gamma }}_{kv}^{\!\top \!}\varvec{{v}}_i+\varepsilon _{ki}, ~~~~\varepsilon _{ki}\mathop {\sim }\limits ^\mathrm{i.i.d.} N(0,\sigma ^2_x), \end{aligned}$$

(2.9)

where $\gamma _{k0}$ is an intercept, $\varvec{{\gamma }}_{kv}=(\gamma _{k1},\ldots ,\gamma _{kp})^{\!\top \!}$ is a $p\times 1$ vector of unknown regression parameters, and $\varepsilon _{ki}$’s are residuals and assumed to be independent of the covariates $\varvec{{v}}_i$ and MEs $\varvec{{u}}_{ij}$’s. The model defined in Eqs. (2.1)–(2.3) together with (2.9) is referred to as a GLMEM.

The above defined model is not identifiable when there are no replicate measurements, i.e., $m=1$. In this case, some identification conditions on parameters are required (Lee and Tang 2006), for example, we may set $\sigma _x^2$ and $\gamma _{k0}$ to be some prespecified values.

Let $\varvec{{y}}=\{y_1,\ldots ,y_n\}$, $\varvec{{x}}=\{\varvec{{x}}_1,\ldots ,\varvec{{x}}_n\}$, $\varvec{{v}}=\{\varvec{{v}}_1,\ldots ,\varvec{{v}}_n\}$, $\varvec{{u}}=\{\varvec{{u}}_1,\ldots ,\varvec{{u}}_n\}$ and $\varvec{{w}}=\{\varvec{{w}}_1,\ldots ,\varvec{{w}}_n\}$ in which $\varvec{{x}}_i=(x_{1i},\ldots ,x_{ri})^{\!\top \!}$,$\varvec{{u}}_i=\{\varvec{{u}}_{i1},\ldots ,\varvec{{u}}_{im}\}$ and $\varvec{{w}}_i=\{\varvec{{w}}_{i1},\ldots ,\varvec{{w}}_{im}\}$ for $i=1,\ldots ,n$. Denote $\varvec{{\theta }}_y=\{\varvec{{\beta }},\phi \}$, $\varvec{{\theta }}_u=\{\tau ,\varvec{{\pi }},\varvec{{\alpha }}^*,\varvec{{\Omega }}\}$, $\varvec{{\theta }}_\gamma =\{\gamma _{10},\ldots ,\gamma _{r0},\varvec{{\gamma }}_{1v},\ldots ,\varvec{{\gamma }}_{rv},\sigma _x^2\}$ and $\varvec{{\theta }}=\{\varvec{{\theta }}_y,\varvec{{\theta }}_u,\varvec{{\theta }}_\gamma \}$. Under the above assumptions, the joint probability density function for $\{\varvec{{y}},\varvec{{w}},\varvec{{u}},\varvec{{x}}\}$ is given by

$$\begin{aligned} P(\varvec{{y}},\varvec{{w}},\varvec{{u}},\varvec{{x}}|\varvec{{v}},\varvec{{\theta }})=\prod _{i=1}^{n}\left\{ p(y_i|\varvec{{x}}_i,\varvec{{v}}_i;\varvec{{\theta }}_y) p(\varvec{{w}}_i|\varvec{{x}}_i;\varvec{{\theta }}_u)p(\varvec{{x}}_i|\varvec{{v}}_i;\varvec{{\theta }}_\gamma )\right\} . \end{aligned}$$

(2.10)

To make Bayesian inference on parameters in $\{\tau ,\varvec{{\theta }}_y,\varvec{{\theta }}_\gamma \}$, it is necessary to specify their corresponding priors. Similar to Lee and Tang (2006), we consider the following priors for parameters $\tau$, $\varvec{{\beta }}$, $\phi$, $\varvec{{\gamma }}_k^*=(\gamma _{k0},\varvec{{\gamma }}_{kv}^{\!\top \!})^{\!\top \!}$ for $k=1,\ldots ,r$, and $\sigma ^2_x$:

$$\begin{aligned}&\displaystyle \tau |a_1,a_2\sim \Gamma (a_{1},a_{2}),~~\varvec{{\beta }}|\phi ,\varvec{{\beta }}^0,\varvec{{H}}_\beta ^0\sim N_{r+p}(\varvec{{\beta }}^0,\phi ^{-1}\varvec{{H}}_\beta ^0),\\&\displaystyle \phi ^{-1}|a_3,a_4\sim \Gamma (a_3,a_4),~~\varvec{{\gamma }}_k^*|\varvec{{\gamma }}_k^0,\varvec{{H}}_{\gamma k}^0\sim N_{p+1}(\varvec{{\gamma }}_k^0,\varvec{{H}}_{\gamma k}^0),~~\sigma ^{-2}_x|c_3,c_4\sim \Gamma (c_{3},c_{4}), \end{aligned}$$

where $a_1,a_2,a_3,a_4,\varvec{{\beta }}^0,\varvec{{H}}_\beta ^0,\varvec{{\gamma }}_k^0,\varvec{{H}}_{\gamma k}^0,c_3$ and $c_4$ are hyperparameters whose values are assumed to be given by the prior information. Thus, we specify standard conjugate priors for parameters $\tau$, $\phi ^{-1}$, $\varvec{{\gamma }}_k^*$ and $\sigma _x^{-2}$. The associated hyperparameters can be determined in a relatively straightforward manner based on previous applications or data-dependent inputs (Raftery 1996; Richarson and Green 1997; Lee and Tang 2006). Particularly, the values of $a_1$ and $a_2$ should be selected carefully because they directly affect the value of $\tau$ which controls the behavior of $\varvec{{u}}_{ij}$. Detailed discussions on selection of $a_1$ and $a_2$ can refer to Chow et al. (2011). Detailed comments on selection of $c_3$ and $c_4$ are given in simulation studies and real example analysis.

Based on the above presented joint probability density function and priors, a Bayesian approach is developed to make statistical inference on parameters in $\{\tau ,\varvec{{\theta }}_y,\varvec{{\theta }}_\gamma \}$ by utilizing the Gibbs sampler together with the Metropolis–Hastings algorithm for our considered GLMEMs.

3 Bayesian inference on GLMEMs

From Eq. (2.10) and the above defined priors, it is easily seen that it is rather difficult to directly make Bayesian inference on parameters in $\{\tau ,\varvec{{\theta }}_y,\varvec{{\theta }}_\gamma \}$ because of the intractable high-dimensional integrals involved. Owing to recent development in statistical computing, the Gibbs sampler is employed to generate a sequence of random observations from the joint posterior distribution $p(\varvec{{\xi }},\varvec{{\Psi }},\tau ,\varvec{{\varphi }}^b,\varvec{{\pi }},\varvec{{L}},\varvec{{\alpha }}^*,\varvec{{\Omega }},\varvec{{u}},\varvec{{\beta }},\phi ,\varvec{{\gamma }},\sigma ^2_x,\varvec{{x}}|\varvec{{y}},\varvec{{w}},\varvec{{v}})$, and Bayesian estimates of unknown parameters and covariates subject to MEs are obtained from the generated sequence of random observations, where $\varvec{{\varphi }}^b=\{\varphi _{1}^b,\ldots ,\varphi _r^b\}$, $\varvec{{\gamma }}=\{\varvec{{\gamma }}_1^*,\ldots ,\varvec{{\gamma }}_r^*\}$ and $\varvec{{L}}=\{L_{ij}:i=1,\ldots ,n,j=1,\ldots ,m\}$. In this algorithm, observations $\{\varvec{{\xi }},\varvec{{\Psi }},\tau ,\varvec{{\varphi }}^b,\varvec{{\pi }},\varvec{{L}},\varvec{{\alpha }}^*,\varvec{{\Omega }},\varvec{{u}},\varvec{{\beta }},\phi ,\varvec{{\gamma }},\sigma ^2_x$, $\varvec{{x}}\}$ are iteratively drawn from the following conditional distributions: $p(\varvec{{\xi }}|\varvec{{\alpha }}^*,\varvec{{\Psi }})$, $p(\varvec{{\Psi }}|\varvec{{\alpha }}^*,\varvec{{\xi }})$, $p(\tau |\varvec{{\pi }})$, $p(\varvec{{\varphi }}^b|\varvec{{\Omega }})$, $p(\varvec{{\pi }}|\varvec{{L}},\tau )$, $p(\varvec{{L}}|\varvec{{\pi }},\varvec{{\alpha }},\varvec{{\Omega }},\varvec{{u}})$, $p(\varvec{{\alpha }}^*|\varvec{{\xi }},\varvec{{\Psi }},\varvec{{\Omega }},\varvec{{L}},\varvec{{u}})$, $p(\varvec{{\beta }}|\varvec{{y}},\varvec{{x}},\varvec{{v}},\phi )$, $p(\varvec{{\Omega }}|\varvec{{\alpha }},\varvec{{\varphi }}^b,\varvec{{L}}$, $\varvec{{u}})$, $p(\phi |\varvec{{\beta }},\varvec{{y}},\varvec{{x}},\varvec{{v}})$, $p(\varvec{{\gamma }}|\varvec{{x}},\varvec{{v}},\sigma ^2_{x})$, $p(\sigma ^2_{x}|\varvec{{x}},\varvec{{v}}$, $\varvec{{\gamma }})$, $p(\varvec{{x}}|\varvec{{y}},\varvec{{v}},\varvec{{u}},\varvec{{w}},\varvec{{\alpha }},\varvec{{\beta }},\phi ,\sigma ^2_{x},\varvec{{\gamma }},\varvec{{L}})$ and $p(\varvec{{u}}|\varvec{{\alpha }},\varvec{{\Omega }}$, $\varvec{{L}},\varvec{{x}},\varvec{{w}},\varvec{{\theta }}_u)$. These conditional distributions are presented in the Appendix.

3.1 Bayesian estimates

Let $\{(\varvec{{\beta }}^{(\ell )},\phi ^{(\ell )}, \varvec{{\gamma }}^{(\ell )},\varvec{{x}}^{(\ell )},{\sigma ^2_{x}}^{(\ell )}): \ell =1,\ldots ,\mathfrak {L}\}$ be observations of $\{\varvec{{\beta }},\phi$, $\varvec{{\gamma }},\varvec{{x}},\sigma ^2_{x}\}$ generated from $p(\varvec{{\xi }},\varvec{{\Psi }},\tau ,\varvec{{\varphi }}^b,\varvec{{\pi }},\varvec{{L}},\varvec{{\alpha }}^*,\varvec{{\Omega }},\varvec{{u}},\varvec{{\beta }},\phi ,\varvec{{\gamma }},\sigma ^2_x,\varvec{{x}}|\varvec{{y}},\varvec{{v}},\varvec{{w}})$ via the preceding presented algorithm. Thus, Bayesian estimates of $\{\varvec{{\beta }},\phi ,\varvec{{\gamma }},\varvec{{x}},\sigma ^2_{x}\}$ can be obtained by

$$\begin{aligned} \hat{\varvec{{\beta }}}=\frac{1}{\mathfrak {L}}\sum _{\ell =1}^{\mathfrak {L}}\varvec{{\beta }}^{(\ell )},\quad \hat{\phi }=\frac{1}{\mathfrak {L}}\sum _{\ell =1}^{\mathfrak {L}}\phi ^{(\ell )},\quad \hat{\varvec{{\gamma }}}=\frac{1}{\mathfrak {L}}\sum _{\ell =1}^{\mathfrak {L}}\varvec{{\gamma }}^{(\ell )},\quad \hat{\varvec{{x}}}=\frac{1}{\mathfrak {L}}\sum _{\ell =1}^{\mathfrak {L}}\varvec{{x}}^{(\ell )},\quad \hat{\sigma }^2_x=\frac{1}{\mathfrak {L}}\sum _{\ell =1}^{\mathfrak {L}}{\sigma ^2_{x}}^{(\ell )}.\nonumber \\ \end{aligned}$$

(3.1)

The consistent estimates of the posterior covariance matrices var$(\varvec{{\beta }}|\varvec{{y}},\varvec{{v}},\varvec{{w}})$, var$(\phi |\varvec{{y}},\varvec{{v}},\varvec{{w}})$, var$(\varvec{{\gamma }}|\varvec{{y}},\varvec{{v}},\varvec{{w}})$ and var$(\sigma ^2_{x}|\varvec{{y}},\varvec{{v}},\varvec{{w}})$ can be obtained from the sample covariance matrices of the above generated observations. For example, $\widehat{\text{ var }}(\varvec{{\beta }}|\varvec{{y}},\varvec{{v}},\varvec{{w}})=\frac{1}{\mathfrak {L}-1}\Sigma _{\ell =1}^{\mathfrak {L}} (\varvec{{\beta }}^{(\ell )}-\hat{\varvec{{\beta }}})(\varvec{{\beta }}^{(\ell )}-\hat{\varvec{{\beta }}})^{\!\top \!}$. The standard errors for components of $\varvec{{\beta }}$ can be obtained from the diagonal elements of the sample covariance matrix.

3.2 Bayesian case influence analysis

In this subsection, we consider Bayesian case-deletion influence analysis based on the case-deletion method given in Cook and Weisberg (1982). For notational simplicity, let $\varvec{{R}}=\{\varvec{{y}},\varvec{{v}},\varvec{{w}}\}$ be a full data set, and $\varvec{{R}}_{(i)}=\{(y_j,\varvec{{v}}_j,\varvec{{w}}_j): j=1,\ldots ,n, j\not = i\}$ be a subset of $\varvec{{R}}$ with the ith individual deleted. To assess the effect of the ith individual on the posterior distribution of parameter vector $\varvec{{\vartheta }}=\{\tau ,\varvec{{\theta }}_y,\varvec{{\theta }}_\gamma \}$, we use the following Kullback–Leibler (K–L) divergence

$$\begin{aligned} KL(i)=\int \log \left\{ \frac{p(\varvec{{\vartheta }}|\varvec{{R}})}{p(\varvec{{\vartheta }}|\varvec{{R}}_{(i)})}\right\} p(\varvec{{\vartheta }}|\varvec{{R}})d\varvec{{\vartheta }}, \end{aligned}$$

as a Bayesian case influence measure, where $p(\varvec{{\vartheta }}|\varvec{{R}})$ and $p(\varvec{{\vartheta }}|\varvec{{R}}_{(i)})$ are the posterior distributions of $\varvec{{\vartheta }}$ for the full data set $\varvec{{R}}$ and the reduced data set $\varvec{{R}}_{(i)}$, respectively. Thus, KL(i) measures the distance (discrepancy) between two posterior distributions $p(\varvec{{\vartheta }}|\varvec{{R}}_{(i)})$ and $p(\varvec{{\vartheta }}|\varvec{{R}})$, which can be regarded as a Bayesian analogue of the likelihood displacement (Cook and Weisberg 1982).

To measure the effect of the ith individual on the posterior mean of $\varvec{{\vartheta }}$, we use the following Cook’s distance

$$\begin{aligned} CD(i)=(\hat{\varvec{{\vartheta }}}-\hat{\varvec{{\vartheta }}}_{(i)})^{\!\top \!}\varvec{{W}}^{-1}_\vartheta (\hat{\varvec{{\vartheta }}}-\hat{\varvec{{\vartheta }}}_{(i)}) \end{aligned}$$

as another Bayesian case influence measure, where $\hat{\varvec{{\vartheta }}}=\int \varvec{{\vartheta }}p(\varvec{{\vartheta }}|\varvec{{R}})d\varvec{{\vartheta }}$ and $\hat{\varvec{{\vartheta }}}_{(i)}=\int \varvec{{\vartheta }}p(\varvec{{\vartheta }}|\varvec{{R}}_{(i)})d\varvec{{\vartheta }}$ are the posterior means of $\varvec{{\vartheta }}$ for the full data set $\varvec{{R}}$ and the deleted data set $\varvec{{R}}_{(i)}$, respectively, and $\varvec{{W}}_\vartheta$ is selected to be the posterior covariance matrix of $\varvec{{\vartheta }}$. A large value of CD(i) corresponds to an influential observation with respect to the posterior mean. Generally, we can use $\bar{D}+d\times SM$ as a benchmark (e.g., see Lee and Tang 2006), where $\bar{D}$ and SM are the mean and standard error of $\{CD(i): i=1,\ldots ,n\}$, and d is a selected constant depending on the problem-by-problem. Specifically, we set $d=3.0$ in our conducted simulation studies and $d=5.0$ in real example analysis.

To compute KL(i), we require calculating the marginal posterior distributions $p(\varvec{{\vartheta }}|\varvec{{R}})$ and $p(\varvec{{\vartheta }}|\varvec{{R}}_{(i)})$. It is rather difficult to directly compute KL(i) because of the MEs involved. It is desirable to develop a computationally feasible formula to reduce computational burden. It is easily shown from independence of individuals that

$$\begin{aligned} p(\varvec{{\vartheta }}|\varvec{{R}}_{(i)})=\frac{\{p_i(\varvec{{\vartheta }})\}^{-1} p(\varvec{{\vartheta }}|\varvec{{R}})}{\int \{p_i(\varvec{{\vartheta }})\}^{-1} p(\varvec{{\vartheta }}|\varvec{{R}}) d\varvec{{\vartheta }}}, \end{aligned}$$

(3.2)

where $p_i(\varvec{{\vartheta }})=p(y_i,\varvec{{v}}_i,\varvec{{w}}_i|\varvec{{\vartheta }})$. Substituting Eq. (3.2) into the definition of KL(i) yields

$$\begin{aligned} KL(i)=\log E_{\vartheta |R} \{p_i(\varvec{{\vartheta }})\}^{-1} + E_{\vartheta |R} \{ \log p_i(\varvec{{\vartheta }})\}, \end{aligned}$$

which indicates that computation of KL(i) can be done using MCMC samples from the full data posterior distribution $p(\varvec{{\vartheta }}|\varvec{{R}})$ via the above developed Gibbs sampler. Specifically, if $\varvec{{\vartheta }}^{(\ell )}$ is the $\ell$th Gibbs sample after $\mathcal {J}$ burn-in iterations for $\ell =1,\ldots ,\mathcal {L}$, thus we get the MCMC approximation of KL(i) as

$$\begin{aligned} KL(i)\approx \log \left[ \frac{1}{\mathcal {L}}\sum \limits _{\ell =1}^{\mathcal {L}}\{p_i(\varvec{{\vartheta }}^{(\ell )})\}^{-1}\right] +\frac{1}{\mathcal {L}}\sum \limits _{\ell =1}^{\mathcal {L}}\log \{p_i(\varvec{{\vartheta }}^{(\ell )})\}, \end{aligned}$$

(3.3)

where $p_i(\varvec{{\vartheta }}^{(\ell )})=p(y_i,\varvec{{v}}_i,\varvec{{w}}_i|\varvec{{\vartheta }}^{(\ell )})$.

On the other hand, to compute CD(i), we need evaluating $\hat{\varvec{{\vartheta }}}$, $\hat{\varvec{{\vartheta }}}_{(i)}$ and $\varvec{{W}}_\vartheta$. It follows from Eq. (3.2) and the definitions of $\hat{\varvec{{\vartheta }}}$, $\hat{\varvec{{\vartheta }}}_{(i)}$ and $\varvec{{W}}_\vartheta$ that $\hat{\varvec{{\vartheta }}}=E_{\vartheta |R}(\varvec{{\vartheta }})$, $\hat{\varvec{{\vartheta }}}_{(i)}=E_{\vartheta |R}[\varvec{{\vartheta }}\{p_i(\varvec{{\vartheta }})\}^{-1}]/E_{\vartheta |Y}\{p_i(\varvec{{\vartheta }})\}^{-1}$ and $\varvec{{W}}_\vartheta =\mathrm{var}_{\vartheta |R}(\varvec{{\vartheta }})$. Similarly, the MCMC approximations of $\hat{\varvec{{\vartheta }}}$, $\hat{\varvec{{\vartheta }}}_{(i)}$ and $\varvec{{W}}_\vartheta$ are given by

$$\begin{aligned} \hat{\varvec{{\vartheta }}}{=}\frac{1}{\mathcal {L}}\sum \limits _{\ell =1}^{\mathcal {L}}\varvec{{\vartheta }}^{(\ell )},\ \ \ \hat{\varvec{{\vartheta }}}_{(i)}{=}\frac{\frac{1}{\mathcal {L}}\sum \nolimits _{\ell =1}^{\mathcal {L}}\varvec{{\vartheta }}^{(\ell )}\{p_i(\varvec{{\vartheta }}^{(\ell )})\}^{-1}}{\frac{1}{\mathcal {L}}\sum \nolimits _{\ell =1}^{\mathcal {L}}\{p_i(\varvec{{\vartheta }}^{(\ell )})\}^{-1}},\ \ \ \varvec{{W}}_\vartheta =\frac{1}{\mathcal {L}-1}\sum \limits _{\ell =1}^{\mathcal {L}}(\varvec{{\vartheta }}^{(\ell )}-\hat{\varvec{{\vartheta }}})(\varvec{{\vartheta }}^{(\ell )}-\hat{\varvec{{\vartheta }}})^{\!\top \!},\nonumber \\ \end{aligned}$$

(3.4)

respectively.

Regardless of KL(i) or CD(i), we need computing $p_i(\varvec{{\vartheta }}^{(\ell )})$. From the definition of our considered model, we obtain

$$\begin{aligned} p_i(\varvec{{\vartheta }})=\int p(y_i,\varvec{{v}}_i,\varvec{{w}}_{i},\varvec{{u}}_{i}, \varvec{{x}}_{i}|\varvec{{\vartheta }})d\varvec{{u}}_{i}d{\varvec{{x}}_i} =E_{u_i,x_i}\{p(y_i,\varvec{{v}}_i,\varvec{{w}}_{i}|\varvec{{\vartheta }},\varvec{{x}}_i,\varvec{{u}}_i)\},\quad \end{aligned}$$

(3.5)

where $E_{u_i,x_i}$ denotes the expectation taken with respect to the joint distribution of $\varvec{{u}}_i$ and $\varvec{{x}}_i$ (denoted by $p(\varvec{{u}}_i,\varvec{{x}}_i|\varvec{{\theta }}_u)$). Monte Carlo approximation of $p_i(\varvec{{\vartheta }}^{(\ell )})$ in Eq. (3.5) can be implemented by using the following steps:

• Step 0 Specifying the initial value $\varvec{{x}}_i^{(0)}$ of $\varvec{{x}}_i$. Generally, we can take $\varvec{{x}}_i^{(0)}$ to be the mean of $\varvec{{w}}_{ij}$’s.

• Step 1 Sampling Gibbs sample $\varvec{{u}}_i^{(t)}$ from the conditional distribution $p(\varvec{{u}}_i|\varvec{{x}}_i^{(t-1)},\varvec{{\theta }}_u^{(\ell )})$.

• Step 2 Drawing Gibbs sample $\varvec{{x}}_i^{(t)}$ from the conditional distribution $p(\varvec{{x}}_i|\varvec{{u}}_i^{(t)},\varvec{{\theta }}_u^{(\ell )})$.

• Step 3 Repeating Steps 1 and 2 for $\mathcal {T}$ times.

• Step 4 Getting the nested Gibbs samples $\{(\varvec{{u}}_i^{(t)},\varvec{{x}}_i^{(t)}): t=1,\ldots ,\mathcal {T}\}$ from $p(\varvec{{u}}_i,\varvec{{x}}_i|\varvec{{\vartheta }}_u)$. Thus, the MCMC approximation of $p_i(\varvec{{\vartheta }}^{(\ell )})$ is given by

  $$\begin{aligned} p_i(\varvec{{\vartheta }}^{(\ell )})\approx \frac{1}{\mathcal {T}}\sum \limits _{t=1}^{\mathcal {T}} p\big (y_i,\varvec{{v}}_i,\varvec{{w}}_i|\varvec{{\vartheta }}^{(\ell )},\varvec{{x}}_i^{(t)},\varvec{{u}}_i^{(t)}\big ). \end{aligned}$$

  (3.6)

Combining Eqs. (3.2)–(3.6) yields the values of KL(i) and CD(i) for all individuals. Index plots of KL(i) and CD(i) can be used to identify influential cases.

4 Numerical examples

4.1 Simulation studies

To investigate the finite performance of the preceding proposed Bayesian approaches under various distributional assumptions of the MEs $\varvec{{u}}_{ij}$ and prior specifications, we conducted the following simulation studies by generating 100 replicated data sets from our defined GLMEMs with sample size $n=200$ together with $m=5$.

In the first simulation study, each of 100 replicated data sets $\{(y_i,\varvec{{v}}_i,\varvec{{w}}_i,\varvec{{x}}_i):i=1,\ldots ,n\}$ was generated from a Poisson distribution with the probability density $p(y_i|\mu _i)=\mu _i^{y_i}\exp (-\mu _i)/y_i!$ and $\eta _{i}=\log (\mu _{i})=\varvec{{x}}_i^{\!\top \!}\varvec{{\beta }}_x+\varvec{{v}}_i^{\!\top \!}\varvec{{\beta }}_v$, where $\varvec{{v}}_i$’s were generated from a multivariate normal distribution with mean zero and covariance matrix $0.25\varvec{{I}}_3$ and components $x_{1i}$ and $x_{2i}$ in $\varvec{{x}}_i$ were generated via Eq. (2.9). In this case, $\phi =1$ relating to Eq. (2.1) is a constant. The true values of $\varvec{{\beta }}_x=(\beta _0,\beta _1)^{\!\top \!}$, $\varvec{{\beta }}_v=(\beta _2,\beta _3,\beta _4)^{\!\top \!}$, $\varvec{{\gamma }}_k^*=(\gamma _{k0},\gamma _{k1},\gamma _{k2},\gamma _{k3})^{\!\top \!}$ and $\sigma _x^2$ were taken to be $\varvec{{\beta }}_x=(0.4,-0.3)^{\!\top \!}$, $\varvec{{\beta }}_v=(0.4,0.3,0.4)^{\!\top \!}$, $\varvec{{\gamma }}_k^*=(0.2,0.2,0.2,0.5)^{\!\top \!}$ for $k=1$ and 2, and $\sigma _{x}^2=1$, respectively. To test the effectiveness of using the TCDP prior to approximate distributions of MEs $\varvec{{u}}_{ij}=(u_{ij1},u_{ij2})^{\!\top \!}$, we considered the following eight distributional assumptions for $u_{ijk}$.

Assumption 1

We assumed the distribution of $u_{ijk}$ to be $u_{ijk}\mathop {\sim }\limits ^\mathrm{i.i.d.}N(0,1.2^2)$ for $k=1$ and 2.

Assumption 2

We assumed the distribution of $u_{ijk}$ to be bimodal: $u_{ijk}\mathop {\sim }\limits ^\mathrm{i.i.d.}0.6N(-0.4$, $0.2^2)+0.4N(0.6,0.2^2)$ for $k=1$ and 2.

Assumption 3

We took the distribution of $u_{ijk}$ to be trimodal: $u_{ijk}\mathop {\sim }\limits ^\mathrm{i.i.d.} 0.3N(0.5,0.1)+0.2N(3,0.1)+0.5N(-1.5 ,0.1)$ for $k=1$ and 2.

Assumption 4

We set the distribution of $u_{ijk}$ to be multimodal: $u_{ijk}\mathop {\sim }\limits ^\mathrm{i.i.d}0.3N(0.5,0.1)+0.2N(3,0.1)+0.1N(-3.5,0.1)+0.4N(-1,0.1)$ for $k=1$ and 2.

The above four assumptions were used to illustrate that even when the assumed distribution is multimodal, our presented TCDP prior can still capture their characteristics.

Assumption 5

We took $u_{ijk}=u_{ijk}^*-1$ with $u_{ijk}^*\mathop {\sim }\limits ^\mathrm{i.i.d.} \Gamma (1,1)$.

Assumption 6

We specified the distribution of $u_{ijk}$ to be $u_{ijk}\mathop {\sim }\limits ^\mathrm{i.i.d.}0.5N(-0.5,0.1)+0.5\Gamma (1,2)$.

Assumption 7

We set $u_{ijk}=0.75(u_{ij1}^*-0.5)+0.25(u_{ij2}^*-1)$ with $u_{ij1}^*\mathop {\sim }\limits ^\mathrm{i.i.d.}\Gamma (4,8)$ and $u_{ij2}^*\mathop {\sim }\limits ^\mathrm{i.i.d.}\Gamma (1,1)$.

Assumption 8

We took $u_{ijk}=u_{ijk}^*-0.5$ with $u_{ijk}^*\mathop {\sim }\limits ^\mathrm{i.i.d.} \mathrm{Beta}(4,4)$.

The above presented four assumptions were designed to generate the skewed distribution for $u_{ijk}$. Based on the generated $u_{ijk}$’s, we obtained data set $\{w_{ijk}: i=1,\ldots ,n,j=1,\ldots ,m,k=1,2\}$ via Eq. (2.3).

The hyperparameter values of the prior distributions for $\tau$ and $\sigma _x^2$ were specified as follows. To ensure that our presented DP mixture approximations were not biased with respect to the selection of our hyperparameters, we set $\varphi _j^a=3$, $\varphi _j^c=150$ and $\varphi _j^d=20$ for $j=1,\ldots ,r$, $c_1=5$ and allowed $c_2$ to be generated randomly from a uniform distribution U(2, 6). For the hyperparameters relating to the prior distribution of $\tau$, we set $a_1=200$ and $a_2=10$ to generate large values of $\tau$ which lead to more unique covariate MEs. For the conjugate prior of $\sigma _x^{-2}$, we set $c_3=10$ and randomly generated $c_4$ from a uniform distribution U(9, 10). For the hyperparameters $\varvec{{\xi }}^0$ and $\varvec{{\Psi }}^0$, we took $\varvec{{\xi }}^0=\varvec{{0}}$ and $\varvec{{\Psi }}^0=\varvec{{I}}_r$ to satisfy the condition of the centered DP procedure. Also, to investigate sensitivity of Bayesian estimates to prior inputs, we considered the following three types of priors for $\varvec{{\beta }}$ and $\varvec{{\gamma }}_k$.

• Type A The hyperparameters corresponding to the priors of $\varvec{{\beta }}$ and $\varvec{{\gamma }}_k$ were taken to be $\varvec{{\beta }}^0=(0.4,-0.3,0.4,0.3,0.4)^{\!\top \!}$, $\varvec{{H}}_{\beta }^0=0.25\varvec{{I}}_{5}$, $\varvec{{\gamma }}_k^0=(0.2,0.2,0.2,0.5)^{\!\top \!}$ and $\varvec{{H}}_{k\gamma }^0=0.25\varvec{{I}}_{4}$. This can be regarded as a situation with good prior information.

• Type B The hyperparameters corresponding to the priors of $\varvec{{\beta }}$ and $\varvec{{\gamma }}_k$ were taken to be $\varvec{{\beta }}^0=1.5\times (0.4,-0.3,0.4,0.3,0.4)^{\!\top \!}$, $\varvec{{H}}_{\beta }^0=0.75\varvec{{I}}_{5}$, $\varvec{{\gamma }}_k^0=1.5\times (0.2,0.2,0.2,0.5)^{\!\top \!}$ and $\varvec{{H}}_{k\gamma }^0=0.75\varvec{{I}}_{4}$. This can be regarded as a situation with inaccurate prior information.

• Type C The hyperparameters corresponding to the priors of $\varvec{{\beta }}$ and $\varvec{{\gamma }}_k$ were taken to be $\varvec{{\beta }}^0=(0,0,0,0,0)^{\!\top \!}$, $\varvec{{H}}_{\beta }^0=10\varvec{{I}}_{5}$, $\varvec{{\gamma }}_k^0=(0,0,0,0)^{\!\top \!}$ and $\varvec{{H}}_{k\gamma }^0=10\varvec{{I}}_4$. This can be regarded as a situation with noninformative prior information.

For each of the generated 100 data sets, the preceding proposed MCMC algorithm with $G=50$ was used to evaluate Bayesian estimates of unknown parameters and covariates subject to MEs for each of three types of priors based on three different starting values of unknown parameters. The estimated potential scale reduction (EPSR) values (Gelman et al. 1996) for all unknown parameters were computed. For the first five test runs, we observed that the EPSR values of all unknown parameters were less than 1.2 after 10, 000 iterations. Hence, $\mathfrak {L}=5000$ observations after 10, 000 burn-in iterations were collected to evaluate Bayesian estimates via Eq. (3.1). Results under eight assumptions together with three types of prior inputs were presented in Table 1, where ‘Bias’ was the absolute difference between the true value and the mean of the estimates based on 100 replications and ‘RMS’ was the root mean square between the estimates based on 100 replications and its true value. Also, for comparison, we calculated Bayesian estimates of $\varvec{{\beta }}$ for each of the above generated 100 data sets under eight distributional assumptions of $u_{ijk}$ on the basis of a GLM without error modelling. The corresponding results were given in Table 2.

Table 1 Performance of parameter estimates in the first simulation study

Table 2 Performance of parameter estimates for a GLM without error modelling in the first simulation study

Table 3 Means and standard deviations (SD) of $u_{ijk}$ and $\hat{u}_{ijk}$ in the simulation studies

Examination of Tables 1 and 2 indicated that (i) Bayesian estimates were reasonably accurate regardless of distributional assumptions of $u_{ij}$ and prior inputs of unknown parameters because their Bias values were less than 0.10 and their RMS values were less than 0.20; (ii) Bayesian estimates were not sensitive to prior inputs of $\varvec{{\beta }}$ and $\varvec{{\gamma }}_k$ under our considered three prior inputs; (iii) Bayesian estimates obtained from the type A prior input behaved better than those obtained from the type B and type C prior inputs in terms of Bias and RMS, but their differences were minor; (iv) Bayesian estimates obtained from the type A and type B prior inputs were slightly better than those obtained from the type C prior input, but their differences were negligible; (iv) our proposed semiparametric Bayesian method produced smaller bias and RMS values than a Bayesian approach to a GLM without error modelling.

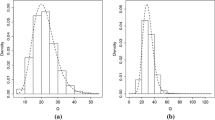
To investigate the accuracy of using TCDP prior to approximate distribution of $u_{ijk}$, we calculated means and standard deviations of $\hat{u}_{ijk}$’s across individuals and plotted the true densities of $u_{ijk}$’s against their corresponding approximated densities for a randomly selected replication. Table 3 presented the estimated means and standard deviations of $u_{ijk}$’s for our considered eight assumptions. To save space, we only plotted densities of $u_{ijk}$ and $\hat{u}_{ijk}$ for Assumption 4 in Fig. 1. Examination of Table 3 and Fig. 1 implied that (i) the TCDP prior approximations to distributions of $u_{ijk}$’s were flexible enough to recover the shapes of $u_{ijk}$’s distributions for our considered eight distributional assumptions of $u_{ijk}$; (ii) the mean and standard deviation of the true distribution of $u_{ijk}$ can be estimated well by our proposed method.

To illustrate our proposed Bayesian case-deletion influence measures, we conducted the second simulation study. In this simulation study, the data set $\{(y_i,\varvec{{v}}_i,\varvec{{w}}_i,\varvec{{x}}_i): i=1,\ldots ,200\}$ was generated by using the same setup as specified in the first simulation study, but outliers were created by changing $y_{i}$ as $y_i+30$ for $i=1,100$ and 150. We calculated the corresponding values of diagnostics KL(i) and CD(i) for the above generated data set including outliers. Results were presented in Fig. 2. Examination of Fig. 2 indicated that cases 1, 100 and 150 were detected to be influential as expected.

4.2 An example

To illustrate our proposed methods, we considered a data set from Framingham heart study, which has been analyzed by Carroll et al. (2006, Section 9.10) and Muff et al. (2015) via a logistic ME model with the normality assumption of covariate ME. The data set consisted of a series of exams taken over two years. Here, we only analyzed the data set from exam 3 with $n=1615$ men aged between 31 and 65. We took $y_i$ to be the indicator for coronary heart disease, which was assumed to follow a Bernoulli distribution, $v_i$ to be the indicator for smoking and $x_i$ to be the transformed (unobserved) long-term blood pressure (i.e., $x_i=\log (\mathrm{SBP}_i-50)$), where SBP was an abbreviation of the systolic blood pressure. Since it is impossible to measure the long-term SBP, measurements at single clinical visits had to be used as a proxy (Muff et al. 2015). Also, due to daily variations or deviations in the measurement instrument, the single-visit measures might considerably differ from the long-term blood pressure (Carroll et al. 2006). Hence, to estimate the magnitude of the error, SBP had been measured twice at different examinations. The two proxy measures for $x_i$ were denoted as $w_{i1}$ and $w_{i2}$, respectively. Following Muff et al. (2015), we fitted the data set via the following logistic ME model (LOGMEM):

$$\begin{aligned} \mathrm{logit}\{\mathrm{Pr}(y_i=1|x_i,v_i)\}=\beta _0+x_i\beta _x+v_i\beta _v, ~~w_{ij}=x_i+u_{ij},~~x_i=\gamma _0+\gamma _v v_i+\varepsilon _i \end{aligned}$$

for $i=1,\ldots ,n$ and $j=1,2$, where $\varepsilon _{i}\mathop {\sim }\limits ^\mathrm{i.i.d.}N(0,\sigma _{x}^2)$.

Fig. 1

Estimated versus true densities of $u_{ij1}$ and $u_{ij2}$ for assumption 4 under three prior inputs: type A (left panel), type B (middle panel) and type C (right panel) in the first simulation study

Fig. 2

Index plots of KL(i) (left panel) and CD(i) (right panel) in the simulation study

To make Bayesian analysis for the above considered LOGMEM, we assumed the following prior distributions for $\varvec{{\gamma }}=(\gamma _0,\gamma _v)^{\!\top \!}$ and $\varvec{{\beta }}=(\beta _0,\beta _x,\beta _v)^{\!\top \!}$: $p(\varvec{{\gamma }})\sim N_2(\varvec{{\gamma }}^0,0.25\varvec{{I}}_2)$ and $p(\varvec{{\beta }})\sim N_{3}(\varvec{{\beta ^0}},0.25\varvec{{I}}_{3})$, where the hyperparameters $\varvec{{\gamma }}^0$ and $\varvec{{\beta }}^0$ were taken to be their corresponding Bayesian estimates obtained from the non-informative priors on $\varvec{{\gamma }}$ and $\varvec{{\beta }}$ (e.g., $p(\varvec{{\gamma }})\sim N_2(\varvec{{0}},20\varvec{{I}}_2)$ and $p(\varvec{{\beta }})\sim N_3(\varvec{{0}},20\varvec{{I}}_3)$). For the hyperparameters $a_1$ and $a_2$, we took $a_1=250$ and set $a_2$ to be a value generated randomly from a uniform distribution U(25, 30) to yield large values of $\tau$ leading to more unique covariate MEs. For the hyperparameters $c_3$ and $c_4$, we randomly generated $c_3$ from a uniform distribution U(1, 10) and randomly sampled $c_4$ from a uniform distribution U(1, 100) to yield relatively diffuse values of $\sigma _x^2$. For the hyperparameters $\varvec{{\xi }}^0$ and $\varvec{{\Psi }}^0$, we took $\varvec{{\xi }}^0=\varvec{{0}}$ and $\varvec{{\Psi }}^0=\varvec{{I}}_2$ to satisfy the condition of the centered DP procedure. Similar to simulation studies, we set $\varphi _j^a=3$, $\varphi _j^c=100$ and $\varphi _j^d=20$ for $j=1,\ldots ,r$, $c_1=5$ and allowed $c_2$ to be generated randomly from a uniform distribution U(2, 6). The preceding presented MCMC algorithm with $G=250$ was used to obtain Bayesian estimates of parameters and MEs $u_{ij}$’s. Similarly, the EPSR values of all unknown parameters were computed by using three parallel sequences of observations generated from three different starting values of unknown parameters. Their EPSR values were less than 1.2 after about 20, 000 iterations. We collected 10, 000 observations after 20, 000 burn-in iterations to evaluate Bayesian estimates of parameters. Results were given in Table 4. Examination of Table 4 showed that the SBP has a positive effect on the coronary heart disease, whilst smoking has a slightly negative effect on the coronary heart disease and the SBP. Also, for comparison, we evaluated Bayesian estimates of parameters in the following logistic model: $\mathrm{logit}\{\mathrm{Pr}(y_i=1|x_i,v_i)\}=\beta _0+x_i\beta _x+v_i\beta _v$ for $i=1,\ldots ,n$ under the above specified prior of $\varvec{{\beta }}=(\beta _0,\beta _x,\beta _v)^{\!\top \!}$, where $x_i=(w_{i1}+w_{i2})/2$. The corresponding results were presented in Table 4, which showed that our considered logistic ME model leaded to a smaller estimate and a smaller SE of parameter $\beta _x$ than the logistic model without ME.

Table 4 Bayesian estimates (Est) and standard errors (SE) of parameters in the real example

To illustrate our proposed case deletion influence measures, we computed the values of diagnostics KL(i) and CD(i), which were presented in Fig. 3. Examination of Fig. 3 indicated that cases 10, 59, 207, 208, 222, 362, 367, 386, 391, 456, 501, 530, 533, 709, 976, 1093, 1096, 1162, 1187, 1336, 1430 and 1502 were detected to be influential by diagnostics KL(i) and CD(i). To investigate the effect of these influential observations on Bayesian estimates of unknown parameters, we also calculated Bayesian estimates of unknown parameters for our considered data set with these influential cases deleted. The corresponding results were given in Table 4. Examination of Table 4 indicated that these influential individuals have a relatively large influence on Bayesian estimates of $\beta _x$ and $\beta _v$.

Fig. 3

Index plots of KL(i) (left panel) and CD(i) (right panel) in the real example

5 Discussion

We discussed Bayesian estimates of unknown parameters and Bayesian case-deletion diagnostics for generalized linear mixed models with covariates subject to MEs. Under the unknown distribution assumptions of random MEs, we used the TCDP mixture model to approximate the distribution of random ME. We also obtained Bayesian estimates of unknown parameters and random MEs and their standard errors, and presented two Bayesian case-deletion influence diagnostics to detect influential observations. Simulation studies and a real example were used to illustrate our proposed methodologies. The empirical results showed that (i) the TCDP mixture model approximation can well capture characteristics of the distribution for random ME; and (ii) our proposed methods can be used to effectively detect influential observations.

This paper considered the balanced repeated measurement for the covariate subject to ME so that we can use the TCDP mixture model to approximate the distribution of random ME. When an unbalanced repeated measurement for the covariate subject to ME is considered, other methods may be employed to address the issue, which is our further work.

Appendix: Conditional distributions

To obtain Bayesian estimates of unknown parameters and covariates subject to MEs in our considered GLMEMs, the Gibbs sampler is adopted to draw a sequence of random observations from the joint posterior distribution $p(\varvec{{\xi }},\varvec{{\Psi }},\varvec{{\varphi }}^b,\varvec{{\pi }},\varvec{{\alpha }}^*,\varvec{{\Omega }},\varvec{{L}}, \tau ,\varvec{{\beta }},\phi ,\varvec{{\gamma }},\sigma ^2_{x},\varvec{{u}},\varvec{{x}}|\varvec{{y}},\varvec{{w}},\varvec{{v}})$. The Gibbs sampler is implemented by iteratively drawing observations from the following conditional distributions: $p(\varvec{{\xi }}|\varvec{{\alpha }}^*,\varvec{{\Psi }})$, $p(\varvec{{\Psi }}|\varvec{{\alpha }}^*,\varvec{{\xi }})$, $p(\tau |\varvec{{\pi }})$, $p(\varvec{{\varphi }}^b|\varvec{{\Omega }})$, $p(\varvec{{\pi }}|\varvec{{L}},\tau )$, $p(\varvec{{L}}|\varvec{{\pi }},\varvec{{\alpha }},\varvec{{\Omega }},\varvec{{u}})$, $p(\varvec{{\alpha }}^*|\varvec{{\xi }},\varvec{{\Psi }},\varvec{{\Omega }},\varvec{{L}},\varvec{{u}})$, $p(\varvec{{\beta }}|\varvec{{y}},\varvec{{x}},\varvec{{v}},\phi )$, $p(\varvec{{\Omega }}|\varvec{{\alpha }},\varvec{{\varphi }}^b,\varvec{{L}},\varvec{{u}})$, $p(\phi |\varvec{{\beta }},\varvec{{y}},\varvec{{x}},\varvec{{v}})$, $p(\varvec{{\gamma }}|\varvec{{x}},\varvec{{v}},\sigma ^2_{x})$, $p(\sigma ^2_{x}|\varvec{{x}},\varvec{{v}}$, $\varvec{{\gamma }})$, $p(\varvec{{x}}|\varvec{{y}},\varvec{{v}},\varvec{{u}},\varvec{{w}},\varvec{{\alpha }},\varvec{{\beta }},\phi ,\sigma ^2_{x},\varvec{{\gamma }},\varvec{{L}})$ and $p(\varvec{{u}}|\varvec{{\alpha }},\varvec{{\Omega }},\varvec{{L}},\varvec{{x}},\varvec{{w}},\varvec{{\theta }}_u)$. The conditional distributions required in implementing the above Gibbs sampler are summarized as follows.

Steps (a)–(h) Conditional distributions related to the nonparametric components

To sample $\varvec{{u}}_{ij}$ in terms of the latent variable $L_{ij}$ for $i=1,\ldots ,n$ and $j=1,\ldots ,m$, we first generate $\varvec{{\alpha }}^*=(\varvec{{\alpha }}^*_1,\ldots ,\varvec{{\alpha }}^*_G)$ and $\varvec{{\Omega }}=(\varvec{{\Omega }}_1,\ldots ,\varvec{{\Omega }}_G)$ from their corresponding posterior distributions and then draw $\varvec{{u}}_{ij}$ from the multivariate normal distribution $N_r(\varvec{{\alpha }}_{L_{ij}}, \varvec{{\Omega }}_{L_{ij}})$ with $\varvec{{\alpha }}_{L_{ij}}=\varvec{{\alpha }}_{L_{ij}}^* -\sum _{g=1}^{G}\pi _g\varvec{{\alpha }}_g^*$. Since it is rather difficult to directly sample observations from the posterior distribution of $(\varvec{{\xi }},\varvec{{\Psi }},\varvec{{\varphi }}^b,\varvec{{\pi }},\varvec{{\alpha }}^*,\varvec{{\Omega }},\varvec{{L}},\tau ,\varvec{{u}})$, the blocked Gibbs sampler is employed to solve the above difficulties. The conditional distributions relating to implement Gibbs sampling of the nonparametric components are given as follows.

• Step (a) The conditional distribution for $\varvec{{\xi }}$ is $p(\varvec{{\xi }}|\varvec{{\alpha }}^*,\varvec{{\Psi }})\sim N_r(\varvec{{\alpha }}_{\xi },\varvec{{\Sigma }}_{\xi })$, where $\varvec{{\Sigma }}_{\xi }=(G\varvec{{\Psi }}^{-1}+{\varvec{{\Psi }}^0}^{-1})^{-1}$ and $\varvec{{\alpha }}_{\xi }=\varvec{{\Sigma }}_{\xi }({\varvec{{\Psi }}^0}^{-1}\varvec{{\xi }}^{0}+\varvec{{\Psi }}^{-1}\sum _{g=1}^{G}\varvec{{\alpha }}_g^*)$.

• Step (b)   For $j=1,\ldots ,r$, the jth diagonal element of $\varvec{{\Psi }}$ given ($\varvec{{\alpha }}^*,\varvec{{\xi }}$) is distributed as $p(\psi ^{-1}_{j}|\varvec{{\alpha }}^*,\varvec{{\xi }})\sim {\Gamma }(c_{1}+G/2,c_{2}+\frac{1}{2}\sum _{g=1}^{G}(\alpha ^*_{gj}-\xi _{j})^{2})$, where $\alpha ^*_{gj}$ is the jth element of $\varvec{{\alpha }}^*_g$ and $\xi _{j}$ is the jth element of $\varvec{{\xi }}$.

• Step (c) Following the same argument of Chow et al. (2011), the conditional distribution $p(\tau |\varvec{{\pi }})$ is given by $p(\tau |\varvec{{\pi }})\sim {\Gamma }~(a_{1}+G-1,a_{2}-\sum _{g=1}^{G}\log (1-\nu _g^{*}))$, where $\nu _g^{*}$ is a random weight sampled from the beta distribution and is sampled in step (e).

• Step (d)   For $j=1,\ldots ,r$, the conditional distribution of $\varphi ^b_j$ is given by $p({\varphi }^b_{j}|\varvec{{\Omega }})\sim {\Gamma }~({\varphi }^c_{j},{\varphi }^d_{j}+\sum _{g=1}^{G}\omega ^{-1}_{gj} )$, where $\omega ^{-1}_{gj}$ is the jth diagonal element of $\varvec{{\Omega }}_g$.

• Step (e) It can be shown that the conditional distribution $p(\varvec{{\pi }}|\varvec{{L}},\tau )$ follows a generalized Dirichlet distribution, i.e., $p(\varvec{{\pi }}|\varvec{{L}},\tau )\sim \wp (a_{1}^{*},b_{1}^{*},\cdots ,a_{G-1}^{*},b_{G-1}^{*})$, where $a_g^{*}=1+d_g$, $b_g^{*}=\tau +\sum _{j=g+1}^{G}d_j$ for $g=1,\ldots ,G-1$, and $d_g$ is the number of $L_{ij}$’s (and thus individuals) whose value equals g. Sampling observations from the conditional distribution $p(\varvec{{\pi }}|\varvec{{L}},\tau )$ can be conducted by (1) sampling $\nu _l^{*}$ from a Beta $(a_l^{*},b_l^{*})$ distribution, (2) sampling $\pi _1,\ldots ,\pi _G$ with the following expressions: $\pi _{1}=\nu _{1}^{*}$, $\pi _g=\nu _g^*\prod _{j=1}^{g-1}(1-\nu _{j}^*)$ for $g=2,\ldots ,G-1$ and $\pi _{G}=1-\sum _{l=1}^{G-1}\pi _l$.

• Step (f) We consider the conditional distribution $p(\varvec{{\alpha }}^{*}|\varvec{{\xi }},\varvec{{\Psi }},\varvec{{\Omega }},\varvec{{L}},\varvec{{u}})$. Let $L_{1}^{*},\ldots ,L_{d}^{*}$ be the d unique values of $\{L_{11},\ldots ,L_{1r},\ldots ,L_{n1},...L_{nr}\}$ (i.e., unique number of “clusters”). For $g=1,\ldots , G$, $\varvec{{\alpha }}_g^*$ is drawn from the following conditional distribution: $p(\varvec{{\alpha }}_g^*|\varvec{{\xi }},\varvec{{\Psi }}) \sim N_r(\varvec{{\xi }},\varvec{{\Psi }})$ for $g\not \in \{L^*_{1},\ldots ,L^*_{d}\}$, and $p(\varvec{{\alpha }}_g^*|\varvec{{\xi }},\varvec{{\Psi }},\varvec{{\Omega }},\varvec{{L}},\varvec{{u}}) \sim N_r(\varvec{{A}}_g,\varvec{{B}}_g)$ with $\varvec{{B}}_g=(\varvec{{\Psi }}^{-1}+\sum _{\{(i,j):L_{ij}=g\}}\varvec{{\Omega }}^{-1}_{L_{ij}})^{-1}$ and $\varvec{{A}}_g=\varvec{{B}}_g(\varvec{{\Psi }}^{-1}\varvec{{\xi }}+\sum _{\{(i,j):L_{ij}=g\}}\varvec{{\Omega }}^{-1}_{L_{ij}}\varvec{{u}}_{ij})$ for $l\in \{L^*_{1},\ldots ,L^*_{d}\}$. Given $\varvec{{\alpha }}^*$, $\varvec{{\alpha }}_g=\varvec{{\alpha }}_g^*-\sum _{j=1}^G\pi _j\varvec{{\alpha }}_j^*$ for $g=1,\ldots ,G$, $\varvec{{\alpha }}^*=\{\varvec{{\alpha }}^*_{1},\ldots ,\varvec{{\alpha }}^*_{G}\}$ and $\varvec{{\alpha }}=\{\varvec{{\alpha }}_{1},\ldots ,\varvec{{\alpha }}_{G}\}$.

• Step (g) The conditional distribution of $\varvec{{\Omega }}$ is similar to the step (f). For $j=1,\ldots ,r$, the jth diagonal element of $\varvec{{\Omega }}_g$ ($g=1,\ldots ,G$) is generated from the following conditional distribution: $p(\omega ^{-1}_{gj}|\varvec{{\alpha }},\varvec{{\varphi }}^b,\varvec{{L}},\varvec{{u}})\sim {\Gamma }(\varphi _j^c,\varphi _j^b)$ for $g\not \in \{L^*_{1},\ldots ,L^*_{d}\}$, and $p(\omega ^{-1}_{gj}|\varvec{{\alpha }},\varvec{{\varphi }}^b,\varvec{{L}},\varvec{{u}})\sim {\Gamma }(\varphi _j^c+d_g/2,\varphi _j^b+\frac{1}{2}\sum _{\{(i,\ell ):L_{i\ell }=g\}}(u_{i\ell j}-\alpha _{gj})^2)$ for $g\in \{L^*_{1},\ldots ,L^*_{d}\}$, where $u_{i\ell j}$ is the jth element of $\varvec{{u}}_{i\ell }$, $\alpha _{gj}$ is the jth element of $\varvec{{\alpha }}_g$ and $d_g$ is the number of $L_{i\ell }$’s whose value equals g for $i=1,\ldots ,n$ and $\ell =1,\ldots ,m$.

• Step (h) The conditional distribution of $L_{ij}$ can be shown to be $p(L_{ij}|\varvec{{\pi }},\varvec{{\alpha }},\varvec{{\Omega }},\varvec{{u}})\mathop {\sim }\limits ^\mathrm{i.i.d.}\mathrm{Multinomial}(\pi ^*_{ij1},\ldots ,\pi ^*_{ijG})$, where $\pi ^*_{ijg}$ is proportional to $\pi _gp(\varvec{{u}}_{ij}|\varvec{{\alpha }}_g,\varvec{{\Omega }}_g)$ and $p(\varvec{{u}}_{ij}|\varvec{{\alpha }}_g,\varvec{{\Omega }}_g)\sim N_r(\varvec{{\alpha }}_g$, $\varvec{{\Omega }}_g)$ for $g=1,\ldots ,G$.

• Step (i) Consider the conditional distribution of $\varvec{{u}}_{ij}$. It is easily shown that the conditional distribution $p(\varvec{{u}}_{ij}|\varvec{{\alpha }},\varvec{{\Omega }},L_{ij},\varvec{{\theta }}_u,\varvec{{w}},\varvec{{x}}_i)\propto p(\varvec{{u}}_{ij}|\varvec{{\alpha }}_{L_{ij}},\varvec{{\Omega }}_{L_{ij}})p(\varvec{{w}}_{ij}|\varvec{{u}}_{ij},\varvec{{x}}_i,\varvec{{\theta }}_u)$ is a non-standard distribution. Thus, we cannot directly sample $\varvec{{u}}_{ij}$ from its conditional distribution. Here, the Metropolis–Hastings algorithm is employed to sample observation $\varvec{{u}}_{ij}$ from its conditional distribution via the following steps. At the tth iteration with a current value $\varvec{{u}}^{(t)}_{i}$, a new candidate $\varvec{{u}}_{ij}$ is generated from the normal distribution $N_m(\varvec{{u}}^{(t)}_{ij},\sigma ^2_{u}\mathbb {D}_{u_{ij}})$, where $\mathbb {D}_{u_{ij}}=(\varvec{{\Omega }}^{-1}_{L_{ij}}+\mathbb {C}_{ij})^{-1}$ with $\mathbb {C}_{ij}=-\partial ^2\log p(\varvec{{w}}_{ij}|\varvec{{u}}_{ij},\varvec{{x}}_i,\varvec{{\theta }}_u)/\partial \varvec{{u}}_{ij}\partial \varvec{{u}}^T_{ij} |_{\varvec{{u}}_{ij}=\varvec{{u}}^{(t)}_{ij}}$. Then, the new candidate $\varvec{{u}}_{ij}$ is accepted with probability

  $$\begin{aligned} \text{ min }\left\{ 1,\frac{p(\varvec{{u}}_{ij}|\varvec{{\alpha }}_{L_{ij}},\varvec{{\Omega }}_{L_{ij}})p(\varvec{{w}}_{ij}|\varvec{{u}}_{ij},\varvec{{x}}_i,\varvec{{\theta }}_u)}{p(\varvec{{u}}^{(m)}_{ij}|\varvec{{\alpha }}_{L_{ij}}, \varvec{{\Omega }}_{L_{ij}})p(\varvec{{w}}_{ij}|\varvec{{u}}^{(m)}_{ij},\varvec{{x}}_i,\varvec{{\theta }}_u)}\right\} . \end{aligned}$$

  The variance $\sigma _{u}^{2}$ can be chosen such that the average acceptance rate is approximately 0.25 or more.

• Step (j) The conditional distribution $p(\phi ^{-1}|\varvec{{y}},\varvec{{x}},\varvec{{v}},\varvec{{\beta }})$ is proportional to

  $$\begin{aligned} \phi ^{-(a_3+p+r-1)}\exp \left\{ -\frac{1}{\phi }\left( a_4+\frac{1}{2}\big (\varvec{{\beta }}-\varvec{{\beta }}^{0}\big )^{T}\big (\varvec{{H}}^{0} _{\beta }\big )^{-1}\big (\varvec{{\beta }}-\varvec{{\beta }}^{0}\big )-\sum \limits _{i=1}^{n}(y_{i}\theta _{i}-b(\theta _{i}))\right) +\sum \limits _{i=1}^{n} c(y_{i},\phi )\right\} , \end{aligned}$$

  which is generally a non-standard or familiar distribution. In this case, the Metropolized independence sampler algorithm (Liu 2001) can be employed to sample observations from the posterior $p(\phi |\varvec{{y}},\varvec{{x}},\varvec{{v}},\varvec{{\beta }})$. At the tth iteration with a current value $\phi ^{(t)}$, a new candidate $\phi$ is drawn from $h(\phi )\sim N({\phi }^{(t)}, \sigma ^2_{\phi })I(0,\infty )$ and is accepted with probability

  $$\begin{aligned} \text{ min }\left\{ 1,\frac{p(\phi |\varvec{{y}},\varvec{{x}},\varvec{{v}},\varvec{{\beta }})h(\phi ^{(t)})}{p(\phi ^{(t)}|\varvec{{y}},\varvec{{x}},\varvec{{v}},\varvec{{\beta }})h(\phi )}\right\} . \end{aligned}$$

  The variance $\sigma _{\phi }^{2}$ can be chosen such that the average acceptance rate is approximately 0.25 or more. Particularly, if $c(y_i,\phi )=c(y_i)/\phi$, we have $p(\phi ^{-1}|\varvec{{y}},\varvec{{x}},\varvec{{v}},\varvec{{\beta }})\sim \Gamma (r+p+a_3,a_4+0.5(\varvec{{\beta }}-\varvec{{\beta }}^{0})^{\!\top \!}(\varvec{{H}}^{0} _{\beta })^{-1}(\varvec{{\beta }}-\varvec{{\beta }}^{0})-\sum _{i=1}^{n}(y_{i}\theta _{i}-b(\theta _{i})+c(y_i)))$. Also, if $c(y_i,\phi )=\zeta c(y_i)$, we obtain $p(\phi ^{-1}|\varvec{{y}},\varvec{{x}},\varvec{{v}},\varvec{{\beta }})\sim \Gamma (r+p+a_3,a_4+0.5(\varvec{{\beta }}-\varvec{{\beta }}^{0})^{\!\top \!}(\varvec{{H}}^{0} _{\beta })^{-1}(\varvec{{\beta }}-\varvec{{\beta }}^{0})-\sum _{i=1}^{n}(y_{i}\theta _{i}-b(\theta _{i})))$, where $\zeta$ is a constant that does not depend on $\phi$ and $y_i$.

• Step (k) The conditional distribution $p(\varvec{{\beta }}|\varvec{{y}},\varvec{{x}},\varvec{{v}},\phi )$ can be expressed as

  $$\begin{aligned} p(\varvec{{\beta }}|\varvec{{y}},\varvec{{x}},\varvec{{v}},\phi )\propto \exp \left\{ \frac{1}{\phi }\sum \limits _{i=1}^{n}(y_{i}\theta _{i}-b(\theta _{i})) -\frac{1}{2\phi }(\varvec{{\beta }}-\varvec{{\beta }}_{0})^{\!\top \!} (\varvec{{H}}^{0}_{\beta })^{-1}(\varvec{{\beta }}-\varvec{{\beta }}_{0})\right\} . \end{aligned}$$

  Similarly, the Metropolis–Hastings algorithm for simulating observations from the conditional distribution $p(\varvec{{\beta }}|\varvec{{y}},\varvec{{x}},\varvec{{v}},\phi )$ is implemented as follows. Given the current value $\varvec{{\beta }}^{(t)}$, a new candidate $\varvec{{\beta }}$ is generated from $N_{p+r}(\varvec{{\beta }}^{(t)},\sigma _{\beta }^2\varvec{{\Sigma }}_{\beta })$ and is accepted with probability $\text{ min }\{1,p(\varvec{{\beta }}|\varvec{{y}},\varvec{{x}},\varvec{{v}}$, $\phi )/p(\varvec{{\beta }}^{(t)}|\varvec{{y}},\varvec{{x}},\varvec{{v}},\phi )\}$, where $\varvec{{\Sigma }}_{\beta }=\phi ^{-1}\left( \frac{1}{2}\sum _{i=1}^nV_i\varvec{{C}}_i^{\!\top \!}\varvec{{C}}_i+ (\varvec{{H}}^0_{\beta })^{-1}\right) ^{-1}$ with $\varvec{{C}}_i=(x_i,\varvec{{v}}_{i}^{\!\top \!})$ and $V_i=\dot{h}^{-2}(\mu _i)\ddot{b}^{-1}(\theta _i)$ in which $\dot{h}(a)=d h(a)/da$ and $\ddot{b}(a)=d^2b(a)/da^2$.

• Step (l) The conditional distribution $p(\varvec{{\gamma }}_k^*|\varvec{{x}},\varvec{{v}},\sigma _{x}^{2})$ is given by $p(\varvec{{\gamma }}_k^*|\varvec{{x}},\varvec{{v}},\sigma _{x}^{2})\sim N(\varvec{{\mu }}_{\gamma k}^*$, $\varvec{{\Omega }}_{\gamma k}^*)$, where $\varvec{{\Omega }}_{\gamma k}^*=(\sum _{i=1}^n\varvec{{v}}_i^*{\varvec{{v}}_i^*}^{\!\top \!}/\sigma _{x}^2+(\varvec{{H}}^0_{\gamma k})^{-1})^{-1}$ and $\varvec{{\mu }}_{\gamma k}^*=\varvec{{\Omega }}_{\gamma k}^*(\sum _{i=1}^n\varvec{{v}}_i^*x_{ki}/\sigma _{x}^2+(\varvec{{H}}_{\gamma k}^0)^{-1}\varvec{{\gamma }}_k^0)$ with $\varvec{{v}}_i^*=(1,\varvec{{v}}_i^{\!\top \!})^{\!\top \!}$.

• Step (m) It is easily shown that the conditional distribution $p(\sigma ^2_{x}|\varvec{{x}},\varvec{{v}},\varvec{{\gamma }})$ is given by $p(\sigma ^{-2}_x|\varvec{{x}},\varvec{{v}},\varvec{{\gamma }})\sim \Gamma (c_{3}+\frac{nr}{2},c_{4}+\frac{1}{2} \sum _{i=1}^{n}\sum _{k=1}^r(x_{ki}-\gamma _{k0}-\varvec{{\gamma }}_{kv}^{\!\top \!}\varvec{{v}}_i)^2)$.

• Step (n) The conditional distribution $p(\varvec{{x}}_i|y_{i},\varvec{{v}}_{i},\varvec{{\gamma }},\varvec{{w}}_{i},\varvec{{\alpha }},\varvec{{\Omega }},\varvec{{\beta }},\sigma ^2_{x},\phi ,\varvec{{L}}_i)$ is proportional to

  $$\begin{aligned} \exp \left\{ \frac{y_{i}\theta _{i}-b(\theta _{i})}{\phi } -\sum \limits _{k=1}^r\frac{(x_{ki}-\gamma _{k0}-\varvec{{\gamma }}_{kv}^{\!\top \!}\varvec{{v}}_i)^2}{2\sigma _x^2} -\frac{1}{2}\sum \limits _{j=1}^m(\varvec{{w}}_{ij}-\varvec{{x}}_{i}-\varvec{{\alpha }}_{L_{ij}})^{\!\top \!}\varvec{{\Omega }}_{L_{ij}}^{-1}(\varvec{{w}}_{ij}-\varvec{{x}}_i-\varvec{{\alpha }}_{L_{ij}})\right\} , \end{aligned}$$

  where $\varvec{{L}}_i=\{L_{ij}: j=1,\ldots ,m\}$. The Metropolis–Hastings algorithm for sampling observations from $p(\varvec{{x}}_i|y_{i},\varvec{{v}}_{i},\varvec{{\gamma }},\varvec{{w}}_{i},\varvec{{\alpha }},\varvec{{\Omega }}$, $\varvec{{\beta }},\sigma ^2_{x},\phi ,\varvec{{L}}_i)$ is implemented as follows. Given the current value $\varvec{{x}}_i^{(t)}$, a new candidate $\varvec{{x}}_{i}$ is generated from $N_r(\varvec{{x}}_{i}^{(t)},\sigma _a^2\varvec{{H}}_{x_i})$ and is accepted with probability

  $$\begin{aligned} \text{ min }\left\{ 1,\frac{p(\varvec{{x}}_{i}|y_{i},\varvec{{v}}_{i},\varvec{{\gamma }},\varvec{{w}}_{i},\varvec{{\alpha }},\varvec{{\Omega }},\varvec{{\beta }},\sigma ^2_{x},\phi ,\varvec{{L}}_i)}{p(\varvec{{x}}_{i}^{(t)}|y_{i},\varvec{{v}}_{i},\varvec{{\gamma }},\varvec{{w}}_{i},\varvec{{\alpha }},\varvec{{\Omega }},\varvec{{\beta }},\sigma ^2_{x},\phi ,\varvec{{L}}_i)}\right\} , \end{aligned}$$

  where $\varvec{{H}}_{x_{i}}=(V_i\varvec{{\beta }}_x\varvec{{\beta }}_x^{\!\top \!}/\phi +\sum _{j=1}^m\Omega ^{-1}_{L_{ij}}+\sigma _x^{-2}\varvec{{I}}_r)^{-1}$ with $V_i=\dot{h}^{-2}(\mu _i)\ddot{b}^{-1}(\theta _i)|_{x_{i}={x_{i}}^{(t)}}$. The variance $\sigma _a^2$ can be chosen such that the average acceptance rate is approximately 0.25 or more.